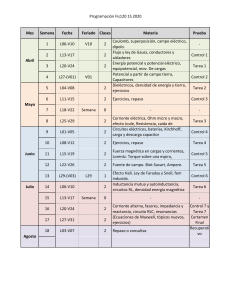
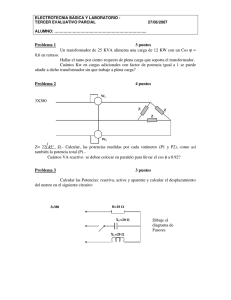
.- Componentes Simétricas Los sistemas trifásicos balanceados existen sólo teóricamente. Es una simplificación para simplificar el análisis de los sistemas eléctricos. Cuando ocurren fallas asimétricas hay cargas desbalanceadas, conductores abiertos, etcétera, en que el desbalance no se puede despreciar y en esos casos hay que utilizar una herramienta matemática debida a J. L. Fortescue quien presentó un método para descomponer un sistema de “n” fasores desbalanceados en la suma de “n” sistemas de fasores balanceados llamados Componentes Simétricas. Según el método de las componentes simétricas un sistema de tres fasores desbalanceados puede descomponerse en la suma de tres sistemas de fasores, dos balanceados de secuencias positiva y negativa y un sistema de fasores del mismo módulo en fase llamado de secuencia cero u homopolar como se muestra en la figura : C B C B A B Fasores Desbalanceados. A = A B Secuencia Positiva. C + C + A Secuencia Negativa. Secuencia Cero. Donde: El sistema de fasores de secuencia positiva coincide con la secuencia del sistema original desbalanceado El sistema de fasores de secuencia negativa tiene secuencia contraria al original. El sistema de secuencia cero tiene la misma fase y el mismo módulo. El sistema de fasores desbalanceados se relaciona con las componentes de secuencia según la matriz de transformación de componentes simétricas. Que desarrollado en forma matricial queda como: Red de Secuencia Positiva: Expresando todo en función de la fase “A”: Red de Secuencia Negativa: Esta formado por tres fasores de igual magnitud y desfasados en 120◦, pero con la rotación de fase o la secuencia invertida, por lo tanto, si la secuencia positiva es a, b, c, la negativa será a, c, b. Red de Secuencia Cero ú Homopolar Composición de las Tensiones por medio de sus componentes Simétricas: Las tensiones del sistema desbalanceado en función de las componentes simétricas quedas expresadas de la siguiente forma: Reeemplazando Vb0, Vb1, Vb2 y Vc0, Vc1 y Vc2 por sus equivalentes en función de las fases “a” se tiene: Y de forma matricial seria: Donde se suele denominar a la siguiente matriz como “A” : De forma inversa, si contamos como dato con las corrientes ó tensiones reales asimétricas podemos hallas sus componentes simétricas