Análisis de varianza y regresión - Universidad de Bogotá Jorge

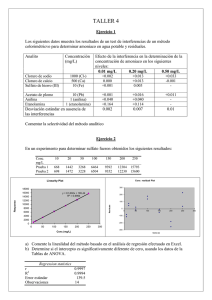
DEPARTAMENTO DE CIENCIAS
BASICAS
AREA DE ESTADISTICA
PRACTICA EI-3
ANALISIS DE VARIANZA Y
REGRESION
ESTADISTICA INFERENCIAL
Objetivo: Que el alumno conozca y comprenda el manejo de un paquete estadístico para realizar
análisis de varianza y pueda construir modelos de regresión.
ANALISIS DE VARIANZA: DISEÑO COMPLETAMENTE ALEATORIO
El propósito del procedimiento de análisis de varianza es analizar la variabilidad de la respuesta y asignar
componentes de esa variabilidad a cada uno de los conjuntos de variables independientes. El objetivo del
análisis de varianza es determinar cuales son las variables independientes de importancia en un estudio, y en
qué forma interactúan y afectan la respuesta.
La validez de las estimaciones y pruebas de las hipótesis para los análisis derivados de modelo lineal, se
apoya en los valores de varios supuestos. Se suponen que los errores experimentales aleatorios son
independientes, siguen una distribución normal con una media igual a cero y tienen una varianza común para
todos los grupos de tratamiento cualquier discrepancia de entre los datos y una o mas de estas suposiciones
afecta las estimaciones de las medias de tratamiento y la pruebas de significación del análisis de varianza. La
suposición de independencia se justifica a través de la asignación aleatoria de los tratamientos a las unidades
experimentales.
Las condiciones ideales rara vez se cumplen en los estudios reales. Las discrepancias menores de los datos
con respecto a la independencia, la distribución normal supuesta y las varianzas homogéneas, generalmente no
ocasionan modificaciones sustanciales en la eficiencia de las estimaciones y en los niveles de significancia de
las pruebas. Es posible que las discrepancias mayores, en especial una heterogeneidad excesiva de la varianza
o alguna heterogeneidad de la varianza con numero de replicas desiguales, afecte en forma importante las
inferencias estadísticas.
EJEMPLO 1: Cuatro grupos de vendedores de una agencia de ventas de revistas fueron sometidos a diferentes
programas de entrenamiento en ventas. Debido a que hubo varias deserciones durante el entrenamiento, el
número de personas fue diferente para cada grupo. Al final del programa de entrenamiento, a cada vendedor le
fue asignada aleatoriamente una zona de ventas de entre un grupo de zonas que tienen aproximadamente el
mismo potencial de ventas. En la siguiente tabla aparece el número de ventas efectuadas por cada uno de los
vendedores durante la primera semana posterior al entrenamiento. Hay suficiente evidencia que indique una
diferencia en los resultados promedios de los cuatro programas de entrenamiento?
GRUPO DE ENTRENAMIENTO
1
2
3
4
65
75
59
94
87
69
78
89
73
83
67
80
79
81
62
88
81
72
83
69
79
76
90
En el editor de datos (hoja de cálculo) definimos en la primera columna todos los valores de la variable de
respuesta (VENTAS), en la segunda columna definimos el código que identificara la clasificación (GRUPO) ,
siguiendo la secuencia: Compare → Analysis of variance → One-Way ANOVA, se define la variable
dependiente como VENTAS y el factor GRUPO → OK → Tabular options → Anova Table, Multiple range
tests,OK, se obtiene lo siguiente:
ANOVA Table
Analysis of Variance
----------------------------------------------------------------------------Source
Sum of Squares Df Mean Square F-Ratio
P-Value
----------------------------------------------------------------------------Between groups
712,586
3
237,529
3,77
0,0280
Within groups
1196,63 19
62,9806
----------------------------------------------------------------------------Total (Corr.)
1909,22 22
La tabla ANOVA descompone la varianza de VENTAS en dos componentes: un componente entre grupos y un
componente dentro de los grupos. El F-ratio, que en este caso es igual a 3,77 es el cociente de la estimación
entre grupos y la estimación dentro de los grupos. Puesto que el p-valor del test F es inferior o igual a 0, 05,
hay diferencia estadísticamente significativa entre las VENTAS medias de un nivel de GRUPO a otro para un
95,0%.
Cuando existen diferencias entre los tratamientos se efectúan las pruebas de rango múltiple, para observar
entre que pares de promedios existen diferencias, el paquete dispone de las pruebas de Tukey, Scheffe,
Bonferroni, Newman-Newman-Keuls y Duncan.
(El procedimiento anterior se puede realizar de varias maneras, entre ellas las siguientes ruta: Compare →
multiple samples → multiple sample comparison → en input: multiple data columns → samples: se define las
columnas donde estan los datos ,ok. Mediante la opción tabular se pueden efectuar los demás procedimientos.
Otra forma de realizar este diseño es de la siguiente forma: Special → Experimental design → create design,
después de esto se debe elegir el tipo de diseño, entre los cuales están single factor categorical para un diseño
completamente aleatorio, Multifactor categorical que corresponde a un diseño de bloques ( no pedir
aleatorizacion –randomize) , Se eligen los dos factores, se declaran sus nombres y su numero de niveles. Se
define la variable de respuesta, y después se da el numero de replicas. Lo anterior generara dos columnas, una
para cada factor (el de tratamiento y el de bloques). Para hacer el análisis, una vez que se haya generado el
archivo de datos, se siguen las siguientes opciones: Special → Experimental design → Analyze design, después
se da el nombre de la variable de respuesta a analizar, y entonces se tendrá acceso a un conjunto de opciones
de análisis tanto graficas como analíticas).
Multiple Range Tests
-------------------------------------------------------------------------------Method: 95,0 percent Student-Newman-Keuls
Count Mean
Homogeneous Groups
-------------------------------------------------------------------------------GRUPO3
6
70,8333
X
GRUPO1
6
75,6667
XX
GRUPO2
7
78,4286
XX
GRUPO4
4
87,75
X
-------------------------------------------------------------------------------Contrast
Difference
-------------------------------------------------------------------------------GRUPO1 - GRUPO2
-2,7619
GRUPO1 - GRUPO3
4,83333
GRUPO1 - GRUPO4
-12,0833
GRUPO2 - GRUPO3
7,59524
GRUPO2 - GRUPO4
-9,32143
GRUPO3 - GRUPO4
*-16,9167
-------------------------------------------------------------------------------* denotes a statistically significant difference.
Esta tabla aplica un procedimiento de comparación múltiple para determinar las medias que son
significativamente diferentes unas de otras. La mitad inferior de la salida muestra la diferencia estimada entre
cada par de medias. El asterisco que se encuentra al lado de l par, indica que éstos muestran diferencias
estadísticamente significativas a un nivel de confianza 95,0%. En la parte superior de la página, se identifican 2
grupos homogéneos según la alineación del signo X en la columna. Dentro de cada columna, los niveles que
tienen signo X forman un grupo de medias entre las cuales no hay diferencias estadísticamente significativas.
Con el click derecho se puede acceder la opción “pane options” y se puede escoger otro de los métodos que
Usted desee de los que el Statgraphics tiene disponible.
PRUEBAS DE NORMALIDAD
Los residuales observados son la base de muchas de las principales herramientas de diagnostico que se usan
para verificar si las suposiciones del modelo lineal son adecuadas. Los residuales son estimaciones de los
errores experimentales, calculados como las diferencias entre las observaciones y las estimaciones de las
medias de los tratamientos. Deben calcularse los residuales, los cuales los podemos calcular siguiendo la ruta:
Compare Analysis of variance One-Way ANOVA click Save results, los residuales aparecerán en el panel inicial
donde esta la información
Los residuales observados son la base de muchas de las principales herramientas de diagnostico que se usan
para verificar si las suposiciones del modelo lineal son adecuadas. Los residuales son estimaciones de los
errores experimentales, calculados como las diferencias entre las observaciones y las estimaciones de las
medias de los tratamientos. Deben calcularse los residuales, los cuales los podemos calcular siguiendo la ruta:
Compare → Analysis of variance → One-Way ANOVA → click Save results, los residuales aparecerán en el
panel inicial donde esta la información
El paquete dispone de varias pruebas de Normalidad, entre ellas las siguientes:
1. Asimetría o Kurtosis estandarizadas: Compare → Analysis of variance → One-Way ANOVA,OK → Tabular
options → Summary statistics,OK, seleccionando con click derecho del mouse “pane options”, Stnd skewness y
Stnd Kurtosis.
Summary Statistics
Count
Stnd. skewness
Stnd. kurtosis
-------------------------------------------------------------------------------GRUPO1
6
0,0636867
-0,57336
GRUPO2
7
0,362472
-0,146676
GRUPO3
6
-0,0326099
-0,998064
GRUPO4
4
-0,613571
0,685427
-------------------------------------------------------------------------------Total
23
-0,407175
-0,593365
La asimetría y/o curtosis estandarizadas están dentro del rango de -2 a +2. Esto indica normalidad significante
en los datos, lo cual no viola la asunción de que los datos proceden de una distribución normal.
Si se deseara efectuar la prueba de Kruskal-Wallis, Ruta: Compare → Analysis of variance →
ANOVA → , Tabular options, Kruskal-Wallis test,OK, se obtiene lo siguiente:
Kruskal-Wallis Test
One-Way
Kruskall-Wallis Test
Sample Size
Average Rank
-----------------------------------------------------------GRUPO1
6
10,5833
GRUPO2
7
12,7143
GRUPO3
6
7,58333
GRUPO4
4
19,5
-----------------------------------------------------------Test statistic = 7,7905 P-Value = 0,0505444
La prueba de Kruskal-Wallis prueba para la hipótesis nula si las medianas son iguales entre los grupos de
entrenamiento. No hay diferencia significativa entre las medianas al 95%.
2.
Gráfica de probabilidad para evaluar la suposición de distribución normal. Secuencia: Plot
Exploratory Plots Normal Probability Plot Data: RESIDUALS OK Pane Options: Using Quartiles, y, direccion
horizontal (el programa da la opción de utilizar como línea de ajuste mínimos cuadrados o cuantiles, y la
dirección de los ejes puede ser horizontal o vertical). En esta gráfica la recta pasa por los cuartiles inferior y
superior de los datos. En esta técnica de tipo exploratorio, se observa si los valores están cercanos a la línea se
dice que la variable tiende a ser Normal. La gráfica siguiente muestra que la distribución de los datos esta
sesgada a la derecha con respecto a la distribución normal estándar.
Normal Probability Plot
RESIDUALS
13
8
3
-2
-7
-12
0,1
1
5
20
50
80
percentage
95
99
99,9
3. Pruebas de bondad de ajuste (Prueba noparametrica): Ruta: describe → Distributions → Distributions
Fitting (Uncensored Data), OK. Data: RESIDUALS, OK . Tabular Options, Goodness of Fit tests OK.
Goodness-of-Fit Tests for RESIDUALS
Goodness-of-Fit Tests for RESIDUALS
Chi-Square Test
-------------------------------------------------------------------------------------------Lower
Upper
Observed
Expected
Limit
Limit Frequency Frequency Chi-Square
-------------------------------------------------------------------------------------------at or below
-7,13486
5
3,83
0,36
-7,13486
-3,17668
4
3,83
0,01
-3,17668 -9,13043E-7
1
3,83
2,09
-9,13043E-7
3,17668
4
3,83
0,01
3,17668
7,13486
5
3,83
0,36
above 7,13486
4
3,83
0,01
-------------------------------------------------------------------------------------------Chi-Square = 2,82618 with 3 d.f. P-Value = 0,419205
Estimated Kolmogorov statistic DPLUS = 0,112651
Estimated Kolmogorov statistic DMINUS = 0,0801477
Estimated overall statistic DN = 0,112651
Approximate P-Value = 0,932265
EDF Statistic
Value
Modified Form P-Value
--------------------------------------------------------------------Kolmogorov-Smirnov D 0,112651
0,559095
>=0.10*
Anderson-Darling A^2 0,308283
0,319647
0,5335*
--------------------------------------------------------------------*Indicates that the P-Value has been compared to tables of critical values
specially constructed for fitting the currently selected distribution.
Other P-values are based on general tables and may be very conservative.
Esta ventana muestra los resultados de los tests ejecutados para determinar si RESIDUALS puede ser
modelado adecuadamente por distribución normal. El test chi-cuadrado divide el rango de RESIDUALS en
intervalos no solapados y compara el número de observaciones en cada clase con el número esperado basado
en la distribución ajustada. El tests de Kolmogorov-Smirnov calcula la distancia máxima entre la distribución
acumulada de RESIDUALS y el CDF de la distribución normal ajustada. En este caso, la distancia máxima es
0,112651. Los otros estadísticos EDF comparan de diferentes maneras la función de distribución empírica con
el CDF ajustado.
Dado que p-valor más pequeño de los tests realizados es superior a .10, no podemos rechazar que
RESIDUALS procede de una distribución normal con un nivel de confianza del 90%.
4.
Pruebas de Normalidad (Prueba noparametrica)
Ruta:describe → Distributions →
Distributions Fitting (Uncensored Data),
Tabular Options, test for normality, OK.
Tests for Normality for RESIDUALS
Computed Chi-Square goodness-of-fit statistic = 6,95652
P-Value = 0,729543
Shapiro-Wilks W statistic = 0,954135
P-Value = 0,35769
OK. Data: RESIDUALS, OK
Z score for skewness = 0,0617506
P-Value = 0,950756
Z score for kurtosis = -1,58326
P-Value = 0,113363
Este cuadro muestra los resultados de varios test ejecutados para determinar si RESIDUALS puede ser
modelado adecuadamente por una distribución normal. El test chi-cuadrado divide el rango de RESIDUALS en
28 clases igualmente probables y compara el número de observaciones en cada clase al número esperado. El
test de Shapiro-Wilks se basa en la comparación de los cuantiles de la distribución normal ajustada con los
cuantiles de los datos. El test de asimetría estandarizada busca la falta de simetría en los datos. El test de
curtosis estandarizada busca la forma de la distribución que sea más plana o más puntiaguda que la
distribución normal.
El p-valor más bajo de los tests realizados es igual a 0.113363. Dado que el p-valor para este test es superior a
0.10, no podemos rechazar que RESIDUALS procede de una distribución normal con un nivel de confianza del
90%.
Histogram for RESIDUALS
frequency
8
6
4
2
0
-14
-9
-4
1
6
11
16
RESIDUALS
PRUEBAS DE IGUALDAD DE VARIANZAS
Al graficar los residuales contra los valores estimados de las medias de tratamiento, se obtiene una evaluación
visual sencilla de la suposición de varianzas iguales en los grupos de tratamiento, en el paquete se logra de la
siguiente manera: Compare → Análisis Of Variance → One-Way Anova : Dependent Variable: VENTAS,
Factor: GRUPO, OK .Gaphical options (Al lado de la opción tabular- Residuals versus Predicted):
Residual Plot
17
residual
12
7
2
-3
-8
-13
70
73
76
79
82
85
88
predicted value
Si la variabilidad de las observaciones alrededor de las medias de tratamientos difiere de un grupo a otro, el
conjunto de residuales correspondiente reflejara las diferencias en la variación. Si las varianzas son
heterogéneas, la grafica de residuales contra los valores estimados a menudo tiene la forma de embudo. La
falta de simetría alrededor del cero indica una distribución asimétrica de las observaciones.
Variance Check
Cochran's C test: 0,378208 P-Value = 0,693018
Bartlett's test: 1,05576 P-Value = 0,81524
Hartley's test: 2,73251
Levene's test: 1,21251 P-Value = 0,332267
Ruta: Compare → Analysis Of Variance →
GRUPO, OK .Tabular options, variance check,Ok
One-Way Anova : Dependent Variable: VENTAS, Factor:
Lo anterior muestra las pruebas para la hipótesis nula de que la desviación típica de VENTAS dentro de cada
uno de los 4 niveles de GRUPO, es la misma. De particular interés están los tres p-valores. Dado que el menor
de los p-valores es superior a 0,05, no hay diferencia estadísticamente significativa entre las desviaciones
típicas para un nivel de confianza del 95,0%.
Por ultimo se pude efectuar una prueba para demostrar que el promedio de los residuales es igual a cero,
Describe → Numeric data → One variable analysis → Data:RESIDUALS,Ok.,Option tabular Hypothesis
tests,Ok.
EJERCICIO 1: Tres métodos clínicos para determinar el contenido de hemoglobina fueron ensayados para
determinar si había diferencias significativas entre los resultados. Se emplearon seis sujetos
(A,B,C,D,E,F),constituyendo cada sujeto un bloque.(gr/100ml)
METODO
A
B
C
D
E
F
1
14
12
16
15
10
11
2
18
16
17
19
12
13
3
15
14
12
14
12
9
a. Pruebe Con una confianza del 94%, si existen diferencias entre los métodos y entre los sujetos.
b. Con una confianza del 95% Efectué las diferentes Pruebas de rango múltiple para bloques y para
tratamientos.
EJERCICIO 2: Se desea comparar el porcentaje de cuentas incobrables de tres diferentes plazas de un
negocio, y así determinar nuevas políticas de crédito. Se observaron nueve diferentes meses sobre el total de la
cartera. Es significativamente diferente el porcentaje de cuentas incobrables en las tres diferentes
plazas? α =0.01
PLAZA OBSERVACIONES
1
2
3
4
5
6
7
8
9
1
3.2
2.1
2.3
3.1
3.0
2.7
2.0
1.7
0.3
2
2.1
2.1
2.0
2.1
2.6
3.8
3.3
3.2
2.0
3
2.3
2.5
2.5
3.0
4.8
2.7
3.0
2.0
2.5
EJERCICIO 3: Que tipo de comerciales captan mejor la atención de los niños? Para dar respuesta a esta
pregunta, se observo la actitud de 15 niños; 5 niños fueron observados mientras veían comerciales de juguetes
y juegos, 5 mientras veían comerciales sobre comida y goma de mascar y 5 mientras veían comerciales
relacionados con ropa para niños. Todos los comerciales tenían una duración de 60 segundos de duración. Se
recolecto la siguiente información:
COMERCIAL
TIEMPO DE ATENCION
JUGUETES Y, JUEGOS
45
40
30
25
45
COMIDA, GOMA DE MASCAR
50
25
55
45
50
ROPA
30
45
40
50
35
Proporcionan estos datos suficiente evidencia que indique una diferencia entre los tiempos medios de atención
de los niños a las tres clases de comerciales?
DISEÑO DE BLOQUES COMPLETAMENTE ALEATORIO
En el paquete estadístico Statgraphics el análisis de los diseños que usan cuando menos un factor de bloques
la correspondiente secuencia es: Compare → Análisis of variance → Multifactor anova. La respuesta observada
y las combinaciones de los factores se capturan manualmente en el editor de datos. Se requiere de una
columna por cada factor, más la columna de la variable de respuesta. Se recomienda capturar los datos y
combinaciones en el orden en que se hayan realizado, ya que con ello se podrá comprobar el supuesto de
independencia de los residuos. Si se capturan los datos en un orden prefijado, se pierde la información sobre la
posible dependencia de una observación a la siguiente.
Ejemplo 2: Un investigador llevo a cabo un estudio para comparar el rendimiento de gasolina de los automóviles
para tres marcas de gasolina,A,B y C. En el experimento se utilizaron cuatro automóviles, todos de la misma
marca y modelo, en cada uno de los cuales se probaron las tres marcas de gasolina. Usando cada marca en el
mismo automóvil se elimina el efecto de la variabilidad entre automóviles. Los datos en millas por galón
MARCA
DE AUTOMOVIL
GASOLINA
1
2
3
4
A
15.7
17.0
17.3
16.1
B
17.2
18.1
17.9
17.7
C
16.1
17.5
16.8
17.8
Presentan los datos suficiente evidencia que indique una diferencia en el rendimiento promedio por galón para
las tres marcas de gasolinas? hay evidencia de una diferencia en el rendimiento promedio para los cuatro
automóviles?
En el editor de datos (hoja de cálculo) definimos en la primera columna todos los valores de la variable de
respuesta (RENDI), en la segunda columna definimos el código que identificara loa bloques (AUTO) y en la
tercera columna (GASOLINA), así:
RENDI
15,7
17,2
16,1
17,0
18,1
17,5
17,3
17,9
16,8
AUTO
1
1
1
2
2
2
3
3
3
GASOLINA
A
B
C
A
B
C
A
B
C
16,1
17,7
17,8
4
4
4
A
B
C
Siguiendo la secuencia: Compare → Analysis of variance → Multifactor ANOVA, se define la variable
dependiente como RENDI, y el factor AUTO, GASOLINA, Tabular options → Anova Table,
Analysis of Variance for RENDI - Type III Sums of Squares
-------------------------------------------------------------------------------Source
Sum of Squares
Df
Mean Square
F-Ratio
P-Value
-------------------------------------------------------------------------------MAIN EFFECTS
A:AUTO
2,52
3
0,84
3,75
0,0792
B:GASOLINA
2,895
2
1,4475
6,46
0,0319
RESIDUAL
1,345
6
0,224167
-------------------------------------------------------------------------------TOTAL (CORRECTED)
6,76
11
-------------------------------------------------------------------------------All F-ratios are based on the residual mean square error.
La tabla ANOVA descompone la variabilidad de RENDI en las contribuciones debidas a varios factores. Puesto
que se ha elegido la suma de cuadrados Tipo III (valor por defecto), se ha medido la contribución de cada factor
eliminando los efectos del resto de los factores. Los P-valores comprueban la importancia estadística de cada
uno de los factores. Dado que un p-valor es inferior a 0,05, este factor tiene efecto estadísticamente
significativo en RENDI para un 95,0%.
Posteriormente se pueden efectuar las pruebas de rango múltiples para GASOLINA. De igual manera se
pueden efectuar las pruebas sobre el cumplimiento de los supuestos de ANOVA.
EJERCICIO 3: las maquinas productoras de papel distribuyen una mezcla delgada de fibras de madera y agua
a una banda ancha de tela de alambre que viaja a velocidades muy altas. Por lo anterior se puede pensar que
la distribución de la fibra, el grosor, la porosidad y otras características varían a lo largo de la banda y producen
variaciones en la resistencia del producto final. Una compañía fabricante de papel diseño un experimento de
cuatro recubrimientos diseñados para mejorar la apariencia del papel para empaque. Debido a que el papel sin
recubrir tiene una resistencia variable y por lo tanto el papel de diferentes secciones del rollo tendrá diferentes
resistencias.
POSICION EN RECUBRIMIENTO
EL ROLLO
A
B
C
D
1
10.4
12.4
13.1
11.8
2
10.9
12.4
13.4
11.8
3
10.5
12.3
12.9
11.4
4
10.7
12.0
13.3
11.4
Proporcionan los datos suficiente evidencia que indique una diferencia en la resistencia promedio del papel
tratado con diferentes recubrimientos? Proporcionan los datos suficiente evidencia que indique una diferencia
en la resistencia promedio para las diferentes posiciones dentro del rollo? Efectué las pruebas de
comparaciones de rangos múltiples, α =0.01
ANALISIS DE REGRESION
Ejemplo 3: Los siguientes datos del año pasado representan a los dias laborables en los que estuvo ausente y
la antigüedad en años en la compañía de cada uno de 7 empleados escogidos al azar.
AUSENCIA : 2 1 5 6 4 9 2
ANTIGÜEDAD : 7 8 2 3 5 3 7
Para estimar una función de regresión se sigue la siguiente secuencia: Relate → (Puede escogerse Simple
regression o Polynomial regression, Multiple regression) → Y: variable dependiente,X:variable
independiente,OK.
Regression Analysis - Linear model: Y = a + b*X
----------------------------------------------------------------------------Dependent variable: AUSENCIA
Independent variable: ANTIGUEDAD
----------------------------------------------------------------------------Standard
T
Parameter
Estimate
Error
Statistic
P-Value
----------------------------------------------------------------------------Intercept
9,14286
1,5027
6,08429
0,0017
Slope
-1,0
0,27501
-3,63624
0,0150
-----------------------------------------------------------------------------
Analysis of Variance
----------------------------------------------------------------------------Source
Sum of Squares
Df Mean Square
F-Ratio
P-Value
----------------------------------------------------------------------------Model
34,0
1
34,0
13,22
0,0150
Residual
12,8571
5
2,57143
----------------------------------------------------------------------------Total (Corr.)
46,8571
6
Correlation Coefficient = -0,851827
R-squared = 72,561 percent
R-squared (adjusted for d.f.) = 67,0732 percent
Standard Error of Est. = 1,60357
Mean absolute error = 0,816327
Durbin-Watson statistic = 2,02222 (P=0,4642)
La salida muestra los resultados del ajuste al modelo lineal para describir la relación entre AUSENCIA y
ANTIGUEDAD. La ecuación del
modelo ajustado es
AUSENCIA = 9,14286 - 1,0*ANTIGUEDAD
Dado que el p-valor en la tabla ANOVA es inferior a 0.05, existe relación estadísticamente significativa entre
AUSENCIA y ANTIGUEDAD
para un nivel de confianza del 95%.
El estadístico R-cuadrado indica que el modelo explica un 72,561% de la variabilidad en AUSENCIA. El
coeficiente de correlación es igual a -0,851827, indicando una relación moderadamente fuerte entre las
variables. El error estándar de la estimación muestra la desviación típica de los residuos que es 1,60357. Este
valor puede usarse para construir límites de la predicción para las nuevas observaciones seleccionando la
opción Predicciones del menú del texto.
El error absoluto medio (MAE) de 0,816327 es el valor medio de los residuos. El estadístico Durbin-Watson
(DW) examina los residuos para determinar si hay alguna correlación significativa basada en el orden en el que
se han introducido los datos en el fichero. Dado que el p-valor es superior a 0.05, no hay indicio de
autocorrelación serial en los residuos.
Si usted desea estimar otro modelo, puede oprimir click derecho, y el menú ofrece otros modelos. En la tabular
options, el menú ofrece otra gama de opciones para efectuar el análisis en regresión.