FIS 231 Guía de ejercicios N°2 Segundo Semestre 2010
Anuncio

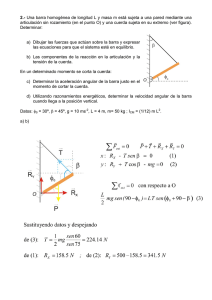
FIS 231 Guía de ejercicios N°2 Segundo Semestre 2010 1.- Un anillo delgado tiene radio 20 [cm] y masa 3 [kg]. Determine el momento de inercia del anillo respecto a un eje: a) que pasa por su centro de masa, como muestra la figura b) paralelo al eje anterior, que pasa por el borde. 2.- El sistema mostrado en la figura, está formado por una barra de longitud “b” y masa despreciable, y dos discos idénticos de masa “M” y radio “r”, adheridos a los extremos de la barra, y paralelos entre sí. Determine, en términos de M y r, el momento de inercia del sistema respecto de un eje paralelo a la barra, y coaxial con ella. 3.- El sistema mostrado en la figura, está formado por dos discos idénticos de radio “r” y masa “M” y un disco menor de radio “ro” y masa M/2, adheridos entre sí como muestra la figura. Determine, en términos de M, r y ro, el momento de inercia del sistema respecto de un eje perpendicular a los discos, y que pasa por sus centros de masa. r ro 4.- La figura muestra una polea con forma de disco macizo, de radio 50 [cm] y masa 4 [kg], que puede girar en torno a un eje que pasa por su centro de masa. Calcule la aceleración angular de la polea en los siguientes casos: a) se cuelga de la cuerda un cuerpo cuyo peso es de 10[N]. b) Se tira la cuerda con una fuerza constante de magnitud 10[N]. 2 Desprecie el roce y use g 10 m/s ]. ¿Son equivalentes los dos casos? a a 1 [kg] 5.- En el sistema mostrado en la figura, el roce entre el bloque y el plano inclinado, y el roce en el eje de la polea pueden despreciarse. La polea es un disco macizo, de radio R y masa M. a) Dibuje diagramas de cuerpo libre para el bloque de masa M, el bloque de masa m y la polea. b) Escriba las ecuaciones de movimiento para cada uno de esos elementos. c) A partir de las ecuaciones halladas en b), encuentre expresiones para la aceleración angular de la polea y las aceleraciones de cada bloque. 10 [N] Roce 0 m M 6.- Una barra de masa 2 [kg] y longitud 120 [cm] puede girar en torno a un eje horizontal fijo que pasa por uno de sus extremos, como se muestra en la figura. El roce puede despreciarse. a) Calcule la tensión de la cuerda que mantiene a la barra en equilibrio en la posición mostrada. b) A continuación se corta la cuerda: ¿cuál es la aceleración angular de la barra en ese instante?. ¿Y en el instante en que pasa por posición horizontal? c) Usando la conservación de la energía, calcule la rapidez angular de la barra, en el instante en que alcanza pasa por la horizontal. 75º 55º Se rompe 7.- Un tablero rectangular homogéneo de altura a, ancho b y masa M está sostenido por dos soportes como se indica en la figura. En cierto instante el tablero se suelta del soporte izquierdo y gira en torno al otro soporte, siendo el roce despreciable. a) ¿Cuál es la aceleración angular del tablero un instante después de soltarse el soporte? b) ¿Cuál es la máxima rapidez angular del tablero, y en qué posición ocurre? c) ¿Cuál es la aceleración angular en la posición determinada en la pregunta b)? a b c 8.- La figura muestra un disco de radio externo “a” con un agujero en su centro de radio “b” y un cilindro con de iguales radios. El espesor del disco es despreciable, y el cilindro tiene altura “c”. Si ambos objetos pueden girar en torno a un eje que pasa por su centro de masa como se indica en la figura, calcule la aceleración de cada objeto en cada sistema, si el bloque tiene masa 2 [kg]. Coordinación FIS 231 - PUCV b a 2 [kg] 2 [kg]