Conceptos Fundamentales Muestras Ordenadas Muestras no

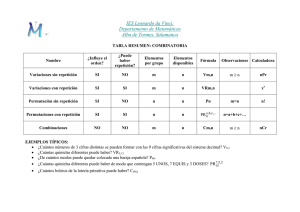
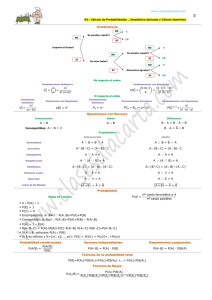
www.clasesalacarta.com
1
Tema 8.- Combinatoria
Conceptos Fundamentales
La Combinatoria es la parte de las Matemáticas que se ocupa de la resolución de problemas de elección y
disposición de los elementos de cierto conjunto, de acuerdo con ciertas reglas.
En todo problema combinatorio hay varios conceptos claves que debemos distinguir:


Población: conjunto de elementos que se están estudiando. Se llama tamaño de la población al número
de elementos de este conjunto.
Muestra: subconjunto de la población. Se llama tamaño de la muestra al número de elementos que la
componen. Los diferentes tipos de muestra vienen determinados por dos aspectos:

El orden, es decir, si es importante que los elementos de la muestra aparezcan ordenados o no.

La posibilidad de repetición o no de los elementos.
El objetivo de la Combinatoria es calcular cuántos tipos de muestras de un determinado tamaño se pueden
extraer de cierta población. Para ello nos basamos en el Principio de Multiplicación: si un procedimiento se
puede separar en r etapas, de modo que el resultado de una de ellas no influye en el resultado de las otras, y en
cada una de estas etapas se obtienen respectivamente n1, n2, n3,…, nr, resultados, entonces el procedimiento
global conduce a n1·n2·n3·…·nr resultados.
Muestras Ordenadas
Variaciones
Sin repetición
Para muestras ordenadas y sin repetición de tamaño k (k<n). Si el tamaño de la población es n y el de la muestra
k (indica el nº de factores que hay que multiplicar), el número de variaciones sin repetición será:
k
Vn =n· n-1 ·…·(n-k+1)
Con repetición
k
VRn = nk
Permutaciones sin repetición
En el caso particular de que se tome una muestra de tamaño igual al tamaño de la población, k = n, las
variaciones se denominan permutaciones sin repetición de n elementos:
Pn = n!
El producto de todos los números enteros desde el 1 hasta el n se denomina factorial de n (n!):
0!=1
1!=1
∄ n!  n < 0
Permutaciones con elementos repetidos
Si queremos calcular el nºo de permutaciones de n elementos de los cuáles hay n1 de una clase,n2 de otra, etc…,
de modo que n1+n2+…+nr = n, entonces hablamos de permutaciones de n elementos, algunos de los cuales están
repetidos, lo que se expresa como:
n , n 2 , nr
PRn1
=
n!
n1 ! · n2 ! ·…· nr !
Muestras no ordenadas y sin repetición: Combinaciones
k
Cn =
k
Vn
n!
=
Pk k! n-k !
á
á
2
Matemáticas _ CCSS _ 2º Bachillerato
Ejemplos
Muestras Ordenadas
Sin Repetición
Variaciones
Permutaciones
En un club de fans hay 34 miembros, hay que elegir al
presidente, al vicepresidente, al tesorero y al secretario ¿De
cuántas formas posibles se pueden cubrir estos 4 puestos?
¿Cuántos números de 5 cifras distintas se pueden formar
con los nº 1, 2, 3, 4, 5?




Ordenadas
Ordenadas

Uso todos los elementos: 5 nº=5 cifras
Faltan elementos: 4 puestos para 34 miembros

Sin repetición: 5 nº = 5 cifras
Sin repetición: 1 persona = 1 cargo
PRn =n! → PR5=5!=120
Vkn =n· n-1 ·…·(n-k+1)
4
VR34 =34· 34-1 · 34-2 · 34-3 =1 113 024 formas
Con Repetición
Variaciones
Permutaciones
Con los nº 1, 2, 3 ¿Cuántos números de 5 cifras se pueden
formar?

Ordenadas

Faltan elementos: 4 puestos para 34 miembros

Con repetición: 3 nº = 5 cifras
Con los nº 5, 5, 5, 6, 6, 6, 6, 7, 7 ¿Cuántos números de 9
cifras se pueden formar?

Ordenadas

Uso todos los elementos: 9 nº=9 cifras

Con repetición: no dicen que sean cifras distintas
5
5
m
VRm
n =n → VR3 =3 =243 números de 5 cifras
PRnn1 , n2, nr =
Muestras NO ordenadas
n!
9!
3,4,2
→ PR9 =
=1260
n1 ! · n2! ·…· nr !
3!·4!·2!
Combinaciones sin repetición
¿Cuántas apuestas de la primitiva (50 casillas) de 1 columna tienes que rellenar para garantizarte el acierto de los 6
resultados?
n!
k
Cn =
k! n-k !
50!

NO importa el orden de los nº  Combinación
6
C50=
=15 890 700

NO se pueden repetir los nº
6! 44 !
1
P acertar los 6 =
15 890 700