UNIDAD 4 Planificación de ecuación dela recta
Anuncio
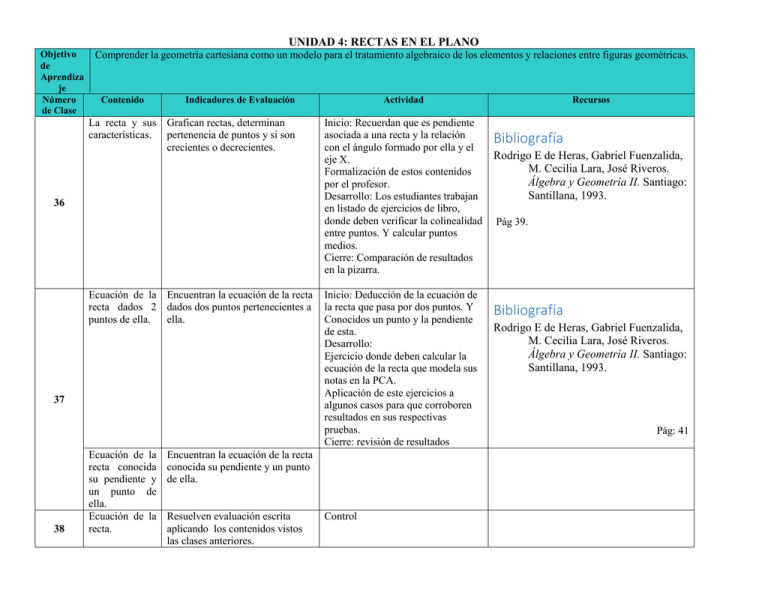
UNIDAD 4: RECTAS EN EL PLANO Objetivo de Aprendiza je Número de Clase Comprender la geometría cartesiana como un modelo para el tratamiento algebraico de los elementos y relaciones entre figuras geométricas. Contenido Indicadores de Evaluación La recta y sus Grafican rectas, determinan características. pertenencia de puntos y si son crecientes o decrecientes. 36 Ecuación de la Encuentran la ecuación de la recta recta dados 2 dados dos puntos pertenecientes a puntos de ella. ella. 37 38 Ecuación de la recta conocida su pendiente y un punto de ella. Ecuación de la recta. Actividad Inicio: Recuerdan que es pendiente asociada a una recta y la relación con el ángulo formado por ella y el eje X. Formalización de estos contenidos por el profesor. Desarrollo: Los estudiantes trabajan en listado de ejercicios de libro, donde deben verificar la colinealidad entre puntos. Y calcular puntos medios. Cierre: Comparación de resultados en la pizarra. Inicio: Deducción de la ecuación de la recta que pasa por dos puntos. Y Conocidos un punto y la pendiente de esta. Desarrollo: Ejercicio donde deben calcular la ecuación de la recta que modela sus notas en la PCA. Aplicación de este ejercicios a algunos casos para que corroboren resultados en sus respectivas pruebas. Cierre: revisión de resultados Encuentran la ecuación de la recta conocida su pendiente y un punto de ella. Resuelven evaluación escrita aplicando los contenidos vistos las clases anteriores. Control Recursos Bibliografía Rodrigo E de Heras, Gabriel Fuenzalida, M. Cecilia Lara, José Riveros. Álgebra y Geometría II. Santiago: Santillana, 1993. Pág 39. Bibliografía Rodrigo E de Heras, Gabriel Fuenzalida, M. Cecilia Lara, José Riveros. Álgebra y Geometría II. Santiago: Santillana, 1993. Pág: 41 Ecuación de la recta en su forma principal , general y Canónica. Despejan y escriben la ecuación de la recta en forma canónica, principal y general. Entienden las ventajas de escribir la ecuación de la recta de distintas formas. Paralelismo entre rectas. Identifican cuando dos rectas son paralelas. Perpendicularid ad entre rectas Ecuación de la recta Identifican cuando dos rectas son perpendiculares. Resuelven guía de ejercicios con los contenidos de la unidad aplicando los contenidos vistos las clases anteriores. Plano Cartesiano y Homotecia 39 40 41 42 43 44 45 46 47 Plano cartesiano. Homotecia. Ecuación de la recta. Sistemas de ecuaciones lineales con 2 incógnitas Sistemas de ecuaciones lineales con 2 incógnitas Sistemas de ecuaciones lineales con 2 incógnitas Plano cartesiano. Homotecia. Resuelven sistemas de ecuaciones lineales con dos incógnitas. Analizan un sistema de ecuaciones y determinan la posición relativa de ambas rectas en el plano cartesiano. Resuelven sistemas de ecuaciones y analizan la posición relativa de las rectas implicadas. Resuelven guía de ejercicios aplicando los contenidos vistos las clases anteriores. Inicio: el profesor muestra a los estudiantes las distintas formas de escribir una ecuación de la recta. Y señala que indican los coeficientes. Desarrollo: realizan guía de ejercicios. Comparan resultados. Guía de ejercicios de ecuación de la recta N° 1 Bibliografía María Blanco, Jorge Botz, Felipe Calderón , Carolina Jammet, Lorna Jimenez, Leonardo Romero. Educación Media 3° Matemática. Santiago: Santillana, 2012. Ecuación de la recta. Sistemas de ecuaciones.

