Ecuaciones de Segundo Grado II
Anuncio
IV BIM – ÁLGEBRA – 5TO. AÑO
Alumno: ………………………………………………………………………………………………………………………………………………… Fecha: ……………………………….
ECUACIONES DE SEGUNDO GRADO II
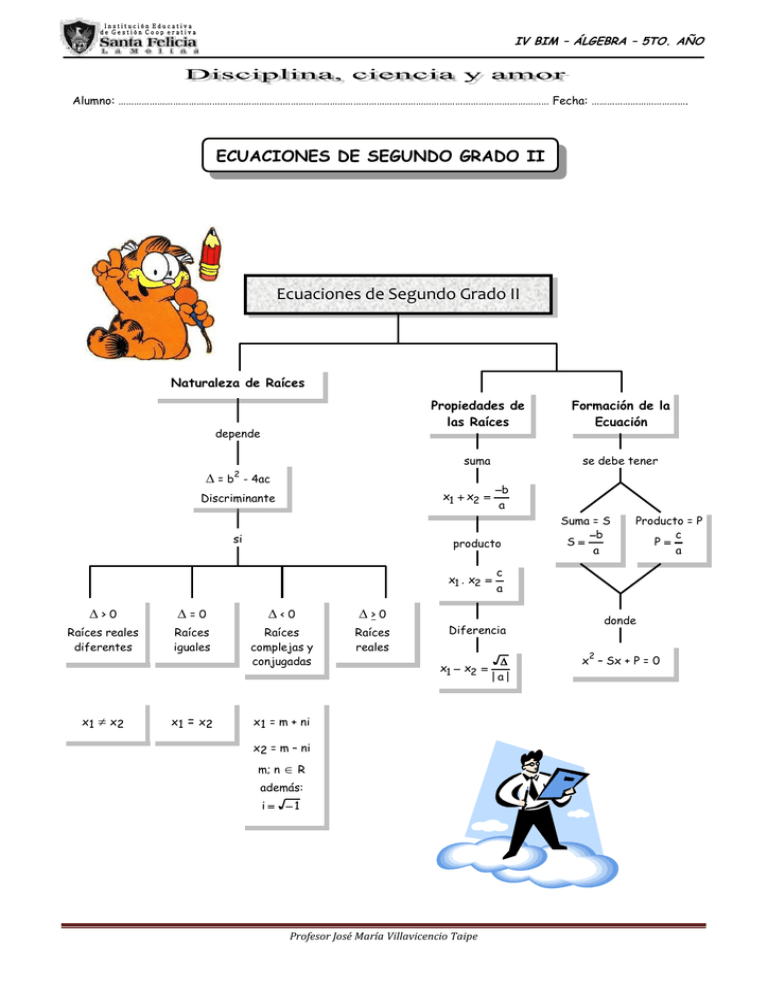
Ecuaciones de Segundo Grado II
Naturaleza de Raíces
depende
Propiedades de
las Raíces
Formación de la
Ecuación
suma
se debe tener
2
= b - 4ac
b
a
x1 x2
Discriminante
si
producto
x1 . x2
>0
=0
<0
>0
Raíces reales
diferentes
Raíces
iguales
Raíces
complejas y
conjugadas
Raíces
reales
x1
x2
x1
= x2
Suma = S
b
S
a
c
a
donde
Diferencia
x1 x2
x1 = m + ni
x2 = m – ni
m; n R
además:
i 1
Profesor José María Villavicencio Taipe
Producto = P
c
P
a
|a|
2
x – Sx + P = 0
IV BIM – ÁLGEBRA – 5TO. AÑO
Observaciones
Raíces Simétricas u
Raíces Recíprocas o
Ecuaciones Cuadráticas
Opuestas
Inversas
Equivalentes
si
si
si las ecuaciones
Una raíz es: x1 = m, la
Una raíz es: x1 = m, la
ax + bx + c = 0 ; a 0
otra es: x2 = -m
otra es: x2
se cumple
x1 + x 2 = 0
2
1
m
2
mx + nx + p = 0 ; m 0
se cumple
tienen
x 1x 2 = 1
Las mismas raíces
o soluciones
se cumple
a b c
m n p
De donde: x1
Ejercicios Resueltos
1.
Ejemplo: En la ecuación x2 + 6x + 5 = 0
Calculemos el DISCRIMINANTE:
6 4
6 4
1; x2
5
2
2
es decir C.S. = {-1; -5} ¡raíces reales y
diferentes!.
2.
Ejemplo:
2
En la ecuación x – 14x + 49 = 0
Calculamos el DISCRIMINANTE:
2
= b – 4ac
2
= b – 4ac
2
= (6) – 4(1)(5)
2
= (-14) – 4(1)(49)
= 16, es decir > 0
Por la fórmula General: x
x
b
2a
6 16
2(1)
= 196 – 196
= 0, entonces las raíces son reales e iguales.
Comprobemos:
La ecuación dada también se escribe así:
2
(x - 7) = 0 ó (x - 7)(x - 7) = 0
Profesor José María Villavicencio Taipe
IV BIM – ÁLGEBRA – 5TO. AÑO
Igualando cada factor a CERO:
x–7=0
x1 = 7
x–7=0
x2 = 7
5.
Ejemplo:
Formar la ecuación de segundo grado si
se tienen las raíces x1 = 2; x2 = -3.
entonces: C.S. = {7; 7}
Solución:
Sabemos:
3.
Ejemplo: En la ecuación x2 – 6x + 25 = 0
S = x1 + x2 = 2 – 3 = -1
P = x1x2 = (2)(-3) = -6
Los coeficientes son: a = 1; b = -6; c = 25
entonces de la ecuación:
2
2
El DISCRIMINANTE es: = b – 4ac
x – Sx + P = 0
2
2
= (-6) – 4(1)(25)
=
x – (-1)x + (-6) = 0
-64, es
2
x + x – 6 = 0 Ecuación de 2º Grado
decir < 0
Lo que significa que las raíces no son reales,
sino COMPLEJAS Y CONJUGADAS.
6.
Ejemplo: Hallar las raíces de la ecuación e indicar
2
4.
que tipo de raíces tiene: x – 100 = 0
Ejemplo:
Indicar la suma y producto de raíces
2
de: x + 5x + 3 = 0
Solución:
Solución:
Factorizando
(x + 10) (x - 10) = 0
Identificamos: a = 1; b = 5; c = 3
Entonces:
S
b
suma de raíces
a
S
5
5
1
P
c
producto de raíces
a
P
3
3
1
x = -10 x = 10
Son simétricos
EJERCICIOS DE APLICACIÓN
1.
Indicar la suma y producto de raíces de cada
una de las ecuaciones:
Rpta.: _______________
b)
2
2
x +1=0
a) x + 2x + 1 = 0
2
Rpta.: _______________
b) x + x + 1 = 0
2
c) 5x + 2x + 3 = 0
c)
2
d) 7x + 2x – 1 = 0
2
e) 3x – 2x + 5 = 0
Rpta.: _______________
2
f) x + 8x + 9 = 0
2.
Indicar de que naturaleza son las raíces de las
ecuaciones siguientes:
a)
2
x + 2x + 1 = 0
2
x + 5x + 2 = 0
d)
2
x –1=0
Rpta.: _______________
e)
2
x –x+1=0
Profesor José María Villavicencio Taipe
IV BIM – ÁLGEBRA – 5TO. AÑO
8.
Rpta.: _______________
f)
2
(b + 5)x + 3bx + b = 0
presenta raíces iguales. Hallar: “b”
2
5x + 3x + 1 = 0
a) 0
d) 8
Rpta.: _______________
g)
Si la ecuación:
2
7x + 4x – 2 = 0
9.
b) -2
e) 6
c) 4
Si la ecuación:
2
x + 3x + 6k – 1 = 0
Rpta.: _______________
h)
no tiene solución real, entonces se cumple:
2
2x + 3x – 3 = 0
5
24
13
d) k
24
a) k
Rpta.: _______________
3.
Si: x1 y x2 son las raíces de la ecuación:
2
x + 5x + 1 = 0
10.
2
E = (x1 + x2) – 2x1x2
4.
b) 21
d) 24
e) 25
13
24
11.
Indique los valores de k si en la ecuación:
b) -2 ; 1/2
e) -2 ; -1
2
5.
b) 25/9
e) N.A.
a)
c) 9/25
b)
2
con raíces “x1” y “x2”; calcular “k”.
k-4
Si: 3(x1x2)
a) 9/2
d) 4
6.
2
c)
c) 5/2
2
d)
qué valor de “a” las raíces serán iguales?
(Raíz doble)
7.
x2 = 1
x1 = 5
;
x2 = -2
x1 = -3
;
x2 = -4
Rpta.: _______________
En la ecuación 3x + 2ax + a – 6 = 0, ¿para
a) ±1
d) ±4
;
Rpta.: _______________
=1
b) 7/2
e) 9
x1 = 3
Rpta.: _______________
Dada la ecuación: 9x + 5x + 1 = 0
b) ±2
e) N.A.
x1 = -2
;
x2 = 2
Rpta.: _______________
c) ±3
e)
x1 3 ;
x2 2 3
Rpta.: _______________
Si una de las raíces de la ecuación:
2
x + (a + 3)x + a + 2 = 0 es (-6), entonces la
f)
otra raíz es:
a) -2
d) -4
b) -1
e) N.A.
x1 2 3 ; x2 2 3
Rpta.: _______________
c) -3
12.
c) 2 ; -1
Formar las ecuaciones de 2º grado a partir de
las raíces x1 y x2.
(m - 2)x – (m + 5)x + 8 = 0
d) 1/4
25
4
e) N.A.
a) 1 ; 2
d) -1/2 ; 1
c) 23
Hallar “m”, si la suma de raíces de la ecuación
es 10.
a) 25
c) k
x2 – (k + 2)x + k + 1 = 0 su discriminante es
igual a la suma de sus raíces.
Indicar el valor de:
a) 20
b) k
Sean las ecuaciones equivalentes:
Profesor José María Villavicencio Taipe
IV BIM – ÁLGEBRA – 5TO. AÑO
2
x + ax + 15 = 0 ……….. (I)
sea igual al producto de las mismas. (k < 0)
2
3x + 2x + b = 0 ……….. (II)
Indicar: “a . b”
a) 45/3
d) 2/3
13.
b) 30
e) 25/3
a) -3
d) -1
c) 35
15.
2
2ax – (8b - 3)x + 18 = 0
2
d)
14.
3
2
2
e)
9
b)
9
2
Hallar el valor de “k” en la ecuación:
2
a) 1
d) 4
x + (b + 5)x + 6 = 0
son equivalentes (tienen las mismas raíces).
1
6
c) 0
(k - 1)x – 5x + 3k – 7 = 0
para que una de las raíces de la ecuación sea
la inversa multiplicativa de la otra.
Calcular “a/b”, si las ecuaciones:
a)
b) -2
e) N.A.
c)
b) 2
e) 6
c) 3
1
2
Hallar el valor de “k” que hace la suma de las
raíces de la ecuación:
2
2
x + kx + 2x – k + 4 = 0
1.
2
Hallar el valor de “a” de modo que las raíces
c) 2x – 2Mx + 1 = 0
de la ecuación:
x2 ( a 3)x
a2
1 0 se difieren en 5.
4
4.
Sean “S” y “P” la suma y el producto de raíces
de la ecuación de incógnita “x”:
2
2.
a) 5/3
b) 7/3
d) 5/6
e) 20/3
(k - a)(x – x) = -(k + a)
c) 10/3
Si: S < P; son números consecutivos. Hallar “k”
en función de “a”.
Indicar la suma de las raíces que verifican la
ecuación:
2
2
x 6x 9 4 x 6x 6
a) 12
b) 16
d) 18
e) 13
c) 15
5.
a) –a
b) 2a
d) 3a
e)
c) a
3a
2
Los límites hacia los que tienden las raíces de
la ecuación:
2
(a - 2)x – (7a - 2)x + 6a = 0
3.
Formar la ecuación de segundo grado, si tiene
cuando “a” crece indefinidamente.
por raíces:
M M2 1
2
d) 2x – 2Mx + 2 = 0
2
e) 2x – Mx + 1 = 0
a) 2x – Mx + 2 = 0
b) 2x – 4Mx + 2 = 0
a) 1 y 6
b) 2 y 3
d) 2 y 6
e) N.A.
2
2
Profesor José María Villavicencio Taipe
c) 1 y 3
IV BIM – ÁLGEBRA – 5TO. AÑO
6.
2n 1 2n 3
Siendo:
;
el conjunto solución
n1
n 1
7.
2
ecuación: x – 5x + 1 = 0
de la ecuación cuadrática en “x”:
2
ax + 2bx + 4c = 0
Calcular el valor de: L
Sabiendo que x1 x2 son las raíces de la
(a 0)
Reducir: N
b2 4 ac
x12 x22
x14 x12 x22 x2 4
( a b c)2
TAREA DOMICILIARIA Nº 5
1.
Indicar la suma y producto de raíces de cada
una de las ecuaciones:
2
7.
2
a) x + 3x + 1 = 0
d) 2x + 5x + 1 = 0
b) x + 5x + 2 = 0
e) x + 7x + 6 = 0
2
2
2
a) 1
d) 9
c) 3x + 4x + 1 = 0
2.
Indicar de que naturaleza son las raíces de las
ecuaciones siguientes:
2
e) 5x + 2x + 1 = 0
b) x + x + 2 = 0
f) x – 25 = 0
c) x + 5x + 1 = 0
g) x + 3x = 0
d) x – 7x + 2 = 0
h) 3x – 7x + 1 = 0
2
2
2
2
9.
4.
b) -4/3
e) -3/4
1
10.
c) 1/3
a) 4
d) 2
5.
11.
64
3
64
d)
19
67
9
19
e)
64
b)
b) -2/3
e) -1/2
c) -3
Hallar “m”, si la ecuación tiene por raíz a la
unidad, m > 0.
2
b) 2
e) 6
c) 3
Dadas las ecuaciones:
2
2
2x + nx + 2 = 0 ………..(II)
Equivalentes (tienen las mismas raíces)
Indicar el valor de: E = m + n
c) 3
c)
19
64
Indicar el valor de “m” si el producto de
raíces es igual a la suma de las mismas en la
2
ecuación: (m + 4)x – 2mx + 3m + 1 = 0
a) 1/2
d) 1/3
b) -2
e) -10
mx + 5x + 10 = 0 ………..(I)
Hallar “k”, si la suma de raíces de la ecuación
es 20.
2
(k - 3)x – (k + 4)x + 30 = 0
a)
6.
b) -2
e) 1
2
2
2
(x1 x2 )2 2x1x2
3x1x2
c) -6
Hallar “m”, si el producto de raíces es 16.
a) 1
d) 4
x + 2ax + a = 0
Indicar:
b) -2
e) -12
4x – 4x + m – m – 2 = 0
Sea x1 y x2 raíces de la ecuación:
2
Hallar “m”, si la suma de raíces de la ecuación
es 8.
2
(m + 2)x – (7m + 6)x + 4m + 5 = 0
a) -1
d) -4
2
x + 4x + 1 = 0
a) 4/3
d) -1/3
c) 3
(m + 1)x – (m + 5)x + 10m + 4 = 0
Siendo x1 y x2 son las raíces de la ecuación:
x x2
Indicar el valor de: A 1
3x1x2
b) 2
e) 10
a) -1
d) -10
2
2
3.
8.
2
a) x – ax + 1 = 0
Hallar “m”, si la ecuación presenta raíz doble.
2
x – (m + 1)x + 25 = 0
c) 2/3
a) 10
d) 11
12.
b) -10
e) 3
c) -11
Indicar el valor de “p” si una de las raíces es
la inversa multiplicativa de la otra.
2
(p + 2)x – 3x + 2p + 1 = 0
a) -1
d) 3
13.
b) 1
e) 4
c) 2
Hallar “a” si la ecuación presenta raíces
2
2
simétricas: x + (a – 2)x + a + b = 0
Siendo: b > 5
Profesor José María Villavicencio Taipe
IV BIM – ÁLGEBRA – 5TO. AÑO
a) 1
d) -1
14.
b) 3
e) 2
c) 4
2
Sea la ecuación: 5x – 2x + 3 = 0
Donde: “x1” y “x2” son sus raíces
Calcular: M = (1 + x1) (1 + x2)
a) 1
d) 4
15.
b) 2
e) 5
c) 3
Formar las ecuaciones de 2º Grado a partir de
las raíces dadas x1 y x2.
a) x1 = -2
x2 = -1
b) x1 = 3
x2 = 4
c) x1 = 5
x2 = 3
d) x1 = 2
x2 =
e) x1 =
x2 = 3
f) x1 = 6
3
3
x2 = -1
Profesor José María Villavicencio Taipe