47 - licimep.org
Anuncio
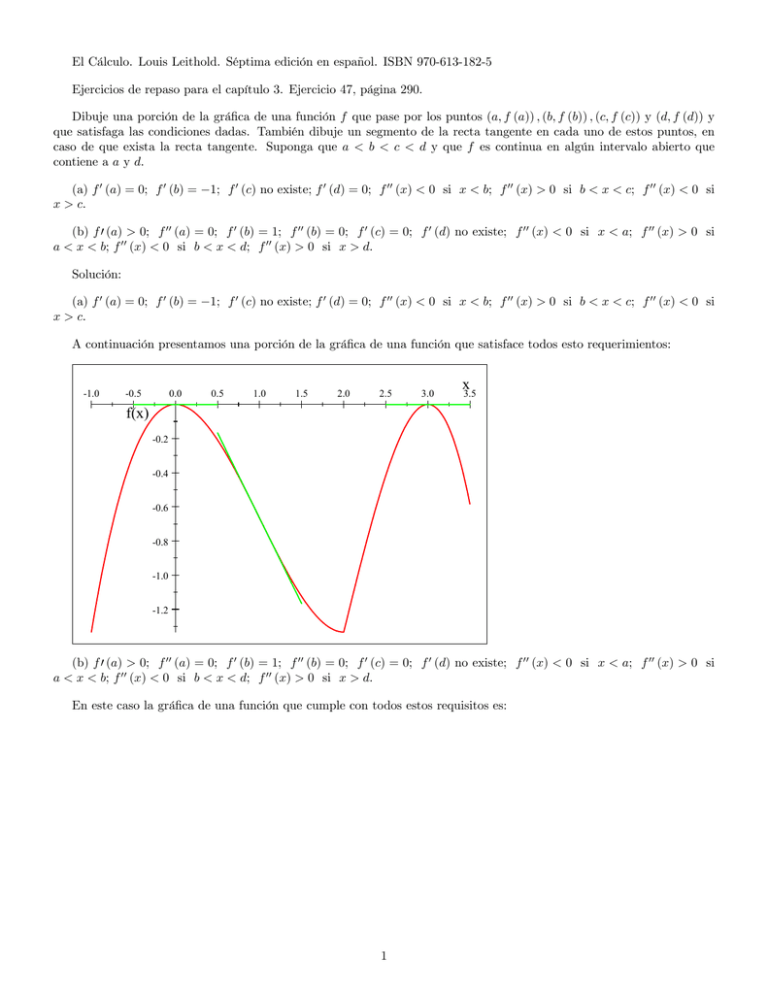
El Cálculo. Louis Leithold. Séptima edición en español. ISBN 970-613-182-5 Ejercicios de repaso para el capítulo 3. Ejercicio 47, página 290. Dibuje una porción de la grá…ca de una función f que pase por los puntos (a; f (a)) ; (b; f (b)) ; (c; f (c)) y (d; f (d)) y que satisfaga las condiciones dadas. También dibuje un segmento de la recta tangente en cada uno de estos puntos, en caso de que exista la recta tangente. Suponga que a < b < c < d y que f es continua en algún intervalo abierto que contiene a a y d. (a) f 0 (a) = 0; f 0 (b) = x > c. 1; f 0 (c) no existe; f 0 (d) = 0; f 00 (x) < 0 si x < b; f 00 (x) > 0 si b < x < c; f 00 (x) < 0 si (b) f 0 (a) > 0; f 00 (a) = 0; f 0 (b) = 1; f 00 (b) = 0; f 0 (c) = 0; f 0 (d) no existe; f 00 (x) < 0 si x < a; f 00 (x) > 0 si a < x < b; f 00 (x) < 0 si b < x < d; f 00 (x) > 0 si x > d. Solución: (a) f 0 (a) = 0; f 0 (b) = x > c. 1; f 0 (c) no existe; f 0 (d) = 0; f 00 (x) < 0 si x < b; f 00 (x) > 0 si b < x < c; f 00 (x) < 0 si A continuación presentamos una porción de la grá…ca de una función que satisface todos esto requerimientos: -1.0 -0.5 0.0 0.5 1.0 1.5 2.0 2.5 3.0 x 3.5 f(x) -0.2 -0.4 -0.6 -0.8 -1.0 -1.2 (b) f 0 (a) > 0; f 00 (a) = 0; f 0 (b) = 1; f 00 (b) = 0; f 0 (c) = 0; f 0 (d) no existe; f 00 (x) < 0 si x < a; f 00 (x) > 0 si a < x < b; f 00 (x) < 0 si b < x < d; f 00 (x) > 0 si x > d. En este caso la grá…ca de una función que cumple con todos estos requisitos es: 1 6 5 4 3 2 1 -0.5 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 x Apendice. (a) f 0 (a) = 0; f 0 (b) = x > c. 1; f 0 (c) no existe; f 0 (d) = 0; f 00 (x) < 0 si x < b; f 00 (x) > 0 si b < x < c; f 00 (x) < 0 si Este problema es sencillo si se resuelve con lápiz y papel, pero si queremos usar un porgrama de gra…cación debemos tener una ecuación en x e y. ¿Cómo se calculan las funciones que gra…camos? Adivinanza: f (x) = Ax3 + Bx2 + Cx Los puntos los tomos como: a = 0; b = 1; c = 2; d = 3 Aplico las condiciones del problema f 0 (0) = C = 0 f 0 (1) = 3A + 2B + C = 1 f (1) = 2 3 f 00 (1) = 6A + 2B = 0 que quedan como el sistema 3A + 2B = 1 6A + 2B = 0 que tiene las soluciones A= B= 1 3 31 23 1 = 2 1 Por lo tanto nos sirve la función: f (x) = 1 3 x 3 x2 2 Como la derivada no debe existir en c (que lo tomé como 2), se construye otra función que pegamos a f , para que quede continua, pero con una derivada diferente. La probamos del mismo tipo g (x) = Ax3 + Bx2 + Cx y las condiciones nos dan g (2) = 8A + 4B + 2C = 4 3 g 0 (3) = 27A + 6B + C = 0 g 00 (2) = 12A + 2B = 0 que se resuelven como 0 1 10 4 1 0 8 4 2 3 C B @ 27 6 1 A B @ 0 A=@ 12 2 0 0 o sea que g (x) = 2 3 x + 4x2 3 1 2 3 C 4 A 6 6x La gra…ca de f y g queda 0.0 0.5 1.0 1.5 2.0 2.5 x 3.0 0.0 f(x) -0.2 -0.4 -0.6 -0.8 -1.0 -1.2 Las dos funciones y sus derivadas f (x) = g (x) = 1 3 x 3 x2 2 3 x + 4x2 3 f 0 (x) = x2 6x 2x g 0 (x) = f 00 (x) = 2x 2x2 + 8x 2 g 00 (x) = 8 6 y gra…cadas para ver que cumpen todos los requisitos: 3 4x y 2 1 0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8 2.0 2.2 2.4 2.6 2.8 3.0 x -1 -2 -3 -4 (b) f 0 (a) > 0; f 00 (a) = 0; f 0 (b) = 1; f 00 (b) = 0; f 0 (c) = 0; f 0 (d) no existe; f 00 (x) < 0 si x < a; f 00 (x) > 0 si a < x < b; f 00 (x) < 0 si b < x < d; f 00 (x) > 0 si x > d. Lo mismo hecho para el segundo inciso, para el (b). f (x) = Ax4 + Bx3 + Cx2 + Dx a = 0; b = 1; c = 2; d = 3 f 0 (0) = D > 0 f 00 (0) = 2C = 0 f 0 (1) = 4A + 3B + 2C + D = 1 f 00 (1) = 12A + 6B + 2C = 0 f 0 (2) = 32A + 12B + 4C + D = 0 C=0 4A + 3B + D = 1 12A + 6B = 0 32A + 12B + D = 0 0 4 @ 12 32 1 3 6 12 1 0 A 1 10 1 B 1 B @ 0 A=B B @ 0 f (x) = 1 4 1 3 4 x + x + x 10 5 5 f 0 (x) = 2 3 3 2 4 x + x + 5 5 5 f 00 (x) = 6 x 5 0 1 10 1 5 4 5 1 C C C C A 6 2 x 5 4 8 6 4 2 -0.5 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 x -2 -4 -6 (b) f 0 (a) > 0; f 00 (a) = 0; f 0 (b) = 1; f 00 (b) = 0; f 0 (c) = 0; f 0 (d) no existe; f 00 (x) < 0 si x < a; f 00 (x) > 0 si a < x < b; f 00 (x) < 0 si b < x < d; f 00 (x) > 0 si x > d. g (3) = f (3) = 23 5 f 0 (3) = 3; 3 10 3 10 g (x) = Ax2 + Bx + C 3 10 g (3) = 9A + 3B + C = g 0 (3) = 6A + B g 00 (x) = 2A 3 , Solution is: 10 9+C = 93 10 93 10 g (x) = x2 g 0 (x) = 2x g 00 (x) = 2 f (x) = f 0 (2) = 0 1 4 1 3 4 x + x + x 10 5 5 f (2) = 8 5 5 6 5 4 3 2 1 -0.5 0.5 1.0 1.5 2.0 2.5 3.0 6 3.5 4.0 x