El Cálculo. Louis Leithold. Séptima edición en español
Anuncio

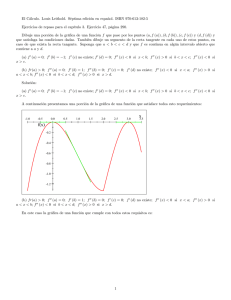
El Cálculo. Louis Leithold. Séptima edición en español. ISBN 970-613-182-5 Ejercicios de repaso para el capítulo 1. Ejercicio 17, página 96. Dados f (x) = x2 x 25 , a = 5, L = 10 5 y " = 0:1, (a) Utiliza argumentos semejantes a los de los ejemplos 1 y 3 de la sección 1.4 del Leithold para determinar una tal que si 0 < jx aj < entonces jf (x) (b) Apoya tu elección de Lj < " del inciso (a) mediante una grá…ca precisa, (c) Con…rma analíticamente, empleando las propiedades de las desigualdades, la elección de del inciso (a). Solución: (a) Queremos los valores de x que hacen que f (x) esté a una distancia " de L; es decir, buscamos x tal que f (x) x2 x L = ", lo que en este problema nos da la ecuación 25 5 10 = 0:1 que reescribimos como (x 5) (x + 5) x 5 10 = x + 5 10 = x 5 = 0:1 que se resuelve como x = 5:1. Ahora "hacia abajo" ponemos, L 10 x2 x f (x) = " que nos da la ecuación 25 = 0:1 5 Factorizando y cancelando factores 10 x2 x 25 = 10 5 (x 5) (x + 5) = 10 x 5 (x + 5) = 5 x = 0:1 cuya solución es x = 4:9 Por lo tanto, si x 2 (4:9; 5:1) entonces f (x) 2 (9:9; 10:1). Así que si tomamos = 0:1, los valores de f (x) estarán más cerca del límite L = 10 que " = 0:1. (b) Haciendo una grá…ca en la vecindad de x = 5 tenemos 1 >0 y 10.5 10.4 10.3 10.2 10.1 10.0 9.9 9.8 9.7 9.6 9.5 4.6 4.7 4.8 de donde es claro que 4.9 5.0 5.1 5.2 5.3 5.4 x = 0:1. (c) Demostraremos ahora analíticamente que dado " = 0:1, la Tenemos que jf (x) Lj = x2 x 25 5 10 = jx + 5 10j = jx 5j < " por tanto, jx 5j < " = y tal como queríamos demostrar, = " = 0:1 2 que necesitamos es 0.1.