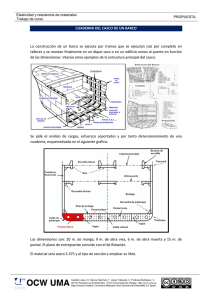
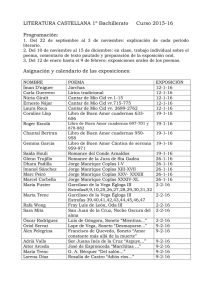
Parte 2. Casco y estructura (4)(1)
Anuncio

El mejor método de analizar las tensiones que se generan en los orificios y sus entornos, es utilizar programas informáticos de cálculo. En estos, debidamente utilizados, se puede apreciar con todo detalle la localización y el reparto general de las tensiones y esto permite optimizar mejor la estructura, aunque una aplicación estricta de los reglamentos es suficiente, si el caso de estudio esta explicado en detalle en las mismas. Para arquitecturas o soluciones no contempladas en los reglamentos, o cuando se requieren análisis mas detallados, es cuando hay que echar mano de estos programas. Escotilla. Un orificio de tamaño grande. Las escotillas son orificios importantes que hay que reforzar-compensar adecuadamente, utilizando cualquiera de los métodos ofrecidos por las Sociedades de Clasificación o Normas vigentes sobre los aparatos a presión. Obsérvese en esta escotilla las trincas de cierre, que son necesarias a efectos de seguridad. Permiten, además, comprimir la junta de estanqueidad sobre su asiento, que en un caso desfavorable, con una la baja presión exterior, y una ligera presión interior podrían permitir el paso de agua, fugas, etc. hacia el interior del habitáculo. Es preceptivo que las escotillas, una vez cerradas puedan soportar una presión interna sin que las trincas se rompan o se suelten, (sobre-presión producida por la descarga de aire u oxigeno en el ambiente del habitáculo). En algunos casos, esta sobre-presión interna puede llegar a ser de unos 200 mbar o quizá mas. Asimismo, el peso propio de las escotillas debe equilibrarse con muelles, contrapesas, resortes, etc. de forma que cueste poco abrirlas, primero, y después levantarlas hasta su posición de estiba por una persona desde dentro del sumergible, (~10 kg max. de peso aparente), de hecho deberán tender a ascender por ellas mismas cuando se las abre, para mas comodidad. La posición de estiba ha de disponer de un pestillo o retención adecuado, seguro, pero fácil de destrincar, que impida el cierre intempestivo de la misma, con balances, al agarrarse, etc. 112 TENSIONES COMBINADAS por criterio de TRESCA En esta Figura se puede observar que las zonas más cargadas son aquellas situadas en el plano crítico o de simetría del conjunto cilindro-brazola y en sus cercanías, o sea por proa y por popa de la brazola de la escotilla y zonas contiguas a esta. En el caso de una escotilla situada en la parte alta de un cilindro (casco principal) estos puntos representan las zonas del lomo (o generatrices más altas) del mismo y la parte de la brazola, en contacto con ellas. Las tensiones máximas discurren en sentido transversal al eje del casco (zona roja). Las tensiones mas bajas (zona azul) corresponden a los laterales de la brazola, que al no estar conectados transversalmente entre si, ceden con facilidad relajando sus tensiones. Con carga exterior, la escotilla tiene a clavarse por todos lados sobre las paredes del cilindro, pero no de modo uniforme, siguiendo la configuración de una silla de montar. De forma general y con respecto a la compensación de los orificios practicados en el casco, hay que puntualizar o respetar las siguientes reglas y detalles constructivos, no siempre claramente estipulados por las diversas normas, en el caso de los sumergibles, y en el contexto de una ejecución utilizando planchas laminadas unidas por soldadura, que es el método mas normal y económico: a) Ley fundamental: Como ya se cita en 1) anterior, la sección total útil de la compensación, es decir el área seccional total añadida mediante los sobreespesores aplicados a cada lado del orificio, según un corte longitudinal por el centro del orificio, (sección por el plano crítico) deberá ser igual o mayor, que el área seccional del material que se ha eliminado a causa de la perforación. Preferentemente deberá del orden del 130% al 150% del área de la sección eliminada ya que el material trabaja en peores condiciones que el original. b) Estos cálculos son solo válidos para penetraciones cuyo diámetro sea inferior a 1/3 del diámetro del cilindro sobre las que se instalan. Para diámetros mayores es preciso recurrir a cálculos mas avanzados. Así, para un casco de un sumergible comercial, de 2,4 m de diámetro, el diámetro de la máxima perforación para la cual estos cálculos son validos, es de unos 800 mm, (750 mm netos) que está en el límite que permite el paso franco de una persona corpulenta provista de chaleco salvavidas (escape), o, en el aspecto comercial, proveer un paso cómodo. 113 c) Los reforzados serán integrales con las planchas que forman el casco o los pasos. Es decir no se permiten planchas dobles, superpuestas o añadidas. No está asegurado que funcionen mecánicamente como un conjunto, que no se cuele el agua de mar entre ellas y se oxiden interiormente lo que pasaría desapercibido, lo cual podría ser peligroso. Esto exige (en una construcción de alta calidad) que se deban hacer unos cortes circulares en el cuerpo principal (cilindro, domo),o rectangulares con las esquinas redondeadas en el forro, mucho más grandes que el orificio que se pretende practicar, (del orden del 200 % en diámetro), se eliminen estos discos y se sustituyan por unos nuevos discos o placas-insertos de la misma superficie, libres de soldadura y un espesor bastante mayor que el típico del cilindro, que rodeen la perforación, al menos en la distancia “L” (ver Tabla 16-V) respecto al borde de la penetración, y sobre los que se perforará el orificio deseado (el taladrado definitivo del orificio se debe hacer después de soldar la placa encastrada anterior, para evitar que por las contracciones de la soldadura, el inserto se alabee demasiado o/y el agujero se ovalice (aparte de que su trazado sobre una plancha plana es mas arriesgado). Puesto que el espesor normal de la plancha del cilindro, en un caso general, es inferior al espesor del inserto, hay que efectuar unas transiciones de espesor suaves, (pendiente < 1/4). El sobre-espesor del reforzado puede aplicarse por la zona externa de la línea de forro, promediado con el espesor medio original o por el interior. En este último caso, el más conveniente desde el punto de vista de mantener las líneas y formas exteriores del casco, el alma de las cuadernas, en la zona correspondiente, hay que recortarla. Si se hace por el exterior, las cuadernas (si son interiores) no hay que tocarlas pero las líneas exteriores del forro ya no son totalmente lisas, y la importancia de esto dependerá del caso. Normalmente, en estos sumergibles, al ser la velocidad muy pequeña, el aspecto hidrodinámico de las formas no es exigente. En el caso de sumergibles muy pequeños, y si los espesores-base asignados son bastante mas grandes que los mínimos necesarios, es posible que no haya necesidad de aplicar estos insertos. d) Es conveniente que el área seccional añadida por el reforzado se encuentre lo mas próxima posible al borde del orificio, sobre todo en los orificios pequeños, (Ver Nota 3 de la Tabla 16-V). Es comprensible que, en las zonas alejadas del orificio, los sobre-espesores añadidos colaboran en un menor grado en la resistencia a la compresión del orificio, aunque en los orificios grandes, sirven para absorber las importantes fuerzas cortantes que se crean, coplanares con el forro. e) Cuando las presiones de servicio son sensiblemente altas, y siendo conscientes de que es muy difícil compensar bien, se debe limitar drásticamente el número de orificios grandes, procurando que todos los orificios sean de diámetro pequeño, respecto al diámetro del cuerpo principal. Los orificios son siempre fuente de fugas, problemas y riesgos, aunque evidentemente, algunos son imprescindibles. Además las ventanas transparentes ofrecen un atractivo sin el cual los sumergibles de recreo carecerían de sentido. f) Las brazolas, o manguitos reforzado que forman el conducto de paso, cuya longitud efectiva máxima es “ℓ “, a cada lado del orificio, (la longitud real puede ser menor) deberán ser de un espesor similar o superior al espesor local del forro (o inserto reforzado del forro). En muchos casos prácticos, no interesa que por el interior o el exterior estos manguitos sobresalgan demasiado (no conviene o no se desea llegar a tener la distancia “ℓ “) por lo que los sobre-espesores habrá que incrementarlos un poco mas, relativamente, para poder así mantener el área seccional requerida de compensación. 114 g) Las costuras longitudinales de forro, es decir las líneas de soldadura de las diversas tracas, deben situarse en lugares alejados de la placa encastrada, o en su defecto del orificio, para que no vayan a intersectar con ella y de ser esto inviable, o no haya otra solución a mano, deberán hacerlo que forma que los cruces entre las soldaduras que contornean los insertos y las de la tracas no formen ángulos cerrados o el contacto sea muy tangencial. h) Las soldaduras de cierre, según la generatriz de los manguitos que forman las brazolas de las escotillas o pasos, si están construidos a base de planchas curvadas y soldadas, conviene que no estén situadas en la generatriz del cilindro principal que pasa por el eje de orificio, o plano crítico (longitudinal). O sea, las soldaduras se desfasarán o decalarán respecto a este plano convenientemente. i) Una vez determinado el espesor y la longitud de la brazola a instalar, si es necesario prolongar el paso (hacia el exterior normalmente), se podrán aplicar los espesores normales, los exclusivamente requeridos para soportar la presión de servicio aunque, si la diferencia de espesores es muy grande, esto habrá que hacerlo de forma escalonada, mediante chaflanes. En caso de una escotilla de acceso, el asiento de la tapa puede formar parte integral de la brazola, por el exterior, o puede estar en el tubo de prolongación de esta, de un espesor adecuado. j) Cuando una brazola (de escotilla) se recorta por el interior del casco para que no estorbe el paso, en cascos muy estrechos, hay que considerar que el área de compensación requerida ha de seguir manteniéndose, por lo menos, en la sección por el plano crítico y en sus cercanías. k) Hay que considerar que las normas de compensación que aparecen en los reglamentos relativas a la compensación de orificios están generalmente pensadas para recipientes sometidos a presión interior y, por consiguiente lisos, sin cuadernas. La aplicación de estas normas a los cascos de los sumergibles, sometidos a presión exterior y provistos de cuadernas, provoca la aparición de problemas suplementarios, y que obliga a prever los inconvenientes que de ello resultan. Es conveniente que no se tengan cuadernas tangenteando o muy cercanas a las brazolas, ya que la soldadura de estas se vuelve muy difícil de ejecutar, por falta de espacio y accesibilidad, y por tanto poco fiable, (estando además, precisamente en la zona del plano critico). Si no hay mas remedio que hacer tangentear una cuaderna, principalmente el alma, y el costado de una brazola hay que recurrir a darle a la brazola unos topes o tacones sobre los que vayan a morir los dos extremos de las almas, soldándolas a tope. Estos tacones deben ser integrales con la brazola, por lo que son difíciles de construir a partir de una brazola obtenida por el curvado de una plancha laminada. Es más fácil de conseguir cuando la brazola es de acero moldeado o forjado. En caso de cualquier interferencia es primordial la buena soldadura de la brazola sobre el casco. Ver gráfico adjunto. l) Las placas transparentes de las ventanas o portillos no colaboran en la resistencia o la compensación. Se consideran meros elementos pasivos, autoportantes, que lo único que hacen es transmitir fuerzas a sus asientos, (aunque tengan una resistencia propia no despreciable). 115 Zonas difíciles de soldar Tacón sobre la brazola Brazola Tacón sobre la brazola, por ambas bandas, cuando las cuadernas tangentean En los sumergibles, los portillos o ventanas transparentes se sitúan, normalmente, alineados a lo largo de la eslora, y bastante juntos, (orificios anidados) por lo que el cálculo del caso de un orificio único, suelto, aislado no es totalmente aplicable y hay que calcular los valores de “L” que se deducen de las normas y hallar los valores de “L” que realmente se pueden asignar, por espacio. Si la separación entre los bordes de dos orificios contiguos es “N”, este valor podría ser inferior a “2 L” y entonces la longitud de compensación de cada orificio individual debería sería igual N/2. En resumen no se admiten solapes en las longitudes efectivas. Asimismo, hay que seleccionar la longitud y espesor de las brazolas, según los espesores de las placas transparentes que se deban montar, mas un margen para los asientos, su montaje, etc. Además, en el caso de orificios alineados y muy juntos, el inserto sobre el casco (con sobre-espesor), conviene que sea alargado, continuo, de una sola pieza y común para todos los orificios, por razones prácticas, con un espesor derivado de la compensación requerida y las distancias “L” de cálculo (máximas efectivas) a considerar, teniendo en cuenta lo anteriormente apuntado sobre el valor de “N/2”, (entre ventanas). Puesto que los cilindros que tratamos están provistos de cuadernas, estas, como ya hemos señalado, pueden interferir en el trazado y el corte de los orificios, ya que, en el caso de escotillas o grandes ventanas transparentes, que pueden tener un diámetro cercano a 700 mm o mas, la separación de las cuadernas se queda muy pequeña y hay que interrumpirlas, (o situarlas extremadamente separadas entre si, lo que exige un espesor mas grande que el óptimo). Para resolver este problema de interferencia ventanas-cuadernas hay dos políticas a seguir: a) Separar las cuadernas bastante, de forma que haya una cuaderna centrada en el espacio que existe entre portillo y portillo. Esto obliga a que estas cuadernas sean relativamente gruesas así como el forro comprendido entre ellas, ya que la distancia entre apoyos, del forro, es bastante elevada, comparativamente. b) Separar las cuadernas el 50% de lo anterior, de forma que las cuadernas entre portillo y portillo sean completas, y existan unas intermedias (incompletas) que 116 vayan a morir al centro de las brazolas de los portillos o ventanas, sobre las que se sueldan. La solución a) es la mas limpia pero exige unos espesores bastante grandes, tanto en cuadernas como en forros. La solución b) es mas compleja y mas arriesgada pero permite reducir algo el espesor del forro entre cuadernas al reducir la luz entre refuerzo y refuerzo. Ahora bien hay que hacer muy bien el contacto de cuaderna-brazola, con cartelas o refuerzos anulares que contorneen la brazola, en prolongación del ala de las cuadernas, soldados al anillo que forma la brazola y que, preferentemente, conecten con el tramo opuesto, interrumpido, de la cuaderna, (como unas gafas). Esta última opción, que ofrece una mayor resistencia tiene el inconveniente de que hay que soldar en lugares muy angostos. K 350. Brazola de escotilla Obsérvese que la brazola, para que no sobresalga mucho por el interior ha sido recortada por proa y por popa del anillo, ajustándola al perfil circular del casco-cuadernas. El recorte máximo ocurre justo en el plano crítico, por lo que el área efectiva de compensación de esta brazola es inferior a la que se podría deducir de sus dimensiones generales. La soldadura de cierre de esta ni la del cilindro base tampoco están en la posición mas aconsejable, aunque al ser las tensiones de compresión el problema es menor. 117 Detalle de cuaderna interrumpida por brazola. En este casco cilíndrico se ha optado por construir algunas cuadernas con barra rectangular maciza de acero. Son más pesadas que las prefabricadas o los perfiles en T pero son muy estables. Lleva una cuaderna interrumpida, que termina en el centro de la brazola, unida a esta soldadura de forma directa. Las cuadernas suelen ir unidas al forro de casco por soldaduras en ángulo. Hay que comprobar que no quedan rendijas o zonas sin soldar por las que pueda entrar la humedad o el agua y almacenarse entre la cuaderna y el forro, lo cual podría inducir corrosiones de difícil detección. Brazola de escotilla con cuaderna interrumpiendo una cuaderna. 118 Detalle de cartelas de refuerzo en extremo interrumpido de la cuaderna intermedia. En los extremos de estas cuadernas interrumpidas conviene que los espesores de alma sean aumentados, al ser grande la carga que actúa en dicho extremo. Cuaderna tangenteando una brazola Asimismo, habrá que reconsiderar el reforzado de compensación, calculado anteriormente, a causa de necesidad de obtener o mantener, además, el momento de inercia combinado de las cuadernas en la zona donde se efectúan las perforaciones. Por consiguiente, la compensación, cuando se trata de un casco cilíndrico provisto de cuadernas, tiene dos vertientes: a) Compensación convencional de la estructura a causa del material eliminado de las ventanas. Es la compensación típica, a efectuar en un cilindro liso, simple, anteriormente descrita, que solo tiene en cuenta las fuerzas de compresión. b) Compensación del momento de inercia mínimo requerido en las cuadernas, (mas su plancha asociada) a efectos de evitar una ovalización anticipada, lo que provocaría un descenso de su presión crítica de inestabilidad general. Por lo general, el reforzado efectuado con motivo del punto a) sirve asimismo como reforzado adecuado para cumplir con este último requisito, pero hay que confirmarlo, comprobando las inercias sobre todo conforme se va avanzando a lo largo de las dos cuadernas mas cercanas al orificio, en el sentido de alejarse del mismo. Hay que señalar que los eventuales momentos de flexión que aparecen en las cuadernas, cuando estas están inicialmente ovalizadas, por construcción (que es lo normal) y se las somete a presión exterior (presión hidrostática real: ley triangular más presión uniforme), introducen tensiones suplementarias en los reforzados de compensación, que hay que evaluar. En general, en cascos sin perforar, intactos, por estar la línea neutra del conjunto cuaderna+plancha asociada, relativamente cercana al forro, este se carga mucho menos en flexión (un 25 %) que el ala de las cuadernas. Además lo hace en una zona en que la tensión transversal en el forro es moderada (zona de contacto forro-cuadernas), por lo cual la tensión en el ala de las cuadernas es el factor que gobierna. En caso 119 de existir orificios y brazolas, las inercia combinada y el reparto de tensiones se puede ver alterado (p.e. desplazamiento de la línea neutra, perdiéndose la circularidad perfecta de esta) por lo que habrá que comprobar estos extremos. Las perforaciones para ventanas o portillos, en los domos (esféricos, elípticos toriesféricos), si se realizan según la dirección de uno de los radios esféricos de que se componen, son mucho mas sencillas de tratar, que el caso de las intersecciones cilindrocilindro, ya que todo se reduce a insertar una brazola o anillo macizo de la conveniente sección recta que mantenga las tensiones y deformaciones en la esfera de base y que sirva de buen soporte para el cristal transparente. La Tabla 16-V del Bureau Veritas (1985) y el Reglas del Germanischer Lloyd anteriormente expuestas, presentan unas reglas de cálculo para domos, que sugiere que hay que dar un sobre espesor al domo, en las proximidades del orifico, aunque no es absolutamente necesario, si la brazola está bien equilibrada en momentos, aunque si es conveniente para eliminar el riesgo de que no lo esté. Un método basado en la resistencia de los materiales, o sea independiente de las exigidas por los Reglamentos, para el cálculo de estas brazolas, (de sección rectangular), se presenta a continuación. Es una solución bastante elemental y consiste en incluir, como siempre, un refuerzo anular (brazola), centrada con el espesor del domo, en el borde del orificio, de una sección recta tal, que cuando se somete a presión el domo completo, incluyendo el “tapón” o pieza que obstruye el orificio, la deformación en el domo (la corona que queda, de acero, principalmente en su borde de contacto con la brazola) sea igual que la que se existe en el domo en estado inicial intacto. Siempre se considera que el cristal o la lámina de plástico no colabora en la resistencia general (se auto-soporta exclusivamente, sin romperse) y lo único que hace es transmitir una carga de borde, fuerza pura sin momento, sobre la brazola, cuya magnitud y dirección dependerá del diseño del mismo y coherente con un equilibrio estático del mismo. La Figura siguiente aclara este concepto. 120 Supongamos que se efectúa una perforación sobre el domo esférico, de acero, centrada con el eje del cilindro-esfera de extremidad, entre los puntos A y B de un radio cercano a R1. Cuando el casco, en estado intacto, se somete a la presión exterior (p), el borde de círculo que pasa por AB, es decir la línea circular que representa el borde de la futura perforación, esta sometido a unas fuerzas de compresión (F) uniformes en todo el borde del anillo, en dirección tangencial (coplanar), equivalentes, por unidad de longitud, a la tensión media de esta esfera por el espesor de pared, o sea F = p·R/2. Fr es del mismo valor y signo opuesto a F. Si ahora se substituye, el sector esférico de acero por un sector idéntico, pero de un material plástico, y este casco mixto se somete a la presión exterior, el sector de plástico está sometido a las mismas fuerzas hidrostáticas que el trozo de acero al que substituye (pero las tensiones de membrana son muy inferiores al deber ser su espesor mucho mayor, el plástico admite un nivel de tensiones muy bajo), pero en resumen, si el contorno del casquete de plástico está bien apoyado en el borde de acero, (apoyo cónico), las fuerzas que ambos se intercambian (de membrana) seguirán siendo las mismas, si se cumple la condición de que las deformaciones, en el disco de acero eliminado y en el plástico son las mismas, lo cual no es siempre cierto, ya que son materiales muy dispares, tanto en lo que respecta a la tensión máxima de servicio como al módulo de elasticidad (Young, E). Para conseguir lo anterior, los bordes del disco de plástico tendrían que poder resbalar sobre la brazola en dirección radial para que pudiese, manteniendo su esfericidad, con un radio ligeramente menor, transmitir la carga requerida de compresión normal sobre el borde de la brazola, (cuyo asiento debería tener forma de cono), lo cual no está asegurado, lo mismo que no lo está el que las líneas medias de los espesores, de uno u de otro material estén en continuidad perfecta. Para materializar este concepto, en la Tabla se presentan los valores de las tensiones máximas admisibles y el módulo de elasticidad de algunos aceros y del plástico acrílico utilizado en las ventanas (según ABS). DEFORMACION DEL ACERO versus METACRILATO Límite de Tension max. fluencia de servicio MATERIAL (MPa) (sigma, MPa), aprox. Acero construcción 240 140 naval A Acero HT (355) 350 210 Acero HY 80 550 320 Acero HY100 690 400 Plástico acrílico (PVHO103 8 1- ABS) a compresión, (C.F.= 8) 60º apertura , 50 bar. Fig. 9 del ABSViewports. Largo plazo. Módulo de elasticidad (E, MPa) Relación sigma/E (aprox) 210000 6,6 * 10-4 206000 206000 205000 2760 1,0 * 10-3 1,5 * 10-3 1,95 * 10-3 2,9 * 10-3 La deformación tiene como valor el cociente entre la tensión y el modulo de Elasticidad de un cuerpo (Ley de Hooke simple, ignorando el efecto de Poisson). Para que dos piezas (barras, domos, etc), una de acero y otra de metacrilato pudieran compaginarse, respecto a sus deformaciones (p.e. sustituir un componente de una estructura en acero por otro de metacrilato, sin que aquella tome deformaciones adicionales), el valor de la deformación en ambas debe ser igual, bajo carga, lo que equivale a que el factor ε = σ / E sea igual. 121 Puede observarse, en la Tabla anterior, que el plástico acrílico (metacrilato) deforma bastante mas que el acero incluso cuando se consideran aceros de muy alto límite elástico, sometidos a una gran tensión. Para un acero HT, la deformación del metacrilato (manteniendo unas tensiones iguales a las máximas admisibles), es del orden de 3 veces superior. En la práctica esto significa que un disco circular de metacrilato, cuando se le somete a una tensión igual a la máxima admisible, en su plano, (p.e. producida por una carga radial uniforme aplicada en su borde) el acortamiento en radio es tres veces superior a la correspondiente si el disco fuese de acero HT. Hay una discordancia importante en las deformaciones que solo se puede resolver dando al disco de plástico un espesor tres veces mayor que el requerido, con el fin de que trabaje con unas tensiones de valor un tercio de las máximas admisibles, lo cual no es práctico. Por dicho motivo, una solución elemental es considerar que el sector de plástico está simplemente apoyado en la brazola y solo le transmite fuerzas en el sentido Fx, fuerzas normales al plano del agujero, que corresponden a la presión que ejerce el mar sobre el disco, multiplicado por el área, uniformemente repartidas por su perímetro. En las ejecuciones en que el plástico dispone de asiento plano (esfera con brida) o angular (bisel), esta hipótesis es la mas adecuada. La brazola estará, entonces, sometida a unas fuerzas exteriores de valor Fx = p·π·R12 / 2·π·R1= p ·R1/2 , por unidad de longitud perimetral, de origen hidrostático, que actúan en una dirección normal al plano del agujero. Debido a la presión exterior que actúa sobre la esfera (corona, parte metálica), el anillo que forma la brazola y sobre el que apoya su borde, estará también sometido a unas fuerzas radiales dirigidas hacia el interior, (fuerzas designadas por T, por unidad de longitud circunferencial de brazola). Se supone que la brazola, ella misma, no tiene que soportar directamente la presión del mar o este efecto es de poco valor. La sección recta del anillo-brazola (A) deberá ser entonces tal que su deformación circunferencial (equivalente a una reducción en radio de la brazola) sea idéntica a la que sufre la esfera, en estado intacto, a lo largo de un circulo menor que tiene el mismo diámetro que la brazola. Con este proceder las tensiones y las deformaciones existentes en la corona de acero se mantienen las mismas que en el estado intacto, y la esfera “no se entera” de la sustitución de su casquete de acero por uno de plástico (o de cualquier otro material, si va simplemente apoyado, con fuerza de apoyo normal al plano de la brazola). La deformación de cualquier circunferencia trazada sobre la superficie de la esfera, bien sea un meridiano, un paralelo, o un círculo menor, es constante y de valor: ε= ∆R (1 − ν ) p ⋅ R = ∗ = ε o = Cte R E 2⋅t Si la sección recta del anillo que forma la brazola tiene un área A, la tensión media en cualquier punto de la sección, para una fuerza radial T es: T * R1 A y la deformación (caso de fuerza uniaxial circular, al considerarse que la brazola es un anillo de pequeño espesor, sin efecto de Poisson) es: σ= εA = T * R1 que debe ser igual a εo. E*A 122 Además resulta que tg(α) = Fx / T, siendo α el semi-ángulo de apertura de la perforación, (cono de apertura), según se desprende de la composición de fuerzas, luego, tg(α) = p ·R1/(2·T) y T / p = R1/ (2· tg(α)) y sabiendo que sen(α) = R1/ R, resulta: A= T * R1 2 * t * T * R1 = = 1,43 * t * R1 * cos(α ) = 1,43 * t * R * sen(α ) * cos( α ) (para v=0,3) E * ε o (1 − ν ) * p * R Cuando el semi-ángulo de apertura es del orden de 90º, o sea el agujero es del mismo diámetro que la semiesfera, el cos(α) se hace cero, ya que la fuerza que ejerce el casquete de plástico ataca de forma normal a la cara de apoyo, por lo que teóricamente no haría falta incluir ninguna brazola, solo un asiento circular. Si el cuerpo metálico original, domo, era una semi-esfera, esta se ha quedado reducida a un anillo metálico estrecho, testimonial, prolongación del cilindro contiguo, que soporta el cristal, que es de un diámetro similar al de la semi-esfera inicial. Como los bordes por donde apoya el cristal, están siempre expuestos a cualquier efecto que los desplace, los deforme o los alabee, siempre es conveniente aplicar algún anillo de refuerzo, pero teóricamente no es necesario. La semiesfera de plástico apoya netamente sobre un aro plano, como lo podría hacer sobre una superficie plana. Asimismo, si el orificio es muy pequeño, sen (α) es muy pequeño y la brazola requerida de refuerzo es muy pequeña, (a efectos de la contracción radial del borde del orificio pero no de las concentración de tensiones, por lo cual una pequeña brazola siempre es necesaria, en el caso límite). Esta formulación de la compensación (brazola calculada para carga normal al plano del agujero) es especialmente útil y adecuada cuando se trata de una escotilla, cuyo asiento es plano. En este caso la escotilla asienta sobre un plano paralelo al del agujero y solo transmite a su borde cargas como las designadas como Fx en la Figura anterior. En la Figura adjunta (del DNV-1988) se presentan las principales fuerzas que hay que considerar en el diseño de una tapa de escotilla, del tipo casquete esférico y su correspondiente anillo perimetral, el cual asienta sobre la brazola fija la casco. Ejerce sobre esta una fuerza normal, en todo el perímetro de valor Fx y la brazola debe estar dimensionada para poder soportar esta. 123 Obsérvese que las leyes de compensación clásicas conducirían, en casos de orificios muy grandes, a unas brazolas de una sección tremendamente grande, y por eso las normas no son aplicables al caso anteriormente citado, en el cual todo el domo metálico desaparece. Una vez añadida la brazola, que debe tener su centro de gravedad en la prolongación de la línea media del forro (de acero), la forma del casquete de plástico es indiferente, pudiéndose instalar un casquete con un radio esférico inferior al que tenia el domo original, formando una ampolla sobre el trazado de les esfera inicial. Si queremos ser mas precisos, en el calculo de la brazola de una ventana, habría que considerar el equilibrio de la misma, que va a recibir el cristal, en este caso de asiento cónico. Tomando como origen el centro de gravedad de la sección recta de la brazola, hay que plantear el equilibrio de fuerzas actuantes, representadas en la Fig. adjunta, tomada de las Reglas del Det Norske Veritas -1982-1988 . La fuerza Fo corresponde a la fuerza de compresión (membrana) que ejerce la esfera (metálica sobre a brazola) o viceversa. Las fuerzas F1 y F2 corresponden a la presión hidrostática. La fuerza F3 es la fuerza normal que transmite el cristal a la brazola, en su apoyo, que se calcula como un sector de esfera (si el cristal es esférico) y la fuerza F4 es la cortante que corresponde al resbalamiento del cristal sobre la brazola, hasta que se encaja totalmente, y que vale F4=µ · F3, siendo µ el coeficiente de fricción entre el metacrilato y el acero, (µ=~0,45). De la figura se puede desprender que si se acepta que el cristal pueda ejercer una fuerza normal sobre su asiento, que es similar a la que hubiese ejercido el casquete metálico que se elimina, (si es capaz de deslizarse perfectamente sobre su asiento), entonces la sección de la compensación del orificio ya no debe ser tan grande (la A que antes se calcula), ya que estas fuerzas ahorran sección de brazola, al oponerse a T. Como existe una fricción (del 45%) y se pierde la continuidad del material, en cualquier caso, hay que poner un anillo de refuerzo, que debe cumplir con unos mínimos de compensación y de rigidez propia (tener una inercia mínima respecto a los ejes x-x e y-y). En algunos casos (dependiendo del valor del ángulo γ) la suma de F3 y F4 podrían equivaler a una fuerza normal al plano del agujero, y se vuelve al caso anterior, de cristal simplemente apoyado. En ciertas aplicaciones es posible compensar a base de solo reforzar el forro de la esfera, como se presenta en la figura siguiente, pero no es lo normal. 124 CASCO del SUMERGIBLE de Greg Money (2000). Es un casco muy complejo de de calcular y construir, con tantos abultamientos, orificios y discontinuidades. Hay que huir de este tipo de cascos, en lo posible. COOLSPHERE del Harbor Branch Oceanographic Institute Se pueden apreciar que las cuadernas van situadas entre ventana y ventana, sobresalientes, y bastante separadas, sin que se aprecien cuadernas intermedias. Un habitáculo compuesto totalmente por una esfera de metacrilato. Visión total. 125 ESCOTILLA Las escotillas son unas penetraciones importantes y origen de importantes deformaciones y eventuales vías de agua. En el Sub-Cat de Subibor, y dado que el cilindro-habitáculo queda sobre el agua, en la situación de superficie, el acceso al mismo se efectúa a través de una gran penetración realizada en el domo de popa, provista de una escotilla circular. Este método es muy conveniente, a la vista de la comodidad que supone el embarque de pasajeros. Además abrir la escotilla no supone un esfuerzo particular. 126 SUMERGIBLE PISCES V del Hawaii Undersea Research Laboratory (HURL) Este vehículo para trabajos submarinos, de alta profundidad, dispone de ventanas transparentes planas con asiento cónico, de gran espesor y un poderoso herramental. 5.5.- Cilindros reforzados por cuadernas. Modos de fallo Conviene tener continuamente presente, en el diseño, los diversos tipos o modos de fallo que pueden producirse por un mal dimensionamiento de los escantillones, una mala distribución de los refuerzos, un deficiente diseño de los detalles o una mala construcción de la estructura. En la mayor parte de los casos estos fallos son catastróficos. Los principales conceptos y modos de fallo que se producen y que hay que combatir a base de un cálculo adecuado de los espesores de forro y del tamaño de los refuerzos (cuadernas) o de los domos, así como otras cuestiones constructivas, en un casco resistente genérico de forma cilíndrica, limitado por domos, son los que se exponen a continuación. Estos cascos o recipientes están sometidos a una presión exterior, aparte de las tensiones directas (tracción, compresión) que deben soportar (y que deben estar por debajo de los límites admisibles del material utilizado), están sujetos, por su forma (nominalmente apléxica), a unos fenómenos denominados de inestabilidad estructural que provocan que la estructura falle o colapse, a tensiones muy inferiores a las máximas admisibles, incluso si la forma geométrica de los mismos es matemáticamente perfecta, sin imperfecciones. Además, como siempre hay algunas imperfecciones, ya sea en las formas, como en el material, o en el montaje, la inestabilidad aparece antes de lo que predice la teoría para formas perfectas y esto hay que compensarlo aplicando factores de reducción, empíricos o experimentales, que son función de las características geométricas del casco (diámetros, espesores, cuadernas, reforzados, etc.) y de los tipos y valores relativos de las imperfecciones mas corrientes que se pueden encontrar en estos recintos. 127 Los fenómenos de inestabilidad o pandeo se dan en el caso de barras, columnas o pilares sometidos a cargas de compresión, en su eje, (campo unidireccional), de anillos con carga radial uniformemente repartida por el exterior, en su plano, en las esferas sometidas a presión exterior, etc. Todos estos cuerpos o superficies trabajan a compresión pura hasta que llega un momento en que de se deforman (imperceptiblemente), aparecen momentos flectores y estos aceleran su deformación. Como se sabe, una barra o columna, si es muy larga y esbelta puede doblarse y “entrar en ruina” mucho antes de alcanzar una compresión sensible de su sección recta. Véase la teoría de Euler. Un Libro muy clásico que trata de estas cuestiones es el de “Theory of Elastic Stability”, de Timoshenko and Gere. En este libro se puede aprender todo lo relativo a la inestabilidad de barras, placas y superficies. En la Figura anexa muestra de forma gráfica lo que ocurre en la mayoría de los fenómenos de inestabilidad, de forma genérica. Cuando una forma apléxica se somete a carga progresiva, las deformaciones o corrimientos diferenciales normales a las superficies de las planchas que integran el casco, y que van destruyendo el aplexismo, crecen muy lentamente, de forma casi imperceptible, hasta que llega un momento en que se incrementan enormemente, incluso si se reduce la carga y no se ha alcanzado el limite de elasticidad en el material. Puesto que el peso de un puente, de una torre o la presión del mar, a una cota dada, son unas cargas constantes, esto significa que el movimiento de deformación va a ser acelerado. En el caso de recintos tridimensionales, esferas, cilindros, etc. ocurre una cosa similar, pudiéndose producir el colapso hacia el interior de forma inesperada, si nos atenemos a las bajas tensiones que puede estar soportando el material. Además el colapso se produce de una forma rápida, acelerada. Una solución elemental para prevenir estos 128 fenómenos es dotar a la estructura de unos amplios escantillones y una cuidada construcción, pero entonces el peso de la misma la puede rendir ineficaz, inútil para el objetivo propuesto, al comerse el peso del casco, exclusivamente, la flotabilidad disponible, que debe asimismo tener capacidad para soportar el peso de la propulsión, otros aparatos, la carga útil (o “payload”), etc. Con el objeto de minimizar el peso (y el coste, en cierta manera) de la estructura es necesario dotarla de espesores ajustados y por consiguiente hay que conocer bien las leyes por las que se rigen tanto las tensiones como la inestabilidad (el pandeo), fenómeno este ultimo que afecta a todos los componentes de la misma, en sus diversos modos. En la Figura nº 19, se presentan los principales modos o tipos de fallo del casco resistente de un sumergible, de forma gráfica. Casi todos son debidos a la inestabilidad estructural anteriormente mencionada. Esta Figura no incluye el fallo de las propias cuadernas por considerarse que este fallo es muy remoto, si estas se dimensionan de forma “armónica”, es decir guardando unas proporciones entre los espesores y las anchuras de los elementos que las integran y que se tratan a continuación, cuestión que es elemental, aunque su cálculo teórico encierre una gran dosis de cálculos matemáticos, (en torsión, pandeo lateral, etc.). Fallo de las cuadernas Las cuadernas son los refuerzos principales del casco y sirven como apoyo y sostén de las tracas del forro. Si las cuadernas fallan, se deforman, se tuercen o se alabean, el forro va a perder su apoyo en ellas, y se va a debilitar, va a ceder hacia dentro y esto podrá conducir a la ruptura total de la estructura. 129 De las formas de cuadernas representadas en la Fig. 4, de carácter general, la mejor es la compuesta por una simple T ya que las otras adolecen de varios defectos. La formada por una doble T, aunque soporta mejor el forro por ser mas ancha y equivale a reducir la clara efectiva, es bastante pesada; además queda una parte del forro que no es “visitable” (contacto forro con ala de la T). Si entra agua no puede ser detectada y puede dar lugar a una corrosión no controlable, no previsible, ni visible hasta que ya es muy tarde. Esto de la “visibilidad” del casco es una constante en todo el sumergible: El casco resistente, hasta el mas mínimo rincón, tiene que ser fácilmente observable e inspeccionable para asegurar que por una entrada de agua fortuita, que quede atrapada o por una corrosión imprevista no acaba debilitándose, perforándose o destruyéndose de forma inadvertida. Hay que tener en cuenta que el agua de mar es bastante corrosiva. Lo mismo pasa con las cuadernas tipo U o en cajón, que pueden almacenar agua. En las llantas con bulbo, muy utilizadas en los buques de superficie, el defecto principal es que su inercia lateral es relativamente pequeña y tienen gran tendencia a acostase sobre un lado, (“stiffener tripping”), bajo carga, lo cual es un inconveniente mayor; por esta causa suele usarse para depósitos pequeños, de poca responsabilidad, en sustitución de las simples pletinas. En algunos casos se ha instalado cuadernas formadas por barras macizas de acero, de sección rectangular, muy compactas, pero son bastante pesadas y su módulo resistente reducido en proporción a su peso, aunque fáciles de construir y muy poco o nada expuestas a problemas de inestabilidad internos. Las cuadernas formadas por una T (simétrica, las mas eficientes), con su alma soldada al casco, bien sean estas exteriores o interiores, independientemente de su tamaño (que está dictado por el modo de fallo denominado de pandeo general, “overall buckling”), deben mantener unas proporciones armónicas entre sus dos componentes (ala y alma) a efectos de que se mantengan con su forma y posición originales hasta que la carga en las mismas (de compresión) esté cercana, al menos, al límite de fluencia del material utilizado. Es evidente que si se diseñan muy robustas (gruesas), es decir se dotan de grandes espesores (en ala y alma), van a resistir mejor la inestabilidad que si son esbeltas y delgadas, pero el objetivo, como ya se apuntó antes, es hacerlas “justas” al objeto optimizar el uso del material, aunque esta optimización, en ciertos sumergibles sencillos, es casi innecesaria y hay que caminar por la senda de la sencillez y la robustez. Hay que tener en cuenta que las cuadernas son la base en la que se apoya la plancha de forro. Si esta base falla, todo falla. Los principales reglamentos dan unas normas respecto a las proporciones que deben guardar sus miembros que, teóricamente, varían un poco con las características mecánicas del acero o material estructural utilizado. Todo se centra en que la relación entre la anchura y el espesor (ratio denominado esbeltez) del ala y del alma deben estar dentro de unos límites máximos y que la anchura de la cuaderna (anchura total del ala) debe estar proporcionada a la altura de la misma. Como término medio (aceros de unos 32 a 55 hbar de límite de fluencia) se deben guardar estas proporciones básicas, como cifras indicativas, para que las cuadernas aguanten bien bajo carga: a) b) c) d) e) Almas (de T) : relación anchura/espesor : < 20 Alas (en T) : relación anchura/espesor : < 10 Espesor del ala > 1,2 del espesor de forro (optimización estructural) Espesor del ala mucho mayor que el espesor del alma (optimiz. de inercia) Relación ancho de ala/altura de la cuaderna : > 65 % (para que no se ladéen) 130 Estas relaciones anchura-espesor, o esbeltez, son función del factor 1 σ y por lo cual, cuanto mas alta es la tensión de fluencia el material utilizado, menor debe ser la esbeltez de los componentes, (almas y alas). Ello se comprende porque cuanto mayor es σy, mayor es la carga a la que se puede someter una cuaderna de unas proporciones dadas y debe ser capaz de resistir sin que se “descomponga”. Existen otras reglas adicionales, mas complejas, que están orientadas a evitar que las cuadernas se “acuesten” (“stiffener tripping”) hacia un lado bien a lo largo de todo su perímetro bien alternativamente, formando ondas, como un festón, o se desplacen uniformemente hacia un costado o hacia otro. Hay otros casos posibles, como puede ser el alabeo en ondas del ala exclusivamente, (en cuadernas con un alma muy gruesa y alas muy delgadas) pero es un caso remoto. Fallo por inestabilidad del forro entre cuaderna y cuaderna, (interframe buckling) En el caso general, se considera que la separación y el escantillonado de las cuadernas son uniformes y constantes, así como el espesor del forro. Para cascos con variaciones en estos parámetros hay que aplicar las fórmulas correspondientes, caso por caso. El escantillonado de las cuadernas afecta principalmente al cálculo de las tensiones en el forro y solo ligeramente al comportamiento del forro respecto a su inestabilidad local, entre cuadernas. Este fallo consiste en una serie de abolladuras alternadas en las tiras transversales o anillos del forro que existen entre cuaderna y cuaderna, dando lugar a que la estructura pierda su forma inicial, su rigidez y se destruya por colapso. Esta deformación, tan aparente, es solo teórica. En la realidad, las ondas no son tan marcadas ni tan uniformes, ni todas las chazas entre cuadernas sufren la deformación anterior. Se le denomina tambien “asymmetric buckling” o “lobar buckling”. Este fallo está normalmente asociado a la existencia de un forro de un espesor ligero combinado con una separación grande de las cuadernas (apoyos locales del mismo), por lo que una forma de combatirlo es aumentar el espesor del forro o/y reducir la clara entre las cuadernas. En este modo de pandeo solo se estudia una de las claras, como representativa del conjunto de las mismas, asumiendo que las restantes se comportan de un modo similar, si las cuadernas están uniformemente repartidas. En caso contrario hay que estudiar los diferentes tipos de clara que existan. Este modo de fallo es poco sensible a las imperfecciones geométricas normales, como puede ser la ovalización de las cuadernas y del forro, pero puede serlo cuando el espesor de las tracas que forman el anillo no es uniforme, las soldaduras de juntas (tracas) están 131 desniveladas, existen abolladuras locales o zonas de curvatura irregular en el forro. No obstante, no se dan exigencias particulares en este sentido que no sean las derivadas de las tolerancias orientadas a tener una buena y cuidada construcción. Las pruebas con modelos se suelen efectuar con cilindros con una ovalización máxima del 0,5 % del radio, más que nada para asegurar que no van a fallar por colapso en modo de inestabilidad general, que es muy sensible a la ovalización inicial, de construcción, con lo cual este tipo de pandeo no podría observarse netamente. Para calcular la presión a la que se produce este modo de fallo, denominado en inglés “interframe buckling”, existen varias fórmulas y procedimientos, aunque el mejor método es el que consiste en hallar y comparar dos parámetros adimensionales, cuya combinación determina la presión efectiva de colapso o de fallo, (dentro de la aproximación experimental relativa a este modo, es decir la dispersión de resultados que se puede obtener si se prueban una serie de cascos idénticos). Aunque todos los Reglamentos aplican unas reglas que son básicamente las mismas, derivadas del cálculo y de la experimentación, aplicaremos aquí los principios del Reglamento del American Bureau o Shipping. Underwater Vehicle Systems, and Hyperbaric Facilities, 1990. Metallic Pressure Boundaries Components, por ser uno de los más simples y compactos, en estas cuestiones. Estas mismas reglas han sido adoptadas por muchos otros Códigos, ya que parte de una base experimental muy amplia. Por un lado está la presión de “plastificación”, Py. Cuando la presión se incrementa hasta progresivamente, llega un momento en el que se crea un estado de tensiones tal que produce la plasticidad (“yielding”) en el medio de las claras (zona central entre dos cuadernas), a mitad del espesor de la plancha. Es decir, las tensiones de compresión en la plancha que forma el forro, rozan o superan el limite de fluencia del material empleado, en la dirección transversal, (circunferencial). Presión denominada Py. Esta presión es ideal, virtual, pues nunca se puede alcanzar, en la práctica, un estado de tensiones tan alto. Por un motivo u otro, el cilindro siempre colapsa antes de alcanzar la presión Py, ya que en este estado se puede considerar que el material se deforma con bastante facilidad, “como un chicle”, al reducirse drásticamente su módulo E, de elasticidad. El material se 132 agota. Es un concepto que se entiende bien, es un “aplastamiento” del material por exceso de la tensiones de compresión. Por otro lado está la presión crítica elástica de inestabilidad, (Pm), es decir la presión teórica a la cual la porción de forro comprendida entre dos cuadernas, se abollaría (pandearía) por inestabilidad estructural si el material fuese perfectamente elástico, es decir si el módulo E de elasticidad pudiese mantenerse indefinidamente constante, independientemente del nivel de tensiones alcanzado, incluso superando el limite de fluencia. Esta presión se denomina presión crítica “clásica” de inestabilidad o presión de Von Mises, y corresponde a la que tiene un cilindro liso relativamente corto (longitud similar a una clara entre cuadernas), simplemente apoyado en sus bordes y sometido a una presión uniforme exterior. La fórmula usada fue inicialmente obtenida por Von Mises y después simplificada por otros autores, entre ellos Windenburg-Trilling, del antiguo David Taylor Model Bassin (DTMB) norteamericano. Es una formula adoptada mundialmente por su sencillez y su relativa buena precisión, en cilindros cortos similares a los que existen en estos sumergibles (entre dos cuadernas) y es la siguiente (para el acero, ν = 0,3): t 0,919 ⋅ E ⋅ ( ) 2 R Pm = L − 0,636 R⋅t Siendo: R el radio del anillo, (medio o exterior) L la distancia entre cuadernas t el espesor de forro (plancha). Obsérvese que en esta fórmula solamente intervienen las características geométricas del anillo y no incluye las características mecánicas de material utilizado, salvo su módulo de elasticidad, E, que se considera constante e invariable. Esta fórmula es válida para los campos: 5,9 < R/t < 250 y 0,04 < L/R < 50, Las medidas normales, típicas en un sumergible o submarino, están dentro de estos límites, con un R/t cercano a 60 -100 y un L/R del orden de 0,1 a 0,3 Par aumentar el valor de Pm, de la formula, para un radio constante, basta aumentar el espesor, t, o disminuir L (la clara) o ambas cosas a la vez, lo cual es coherente con los resultados experimentales. Esta presión es totalmente teórica. Por otro lado está la presión experimental mínima de colapso (Pc) o de destrucción, que es la presión (en este modo de fallo) que se necesita conocer, para el anillo en cuestión. El valor de Pc, se obtiene aplicando una regresión. Es un valor estadístico. Con Py, Pm y Pc se forman los parámetros adimensionales (Pm / Pv) y (Pc / Py), los cuales están interrelacionados por las función representada por la curva de la Figura anterior, lo que permite el cálculo de Pc, o presión de colapso mínima experimental (o presión de destrucción calculada). La curva siguiente representa el umbral inferior del parámetro Pc/Py en función de Pm/Py. Esta curva se ha obtenido a base de analizar y correlacionar cientos de pruebas de presión realizadas sobre modelos de cilindros, tomando los valores más desfavorables, es 133 decir los mas bajos, (“lower bound”), por lo que goza de bastante fiabilidad a efectos de diseño. RESISTENCIA DEL CASCO ENTRE CUADERNA Y CUADERNA 1,000 0,900 0,800 0,700 Pc / Py 0,600 0,500 0,400 0,300 0,200 0,100 0,000 0 0,5 1 1,5 2 2,5 3 3,5 4 4,5 5 Pm / Py Esta curva viene a indicar que, tomando como referencia el valor Py, (presión de plastificación), cuando Pm es mucho mas alto que Py, el cilindro es muy estable y la presión de colapso se acerca mucho a la de fallo por plastificación pura, que es la forma convencional de rotura de una estructura. La curva tiene una asíntota horizontal a partir de (Pm/Py)=3, con un Pc=0,833*Py, constante, o sea que no se obtienen ganancias apreciables en la presión de destrucción cuando se pasa de (Pm/Py) =3, para Py = Cte. Para valores de (Pm/Py) del orden de 1, ver curva, la presión de colapso experimental es del orden de solo 0,5*Py, lo que indica que el pandeo por inestabilidad es el que gobierna y la presión de destrucción experimental anda por valores cercanos al 50% de Py . Para valores intermedios de (Pm/Py), p.e. (Pm/Py) del orden de 2, la presión de colapso calculada es de Pc= 0,75* Py. Es un caso corriente. Según esta formulación, por muy grande que sea Pm, con respecto a Py, la presión calculada de colapso nunca supera el 83% de Py. En otras formulaciones se admiten unos valores un poco más altos, cuando el parámetro (Pm/Py), es superior a 3. En general, en las construcciones más recientes, el valor de (Pm/Py) está comprendido entre 2 y 2,5, lo que significa una Pc del orden 75-80 % de Py. Siguiendo el ABS, al valor obtenido de Pc se le aplica un factor reductor (η) de 0,8 para convertirlo en la presión máxima (admisible) de servicio (Pa) del casco o del anillo en cuestión, con objeto de evitar o prevenir el colapso en este modo (exclusivamente), lo que equivalente, a aplicar un factor de seguridad de F.S.= 1,25, lo que parece ciertamente poco sobre todo en los minisubs de baja cota, ya que el valor absoluto de la subreinmersión aceptable es muy escaso. Por ejemplo, en un sumergible de 50 m de cota de servicio, la cota de colapso calculada en este modo sería de unos 50*1,25 = 62,5 m, (12,5 metros mas que la máxima admisible) lo cual significa que si el piloto del sumergible se excede un poco en la inmersión, se despista, o los indicadores tienen algún error, se entra rápidamente en una zona de alto riesgo. 134 Fallo por pandeo en compresión axial, (axial buckling) Puesto que los domos de extremos de un casco cilíndrico lo comprimen axialmente, puede ocurrir que el forro se arrugue, en forma de ondas, de un modo parecido a lo que ocurre en el pandeo entre cuadernas. El casco se contrae axialmente y se forman unos hoyos entre cuaderna y cuaderna. Si esto ocurre a tensiones por debajo de la tensión de fluencia, es debido a una inestabilidad estructural. Es normal que suceda en cilindros de una pared muy fina respecto a su diámetro. Algunos reglamentos lo denominan “symmetric buckling” para distinguirlo del pandeo entre cuadernas. Es un pandeo cuyas deformaciones tienden a estar alrededor de un eje de revolución. 2 ⋅E ⋅ t2 La ecuación que gobierna es la formula clásica: Pcr = 3 ⋅ (1 − ν 2 ) ⋅ R 2 siendo Pcr la presión crítica de compresión, aplicada en los domos o mamparos extremos. De la ley de cilindros se deduce que la tensión crítica longitudinal será σcr = Pcr·R/2·t En conclusión, para ν=0,3, acero, la tensión crítica elástica (teórica) vale: σ cr = 0,605 ⋅ E ⋅ t / R Que es similar a la correspondiente al pandeo entre cuadernas, deducida según la teoría clásica, pero con la particularidad de que le numero de ondas es diferente, así como su constitución. Esta tensión crítica hay que corregirla para obtener la tensión práctica o experimental de colapso. Esta corrección es función de un parámetro, Z, denominado de Batdorf que es función, para cilindros simples, de su longitud, del radio y del espesor. Este modo de inestabilidad apenas se da en cilindros dotados de cuadernas, proyectados para soportar una presión exterior, pero hay que comprobarlo. Fallo por inestabilidad general, (overall buckling) Este tipo de fallo corresponde al fallo conjunto de un tramo largo de casco compuesto por un forro cilíndrico dotado de sus respectivas cuadernas, limitado por unos mamparos planos o curvos, domos. Cuando el casco dispone de cuadernas muy fuertes (“deep frames”) o mamparos intermedios, hay que verificar cada tramo de casco comprendido entre estos elementos fuertes, por separado. La longitud (Lc) que se usa para cálculo es la distancia entre dos apoyos fuertes contiguos. La deformación correspondiente que esta inestabilidad provoca es una ovalización general del cilindro (y sus cuadernas), que se extiende entre mamparo y mamparo (o apoyo y apoyo (*)), progresiva, lo cual provoca la ruina del conjunto por aplastamiento. (*) Se tiene la hipótesis de que los mamparos o apoyos son muy fuertes y se mantienen perfectamente circulares. Se habla en términos genéricos de mamparos de apoyo de los extremos del cilindro reforzado estudiado pero bien pudieran ser cuadernas reforzadas de las convenientes características, situadas en los extremos o puntos intermedios del cilindro en cuestión. En el caso de domos, para el cálculo de la inestabilidad, el borde de conexión de los mismos no es el límite de la longitud de calculo (Lc) sino que incluye además un 40% de la altura (h) del domo. O sea, en el caso de dos domos, uno en cada extremo de un cilindro, la longitud efectiva de cálculo no es la longitud del cilindro sino esta mas el 40% de la altura de un domo mas el 40% de la altura del otro. 135 Algunos mamparos planos pueden permitir un desplazamiento axial diferencial, entre una posición angular y otra, lo que es perjudicial para el colapso general, pero ya se cuenta con ello. Según sea la longitud del cilindro reforzado (o la distancia efectiva entre mamparos) se producirán “ovalizaciones” de dos ondas (elipse, las mas corrientes, en cilindros largos) o más ondas (figuras onduladas en forma de estrella), en cilindros “cortos”. Esta inestabilidad se achaca a la debilidad de las cuadernas y, en segundo término, a una separación excesiva de los mamparos, por lo que unas cuadernas numerosas y fuertes, junto con una separación pequeña o moderada de los mamparos, retrasan o evitan este modo de pandeo. En general, reducir la distancia entre mamparos o la distancia entre cuadernas es poco práctico, por lo que, para aumentar la resistencia frente a este tipo de fallo lo que normalmente se hace es incrementar la sección recta de las cuadernas o introducir bulárcamas intermedias (“deep frames”). Gran parte de los cascos cilíndricos construidos tienden a fallar según este modo, por lo cual hay que prestarle un particular atención. En teoría, en cilindros matemáticamente circulares, o en cuadernas, este fallo se puede producir, si la presión es lo suficientemente alta. Existe una presión o una fuerza radial crítica elástica. Este comportamiento deriva del concepto de inestabilidad estructural. Es un hecho físico, demostrado matemáticamente. Además, incluso con cuadernas de un alto escantillón se produce la rotura general del anillo, por aplastamiento, cuando existe una ovalización inicial, en las mismas, más o menos pronunciada. Esta rotura deriva de la existencia de unos momentos flectores muy grandes en las cuadernas, que provocan que estas se plieguen, como lo haría un anillo de goma o plástico cuando se aprieta, con los dedos, en dos puntos diametralmente opuestos. Es un concepto de rotura corriente, como ocurre en vigas o pórticos sobrecargados por momentos flectores, etc. Es evidente que para reducir este último modo de rotura es conveniente tener la máxima circularidad posible, pero en la práctica siempre existe una cierta ovalización inicial (por inexactitudes de construcción, contracción de las soldaduras, etc.). Como estos dos efectos (inestabilidad pura y ovalización progresiva en carga) existen simultáneamente, y producen efectos similares, hay que combinarlos para poder sacar alguna ley de rotura, en este modo, que sea útil, aplicable y mas o menos precisa. Después de algunos intentos, se ha conseguido obtener una inter-relación entre la presión crítica elástica de pandeo general relativa a un cilindro reforzado teóricamente perfecto, la ovalización que el anillo reforzado tiene debido a las inevitables imperfecciones de su construcción, y la presión real o experimental de colapso. La fórmula clásica que determina la presión de pandeo general (en régimen elástico), de un cilindro relativamente largo, provisto de cuadernas regularmente espaciadas es la siguiente: E ⋅ Icomb P1 = (n 2 − 1) ∗ R 3 ⋅ L1 Siendo n nº entero = nº de ondas que se forman en el colapso (n=2 para la forma oval), E el módulo de elasticidad del material utilizado, I comb la inercia combinada de las cuadernas mas su ancho asociado de plancha, R el radio del cilindro en cuestión, L1 la clara de cuadernas (supuesta constante a lo largo del cilindro). 136 Como P1 es función de (n2-1), cuanto mayor es el valor de n (n =2, 3, 4, ....), mucho mayor es el valor de P1. En la fórmula anterior, el cilindro se idealiza como un simple anillo corto, compuesto por una cuaderna mas una clara (longitud L1) de forro (cuaderna tipo, con una semi-clara a cada lado de la cuaderna) y se aplica la formula de los anillos compactos. El cilindro total estaría compuesto por la suma de numerosos anillos simples, independientes, dispuestos en línea, que se moverían de la misma forma, sincronizados. Esta formula ha sido derivada de la inicialmente propuesta por Fölpp, a principios del siglo XX, para simples anillos de sección compacta, circular o rectangular, la cual fue ajustada y ligeramente modificada por diversos autores (Bress, Von Sanden, etc), para poder usarla con secciones similares a las utilizadas en submarinos, (cuadernas mas forro). Un punto conflictivo que presenta es la determinación precisa de la inercia combinada, ya que el ancho (efectivo) asociado de plancha ha sido difícil de determinar con exactitud. 137 Históricamente, se le han asignado valores convencionales, similares a los que se usan en la construcción naval, ancho igual a 30 espesores de plancha, etc. Además, se ha demostrado que el ancho efectivo puede tomar diversos valores, en función del número de ondas que se forman en la iniciación del colapso, (Biljaard y otros). Un valor muy convencional y bastante aproximado es L ef = 1,55· R·t , que corresponde a una flexión en una sola onda, o sea, una flexión convencional. Los valores mas corrientes que se toman, en la práctica, si no se quiere recurrir a fórmulas mas complejas y avanzadas, ya que las diferencias son despreciables, oscilan entre L ef = 1,4· R·t y L ef = 1,55· R·t , para “n” entre dos y cuatro, aunque Lef, puede ser bastante menor si el número de ondas criticas es muy alto, pero esto solo ocurre en casos muy teóricos. Lef suele ser inferior a la clara real (L1). Si no lo fuese, es la clara real la que hay que tomar como ancho efectivo, para que no se solapen estos anchos en dos claras contiguas. Incluso hay algunos reglamentos que limitan la Lef máxima al 75% de la clara. La formula anterior, que define la presión de colapso, elástica, P1, es imperfecta, en los cilindros finitos, reales, ya que considera que todas las secciones del cilindro estudiado, compuesto por una infinidad de anillos individuales, elementales, independientes, de longitud unitaria igual a la clara L1, puestos unos a continuación de los otros, se deforman de la misma forma, a todo el largo, cuando no es así. Cuando existen mamparos moderadamente separados o muy juntos, esta hipótesis no es cierta, ya que las secciones intermedias, alejadas de los mamparos, pueden ceder mas (son mas libres para tomar una ovalización) que las que están en las inmediaciones de los mismos. Estos se mantienen circulares y obligan a las cuadernas contiguas a mantenerse quasi-circulares. En consecuencia, durante el pandeo, el forro, que adquiere una configuración oval progresiva hacia el centro del cilindro, como se observa en la Figura anterior. Es similar a lo que ocurre si tomamos una lata cilíndrica de refresco o de cerveza y la apretamos por el centro con los dedos: los extremos, la tapa y el fondo, se mantienen casi circulares y por el centro la lata se chafa, se aplasta un poco. Eso es lógico y fácilmente observable cuando estos cilindros se someten a una prueba de presión en tanque. 138 La forma en que se ovalizan los cilindros reforzados sometidos a presión exterior, supuestamente progresiva desde los extremos del anillo hacia el centro, ha sido objeto de variadas interpretaciones, sobre todo el asunto de si la ovalización, a partir de los mamparos, es realmente progresiva o no, o que ley de progresividad existe, lo cual podría influir sensiblemente en los resultados teóricos a obtener y a verificar. El forro, arrastrado por las cuadernas, absorbe una energía (se generan unas fuerzas cortantes en el plano de la plancha) que impide, en cierto grado, que el anillo se ovalice con tanta facilidad como cuando los anillos elementales eran totalmente independientes. Se ha verificado teóricamente (S. Kendrick y otros investigadores) que cuando el cilindro es muy largo, la contribución del forro a la energía requerida para su deformación (ovalización) es muy pequeña, por lo cual la formula anterior (de P1) es bastante exacta pero cuando la separación entre apoyos (mamparos) es pequeña los errores son sensibles, y las presiones críticas deducidas por la fórmula, muy inferiores a las reales. En conclusión, ha habido que modificar la formula de los anillos simples para incluir la contribución ofrecida por el forro y así estar mas cercanos a los resultados experimentales. El perfeccionamiento de la formula (a veces no todos los fenómenos se pueden resumir en una fórmula sencilla) se ha conseguido, a base de numerosos estudios teóricos, y al final se ha obtenido una resultado bastante aproximado al real añadiéndole un término adicional a la fórmula inicial (P1), y que representa la “reactancia” del forro a ser deformado. Se computa este término como un incremento de la presión crítica, sobre el valor P1, o valor asignado a la cuaderna tipo o cuaderna base. En resumen, la formula que permite calcular la presión crítica de pandeo general, (en régimen elástico), debida finalmente a Bryant, se compone de dos términos y es la siguiente: PBryant = Pn = P1 + P2 Siendo P1 la presión crítica elástica de un anillo elemental (anteriormente presentada) y P2 = E⋅t R 2 2 (n − 1 + λ 2) ∗ (n 2 λ2 + 1) 2 Siendo λ = π ·R / L2 L2 = la distancia entre mamparos (o longitud efectiva del compartimento) Hay que probar con diversos valores de n, ascendentes, (n= 2, 3, 4, etc.) y comprobar cual minimiza la expresión de Pn, lo que permite hallar la presión crítica a la que el cilindro falla por inestabilidad general, (en régimen elástico), así como el número de ondas con que se produce el colapso. Como puede observarse, cuando el valor de n (nº de ondas) aumenta, el primer término debido a la cuaderna más área asociada de foro, (P1) crece rápidamente mientras que el término de forro disminuye. Asimismo, cuando L2 es muy grande, el término P2 se hace muy pequeño. Esta fórmula está considerada de una precisión bastante buena para el cálculo de la presión de pandeo elástico (teórico) de cilindros provistos de cuadernas totalmente circulares, sin imperfecciones en el material, sin tensiones internas, sometidos a una presión uniforme exterior y bajo la hipótesis de una elasticidad perfecta, es decir el modulo de Young, E, se mantiene constante, independientemente de la tensión alcanzada cuando el cilindro se le somete a la presión exterior Pn. 139 Como no intervienen las tensiones que se generan en el cilindro y cuadernas durante la carga progresiva, hasta llegar a Pn, podría ocurrir que antes de llegar a esta presión las tensiones fuesen tan altas que el cilindro rompiese por tensiones, (plastificación general), y entonces nunca se sabría si la formula es correcta, experimentalmente hablando, o no. Habría que introducirle unos factores de corrección para que fuese aplicable en el campo inelástico, o semi-plástico, como ocurre en le caso de barras o columnas sometidas a compresión. Existen algunas teorías la respecto, más o menos acertadas. Dentro de que es una fórmula de pandeo o inestabilidad en el campo elástico puro, se la ha aceptado universalmente como una formula de referencia. El Reglamento ABS utiliza una fórmula semejante, para Pn, que, en el fondo es la misma, presentada de otra forma. El ABS, para pasar de Pn (presión critica de colapso en régimen elástico) a la presión máxima de servicio (Pa) aplica un factor corrector (η) de 0,5, lo que representa un factor de seguridad, sobre la máxima operativa, de F.S.=2. Se estipula una ovalización máxima del 0,5% del radio,(*). COLAPSO POR PANDEO GENERAL (Iniciación, 2 ondas) (*) La ovalización está definida como la máxima desviación de cualquiera de los puntos de la forma real de una cuaderna respecto a una circunferencia de radio igual a su radio medio (supuestamente muy cercano a R, o radio nominal, teórico). Esta desviación se mide en el sentido radial. Cuando la cuaderna tiene forma de ovalo, o elipse, (n=2) esta ovalización es equivalente a la diferencia de las dimensiones de los dos ejes (mayor y menor, que hay que identificar sobre el trazado de la cuaderna) dividida por 4. Cuando el numero de ondas esperado en el colapso es mayor que 2, hay que hacer lo mismo, pero comparando la forma con la figura estrellada correspondiente (n=3, estrella de tres puntas, etc). El asunto es complejo ya que lo que interesa es la ovalización del anillo completo, compuesto de numerosas cuadernas. Si estas tienen sus correspondientes ovalizaciones orientadas en el mismo sentido, la ovalización general es de un valor medio de estas, pero si las orientaciones son fortuitas, el valor resultante es poco indicativo o fiable (puede ser cero), siendo las más representativas o críticas las situadas en el centro del anillo, que es donde mas deforma el anillo en caso de pandeo. Hay que aclarar que la deformación “de pandeo” que se cita, ovalización creciente, etc. es solo de iniciación, de arranque. Una vez arrancado el movimiento, traspasado un umbral, el colapso es sumamente acelerado y es inútil de hablar de ovalizaciones progresivas. 140 Esta fórmula ofrece una aproximación bastante buena de la presión de colapso, pero en cilindros “teóricamente” perfectos, como ya se indicó. Para pasar a cilindros “reales” hay que considerar las imperfecciones con cierto detalle, tales como las ovalizaciones iniciales, el carácter lineal de la presión hidrostática, etc. por lo que hay que perfeccionar aún mas este cálculo. Como se parte de la hipótesis cierta de que la ovalización de las cuadernas (ovalización inicial mas la ovalización progresiva, en carga) es la que desencadena este modo de pandeo, este perfeccionamiento se obtiene mediante la limitación de las tensiones máximas en las alas de las cuadernas. Las cuadernas, ya ligeramente ovalizadas, en su estado inicial, sin carga, por motivos de su construcción (es prácticamente imposible construir cuadernas completamente circulares, o estas se deforman durante el montaje), están sujetas, desde el mismo momento en que el sumergible hace inmersión, a unos momentos flectores en su plano, que pueden ser importantes, que progresan con la inmersión, muy despacio hasta que la compresión en las alas (suma de la tensión circular “normal” y la proveniente de los momentos), en ciertos puntos, es excesivamente alta y la resistencia mecánica del material se agota, produciéndose una ovalización rápida que produce un plegado en su plano, es decir la forma de elipse inicial va a pronunciarse fuertemente hasta aplastarse rápida y totalmente. Una serie de estudios han permitido calcular las tensiones combinadas en el ala de las cuadernas a efectos de determinar este modo de fallo con más precisión, o completar la información ofrecida por Pn acerca de la presión crítica de colapso general, cuando se tiene en cuenta ya cualquier tipo de ovalización inicial de las mismas (supuestamente, las ovalizaciones de las cuadernas están todas orientadas en la misma dirección radial). Si Pt, es la presión que produce la fluencia del ala de las cuadernas (o sea la ruina del casco completo), debe satisfacer la expresión siguiente: σy = Pt ⋅ σ y E ⋅ c ⋅ δ ⋅ (n 2 − 1) ⋅ Pt + Pyf (Pn − Pt ) ⋅ R 2 Siendo como siempre: σy la tensión de fluencia del material utilizado, R el radio medio del cilindro en cuestión, E el modulo de Young, y n el numero de ondas crítico obtenido en el pandeo, y Pn la presión crítica de Bryant correspondiente, ya vista, y : c : la distancia desde el eje neutro de la sección combinada de cuaderna mas forro efectivo hasta la fibra mas alejada del ala de la cuaderna (cara interior de la cuaderna en el caso de cuadernas interiores, o la mas exterior en el caso de cuaderna exteriores). Ver croquis de la cuaderna tipo. El eje neutro se define como la recta que, paralela al eje del cilindro, pasa por el centro de gravedad de la sección recta de la cuaderna más su ancho efectivo de forro. δ : es la ovalización máxima admisible, del 0,5 % del radio del cilindro, o 0,005 R. Pyf : es la presión que produce la fluencia en la platabanda o ala de las cuadernas, supuestas estas totalmente circulares, y que vale: Pyf = σy ⋅ t ⋅ Rf 2 R ⋅ (1 − (ν / 2) − γ ) Siendo 141 Rf : radio de la cuadernas, medido en la fibra mas alejada del forro (o sea: radio de la cara interior del ala de las cuadernas, cuando estas son interiores). γ : parámetro de tensiones, formula compleja, según se define en el Reglamento ABS, que se obtiene de la ecuación de la deformación de una clara-tipo. Se ha conseguido aunar en una sola expresión los dos conceptos que provocan el fallo del cilindro reforzado: la presión crítica de inestabilidad (Pn) y la ovalización inicial, definida por δ. El primer término de esta fórmula, se refiere a la compresión que soporta el ala de la cuaderna debido a la presión exterior (supuesta uniforme) y el segundo a la componente adicional debida a la flexión producida por la ovalización inicial mas la autogenerada (es decir una mayor compresión crea una mayor flexión que supone una mayor ovalización y así sucesivamente, fenómeno no lineal), en el número de ondas considerado. Obsérvese que Pt es, en resumen, la presión a la cual las cuadernas (y de paso todo el casco) entrarían en ruina, por plastificación en un anillo que tiene una presión critica elástica de valor Pn, basándonos en su ovalización inicial, con lo cual puenteamos el problema de encontrar una formula de inestabilidad pura en el campo inelástico. A la presión de colapso obtenida, Pt, se le aplica un coeficiente reductor de η =0,5 para obtener la presión máxima admisible, o presión máxima de servicio Pa, referente al comportamiento del forro-cuadernas, asumiendo una ovalización inicial nominal, frente a la inestabilidad general del anillo. Fallo del forro por plastificación (shell yielding) Es el tipo fallo más elemental y convencional, y es debido a un estado general o local de tensiones muy alto, cercano al límite de fluencia del material. Es un caso de rotura similar al que le ocurriría a una viga apoyada en sus extremos con carga lateral, cuando esta se incrementa hasta valores muy altos. Si la estructura está razonablemente bien dimensionada, y no se destruye por inestabilidad prematuramente, cuando se va aumentando la presión exterior, las tensiones se van incrementando progresivamente hasta un límite en que se alcanza la tensión de fluencia en algunos puntos o áreas, que se van extendiendo, hasta que la estructura entra en ruina al ser incapaz de auto sustentarse. La forma teórica que adquiere el cilindro en este modo de fallo es de una especie de acordeón, apretándose las cuadernas unas con otras hasta formar una especie fuelle. Este fallo es difícil de visualizar en las pruebas con modelos, ya que cuando se alcanza el límite de fluencia en ciertas partes de la estructura del forro, los otros modos de fallo, de inestabilidad, comienzan a tener efecto (debido a la reducción drástica del modulo de Young, E, que es el que determina la tensión crítica, en los pandeos), mezclándose con el de plastificación pura, obteniéndose formas de fallo o destrucción que corresponden mas bien a estos últimos modos de inestabilidad. Hay que puntualizar que en las figuras presentadas solo se indican los modos incipientes de fallo, es decir la deformación inicial y preliminar que se produce y que finalmente es la que determina el fallo total de la estructura. En un tanque de pruebas esta deformación incipiente queda paralizada al cancelarse la presión, con el fin de que anillo que se analiza no se destruya total y brutalmente. Al hacerse las pruebas en un tanque de presión, con caudal de agua bajo control, en cuanto se nota una alteración de las condiciones (bien con galgas extensiométricas o bien con sensores muy precisos de deformación), la prueba se para, es decir, la presión se cancela. Al ser el agua incompresible y de un 142 volumen controlado, cuando el cilindro tiende a aplastarse, la presión se reduce a cero, por lo que se puede apreciar visualmente la deformación incipiente del mismo. En el mar, al ser la masa de agua disponible ilimitada la presión exterior se mantiene durante todo el “recorrido” de aplastamiento, por lo cual el movimiento de deformación es acelerado y brutal, y no habría forma de determinar, con certeza qué tipo de fallo ocurrió o como comenzó a destruirse el cilindro. 5.6.- Esferas y domos. Modos de fallo Los modos de fallo más corrientes en estos domos, que no llevan refuerzos, son abolladuras locales, como le ocurre a un balón casi desinflado. Estas abolladuras, al incrementar enormemente las tensiones en las planchas que forman las esferas o los domos, provocan el colapso repentino de las mismas hacia el interior (o implosión). La forma más directa de prevenir este tipo de colapso es dotar a estas estructuras, como primera medida, de los espesores necesarios y como segunda realizar una construcción muy esmerada, verificando que mantiene una gran esfericidad y que no hay zonas con falta de curvatura, ya que las esferas son muy sensibles a las imperfecciones. Hay numerosos estudios al respecto, (Budiansky, Weinitschke, Bushnell, Wang, Huang, etc.) Estos domos, sobre todo en la proa, a veces, deben estar atravesados por numerosas perforaciones, entre ellas en los submarinos militares, las de los tubos lanzatorpedos, las bombas de impulsión, etc. y, en los de recreo, por portillos y ventanas, de un diámetro considerable, que modifican grandemente el estado inicial de tensiones, y crean puntos de concentración de esfuerzos, que merecen unos estudios particulares. La teoría que liga las imperfecciones en las formas (faltas de esfericidad) y la presiones de colapso correspondientes es bastante compleja, y ha habido que recurrir a numerosas pruebas y experimentos, para poder sacar conclusiones razonablemente fiables. La dificultad principal es que las potenciales irregularidades geométricas que expresan una falta de esfericidad son extremadamente numerosas. 143 Ejemplo de fallo por inestabilidad de un domo esférico, construido en metacrilato. Se puede observar, en el grafico anterior, un caso típico, que la presión de colapso baja de 22 MPa a 17,7 MPa, al pasar la imperfección inicial de 10 mm a 16,5 mm. Y todavía habría mas contraste si se pasase de 5 a 10 mm. 144 5.7.- Otros modos de fallo Por concentración de tensiones Uno de los modos de fallo mas corrientes, y que no tiene relación alguna con la inestabilidad estructural, es el fallo por concentración de tensiones, que acaba manifestándose mediante grietas y fisuras mas o menos profundas en el casco, lo que generalmente se traduce en humedades, goteos, entradas de agua y que, si se abandona su reparación inmediata, y las fisuras se propagan, se pueden convertir en verdaderas y potentes vías de agua. Afortunadamente, el casco de un sumergible está sometido a compresión y las grietas que se forman tienden a comprimirse por lo que las fugas se ven relativamente impedidas. Si el caso fuese el opuesto estas grietas serían un asunto mucho mas grave. La concentración de tensiones puede estar asociada, como ya se ha mencionado, a los orificios y penetraciones efectuadas sobre el casco. Con su compensación se reducen, en cierto modo, sus efectos perniciosos sobre las tensiones. En otros casos la concentración de tensiones está asociada a la combinación y contacto de una estructura muy elástica, cargada y descargada, más o menos frecuentemente, con una estructura muy rígida, poco deformable. Tal es el caso de unión de los polines de maquinas importantes, muy robustos, con partes del forro del submarino, o de tanques estructurales y el forro. Las planchas de forro y cuadernas que forman los anillos del casco, al contraer y dilatar estos, a causa de los cambios de inmersión del sumergible, están expuestas a movimientos relativos respecto a algunas estructura interiores, que estando rígidamente unidas a ellos son obligadas a moverse también, lo cual produce una concentración puntual o localizada de tensiones, originada por la incompatibilidad de los movimientos absolutos de ambas estructuras. El concepto mas elemental es que unas estructuras se “clavan” en las otras, de forma periódica, sometiendo a las piezas de contacto o de unión a tensiones mas altas de lo previsto y conveniente. Por este motivo, una de las ocupaciones que el proyectista debe tener es analizar los diversos detalles constructivos y determinar como interactúan las diversas estructuras que componen una zona del buque, de modo que las contracciones del casco no se vean impedidas por elementos muy rígidos que actúen como “punzonadores” o “puntos duros” del mismo. El casco resistente tiene siempre que estar libre para moverse, debe poder “respirar”, contraerse y dilatar, sin impedimentos. Puesto que hay que instalar equipos interiores o exteriores lo cuales deben ir soportados de alguna manera en el casco, hay que procurar que su peso y los esfuerzos que desarrollan, descansen prioritariamente sobre las cuadernas, en un montaje que reparta dichos esfuerzos, y no directamente sobre las planchas del forro, y además han de hacerlo de forma que dejen la máxima libertad de movimiento a dichas cuadernas. Problema, a veces, irresoluble, por lo cual siempre hay fenómenos de concentración de esfuerzos en los cascos de los sumergibles. 145 Sujetar cargas importantes o soportar aparatos pesados directamente sobre el forro (mediante soldaduras, etc.) es una práctica desaconsejable, ya que el foro no está pensado (dimensionado) para soportar cargas que no sean las propias de la compresión hidrostática. Asimismo, la instalación de quillas interiores o travesaños longitudinales entre las cuadernas puede generar efectos de concentración de esfuerzos en el material. El casco contrae longitudinalmente, las cuadernas se acercan entre si, y si una barra o quilla se instala sobre las cuadernas (sobre sus alas) en dirección longitudinal, las cuadernas van a estar sometidas a unas fuerza alternadas, intentando inclinarlas hacia un lado y hacia otro. Las almas de las cuadernas, bastante delgadas, no están pensadas para este esfuerzo y, eventualmente, se puede producir una agrietamiento en la soldadura del pié de las mismas, la que las une al forro. Un método muy utilizado para independizar los soportes de los equipos del casco es montarlos sobre elementos flexibles, tacos elásticos, etc. siendo estos lo que absorben los movimientos diferenciales entre el casco y los soportes, pero, aparte de incrementar el coste, estos montajes exigen mas espacio. Por fatiga Como ya se ha apuntado, una concentración de esfuerzos o tensiones, combinada con movimientos cíclicos de los componentes sujetos a la misma, puede producir a medio o largo plazo fisuras o agrietamientos por fatiga, en función del nivel de tensiones y el número de ciclos. En general, las tensiones máximas a las que está sometido el material (acero principalmente), siguiendo las formulaciones que figuran en los diversos reglamentos de diseño y construcción de estos aparatos, solo darán lugar a fenómenos de fatiga, con los aceros autorizados por los reglamentos, a un numero elevado de ciclos (>30000), entendiéndose como ciclo una maniobra de inmersión hasta la máxima profundidad operativa seguida de otra de emersión. En la mayoría de los casos no se superan los 10 o 12000 ciclos, por lo que no hay que temer un alto índice de fatiga del material. Aceros hay de muchos tipos, unos mas sensible a la fatiga que otros, pero en términos generales, cuanto mayor es el limite de elasticidad de un acero, menor es su resistencia a la fatiga, ya que las tensiones a las que se le somete serán mas altas, en proporción a su carga de rotura. Hay curvas o fórmulas que, para cada acero, relacionan el campo de tensiones alternadas al que está sometido y el número aproximado de ciclos que puede soportar. Son curvas decrecientes con el número de ciclos. O sea, cuanto mayor sea el número de ciclos que se esperan tener, en un material muy cargado, el nivel de carga alternada que puede soportar es menor. Se suelen denominar curvas S-N. Estas curvas se obtienen a través de una serie de ensayos donde una probeta del material se somete a tensiones cíclicas con una amplitud máxima relativamente grande (aprox. 2/3 de la resistencia de tracción). Se cuentan los ciclos hasta rotura. Este procedimiento se repite en otras probetas a amplitudes máximas decrecientes. 146 La rotura por fatiga tiene aspecto frágil aun en metales dúctiles, puesto que no hay apenas deformación plástica asociada a la rotura. El proceso consiste en un inicio, y posterior propagación, de fisuras. La superficie de fractura es perpendicular a la dirección del esfuerzo. Los resultados se representan en un diagrama de tensión, S, frente al logaritmo del número N, de ciclos, hasta la rotura para cada una de las probetas. Los valores de S se toman normalmente como amplitudes de la tensión σa. A mayor tensión, menor número de ciclos hasta rotura. En algunas aleaciones férreas y en aleaciones de titanio, la curva S-N se hace horizontal para valores grandes de N, es decir, existe una tensión límite, denominada límite de fatiga, por debajo del cual la rotura por fatiga no ocurrirá, por muy altos que sea el nº de los ciclos. Los coeficientes de seguridad que se aplican tienen en cuenta, a veces, esta tensión límite. Solamente en el caso de un vehiculo utilizando materiales muy avanzados o con formas muy atípicas es preciso hacer un estudio de fatiga. No obstante el esfuerzo excesivo siempre existe, en un mayor o menor grado, en ciertas zonas localizadas, debido a que su diseño, es difícil de perfeccionar y resultan indefectiblemente sobrecargadas. Tal es el caso de las zonas de contacto de un anillo cilíndrico y un mamparo resistente plano, ya sea de extremidad o intermedio. El forro contrae radialmente, bajo presión mientras que el mamparo (disco de acero muy reforzado) apenas lo hace. Los tramos de forro cercanos al mamparo deben deformarse excesivamente para poder mantener la continuidad física con el mamparo y, consecuentemente deben soportar unas tensiones superiores a las medias, que incluso superan el límite de fluencia. Reducirlas es prácticamente imposible, aunque se instalen fajas, espesores crecientes, etc. por lo que el problema de fatiga subsiste. Por ese motivo la aparición de grietas o fisuras producidas por la fatiga nunca se puede descartar y hay que estar atentos a las mismas durante toda la vida útil del buque, principalmente cuando ya tiene un gran número de años de servicio. Los coeficientes de seguridad que se aplican, relativos a las tensiones (del orden de 1,75 a 1,95, respecto a la tensión de fluencia), para cotas de inmersión de hasta unos 300-400 m, y siguiendo los reglamentos, son adecuados par el 98 % de la superficie del casco pero siempre hay puntos duros que pueden fallar a fatiga. Cuando el coeficiente de seguridad local de una zona de la estructura es alto (>2) el problema de fatiga no da lugar a agrietamientos. Esto se deriva de la configuración de la curvas S-N para la mayoría de los aceros empleados en los sumergibles. Sin embargo, en sumergibles de cota elevadas y con el fin de aprovechar el material del casco al máximo, ya que los márgenes de sobre-inmersión accidental se amplían, los coeficientes de seguridad de las tensiones se reducen bastante, (~1,6), dando lugar a que la fatiga pueda aparecer a un número moderado de ciclos. Existen submarinos muy avanzados, de gran profundidad en que el casco se somete al límite de su resistencia. En estos casos es necesario llevar una contabilidad de las inmersiones que realiza. Por cargas dinámicas Las cargas dinámicas son todas aquellas que tienen su origen en golpes, colisiones, etc. Los submarinos de recreo están expuestos a pequeños golpes con las rocas circundantes, contra el muelle, contra el buque auxiliar, en los atraques, etc.. Los eventuales golpes, los mas comunes, son golpes ligeros por su baja velocidad, en general, salvo alguna colisión accidental con otro buque (en las operaciones de emersión, normalmente). 147 Como una colisión de cierta importancia jamás se puede descartar, ya que la densidad de navegación por las costas y puertos es mas elevada que en alta mar, y por tanto el riesgo, este apartado tiene una cierta influencia sobre el proyecto de estos sumergibles, como pasa con cualquier otro buque. En primer término, es deseable que sean capaces de resistir sin daños aparentes, los golpes, de servicio, más habituales y para ello es importante el uso de cintones de defensa, parapetos, barras para golpes, etc. De especial importancia es la protección de las ventanas transparentes, que suelen ser más frágiles que el acero. En un choque se producen unas aceleraciones que tienen una amplitud que es función del tiempo. El gráfico de aceleración dispone de un tramo ascendente y corto seguido de otro decreciente y largo. Todo ello ocurre en milisegundos. Con el fin de simplificar el cálculo del choque entre objetos, muy complejo si se aplica el diagrama de amplitud de la aceleración, se ha creado una aceleración “estática” equivalente o aceleración permanente, (ASE: Acceleration Static Equivalent), con lo cual el problema se reduce a calcular o verificar el efecto que una aceleración estática (o sea permanente) tendría sobre el objeto en cuestión. Decir permanente no significa que sea eterna. Con demostrar que la puede soportar durante unos segundos es suficiente. Algunos reglamentos estipulan golpes o colisiones produciendo aceleraciones “estáticas, ASE” radiales del orden de 2 g y longitudinales de 3 g, que los sumergibles deben soportar sin que exista riesgo de hundimiento o perdida excesiva de la estabilidad y el francobordo. Esto equivale a afirmar que los objetos sometidos a estas aceleraciones “estáticas”, van a pesar el doble o el triple de su peso real, aparentemente en la dirección del choque, durante un corto e indeterminado periodo temporal. Estos bajos valores de “g” no autorizan a poder resistir cualquier choque. Son unos mínimos, a efectos de que el artefacto tenga “algo” de aguante frente a un choque “corriente”. No se especifica bien como se materializan, abordo, estos choques, en la mayoría de los Reglamentos. En lo que respecta a los equipos del sumergible se entiende que estos deberán, al menos, seguir sobre sus soportes o bancadas sin soltarse de ellas y eventualmente seguir funcionando a su régimen normal, al menos provisionalmente. Por consiguiente, los anclajes de sujeción, polines, abrazaderas, tornillos y bulones, de los aparatos de propulsión, ejes, sistemas hidráulicos, generadores, botellas de aire comprimido, (de todos los aparatos de mando y control, los esenciales y/o peligrosos), etc. deberán estar preparados para soportar estas cargas extraordinarias, sin deformarse y, en el caso limite, partirse o soltarse, manteniendo en su sitio, al menos, los elementos que soportan. Si el nivel de choque estipulado es de 3 “g” esto significa que, p.e. un polín debe aguantar el triple de lo que pesa el equipo que soporta, al menos, así como los pernos de sujeción, etc. en la dirección exigida (p.e. línea proa-popa). En lo que respecta a las estructuras, se entiende que las interiores no se deberán deformar sensiblemente (incluyendo los soportes de los equipos), los tanques no fugarán y los mamparos no se abollarán. El casco resistente (incluyendo los portillos de plástico), deberá estar protegido, en lo posible, por las estructuras exteriores que deberán ser las primeras en deformarse, a efectos de amortiguar y absorber la mayor parte del choque. Se entiende que el choque sobre estas, las primeras que deben entrar en contacto con el elemento que golpea (buque, muelle, etc.), es equivalente a un empuje estático (en sentido longitudinal) que equivale al peso total del sumergible multiplicado por 3. La energía de deformación de estas deberá ser lo suficientemente alta para que el casco resistente no entre en contacto con el objeto sobre el que se choca (en dirección proa-popa). Evidentemente, los anclajes de las superestructuras, tanques de lastre y otros elementos estructurales situados en el 148 exterior deberán ser capaces de mantenerse íntegros, sin que los elementos que los enlazan al casco principal se partan y se suelten, aunque se pueden consentir abolladuras, desperfectos, deformaciones en los anclajes, etc. En superficie, los tanques de lastre, que suelen rodear al casco resistente, son los mas expuestos, principalmente los de los extremos, y este tipo de avería obliga a verificar la flotabilidad y la estabilidad y el francobordo con algunos de ellos estos rotos o perforados. En inmersión no es tan probable que se produzca un choque, y si este se produce sería de un valor muy moderado, (contra las rocas circundantes, a muy baja velocidad), pero que también hay que prever. Otro concepto de choque que se podría aplicar a la estructura y equipos exteriores sería el de los golpes de mar, en superficie, que suponen una sobre-presión por el impacto de las olas sobre las planchas y objetos exteriores o sobre el propio casco resistente. Esta sobre-presión, presión dinámica, tiene valores que oscilan entre 12000 Pa (0,12 bar) y los 50000 Pa, (0,5 bar), con una distribución irregular sobre las planchas y estructuras exteriores. Producen abolladuras que pueden ser importantes, pueden deformar casetas, arrancarlas, deformar los tanques, etc. Normalmente estos aparatos no están autorizados a navegar con mal tiempo, por lo que estos efectos se podrían excluir, salvo en los sumergibles de alta mar en que es inevitable que exista un cierto nivel de oleaje durante su lanzamiento y recogida. Por los motivos anteriores, es aconsejable que las estructuras exteriores, aunque no deban ser resistentes a la presión de inmersión, aparte de cumplir con su servicio, tengan una cierta consistencia mínima que las haga inmunes a pequeños choques y golpes de mar. En los sumergibles y submarinos militares, considerar el efecto de las cargas dinámicas, principalmente originadas por explosiones submarinas, de minas, etc. es un asunto muy importante, ya que deben estar, hasta cierto punto, preparados para resistirlas o, al menos, que sus efectos no produzcan averías graves. Todo ello, evidentemente, hasta ciertos límites máximos. Se calculan para 60, 100, 200 o mas “g” según el caso. Se utilizan conceptos como el factor de choque, espectros de choque, los desplazamientos máximos de los equipos originados por la transmisión de un choque hacia el interior del sumergible, etc. 149