representacion de los poliedros.

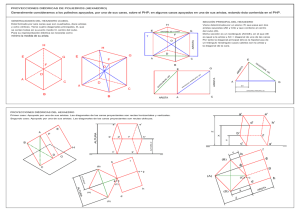
FIEPFIESENTAGItrN TTIEtrRIEA trE LOS FELIEDROSAntes de la represent¡ción de los poliedros, estudiaremos su constituci6n,
secciones principales y relaciones métricas de cada uns de ellos para, a partir de ellas, deducir las propiedades y particularidades de sus proyecciones.
POL|EIIROS RE6UIÍRES COI{VEHOS.
cntri
TETRAEDRO
CUEO O EXAEDRO._
ñt!_
4\ff.
aHtsTÁs
Irls-
UERTICES
E
¡l
1Z
I
t2
6
CICTNEDRO.
SECClf}lil FR|HCltráL
Triánoulo isssceles de
lado desigual = arista y
dos lados iguales = h.
Rectánoulo de lado mensr
= arista y lado mayor = dia'
gonal de unü cara.
Mlgde lado = h, diagonal menor = arista y diagonal mayor la propia.
Exáouno irreuular. de dos
ICOSÁEDRO
3Ú
1Z
DODECAEDRO.-
lados lguales opueslos
=
aristr, y cuatro iguales = h.
Exáoano irreoular. de dos
1
3ü
¡0
lados iguales opuestos =
arista, y cuatro iguales = n
SECCIOHES FRIHCIFALES.
Llamam¡s sección principal del poliedro en cuestión, la producida For un plano que
pa$a pür dns aristas opuestas {cubo o exaedro, icosaedrs y dodecaedrol, por una
arista y el punto medio de la opuesta ftetraedrol, o por unt diagonal y es perpendicul¡r a dos aristas en su punto medio [octaedrof.
En estas secciones lencmos, una vez dibujadas, lodos los datos necesario* del
poliedro de que se trale, para prder dibujar las proyccciones a partir de una arista
como dato del ejercicia. Scn la llave que nos abre la solución del problema.
FOSICIOI'IES TIPICáS DE LOS POLIEDROS.
Las posiciones típicas de los poliedros con respecto a los planos de proyecciñn
vertical y horizontal son:
- ton una cara apoyada en el horizontal.
- Con una arista apoyada en el trorizsntal.
- Con un vÉrtice apoyado en el horizonta¡ y ü¡rE diagonal perpendicular a é1,
- lguales posiciones anteriores con respecto al vertical de prq¡ección,
Aqui estudiaremos los tres primeros casos relativos al horizqntal, dejando los relativos al vertical como práctica a re alizar por el alumno, dada la similitud con los
tres primeras y como comprobación de lo aprendido.
De la correcta identificación de cuál es cada uno de lss paliedros, cómo es, cómo
sün sus carari, cuántas tiene, cuóntas aristas y vÉrtices lo componen, cómo es y
cúmo se dibuja su sección principal, depende que podamos dibuiar o no sus pro-
ycccioncs, pues si dominamos la geometría dcscriptiva del sistema diédrico
parte nos resultar$ la mis st¡cilla.
lgualmente podremos dibujar una perspectiva del poliedro, a partir de que conozeamos una de sus aristas, si sabemos todo lo anterior.
Hoja apÉndice 3.
FIEPFIESEHTAEION BIEBFIIEA trE LES POLIEtrRESPOL¡EDROS REGULARES COT{VEXOS.
- TETRAEDRO.
Poliedro formado por cuatro caras triangulares equiláteras, seis aristas
tro vÉrtices.
y
cua-
$ección p¡incinal.
Llamamos sección principal a la producida pur cualquiera de Ios planos que
pasan por una adsta [A-Ef y por el punto medio de la opuesta lMl- Dichu
plano es perpendicular r l¡ flr¡$tfl fC-Dl que conüene al punto medin.
Está formada [a sección principalf pür una arista del letraedro [A-Bl y dos
alturas thl-Al lhil-Bl de triángulos equiláteros fcaras del tetraedrol.
La distancia hl-H entre dss aristas opuestas es el diámetrs de la eslera
tangente a todas las aristas.
El ortocentro deltriángulo isósceles hlAB es el centro del poliedro, y las
distancias desde él a las caras [igualesl el radio de la eslera inscrita.
La altura h del vértice A sobre el lada ME o la delvÉrtice B sobre MA es la aF
tura del tetraedro,
Fosiciones tiFicas del tetraedro.
ilfia ESíE Afrfil/ad8 #1
Dibujaremos un triángulo equilátero de lado = arista, y For su ortorentro se traz
rá una perpendicular de magnitud la altura h anteriormente hallada, nbteniendo
vártice aZ-al,que, unido a los tres anteriores nus dibuia el tetrtedro.
tsn uns srisla yertitsl
Dibuiamos la recta vertical bl-cZ, bl=cl de magnitud la arisla de! tetraedro.
La arista cpuesla a la arista B-C [arista A-Dl es una rec{a horizontal quÉ \rE
mos En su proyección horizcnlal en verdadera magnitud, y a una distuncia de
la arista E-C {en proyeceión hnrizontal bl=cll igual a la magnitud M-H. Esta
arista horizontal tiene de cota la mitad de la arista dada, pudiÉndose por tanto
dibujar en el verticrl. Unienda los cuatro vértices completamns el letraedro.
En proyección horiznntal resulta el contorno un triángulo secciñn principal.
tan dos a¡islas Éon'Eenlslss.
Una de las rristas sÉ suFrine
en el mismo plano horizantal,
la C-D, siendo la más baja y
üÉndose en verdadera magnitud cl -dl .
La opuesta A-B tamhiÉn en
verdadera magnitud al -bl,
se verá normal a la anterior y
con sus puntüs medins M-ft|'
coincidentes. Su cnta será la
En planta, uniendo los cuatro vÉrtices,
se obtirne el cuadradn d¿ lado la mag-
nitud l.J-H=h'.
distancia lvl-H antes hallada,
Hoja aFéndice 4
F|EPRESENTAEIOH trE POLIEtrRtrS.
FO LIE
DROS RE€ULüRE$ CüfrlVEXO S.
-CUEO O E}$EDRO.
Prliedro formado por seis calas cuadradss, ochn vártices y dnce aristas.
Tiene su sección urincinal en el plano, que Fasü por dns aristas opuestas,
sección que está lsrmada por un rectángulo de dimensiones, la arista y la
diagonal de un ru¿drado [una cara del cubof.
La diagonal de eete rectángulo es el diámstro 2R de la esfera circunscrita.
La diagonal de una de las EErEs es el diámetro tR' de la esfera tangente a
A
las ffistas,
El diámetru 2r es el de la esfera tangente a las caras del cuba = arista.
La proyección de rn vÉrtice B sobre la diagonalA-C está a la tercera parte de
dicha diagonal. La distancia s es la distancla de un vértice a la diagonal A-C.
Dibujamas en primer lugar la diagonalA-C, aZ-cZ, al-eI, deducida
de la seccién principal.
Lr dividimo* e* tres partes iguales dibujando paralelas a la L.T.
por los puntos de división, sobre Eada una de las cuales estarán
lrcs vÉrticcs del cubo.
Con radio s dibujamos una circunferencia en el horizontal de centro aI=cl . En ella estarán las proyecciones horizontales de seis
vÉrtices [tres altos y tres baios] separadas 60-!.
Sl suponemos que las arlstas AE, AH, ÁF ssn las más altas, referiremos los vÉrtice s E, H, F a la paralela superior de las traeadas
anteriormente, y los vértices G, D, E a Ia paralela inlerior.
Los tres vÉrtices suprriorcs lss unimos con cl extremo superior
de la diagonal, A [a2-a1lLos tres vÉrtices inferiores los unlmos con el extremo inferior de
la diagonal C [c2-c11.
Por último cnmprabamss las partes victas y ocultas del exaedro.
taa sna tata aptyada en elplane harízanial,
Esta posición es la más sencilla, pues la proyección horizontal
resulla¡á un ctadradu de lado la arista del eubo, y la proyección
vertic-¡|, que nbtendremos trazando perpendiculares al plano horizontal lrectas verticalÉsl por los vÉrtices, limitadas por la base superior del exaedr* [que teremos como una rertal a una distancia de
la base inferior igual a la arista del cubu.
Dibujamos en primer lugar la
SECClOltl PRINCIPAL del exaedro
a representar en diÉdrica, tomando
coma datos los relativos
arista,
a É1.
arista.
el
=gl
Dibujamos la arista delplano ho¡izontalcl-gl, c2-gZ; la más alta y
epuesta a la dibujada se proyectará sobrr ella según al-el, y en
proyrcci6n vertical sobre las verticales por cZ-g2 y a una altura
lcotal igual a la diagonal "d" dE una cara.
En esta posición, otra seccién principal horizrntal se verá En verdadera magnitud en el plano horizontal, y con al=cl-eI
=gl como
eje central del rec{ángulo sección.
Los cuatro vértices de esta sección principal E, F, H, D están en la
Hoia aFÉndice 5.
línea intermedia entre A-C, E-G.
REPRESENTAGION DE POLIEtrROS.
POLIEDROS REGULARES CONVEXOS.
- OCTAEDRO.
Consta de ocho caras triángulos equiláteros, seis v6rtices y doce aristas.
La sección principal está contenida en un plano que pasa por una
diagonal y es perpÉndicular a dos arislas opuestas É$ su punto
medio. Plano A-E-C.
Está formada por cuatro lados iguale$, es un romho, de lado igual
a la altura A-B de un triángulo equilátero de cara, siendu las diagonales, la menor una a¡ista del octaedrr y la mayor la diagonal del
mismo = r Vf
R = Radio de la esfera circunscrita.
r = Radio de la esfera tangente a las caras
r'= Radiq de la esfera tangente a las aristas,
En la figura de la derecha
se ha dibujado la sección
principal en verdadera magnitud.
Se ha tomado como punto
de partida un triángulo equF
Iátero, al que se le ha hallado la altura.
Didra altura se ha empleado
csmo lado del rombo cuya
diagonal menor es igual al
lado de dicho triángulo, lo
que equivale a la arista del
sstaedro. El resto de elementos son fácilmente deducibles de la figum.
Can sns díeganel van#a!.
Posici¡nes duicas del octaedro.
tan ans rera spnyade nn alrtatizanlsl
2r = dislancia entre dos lados del rombn sección pdncipal.
Hnje epéndice 6.
REPRESENTAGIEN DE POLIEtrROS.
POLIEDROS REGULüRES CO¡IVEXOS.
- OCTAEORO.
Fosiciones tínicas del octaedro.
tsn
t¡¡ta
Puede suceder ctrmo sÉ aprecia en la figura de la derecha, quÉ el plano
vertical de la sección pf¡ncipal no sea perpendicular al vertical de
proyección. Es decir, no safi un plano de perfil el que contiene a dicha
secci6n principal.
tan anplaae díaganal
al
tnflinly
una atista en elpÍana
=b
dl
=cl
rtaritantel
Dentrs de este plano diagonal eelará un cuadrado de lado la arista,
dibujamrs la proyección vertical a2, bZ, cZ, dt de dicho cuadrado y
la proyección horiznntalde el, aI=bl, cl=dl.
Los vÉrtices el y fl estarán sobre la mediatriz del lado del cuadrado
anterior, y a una distancia de el en verdadera magnitud igual a R.
A continuaciñn dibujamos las proyecciones verticales eZ y 12, tambie n sobre la mediatriz del lado del cuadrads, cuidando dibujar correctamente las partes vistas y ocultrs del poliedro.
Hoja apéndice 7.
- tcosAEtlRü.
Este polie drs está formado por veinte caras triángulos e quiláte¡os, lreinta aristas y doce vÉrtices.
Su sección principal pasa por dos aristas opuestas y rerulta un exágono irregular en el que:
.
arista
d = diagonal del pentágono
\ ',
regular de lado la arista
Partimos como dato de la arista del ICOSAEDRO para dibujar un
pentágono regular de lado la arista dada.
Tsmamss la diagonal de este pentágono para cunstruir la
SECCIOH PRlttlClPAL de la siguiente manera:
de|ICOSAEDRO.
COHSTRUCCIOiI DE LA SECCI0N FRllrlClPAL.
l¡.- Dibuiamos una circunferencia de diámetro
la diagonal del pentágono hallada anterior-
mentt.
2s.- Trazamos dos iangentes a la misma, para-
lelas entre sí, y de rna magnitud igual a la
arista del ICOSAEDRCI.
3s.- Unimos los extremos del diámetro paralelo
a las tangentes, extremos I y 4, con los extremcs de las aristas 2, 3 y 5, 6.
= altura del triángulo equilatero [cara de este poliedrol.
La distrncia entre los vértices 2-5 ó los 3-E será 2R = diámetro de la esfera circuns-
crita.
La distancia 1-4 será 2r' = diámetro de la esfera tangente a las arist¡s.
La distancia enlre los ladss 3-4 y l-E será 2r = diámetro de la esfera tangenle a las
caras.
La perpendiculartrazada desde el centro del exágono dlbujado a los ladss 1-S ó
sus análogos tiene su pie en el puntr lerce¡a parte de l-6 a partir de l, pues es el
cenlro de una cara del irnsaedrp.
procuramos determinar l¡s vÉrEn las posiciones que dihuiaremos a
tice s por sus alturas referidas a las posturas corrcspondientes de la secciñn prin-
cipal.
e legida y fijada una sección principal en el icosaedro existen otras dos
idÉnticas formando un triedro trirrectángulo, y como en cada una hay cuatro vértices del poliedro, el dihujo de estas secciones principales nos permite tener todos
los vÉrtice s de I icosae dro [121.
Una vez
Fosiciones típicas del icosaedro.
tan ute en'sle tn anplena hon'za*ief
¡ry¡lireÍ.
arista.
yle sem'óaprtbdgtlgacpeseparella
Dibujamos una sección principal en verdadera magnitud en el plano horizontal.
Proyección 1 2-3-4-5-6-7-S-9-1 0-l I-I 2
Referimos al mismo plano en proyecciün
vertical los puntos 2'-3'-5'-6'.
Como la sección principal es perpendicular
en el punto medio a dos rristas, en los vértices l-7 y 4-8 del exágnnn sección, quedarán vertieales y situadas la mitad pnr encima, y la mitad por debajo del plano 3'-6'.
Estas aristas son la 4{, 418'y la l-1, lll'.
Las aristas horizontales más alta y más baja se verán verticalmente snparf,das del
plano 3'-E'una magnitud dlZ y simétrieas
respecto al centrs del icosaedro; ss dsc¡r,
en 911 1'y I 0'-12', en prnyecciún horiznntrl
normales a las ya dibujadas 2-3 y 5-6 y can
su punto med¡o sobre el E€ntro del poliedro.
En esta posición, la proyección horizontal tiene un contorno qüe es una sección
principal. pue$ cualro rüras son verticales y cuatro aristas son hsrizontales.
Hoja apÉndice
E.
REPRESENTAEION DE POLIEDFIOS.
FOLIEDHOS REGULARES CCIHVEXOS.
En esta postura, una de las secciones principales que
pase por esta diagonal podrá dibuiarse ean su propia
diagonal perpendicular a la línea de tierra, y las perpendiculares pur lns vÉrtices a la diagonal nos determinan
los puntos H, que nos dan la altura a que sE proyectarán
grupos de cinco vÉrtices separados del eje o diagonal
una magnitud s.
Par lo tanto, dibujamos en proyección horiznntal una
cirrunferencia de radio s, sobre la que se ensontrarán
dos pentáganos regulares con sus vÉrtices girados 361,
para lo que dividimus la circunferencia en diez psrtes
- ICOSÁEBRO.
Posiciones fipicas del icos¿edrs.
ilfi#
iguales.
Estos pentágonos 2-3-4-5-6 y sus análogos están a diferente
altura, pues si uno lo suponemos en 2'-3'-4'-5'-6', horizonlal H superior, el otrs se referirá a la hurizuntal H inferior.
Diagonal de la
lt vÉrtices, los unimos cada uno csn los cinco más
próximos, farmando triángulas y ángulos poliedros pentaedros.
Conviene unir cada arista en proyección vertical y en proyección horizontal,
pues al hacerlo todo de vez Én el vertical y despues en el horizontal se presta
a mayor confusión.
Como ya lenemss los
ta*
ane ters spayada en
Como FRIIJEFA OtrERACIOH a realizar, dibujaremos la SECCIOH PRIHCIFAL
con uno de los lados altura del equilátero [hl, apoyado en la líne a de tierra,
[equivalente a la ca¡a apoyada en el plano horizontall
lrazrmos unff perpendicular al lads h que pase
por el centro del palígono sección principal [punto donde se corten dos diagonalesl. Esla recta es la que une los puntos medios
de dos caras opuestas, y sobre ella llevamos mediante perpendiculares los puntos 1, Z, 3 y 4. El punto 3 sale de la intersección de las dns diagonale s quc se aprecian en la fig, Estos
i puntos determinarán en la proyección vertical las alturas a las
j que se situarán los vÉdices del icosae dro.
Una vez terminada la operación anterior, acnmetemus la
SEGUIIDA OPERACION -A-, consistente en dibujar la circunferencia que circunscribe al triángulo equilátero, cara del icosaedro, como paso prcvio para poder dibujar en proyección horieon'tal ISEGUIIIDA OFERACIOH -EJ el triángulo cara del icosaedro.
A continuaciún
A rsntinuación, ya podemos co-
Terminadas las operaciones previas a la resolución del ejercicio, dibujaremos la cara apoyad¡ en el horizontal, un triángulo igual al
pero girado 6¡r ¡-2-31
Referenciamos los puntos anteriores l-Za la proyección ve rtical, 1'-2'-3' en la L.T. y 4a
5aE'a una altura Zr con respecto a los anteriores-
El resto de puntos [I y srs análogosl se llevarán del modo siguiente: los que están enfrente
de los vÉrtices del triángulo superior [4-5-61 al
plano intermedio bajo, y los otros tres al plano
intermedio alto.
Solo queda unir, formando triángulos y ángulos
poliedrns de cinco aristas.
menzar a dibujar la proyección
horizontal ISEGUIIIDA OFERACIOH -BJ, que podemos ir dibujando en el lugar que destinemos
para resolver delinitivamente el
ejercicio.
Fara ello trazamos una circunferencia de radio s [obtenido en la
sección principall, que dividirem$s en seis partes iguales.
Situaremos la cara supe rior del
icosaedro, trazando la circuolerenda circunscrila de radio c hallada en el pasa anterior.
Húja aFÉndice g.
POLIEDROS RECUI-ARES COIIIVEHOS.
- DODECAEDROEste poliedro está formado por doce caras pentágonss regulares, treinta aristas [igual que el icosaedrol y veinte vÉrtices; los ángulos poliedrns ssn triedros cuyo ingulo de caras vale 108s.
La sección principal, parecida a la del icnsaedro, pasa tambien por dos aristas
opueslas y es un exágono irre sular que tiene dos lados iguales opuesto* [dos
aristasl de magnitud la arista del policdro y otros cuatro iguales e iguales a la
mediana del pentágo$o Eara del dodecaedro lml.
La distancia entre las dos aristas
de la sección principal, es igual a
. arista
la Diagonal de un pentügono de laCO}ISTRUCCION DE LA SECCIOH PRIHCIFAL.
do, la diagonal de una de las caras
pentagonales del dodecaedro.
tr
E
Así pues, para dibujar la sección
principal, dibujaremos 1! un pentágonu de lado la arista dada del dodecaedro, es decir, dibuiamos una
cara pentaganal regular del poliedro,
y en 2! lugar dibuiamos otro pentágona regular de lado
una diagonal del ls, obteniendo en
esta construcción la distancia que
hay entre las dos aristas = Diagonal.
A continuación
I AflStá
T-T
r
SECCION PHI HCIPÁ
D
,tl \rÉ
I
a
g
..1
'¿f
o
n
.
*i '
Con las construcciones I !
a
¡
y
2s, eslamos en situación de
dibujrr la sección
principalA.
En la sección principal B se han hallado los puntos HZ y H4, a cuya altura
estarán Z y 4 vértices, que nos campletan los Z0 que ti*ne el dodecaedro.
La dislancia entre dos lados paralelos m [medianas del pentágona cara del
dndecaedrol será el diimet¡o de la esftra inscrita [tangente a la* carasl, y
la diagcnal mqÉor de la sección principal el diámetru de la eslera cireunscrita [pasa por lns vértices del dodecaedrol.
La distancia entre las dos aristas parolelas de la sección principal = Diagonal
¿s¡ tE prntágono es el diámetro de la eslera tangente a las aristas.
Hoja aFéndice 10
REPRESEHTACION tTE POLIEtrROS.
POLIET}ROS REGUI.ARES COHVEXO$.
- DODECAEDRO.
-
Los v*rtices 5 y sus tres análogos son los de I plano intermedio [otra sección
principall, en prayección vertical 5'y sus tres análugus.
Los vÉrtices l6 y I f son los extremos de una arista vertical" llevados, camu
sus análogos, a los planos HZ intermedios fl 6'y 17J, y los vÉrtices l0 y análogos deb:rán llevarse a los planos H4, cuatro arriba y cuatro abajo.
la
uni6a ordenade" simullónea cn alztda
yplanl*
larmando petrtóganas
i ngaio s paliedro s *íed¡os. nas dele¡mina¡ó la s pnTnrrñr*e s del
tan ana tara apa¡nda
y
t* etpkna harizonlal
Dibujamas la sección principal con urn de los cuatro lados iguales m [mediana del pentógono-cara del dodecaedrnl adosado a la línea de tierra.
Trazamos la perpendicular por el centru de la sección a la línea de tierra, recta P. Fara ello dibujamos d¡s diagonales que al cortarse nos den el punto
medio.
El eje P [rroquis derrdrrl caincidirá en la prnyección horizuntal con el cenlro
del pentágono.
Sobre el nje P llevamos los vÉrtices de la *ección para determinar los planos
H de las alturas a las que se Eneontradn grupos de cinco vértices del dode-
c¡edro.
En esia secciin hallamos tambiÉn el radio s de la circunferencia que er proyecci6n horizontal contendrá diez vértices del dndecaedro, distribuídos según
un decágono regular.
Hoja apÉndice 11
.
FOLIEDROS REGULARES COTIIVEXSS.
- DODECAENRO.
Posiciones tíoicas del dodecaedro.
tea a*a rtrc apoy*da tn etptan* hafizanlaf"
61
1ü'' ,7'
s:.fi'
Una vez dibujada la seccién principal,
trazamos con cÉntrü en p fproyección
horizontal de Pl una circunferencia de
radio s, y otra concÉntica de radio r =
al radio de lt circtnferencia que circunscribe a un pentágons cara del poliedro.
l',n
I
Dibujamos un pentágúno regular inscrito en la circunferencia de
radin r, proyección horizontal de la cara apryada en el plano horizo ntal, I -2-3-{-5, proyección vertica I t'-2'-3'-4'-5'.
Dihujamos otro concÉntrico girado 35! respecto al anterior, proyeccién horizontal de la cara del dodecaedrs situada en un plano
paralelo al horizontal a rna altura [en proyección verticafl igual
a la altura de la sección principal, 6-7-8-9-10, E'-7--8--g'-l['.
Sobre la circunferencia de radio s obtenernss los I ll vÉrtices que
faltan, lI-IZ-l 3-l¡l-15-tE-l ¡-18-19-2[ según un decágono regular
que tendrá sus vÉrlices enfrent¡dos con los de los dos pentágonos dihujadoe en el pasa anterior.
Los vértices enfrenladcs a los l-Z-3-4-5 se llevarán al plano H intermedio inferior
I U '-l ¡l'-16'-1 8'-U 0', y los otros cinco, situados enfrente del 6-7{-9-10, se llevarán
al plano H intermedin superior 11113'-15'-17'-l g'.
Una vez ten¿mos lodss los vÉrtic=s unimss metódicamente formando pentágonos
y triedros en cada vártice.
fiTTA
Dibujamos la sección principal con una
1E:
diagonal msyor perpendicular a la L-T.
Obtnnemos las cotas de los grupos de
vÉrtices Hl. HI y H6.
Con centro en 2=l trazamos, primeramente,
una circunferencia de radio s, sobre la que
estarán tres vÉrtices próximos al más alto,
y análagamente, tres próximos al más bajo
distr¡buídos los seis a 6lls, en proyección
hsrizontal.
Después dibujamos una circunferencia de
radio t a la que serán tangentÉs En Froyección horizontal tres aristas supe riores
y otras tres inferiores. El punto de tangencia
lo obtenemos prolongando las divisinnes
a Eüs hechas a la circunferencia de radio
Las circunferencias menorÉs se han
llevar llZ arista a un lado y otrü. ".
.r.5
Completamos la planta, comprobando
llneas scn vistas y cuáles ocultas.
A continuaci6n dibujamns el alzado seg. la fig.
3'
Hoja apéndice 1?.