resumen matrices 2 - IES Gabriela Mistral

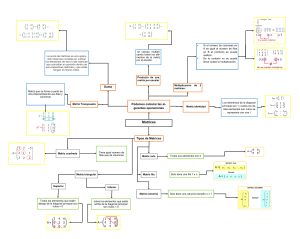
RESUMEN DE MATRICES
•
Se denomina matriz a todo conjunto de números dispuestos en forma
rectangular, formando filas y columnas
Am ,n
 a11

a
=  21

a
 m1
a12
a 22
am 2
a1n 

a2n 


a mn 
a23 indica el elemento que ocupa la fila 2 y
la columna 3
• Cada uno de los números de que consta la matriz se denomina elemento. Un
elemento se distingue de otro por la posición que ocupa, es decir, la fila y la
columna a la que pertenece.
• El número de filas y columnas de una matriz se
denomina dimensión de una matriz. Así, una matriz
será de dimensión: 2x4, 3x2, 2x5,... siendo el primer
número, el número de filas y el segundo número,
el número de columnas
• Sí la matriz tiene el mismo número de filas
que de columnas, se dice que es cuadrada y
su dimensión: 2, 3, ...
A 42
1

0
=
2

3

4

1
2

0 
2 0
1


A3 =  − 1 1 4 
 2 − 1 3


• El conjunto de matrices de m filas y n columnas se denota por Am,n, y un
elemento cualquiera de la misma, que se encuentra en la fila i y en la columna j,
por aij.
• Dos matrices son iguales cuando tienen la misma dimensión y los elementos
que ocupan el mismo lugar en ambas, son iguales.
a1n )
• Matriz fila: Sólo tiene una fila y n columnas, A1n = (a11 a12 a13
•
•
•
Matriz columna: Tiene m filas y sólo una columna.
Matriz nula: todos los elementos son ceros.
Diagonal principal: Es la línea de la forma: aii : a11, a22, a33….ann
• Matriz triangular superior: los elementos
situados por debajo de la diagonal
principal son ceros.
 1 −1 3 


B3 =  0 2 − 1
0 0
4 

• Matriz triangular inferior: los elementos situados por encima de la diagonal
principal son ceros.
• Matriz diagonal: todos los elementos situados por encima y por debajo de la
diagonal principal son nulos. Sólo tiene sentido en matrices cuadradas
• Matriz identidad es una matriz diagonal en la que los elementos de la diagonal
principal son iguales a 1. Se denota por Im.
• Dada una matriz A, se llama Matriz Transpuesta de A y se denota por At , a la
matriz que se obtiene cambiando ordenadamente las filas por las columnas.
1 0 − 2

A23 = 
5 −1 3 
A t 32
5
 1


=  0 − 1
− 2 3 


Propiedades de la Matriz Transpuesta:
( )
t
1) La transpuesta de la transpuesta es la matriz original: At = A
2) La transpuesta de la suma es la suma de
las transpuestas:
( A + B )t
= At + B t
3) La transpuesta del producto es el producto de las transpuestas en orden
t
inverso: ( A ⋅ B ) = B t ⋅ A t
NOTA: El producto de marices NO es conmutativo.
• Matriz simétrica: es una matriz cuadrada que verifica: At=A
• Matriz antisimétrica o hemisimétrica es una matriz cuadrada que verifica:
At=-A
• La matriz Inversa de una matriz dada A, se denota por A-1 y es aquella que
cumple: A ⋅ A −1 = A −1 ⋅ A = I
• Rango de una matriz es el máximo número de líneas (filas o columnas)
linealmente independientes, que tiene la matriz.
OPERACIONES CON MATRICES
• SUMA: Dadas dos matrices de la misma dimensión, A=(aij) y B=(bij), se define
la matriz suma como: A+B=(aij+bij). Es decir, aquella matriz cuyos elementos se
obtienen: sumando los elementos de las dos matrices que ocupan la misma
posición.
 2 − 3
 ;
A = 
1 5 
 1 4
 ;
B = 
 − 2 3
 3 1
 ;
A + B = 
 −1 8
1 − 7 

A − B = 
3 2 
•
Multiplicación por un número: Dada una matriz A = (aij) y un número real k
R, se define el producto de un número real por una matriz: a la matriz del mismo
orden que A, en la que cada elemento está multiplicado por k.
 0 2
 ;
A = 
 −1 1
k = 3;
 0 6

k ⋅ A = 
 − 3 3
• Multiplicación de matrices: Dos matrices Am,n Bn,p se dicen multiplicables si el
número de columnas de A coincide con el número de filas de B. La dimensión de la
matriz producto es (A B)m,p
El elemento cij de la matriz producto se obtiene multiplicando cada elemento de la
fila i de la matriz A por cada elemento de la columna j de la matriz B y
sumándolos.(fila por columna)
 0 2
 ;
A = 
 −1 1
 1 4
 ;
B = 
 − 2 3
0⋅ 4 + 2⋅3 
 0 ⋅1 + 2 ⋅ (−2)

A ⋅ B = 
 (−1) ⋅1 + 1 ⋅ (−2) (−1) ⋅ 4 + 1 ⋅ 3 
El producto de matrices no cumple la propiedad conmutativa y en general, el orden
de los factores si altera el producto