k - Simfit
Anuncio

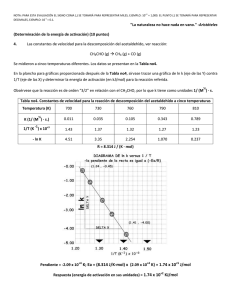
Ejercicio resuelto Ejercicio 1. TRABAJO DIRIGIDO Nº 3 (Fisicoquímica II, Curso 2009-2010 , Grupo B) El diazepam es un ansiolítico que se descompone por hidrólisis para dar distintos productos de reacción: Diazepam t Productos Para estudiar su estabilidad en unas condiciones, se ha medido, a dos temperaturas, la concentración de Diazepam a diferentes tiempos. Los resultados fueron los siguientes: Temperatura = 80.0 ºC Tiempo / min 0.0 45.0 90.0 120.0 Temperatura = 90.0 ºC [Diazepam] / mol L-1 0.2000 0.1332 0.0889 0.0679 Tiempo / min 0.0 45.0 90.0 120.0 [Diazepam] / mol L-1 0.2000 0.0885 0.0386 0.0228 a) Determine el orden de la reacción de descomposición por un método numérico. b) Calcule gráficamente el valor de las contantes de velocidad a 80.0 y 90.0 ºC (puede hacerlo sobre una misma gráfica para apreciar mejor las diferencias). Compruebe los valores obtenidos por regresión lineal por mínimos cuadrados. c) ¿Cuanto vale la energía de activación de la reacción? d) ¿Cuál será el tiempo de caducidad de una disolución de diazepam en esas condiciones si se va a conservar a la temperatura ambiente (25.0 ºC), considerándo un 10 % como el máximo de descomposición permitida? ______________________________________________________________________________ a) Aplicando el método de integración para orden uno, comprobemos si los datos cinéticos cumplen dicho orden a las dos temperaturas: Temperatura 80.0ºC Temperatura 90.0ºC [A] 0 1 k = 1t ln = ln 0.2000 M = 0.00903 min −1 [A] t 45 min 0.1332 M [A] 0 1 k = 1t ln = ln 0.2000 M = 0.0181 min −1 [A] t 45 min 0.0885 M [A] 0 1 k = 1t ln = ln 0.2000 M = 0.00900 min −1 [A] t 90 min 0.0889 M [A] 0 1 k = 1t ln = ln 0.2000 M = 0.0183 min −1 [A] t 90 min 0.0386 M [A] 0 [A] 0 1 1 k = 1t ln = ln 0.2000 M = 0.00900 min −1 k = 1t ln = ln 0.2000 M = 0.0181 min −1 [A] t [A] t 120 min 0.0679 M 120 min 0.0228 M Como puede observarse, las k se mantienen constantes a ambas temperaturas, por lo que concluimos que la reacción es efectivamente de orden uno a ambas temperaturas. b) Para calcular gráficamente las dos constantes, procedemos a hacer las respectivas gráficas en papel milimetrado. Para ello, recordemos que: ln [A] 0 = kt [A] t Hoja de problemas nº 1 (continuación) que tiene la forma de una línea recta: y = pendiente $ x de manera que representando ln [A] 0 [A] t frente a t podremos obtener las respectivas k a las dos temperaturas. Para ello hacemos la siguiente tabla auxiliar: Temperatura = 80.0 ºC Tiempo / min 45.0 90.0 120.0 ln [A] 0 [A] t 0.4065 0.8108 1.080 Temperatura = 90.0 ºC Tiempo / min ln 45.0 90.0 120.0 [A] 0 [A] t 0.815 1.645 2.172 Por tanto, los valores de las constantes de velocidad a las dos temperaturas son: k 80.0 o C = 9.1 $ 10 −3 min −1 k 90.0 o C = 1.8 $ 10 −2 min −1 Los valores obtenidos por regresión lineal por mínimos cuadrados son: O.O. = 5.75 $ 10 −4 O.O. = 9.59 $ 10 −4 pend. = 9.00 $ 10 −3 pend. = 1.82 $ 10 −2 r = 0.9999 r = 0.9999 c) La energía de activación la calcularemos por la Ecuación de Arhenius: ln −2 E Ea k2 1 − 1 = − a 1 − 1 u ln 1.82 $ 10 −3 = − cal R T2 T1 9.00 $ 10 k1 1.987 K$mol 363 K 353 K 0.6898 = − Ea cal (−7.80 $ 10 −5 K −1 ) u E a = 17.6 $ 10 3 mol u E a = 17.6 cal 1.987 K$mol Kcal mol d) Para calcular el tiempo de caducidad, hacemos lo siguiente: i. Calculemos primero la k a 25.0oC 3 cal −3 17.6 $ 10 mol 1 − 1 ln 9.00 $ 10 = − u k 1 = 8.84 $ 10 −5 min −1 cal 298 K 353 K k1 1.987 K$mol ii. Calculemos ahora el tiempo de caducidad: [A] 0 [A] 0 1 t c = 1 ln u tc = ln = 1.19 $ 10 3 min −5 −1 x[A] 0.90[A] k 8.84 $ 10 min 0 0 que finalmente podríamos escribir como: t c = 19.8 h