Índice 1. INTEGRACIÓN - Escuela de Matemáticas UIS

Índice
1. INTEGRACIÓN
1.1. Conceptos básicos de la Integral . . . . . . . . . . .
1.2. Suma de Riemann (Integral Definida) . . . . . . .
1.3. Integración por sustitución Simple o Compuesta .
1.4. Integración por Partes . . . . . . . . . . . . . . . .
1.5. Integrales que contienen Funciones Trigonométricas
1.5.1. Integrales de senos y cosenos . . . . . . . .
1.5.2. Integrales de Secantes y de Tangentes . . .
1.6. Integración por Sustitución Trigonométrica . . . .
1.7. Integración por Fracciones Parciales . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1
3
6
13
19
21
21
22
23
25
CÁLCULO INTEGRAL
Profesor Marcos Alejo Sandoval
email: marcosalejo@gmail.com
Universidad Los Libertadores
1.
INTEGRACIÓN
INTRODUCCIÓN
Las matemáticas en general, contribuyen en el desarrollo del ingenio y la capacidad de análisis que todo futuro
ingeniero necesita. Parte fundamental en la construcción del pensamiento matemático que todo ingeniero debe
tener consiste en la comprensión conceptual del cálculo integral.
En esta unidad temática iniciaremos el estudio de la integral, vamos a encontrar como inicialmente la integral
es vista simplemente como una antiderivada o operación inversa de la derivada, de acuerdo a ese aspecto, si
tenemos una derivada cualquiera, lo importante es encontrar la función o funciones cuya derivada es la ya dada.
Cuando hemos tenido una comprensión acerca de las antiderivadas, podemos conceptualizar a la integral como el
área bajo la curva de una función, para esto utilizaremos el método de aproximación por "sumas de Riemann";
y por último, estudiaremos los diferentes procesos para desarrollar diferentes tipos de integrales, por medio
de unas técnicas básicas como son técnica de integración por sustitución, por partes, técnica de funciones
trigonométricas, por fracciones parciales y por sustituciones especiales.
OBJETIVO GENERAL
Brindar un apoyo holístico a los estudiantes, en el desarrollo de la comprensión de los conocimientos del cálculo
integral; para así fortalecer su visión analítica, que pueda plantear y solucionar cualquier situación problema
que involucre estos saberes.
OBJETIVOS ESPECÍFICOS
-Estudiar el concepto de la integral.
-Comprensión geométrica de la integral
-Desarrollar integrales utilizando las técnicas de integración
PALABRAS-CLAVE: Antiderivada, Sumas de Riemann, Técnicas de integración, Teorema Fundamental del
Cálculo
1
CONOCIMIENTOS PREVIOS
Para el estudio del cálculo integral, el estudiante debe estar familiarizado con el concepto de función, es importante que él tenga claro cuáles son la funciónes constante, idéntica, polinómica, logarítmica, exponencial,
trigonométricas.
También, el estudiante requiere conocimientos en derivación como su definición, sus propiedades, las fórmulas
de derivación, la derivada de las funciones en general y de una función compuesta.
Otro factor importante en la fácil comprensión del cálculo integral, es la construcción de gráficos en el plano
x − f (x), especialmente de las diferentes funciones.
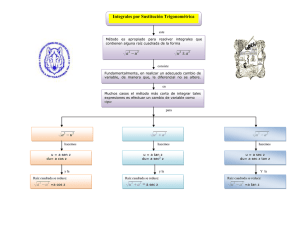
MAPA TEMÁTICO
INTEGRACIÓ
INTEGRACIÓN
Concepto básico de la integral
Operación inversa de la
derivada: Antiderivada
Integral
Indefinida
Notación
Propiedades de
las integrales
Área bajo la curva:
Sumas de Riemann
Integral definida
Teorema
Fundamental
del Cálculo
Reglas de
integración
Técnicas de
integración
Por sustitución
trigonométrica
Por partes
Por sustitución
trigonométrica
2
Con contenido Por Fracciones Por sustituciones
Trigonométrico
Parciales
especiales
1.1.
Conceptos básicos de la Integral
Al utilizar operaciones básicas como la suma, el producto, la potenciación, la exponenciación, podemos mediante
un proceso inverso, volver al operando inicial.
En el caso de la derivada, descubriremos una operación inversa que me determina cuál es la función de la cual
obtengo esa derivada.
Iniciemos con una funcion sencilla:
Si f (x) = x2 , entonces su derivada es f (x) = 2x
Ahora, si tenemos f (x) = 2x, su operación inversa, sería el proceso que el que se llega nuevamente a f (x) = x2 .
Esta operación recibe el nombre de antiderivada.
Definición: Sea f (x) una función y f (x) su derivada, entonces f (x) se llama una ANTIDERIVADA de f (x).
Ejemplo: Encontrar una función f (x) cuya derivada es f (x) = 7x6 . En otras palabra, encontrar una antiderivada para f (x) = 7x6 .
dy
Solución: Basta observar que para y = x7 , entonces dx
= 7x6 .
7
y si tuvieramos y = x + C, donde C es una constante, y = 7x6
Por consiguiente,
la antiderivada de y = 7x6 es y = x7 + C, donde C es una constante.
Como podemos observar,
√ una función puede tener muchas antiderivadas. Por ejemplo, las funciones f (x) =
x7 + 3, f (x) = x7 + 3 2, f (x) = x7 − π y f (x) = x7 son antiderivadas de 7x6
Graficamente podemos observar algunas antiderivadas de f (x) = 2x
La antiderivada en su forma general es f (x) = x2 + C
4
y
La gráfica corresponde con las funciones:
f (x) = x2 + 2
f (x) = x2 + 1
f (x) = x2
f (x) = x2 − 1
f (x) = x2 − 2
f (x) = x2 − 3
3
2
1
x
−4
−3
−2
−1
1
2
3
4
5
−1
−2
−3
−4
Si f (x) = 0 para todo x en un intervalo (a, b), entonces f (x) = C, en todo este intervalo donde C es una
constante.
Como la razón de cambio de la función f (x) en un intervalo dado es 0, la función es una constante arbitraria
C.
Teorema: Si f (x) = g (x) para todo x ∈ (a, b), entonces f (x) = g (x) + C.
donde C es una constante.
Esto es, si las derivadas de dos funciones son iguales, las funciones se diferencian de una constante aditiva.
Corolario: La antiderivada más general de f está definida por
f (x) + C
donde f es una antiderivada particular de f y C es una constante arbitraria. Todas la antiderivadas de f se
pueden obtener de esta, dando valores a C particulares. Se le llama familia de antiderivadas.
3
Ejemplos:
Encuentre la familia de antiderivadas de las siguientes funciones:
1. g (x) = 3x2
Debemos encontrar una G (x) tal que G (x) = g (x)
Sabemos 3x2 es la derivada de x3 , entonces una antiderivada de g (x) = 3x2 es x3 . De forma general, la
familia de antiderivadas de g (x) es
G (x) = x3 + C
2. h (x) = cos x
Debemos encontrar una H (x) tal que H (x) = h (x)
d
Sabemos, dx
[sen (x)] = cos x, entonces una antiderivada para h (x) = cos x es sin x. De forma general, la
familia de antiderivadas de h (x) es
H (x) = sin x + C
3. v(t) = 540 − 5t2
Debemos encontrar una V (t) tal que V (t) = v(t). Para el caso la solución es:
5
V (t) = 540t − t3 + C
3
Por qué?
Ejercicios
Encuentre la familia de antiderivadas de las siguientes funciones:
1. f (x) = x
4. v(t) = 2t2 − 34
2. g(x) = 3 cos x
3. h(x) = 5x11
5. v(t) = sec2 t
Notación de las Antiderivadas
El símbolo utilizado para simbolizar la antiderivada de una función es
...dx
.
Leibniz, uno de los protagonistas en la creación del cálculo integral diseñó este símbolo, que goza de gran
popularidad quien escribía de la siguiente forma:
f (x) dx
Siguiendo el lenguaje de Leibniz , ahora usaremos el término de integral indefinida para referirnos a la
antiderivada, por consiguiente, integrar es antiderivar.
Teorema (Regla de potencias)
Si r es un número Real cualquiera diferente de −1, entonces
xr+1
xr dx =
+C
r+1
4
Ejemplos:
x3+1
x4
+C =
+C
3+1
4
4+1 5
x
x
4
+ C = 125
+ C = 25x5 + C
2.
125x dx = 125
4+1
5
−1 −2+1 x
x
5
=5
+ C = −5x−1 + C = − + C
3.
5x−2 dx = 5
−2 + 1
−1
x
1.
x3 dx =
Nota: En el caso de que r = 0, tenermos lo suguiente:
x0+1
x0 dx =
+C =x+C
1
en conclusión,
dx = x + c
Propiedades de las integrales indefinidas
Sean f (x) y g (x) funciones contínuas, y c ∈ , se tiene que
1.
[f (x) + g (x)] dx = f (x) + g (x)
2.
3.
cf (x) dx = c
f (x) dx
[f (x) − g (x)] dx =
f (x) dx −
g (x) dx
Tabla de integrales indefinidas básicas
1.
kdx = kx + C
2.
3.
4.
5.
6.
7.
xn dx =
xn+1
+C
n+1
(n = −1)
1
dx = ln |x| + C
x
8.
9.
10.
ex dx = ex + C
ax dx =
x
a
+C
ln a
senxdx = − cos x + C
cos xdx = senx + C
11.
12.
13.
sec2 xdx = tan x + C
csc2 xdx = − cot x + C
sec x tan xdx = sec x + C
csc x cot xdx = − csc x + C
1
dx = tan−1 x + C
x2 + 1
√
2
1
dx = sen−1 x + C
1 − x2
Ejemplos
Encuentre la antiderivada o integral indefinida en cada una de las expresiones dadas:
1. f (x) = (x − 1)3
Solución:
5
3
(x − 1)3 dx =
x − 3x2 + 3x − 1 dx
x4
3x3
3x2
= x3 dx − 3x2 dx + 3xdx − 1dx =
−
+
−x+C
4
3
2
3x2
x4
− x3 +
−x+C
=
4
2
sec x
2.g (x) =
cos x
sec x
1
dx, reemplazamos
= sec x
cos
x
cos
x
2
sec x sec xdx = sec xdx = tan x + C
4
3.h (x) = 3
3x
4
4 1
4 −2
dx =
dx =
x dx
2
2
3x
3 x
3
4
−4
= (−1) x−1 + C =
+C
3
3x
4. v (t) = π (16 cos t − 4t)
π (16 cos t − 4t) dt = π (16 cos t − 4t) dt = π 16 cos tdx − 4tdt
4t2
= π 16sent −
+ C = 16πsent − 2πt2 + C
2
5. s (t) = 3sen2 x 1 − cos2 x
3sen2 x
3sen2 x
dx =
dx
2
(1 − cos x)
sen2 x
3dx = 3x + C
Ejercicios:
Encuentre la antiderivada de las siguientes funciones:
1. y = (x − 1) (x − 2)
√
3
2. y = x19 + 2
3. y =
1.2.
3
x7
4. y = π x +
3 cos x
sen2 x
5. y = 3ex − 2
Suma de Riemann (Integral Definida)
Si intentamos conocer el área de una región, una alternativa sería subdividir esta región en regiones cuyas áreas
sean conocidas.
Problema: Hallar el área de la región S que está debajo de la curva y = f (x), desde a hasta b
Esto significa, que debemos hallar el área de la región comprendida entre el eje x, cuyo límite inferior es a y el
límite superior es b, además la función debe ser contínua y f (x) ≥ 0
6
S = {(x, y) | a ≤ x ≤ b, 0 ≤ y ≤ f (x)}
No es fácil hallar el área de una región con lados curvos, sabemos encontrar el área de un rectánculo, de un
triángulo, pero no de una región curva.
Podemos iniciar aproximando el área bajo la curva dividiendo la región en rectángulos de la siguiente manera:
A = a1 + a2 + a3 + a4 + a5
Como vemos en el gráfico anterior, estamos aproximando el área de la curva, por medio de la suma de estos
rectángulos; calculando la altura f (x) sobre el lado derecho de cada rectángulo. Pero, podría ser de otras formas.
7
B = b1 + b2 + b3 + b4
Como vemos en el gráfico anterior, estamos aproximando el área de la curva, por medio de la suma de estos
rectángulos; hemos calculador la altura f (x) por izquierda de cada rectángulo.
Sea S la región bajo la curva, entonces para el caso
A < Área de S < B
y al aumentar el número de rectángulos en el intervalo (a, b), nos estaremos aproximando cada vez más al área
real.
Si el ancho de cada rectángulo es lo suficientemente pequeño o muy cercano a cero; el número de rectángulos
en una región tiende a ∞.
Apliquemos esta idea a la región más general S. Empecemos a subdividir S en n franjas S1 , S2, S3,..., Sn de
anchos iguales. el ancho del intervalo [a, b] es b − a, de modo que el ancho de cada una de las n franjas es:
∆x =
b−a
n
Estas franjas dividen el intervalo [a, b], en n subintervalos
[x0 , x1 ] ,
[x1 , x2 ] ,
[x2 , x3 ] ,
...,
[xn−1 , xn ]
donde x0 = a y xn = b
Obtengamos una aproximación de la i_ésima franja, Si ,con un rectángulo con ancho ∆x y altura f (xi ), que
es el valor de f en los extremos de la derecha
8
El área del i_ésimo rectángulo es f (xi ) ∆x
Podemos decir que el área de toda la región S se aproxima con la suma de las áreas de estos rectángulos
Rn = f (x1 ) ∆x + f (x2 ) ∆x + f (x3 ) ∆x + ... + f (xn ) ∆x
Si la cantidad de rectángulos tiende a infinito, podemos definir el área de una región S de la siguiente manera:
Definición
El área A de la región S, que se encuentra entre la función f y el eje x es:
A =
A =
A =
lı́m Rn
n→∞
lı́m [f (x1 ) ∆x + f (x2 ) ∆x + f (x3 ) ∆x + ... + f (xn ) ∆x]
n→∞
lı́m
n→∞
n
f (xi )∆x
i=1
De hecho, en vez de utilizar los puntos laterales de cada triángulo, podemos tomar la altura del i_ésimo
rectángulo como el valor de f en cualquier número x∗i en el i_ésimo subintervalo [xi−1 , xi ]
9
Podemos escribir la expresión del área de la siguiente forma
A = lı́m
n→∞
n
f (x∗i )∆x
i=1
A este tipo de límite le damos nombre y notación especial.
Definición (Suma de Riemann o Integral Definida)
Si f es una función
contínua definida para a ≤ x ≤ b, dividimos el intervalo [a, b] en n subintervalos de igual
b−a
ancho ∆x =
. Denotamos con x0 , x1 , x2 ..., xn los puntos extremos de estos subintervalos y elegimos los
n
puntos muestra x∗1 , x∗2 , ..., x∗n en estos subintervalos, de modo que si x∗i se encuentra en el i_ésimo subintervalo
[xi−1 , xi ]. Entonces la integral definida o Suma de Riemann de f , desde a hasta b es
b
f (x) dx = lı́m
n→∞
a
n
f (x∗i ) ∆x
i=1
Es el nombre de Suma de Riemann en honor al matemático Bernhard Riemann (1826-1866)
Si f toma tanto valores positivos como negativos, entonces la suma de Riemann es la suma de las áreas de los
rectángulos que se encuentran arriba del eje x y los negativos de las áreas de los rectángulos que están debajo
del eje x. Puede interpretarse como una diferencia de áreas.
b
a
f (x) dx = A1 − A2
Ejemplo
Exprese
lı́mn→∞
n
i=1
π x16
i + cot xi ∆x, como una integral en el intervalo 2 , π
Podemos darnos cuenta que esta expresión tiene la forma de una Suma de Riemann, ahora debemos identificar
la función y los puntos muestra de la siguiente manera:
f (x) = x16 + cot x
x∗i = xi
a = π2 , b = π
Luego
π
16
lı́mn→∞ ni=1 x16
+
cot
x
∆x
=
x + cot x dx
i
i
π
2
10
Ejemplo 1
Exprese
n
lı́mn→∞
i=1
Solución
f (x) = ln x
x∗i = xi
a=1 , b=5
[ln xi ] ∆x, como una integral en el intervalo [1, 5]
lı́mn→∞
n
i=1 [ln xi ] ∆x =
5
ln xdx
1
Ejemplo 2
Exprese
lı́mn→∞
f (x) = e−2x − cos5 x
x∗i = xi
√
a=0 , b= 37
n
i=1
√ e−2xi − cos5 xi ∆x, como una integral en el intervalo 0, 3 7
lı́mn→∞
n
i=1
−2xi
e
5
− cos xi ∆x =
0
√
3
7
−2x
e
− cos5 x dx
Ejemplo 3
b
b
a.Exprese a f (x) dx = a xdx como una Suma de Riemann, tomando los puntos extremos derechos como
a = 1 , b = 2; n = 5
b. Evalúela la integral usando la definición de integral definida
Solución:
a. Para expresar la función como una suma de Riemann es necesario conocer los límites de la integral y la
función y el ancho del intervalo.
→Ancho del intervalo
∆x =
b−a
2−1
1
=
= = 0, 2
n
5
5
De modo que la suma de Riemann es
5
R6 =
f (xi )∆x
i=1
R5 = f (1,2)∆x + f (1,4)∆x + f (1,6)∆x + f (1,8)∆x + f (2)∆x
R5 = 1,2∆x + 1,4∆x + 1,6∆x + 1,8∆x + 2∆x
R5 = ∆x (1,2 + 1,4 + 1,6 + 1,8 + 2)
R5 = 0,2 (8)
R5 = 1,6
b.
2
1
∆x =
xdx = lı́m
n→∞
n
f (xi ) ∆x
i=1
b−a
,evaluándo en toda el intervalo tenemos,
n
11
1
n entonces
∆x =
n
3i 1
xdx = lı́m
f
n→∞
n n
1
i=1
n 3i 1
1 n 3i
= lı́mn→∞
= lı́mn→∞
i=1
i=1 n
n n
n
3 n
1 3n2 + 3n
= lı́mn→∞ 2
i = lı́mn→∞ 2
i=1
n
n
2
3n2 + 3n
3
=
= lı́mn→∞
2n2
2
2
Propiedades de las integrales definidas
Sean f (x) y g (x) funciones contínuas, y c ∈ , se tiene que
1.
b
f (x) dx = −
a
2.
a
a
f (x) dx
5.
b
f (x) dx = 0
a
3.
b
cdx = c(b − a)
a
4.
a
6.
b
[f (x) + g (x)] dx =
a
b
f (x) +
b
g (x)
7.
a
b
cf (x) dx = c
a
b
f (x) dx
a
b
[f (x) − g (x)] dx =
a
c
f (x) dx +
a
a
b
f (x) −
b
f (x) dx =
c
b
g (x)
a
b
f (x) dx
a
TEOREMA FUNDAMENTAL DEL CÁLCULO
Este teorema proporciona la relación entre la derivación y la integración. Aunque la derivación se obtiene del
estudio de las tangentes y la integración del estudio del área; como procesos matemáticos son inversos.
El teorema fundamental del cálculo presenta la relación inversa precisa entre la derivada e integral.
Teorema parte 1:
Si f es continua en [a, b] , la función g definida por
x
g (x) = a f (x) dx,
a≤x≤b
es continua en [a, b] y derivable en (a, b), y g (x) = f (x)
Teorema parte 2
Si f es continua en [a, b], entonces
b
a
f (x) dx = F (b) − F (a)
donde F es cualquier antiderivada de f , esto es, una función tal que F = f
Nota: Tener en cuenta que la función debe ser continua
Ejemplos
x
1. Determine la derivada de h (x) = 0 (4sent − 3 cos t)3dt
Solución: como f (t) = 4sent − 3 cos t es continua y aplicando el Teorema Fundamental del Cálculo
(parte 1), tenemos que
h (x) = 4senx − 3 cos x
b
x
2. Determine la derivada de R (x) = 0 cos (3m) dm + b cos (3m) dm
Solución: Aplicando propiedad aditiva de las integrales definidas tenemos que
12
b
0
cos (3m) dm +
x
b
cos (3m) dm =
x
0
cos (3m) dm
entonces como f (m) = cos (3m) es continua y aplicando el Teorema Fundamental del Cálculo (p 1),
tenemos que
R (x) = cos (3x)
π
3. Evalúe al integral 0 2 cos xdx
Solución: La función es continua en todo el intervalo y la antiderivada de f (x) = 2 cos x es
F (x) = 2senx, por lo tanto
π
2 cos xdx = 2senx]π0 = 2senπ − 2sen0 = 0
0
4. Evalúe la integral
3 x3
dx
−2 64
Solución: La función es continua en todo el intervalo y la antiderivada de f (x) =
F (x) =
x4
, por lo tanto
256
x3
es
64
3 x3
x4 3
34
(−2)4
81
16
65
=
dx
=
]
−
=
−
=
−2
−2 64
256
256
256
256 256
256
Ejercicios
1-5. Encuentre la derivada de las siguientes funciones
x
dt
1. g(x) =
32
16
0 y t + t + 2
2. h(y) =
log4 162x dx
0
x
3. j(x) =
cos3 y 8
y
dδ
2
0x sen δ
1
t
5. l(x) =
−
e
dt
2t7 + 1
0
4. g(y) =
0
6-10 Evalúe las siguientes integrales utilizando parte del teorema fundamental del Cálculo
6.
7.
3
−3
π
2
dx
135x2 − 1
4senxdx
0 5 t
1
8.
dx
5
2
2
9.
10.
3π
2
cos x sec xdx
π
1
2
dx
x
TECNICAS DE INTEGRACIÓN
1.3.
Integración por sustitución Simple o Compuesta
En el anterior tema, analizamos las relaciones que existen entre la derivada y la integral; aprendimos a evaluar
integrales definidas y sabemos hacer el proceso con funciones básicas y utilizando las propiedades.
Existen algunas Técnicas de integración que son de gran ayuda para evaluar integrales de funciones compuestas.
Comenzaremos el estudio de las técnicas de integración con la Sustitución Simple o Directa.
Regla de sustitución simple o directa de las integrales indefinidas
Si u = g(x) es una función diferenciable, cuyo rango es un intervalo I y f es continua sobre I, entonces
13
f (g(x)g (x)) dx =
f (u)du
Ejemplo 1 Encuentre 2x x2 + 5 dx
Solución: Como sabemos, la derivada de x2 + 5 es 2xdx, entonces haremos la sustitución siguiente:
u = x2 + 5
Ahora sustituimos en la integral
Resolvemos
du = 2xdx
2x x2 + 5 dx =
udu
2
2
x +5
u2
udu =
+C =
+C
2
2
Debemos dar solución en
variable original
√ de la
función
Ejemplo 2 Encuentre x2 2 x3 − 7 dx
Solución: Como sabemos, la derivada de x3 − 7 es 3x2 dx, entonces haremos la sustitución:
u = x3 − 7
Sustituyendo en la integral
du = 3x2 dx ⇒
du
= x2 dx
3
√
2
2
3
x
x − 7 dx =
udu
2
Resolvemos
Ejemplo 3 Encuentre
2
3
3
2 x3 − 7 2
2u 2
(u) du =
+C =
+C
3
3
1
2
8 dx
(x + 5)
Solución: tomando: u = (x + 5)
Sustituimos en la integral tenemos
du = dx
2
(x + 5)
8 dx =
2du
u8
Luego
2du
=
u8
2u−8 du = 2
u−7
2
−2
= − (x + 5)−7 =
−7
7
7(x + 5)7
14
1 + 8x
√
dx
2
5 + x + 4x2 Solución: Como sabemos, la derivada de 5 + x + 4x2 es (1 + 8x), entonces haremos la sustitución siguiente:
Ejemplo 4 Encuentre
Ahora sustituimos en la integral
u = 5 + x + 4x2
√
2
du = (1 + 8x) dx
1 + 8x
dx =
5 + x + 4x2
du
√
2
u
Luego
du
√
=
2
u
1
(u)
−1
2
du = 2
u2
2
+ C = 2 5 + x + 4x2 + C = 2 5 + x + 4x2 + C
1
Ejemplo 5 Encuentre sen2 x cos xdx
Solución: Como sabemos, la derivada de (senx) es (cos x) dx, entonces haremos la sustitución siguiente:
u = (senx)
du = (cos x) dx
Ahora sustituimos en la integral
Resolvemos
Ejemplo 6 Encuentre
sen2 x cos xdx =
u2 du =
u2 du
u3
sen3
+C =
+C
3
3
√
ex 2 3 + ex dx
Solución: Como sabemos, la derivada de (3 + ex ) es ex dx, entonces haremos la sustitución siguiente:
u = (3 + ex )
du = ex dx
Ahora sustituimos en la integral
Resolvemos
√
2
√
√
ex 2 3 + ex dx = 2 udu
udu =
3
1
u 2 du =
2u 2
=
3
2
3
Ejemplo 7 Encuentre ex cos ex dx
Solución: tomando :u = ex
du = ex dx
Ahora sustituimos en la integral
x
e cos ex dx = cos udu
Resolvemos
15
3
(3 + ex ) 2
cos udu = sin u + C = sin ex + C
Ejemplo 8 Encuentre sec2 (x) tan (x) dx
Solución: Como sabemos, la derivada de (sec x) es (sec (x) tan (x)), entonces haremos la sustitución
siguiente:
u = sec x
du = sec x tan xdx
Ahora sustituimos en la integral
Resolvemos
Ejemplo 9 Encuentre
sec2 (x) tan xdx =
udu =
udu
u2
sec2 x
+C =
+C
2
2
cos x cos(senx)dx
Solución: Como sabemos, la derivada de (sin x) es (cos xdx), entonces haremos la sustitución siguiente:
u = sin x
du = cos xdx
Ahora sustituimos en la integral
Resolvemos
Ejemplo 10 Encuentre
√
4
cos x cos(senx)dx =
cos udu
cos udu = sin u + C = sin(sin x) + C
x
dx
x+1
Solución: Como sabemos, la derivada de (x + 1) es (dx), entonces haremos la sustitución siguiente:
u=x+1
despejando tenemos x = u − 1
du = dx
Ahora sustituimos en la integral
Resolvemos
u
√
4 u dx
−
(u−1)
√
4 u dx
1
√
4 u dx
=
=
u
√
4 u dx
√
4
u3 dx −
7
−
1
√
4 u dx
7
1
√
4 u dx
3
=
4 (x + 1) 4
4 (x + 1) 4
=
−
+C
7
3
Ejercicios
x
1.
e sec ex dx
x
dx
2.
2
x +1
16
3
4u 4
4u 4
−
+C
7
3
cos (ln x) dx
x
4.
csc 2tdt
3.
esin z
dz
sec z
Regla de sustitución simple o directa de las integrales definidas
Si g es continua en [a, b] y f lo es en la imagen de u = g(x), entonces
b
g(b)
f (g(x)g (x))dx =
f (u)du
5.
a
g(a)
Ejemplo 1 Encuentre 0 (2x + 3) x2 + 3x dx 2
Solución:
2 Como
sabemos, la derivada de x + 3x es (2x + 3), entonces haremos la sustitución siguiente:
u = x + 3x
du = (2x + 3) dx
2
Como la integral es definida, debo encontrar los nuevos límites
Si x = 0 ⇒ u = 0
,
x = 2 ⇒ u = 10
Ahora sustituimos en la integral
2
0
Resolvemos
10
(2x + 3) x2 + 3x dx = 0 udu
10
0
Ejemplo 2 Encuentre
1
udu =
u2 10
| = 50 | 5
2 0
cos (πt) dt
0
Solución: Como sabemos, la derivada de (πt) es (πdt), entonces haremos la sustitución siguiente:
du
u = (πt)
du = πdt ⇒ dt =
π
Como la integral es definida, debo encontrar los nuevos límites
Si t = 0 ⇒ u = 0
,
t=1⇒u=π
Ahora sustituimos en la integral
1
cos πtdt =
0
Resolvemos
0
Ejemplo 3 Encuentre
π
π
0
cos udu
π
cos udu
1
π
= [sin u]0 = 0
π
π
π
4
sin 4tdt
0
Solución: Como sabemos, la derivada de (4t) es (4dt), entonces haremos la sustitución siguiente:
du
u = (4t)
du = 4dt ⇒ dt =
4
Como la integral es definida, debo encontrar los nuevos límites
Si t = 0 ⇒ u = 0
,
t = π4 ⇒ u = π
Ahora sustituimos en la integral
17
π
4
sin 4tdt =
π
sin udu
4
0
0
Resolvemos
π
0
1
1
sin udu
1
π
= [− cos u]0 = − [−1 − 1] =
4
4
4
2
1
dx
(x
−
2)3
0
Solución: Como sabemos, la derivada de (x − 2) es (dx), entonces haremos la sustitución siguiente:
u = (x − 2)
du = dx
Como la integral es definida, debo encontrar los nuevos límites
Si x = 0 ⇒ u = −2
,
x = 1 ⇒ u = −1
Ejemplo 4 Encuentre
Ahora sustituimos en la integral
0
1
dx
=
(x − 2)3
−1
−2
du
u3
Resolvemos
−1
u−3 du =
−2
Ejemplo 5 Encuentre
0
1
2
−u−2
2
−1
−2
sin−1 x
√
dx
1 − x2
−1
3
1
1 1
= − 2
=− + =−
2u −2
2 8
8
Solución: Como sabemos, la derivada de sin−1 x es √
u = sin−1 x
1
du = √
dx
1 − x2
1
dx, entonces haremos la sustitución siguiente:
1 − x2
Como la integral es definida, debo encontrar los nuevos límites
Si x = 0 ⇒ u = 0
,
x = 12 ⇒ u = π
Ahora sustituimos en la integral
0
1
2
sin−1 x
√
dx =
1 − x2
Resolvemos
u2
2
π
=
0
Ejercicios
1.
π
6
2sin x cos xdx
0
2.
0
π
2
cos xdx
1 + sin2 x
18
π2
2
0
π
udu
1
2
x10x dx
√
34
cos 1 − x
√
4.
dx
1−x
0
π2
sin x
5.
dx
16 + cos2 x
0
3.
1.4.
0
Integración por Partes
Si fracasa la integración por sustitución, puede intentarse una doble sustitución, mejor conocida como integración
por partes.
Este método se basa en la fórmula diferencial de un producto.
d (u.v) = udv + vdu
de donde, udv = d(u.v)
− vdu
integrando tenemos, udv = u.v − vdu + C
Se trata, de encontrar una integral vdu, en lugar de la propuesta originalmente udv. El método, como es natural,
solo tiene aplicación, si la segunda integral es más sencilla que la primera.
Ejemplo 1 Encuentre xex dx
Solución: Para aplicar la integración por partes, queremos escribir el integrando de la forma udv.
Hay varias formas de hacerlo, y lo esncial es encontrar la que me simplifique a una más sencilla; ahora muestro
las diferentes formas:
1. u = x
dv = ex dx
x
2. u = e
dv = xdx
3. u = 1
dv = xex dx
x
4. u = xe
dv = dx
Siguiendo las normas, elegimos la primera opción, puesto que ex es la parte más complicada del integrando que
se ajusta a una fórmula básica de integración.
Por tanto,
u=x
dv = ex dx
⇒
⇒
du =dx
v = dv = ex dx = ex
Utilizando la técnica de integración por partes tenemos,
= u.v − vdu
udv
x+ C
x
x
xe
dx
=
xe
−
e dx
x
xe dx = xex − ex + C
Ejemplo 2 Encuentre x2 ln xdx
En este caso se integra más fácilmente x2 que lnx; además, la derivada de lnx es sencilla.
Entonces,
1
u = ln x
⇒
du = dx
x
x3
dv = x2
⇒
v = dv =
3
udv = u.v − vdu + C
19
x3 1
x2
x3
x3
x3
x3
ln x −
dx =
ln x −
dx =
ln x −
+C
3
3 x
3
3
3
9
x2 ln xdx =
Ejemplo 3 Encuentre ln xdx
En este caso se integra más fácilmente dx que ln x; además, la derivada de lnx es sencilla.
Entonces,
1
u = ln x
⇒
du = dx
x
dv = dx
⇒
v = dv = dx = x
vdu + C
1
ln xdx = x ln x − x dx = x ln x − dx = x ln x − x + C
x
Ejemplo 4 Encuentre x cos xdx
En este caso se integra más fácilmente cos x; además, la derivada de x es dx.
Entonces,
u=x
⇒
du = dx
dv = cos xdx
⇒
v = dv = cos xdx = sin x
udv = u.v −
udv = u.v − vdu + C
x cos xdx = x sin x − sin xdx = x sin x − − cos x = x sin x + cos x + C
Ejemplo 5 Encuentre
Entonces,
u = sec x
dv = sec2 xdx
⇒
sec3 xdx
(caso especial)
du = sec
x tan xdx
v = dv = sec2 xdx = tan x
⇒
= u.v − vdu + C
sec3 xdx =
sec x sec2 xdx = sec x tan x − tan x sec x tan xdx
= sec x tan x − tan x sec x tan xdx = tan x sec x − tan2 x sec xdx
2
= tan x sec x −
sec x − 1 sec xdx
3
= tan x sec x − sec xdx + sec xdx
udv
y como
3
=
3
tan x sec x − sec xdx + sec xdx =⇒
sec3 xdx + sec3 xdx = tan x sec x + sec xdx
3
2 sec xdx = tan x sec x + sec xdx = tan x sec x + ln [sec x + tan x] + c
sec xdx
20
entonces
Ejercicios
1. ln xdx
xex
2.
dx
+ 1)2
(x
3. x2 ln2 xdx
4. xex dx
2
5. x3 ex dx
2
6. x sin xdx
1.5.
1.5.1.
sec3 xdx =
1
[tan x sec x + ln (sec x + tan x)] + c
2
Integrales que contienen Funciones Trigonométricas
Integrales de senos y cosenos
1. Si la potencia del seno es positiva e impar, quédese con un factor seno y convierta los restantes
factores en cosenos.
Ejemplo
2
4
sin3 x cos4 xdx = sin
x cos 2x (sin
x) dx (guardar sin x)
= 1 − cos x cos4 x (sin x) dx
= cos4 x − cos6 x (sin x) dx
4
6
= cos
x4sin xdx − cos x
sin xdx
= − cos x (− sin x) dx + cos6 x (− sin x) dx (sea u = cos x ⇒ du = − sin xdx)
cos5 x cos7 x
sin3 x cos4 xdx = −
+
+c
5
7
2. Si la potencia del coseno es positiva e impar, quédese con un factor coseno y convierta los
restantes factores en senos.
Ejemplo
sin2 x cos5 xdx = sin2 x cos4 x (cos x) dx (guardar cos x)
2
= sin2 x cos2 x cos xdx
2
= sin2 x 1 − sin2 x cos xdx
= sin2 x 1 − 2 sin2 x + sin4 x cos xdx
2
=
sin x − 2 sin4 x + sin6 x cos xdx
= sin2 x cos xdx − 2 sin4 x cos xdx + sin6 x cos xdx (sea u = sin x ⇒ du = cos xdx)
sin3 x 2 sin5 x
sin7 x
sin2 x cos5 xdx =
−
+
c
3
5
7
3. Si la potencia de ambos seno y coseno son pares y no negativas, utilice las siguientes
identidades:
sin2 x =
1 − cos 2x
2
y cos2 x =
A continuación se procede como en el caso número 2.
Ejemplo
1 − cos 2x
1 + cos 2x
sin2 x cos2 xdx =
dx
2
2
21
1 + cos 2x
2
1
1 − cos2 2x dx
4
1
1
dx −
cos2 2xdx
=
4
4
1
1 1 + cos 4x
dx
= x−
4
4
4
1
1
1
= x− x−
sin 4x+ c
4
16
16
=
Ejercicios
1. sin5 2x cos 2xdx
2. cos2 3xdx
3. sin4 x cos2 xdx
4. cos3 x sin xdx
5. sin4 x cos4 xdx
6. sin2 x cos4 xdx
1.5.2.
Integrales de Secantes y de Tangentes
1. Si la potencia de la secante es positiva y par, quédese con un factor de la secante al cuadrado
y convierta los restantes factores en tangentes.
Ejemplo
3
4
si u = tan 3x ⇒ du = 3 sec2 3xdx
Entonces:
sec4 3x tan3 3xdx
3
2
2
sec 3x tan xdx = sec 3x
tan
3x
sex
3x
dx
=
1 + tan2 3x tan3 3x sec2 3x dx
1 3
=
tan 3x + tan5 3x 3 sec2 3x dx (sea u = tan 3x ⇒ du = 3 sec2 3xdx)
3
1
1
tan3 3x 3 sec2 3x dx +
tan3 3x 3 sec2 3x dx
=
3
3
1 tan4 3x tan6 3x
=
+
+c
3
4
6
2. Si la potencia de la tangente es positiva e impar, quédese con un factor secante-tangente y
covierta los restantes factores en secantes.
Ejemplo
tan3 x
1
3 3 √
dx = (sec x)− 2 tan3 xdx = (sec x)− 2 tan2 x (sec x tan x) dx = (sec x)− 2 sec2 x − 1 (sec x tan x) dx
sec x
3 1
3
= (sec x)− 2 sec2 x − 1 (sec x tan x) dx =
(sec x) 2 − (sec x)− 2 (sec x tan x) dx
(sea u = sec x ⇒ du = sec x tan xdx)
tan3 x
3
−3
√
dx = (sec x) 2 + 2 (sec x) 2 + c
sec x
3. Si no hay factores de la secante y la potencia de la tangente es positiva y par, convierta un
factor tangente cuadrado en secantes.
Ejemplo
2
2
2
2
tan4 xdx = tan2 x tan2 xdx =
tan
x
sec
x
−
1
dx
=
tan
x
sec
xdx
−
tan2 xdx
= tan2 x sec2 xdx − sec2 x − 1 dx
22
(sea u = tan x ⇒ du = sec2 xdx)
tan3 x
tan4 xdx =
− tan x + x+ c
3
4. si no se está en ninguna de las tres situaciones previas, intente reescribir el integrando en términos
de senos y cosenos.
Ejemplo
sec x
1
cos x 2
dx
=
dx = (sin x)−2 cos xdx = −(sin x)−1 + c = − csc x+ c
2
cos x
sin x
tan x
Ejercicios
1.
2.
3.
4.
5.
sec3 xdx
sec4 5xdx
tan2 x sec2 xdx
csc2 3x cot 3xdx
sec6 4x tan 4xdx
1.6.
Integración por Sustitución Trigonométrica
Este método se utilixa cuando la función integrando contiene expresiones de la forma:
+
a2 − x2
+
x2 − a2
ax2 + bx + c
El objetivo con las sustituciones trigonométricas consisite en eliminar los radicales del integrando.
Ejemplo 1 Encuentre
√
3 − x2
dx
x2
√
x
dx
En el triángulo anterior sin θ = √ , derivando se obtiene cos θdθ = √ ⇒ 3 cos θdθ = dx
3
3
√
√
√
3 − x2
√
y cos θ =
⇒
3 cos θ = 3 − x2 , luego la integral quedaría de la siguiente forma:
3
√
√
√
2
3 cos θ
3 cos θ
3 − x2
cos2 θ
2
dx
=
dθ
=
dθ
=
cot
θdθ
=
csc θ − 1 dθ
2
2
2
x
3 sin θ
sin θ
2
csc θ − 1 dθ = − cot θ − θ+c reemplazando del triángulo se obtiene que
√
√
3 − x2
3 − x2
x
dx = −
− arcsin √
+c
x2
x
3
Ejemplo 2 Encuentre
dx
√
x 4 + x2
23
x
dx
En el triángulo anterior tan θ = , derivando se obtiene sec2 θdθ =
⇒ 2 sec2 θdθ = dx
2
2
√
√
4 + x2
y sec θ =
⇒ 2 sec θ = 4 + x2 , luego la integral quedaría de la siguiente forma:
2
1
2
dx
√
=
x 4 + x2
1 2 sec2 θ
1
1
(sec θ)
1
cos θ
θ
cos
dθ
=
dθ =
dθ =
dθ
sin
θ
(2 tan θ) (2 sec θ)
2
tan θ
2
2
cos θ sin θ
cos θ
cos θ
1
dθ
1
dθ =
=
csc θdθ
cos θ sin θ
2 sin θ
2 √
4 + x2
dx
1
2
√
=
ln
−
+c
2
x
x
x 4 + x2
Ejemplo 3 Encuentre
√
reemplazando del triángulo se obtiene que
x2
dx
x2 − 9
x
dx
En el triángulo anterior sec θ = , derivando se obtiene sec θ tan θdθ =
⇒ 3 sec θ tan θdθ = dx
3
3
√
√
x2 − 9
y tan θ =
⇒ 3 tan θ = x2 − 9, luego la integral quedaría de la siguiente forma:
3
x2
√
dx =
x2 − 9
2 2 3 sec θ (3 sec θ tan θ)
dθ = 9 sec3 θdθ
3 tan θ
1
Como ya vimos,
sec3 θdθ = [tan θ sec θ + ln (sec θ + tan θ)] + c
Luego,
2
1
9 sec3 θdθ = 9
[tan θ sec θ + ln [sec θ + tan θ]] +c Reemplazando del triángulo se obtiene que:
2
√
√
1
x2 − 9 x
x
x2 − 9
1
9
[tan θ sec θ + ln [sec θ + tan θ]] +c = 9
+ ln
+
+c
2
2
3
3
3
3
√
x2
x x2 − 9
√
dx = 27
+ ln x + x2 − 9 +c
6
x2 − 9
Ejercicios
dx
√
1.
2
x − 6x + 10
(complete cuadrado)
dx
2.
2
2
(x + 1)
dx
3.
3
2
(x − 4x) 2
dx
4. √
x3 x2 − 9
24
1.7.
Integración por Fracciones Parciales
En este método se podrá ver cómo se integra cualquier función racional (como razón de polinomios)
expresándola como una suma de fracciones más simples, llamadas fracciones parciales.
Para ver cómo funciona en general el método de fracciones parciales, trabajaremos sobre una función
racional.
f (x) =
P (x)
Q(x)
en donde P y Q son polinomios
Es posible expresar a f (x) como una suma de fracciones más sencillas, siempre que el grado de P
sea menor que el grado de Q. Esa función racional se llama propia.
si P (x) = an xn + an−1 xn−1 + ... + a1 x + a0 en donde an es diferente de cero, el grado de P (x) es n.
f (x) es impropia si el grado de P (x) es mayor o igual al gardo de Q(x), el primer paso es dividir Q(x)
entre P (x), hasta obtener un residuo R(x), tal que el grado de R(x) sea menor que el grado de Q(x).
P (x)
R(x)
Es decir,
f (x) =
= S(x)+
, en donde R y S son polinomios.
Q(x)
Q(x)
Caso 1 El denominador Q(x) es un producto de factores lineales distintos.
x2 + 2x − 1
dx como el grado del numerador es menor que el grado del
2x3 + 3x2 − 2x
denominador no necesitamos dividir.
Ejemplo Evalue
2x3 + 3x2 − 2x = x 2x2 + 3x − 2 = x(2x − 1) (x + 2)
Como los tres factores lineales son distintos, la descomposición en fracciones parciales queda:
x2 + 2x − 1
A
B
C
= +
+
, hallamos los valores A, B, C
x(2x − 1) (x + 2)
x
2x − 1 x + 2
x2 + 2x − 1 = A(2x − 1) (x + 2) + Bx(x + 2) + Cx(2x − 1) = (2A + B + 2C)x2 + (3A + 2B − C)x − 2A
igualamos los coeficientes de x2 , x y también de las constantes.
2A + B + 2C
=1
3A + 2B − C
=2
−2A
= −1
Al resolver el sistema obtenemos:
1
luego,
A = 12 , B = 15 , C = 10
x2 + 2x − 1
dx =
2x3 + 3x2 − 2x
11 1 1
1 1
1
1
1
+
−
dx = ln (x) +
ln (2x − 1) −
ln (x + 2) + c
2 x 5 2x − 1 10 x + 2
2
10
10
25
Caso 2
Q(x) es un producto de factores lineales, algunos de los cuales se repiten.
Ejemplo Evalue
x2 + 2x + 3
dx
(x − 1) (x + 1)2
la descomposición en fracciones parciales queda:
x2 + 2x + 3
A
B
C
+
+
x
−
1
x
+
1
(x − 1) (x + 1)
(x + 1)2
2
2
x + 2x + 3 = A (x + 1) + B (x + 1) (x − 1) + C (x − 1) = A (x + 1)2 + B x2 − 1 + C (x − 1) =
(A + B)x2 + (2A + C) x + (A − B − C)
2
=
A+B
=1
2A + C = 2
A−B−C =3
Al resolver el sistema obtenemos:
A = 32 , B = − 12 , C = −1 luego,
x2 + 2x + 3
(x − 1) (x + 1)
Caso 3
2 dx =
3
2
1
1
dx + −
x−1
2
1
dx −
x+1
1
(x + 1)2
dx =
3
1
1
ln (x − 1) − (x + 1) +
+c
2
2
x+1
Q(x) contiene factores cuadráticos irreductibles, ninguno de los cuales se repite
Ejemplo Evalue
x2
2 dx
(x2 + 1)
la descomposición en fracciones parciales queda:
x2
Ax + Bx
Cx + D
2 = x2 + 1 +
2 + 1)2
(x2 + 1)
(x
x2 = Ax + Bx x2 + 1 + Cx + D
2
x = Ax3 + Bx2 + (A + C) x + (B + D)
Igualando los coeficientes obtenemos:
A = 0,
B = 1,
C = 0,
D = −1
de modo que la integral queda:
1
1
1
1
1
dx
=
dx
−
dx
=
dx
−
dx = arctan x − (arctan x+)
2
2
2
2
2
2
2
2
x +1
x +1
2
(x + 1)
(x + 1)
(x + 1)
1
x
x2
2 dx = arctan x − 2 arctan x + (x2 + 1) + c
(x2 + 1)
x2
Caso 4 Q(x) contiene un factor cuadrático irreductible repetido.
Ejemplo Evalue
1 − x + 2x2 − x3
dx
2
x (x2 + 1)
la descomposición en fracciones parciales queda:
26
1 − x + 2x2 − x3
A
Bx + C
Dx + E
= + 2
+
2
x
(x + 1) (x2 + 1)2
x (x2 + 1)
2
1 − x + 2x2 − x3 = A x2 + 1 + (Bx+ C) x2 + 1 x + (Dx
+ E) x
−x3 + 2x2 − x + 1 = A x4 + 2x2 + 1 + B x4 + x2 + C x3 + x + Dx2 + Ex
−x3 + 2x2 − x + 1 = (A + B) x4 + Cx3 + (2A + B + D) x2 + (C + E) x + A
Igualando los coeficientes obtenemos:
A = 1,
B = −1,
C = −1,
D = 1, E = 0
de modo que la integral queda:
1
dx
x+1
x
x
dx
xdx
dx =
− 2
+
−
−
+
2
2 dx =
2+1
2+1
2
2
2
x
x
+
1
x
x
x
x (x + 1)
(x + 1)
(x + 1)2
2
3
1 1
1 − x + 2x − x
dx = ln (x) − ln x2 + 1 − tan−1 x −
+c
2
2 + 1)
2
2
2
(x
x (x + 1)
1 − x + 2x2 − x3
Ejercicios
1
1.
dx
2−1
x
3
2.
dx
2+x−2
x
x+2
3.
dx
2
x −24
6x − 3x + 14
4.
dx
3 − 2x2 + 4x − 8
x
6x2 + 1
5.
dx
2 (x − 1)3
x
x3
6.
2 dx
2
(x − 24)
3x + 2x − 2
7.
dx
(x − 1) (x2 + x + 1)
27