Convertir expresión a puertas lógicas Variables y funciones lógicas

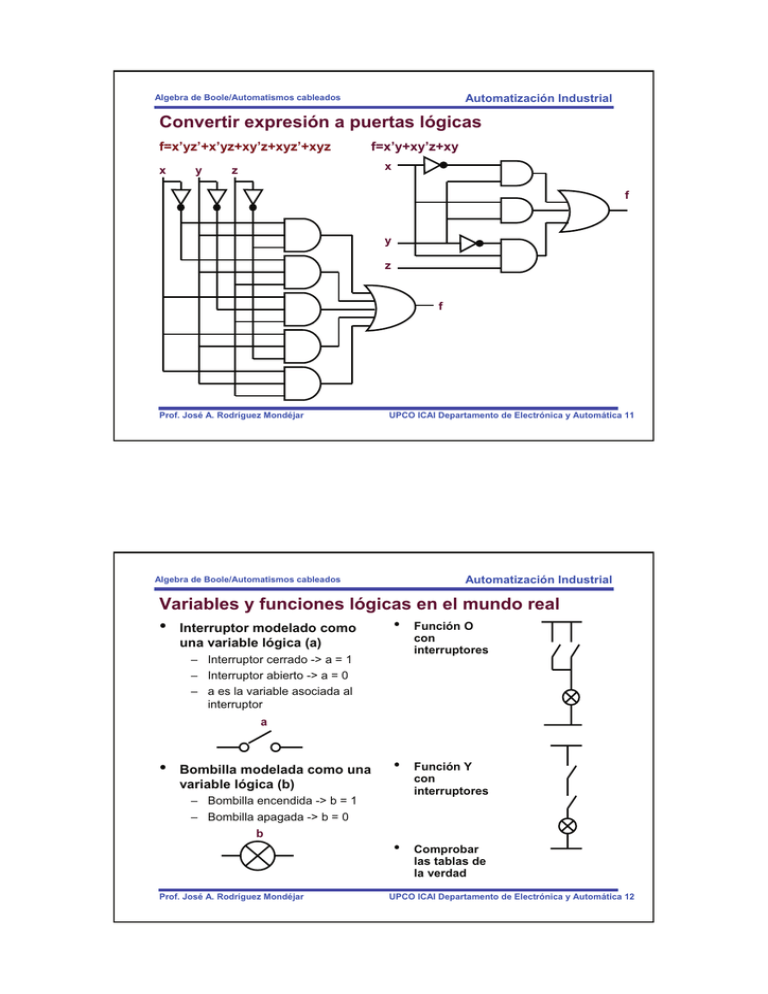
Automatización Industrial
Algebra de Boole/Automatismos cableados
Convertir expresión a puertas lógicas
f=x’yz’+x’yz+xy’z+xyz’+xyz
x
y
f=x’y+xy’z+xy
x
z
f
y
z
f
Prof. José A. Rodríguez Mondéjar
UPCO ICAI Departamento de Electrónica y Automática 11
Automatización Industrial
Algebra de Boole/Automatismos cableados
Variables y funciones lógicas en el mundo real
• Función O
• Interruptor modelado como
con
interruptores
una variable lógica (a)
– Interruptor cerrado -> a = 1
– Interruptor abierto -> a = 0
– a es la variable asociada al
interruptor
a
•
Bombilla modelada como una
variable lógica (b)
•
Función Y
con
interruptores
•
Comprobar
las tablas de
la verdad
– Bombilla encendida -> b = 1
– Bombilla apagada -> b = 0
b
Prof. José A. Rodríguez Mondéjar
UPCO ICAI Departamento de Electrónica y Automática 12
Automatización Industrial
Algebra de Boole/Automatismos cableados
Función complemento
•
•
Se puede realizar la función
complemento de forma
mecánica: se dispone de la
variable complementada y sin
complementar
mecánicamente( contacto
abierto, contacto cerrado).
En muchos casos resulta
difícil con interruptores y sin
provocar cortocircuitos
realizar la función
complemento: manejar f1 y
f1’ en el mismo circuito,
donde f1’ se ha construido a
partir de f1. En estos casos
se necesitan relés (caso de
circuito eléctrico).
Prof. José A. Rodríguez Mondéjar
Físicamente es el mismo
pulsador: 2 contactos (NO y NC)
b
b
f2=b
a
f1=ab’
UPCO ICAI Departamento de Electrónica y Automática 13
Automatización Industrial
Algebra de Boole/Automatismos cableados
Lógica positiva/Lógica negativa
•
Si una variable lógica está a 1 significa que la acción o
estado asociado a dicha variable se está cumpliendo. Si es
0 indica que no se cumple.
– En electrónica 1 significa tensión positiva ( típico 5V) y 0 significa
tensión cero o tensión negativa.
– Interruptor abierto igual a 0.
– Interruptor cerrado igual a 1.
•
Lo anterior es una convención. Se puede cambiar 0 por 1.
– Lógica negativa: 1 - 0 voltios, 0 - 5 voltios.
– 1 - Interruptor abierto 0 - Interruptor cerrado. Típico para detectar
fallos de alimentación.
Alimentación
Planta
Prof. José A. Rodríguez Mondéjar
Unidad de
control
Bombilla alarma
UPCO ICAI Departamento de Electrónica y Automática 14
Automatización Industrial
Algebra de Boole/Automatismos cableados
Simplificación
•
Problema: Juan quiere
instalar 2 interruptores en su
habitación (a y b) para
encender una bombilla (f) de
tal forma que sólo se
encienda cuando:
a
a
a
b
– a y b están simultáneamente
cerrados.
– a está cerrado
•
•
Juan que es un lanzado hace
la instalación
Juan está muy contento
porque la instalación
funciona perfectamente hasta
que llega su amigo Antonio y
le pregunta para qué sirve el
interruptor b
Prof. José A. Rodríguez Mondéjar
a
b
f
0
0
0
0
1
0
1
0
1
1
1
1
f = ab + a = a(b+1) = a·1 = a
UPCO ICAI Departamento de Electrónica y Automática 15
Automatización Industrial
Algebra de Boole/Automatismos cableados
Propiedades útiles del Algebra de Boole
•
Idempotencia
•
– a+a=a
– a·a=a
•
Maximalidad del 1
– a+1=1
•
Minimalidad del 0
•
Involución
•
Leyes de Morgan
– a+ab=a
– a(a+b)=a
•
– a+0=a
– a’’=a
–
–
–
–
(a+b)’=a’b’
(ab)’=a’+b’
(a+b+c+...)’=a’b’c’...
(abc...)’=a’+b’+c’+...
Prof. José A. Rodríguez Mondéjar
Absorción
•
Todas estas propiedades se
comprueban mediante la
aplicación de las propiedades
del Algebra de Boole
(postulados de Hungtinton) o
recurriendo a las tablas de la
verdad (en todos los casos
posibles se cumple la
igualdad).
Permiten simplificar
fácilmente.
UPCO ICAI Departamento de Electrónica y Automática 16
Automatización Industrial
Algebra de Boole/Automatismos cableados
Simplificando
•
f=x’yz’+x’yz+xy’z+xyz’+xyz
–
–
–
–
•
Asociativa y distributiva: f=x’y(z’+z)+xy’z+xy(z’+z)
Complemento: f=x’y+xy’z+xy
Complemento: f=y(x’+x)+xy’z
f=y+xy’z
f=(x’y’z’+x’y’z+xy’z’)’
–
–
–
–
Asociativa y distributiva: f=(x’y’(z’+z)+xy’z’)’
Complemento: f=(x’y’+xy’z’)’
Leyes de Morgan: f=(x’y’)’(xy’z’)’
Leyes de Morgan: f=(x+y)(x’+y+z)
–
–
–
–
f=xx’+xy+xz+yx’+yy+yz
f=xz+y+xy+yx’+yz
f=xz+y(1+x+x’+z)
f=xz+y Es equivalente a la de arriba (ver tabla de la verdad)
Prof. José A. Rodríguez Mondéjar
UPCO ICAI Departamento de Electrónica y Automática 17
Automatización Industrial
Algebra de Boole/Automatismos cableados
Implantaciones alternativas de f
A
F = A' B C + A B' C' + A B' C + A B C' + A B C
B
F1
C
Suma de productos canónica
F2
Suma de productos minimizada
F3
F4
Prof. José A. Rodríguez Mondéjar
Producto de sumas canónica
Producto de sumas minimizado
UPCO ICAI Departamento de Electrónica y Automática 18