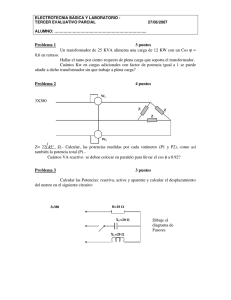
Electrotecnia. Problemas
Anuncio

AULA POLITÈCNICA 97 Electrotecnia. Problemas AULA POLITÈCNICA / TECNOLOGÍA ELÉCTRICA Y ELECTRÓNICA Xavier Alabern Morera Jordi-Roger Riba Ruiz Electrotecnia. Problemas EDICIONS UPC 11 Circuitos trifásicos 1 Circuitos trifásicos © Los autores, 2006; © Edicions UPC, 2006 12 Problemas de electrotecnia 1.1 Problema 1 Una carga equilibrada trifilar conectada en estrella y de impedancia 40 ∠ 30º Ω por fase está conectada a una red trifásica equilibradade secuencia directa RST de 400 V i 50 Hz. a) Calcular las corrientes de línea. b) Calcular las potencias activa, reactiva y aparente totales que consume la carga. IR Z IS Z IT Z R S T Figura 1.1.1 Resolución: a ) Cálculo de las corrientes de línea: IR = VRN 400 / 3 < 0º = = 5,7735∠ − 30º A Z 40 < 30º IS = VSN 400 / 3 < −120º = = 5,7735∠ − 150º A 40 < 30º Z IT = VTN 400 / 3 < 120º = 5,7735∠90º A = Z 40 < 30º b ) Cálculo de las potencias totales: PTOT = 3 .Vlínea.Ilínea.cosϕ = 3 .400.5,7735.cos30º = 3464,10 W QTOT = 3 .Vlínea.Ilínea.sinϕ = 3 .400.5,7735.sin30º = 2000,00 VAr STOT = 3 Vlínea.Ilínea= 3 .400.5,7735 = 4000 VA © Los autores, 2006; © Edicions UPC, 2006 N 13 Circuitos trifásicos 1.2 Problema 2 Una carga equilibrada trifilar conectada en triángulo y de impedancia 40 ∠ 30º Ω por fase está conectada a una red trifásica equilibrada de secuencia directa RST de 400 V i 50 Hz. a) Calcular las corrientes de fase de la carga. b) Calcular las corrientes de línea. c) Calcular las potencias activa, reactiva y aparente totales que consume la carga. IR R R IRS S ITR Z IS Z I ST S T IT T Z Figura 1.2.1 Resolución: a ) Cálculo de las corrientes de fase de la carga (se toma como origen de fases VRN = VRN ∠0º ): I RS = I ST = I TR = V RS Z V ST Z = 400∠30º = 10∠0º A 40∠30º = 400∠ − 90º = 10∠ − 120º A 40∠30º VTR 400∠150º = 10∠120º A = 40∠30º Z b ) Cálculo de las corrientes de línea: I R = I RS − ITR = 17,32∠ − 30º A I S = I ST − I RS = 17,32∠ − 150º A IT = ITR − I ST = 17,32∠ + 90º A c ) Cálculo de las potencias totales: PTOT = 3 .Vlínea.Ilínea.cosϕ = 3 .400.17,32.cos30º = 10392 W QTOT = 3 .Vlínea.Ilínea.sinϕ = 3 .400.17,32.sin30º = 6000 VAr STOT = 3 Vlínea.Ilínea= 3 .400.17,32 = 12000 VA © Los autores, 2006; © Edicions UPC, 2006 14 Problemas de electrotecnia 1.3 Problema 3 Una carga desequilibrada trifilar conectada en estrella está conectada a una red trifásica equilibrada de secuencia directa RST de 400 V i 50 Hz. a) Calcular las corrientes de línea. b) Calcular las potencias activa, reactiva y aparente totales que consume la carga. IR Z R = 20. 2∠45º Ω IS Z S = 20∠90º Ω IT ZT = 20. 2∠ − 45º Ω R N’≠N S T Figura 1.3.1 Resolución: a ) Al ser una carga desequilibrada trifilar en estrella, el centro de la estrella no coincide con el neutro. I R + I S + IT = 0 → V RN ' V SN ' VTN ' + + =0 ZR ZS ZT 400 400 ∠0º − ∠ − 120º + VSN ' 3 3 400 400 = ∠120º − ∠ − 120º + VSN ' 3 3 VRN ' = VRN − VSN + VSN ' = VTN ' = VTN − VSN + VSN ' Del sistema de ecuaciones anterior resulta: VRN ' = 386,4∠15º V VSN ' = 103,5∠ − 75º V VTN ' = 301,3∠84,9º V Ahora ya se pueden calcular las corrientes de línea: IR = VRN ' = 13,66∠ − 30 º A ZR IS = VSN ' = 5,18∠ − 165 º A ZS IT = VTN ' = 10,65∠129,9º A ZT b ) Cálculo de las potencias totales: S total = V RN ' .I *R + V SN ' .I *S + V TN ' .I *T = 6000 +j.2000 = 6324,56 ∠ 18,4º VA Stotal = 6324,56 VA Ptotal = 6000 W Qtotal = 2000 VAr © Los autores, 2006; © Edicions UPC, 2006 15 Circuitos trifásicos 1.4 Problema 4 Una carga desequilibrada trifilar conectada en triángulo está conectada a una red trifásica equilibrada de secuencia directa RST de 400 V i 50 Hz. a) Calcular las corrientes de fase de la carga. b) Calcular las corrientes de línea. c) Calcular las potencias activa, reactiva y aparente totales que consume la carga. IR R R IRS S IS ITR ZRS=40<0º Ω ZTR=40<0º Ω I ST S T IT T ZST=40<30º Ω Figura 1.4.1 Resolución: a ) Cálculo de las corrientes de fase de la carga (se toma como origen de fases VRN = VRN ∠0º ): I RS = V RS 400 < 30º = 10 < 30º A = 40 < 0º Z I ST = V ST 400 < −90º = = 10 < −120º A Z 40 < 30º I TR = VTR 400 < 150º = = 10 < 150º A Z 40 < 0º b ) Cálculo de las corrientes de línea: I R = I RS − I TR = 17,32 < 0º A I S = I ST − I RS = 19,32 < −135º A I T = I TR − I ST = 14,14 < 105º A c ) Cálculo de las potencias totales: S total = V RS .I *RS + V ST .I *ST + V TR .I *TR = 11464,1 +j.2000,0 = 11637,5<9,90º VA Stotal = 11637,5 VA Ptotal = 11464,1 W Qtotal = 2000,0 VAr © Los autores, 2006; © Edicions UPC, 2006 16 Problemas de electrotecnia 1.5 Problema 5 El esquema representa la alimentación en media tensión de tres cargas trifásicas equilibradas, cuyas características están dadas por sus potencias. Con el interruptor D abierto, la lectura del voltímetro VG es de 1202,5 V. Se desea saber: a) Impedancia equivalente por fase de la carga, en el supuesto de que esté conectada en estrella. b) Indicaciones de los vatímetros W1 y W2 A continuación se cierra el interruptor D (que equivale a conectar en el circuito una batería de condensadores). Se pregunta: c) Nuevas lecturas de los vatímetros y del voltímetro VG (en el supuesto que la tensión en bornes de la carga se mantuviera constante). carga 1 100 kVA cos φ = 0,6 (ind.) G Z l = 1,2 + j1,6 Ω carga 2 W1 R G Z l = 1,2 + j1,6 Ω VG S 40 kW cos φ = 1 W2 G Z l = 1,2 + j1,6 Ω T D 0 - j90 kVA 20 + j10 kVA carga 3 Figura 1.5.1 Resolución: a) Nomenclatura utilizada: C: carga G: generador S: simple En primer lugar, se reducirán las tres cargas conectadas al extremo de la línea a una sola equivalente: carga 1 S1 = 100 ∠ 53,13º = (60 + j80 ) kVA carga 2 S 2 = 40 ∠ 0º = (40 + j 0 ) kVA carga 3 S 3 = 22,36 ∠ 26,56º = (20 + j10 ) kVA (cos φ = 0,6; φ = 53,13º) (tg ϕ = 10 ; ϕ = 26,56º ) 20 S T = (120 + j 90 ) kVA = 150 ∠ 36,87 º kVA © Los autores, 2006; © Edicions UPC, 2006 17 Circuitos trifásicos que, por fase, representa una potencia de: S Cf = SC = 40 + j 30 = 50 ∠ 36,87 º kVA 3 La tensión simple o de fase vale: U GS = UG 3 = 1202,5 3 = 694,26 V U GS = 694,26 ∠ δº V Y si se toma la tensión simple en bornes de la carga como origen de fases: U CS = U CS ∠0º V La impedancia por fases de la línea es de la forma: Z l = (1,2 + j1,6) Ω = 2 ∠ 53,13º Ω Pudiéndose ahora plantear la siguiente ecuación vectorial: U GS = U CS + Z l · I siendo, I* = S Cf 50000 ∠ 36,87 º = U CS ∠ 0º U CS I= 50000 ∠ − 36,87 º U CS y sustituyendo se obtiene, 694,26∠ δ º = U CS∠ 0º +2 ∠ 53,13º · 50000 ∠ − 36,87 º U CS igualando partes reales e imaginarias entre sí, queda: 96000 ⎫ U CS ⎪⎪ ⎬ 28000 ⎪ 694,26 sen δ = ⎪⎭ U CS 694,26 cos δ = U CS + que resuelta, nos da: U CS = ± 200 V U CS = ± 500 V Los valores negativos no tienen sentido físico. El valor UCS = 200 V no se considera, puesto que es ilógico que la caída de tensión en la línea sea superior a la caída de tensión en la carga. Por tanto, la corriente que circula por la línea vale: I= 50000 ∠ − 36,87 º = 100 ∠ − 36,87 º = (80 − j 60) A 500 y si se recuerda que por fase S Cf = 50000 ∠ 36,87 º VA = (40000 + j 30000) VA resulta, teniendo en cuenta que S Cf = P Cf + Q Cf : © Los autores, 2006; © Edicions UPC, 2006 18 Problemas de electrotecnia RC = PCf I X LC = 2 = 40000 =4Ω 100 2 QCf 30000 = =3Ω 100 2 I2 Z Cf = (4 + j 3) Ω = 5 ∠ 36,87º Ω b ) Si se tiene en cuenta la disposición de los dos vatímetros (conexión Aron) la forma de conocer las lecturas de cada uno de ellos es la siguiente: Carga: PTC = 40000 · 3 = 120000 W QTC = 30000 · 3 = 90000 var Línea: Pl = 3 Rl I 2 = 3 · 1,2 · 100 2 = 36000 W Ql = 3 X l I 2 = 3 · 1,6 · 100 2 = 48000 VAr La potencia suministrada por el generador será PG = PTC + Pl = 156000 W = 156 kW QG = QTC + Ql = 138000 var = 138 k VAr S G = 208,278 ∠ 41,5º k VA y teniendo en cuenta la disposición de los vatímetros, W1 + W2 = PG ⎫ ⎬ (W1 − W 2 ) 3 = QG ⎭ W1 + W 2 = 156 ⎫ ⎬ W1 − W 2 = 138 / 3 ⎭ W1 = 117,8 kW W2 = 38,2 kW c) Al conectar los condensadores, la potencia aparente total del conjunto de la carga será S 'TC = S TC + S cond S 'TC = 120000 + j 90000 − j 90000 = 120000 ∠ 0º VA Y puesto que la tensión en bornes de la carga se supone constante y de valor por fase 500 V, la nueva corriente de línea vale I '* = 120000 ∠ 0º = 80 ∠ 0º A 3 · 500 ∠ 0º Las nuevas pérdidas de potencia en la línea en estas condiciones serán P' l = 3 · 1,2 · 80 2 = 23040 W Q 'l = 3 · 1,6 · 80 2 = 30720 VAr Y el generador aportará una nueva potencia de P 'G = 120000 + 23040 = 143040 W Q' G = 30720 VAr S 'G = 143040 + j 20720 = 146301,6 ∠ 12,12º VA © Los autores, 2006; © Edicions UPC, 2006 19 Circuitos trifásicos Las nuevas indicaciones de los vatímetros serán, W '1 +W ' 2 = 143040⎫ 30720 ⎪⎬ W '1 −W ' 2 = 3 ⎪⎭ W '1 = 80,3881 kW W ' 2 = 62,6519 kW y la nueva indicación del voltímetro será V 'G = U GC = S 'G I' · 3 = 146301,6 = 1055,84 V 80 · 3 Æ V ' G = 1055,84 V Se observa pues, que como resultado de corregir totalmente la componente reactiva de la carga mediante los condensadores, la potencia activa absorbida del generador, solamente disminuye en 13 kW mientras que la reactiva se ha rebajado en ~ 107 kVAr. © Los autores, 2006; © Edicions UPC, 2006 20 Problemas de electrotecnia 1.6 Problema 6 Un sistema trifásico equilibrado, de secuencia directa RST a 50 Hz, alimenta: 1. Tres calefactores de un horno eléctrico conectados en triángulo, con factor de potencia unidad y que consumen 3,74 kW cada uno. 2. Un motor eléctrico de rendimiento 83% conectado en triángulo a la tensión compuesta de 208 V y que proporciona una potencia mecánica de 25 CV, con factor de potencia 0,8. La línea de alimentación tiene una impedancia por fase Z1 = R1 + jX 1 . En bornes de salida del generador, se conectan tres vatímetros de la forma que se especifica a continuación y que dan las siguientes lecturas: W1 : Bobina amperimétrica con corriente de la fase R Bobina voltimétrica con tensión RT Lectura: ilegible W2 : Bobina amperimétrica con corriente de la fase R Bobina voltimétrica con tensión ST Lectura: 15200 W W3 : Bobina amperimétrica con corriente de la fase S Bobina voltimétrica con tensión ST Lectura: 15570 W Se pregunta: a) Impedancia de la línea b) Tensión en bornes del generador Resolución: a) Se determinan las potencias eléctricas consumidas por las cargas conectadas al circuito. Motor: Pmec = 25 CV PM = η = 83% cos φM = 0,8 25 · 736 = 22168,7 W 0,83 tg φM = 0,75 QM = PM tg ϕ M = 22168,7 · 0,75 = 16626,5 VAr S M = 22168,7 + j16626,5 = 27710,9 ∠ 36,87 º VA Horno: P’H = 3,74 kW/fase cos φH = 1 PH = 3 P ' H = 3 · 3740 = 11220 W φH = 0 QH = 0 VAr S H = 11220 + j 0 = 11220 ∠ 0º VA En consecuencia, la carga total conectada al circuito será S C = S M + S H = 33388,7 + j16626,5 = 37299,41 ∠ 26,47º VA Si se toma la tensión en bornes de la carga, como origen de fases U C = U C ∠ 0º V , la corriente que circula por la línea de alimentación se obtiene a partir de © Los autores, 2006; © Edicions UPC, 2006 21 Circuitos trifásicos I* = SC UC 3 = 37299,41 ∠ 26,47 º 3 · 208 ∠ 0º = 103,5 ∠ 26,47 º I = 103,5 ∠ − 26,47 º = (92,65 − j 46,133) A Analicemos a continuación las potencias que proporciona el generador, para lo cual basta observar que los vatímetros W1 y W3 están conectados según el método de Aron, y por tanto se cumple para cualquier sistema equilibrado que: PG = W1 + 15570 ⎫ ⎪ QG = W1 − 15570⎬ ⎪⎭ 3 PG = W1 + W3 ⎫ ⎪ QG = W1 − W3 ⎬ ⎪⎭ 3 (1) la lectura del vatímetro W1, según el enunciado, no es posible. El vatímetro W2 está montado de forma que en un sistema trifásico equilibrado su indicación es, W2 = QG 3 = 15200 W expresión que sustituida en la ecuación 1 resulta: ⎫ ⎬ W1 = 30770 W 15200 = W1 − 15570⎭ PG = W1 + 15570 PG = W1 + W3 = 30770 + 15570 = 46340 W QG = 3 · 15200 = 26327,2 VAr Por lo que el generador suministra una potencia total que en forma compleja vale S G = 46340 + j 26327,2 = 53296,5 ∠ 29,6º VA con un factor de potencia cos φG = 0,8695. Las tres fases de la línea absorben una potencia que vale Pl = PG − PC = 46340 − 33388,7 = 12951,3 W Ql = QG − QC = 26327,2 − 16626,5 = 9700,7 VAr S l = 12951,3 + j 9700,7 = 16181,46 ∠ 36,84º VA Los parámetros por fase de la línea serán de la siguiente forma: Rl = Pl 3I 2 = 12951,3 = 0,403 Ω 3 · 103,5 2 Xl = Ql 9700,7 = = 0,302 Ω 2 3I 3 · 103,5 2 Z l = 0,403 + j 0,302 = 0,5036 ∠ 36,84º Ω b) La tensión en bornes del generador se puede deducir de UG = SG 3·I* = 53296,5 ∠ 29,6º 3 · 103,5 ∠ 26,47 º = 297,3 ∠ 3,13º V U G = 297,3 ∠ 3,13º V = (296,86 − j16,23) V → UG = 297,3 V recordando que el origen de fases es precisamente la tensión en bornes de la carga. © Los autores, 2006; © Edicions UPC, 2006 22 Problemas de electrotecnia 1.7 Problema 7 Seis impedancias idénticas, de valor Z = (12 + j16) Ω cada una, se conectan como se indica en el esquema adjunto, al extremo final de una línea trifásica alimentada por un generador equilibrado y a secuencia directa que proporciona en bornes de la carga así constituida una tensión entre fases de V C = 200 3 V . La alimentación se realiza mediante una línea trifásica, cuya impedancia por fase es Z l = (1 + j1) Ω . Con el interruptor K abierto, determinar: a) Las indicaciones de todos los aparatos de medida b) Potencia aparente, en forma compleja, suministrada por el generador que alimenta la carga. Para mejorar el factor de potencia de la carga hasta la unidad, se cierra el interruptor K, que conecta una batería de condensadores y en este caso se pide: c) Características de la batería de condensadores. d) Potencia aparente en forma compleja, que proporciona ahora el generador y nueva tensión en G bornes del mismo. Z A11 Vl G Z G Zl W1 R G Z G Z A1 AG A2 G Zl VG G Z VC W2 S G Zl G Z T K C C C Figura 1.7.1 Resolución: a) Las seis impedancias así conectadas dan lugar a una impedancia de carga cuyo valor por fase es Z C estrella = Z ·Z Z +Z 3 =Z 4 3 © Los autores, 2006; © Edicions UPC, 2006 23 Circuitos trifásicos siendo, Z = 12 + j16 = 20 ∠ 53,13º Ω Z C estrella = 12 + j16 20 = ∠ 53,13º = 5 ∠ 53,13º Ω = (3 + j 4) Ω 4 4 El esquema anterior puede reducirse a otro monofásico, constituido por fase y neutro, como se aprecia en la figura 1.3.2 G Zl R G IG VGS G Z C estrella VCS Figura 1.7.2 Z T = Z l + Z C estrella = (1 + j1) + (3 + j 4) = 4 + j 5 = 6,4 ∠ 51,34º Ω La corriente por fase vale 200 3 IG = 3 ∠ 0º Z C estrella = 200 ∠ 0º = 40 ∠ − 53,13º A 5 ∠ 53,13º AG = 40 A Æ y por tanto el amperímetro AG marca 40 A. La caída de tensión en la línea en valor simple será U l = Z l · I G = 2 ∠ 45º · 40 ∠ − 53,13º = 40 2 ∠ − 8,13º = (56 − j8) V La indicación del voltímetro V1 será, pues, 40. 2 = 56,5685 V V1 = 56,5685 V Æ La tensión simple en bornes del generador vale → U GS = U CS + Z l · I = 200∠0º +40 2∠ − 8,13º = 256 − j8 U GS = 256,125 ∠ − 1,8º V La indicación del voltímetro VG será V G = 3 U GS = 3 · 256,125 = 443,62 V Æ V G = 443,62 V El amperímetro A2 marcará I2 = U CS Z = y como vector será: 200 = 10 A 20 I2 = Æ A2 = 10 A U CS 200 ∠ 0º = = 10 ∠ − 53,13º = (6 − j8) A 20 ∠ 53,13º Z © Los autores, 2006; © Edicions UPC, 2006 24 Problemas de electrotecnia El amperímetro A11 indicará I 11 = U CC Z = 200 3 = 10 3 A 20 Æ A11 = 10 3 A Æ A1 = 30 A y el amperímetro A1 marcará I 1 = I 11 · 3 = 10 3 · 3 = 30 A Los vatímetros conectados según el método Aron indicarán: W1 + W2 = PG ⎫ Q ⎪ W1 − W2 = G ⎬ 3 ⎪⎭ Determinemos, en primer lugar, las potencias absorbidas por la carga y la línea: PC = 3 RC I G2 = 3 · 3 · 40 2 = 14400 W Pl = 3 Rl I G2 = 3 · 1 · 40 2 = 4800 W PG = PC + Pl = 19200W y por el teorema de Boucherot QC = 3 X C I G2 = 3 · 4 · 40 2 = 19200 VAr Ql = 3 X l I G2 = 3 · 4 · 40 2 = 4800 VAr QG = QC + Ql = 24000 VAr Por tanto, resulta W1 + W2 = 19200 ⎫ 24000 ⎪⎬ W1 − W2 = 3 ⎪⎭ b) Æ W1 = 16528,2 W W 2 = 2671,8 W S G = PG + jQG = 19200 + j 24000 = 30735 ∠ 51,34º VA c) Como se ha visto en el apartado a), la potencia aparente absorbida por la carga es de la forma: S C = PC + jQC = 14400 + j19200 = 24000 ∠ 53,13º VA Para que el factor de potencia de la carga sea la unidad, se deberá cumplir que S C = 14400 + j 0 = 14400 ∠ 0º VA en consecuencia, la batería de condensadores tendrá que aportar una potencia reactiva de QC cond = 19200 VAr (−) que, por fase, vale 2 QCf cond = V fC 19200 = 6400 VAr (−) = = V fC 2 ⋅ 2π ⋅ f ⋅ C 3 XC © Los autores, 2006; © Edicions UPC, 2006 25 Circuitos trifásicos La capacidad de dichos condensadores, sabiendo que están conectados en triángulo a la tensión compuesta de 200 3 V y frecuencia de 50 Hz, es C= 10 6 · 6400 ( 2 ⋅ π⋅ 50 ⋅ 200 3 ) 2 = 169,765 µF/fase Æ C = 169,765 µF/fase cuya reactancia por fase vale XC = 10 6 = 18,75 Ω 2 ⋅ π⋅ 50 · 169,765 → X C = − j18,75 = 18,75 ∠ 90º A d) La reactancia capacitiva de los condensadores proporciona I f cond = 200 3 ∠ 0º = 18,475 ∠ 90º A 18,75 ∠ − 90º la intensidad de línea valdrá I C cond = 3 · 18,475 = 32 A La corriente I G que suministraba el generador, antes de mejorar el factor de potencia de la carga, valía I G = 40 ∠ − 53,13º = (24 − j 32) A Una vez compensado el factor de potencia, la nueva corriente pasa a ser I 'G = 24 + j 0 = 24 ∠ 0º A siendo la nueva potencia absorbida por la carga de la forma S 'G = 14400 + j 0 = 14400 ∠ 0º VA En la línea se producirán ahora unas pérdidas de potencia que valen P 'l = 3 · 1 · 24 2 = 1728 W Q' l = 3 · 1 · 24 2 = 1728 VAr La potencia que suministra en estas condiciones el generador, según el teorema de Boucherot, valdrá P 'G = P 'C + P 'l = 14400 + 1728 = 16128 W Q'G = Q'C +Q'l = 0 + 1728 = 1728 VAr S 'G = 16128 + j1728 VA = 16220,3 ∠ 6,116º VA Por tanto, la nueva tensión en bornes del generador será U 'G = S 'G 3 · I 'G = 16220,3 3 · 24 = 390,2 V Æ U 'G = 390,2 V © Los autores, 2006; © Edicions UPC, 2006 26 Problemas de electrotecnia 1.8 Problema 8 Un generador trifásico equilibrado alimenta, a la tensión constante de 1810 V, una línea a la que están conectados dos receptores equilibrados A y B, como se representa esquemáticamente en la figura. El receptor A consume permanentemente una potencia de 376,2 kW. Con los interruptores K1 y K2 cerrados, se mide en el amperímetro A3 una corriente de 70 A y el factor de potencia en bornes del generador es 0,8 (inductivo). a) Calcular las lecturas de los amperímetros A1 y A2 y el factor de potencia del receptor A. Se abren los dos interruptores K1 y K2, y una vez alcanzado el régimen permanente, se mide un factor de potencia en bornes del generador de 0,96 (capacitivo). b) Calcular el valor de X4. X3 A3 X3 K1 X4 X4 K2 X4 X3 receptor B ~ A1 50 Hz A2 PA = 376,2 kW receptor A 1810 V Figura 1.8.1 Resolución: a) Con los dos interruptores K1 y K2 cerrados, la única potencia activa proporcionada por el generador es la consumida por el receptor A, puesto que el receptor B es una capacidad pura. Por tanto, PG = PA = 376,2 kW La corriente suministrada por el generador será: © Los autores, 2006; © Edicions UPC, 2006 27 Circuitos trifásicos PG I G = I1 = 3 U G cos ϕ = 376200 3 · 1810 · 0,8 = 150 A Æ A1 = 150 A al ser el factor de potencia 0,8 inductivo φG = -36,87º I G = 150 ∠ − 36,87º = (120 − j 90) A La potencia reactiva suministrada por el generador vale QG = PG tg ϕ G = 376,2 · 0,75 = 282,15 k VAr Y su potencia aparente, S G = 376,2 + j 282,15 = 470,25 ∠ 36,87º kVA La potencia reactiva del receptor B, con los interruptores K1 y K2 cerrados, se puede calcular a partir de QB = − 3 U G I B IB = I3 I 3 = 70 A Q B = − 3 · 1810 · 70 = −219,45 k VAr y con este valor puede determinarse la reactancia capacitiva: X3 = QB − 3 I B2 = − 2194450 = 14,93 Ω − 3 · (70) 2 Por tanto, la potencia reactiva absorbida por el receptor A se obtendrá como diferencia entre la proporcionada por el generador y la absorbida por el receptor B. Q A = QG − Q B = [282,15 − (− 219,45)] = 501,6 k VAr Por tanto, la potencia aparente del receptor A vale S A = (376,2 + j 501,6) kVA = 627 ∠ 53,13º kVA SA = 3 U G · IA * IA* = 627000 ∠ 53,13º 3 · 1810 ∠ 0º = 200 ∠ 53,13º A I A = I 2 = 200 ∠ − 53,13º = (120 − j160) A A2 = 200 A La lectura del amperímetro A2 será de 200 A. Æ También se puede calcular I A a partir de I A = I G − I B = 150∠ − 36,87 º −70∠90º = (120 − j160) A b) Al abrir los interruptores K1 y K2, no se modifica la potencia activa suministrada por el generador, ya que sólo se introduce en el circuito una reactancia inductiva: P ' G = PG Como consecuencia, la corriente suministrada por el generador valdrá I 'G = P 'G 3 U G cos ϕ 'G = 376200 3 · 1810 · 0,96 = 125 A cos ϕ = 0,96(c) I G = 125 ∠ 16,26º = (120 + j 35) A © Los autores, 2006; © Edicions UPC, 2006 ϕ = −16,26º 28 Problemas de electrotecnia Al no variar la impedancia del receptor A, ni la tensión de alimentación, tampoco varía la corriente que consume y, por lo tanto, I ' A = I A = (120 − j160) A Igualmente no varía la potencia reactiva consumida por el receptor, o sea, Q' A = Q A . Resulta, pues, I 'B = I 'G − I 'A = (120 + j 35) − (120 − j160) = j195 = 195∠90º A La indicación del amperímetro A3 es de 195 A. La potencia reactiva suministrada por el generador en estas condiciones vale Q'G = P 'G tg ϕ 'G = 376,2 · (−0,292) = −109,725 k VAr S G = 376,2 − j109,725 = 391,875 ∠ − 16,26º kVA La potencia absorbida por los condensadores del receptor B será Q' X 3 = −3 X 3 I ' 2B = 3 · 14,93 · 195 2 = −1703,140 k VAr Por diferencia entre la potencia reactiva que suministra el generador y las absorbidas por los condensadores del receptor B y del receptor A, se obtendrá la potencia reactiva absorbida por las bobinas del receptor B: Q'X 4 = Q'G −Q'X 3 −Q'A = −109,725 − (−1702,98) − 501,6 QA = Q' A Q X 4 = 1091,65 k VAr La corriente que pasa por las reactancias X4 vale: I 'X 4 = I 'B / 3 A partir de QX4 se puede obtener X4 como se indica: X4 = Q' X 4 3 I ' 2X 4 = Q' X 4 I ' 2B = 1091650 195 2 = 28,71 Ω → X 4 = 28,71 Ω © Los autores, 2006; © Edicions UPC, 2006 29 Circuitos trifásicos 1.9 Problema 9 Una pequeña instalación industrial se alimenta mediante un generador trifásico equilibrado de secuencia directa, a la frecuencia de 50 Hz. A ~ B C W W IAIA IBIB IC N D1 FA Z D2 Z D3 FB FC M ~ Z Z Z Figura 1.9.1 Dicha instalación está constituida por los consumos siguientes: 1. Un grupo de lámparas incandescentes de 100 W cada una a 220 V, conectadas en estrella con un total de 44 lámparas por fase. 2. Un motor conectado en estrella y que trabajando a plena carga proporciona una potencia mecánica de 11 kW con rendimiento del 83,33% y factor de potencia 0,8 inductivo. 3. Un receptor inductivo constituido por seis impedancias iguales Z y conectadas como se esquematiza en la figura. Con el interruptor D3 cerrado, el amperímetro IA marca 22 A y el vatímetro 2904 W. Se pide: a) Formas binómica y polar de las impedancias Z b) Lecturas de los aparatos de medición al cerrar el interruptor D2 permaneciendo D3 cerrado. Finalmente, se cierra D1, pero por fallo en el fusible FB, queda fuera de servicio la iluminación en la fase B. c) Nuevas lecturas de los aparatos de medición d) Componentes simétricas de las corrientes de línea © Los autores, 2006; © Edicions UPC, 2006 30 Problemas de electrotecnia Resolución: a) La impedancia por fase a considerar vale: Zf = Uf IA = 220 = 10Ω 22 Esta impedancia provoca un retraso de la intensidad respecto a la tensión simple dada por: cos ϕ c = WA 2904 = = 0,6 Uf ⋅ IA 220 · 22 senϕ C = 0,8 ϕC = 53,13º Z f = 10 ∠53,13º = ( 6 + 8 j) Ω (1) Por otra parte y por fase, se tiene: Zf = Z· Z 3 = Z 4 Z+Z 3 (2) Igualando las expresiones (1) y (2), resulta: Z = 10∠53,13º · 4 = 40 ∠53,13º = ( 24 + 32 j) Ω y la corriente de la fase A será: IA = 22 ∠ − 53,13º = ( 13,2 − 17 ,6 j) A La potencia aparente por fase que consume el receptor C será de la forma: Q fC = 2904 ⋅ tg ϕ C = 3872 VAr PfC = 2904W SCf = 2904 + 3872 j = 4840∠53,13º VA y en total: SC = 3SCf = 14520∠53,13º VA = ( 8712 + 11616 j) VA b) La potencia consumida por el motor es: Su potencia reactiva es: Pb = 11000 = 13200 W 0,8333 Qb = 13200 ⋅ tgϕ b = 9900 VAr S b = 13200 + 9900 j = 16500∠36,87º VA El vatímetro conectado al circuito indicará en este caso: W = 2904 + 13200 = 7304 W 3 Para obtener las intensidades de corriente que marcan los diferentes amperímetros, se aplicará el teorema de Boucherot: I A* = Sc + Sb 3Uf = 8712 + 11616 j + 13200 + 9900 j 3 ⋅ 220∠0º → I A = 46 ,53∠ − 44 ,5ºA Igualmente se podría haber calculado esta intensidad, calculando la que consume el motor y sumándole la que consume la carga, ya calculada previamente en el apartado a. Efectivamente; © Los autores, 2006; © Edicions UPC, 2006 31 Circuitos trifásicos Sb I B* = 3Uf = 16500∠36 ,87º = ( 20 + 15 j)A 3 ⋅ 220∠0º I A = 20 − 15 j + 13,2-17 ,6 j = 46,53∠ − 44,5ºA → I B = ( 20 − 15 j) A que coincide con la anterior. Como el sistema es equilibrado, los valores numéricos indicados por lo amperímetros son iguales, pero están desfasados entre sí en ángulos de 120º. I A = 46,53∠ − 44,5ºA I B = 46,53∠ − 164,5ºA I C = 46,53∠75,5ºA IA = IB = IC = 46,53 A Por tanto: c) Las lámparas consumen una potencia, que por fase, vale: S af = 4400∠0º VA Pa f = 44 ⋅100 = 4400 W Por lo que si no se fundiese ningún fusible, la corriente consumida sería de: S af IA = Uf = 20 A Al fallar la fase B se tiene: IaA = 20∠0º A = 20 A IaB = 0∠ − 120º A = 0 A IaC = 20∠120º A = ( −10 + 17,32 j ) A que representan las intensidades por fase, correspondientes a la carga a. Para calcular en las nuevas condiciones la corriente por fase, se tendrá: I A = I aA + I bA + I cA = 20∠0º +46,53∠ − 44,5º = 62,4∠ − 31,5º A lectura: IA = 62,4 A I B = I bB + I cB = 46,53∠ − 164,5º A lectura: IB = 46,53 A I C = 46,53∠75,5º +20∠120º = 62,4∠88,5º A lectura: IC = 62,40 A El vatímetro indicará: W =V AN ⋅ I A ⋅ cos(ϕV AN − ϕI ) = 220 ⋅ 62,4 ⋅ cos 31,5º = 11704 W A → y la corriente en el neutro vale: I N = I A + I B + I C = 10 + 10 3 j = 20∠60º A d) Cálculo de las componentes simétricas de la corriente: Homopolares: I OA = I OB = I OC = I N 10 + 10 3 j = = 3,3 + 3,3 3 j = 6,6∠60º A 3 3 Vector clave del sistema directo: I1A = 1 ⎡ ⋅ I A + aI B + a2 IC ⎤ ⎥⎦ 3 ⎢⎣ © Los autores, 2006; © Edicions UPC, 2006 W = 11704 W 32 Problemas de electrotecnia I A = 62,4∠ − 31,5º = 53,2 − 32,6 j A a I B = 1∠120 º⋅46,53∠ − 164,5º = 33,2 − 32,6 j a 2 I C = 1∠120º⋅62,4∠88,5º = 53,2 − 32,6 j y sustituyendo resulta: I1 A = 46,5 − 32,6 jA = 56,8∠ − 35º A I 1B = a 2 I 1 A = 56,8∠ 205 º A I 1C = a.I 1 A = 56,8∠85º A Vector clave del sistema inverso: I2A = 1 ⎡ ⎤ ⋅ ⎢ I A + a 2 .I B + a.I C ⎥ 3 ⎣ ⎦ Como I A = 62,4∠ − 31,5º = 53,2 − 32,6 j A a 2 .I B = 1∠240º⋅46,53∠ − 164,5º = 46,53∠75,5º a.I C = 1∠120º⋅62,4∠88,5º = 62,4∠208,5º sustituyendo resulta: I 2 A = 6,6∠ − 60º A I 2 B = a.I 2 A = 6,6∠60º A I 2C = a 2 I 2 A = 6,6∠180º A © Los autores, 2006; © Edicions UPC, 2006 33 Circuitos trifásicos 1.10 Problema 10 Cuando la carga simétrica de la figura se alimenta por los bornes R, S, T con un sistema simétrico de tensiones, las indicaciones de los aparatos de medida son lo siguientes: Voltímetro V1 = 400 V Voltímetro V2 = 420 V Vatímetro W1 = 15.285,5 W Vatímetro W2 = 6.047,8 W Amperímetro A1 = 38,49 A Se pide: a) Los valores de R∆ y XL∆ b) ¿Cuál es la indicación del voltímetro V3 en este caso? c) Valor de XCλ R A1 W1 XCλ V1 R∆ XL∆ XL∆ R∆ XL∆ R∆ XCλ W2 S XCλ V2 T V3 Figura 1.10.1 Resolución: a) El triángulo central de la carga lo pasamos a estrella, siendo la impedancia equivalente por fase, conexión en estrella: Zλ = U1 3I1 = 400 = 6Ω 3 ⋅ 38,49 Para el cálculo del argumento nos basamos en las indicaciones de los vatímetros W1 y W2, que forman una conexión Aron: P = W1 + W2 = 15285,5 + 6047 ,8 = 21333,3 W Q = 3 (W1 − W2 ) = 3( 15285 ,5 − 6047 ,8 ) = 16000 ,2 VAr tgϕ = Q = 0,75 P → cos ϕ = 0,8 → senϕ = 0,6 → Luego: Z λ = 6∠36,87º Ω = 4,8 + j 3,6 Ω © Los autores, 2006; © Edicions UPC, 2006 ϕ = 36,87 º 34 Problemas de electrotecnia Esta impedancia se puede expresar como: Por tanto: Z λ = R λ + j ( X L λ − X Cλ ) → Rλ = 4,8Ω R ∆ = 3 ⋅ Rλ = 14,4Ω De la indicación del voltímetro V2, se puede calcular XL: X L∆ = U2 I∆ = U2 I1 / 3 = 3 ⋅U 2 I1 = 3 ⋅ 420 = 18,9 Ω 38,49 → X L∆ = 18,9 Ω b) La impedancia de una fase del triángulo es: ZL ∆ = R∆ + j X L∆ = 14,4 + j18,9 = 23,761∠52,696 Ω Y, en consecuencia, la indicación del voltímetro V3 es: I 38,49 ⋅ 23,761 = 528,02 V U 3 = I ∆ ⋅ Z L∆ = 1 ⋅ Z L∆ = 3 3 → U 3 = 528,02 V c) El valor total de la impedancia en estrella vale: Z λ = Rλ + j ( X Lλ − X cλ ) Del apartado a: Z = 4,8 + j3,6 Ω λ Luego la parte imaginaria: X Lλ − X cλ = 3,6 Ω y puesto que: X Lλ = X L∆ 3 = 18,9 = 6,3 Ω 3 Resulta: X cλ = 6,3 − 3,6 = 2,7 Ω © Los autores, 2006; © Edicions UPC, 2006 35 Circuitos trifásicos 1.11 Problema 11 Un generador trifásico de secuencia directa y equilibrado en tensiones alimenta una carga trifásica. A esta carga se conectan tres cargas equilibradas I, II, III, según se indica en la figura. Las cargas I y II son desconocidas y de la carga III se conoce el valor de la impedancia por fase, que vale: con un cos ϕ3 = 0,5 (inductivo) Z 3 = 15 3 / 2 Cuando los interruptores K1 y K2 están abiertos, las indicaciones de los vatímetros son: W1 = 3 3 kW W 2 = 0 kW Además, se sabe que el voltímetro marca V = 300V. Se pide: a) Potencia activa y reactiva consumida por el receptor I, el valor que indicará el amperímetro A1 y el factor de potencia de la carga. Si a continuación se cierra K1, manteniendo K2 abierto las indicaciones de los vatímetros en este caso son: W1 = 4 3 kW , W2 = 2 3 kW . Para este caso, se pide: b) Factor de potencia de la carga c) Potencias activas y reactiva del receptor II y la indicación de A2 Finalmente, cerrando también el interruptor K2, se pide: d) Indicación del amperímetro A3 e) Potencias activa, reactiva y aparente del generador f) Factor de potencia de la carga g) Lectura del amperímetro AR R WI1A AR V S W2 T A1 A2 I A3 K1 II K2 Z3 Z3 Z3 III Figura 1.11.1 Resolución: a) Por estar conectados los vatímetros según el método de Aron y ser un sistema equilibrado en tensiones y en cargas, se verifica: P = W1 + W2 © Los autores, 2006; © Edicions UPC, 2006 36 Problemas de electrotecnia Q = (W1 − W2 ) ⋅ 3 Resulta PI = 3000 3 W Q I = 3 ⋅ 3000 3 = 9000 VAr y, por tanto, la potencia aparente: S I = PI + jQ I = 3000 3 + 9000 jVA = 6000 3∠60 º VA El módulo de la potencia aparente de un sistema trifásico, en función de la tensión entre fases UG y la corriente de la línea I1, vale: S I = 3 ⋅ U G ⋅ I1 Sustituyendo valores: I1 = 6000 3 300 3 = 20 → A1 = 20 A El factor de potencia es cos φ1, y el valor de φ1 se obtiene de: tgϕ1 = QI 9000 = =+ 3 PI 3000 3 ϕ1 = 60º → Por tanto: cos ϕ1 = cos 60º = 0,5 (i) b) Al conectar el receptor II se produce una modificación del valor de la carga, lo que puede ocasionar una modificación del desfase entre la tensión y las corrientes de las respectivas fases y, en tal caso, un nuevo valor del factor de potencia dado por: tgϕ 2 = QII = PII Resultando 3 (W1 − W2 ) = W1 + W2 3 (4 3 − 2 3 ) 4 3+2 3 = 3 3 ϕ 2 = 30º cos ϕ 2 = cos 30º = 0,866 c) Los vatímetros medirán la potencia total consumida por las cargas I, II, por tanto: PII = (W1 + W 2 ) − PI = 4000 3 + 2000 3 − 3000 3 = 3000 3 W → PII = 3000 3 W Q II = (W1 − W2 ) ⋅ 3 − Q I = 3 ( 4000 3 − 2000 3 ) − 9000 = −3000 VAr → Q II = −3000 VAr y como consecuencia: S II = PII + jQII = 3000 3 − 3000 j = 6000∠ − 30º VA y como en el caso anterior: I2 = S II 3U G = 6000 3 ⋅ 300 = 20 3 → A2 = 20 A 3 y como en el vector S II tiene un ángulo de fase de (-30º), el vector corriente I 2 vale: I2 = 20 ∠30º A (carga capacitiva) 3 d) Al quedar conectadas todas las cargas, la corriente I3 vale: © Los autores, 2006; © Edicions UPC, 2006 37 Circuitos trifásicos I3 = U GS Z3 U GS = I3 = Siendo UGS la tensión del sistema trifásico, es decir: U 300 = V 3 3 300 40 = A 3 15 3 3⋅ 2 → A3 = 40 A 3 e) Puesto que se conocen las potencias trifásicas activa, reactiva y aparente consumidas por las cargas I y II, encontraremos la potencia total consumida por todas las cargas calculando previamente la correspondiente a la carga III, que es tres veces el valor de la potencia de una cualquiera de sus fases (carga equilibrada): 300 40 ⋅ ⋅ 0,5 = 2000 3 W 3 3 300 40 3 ⋅ I 3 senϕ 3 = 3 ⋅ ⋅ ⋅ = 6000 VAr 3 3 2 PIII = 3 ⋅ U GS ⋅ I 3 cos ϕ 3 = 3 ⋅ QIII = 3 ⋅ U GS Las potencias activa y reactiva suministrada por el generador corresponden a las absorbidas por las cargas y, por consiguiente: PG = PI + PII + PIII = 3000 3 + 3000 3 + 2000 3 = 8000 3 W QG = QI + QII + QIII = 9000 − 3000 + 6000 = 12000 VAr S G = 8000 3 + 12000 jVA = 18330 ,3∠40,89 º VA f) El factor de potencia correspondiente a la carga es: cos ϕ = cos 40,89º = 0,756 g) Cálculo de la intensidad de corriente que circula por el amperímetro: I R = I 2 + I3 = IR = IR = 20 3 20 cos 30º + 3 ∠30º + 20 3 40 ∠ − 60º 3 sen30º j + 40 40 cos(−60º ) + sin(−60º ) j 3 3 20 ⎞ 10 3 3 40 1 ⎛⎜ 20 1 40 3 ⎞⎟ ⎛ j = ⎜10 + j + + ⋅ − ⋅ ⎟− ⎜ ⎟ 3 ⎠ 3 3 2 ⎝ 3 2 3 2 ⎠ 3 2 ⎝ 20 I R = 17,64∠ − 19,10º A AR = I R = 17,64 A © Los autores, 2006; © Edicions UPC, 2006 38 Problemas de electrotecnia 1.12 Problema 12 El generador, de secuencia directa, del circuito representado en la figura mantiene siempre la tensión compuesta de 250V a la frecuencia de 50 Hz. Se conecta el interruptor K1, manteniendo abiertos K2 y K3, y se observan las siguientes indicaciones de los aparatos de medida: W3 = −4 3 kW A1 = 20 3 A RECEPTOR C XL XL XL K3 A3 A3 A3 R G S W1 W3 W2 A2 A ZB A A2 A A2 ZB IB>10 ZB T K2 A1 A1 A1 RECEPTOR B cos φB = 0,28 K1 RECEPTOR A Figura 1.12.1 Se pide: a) Indicaciones de los otros aparatos de medida conectados al circuito (A, W1 y W2). A continuación, con K1 conectado, se conecta K2, quedando K3 desconectado. En este estado la potencia aparente absorbida del generador es 5/6 de la anterior, siendo cos ϕ B = 0,28 y IB > 10A. b) Calcular los valores de la impedancia Z B y la corriente IB. c) Las nuevas indicaciones de los aparatos de medida (A, A2, W1, W2 y W3). Finalmente, con K1 y K2 conectados, se conecta K3. En este estado el factor de potencia de la instalación es 0,8. d) Características del receptor C (XL, L) e) Nueva indicación de los aparatos de medida (A, A3, W1, W2 y W3) © Los autores, 2006; © Edicions UPC, 2006 39 Circuitos trifásicos Resolución: a) Si el receptor A absorbe una corriente I1 = 20 3 A , a la tensión compuesta de 250 V, el módulo de la potencia trifásica aparente vale: S A = 3.U .I 1 = 3 ⋅ 250 ⋅ 20 3 = 15000 VA La potencia trifásica reactiva absorbida por este receptor se obtiene a partir de la indicación del vatímetro W3 y vale: Q A = 3W3 = − 3 ⋅ 4 3 = −12kVAr = −12000VAr Con lo que la potencia trifásica activa absorbida por el receptor se obtiene de: PA = S A2 − QA2 = 15000 2 − 12000 2 = 9000W siendo cos ϕ A = 0,6 (capacitivo) (deducido a partir de los valores de PA y QA) y: S A = 9000 − 12000 jVA = 15000∠ − 53,13º VA A continuación, encontraremos las expresiones vectoriales de las corrientes absorbidas, para ello tomamos como origen de fases la tensión simple: U RN = I *1 = UC 3 ∠0º V SA 3 ⋅ U C / 3∠0º = 3 ⋅ 15000∠ − 53,13º = 20 3∠ − 53,13º 3 ⋅ 250∠0º I 1 = 20 3∠53,13º = 12 3 + 16 3 j A A = A1 = 34,6 A Las indicaciones de los amperímetros son: El vatímetro W1 indica: W1 = U RS .I R cos(ϕU RS − ϕ I R ) = 250 ⋅ 20 3 cos(30º −53,13º ) = 7964,10 W El vatímetro W2 indica: W2 = U ST .I S cos(ϕU − ϕ I ) = 250 ⋅ 20 3 cos(−23,13º ) = 7964,10 W ST S Si los vatímetros se hubiesen conectado según el método Aron, las indicaciones habrían sido: W1 + W2 = 9000 W1 − W2 = −12000 / 3 = −6928,2 De aquí que: 2W1 = 2071,8 W1 = 2071,8 / 2 = 1035,9 W 2W2 = 15928,2 W2 = 15928,2 / 2 = 7964,1 W b) Al conectar el receptor K2, permaneciendo cerrado K1 y abierto K3, la potencia aparente absorbida por los receptores A y B es 5/6 de la que consumían, de manera que la potencia aparente es: S A+ B = 5 5 ⋅ S A = ⋅ 15000 = 12500 VA 6 6 Con lo que se puede escribir la siguiente ecuación vectorial referida a las potencias trifásicas: 12500∠α = 3R B ⋅ I B 2 + 9000 + j.(3 X B I B 2 − 12000) © Los autores, 2006; © Edicions UPC, 2006 40 Problemas de electrotecnia En esta expresión se ha considerado Z Bλ = RBλ + jX Bλ como una impedancia de fase de la estrella equivalente del receptor B, de manera que IB es la corriente de la línea del receptor B solamente. Puesto que cos ϕ B = 0,28 senϕ B = 0,96 ϕ B = 73,74º se pueden expresar los valores de RBλ y XBλ en función de una sola incógnita ZBλ: RBλ = Z Bλ ⋅ cos ϕ B = 0,28 ⋅ Z Bλ X Bλ = Z Bλ ⋅ senϕ B = 0,96 ⋅ Z Bλ Y de este modo, se puede desdoblar la ecuación vectorial anterior en parte real y parte imaginaria de la siguiente manera: 12500 cos α = 9000 + 3 ⋅ 0,28Z Bλ I B 2 = 9000 + 0,84 I B 2 Z Bλ 12500 senα = −12000 + 3 ⋅ 0,96 Z Bλ I B 2 = −12000 + 2,88 I B 2 Z Bλ U Puesto que, por otra parte: I B = IB2 = 3Z Bλ = 250 3Z Bλ 2 250 62500 = 3Z Bλ 3Z Bλ 2 Y sustituyendo, obtenemos un sistema de dos ecuaciones con dos incógnitas: 12500 cos α = 9000 + 0,84 62500 3Z Bλ 12500 senα = −12000 + 2,88 2 Z Bλ = 9000 + 62500 3Z Bλ 2 17500 Z Bλ Z Bλ = −12000 + 60000 Z Bλ Operando: 12,5Z Bλ cos α = 9 Z Bλ + 17,5 12,5Z Bλ senα = −12 Z Bλ + 60 Elevando al cuadrado y sumando, se obtiene: 156,25Z Bλ 2 = 81Z Bλ 2 + 315Z Bλ + 306,25 + 144 Z Bλ 2 + 3600 − 1440 Z Bλ 68,75Z Bλ 2 − 1125Z Bλ + 3906,25 = 0 Así pues, se han encontrado dos valores posibles de ZBλ: Z B1λ = 11,36 Ω Z B 2λ = 5 Ω Puesto que ZB no está conectada en estrella, sino en triángulo, el valor por fase es: Z B∆ = 3Z Bλ = Z B1∆ = 34,09Ω Z B 2 ∆ = 15Ω Para los dos valores de la impedancia calculada, la corriente de fase respectiva al triángulo de impedancias vale: I 1B = U Z B1∆ = 250 = 7,33 A < 10 A 34,09 I 2B = U Z B 2∆ © Los autores, 2006; © Edicions UPC, 2006 = 250 = 16,66 A > 10 A 15 41 Circuitos trifásicos Y puesto que se nos impone que IB > 10 A, la solución para ZB∆ es Z B∆ = 15Ω . De manera que: Z B = 15∠ϕ B = 4 ,2 + j14,4Ω = 15∠73,74º Ω y, por tanto, la corriente para cada fase del triángulo de impedancias del receptor B es: I B = 16,66 A c) Los amperímetros A2 indican: I 2 = I B 3 = 16 ,66 3 = 28,87 A = 50 / 3 A → I 2 = 50 / 3 A Para calcular la lectura de los otros aparatos de medida, analicemos en primer lugar las potencias que se tienen: Potencias activas Potencias reactivas 17500 = 12500 5 60000 12500 senα = −12000 + =0 5 12500 cos α = 9000 + cos α = 1 en consecuencia: senα = 0 α = 0º Lo que quiere decir que al conectar dos receptores A y B el circuito entra en resonancia y la potencia aparente necesaria es de la forma: S ' A+ B = 12500∠0º VA = (12500 + 0 j )VA Q ' A+ B = 0VAr W '3 = 0 Q ' A+ B = 3W ' 3 Los amperímetros A indican, en este caso: I '* = S ' A+ B 3U = 12500∠0º 3 ⋅ 250∠0º = 50 3 → ∠0º A 50 I' = 3 A De manera que: I’ = I2 Los vatímetros indicarán ahora: W '1 = W '2 = U RS .I R cos( ϕU RS − ϕ I ' R ) = 250 ⋅ 50 3 ⋅ cos 30º = 6250 W → W’1 = W2’ = 6250 W d) Al conectar K3, dejando K1 y K2 cerrados, se introducen en el circuito tres reactancias puras conectadas en estrella, de manera que la potencia activa del circuito no variará respecto al segundo caso. Por tanto: P' ' A+ B + C = 12500W Q ' ' A+ B +C = 12500tgϕ ' ' y puesto que ahora cos ϕ ' ' = 0,8 ϕ ' ' = 36,87 º tgϕ ' ' = 0,75 Q' ' A+ B +C = 12500 ⋅ 0,75 = 9375 VAr Y, por tanto, la potencia aparente en forma compleja es: S' ' = P' ' + jQ' ' = ( 12500 + 9375 j ) VA = 15625∠36,87º VA Con ello, el receptor C absorbe del generador una potencia que vale: SC = ( 0 + 9375 j )VA = 9375∠90º VA Ahora se cumplirá: S C = 3 ⋅ U C ⋅ I *3 © Los autores, 2006; © Edicions UPC, 2006 42 Problemas de electrotecnia De donde: I *3 = 9375∠90º 3 ⋅ 250∠0º = 37,5 3 → ∠90º I3 = 37,5 3 ∠ − 90º A = 12,5 3∠ − 90º A Los amperímetros A3 indican 12,5 3 A = 21,65 A Las reactancias conectadas al circuito en estrella tienen un valor por fase de: 250 XL = US I3 = ∠0 º 250∠0º 3 = 6,66̂∠90º Ω = 12,5 3∠ − 90 º 12,5 ⋅ 3∠ − 90º X L = 6,6ˆ6∠90º Ω = ( 0 + j 6,6ˆ6 ) Ω fase que se podría haber determinado a partir de la potencia aparente absorbida por el receptor C de la manera siguiente: SC = 3X L I 32 → XL = 9375 X L = 6,6ˆ6 Ω → 2 3 ⋅ ( 12,5 3 ) Y como se cumple que: X L = ωL = 100πL L= 6 ,6ˆ6 = 0,02122 H 100π → L = 21,22 mH las nuevas indicaciones de los amperímetros A, en este tercer caso, son: I "* = I" = S" 3 ⋅ U C ∠0º 62,5 3 = 15625∠36,87 º 3 ⋅ 250∠0º = 62,5 3 ∠36,87 º → ∠ − 36,87º = 36 ,08∠ − 36 ,87º A Ahora el vatímetro W3 indica: W " 3 = Q" 3 = 9375 3 I" = 36,08 A = 3125 3 W Los vatímetros W1 y W2 indican, en este tercer caso: W ' '1 = W ' ' 2 = U RS I R cos(ϕU RS − ϕ I ' RS ) = 250 ⋅ 62,5 3 ⋅ cos[30º +36,87 º ] W ' '1 = W ' '2 = 3543,66 W © Los autores, 2006; © Edicions UPC, 2006 43 Circuitos trifásicos 1.13 Problema 13 El generador trifásico de la figura genera unas tensiones senoidales de secuencia directa y tiene una impedancia interna que se puede despreciar. Está conectado mediante una línea de resistencia 2 Ω y una inductancia desconocida a una carga equilibrada y conectada en triángulo con una impedancia por fase de 16,97 Ω. Las indicaciones de los aparatos de medida son: W4 = 2904 W y V1 = 380 V . También se conocen la suma de las indicaciones de los aparatos W1 y W2, que es de 5808 W. Se pide: a) Corriente de línea y corriente que circula por la carga b) Indicación del vatímetro W3 c) Valor de la inductancia X1 de la línea d) Indicación del voltímetro V2 Xl R=2Ω W4 W1 W3 V2 V1 R=2Ω Xl R=2Ω Xl Carga inductiva equilibrada conectada en triángulo W2 Figura 1.13.1 Resolución: a) Tal como están conectados los vatímetros W1 y W2, se puede determinar la potencia activa total consumida por la carga (conexión de Aron): P = W1 + W 2 = 5808 W y por fase vale P f = 5808 = 1936 W 3 Por otro lado, el vatímetro W4 nos da la potencia por fase que suministra el generador y que es de 2904W, lo que quiere decir que la potencia consumida por fase por la línea es: Plf = 2904 − 1936 = 968 W y conociendo el valor de la resistencia, se puede determinar la corriente de línea: I l = Plf / R = 968 / 2 = 22 A Al estar la carga en triángulo, la intensidad en ella es: IC = 22 / 3 = 12,70 A b) A continuación, se determina la inductancia de la línea X1 y la resistencia y la inductancia de la carga. La corriente por fase vale 12,70 A y la potencia activa por fase es de 1936W; por tanto, la resistencia vale: © Los autores, 2006; © Edicions UPC, 2006 44 Problemas de electrotecnia R= 1936 12,70 2 = 12 Ω Además, R 2 + X C 2 = 16,97 2 X C = 16 ,97 2 − 12 2 = 12 Ω En definitiva, Z C = 12 + 12 j Ω = 16 , 97 ∠ 45 º Ω Representando el circuito monofásico correspondiente, se obtiene: 3 ⋅ 2Ω 3⋅ X l Z C = 12 + 12 jΩ 380∠0º Figura 1.13.2 Por tanto: ZT = U I = 380 = 29 ,92 Ω 12 ,70 y también: 29,92 = (3 ⋅ 2 + 12)2 + (3 X 1 + 12)2 resultando: X 1 = 4 Ω El vatímetro W3 indica la potencia reactiva total del circuito dividida por 3 . QT = 3 ⋅ I 2 ⋅ X T = 3 ⋅ 12 ,70 2 ⋅ (4 ⋅ 3 + 12 ) = 11612,88 VAr Por consiguiente, la indicación del vatímetro W3 es: W3 = QT / 3 = 6704,7 W c) La inductancia de la línea ya ha sido determinada y su valor es: d) La indicación del voltímetro V2 es: U 2 = Z C I f = 12,70 ⋅16,97 = 215,52 V © Los autores, 2006; © Edicions UPC, 2006 X1 = 4 Ω 45 Circuitos trifásicos 1.14 Problema 14 En el circuito representado en la figura se conocen las indicaciones de los siguientes equipos de medida: A1 = 10 A W = 15588 W Por otra parte, se conoce el módulo de la diferencia vectorial entre las tensiones V1 y V 2 , que vale 3000V, y se sabe la secuencia de generación es directa. También se sabe que la potencia activa que cede el generador es de 90 kW y que la potencia reactiva es de 27 kVAr. El voltímetro VG indica una lectura de 3059,41V y la impedancia interna del generador ZG es totalmente reactiva. Zl W E3 V1 ZG + ZG + A2 V3 E1 VG ZC ZC Zl ZC A1 + E2 ZG V2 V3 Zl Figura 1.14.1 Se pide: a) Impedancia de la línea b) Impedancia de la carga c) Impedancia interna del generador d) Lectura del voltímetro V3 e) Lectura del amperímetro A2 Resolución: a) Por la disposición del vatímetro W, se puede calcular la potencia reactiva de la carga, ya que: W = QC / 3 QC = 3 ⋅ W = 3 ⋅15588 = 27000 VAr Como se puede observar, la potencia reactiva del generador y la potencia reactiva de la carga coinciden, cosa que indica que la línea se puede considerar como una resistencia pura. Por otro lado, como se conoce la corriente de fase de la carga, se puede determinar la corriente de la línea. © Los autores, 2006; © Edicions UPC, 2006 46 Problemas de electrotecnia Il = I fc arg a ⋅ 3 = 10 3 = 17 ,32 A A continuación, se halla cuanto vale la diferencia vectorial entre V1 y V2. Al ser una carga equilibrada las corrientes de línea son iguales, pero desfasadas 120º, tal como se representan en la figura siguiente: Figura 1.14.2 Las caídas de tensión en las líneas son: V1 = I R ⋅ R = 17,32∠0º⋅R V 2 = I s ⋅ R = 17,32∠ − 120º⋅R V1 − V 2 = 17,32∠0º⋅R − 17,32∠ − 120º⋅R = R(17,32∠0º −17,32∠ − 120º ) = R ⋅ 30∠30º V1 − V 2 = 30 R Por otro lado y según el enunciado del problema, la anterior expresión vale 3000 y por tanto: → 30 R = 3000 R = 100 Ω b) Para calcular la impedancia de la carga, se calcula en primer lugar la potencia absorbida por la línea: Pl = 3 ⋅ I l 2 ⋅ R = 3 ⋅17 ,32 2 ⋅100 = 90000 W potencia que coincide con la proporcionada por el generador, lo que indica que la potencia activa absorbida por al carga es nula, es decir, se trata de una carga inductiva pura. A continuación, se calcula el valor de esta carga inductiva: XC = QCf If2 27000 = 10 2 3 = 90 Ω c) El circuito se puede estudiar transformándolo en el equivalente monofásico: © Los autores, 2006; © Edicions UPC, 2006 47 Circuitos trifásicos 300Ω Z C = 90 j ZG EG Figura 1.14.3 Si se plantea la segunda ley de Kirchhoff para la fase R, se obtiene: E R = I R .( Z G + 300 + 90 j ) Pero teniendo en cuenta que Z G es una reactancia pura, se puede hacer la siguiente representación vectorial donde I R es la corriente de la fase R. En consecuencia: E R 2 = (I R ⋅ R )2 + [I R (90 + X G )]2 y sustituyendo valores: 3059,412 = (10 ⋅ 300)2 + [10(90 + X G )]2 y resolviendo: X G = −30Ω es decir, es una impedancia capacitiva d) El voltímetro V3 indica: U 3 = I f ⋅ X C = 10 ⋅ 90 = 900 V e) La lectura del amperímetro A2 es: I 2 = 10 3 = 17,32 A © Los autores, 2006; © Edicions UPC, 2006 48 Problemas de electrotecnia 1.15 Problema 15 En el circuito de secuencia directa representado en la figura hay conectadas dos cargas trifásicas equilibradas, cuyas impedancias por fase son Z 1 = ( 30 − j10 ) Ω y Z 2 = ( 20 + j10 ) Ω respectivamente. La impedancia por fase de la línea es Z L = ( 1 + j ) Ω . Además, se conoce que la tensión de la línea es de 220V. Se pide: a) Las indicaciones de los aparatos de medida A, V1, V2, A1 y A2. b) Las potencias activa y reactiva absorbidas por cada carga y la lectura del vatímetro. c) La potencia perdida en la línea. d) La capacidad por fase de una batería de condensadores conectados en triángulo, que se habría de conectar en paralelo con las cargas para conseguir un factor de potencia igual a la unidad. R Z1 ZL A A1 W S ZL Z1 T ZL Z1 V1 A2 Z2 Z2 Z2 V2 Figura 1.15.1 Resolución: a ) El circuito se estudia transformándolo en el correspondiente monofásico, representado en la figura, teniendo en cuenta que las cargas Z 1 y Z 2 están conectadas en paralelo. La tensión del circuito monofásico es la tensión simple, es decir, R 220 / 3 V . ZL UG = 220 3 V Z2 Z1 N Figura 1.15.2 © Los autores, 2006; © Edicions UPC, 2006 49 Circuitos trifásicos Siendo: Z L = 1 + j = 2∠45º Ω Z 1 = 30 − 10 j = 31,62∠ − 18,43º Ω Z 2 = 20 + 10 j = 22 , 36 ∠ 26 , 56 º Ω A continuación, se busca la Z P equivalente a las impedancias en paralelo Z 1 y Z 2 . ZP = Z1 ⋅ Z 2 Z1 + Z 2 = 31,62∠ − 18,43º ⋅22,36∠26,56º = 10 2∠8,13º Ω = 14 + 2. j Ω 30 − 10 j + 20 + 10 j La impedancia equivalente total por fase del circuito es: Z T = Z L + Z P = 1 + j + 14 + 2 j = 15 + 3 j = 15,3∠11,31º Ω En consecuencia, la corriente que circula por el circuito es: I= UG ZT 220 / 3∠0º = 8,3∠ − 11,31º = 8,14 − 1,63 j A 15,3∠11,31º = La tensión simple en bornes de las cargas es U C = U G − U L , además se sabe que: U L = Z L .I = 2∠45º ⋅8,30∠ − 11,31º = 11,74∠33,69º V U L = 9 ,77 + 6 ,51 j V En consecuencia: UC = 220 3 − 9 ,77 − 6,51 j = 117 ,25 − 6 ,51 j = 117 ,43∠ − 3,18º V La corriente que absorbe la carga 1 es: I1 = UC Z1 = 117 ,43∠ − 3,18º = 3,71∠15,25º = 3,58 + 0 ,98 j A 31,62∠ − 18,43º y la absorbida por la carga 2 es: I2 = UC Z2 = 117 ,43∠ − 3,18º = 5,25∠ − 29 ,74º = 4,56 − 2 ,61 j A 22,36∠26 ,56º Las tensiones en cada carga son: U1 = Z1 I1 = 31,621∠ − 18,43º ⋅3,71∠15,25º = 117,43∠ − 3,18º V U 2 = Z 2 I 2 = 22,36∠26,56º ⋅5,25∠ − 29,74º = 117,43∠ − 3,18º V Como era de esperar: U 1 = U 2 = U C Resultan, por tanto, las siguientes indicaciones de los aparatos de medida: Amperímetro A: 8,3 A Voltímetro V1: 117,43 V Voltímetro V2: 117,43 V Amperímetro A1: 3,71 A Amperímetro A2: 5,25 A © Los autores, 2006; © Edicions UPC, 2006 50 Problemas de electrotecnia b) Las potencias consumidas en la impedancia Z 1 son: Potencia activa trifásica: P1 = 3 ⋅ R1 ⋅ I 1 2 = 3 ⋅ 30 ⋅ 3,712 = 1241 W Potencia reactiva trifásica: Q1 = 3 ⋅ X 1 ⋅ I 1 2 = 3 ⋅10 ⋅ 3,712 = 413,69VAr (−) Las potencias consumidas en la impedancia Z 2 son: Potencia activa trifásica: P2 = 3 ⋅ R 2 ⋅ I 2 2 = 3 ⋅ 20 ⋅ 5,25 2 = 1654 ,77 W Potencia reactiva trifásica: Q2 = 3 ⋅ X 2 ⋅ I 2 2 = 3 ⋅10 ⋅ 5,25 2 = 827 ,38 VAr La potencia aparente total trifásica de las dos cargas: S C = S1 + S 2 = 1241 − 413,69 j + 1654,77 + 827,38 j S C = 2985,77 + 413,69 j = 2925,17∠8,13º VA que se puede también calcular como: SC = 3 ⋅ UC ⋅ I * = 3 ⋅117,43∠ − 3,18 ⋅ 8,30∠11,31º = 2925,17∠8,13º V.A La indicación del vatímetro W, teniendo en cuenta como está conectado, es: W = Q'C / 3 = 413,69 / 3 = 238,84 W c) La potencia aparente perdida en la línea es: S L = 3 ⋅ U L ⋅ I * = 3 ⋅ 11,74∠33,65 ⋅ 8,30∠11,31º = 292,27∠45 = ( 206,67 + 206,67 j ) VA S L = 206,67 + 206,67 j VA d) Se ha de tener en cuenta que la potencia aparente que corresponde al conjunto de las cargas 1 y 2 es S C = ( 2895,77 + j 413,69 ) VA y que se ha de compensar el factor de potencia hasta la unidad, lo que quiere decir que hay que tomar una potencia reactiva trifásica inductiva del conjunto de las cargas 1 y 2, pero cambiada de signo, es decir, una potencia reactiva trifásica capacitiva Q'C = 413,69 VAr , que por fase vale: QCf = 413,69 / 3 = 137,90 VAr(−) Por tanto, la capacidad total de los condensadores por fase conectados en triángulo vale: CµF = Qcf W ( U C 3 )2 = 137 ,90 ⋅106 2π 50( U C 3 )2 = 137 ,90 ⋅ 106 100 ⋅ 3,14( 117 ,43 3 )2 = 10,61 µF C µF = 10,61 µF © Los autores, 2006; © Edicions UPC, 2006 51 Circuitos trifásicos 1.16 Problema 16 Se quiere mejorar el factor de potencia de una instalación eléctrica que alimenta a 3 kV, 50 Hz, una carga inductiva de 250 kVA, cosφ = 0,8, hasta la unidad, a base de conectar una batería de condensadores conectados en estrella. S = 250 kVA cos φ = 0,8 (i) C C C C C C Figura 1.16.1 En el supuesto que cada rama de la batería de condensadores esté formada por dos condensadores iguales conectados en paralelo, tal como se indica en la figura 1, se pide: a) Potencia de la batería de condensadores para conseguir el fin propuesto b) Potencia de cada condensador c) Reactancia de cada condensador d) Capacidad de cada condensador e) Corrientes por fase en la batería de condensadores f) Tensión en bornes de cada condensador En el caso de que uno de los condensadores de la fase R se elimine, dejando abierto el circuito, se pide: g) Corrientes por fase en la batería de condensadores h) Tensiones simples en bornes de los condensadores i) Incremento de la tensión a que están sometidos los condensadores de la fase R en tanto por ciento respecto a la del apartado f) © Los autores, 2006; © Edicions UPC, 2006 52 Problemas de electrotecnia Resolución: a) La potencia reactiva de la carga es Q L = S ⋅ senϕ . QL = 250 ⋅ 0 ,6 = 150 kVAr(+) Por tanto, la batería de condensadores tiene una potencia de: QCT = 150 kVAr(−) b) Esta potencia se tendrá que repartir entre el número total de condensadores, que en nuestro caso es de 6, y por tanto: QCT 150 = = 25 kVAr n 6 QC = c) La reactancia del condensador se puede obtener a partir de su potencia y de la tensión de alimentación por fase US: QC = X C ⋅ I C UC US = 3 XC = = 2 ⎞ U 2 ⎟ = S ⎟ XC ⎠ ⎛U = X C ⋅ ⎜⎜ S ⎝ XC 2 3 3 → XC = US2 QC kV = 3 kV ( 3 ⋅1000 ) 2 = 120 Ω 25000 X C = 120 Ω d) La frecuencia de la red es f = 50Hz, por tanto: C= 1 1 = = 26,53 µF 2πfX C 100π ⋅ 120 e) Los módulos de las corrientes de fase en la batería de condensadores son iguales entre sí y de valor: If = US X CT en la cual la reactancia XCT representa la reactancia equivalente a la de los condensadores en paralelo de una fase, es decir, a la reactancia por fase. X CT = Y por tanto: X C 120 = = 60 Ω 2 2 If = 3 .10 3 = 28,868 A 60Ω © Los autores, 2006; © Edicions UPC, 2006 53 Circuitos trifásicos f) La tensión en bornes de cada condensador es la tensión de fase: U C = U S = 3 kV g) Se toma como origen de ángulos la tensión simple de la fase R, tal como se representa en la figura. Figura 1.16.2 U RN = 3∠0º kV U SN = 3∠ − 120º kV U TN = 3∠120º kV Las tensiones compuestas valen: U RS = 3∠30º kV U ST = 3∠ − 90º kV UTR = 3∠150º kV Eliminando un condensador de la rama de la batería de condensadores conectada a la fase R, la carga se convierte en desequilibrada cuyas impedancias por fase valen, respectivamente: Z R = − jX C Z R = −120 j = 120∠ − 90º Ω ZS = − j XC 2 Z S = −60 j = 60∠ − 90º Ω ZT = − j XC 2 Z T = −60 j = 60∠ − 90º Ω Figura 1.16.3 © Los autores, 2006; © Edicions UPC, 2006 54 Problemas de electrotecnia La figura anterior se puede simplificar obteniéndose el circuito siguiente (resolviendo por el método de las mallas): Figura 1.16.4 U RS = I 1 ( Z R + Z S ) − I 2 ⋅ Z S 3000∠30º = I 1 ⋅180∠ − 90º − I 2 ⋅ 60∠ − 90º U ST = I 2 ( Z S + Z T ) − I 1 ⋅ Z S 3000∠ − 90º = − I 1 ⋅ 60∠ − 90º + I 2 ⋅120∠ − 90º Expresado en forma matricial resulta: ⎡ 3000∠30º ⎤ ⎡ 180∠ − 90º − 60∠ − 90º ⎤ ⎡ I 1 ⎤ ⎢3000∠ − 90º ⎥ = ⎢− 60∠ − 90º 120∠ − 90º ⎥ ⎢ ⎥ ⎦ ⎣⎢ I 2 ⎦⎥ ⎦ ⎣ ⎣ Por tanto: I1 = j17 ,321 = 17 ,321∠90º A → ⎡ 17,321∠90º ⎤ ⎡0 + 17,321 j ⎤ I =⎢ ⎥=⎢ ⎥A ⎣26,458∠19,107º ⎦ ⎣25 + 8,660 j ⎦ I 2 = 25 + j8,660 = 26 ,458∠19 ,107º A De la figura anterior se deduce: I R = I 1 = 17 ,321∠90º A I S = I 2 − I 1 = 25 + j8,660 − j17 ,321 = 25 − j8,661 = 26 ,458∠ − 19 ,107º A I T = − I 2 = 26 ,458∠199 ,107º A Figura 1.16.5 © Los autores, 2006; © Edicions UPC, 2006 55 Circuitos trifásicos h) Las tensiones simples en bornes de los condensadores son las tensiones U R 0 , U S 0 y U T 0 respectivamente. U R 0 = Z R ⋅ I R = 120∠ − 90º ⋅17 ,32∠90º = 2078,52∠0º V U S 0 = Z S ⋅ I S = 60∠ − 90º ⋅26 ,458∠ − 19 ,107º = 1587 ,48∠ − 109 ,107º V U T 0 = Z T ⋅ I T = 60∠ − 90º ⋅26 ,458∠199,107º = 1587 ,48∠109 ,107º V Los condensadores de la fase R están sometidos a sobretensión respecto del caso anterior y los de las otras fases trabajan a una tensión inferior. i) El incremento en tensión en tanto por ciento es: u% = U RN − U RO ⋅ 100 con U RN = 3 kV U RN u% = 1732,05 − 2078,52 ⋅100 = 20% 1732 ,05 → u% = 20% © Los autores, 2006; © Edicions UPC, 2006 56 Problemas de electrotecnia 1.17 Problema 17 El circuito de la figura está constituido por un generador trifásico equilibrado, de secuencia directa y frecuencia de 50 Hz, alimentando una carga trifásica equilibrada. La impedancia de la línea es Z 1 . La tensión en bornes de la carga indicada por el voltímetro V2, es de 658,18V. También se conocen las indicaciones de lo vatímetros W1 y W2 que son iguales y valen 5000 W. Por otro lado, se ha comprobado experimentalmente que las pérdidas totales que se producen en la línea corresponden al 10% del consumo de la carga. En un momento determinado se produce un cortocircuito entre las tres fases, quedando en contacto los puntos A, B y C; en este momento se puede observar que la indicación del vatímetro W1 es cero. R S T A1 A2 D Z1 V1 Z1 A3 W1 Z1 A B V2 W2 RECEPTOR INDUCTIVO C Figura 1.17.1 Calcular: a) Impedancia por fase de la carga o receptor, en el supuesto de estar conectada en triángulo. b) Impedancia por fase del receptor, en el caso de estar conectada en estrella. c) Impedancia de la línea Z 1 d) Tensión en bornes del generador indicada por el voltímetro V1 e) Con el receptor conectado en estrella, se produce un cortocircuito entre el punto D y el neutro de la estrella del receptor. Calcular para este caso la lectura de los amperímetros A1, A2 y A3. Resolución: En un momento determinado, según dice el enunciado, se produce un cortocircuito entre A, B y C, y el vatímetro W1 en este momento indica una lectura cero; por tanto, en este instante sólo se tiene el consumo de la línea. Por la disposición del vatímetro W1 y por el hecho de la carga total Z1 sea equilibrada ( se está en el caso de cortocircuito, la potencia reactiva total es: Q = 3.W1 = 0 Es decir, la impedancia Z 1 no consume energía reactiva, en consecuencia Z 1 es totalmente resistiva. Por otro lado, y por su disposición, multiplicando por línea-receptor. 3 indica la potencia reactiva del conjunto © Los autores, 2006; © Edicions UPC, 2006 57 Circuitos trifásicos Q = 3W1 = 3 ⋅ 5000 VAr Pero si, como se ha dicho, la línea es totalmente resistiva, QT corresponderá en su totalidad al receptor, es decir: QC = 3 ⋅ 5000 VAr Conocida la potencia reactiva absorbida por el receptor y la lectura del vatímetro W2 se podrá calcular la potencia absorbida por la carga. Si se dispusiera de otro vatímetro WA entre la impedancia de la línea y el receptor en la fase R, y conectada la bobina voltimétrica entre las fases R y T, estaríamos frente a una conexión Aron en que: QC = 3 (W A − W 2 ) PC = W A + W 2 Despejando WA y sustituyendo, resulta: QC = 3 ( PC − 2W 2 ) → PC = QC + 3 ⋅ 2W 2 Y sustituyendo los valores correspondientes, resulta: 3 ⋅ 5000 + 3 ⋅ 2 ⋅ 5000 PC = 3 = 15000 W Se puede calcular a continuación el factor de potencia de la carga: tgϕ C = QC 3 ⋅ 5000 3 = = PC 15000 3 → ϕ C = 30º Para calcular la corriente de la línea se hará de la siguiente manera: PC = 3U l I l cos ϕ C → I l= PC 3U l cos ϕ C = 15000 3 3 ⋅ 658,18 2 a) Si la carga está conectada en triángulo, se tendrá: Figura 1.17.2 Z c∆ = es decir: Uc I1 / 3 = 658,18 15,19 / 3 = 75 Ω Z C∆ = 75∠30º Ω © Los autores, 2006; © Edicions UPC, 2006 = 15,19 A 3 58 Problemas de electrotecnia b) Si está conectada en estrella: Z Cλ = Z C∆ 75∠30º = = 25∠30º Ω 3 3 c) Se sabe que la impedancia de la línea es totalmente resistiva y, por otro lado, se conocen las pérdidas que se producen. Pl = 0 ,1 ⋅ PC = 0,1 ⋅15000 = 1500 W De aquí se puede calcular la resistencia Rl. Pl = 3 ⋅ I 2 ⋅ Rl Rl = 1500 3 ⋅15,19 2 = 2 ,167 Ω d) Para calcular la indicación del voltímetro V1, representamos el circuito equivalente monofásico correspondiente: Figura 1.17.3 U 1S = U 2 S + Z l ⋅ I U 1S = 658,18∠0º 3 + 2,167∠0º⋅15,19∠ − 30º U 1S = 408,83 V Por tanto, el voltímetro V1 conectado entre las dos fases indicaría: V1 = 3 ⋅ 408,83 = 708,12 V e) El circuito correspondiente cuando se produce un cortocircuito entre el punto B y el neutro de la estrella es: © Los autores, 2006; © Edicions UPC, 2006 59 Circuitos trifásicos N N’ = R Zl Figura 1.17.4 Siendo ER , E S y ET las tensiones de fase, es decir: ER = 708,12∠0º 3 = 408,83∠0º V E S = 408,83∠ − 120º V ET = 408,83∠120º V Z TOT = Z l + Z c = ( 2 ,167 + 0. j ) + 25 < 30º = 26 ,90 < 27 ,69º Ω IS = VSR 708,12 < 210º = = 26,32 < 182,31º A Z TOT 26,90 < 27 ,69º IT = VTR 708,12 < 150º = 26,32 < 122,31º A = Z TOT 26,90 < 27 ,69º I R = −( I S + I T ) = 45,59 < −27 ,68º A Las indicaciones de los amperímetros son: A1 : 45,59A A2 : 26,32 A A3 : 26,32 A © Los autores, 2006; © Edicions UPC, 2006 60 Problemas de electrotecnia 1.18 Problema 18 El sistema trifásico a 380 V de la figura es de secuencia directa y alimenta dos cargas equilibradas mediante una línea de impedancia Z L = 1,5 + j1,5Ω . La carga en triángulo presenta unas impedancias por fase de 90 + j45 Ω, mientras que la carga en estrella tiene unas impedancias por fase de 45 - j15 Ω. Se pide: a) La lectura del amperímetro A b) La lectura del voltímetro V c) Las lecturas de los vatímetros W1, W2 y W3 R ZL S ZL T ZL A W2 V W3 W1 Figura 1.18.1 Resolución: a) Impedancias de las cargas equivalentes en estrella: Z 1λ = 90 + j 45 = 30 + j15 = 33,541 ∠ 26 ,565º Ω 3 Impedancia en paralelo de las dos cargas: Z Pλ = Z 2 λ = 45 − j15 = 47 ,434 ∠ − 18,435º Ω Z 1λ ·Z 2 λ Z1λ + Z 2 λ = 21,21 ∠ 8,13º = 21 + j 3 Ω Impedancia global del circuito por fase: Z T = Z l + Z P λ = 1,5 + j1,5 + 21 + j 3 = 22 ,5 + j 4 ,5 = 22 ,94 ∠ 11,31º Ω Origen de fases: U f = 380 / 3 ∠ 0º V Zl Circuito equivalente por fase: 380 3 ∠ 0º V U fc © Los autores, 2006; © Edicions UPC, 2006 Z Pλ 61 Circuitos trifásicos I= 380 / 3∠ 0º = 9 ,56 ∠ − 11,31º A 22 ,94∠ 11,31º → A = 9,56 A b) Tensión en bornes de la carga U f c = U f g − Il ⋅ Zl = 380 ∠ 0º − ( 9 ,56 ∠ − 11,31º )·( 1,5 + j1,5 ) = 202 ,835 ∠ − 3,1786 V 3 Lectura del voltímetro: 202,835 · 3 = 351,32 V → V = 351,32 V c) S = 3·U f c ·I *f c = 3 · 202 ,835∠ − 3,1786º · 9 ,56∠ 11,31º = 5817 ,30∠ 8,1314º = 5758,81 + j822 VA Conexión Aron: P = W1 + W2 ⎫ ⎬ Q = 3( W1 − W2 )⎭ 5758,81 = W1 + W2 ⎫ ⎬ 822 = 3( W1 − W2 )⎭ → Del sistema anterior resulta W1 = 3116,69 W W2 = 2642,11 W De la disposición de W3 resulta, Q = 3 · W3 → W3 = 822 3 = 474,58 W → W3 = 474 ,58 W © Los autores, 2006; © Edicions UPC, 2006 62 Problemas de electrotecnia 1.19 Problema 19 Una red trifásica de 400 V y 50 Hz alimenta dos cargas según muestra la figura adjunta. Con el interruptor K1 cerrado y el K2 abierto, se tiene W2 = 0,6.W1. Se pide: a) La lectura del amperímetro b) La lectura del voltímetro Con los interruptores K1 y K2 cerrados, se pide: c) La nueva lectura del amperímetro d) Las nuevas lecturas de los vatímetros R A W1 S W2 T K1 2,5 Ω 5Ω V CARGA 1 60 kVA cosϕ1 = 0,5 (i) (1000.π)−1 F Figura 1.19.1 Resolución: a) Por estar W1 y W2 en conexión Aron: PTOT = W1 + W 2 = 60000 ⋅ 0,5 = 30000W W1 = 18750 W W 2 = 0,6 ⋅ W1 W 2 = 11250 W QTOT = 3( W1 − W2 ) = 12990 ,38 VAr tgϕ TOT = QTOT 12990,38 = PTOT 30000 PTOT = 3Vlin ⋅ I lin ⋅ cos ϕ TOT b) → → ϕ TOT = 23,41º → I lin = 47,185 A Pcàrrega = 3Vlin ⋅ I lin ⋅ cos ϕ 30000 = 3 ⋅ Vlin ⋅ 47,185 ⋅ 0,5 → Vlin càrrega = 734,15 V © Los autores, 2006; © Edicions UPC, 2006 cos ϕ TOT = 0,9177 63 Circuitos trifásicos c) T XC = 1 1 = = 10 Ω 2.π . f .C 2.π .50.( 1000.π ) −1 I RT = V RT 400∠ − 30º = = 40∠60º A 10∠ − 90º 10∠ − 90º R R S V 400∠90º ITS = TS = = 160∠90º A 2 ,5 2 ,5 V 400∠210º = 80∠210º A I SR = SR = 5 5 La figura siguiente muestra las intensidades en la carga 2: IS2 IR2 IT2 2,5 Ω 5Ω ISR ITS (1000.π)−1 F IRT Figura 1.19.2 I R 2 = I RT − I SR I R1 = 47,185∠ − 23,41º A I R = I R1 + I R 2 = 47,185∠ − 23,41º +40∠60º −80∠210º = 144,07∠22,93º A = 144,07 A I S1 = 47 ,185∠ − 143,41º A I S 2 = I SR − I TS I S = I S1 + I S 2 = 47 ,185∠ − 143,41º +80∠210º −160∠90º = 252 ,05∠ − 115,06º A d) ( ) W1 = 34737,6 W ( ) W2 = 91329,3 W W1 = V RT ⋅ I R ⋅ cos ϕ VRT − ϕ I R = 400 ⋅144,07 ⋅ cos(− 30º −22,93º ) → W 2 = V ST ⋅ I S ⋅ cos ϕ VST − ϕ I S = 400 ⋅ 252,05 ⋅ cos(− 90º +115,06º ) → © Los autores, 2006; © Edicions UPC, 2006 64 Problemas de electrotecnia 1.20 Problema 20 El sistema trifásico con U = 400 V (tensión fijada para todo el problema) y 50 Hz de la figura es de secuencia directa y alimenta dos cargas equilibradas y una carga desequilibrada. a) Con el interruptor K1 cerrado y el interruptor K2 abierto, se pide el factor de potencia global de la carga, las lecturas de los amperímetros y la lectura del voltímetro UG. b) Con los interruptores K1 y K2 cerrados, determinar las nuevas lecturas de los amperímetros. R S T RL = 0,4 Ω UG 0,4 Ω U RL = 0,4 Ω R AR S AS T AT K1 20 kVA cosϕ = 0,8 (i) 31,8 µF 31,8 µF K2 50 Ω 25 Ω 50 Ω 31,8 µF Figura 1.20.1 Resolución: a) XC = 1 1 = = 100 Ω Cω 31,86 ⋅10 − 6 ⋅ 2π ⋅ 50 P2 = 0 W Q2 = 3 ⋅ 400 2 U2 = 3⋅ = 4800 VAr (capacitiva ) 100 XC P1 = 20000 ⋅ 0,8 = 16000 W Q1 = S1 ⋅ sin ϕ 2 = 20000 ⋅ sin 36,87º = 12000 VAr (inductiva) PT = P1 + P2 = 16000 W QT = Q1 + Q2 = 12000 − 4800 = 7200 VAr tgϕ T = QT 7200 = = 0,45 PT 16000 → ϕ T = 24,22º → ST = PT + jQT = 16000 + j 7200 = 17545,37∠24,22º VA Vamos a considerar la carga total conectada en estrella. Tomando URN como origen de fases resulta: U RN = 400 / 3∠0 º V ST = 3 ⋅ U RN ⋅ I RN * I RN * = 17545,37∠25,22º = 25,32∠24,22º A 3 ⋅ 400 / 3∠0º Por lo tanto, resulta: AR = AS = AT = 25,32 A © Los autores, 2006; © Edicions UPC, 2006 cos ϕ T = 0,911 65 Circuitos trifásicos U GRN = U RN + I R .RL = 400 / 3∠0º +25,32∠ − 24,32º⋅0,4∠0º = 240,21∠ − 0,99 V U G = 3 ⋅ 240,21 = 416,05 V b) U RN = 400 ∠0º V 3 U SN = 400 ∠ − 120º V 3 I RS = U RS 400∠30º = 16∠30º A = Z RS 25∠0º I ST = U ST 400∠ − 90º = 8∠ − 180º A = Z ST 50∠90º I TR = U TR 400∠150º = 8∠240º A = Z TR 50∠ − 90º U TN = I R 2 = I RS − I TR = 16∠30º −8∠240º = 17,86 + j14,93A I S 2 = I ST − I RS = 8∠ − 180º −16∠30º = −21,86 − j8 A I T 2 = I TR − I ST = 8∠240º −8∠ − 180º = 4 − j 6,93 A Resultando: I R ' = I R1 + I R 2 = (17,86 + j14,93) + 25,32∠ − 24,22º = 41,20∠6,32º A AR = 41,20 A I S ' = I S1 + I S 2 = (− 21,86 − j8) + 25,32∠ − 24,22º −120 º = 48,13∠ − 151,72º A As = 48,13 A I T ' = I T 1 + I T 2 = (4 − j 6,93) + 25,32∠ − 24,22º −240º = 18,32∠85,3º A AT = 18,32 A © Los autores, 2006; © Edicions UPC, 2006 400 ∠120º V 3 66 Problemas de electrotecnia 1.21 Problema 21 Se conocen los datos siguientes de la figura adjunta: W1 = 26145 W, W3 = 12235 W, V2 = 380 V. Se pide: a) La lectura del vatímetro W2 b) La potencia activa consumida por la carga B c) La lectura del amperímetro d) La lectura del voltímetro V1 R S RΩ W1 A V1 W2 W3 V2 RΩ RΩ T Carga A PA = 12500 W cosϕA = 0,6 (i) Carga B PB = ? cosϕB = 0,8 (i) Figura 1.21.1 Resolución: a) Q A− B = 3 ⋅ W3 = 3 ⋅12235 = 21191,64 VAr QB = QA− B − QA = 21191,64 − 12500 ⋅ tg [arccos 0 ,6] = 4524 ,97 VAr Por otro lado: QT = QA− B = 21191,64 VAr QT = 3 ⋅ (W1 − W2 ) → W1 − W 2 = QT 3 = 21191,64 3 = 12235 W W 2 = W1 − 12235 = 26145 − 12235 = 13910 W b) PB = 4524 ,97 QB = = 6033,29 W tgϕ B tg (arccos 0 ,8) → PB = 6033,29 W © Los autores, 2006; © Edicions UPC, 2006 67 Circuitos trifásicos c) tgϕ AB = I= QAB 21191,64 = = 1,1434 PAB 18533,25 PA− B → 3 ⋅V 2⋅ cos ϕ AB → ϕ AB = 48,828º I= 18533,25 3 ⋅ 380 ⋅ 0 ,658 → = 42 ,77 A cos ϕ AB = 0,658 → d) PA− B = PA + PB = 12500 + 6033,14 = 18533,29 W PT = W1 + W 2 = 26145 + 13910 = 4055 W PR = PT − ( PA + PB ) = 40055 − ( 12500 + 6033,25 ) = 21521,71 W PR = 3 ⋅ R ⋅ I 2 → V 1f = V 2 f + I ⋅ R = R= 380 3 21521,71 3 ⋅ 42,77 2 = 3,82Ω ∠0º +42 ,77∠ − 48,28º ⋅3,82 = 353,835∠ − 20 ,71º V V1 = 3 ⋅ V1 f = 3 ⋅ 353,835 = 611,82 V © Los autores, 2006; © Edicions UPC, 2006 A = 42,77 A 68 Problemas de electrotecnia 1.22 Problema 22 En el circuito trifásico de la figura la impedancia de línea vale Z L = 4 + j.3 Ω . Se conocen las lecturas de los aparatos de medida: A1 = 1,633 A, A2 = 5,773 A, W1 = 6928,2 W, W2 = 12000 W, U = 6000 V. Con el interruptor abierto determinar: a ) La potencia aparente de las cargas. b ) La lectura del amperímetro general A. c ) La lectura del voltímetro U1 d ) Al cerrar el interruptor, determinar la capacidad de los condensadores para mejorar el factor de potencia global hasta la unidad. Suponer que la tensión U se mantiene inalterable respecto al apartado anterior y que la frecuencia es de 50 Hz. ZL R S U1 A U ZL ZL T A1 A2 W1 W2 K C Carga equilibrada 1 capacitiva Carga equilibrada 2 inductiva C C Figura 1.22.1 Resolución: a) Q1 = − 3 ⋅ W1 = − 3 ⋅ 6928,3 = −12000 VAr (cap) y también: Q1 = 3 ⋅ U ⋅ I1 ⋅ sin ϕ1 tgϕ1 = P1 Q1 12000 sin ϕ1 = 3 ⋅ 6000 ⋅ 1,633 = 0,707 ϕ1 = 45º P1 = Q1 ⋅ tg 45º = 12000 ⋅ 1 = 12000 W S1 = 12000 − j12000 = 16970,56∠ − 45º VAr W2 = U 3 ⋅ I 2 ⋅ cos ϕ 2 cos ϕ 2 = 12000 = 0,6 6000 ⋅ 5,773 3 © Los autores, 2006; © Edicions UPC, 2006 ϕ 2 = 53,12º 69 Circuitos trifásicos P2 = 3 ⋅12000 = 36000 W Q2 = P2 ⋅ tgϕ 2 = 36000 ⋅ tg 53,12º = 47982,37 VAr S 2 = 36000 + j 47982,37 = 59985,89∠53,12º ST = S1 + S 2 = 48000 + 35982,37 = 59989,42∠36,89º ST = 59989,42∠36,89º b) I= ST 3 ⋅U = 59989,42 3 ⋅ 6000 = 5,772 A I = 5,772 A c) Orígen de fases: Uf = 6000 3 ∠0 º I = 5,772∠ − 36,86º U1 f = U f + ZC ⋅ I U1 f = 6000 3 ∠0º + (4 + j 3) ⋅ 5,772∠ − 36,86º = 3492,97∠0º V U 1 = 3 ⋅ U 1 f = 6050 V d) QC = −Q = 35982,37 VA QC U 2 U 2 = = = U 2 ⋅ Cω 1 3 XC Cω C= U 2 ⋅ 2 ⋅ π ⋅ f 6000 2 ⋅ 2 ⋅ π ⋅ 50 = = 1,06 µF QC 35982,37 3 3 © Los autores, 2006; © Edicions UPC, 2006 70 Problemas de electrotecnia 1.23 Problema 1.23 Dado el circuito de la figura, alimentado por un sistema trifásico equilibrado de tensiones de secuencia directa, se conocen las lecturas V = 400 V, W1 = 7173,8 W y W2 = 3926,2 W. Con los interruptores K1 y K2 abiertos, determinar: a) El número de lámparas de incandescencia por fase de la carga IV. Si se cierran los interruptores K1 y K2, calcular: b) La lectura del amperímetro AN. c) Las lecturas de los vatímetros WA y WB. AR R WA W1 V W2 WB S T N AN K1 Motor I FP = 0.8 (i) 2309,4 W K2 Motor III FP = 0.8 (i) Carga II 30 lámparas de 230V y 60 W en paralelo Carga IV Lámparas de 400 V y 60 W en ∆ Figura 1.23.1 Resolución: a) P3− 4 = W1 + W2 = 7173,8 + 3926,2 = 11100 W Q3− 4 = (W1 − W2 ) ⋅ 3 = 3 ⋅ (7173,8 − 3926,2 ) = 5625 VAr La carga IV es puramente resistiva, por lo que se cumple que Q4 = 0 VAr. Q3− 4 = Q3 + Q4 Q3 = Q3− 4 = 5625 VAr P3 = Q3 5625 = = 7500 W tgϕ3 tg (ar cos 0,8) P4 = P3− 4 + P3 = 11000 − 7500 = 3600 W P4 fase = 3600 = 1200 W 3 Pbombilla = 1200 = 20 bombillas 60 © Los autores, 2006; © Edicions UPC, 2006 71 Circuitos trifásicos b) P3− 4 = 3 ⋅ U ⋅ I 3− 4 ⋅ cos ϕ3− 4 tgϕ3− 4 = 5625 Q3− 4 = = 0,5067 P3− 4 11100 P3− 4 I 3− 4 = 3 ⋅ U ⋅ cosϕ3− 4 = 11100 3 ⋅ 400 ⋅ 0,892 ϕ3− 4 = −26,874º = 17,961 A T Origen de fases: U RN = cos ϕ3− 4 = 0,892 400 3 ∠0º V R S I (3− 4) R = 17,961∠ − 26,874 º A I (3− 4 ) S = 17,961∠ − 26,874 º −120 º A I (3− 4 )T = 17,961∠ − 26,874 º −240 º A Consumo monofásico 1: I1R = P1 2309,40 = = 12,5 A VRN .cos ϕ1 400 ⋅ 0 ,8 3 cos ϕ1 = 0,8 ϕ1 = 36,87º I 1R = 12,5∠ − 36,87º A I 1N = −12,5∠ − 36,87º = 12,5∠ − 36,87º −180º = 12,5∠143,13º A Consumo monofásico 2: I 2S = 30 ⋅ 60 = 7,794 A 400 ⋅1 3 I 2 S = 7,794∠ − 120º A I 2 N = −7,794∠ − 120º = 7,794∠60º A I N = I 1N + I 2 N = 12,5∠143,13º +7 ,794∠60º = −10 + j 7 ,5 + 3,897 + j 6 ,75 = = −6,1 + j14,25 = 15,5∠113,17º A AN = 15,5 A © Los autores, 2006; © Edicions UPC, 2006 72 Problemas de electrotecnia c) ( WA = U RT ⋅ I R ⋅ cos U RT ⋅ I R ) U RT = 400∠ − 30º V I R = I 1R + I (3− 4) R = 12,5∠ − 36,87 º +17,961∠ − 26,874 º = 30,348∠ − 30,98º A WA = 40 ⋅ 30,348 ⋅ cos(− 30 − ( −30,98 )) = 12131,95 W ( WB = U SN ⋅ I S ⋅ cos U SN ⋅ I S ) U SN = 400 3 ∠ − 120º V I S = I 2 S + I (3− 4) S = 7,794∠ − 120º +17,961∠ − 146,874 = 25,156∠ − 138,83º A WB = 400 3 ⋅ 25,156 ⋅ cos(− 120 − ( − 138,83 )) = 5498,6 W o también: WB = P3+ 4 11000 + P2 = + 30 ⋅ 60 = 5500 W 3 3 © Los autores, 2006; © Edicions UPC, 2006 73 Circuitos trifásicos 1.24 Problema 24 Dado el circuito de la figura, alimentado por un sistema trifásico equilibrado de tensiones de secuencia directa a 50 Hz, se conocen las lecturas V = 400 V, W1 = 7173,8 W i W2 = 3926,2 W. La carga IV está formada por un total de 12 condensadores conectados en triángulo, formando una carga equilibrada. Con los interruptores KI i KII abiertos, determinar: a) Capacidad de cada uno de los 12 condensadores de la carga IV( todos los condensadores soportan una tensión de 400 V). Si se cierran los interruptores KI i KII, calcular: b) La lectura de los amperímetros AN i AS. c) Las lecturas de los vatímetros WA i WB. R S WA AS WB V W1 W2 T N AN KII KI Motor I FP = 0.8 (i) 3000 W Carga II 20 lámparas de 230V y 60 W en paralelo Motor III FP = 0.8 (i) Figura 1.24.1 Resolución: a) PIII + IV = W1 + W2 = 11100 W Q III + IV = 3 ⋅ (W1 − W2 ) = 3 ⋅ (7173,8 − 3926,2) = 5625 VAr PIV = 0 PIII = 11100 W Q III = PIII ⋅ tgϕ III = 11100 ⋅ tg (ar cos 0,8) = 8325 VAr Q IV = 5625 − 8325 = −2700 VAr Q IV = −225 VAr 12 2 UC 400 2 225 = = 1 1 2π ⋅ 50C 2π ⋅ 50C QC = C = 4,48 µF b) © Los autores, 2006; © Edicions UPC, 2006 Carga IV Condensadores en ∆ 74 Problemas de electrotecnia S III + IV = 11100 + j 5625 = 12443,9∠ − 26,87 º W IR = 12443,9 Si UR = 3 ⋅ 400 = 17,96 A 400 ∠0º V 3 I R = 17,96∠ − 26,87 º A I S = 17,96∠ − 146,87 º A I T = 17,96∠ − 226,87 º A Motor I: 3000 = 16,238 A 400 ⋅ 0,8 3 400 ∠ − 120º U SN = 3 FPI = 0,8 (i) → ϕ I = 36,87 º II = I I = 16,238∠ − 120º −36,87º = 16,238∠ − 157,87º A Carga II: I II = 20 ⋅ 60 1200 ⋅ 3 = = 5,196 A 400 400 3 U TN = 400 3 ∠ − 240º I II = 5,196∠ − 240º A Las lámparas e incandescencia tienen FPII = 1 ( ) → ϕ II = 0º I N = − I I + I II = −(16,238∠ − 157,87º +5,196∠ − 240º ) = 17,63∠6,11º A AN = 17,63 A I S ' = I S ' + I I = 17,96∠ − 146,89º16,238∠ − 156,87º = 34,065∠ − 151,61º A AS = 34,064 A c) ( ) ( ) W A = U ST ⋅ I R ⋅ cos U ST , I R = 400 ⋅ 17,96 ⋅ cos(− 90º −(− 26,7º )) = 3246,93 W W A = 3246,93 W W B = U SN ⋅ I S '⋅ cos U SN , I S ' = 400 3 ⋅ 34,065 ⋅ cos(− 120 º −(− 151,61º )) = 6700 W W B = 6700 W © Los autores, 2006; © Edicions UPC, 2006 75 Transformadores monofásicos 2 Transformadores monofásicos © Los autores, 2006; © Edicions UPC, 2006 76 Problemas de electrotecnia 2.1 Problema 1 Un transformador monofásico de 44 kVA, 2200/220V absorbe en vacío 176 W, alimentado a una tensión de 2200 V. Se conocen los valores de les caídas de tensión relativas en la resistencia y la reactancia de cortocircuito que valen 1,4% y 2,1% respectivamente. Determinar la potencia absorbida por el transformador y el rendimiento cuando su secundario alimenta una carga de 30 kW, con una tensión de 220 V, presentando un factor de potencia de 0,8 inductivo. Resolución: I1n = 44000 2200 ε Rcc = ε Xcc = 1,4 100 2,1 100 = 20 A = = rt = R1cc · I1n U 1n X 1cc · I1n U 1n 2200 = 10 220 Æ R1cc = Æ X 1cc = Æ I 2 n = I1n · rt = 200 A 1,4 · 2200 100 · 20 2,1 · 2200 100 · 20 = 1,54 Ω = 2,31 Ω Corriente absorbida por la carga, I2 = P2 30000 = = 170,45 A V 2 ⋅ cos ϕ 2 220 · 0,8 Æ I 2/ = 170,45 U1 U'2 X1cc · I'2 -36,87º I'2 R1cc · I'2 Fig. 2.1.1 cos ϕ C = 0,8 / / Æ ϕ C = − 36,87 º / U 1 = U 2 + R1 cc · I 2 + X 1 cc · I 2 U 1 = 2200 ∠ 0º + (1,54 + j 2,31) · 17,045 ∠ − 36,87 = 2244,67 ∠ 0,4º V ⎛V P1 = P2 + PFe + PCu = P2 + PO ⎜ 1 ⎜V ⎝ 1n 2 ⎞ ⎟ + I' 2 · R 2 1CC ⎟ ⎠ © Los autores, 2006; © Edicions UPC, 2006 rt = 17,045 A 77 Transformadores monofásicos P1 = 30000 + 176 ⎛⎜ 2 2244,67 ⎞ 2 ⎟ + 1,54 · 17,045 = 30000 + 183,22 + 447,41 = ⎝ 2200 ⎠ = 30630,64 W Æ P1 = 30630,64 W P 30000 = 97,94% η = 100 ⋅ 2 = 100 ⋅ P1 30630,64 © Los autores, 2006; © Edicions UPC, 2006 78 Problemas de electrotecnia 2.2 Problema 2 Un transformador monofásico de 200 kVA, 6600/ 384 V, alimenta a 384 V una carga que tiene un factor de potencia igual a la unidad. El rendimiento del transformador es del 98%, tanto si presenta un índice de carga C = 1 como si el índice de carga es de 0,5. El factor de potencia de la impedancia de cortocircuito es de 0,2079. La corriente de vacío que absorbe el transformador es de 0,84 A estando el transformador alimentado a 6600 V. Se piden los parámetros del circuito equivalente Rcc, Xcc, RFe, Xµ (valores referidos al primario del transformador). Resolución: I1n = η= 200000 6600 = 30,30 A ⎛V PFe = Po ⎜⎜ 2 ⎝ V2n P2 P2 + PFe + PCu 2 ⎞ ⎟ = Po ⎟ ⎠ PCu = C 2 PCC Situación 1: P2 = V2 ⋅ I 2 ⋅ cos ϕ 2 = V2n ⋅ I 2n ⋅1 = Sn Situación 2: P2 = V2 ⋅ I 2 ⋅ cos ϕ 2 = V2n ⋅ I 2n ⋅ 0,5 = 0,5Sn ⎫ 200 · 10 3 ⎪ 3 200 · 10 + PO + PCC ⎪ ⎬ 200 · 10 3 · 0,5 ⎪ 0,98 = 200 · 10 3 · 0,5 + PO + 0,5 2 · PCC ⎪⎭ 0,98 = PO = U 12O R1 Fe Æ R1Fe = PO = 1360,54 W PCC = 2721,09 W 6600 2 = 32016,70 Ω 1360,54 Æ R1Fe = 32016,70 Ω S O = U 1n · I1O = 6600 · 0,84 = 5544 VA QO = S O2 − PO2 = 5544 2 − 1360,54 2 = 5374,46 X 1µ = U 12O 6600 2 = = 8104,99 Ω QO 5374,46 PCC = I12n · R1CC Æ R1CC = cos ϕ CC = 0,2079 tg ϕ CC = X 1CC R1CC X 1µ = 8104,99 Ω PCC 2721,09 = = 2,96 Ω 30,30 2 I12n Æ ϕCC = 78º Æ Æ R1CC = 2,96 Ω Æ Æ tg ϕ CC = 4,7 X 1 CC = 4,7 · 2,96 = 13,93 Ω Æ X 1 CC = 13,93 Ω © Los autores, 2006; © Edicions UPC, 2006 79 Transformadores monofásicos 2.3 Problema 3 De la placa de características de un transformador monofásico reductor de tensión, se han obtenido los datos siguientes: Tensiones 3300 V / 220 V Corrientes 3,03 A / 45,45 A Potencia aparente Frecuencia 10 kVA 50 Hz εCC = 5 % Tensión de cortocircuito Por medidas efectuadas, se sabe que los valores óhmicos de las bobinas primaria y secundaria son respectivamente 5 Ω y 0,02 Ω. Se hace el ensayo del transformador en cortocircuito, intercalando un amperímetro entre los terminales del primario, alimentándolo por el secundario. Cuando el amperímetro indica 3,03 A, en el secundario quedan aplicados 11 V. + A AT BT V Figura 2.3.1 a) Comprobar la coherencia de los datos obtenidos de la placa de características. b) Calcular la relación de transformación. c) Calcular los valores de RCC y XCC reducidos al primario y al secundario. d) Valor de la tensión que se ha de aplicar al primario del transformador para que el secundario alimente a la tensión nominal una carga de 7 kW, constituida por lámparas de incandescencia de 220 V. Resolución: a) En primer lugar, verificaremos si los datos de placa son coherentes: Las corrientes nominales han de ser: I 1n = Sn 10000 = = 3,03 A U 1n 3300 I 2n = Sn 10000 = = 45,45 A U 2n 220 © Los autores, 2006; © Edicions UPC, 2006 80 Problemas de electrotecnia En el ensayo de cortocircuito encontramos que la tensión UCC de cortocircuito es de 11 V, tensión que referida a la nominal, representa: ε CC = 11 ⋅100 = 5% 220 Así pues, los datos de la placa de características son coherentes con el resto de los datos. b) Por definición, la relación de transformación es el cociente entre las tensiones en los devanados de alta y baja cuando el transformador trabaja en vacío. rt = U 1n I 2n 3300 45,45 = = = = 15 U 2n I1n 220 3,03 → rt = 15 c) Los valores de la resistencia RCC, reactancia XCC e impedancia ZCC de cortocircuito del transformador se pueden dar referidos tanto al lado de A.T. como al de B.T. Considerando el transformador por el lado de baja tensión, se tiene: R 2CC = R 2 + R1 rt 2 = 0,02 + 5 15 2 = 0,0422Ω R 2CC = 0,0422Ω ( en B.T. ) Por otro lado, el valor de Z2CC se encuentra a partir del ensayo de cortocircuito: U 2CC = I 2 n ⋅ Z 2CC 11 = 45,45 ⋅ Z 2CC Z 2CC = 0,242Ω ( en B.T. ) Y en consecuencia: X 2CC = Z 2CC 2 − R 2CC 2 = 0,242 2 − 0,0422 2 = 0,238Ω X 2CC = 0,238Ω ( en B.T. ) Para referir estos tres valores al primario, o al lado de A.T., sólo hace falta multiplicarlos por el cuadrado de la relación de transformación: R1CC = rt 2 ⋅ R 2CC = 15 2 ⋅ 0,0422 = 9,5Ω X 1CC = rt 2 ⋅ X 2CC = 15 2 ⋅ 0,238 = 53,55Ω Z 1CC = rt 2 ⋅ Z 2CC = 15 2 ⋅ 0,242 = 54,45Ω d) Como la carga está formada únicamente por lámparas de incandescencia, o sea, resistencias puras, su factor de potencia es la unidad, y la corriente de carga es, pues: P2 = V 2 ⋅ I 2 RC = 7000 = 220 ⋅ I 2 I 2 = 31,82 A U2 220 = = 6,91Ω I2 31,82 Ahora se está en condiciones de dibujar el circuito equivalente del transformador, reducido al secundario: © Los autores, 2006; © Edicions UPC, 2006 81 Transformadores monofásicos X2CC (en B.T.) R2CC (en B.T.) U’1 U2 RC = 6,91Ω I2 = 31,82 A Figura 2.3.2 Se deduce, lógicamente, la tensión de alimentación que se ha de aplicar, pero reducida al secundario. U '1 = (U C + R2CC ⋅ I 2 )2 + ( X 2CC ⋅ I 2 )2 = (220 + 0,0422 ⋅ 31,82)2 + (0,238 ⋅ 31,82)2 Esta tensión, referida al primario, es: U1 = rt ⋅ 221,47 = 3322V U1 = 3322 V © Los autores, 2006; © Edicions UPC, 2006 = 221,47V 82 Problemas de electrotecnia 2.4 Problema 4 Se dispone de un transformador monofásico en cuya placa de características constan los datos siguientes: Potencia nominal Sn = 30 kVA Tensión nominal en el primario U1n = 15 kV Tensión nominal en el secundario U2n = 380 V Tensión de cortocircuito en valor relativo εCC = 3 % Pérdidas en cortocircuito PCC = 150 W Pérdidas en vacío PO = 75 W Corriente de excitación en valor relativo iO = 4 % Determinar, suponiendo que la frecuencia es f = 50 Hz: a) Intensidades nominales en cada bobinado b) Valores de la corriente en vacío IO según por qué bobinado se alimente el transformador c) Relación de transformación d) Corrientes en primario y en secundario en caso de cortocircuito franco en un arrollamiento, suponiendo el otro alimentado a tensión nominal e) Rendimientos a plena y a ¾ de carga, si el transformador alimenta a tensión nominal un consumo puramente óhmico f) Rendimientos a plena y al 60% de carga, si el transformador alimenta a tensión nominal un consumo capacitivo de cos φ = 0,8 g) Para un factor de potencia dado, determinar el índice de carga que da un rendimiento máximo h) Valores de εRCC y εXCC, dibujando el correspondiente esquema del ensayo de cortocircuito i) Caída de tensión relativa a plena carga y a ¾ de carga, si alimenta una carga de cos φC = 0,866 (i) Resolución: a) La potencia aparente nominal es S n = U 1n ⋅ I 1n , y si se supone que el rendimiento es del 100%, también es S n = U 2 n ⋅ I 2 n . Por tanto: I 1n = Sn 30000 = = 2A U 1n 15000 I 2n = Sn 30000 = = 78,95 A U 2n 380 b) Si, como es normal, el transformador se alimenta por el primario, siendo io = 0,04 (4%). Se tiene: I 01 = I 1n ⋅ i o = 2 ⋅ 0,04 = 0,08 A si, por el contrario, la alimentación se hace por el secundario, entonces: I 02 = I 2 n ⋅ i o = 78,95 ⋅ 0,04 = 3,158 A © Los autores, 2006; © Edicions UPC, 2006 83 Transformadores monofásicos c) La relación de transformación se puede calcular directamente a partir de los datos del enunciado: rt = U 1n 15000 = = 39,474 U 2n 380 d) Si el cortocircuito franco se produce en el secundario, el esquema equivalente es: R1CC X1CC U1 Figura 2.4.1 y como: ε CC = U 1CC U 1n y Z 1CC = U 1CC I 1n y también: U 1n = I 1(CC ) ⋅ Z 1CC o sea que: I 1(CC ) = Z 1CC = U 1CC U = 1n I 1n I 1(CC ) I U 1n 2 ⋅ I 1n = 1n = = 66,6 A ε CC 0,03 U 1CC y análogamente: I 2(CC ) = U 2n I 78,94 ⋅ I 2n = 2n = = 2631,3 A ε CC 0,03 U 2CC Se puede llegar al mismo resultado para I 2(CC ) , teniendo en cuenta que entre I 1(CC ) e I 2(CC ) hay la misma relación que entre I 1 e I 2 , es decir, que si I 1(CC ) I1 1 1 = , como se puede = , también I 2(CC ) rt I 2 rt comprobar seguidamente: I 2(CC ) = rt ⋅ I 1(CC ) = 39,474 ⋅ 66,6 = 2631,6 A e) Si C representa el índice de carga, es decir: C = C = 1 a plena carga I2 I 2n C = 0,75 a ¾ de carga Recordando que el rendimiento η vale: P P2 P2 = η= 2 = P1 P2 + PFe + PCu P2 + Po + C 2 ⋅ PCC ⎛V PFe ≅ Po ⎜⎜ 2 ⎝ V 2n 2 ⎞ ⎟ = Po ⎟ ⎠ aplicado a los dos casos y teniendo en cuenta que la carga es óhmica y se alimenta a tensión nominal, se obtiene: © Los autores, 2006; © Edicions UPC, 2006 84 Problemas de electrotecnia A plena carga (C = 1): 30000 = 0,9926 30000 + 75 + 150 η1 = → η1 = 99,26 % → η 0,75 = 99,29 % A ¾ de carga (C = 0,75): η 0,75 = 30000 ⋅ 0,75 30000 ⋅ 0,75 + 75 + 0,75 2 ⋅150 = 0,9929 f) En este caso, al ser cos φC = 0,8 capacitivo y los índices de carga, C=1 y C=0,6, respectivamente: A plena carga: η1 = 30000 ⋅ cos ϕ C 30000 ⋅ 0,8 = 0,9907 → η 1 = 99,07 % = 30000 ⋅ cos ϕ C + 75 + 150 30000 ⋅ 0,8 + 75 + 150 A un 60% de la carga: η 0, 6 = 30000 ⋅ 0,8 ⋅ 0,6 30000 ⋅ 0,8 ⋅ 0,6 + 75 + 0,6 2 ⋅150 = 0,9911 → η 0,75 = 99,11 % g) Para un factor de potencia cos φC, el rendimiento vale, según la fórmula indicada en el punto (e): η= P2 2 P2 + Po + C ⋅ PCC = U 2 n ⋅ I 2 cos ϕ C U 2 n ⋅ I 2 cos ϕ C + Po + C 2 ⋅ PCC pero como I 2 = C ⋅ I 2 n η= U 2 n ⋅ I 2 n ⋅ C ⋅ cos ϕ C 2 U 2 n ⋅ I 2 n ⋅ C ⋅ cos ϕ C + Po + C ⋅ PCC = U 2 n ⋅ I 2 n ⋅ cos ϕ C P U 2 n ⋅ I 2 n ⋅ cos ϕ C + o + C ⋅ PCC C El valor máximo del rendimiento se obtiene cuando la expresión siguiente es mínima: ⎛P Min⎜⎜ o + C ⋅ PCC ⎝C y el mínimo de ⎞ ⎟⎟ ⎠ y= Po + C ⋅ PCC C es P dy = − o2 + PCC = 0 dC C por lo tanto, independientemente de cos φC, el máximo se obtiene para C= Po 75 = = 0,7071 PCC 150 © Los autores, 2006; © Edicions UPC, 2006 → C= Po PCC 85 Transformadores monofásicos h) X1CC R1CC Figura 2.4.2 Por definición, ε RCC = o sea que R1CC ⋅ I 1n R1CC ⋅ I 21n PCC = = U 1n U 1n ⋅ I 1n Sn ε RCC = PCC 150 = = 0,005 Sn 30000 → εRCC = 0,5 % y el triángulo vectorial: εCC εXCC εRCC Conocemos los valores de εCC y de εRCC, y por lo tanto, ε XCC = ε CC 2 − ε RCC 2 = 0,03 2 − 0,005 2 = 0,0296 → εXCC = 2,96 % i) La caída relativa de tensión en el transformador se puede calcular por la expresión aproximada, al ser εCC < 4%: ∆u = C [ε RCC cos ϕ c + ε XCC senϕ c ] en la que cos φC = 0,866, φC = 30º y sen φC = 0,5 A plena carga, por lo tanto, como C=1 ∆u1 = 1[0,5 ⋅ 0,866 + 2,96 ⋅ 0,5] = 1,913% A ¾ de carga, como C=0,75 ∆u 0,75 = 0,75[0,5 ⋅ 0,866 + 2,96 ⋅ 0,5] = 1,435% © Los autores, 2006; © Edicions UPC, 2006 86 Problemas de electrotecnia 2.5 Problema 5 Un transformador monofásico de 20 kVA de potencia trabaja a 50 Hz y sus tensiones de alimentación en alta y baja tensión son de 3800 V y 380 V, respectivamente. La resistencia del bobinado primario es de 5Ω y su reactancia de dispersión es de 25Ω. La corriente en vacío medida desde el lado de alta tensión es de 0,5 A y las pérdidas en vacío son de 1200 W. Determinar la tensión en el secundario cuando el transformador trabaja en vacío, si la aplicada al bobinado de alta tensión es de 3800V. Nota: Trabajar con el circuito equivalente exacto del transformador. Resolución: El circuito equivalente exacto del transformador reducido al primario es: R1 Xd1 X’d2 R’2 Io I’2 I1 RFe U1 IFe Xµ Iµ U’2 Figura 2.5.1 siendo: y X ' d 2 = rt 2 ⋅ X d 2 (Reactancia del secundario reducida al primario) R' 2 = rt 2 ⋅ R 2 (Resistencia del secundario reducida al primario) U ' 2 = rt ⋅ U 2 (Tensión en el secundario reducida al primario) rt = U 1n 3800 = = 10 U 2n 380 (Relación de transformación) Como se trabaja en vacío, la corriente en el secundario es nula; por lo tanto I’2 = 0; la tensión del primario U1 en forma vectorial se puede obtener de la siguiente forma: U 1o = R1 ⋅ I 1o + j ⋅ X d 1 ⋅ I 1o + U ' 2o © Los autores, 2006; © Edicions UPC, 2006 87 Transformadores monofásicos A partir de las pérdidas en vacío, se puede encontrar el ángulo que forman la tensión U 1 y la corriente I1 . ( Po = U 1o ⋅ I 1o ⋅ cos ϕ U 10 − ϕ I10 ( ) cos ϕU 10 − ϕ I 10 = ) Po 1200 = = 0,6315 U1o ⋅ I1o 3800 ⋅ 0,5 ϕ = ϕ U 1 o − ϕ U 1 o = 50 ,83 º Si se toma como origen de ángulos el correspondiente a la corriente I 1o = 0,5∠0º A , se tiene U 1o = 3800∠50,83º V . El diagrama vectorial es: U’2 α U1 Xd1 I1 R1 I1 I1 Figura 2.5.2 Proyectando los vectores sobre el eje de las abcisas, se obtiene: R1 ⋅ I 1o + U ' 2o ⋅ cos α = U 1o ⋅ cos ϕ Y sobre el eje de las ordenadas: X d 1 ⋅ I 1o + U ' 2o ⋅senα = U 1o ⋅ senϕ y sustituyendo valores, resulta: ⎧5 ⋅ 0,5 + U ' 2o ⋅ cos α = 3800 ⋅ cos 50,83º ⎫ ⎨ ⎬ ⎩25 ⋅ 0,5 + U ' 2o ⋅senα = 3800 ⋅ sen50,83º ⎭ y por lo tanto: U ' 2o ⋅ cos α = 2397,50 U ' 2o ⋅senα = 2933,68 Resolviendo el sistema, resulta: α = 50,74 º U ' 2o = 3788,74 V En consecuencia, U 2o = U ' 2o 3788,74 = = 378,87 V 10 rt © Los autores, 2006; © Edicions UPC, 2006 88 Problemas de electrotecnia 2.6 Problema 6 Un transformador monofásico de 125 kVA y 3000 V/380 V alimenta una carga de 116046 VA y factor de potencia 0’8 (i) a 378 V. En esta situación la potencia absorbida por el transformador es de 94655 W. Datos del ensayo de cortocircuito: 8 V, 240 A, 480 W (medidas realizadas desde el lado de baja tensión). Se sabe que el factor de potencia de la rama en paralelo del circuito equivalente es 0’2. Se pide: a ) Valores de los parámetros R1cc y X1cc, reducidos al lado de alta tensión. b ) Tensión de alimentación del transformador cuando alimenta la carga del enunciado. c ) Valores de los parámetros R1Fe y X1µ, reducidos al lado de alta tensión. Resolución: a) I 1n = rt = 125000 = 41,66 A 3000 I 2n = 125000 = 328,747 A 380 3000 = 7,8947 380 Carga: S 116046 I2 = C = = 307 A U2 378 I 2 = 307∠ − 36,87º A I' 2 = 38,88 A PC = S C ⋅ cos ϕC = 116046 ⋅ 0,8 = 92836,8 W Prueba de cortocircuito ( parámetros reducidos al primario ): Z1CC ⎛ 3000 ⎞ 8⋅⎜ ⎟ 380 ⎠ ⎝ = 2,077 Ω = ⎛ 380 ⎞ 240 ⋅ ⎜ ⎟ ⎝ 3000 ⎠ P R1CC = CC = I 21CC 480 ⎛ 380 ⎞ 2402 ⋅ ⎜ ⎟ ⎝ 3000 ⎠ R1CC = 0,519 Ω X 1CC = Z 21CC − R 21CC = 2,011 Ω X1CC = 2,011 Ω © Los autores, 2006; © Edicions UPC, 2006 2 = 0,519 Ω 89 Transformadores monofásicos b ) En las condiciones de la carga: 2 PCu = R1CC ⋅ I' 2 = 0,519 ⋅ 38,88 2 = 784 ,5486 W PFe = Pabs − PC − PCu = 94655 − 92836,8 − 784,5489 = 1033,65 W R1CC X1CC I '2 = 38 ,88∠ − 36 ,87º A 378 · ( 3000 / 380 ) = 2984 ,21∠ 0º V R1Fe X1µ Figura 2.6.1 U 1 = 2984,21∠0º +(0,5197 + j 2,011)·38,88∠ − 36,87 º = 3047,27 + j 50,43 U 1 = 3047,48 V c) R Fe = U 1 2 3047,48 2 = = 8986,01 Ω 1033,65 PFe Q µ = PFe ⋅ tgϕ o = 1033,65 ⋅ tg [arccos 0,2] Q µ = 5063,83 VAr Xµ = U12 3047,482 = = 1834,25 Ω Qµ 5063,83 X µ = 1834,25 Ω © Los autores, 2006; © Edicions UPC, 2006 90 Problemas de electrotecnia 2.7 Problema 7 Un transformador monofásico de baja tensión 380 V/220 V y potencia nominal 5000 VA tiene una corriente de vacío del 5% de la nominal y las pérdidas de vacío son de 150 W. Se conecta al transformador por la parte del secundario una carga con un consumo de 2000 VA, un factor de potencia 0,96 inductivo, y la tensión aplicada al consumo es de 200 V. Para las condiciones indicadas, se sabe que la potencia activa absorbida por el primario del transformador es de 2100 W y la reactiva es de 800 VAr. Calcular: a) Valores de εRCC y de εXCC b) Tensión aplicada al transformador en el lado de alta tensión Resolución: a) En primer lugar, se determinan las corrientes nominales primaria y secundaria del transformador. La corriente nominal primaria es: I 1n = Sn 5000 = = 13,158 A U 1n 380 La corriente nominal secundaria es: I 2n = Sn 5000 = = 22,727 A U 2n 220 La relación de transformación es: rt= U 1n 380 = = 1,727 U 2 n 220 Como se puede comprobar, el valor nominal de la corriente del secundario también se puede calcular del siguiente modo: I 2 n = I 1n ⋅r t = 13,158 ⋅1,727 = 22,727 A que coincide con el valor encontrado anteriormente. La corriente de vacío es: I 1o = i o ⋅ I 1n = 0,05 ⋅13,158 = 0,658 A Como se conocen las pérdidas en vacío, se puede determinar el factor de potencia del circuito equivalente en vacío: Po = U 1n ⋅ I 1o ⋅ cos ϕ o cos ϕ o = Po 150 = = 0,6 U 1n ⋅ I o 380 ⋅ 0,658 siendo ϕ o = 53,13º © Los autores, 2006; © Edicions UPC, 2006 91 Transformadores monofásicos Las pérdidas de potencia reactiva en el ensayo en vacío, a la tensión de 380 V, son: Qo = Po ⋅ tgϕ o = 150 ⋅ tg 53,13º = 200VAr Cuando se conecta la carga, la tensión en el secundario es de 200 V y, por lo tanto y en primera aproximación, despreciando la caída de tensión interna, se ha de aplicar al primario una tensión de U 1o = U 2o ⋅ rt U 1o = 200 ⋅1,727 = 345,45V Las pérdidas en vacío en estas condiciones, en que la tensión aplicada no es la nominal, son: ( Po ) 220V ⎛ U 2 n =⎜ ( Po ) 200V ⎜⎝ U 2 2 ⎞ ⎛ 220 ⎞ ⎟⎟ = ⎜ ⎟ ⎝ 200 ⎠ ⎠ 2 2 2 ⎛ 200 ⎞ ⎛ 200 ⎞ ( Po ) 200V = ( Po ) 220V ⎜ ⎟ = 123,97W ⎟ = 150 ⋅ ⎜ 220 ⎝ 220 ⎠ ⎝ ⎠ 2 2 ⎛ 200 ⎞ ⎛ 200 ⎞ (Qo ) 200V = (Qo ) 220V ⎜ ⎟ = 200 ⋅ ⎜ ⎟ = 165,29VAr ⎝ 220 ⎠ ⎝ 220 ⎠ La carga conectada al secundario tiene las siguientes características: P2 = S 2 ⋅ cos ϕ C = 2000 ⋅ 0,96 = 1920W Q2 = S 2 ⋅ senϕ C = 2000 ⋅ 0,28 = 560VAr La corriente en el secundario es: I2 = S 2 2000 = = 10 A U2 200 y por lo tanto, el índice de carga C en estas condiciones es: C= I2 10 = = 0,44 I 2 n 22 ,727 La corriente secundaria I’2 referida al primario es: I '2 = I2 10 = = 5,789 A rt 1,727 Las pérdidas en el cobre se pueden calcular a partir de la potencia absorbida por el transformador, de la potencia cedida a la carga y las pérdidas en vacío. PCu = P1 − P2 − ( Po ) 200V = 2100 − 1920 − 123,97 = 56,03W A partir de las pérdidas en el cobre, se puede determinar la resistencia de cortocircuito referida al primario. R1CC = PCu I '2 2 = 56,03 5,789 2 = 1,67Ω U R1CC = R1CC ⋅ I1n = 1,67 ⋅13,158 = 22V ε RCC = U R1CC 22 = = 0,057 U 1n 380 → εRCC = 5,7 % © Los autores, 2006; © Edicions UPC, 2006 92 Problemas de electrotecnia La ε X CC se determina a partir de las potencias reactivas. QCu = Q1 − Q2 − (Qo ) 200V = 800 − 560 − 165,29 = 74,71VAr X1CC = QX 1CC I '2 2 = 74,71 5,7892 = 2,235Ω La caída de tensión en esta reactancia tiene un valor de: U X 1CC = X 1CC ⋅ I 1n = 2,235 ⋅13,158 = 29,40V En consecuencia, el valor relativo de la componente reactiva de la tensión de cortocircuito es: ε X CC = U X 1CC U 1n = 29,40 = 0,0773 380 → εRCC = 7,73 % Si se quiere calcular el valor relativo de la tensión de cortocircuito, puede hacerse así: ε CC = ε 2 RCC + ε 2 XCC = 0,057 2 + 0,07732 = 0,096 → εCC = 9,6 % b) La tensión que se ha de aplicar al bobinado primario es: U1 φC I’2 X’CC I’2 U’2 R’CC I’2 Figura 2.7.1 cos ϕ = 0,96 ϕ = 16,26º U 1 = U ' 2 + I ' 2 ⋅ Z 1CC = 200 ⋅1,727∠0º +5,789∠ − 16,26º⋅(1,67 + j 2,235) = 345,45 + 0 j + 12,90 + 9,71 j U1 = 358,48∠1,55º V Nota: En primer lugar se ha considerado que se había aplicado al transformador una tensión de 345,45 V, lo cual ha permitido determinar los valores R1CC y X1CC. Al efectuar los cálculos se ha determinado que la tensión de alimentación realmente es de 358,48 V. A partir de este dato, y por aproximaciones sucesivas, se podría calcular con exactitud los valores de R1CC y X1CC. © Los autores, 2006; © Edicions UPC, 2006 93 Transformadores monofásicos 2.8 Problema 8 En la placa de características de un transformador monofásico se encuentran, entre otros, los siguientes datos: S n = 100kVA U 1n = 3kV U 2 n = 220V Las lecturas del ensayo en vacío dan los valores siguientes: i o = 6% Po = 500W Las lecturas del ensayo de cortocircuito aportan los datos siguientes: ε CC = 5,7% PCC = 2500W a) Si el transformador se alimenta por el lado de baja tensión y se produce en el lado de alta un cortocircuito franco, se registra una intensidad de corriente de I1(CC) = 350 A. En estas condiciones, encontrar la impedancia de cortocircuito Z1CC y la tensión U2 de alimentación. A1 + AT BT V2 Generador 3000 V / 220 V 100 kVA Figura 2.8.1 b) Si el transformador se conecta a la red por el lado de alto tensión y alimenta una carga inductiva de cos φC =0,8, conectada al lado de baja tensión, en estas condiciones se tienen los valores siguientes en régimen permanente: U 1 = 2,8kV U 2 = 200V Encontrar el valor de la corriente I2 correspondiente al lado de baja tensión. Resolución: a) En primer lugar se van a determinar los restantes datos del transformador partiendo de los valores obtenidos de su placa de características. La corriente nominal primaria es: I 1n = La corriente nominal secundaria es: I 2n = Sn 100000 = = 33,33 A U 1n 3000 Sn 100000 = = 454,55 A U 2n 220 © Los autores, 2006; © Edicions UPC, 2006 94 Problemas de electrotecnia La relación de transformación: rt = La corriente de vacío: U 1n 3000 = = 13,64 U 2n 220 I 1o = i o ⋅ I 1n = 6 ⋅ 33,33 = 2 A 100 La impedancia de cortocircuito Z1CC referida al primario se obtiene a partir de la tensión de cortocircuito: Z 1CC = U 1CC U 1n ε CC 3000 ⋅ 5,7 = 5,13Ω = = I 1n I 1n 100 ⋅ 33,33 Ya que la intensidad de corriente que pasa por el primario, en caso de producirse el cortocircuito franco, es I1(CC) = 350A, la tensión a que está sometido el primario es U2CC, que vale: ⎞ I1(CC ) ⋅ Z1CC ⎛Z = 131,67 V U 2(CC ) = I 2(CC ) ⋅ Z 2CC = rt ⋅ I1(CC ) ⋅ ⎜⎜ 1CC 2 ⎟⎟ = rt rt ⎠ ⎝ ( ) b) En primer lugar se puede hallar ε RCC , o sea, la componente óhmica de la tensión de cortocircuito en valor relativo del transformador a partir de las pérdidas de potencia activa del ensayo de cortocircuito. ε RCC = PCC 2500 = = 0,025 Sn 100000 Y por lo tanto: 2 2 ⎛ 5,7 ⎞ ⎛ 2,5 ⎞ ⎟ −⎜ ⎟ = 0,0512 ⎝ 100 ⎠ ⎝ 100 ⎠ ε XCC = ε 2CC − ε 2 RCC = ⎜ Debido a que no se conoce el índice de carga del transformador, se puede aplicar la fórmula aproximada que da la caída de tensión en valor unitario, que es: U1 U 2 − = C ⋅ [ε RCC ⋅ cos ϕC + ε XCC ⋅ senϕC ] U1n U 2 n Sustituyendo los valores numéricos dados en el enunciado, se tiene: 2,8 200 5,12 ⎤ ⎡ 2,5 − = C⋅⎢ ⋅ 0,8 + ⋅ 0,6⎥ 3 220 100 ⎦ ⎣100 Haciendo operaciones se obtiene el valor del índice de carga: ( 47,8% ) C = 0,4780 y, en consecuencia, la corriente I2 en el lado de baja tensión es de: I 2 = C ⋅ I 2n = 47,80 ⋅ 454,55 = 217,26 A 100 I 2 = 217,26 A © Los autores, 2006; © Edicions UPC, 2006 95 Transformadores monofásicos 2.9 Problema 9 Un transformador monofásico, cuya tensión nominal primaria es de 6 kV, su tensión nominal secundaria de 380 V y su potencia nominal de 200 kVA, tiene un rendimiento del 0,98 trabajando a plena carga. Cuando trabaja a media carga, el rendimiento es de 0,985 y el factor de potencia de la carga es siempre la unidad. En ambos casos la carga se supone alimentada a la tensión nominal secundaria del transformador. La caída de tensión a plena carga con un factor de potencia de la carga igual a 0,8 inductivo es del 4%. El factor de potencia cuando trabaja en vacío vale 0,22 (i). Calcular: a) Resistencia y reactancia de cortocircuito b) Parámetros que definen el circuito equivalente del transformador c) Dibujar el circuito equivalente reducido al lado de baja tensión Resolución: a) El rendimiento de un transformador viene definido por la expresión: η= U 2 ⋅ I 2 n ⋅ C ⋅ cos ϕ C ⎛V U 2 ⋅ I 2 n ⋅ C ⋅ cos ϕ C + Po ⎜⎜ 1 ⎝ V1n 2 ⎞ ⎟ + C 2 ⋅ PCC ⎟ ⎠ = S n ⋅ C ⋅ cos ϕ C S n ⋅ C ⋅ cos ϕ C + Po + C 2 ⋅ PCC y el índice de carga del transformador es C = 1, en el caso de que trabaje a plena carga, y C = 0,5, en el caso de que trabaje a media carga. En consecuencia, para los dos casos planteados se tiene: 200000 200000 + Po + PCC Plena carga: 0,98 = Media carga: 0,985 = 200000 ⋅ 0,5 200000 ⋅ 0,5 + Po + PCC ⋅ 0,5 2 Resolviendo el sistema de ecuaciones anteriores, resulta: Po = 666,66W La corriente nominal primaria del transformador es: I 1n = PCC = 3333,33W Sn 200000 = = 33,33 A U 1n 6000 Trabajando el transformador a plena carga y con un factor de potencia igual a 0,8 inductivo, presenta una caída de tensión del 4%, es decir: 0,04 = U 1n − U ' 2 6000 − U ' 2 = 6000 U 1n U ' 2 = 5760V y utilizando la expresión aproximada de Kapp, se tiene: U1 = U '2 + R1CC I '2 cos ϕC + X1CC I '2 senϕC © Los autores, 2006; © Edicions UPC, 2006 96 Problemas de electrotecnia U1 XCC I φc U’2 RCC I Figura 2.9.1 Es decir: 6000 = 5760 + R1CC ⋅ 33,33 ⋅ 0,8 + X 1CC ⋅ 33,33 ⋅ 0,6 pero R1CC = PCC I 21n 3333,33 = 33,3 2 = 3Ω De aquí se puede encontrar el valor de XCC: 6000 = 5760 + 3 ⋅ 33,33 ⋅ 0,8 + X 1CC ⋅ 33,33 ⋅ 0,6 → X 1CC = 8 Ω b) Para definir el circuito equivalente, hace falta encontrar RFe, y Xµ. Se sabe que cuando el transformador trabaja en vacío y en condiciones nominales, tiene unas pérdidas de Po = 666,66 W. Po = U 1n 2 R1Fe de donde R1Fe = U 21n 6000 2 = = 54000 Ω Po 666,66 Por otra parte: Po = I 1o ⋅ U 1n ⋅ cos ϕ o Z 1o = I 1o = U 1n 6000 = = 11881,18Ω I 1o 0 ,505 Po 666,66 = = 0,505 A U 1n ⋅ cos ϕ o 6000 ⋅ 0,22 con ϕ o = 77,29º 1 y teniendo en cuenta que RFe y Xµ están en paralelo, resulta: y despejando X µ queda: Z 1o = 1 R1Fe + 1 X 1µ Z 10 ⋅ R1Fe 11881,18∠77,29º⋅54000∠0º = = 12179,62∠90º Ω R1Fe − Z 10 54000∠0º −11881,18∠77,29º X 1µ = c) El circuito equivalente reducido al secundario corresponde a los valores encontrados anteriormente, y sólo hay que dividir por el cuadrado de la relación de transformación. rt = 6000 = 15,789 380 R2CC = R 2 Fe = 3 15,789 2 54000 15,789 2 = 1,20 ⋅10−2 Ω X 2CC = = 216,60Ω X 2µ = 8 15,789 2 12179,62 15,789 2 = 3,21⋅10 −2 Ω = 48,85Ω © Los autores, 2006; © Edicions UPC, 2006 97 Transformadores monofásicos -2 1,2·10-2 Ω 3,21·10 Ω U’1 216,6Ω 48,55 Ω Figura 2.9.2 © Los autores, 2006; © Edicions UPC, 2006 U2 98 Problemas de electrotecnia 2.10 Problema 10 En el circuito cuyo esquema se representa en la figura, los datos que se conocen del transformador son los siguientes: Sn = 7,2 kVA PCC = 108 W U1n = 600 V U2n = 300 V Po = 36 W εCC = 0,039 ( 3,9% ) IA2 G V1 V2 WA2 CARGA A inductiva K1 IB2 K2 WB2 CARGA B capacitiva Figura 2.10.1 Con los interruptores K1 cerrado y K2 abierto, se registran las lecturas siguientes en los aparatos de medición: WA2 = 1267,2 IA2 = 6,6 A V2 = 240 V Calcular: a) El rendimiento del transformador y la lectura del voltímetro V1. Se cierra a continuación el interruptor K2 permaneciendo cerrado K1, regulándose el generador de alimentación de forma que las lecturas de los voltímetros permanezcan invariables y obteniéndose además en este caso las siguientes: WB2 = 2880 W IB2 = 15 A Calcular: b) Nuevos valores del rendimiento del transformador y de la lectura del voltímetro V1 en este estado de conexión. c) Valores de las magnitudes S’n, U’1n, U’2n, P’o, P’CC y ε’CC del banco trifásico conexionado estrellatriángulo, constituido por tres unidades monofásicas de características idénticas al transformador dado. d) Determinar para el banco trifásico del apartado anterior, las intensidades de corriente de cortocircuito permanente que se establecen en la línea y en los arrollamientos de alta y baja tensión, en el supuesto de que, durante el defecto, se mantiene en el primario la tensión nominal. Resolución: a) El factor de potencia de la carga A se obtiene de inmediato a partir de: © Los autores, 2006; © Edicions UPC, 2006 99 Transformadores monofásicos cos ϕ CA = W A2 1267,2 = = 0,8 U 2 I A2 240 ⋅ 6,6 ϕ CA = 36,87 º senϕ CA = 0,6 Se observa así mismo que el transformador alimenta la carga A a una tensión que es inferior a su tensión nominal U2<U2n. En consecuencia, las pérdidas en el hierro serán menores que las obtenidas en el ensayo de vacío, ya que dichas pérdidas son proporcionales al cuadrado del flujo, al cuadrado de la inducción y en consecuencia al cuadrado de la tensión, pudiéndose escribir que: 2 2 ⎛U ⎞ ⎛ 240 ⎞ PFe = Po ⎜⎜ 2 ⎟⎟ = 36⎜ ⎟ = 23,04 W ⎝ 300 ⎠ ⎝ U 2n ⎠ La corriente nominal en el secundario del transformador vale: I 2n = Sn 7200 = = 24 A 300 U 2n y la corriente nominal en el primario: I1n = I 2 n 24 S n 7200 = = = = 12 A 2 U 1n 600 rt al ser la relación de transformación: U 1n 600 = =2 U 2 n 300 rt = por lo que el índice de carga del transformador es: I A2 6,6 = = 0,275 24 I 2n C= Y puesto que, en estas condiciones, el factor de potencia de la carga es 0,8 inductivo, la corriente IA2 en forma vectorial es: I 2 A = 6,6∠ − 36,87º A Y el índice de carga en forma compleja es de la forma: C = 0,275∠ − 36,87 º A Con estos datos, ya se puede determinar el rendimiento, al ser: η= PC 1267,2 = PC + PFe + PCu 1267,2 + 23,04 + 0,275 2 ⋅108 η= 1267,2 = 0,976 1267,2 + 23,04 + 8,1675 → η= 97,6 % Siendo εCC = 3,9%, se van a determinar a continuación sus dos componentes, εRCC y εXCC, que valen: ε RCC = PCC 108 ⋅ 100 = ⋅ 100 = 1,5% Sn 7200 ε XCC = ε CC 2 − ε RCC 2 = 3,9 2 − 1,5 2 = 3,6% Por lo tanto: tgϕ CC = ε XCC 3,6 = = 2,4 ε RCC 1,5 ϕ CC = 67,38º © Los autores, 2006; © Edicions UPC, 2006 100 Problemas de electrotecnia En la forma vectorial se tiene: ε CC = 3,9 ⋅ 10−2 ∠67 ,38º = ( 1,5 + j 3,6 )10−2 Para el cálculo de la tensión en el primario del transformador, se aplicará el método exacto: U 1 = U ' 2 + I ' 2 ⋅ Z 1CC (U (I U ' 2 = U 2 ⋅ rt = 480∠0º I I '2 = 2 rt = 3,3∠ − 36,87 º ) 2 = 240∠0º 2 = 6,6∠ − 36,87º ) V Z1CC = ε CC ⋅ 1n = 1,95∠67,38º I1n U 1 = 480∠0º +3,3∠ − 36,87º⋅1,95∠67,38º = 480 + 0 j + 5,54 + 3,27 j V Resultando: U1 = 485,55 V b) El factor de potencia de la carga B vale: cos ϕ CB = WB2 2880 = = 0,8 U 2 I B 2 240 ⋅15 ϕ CB = −36,87º senϕ CB = −0,6 Con ello será: I B 2 = 15∠36,87º A Al cerrar ambos interruptores y regularse el generador de forma que las lecturas anteriores permanezcan invariables, se puede aplicar ahora el método de la superposición, siendo la corriente que recorre el secundario del transformador con las dos cargas conectadas: I 2 = I A2 + I B 2 = 6,6∠ − 36,87º +15∠36,87º = 5,28 − 3,96 j + 12 + 9 j = [17,28 + 5,04 j ] A I 2 = 18∠16,26º A y el nuevo índice de carga vale: C' = I2 18 = ∠16,26º = 0,75∠16,26º I 2 n 24 El rendimiento en este segundo caso, con ambas cargas conectadas, vale: η' = W A2 W A2 + W B 2 1267,2 + 2880 = + W B 2 + PFe + PCu 1267,2 + 2880 + 23,04 + 0,75 2 ⋅108 η' = 4147,2 = 0,9802 4147,2 + 23,04 + 60,75 → η’ = 98,02 % Para determinar el nuevo valor de la tensión primaria aplicada al transformador, al utilizar la misma expresión del apartado a), se obtiene: U 1 = U ' 2 + I ' 2 ⋅ Z 1CC En la que tomando U 2 ' = rt .U 2 ∠0º = 480∠0º V I 2' = I 2 / rt = 9∠16 ,26º A Z1CC = 1,95∠67 ,38º Ω © Los autores, 2006; © Edicions UPC, 2006 101 Transformadores monofásicos resulta: U1 = 482,26∠2,07º V c) La potencia nominal del banco trifásico será tres veces la potencia de uno de los transformadores; por tanto: S ' n = 3S n = 3 ⋅ 7,2 = 21,6 kVA La tensión compuesta o de línea en el primario del banco trifásico, al estar conectado en estrella, será: U '1n = 3 ⋅ U1n = 3 ⋅ 600 = 1039,23 V La tensión secundaria en el banco trifásico, al estar éste devanado conectado en triángulo, será la misma del transformador monofásico, por lo tanto: U ' 2n = U 2n = 300 V La potencia P’o en el ensayo en vacío será tres veces la potencia Po del transformador dado; por lo tanto: P' o = 3 ⋅ Po = 3 ⋅ 36 = 108 W De la misma forma, en el ensayo en cortocircuito se cumplirá: P 'CC = 3 ⋅ PCC = 3 ⋅ 108 = 324 W Y en estas condiciones, las tensiones de cortocircuito serán las mismas para el transformador único que para el banco trifásico, por lo que: ε ' CC = ε CC = 0,039 ε’CC = 3,9 % d) El esquema en representación unifilar, supuesta la conexión estrella-estrella, tratándose de cortocircuito primario, en el que la impedancia por fase a considerar es la de cortocircuito, referida al primario, es el de la figura siguiente: ZCC1 600V Figura 2.10.2 Por lo que en el primario, al estar conectado en estrella, se tiene: I 1CCfase = I 1CClínea = U 1nfase Z 1CC Expresión en la que únicamente falta por calcular la impedancia de cortocircuito del transformador referida al primario, que vale: Z 1CC = ε CC ⋅U 1n I 1n = 0,039 ⋅ 600 = 1,95Ω 12 © Los autores, 2006; © Edicions UPC, 2006 102 Problemas de electrotecnia Por lo tanto será: I1CCfase = I1CClínea = V1nfase Z1CC = 600 = 307,69 A 1,95 → I 2CClínea = rt ⋅ I1CClínea = 615,38 A En el secundario, tanto en estrella como en triángulo, la intensidad de línea en cortocircuito es la corriente de línea en el primario, multiplicad por la relación de transformación. I 2CCfase = I 2CClínea 3 = 615,38 = 355,29 A 3 © Los autores, 2006; © Edicions UPC, 2006 103 Transformadores monofásicos 2.11 Problema 11 Dos transformadores monofásicos están conectados en paralelo y alimentan por el lado de baja tensión una carga eléctrica de 200 kW con un factor de potencia 0,8 inductivo. La tensión de alimentación de la carga es de 370 V. Las características de los transformadores se dan en la tabla siguiente: Transformador Sn (kVA) U1n (V) U2n (V) εCC (%) PCC (kW) Po (kW) A 125 6000 380 4,2 1 0,4 B 140 6000 380 4 1,2 0,5 Calcular: a) La impedancia de cortocircuito de cada transformador b) La intensidad de corriente que suministra a la carga cada uno de los transformadores c) La tensión de alimentación del devanado de alta tensión ( primario ) d) Potencia aparente suministrada por cada transformador e) Rendimiento de cada transformador Resolución: a) Se calculan, en primer lugar, las intensidades de corriente nominales de cada transformador, referidas al lado de baja tensión: S An = U 2 An ⋅ I 2 An I 2 An = S An 125000 = = 328,95 A U 2 An 380 S Bn = U 2 Bn ⋅ I 2 Bn I 2 Bn = S Bn 14000 = = 368,42 A U 2 Bn 380 A partir de los datos de las pérdidas del ensayo de cortocircuito, PCC, se pueden determinar las resistencias de cortocircuito, RCC, de cada uno de los transformadores. El circuito equivalente de un transformador es: RCC XCC Figura 2.11.1 © Los autores, 2006; © Edicions UPC, 2006 104 Problemas de electrotecnia Transformador A: PCCA R 2CCA = Transformador B: I 2 = 2 An PCCB R 2CCB = I 2 = 2 Bn 1000 328,95 2 = 0,924 ⋅10 − 2 Ω 1200 = 0,884 ⋅10 − 2 Ω 368,42 2 Por otra parte: ε CC = I 2 n ⋅ Z 2CC U 2n siendo Z 2CC = U 2 n ⋅ ε CC I 2n que aplicado a cada transformador resultan: Z 2CCA = U 2 An ⋅ ε CCA 380 ⋅ 0,042 = = 4,85 ⋅10 − 2 Ω 328,95 I 2 An Z 2CCB = U 2 Bn ⋅ ε CCB 380 ⋅ 0,04 = = 4,12 ⋅10 − 2 Ω 368,42 I 2 Bn y de aquí: X 2CCA = Z 2 2CCA − R 2 2CC = X 2CCB = (4,85 ⋅10 ) − (0,924 ⋅10 ) −2 2 (4,12 ⋅10 ) − (0,884 ⋅10 ) −2 2 −2 2 −2 2 = 4,71⋅10 − 2 Ω = 4,02 ⋅10 − 2 Ω Por lo tanto, las impedancias de cortocircuito de los transformadores son, respectivamente: ( ) Z 2CCB = (0,884 ⋅10 −2 + 4,02 ⋅10 −2 j ) = 4,12 ⋅10 −2 ∠77,63º Ω Z 2CCA = 0,924 ⋅ 10 −2 + 4,71 ⋅ 10 −2 j = 4,8 ⋅ 10 −2 ∠79,02 º Ω b) El circuito equivalente reducido al lado de baja tensión del conjunto de los dos transformadores que alimentan la carga es: ZCCA ZCCB U’1 U2 = 370 V ZC Figura 2.11.2 Tomando como origen de ángulos la tensión de alimentación de la carga, 370 V, la intensidad de corriente absorbida por la carga vale: IC = 200000 = 675,675 A 370 ⋅ 0,8 © Los autores, 2006; © Edicions UPC, 2006 105 Transformadores monofásicos con un factor de potencia de 0,8 inductivo, es decir, φC = 36,87º. Por tanto, I C = 675,675∠ − 36,87 º A La impedancia equivalente de Z CCA y Z CCB en paralelo vale: Z 2CCeq = Z 2CCA ⋅ Z 2CCB 4 ,85 ⋅ 10 −2 ∠79 ,02º ⋅4 ,12 ⋅ 10 −2 ∠77 ,63º = 2 ,223 ⋅ 10 − 2 ∠78,27º Ω = Z 2CCA + Z 2CCB 4 ,85 ⋅ 10 − 2 ∠79 ,02º +4 ,12 ⋅ 10 − 2 ∠77 ,63º El diagrama vectorial es: Z2CCeq U’1 78,22º ZCCeq IC U2 36,87º IC U '1 = U 2 + Z 2 cceq ⋅ I C = 370 ∠0º +2,223 ⋅ 10 −2 ∠78,27 º⋅675,675∠ − 36,87 º = 381,43∠1,50 º V Tensión que pasada al primario resulta: U1 = U '1⋅rt = 381,43 ⋅ 6000 = 6022 ,78 V 380 La intensidad de corriente I A es: I2A = La intensidad de corriente I B es: I 2B = Se puede comprobar que: Z 2CCeq ⋅ I C = 310,23∠ − 37,62º A Z 2CCA Z 2CCeq ⋅ I C Z 2CCB = 365,19∠ − 36,23º A IC = I A + I B Por consiguiente las intensidades de corriente que proporcionan los transformadores A y B a la carga son respectivamente 310,2 A y 365,2 A. c) La tensión del lado de alta tensión ya ha sido calculada en el apartado anterior y es de 6022,8 V. d) Las potencias aparentes valen: S A = U 2 ⋅ I A * = 370∠0º⋅310,23∠37,6º = 114785,1∠37,6º VA S B = U 2 ⋅ I B * = 370∠0º⋅365,19∠36,25º = 135120,3∠36,23º VA e) Los rendimientos se calculan a partir de la expresión: η= Putil Putil + PFe + PCu Se ha de tener en cuenta que los transformadores no trabajan en condiciones nominales de tensión y carga. Por tanto, es necesario calcular las respectivas pérdidas en el cobre y en el hierro de cada uno de los transformadores. Es decir, hay que tener en cuenta que tensión ( la misma por estar en paralelo) e intensidad de corriente suministran respectivamente a la carga. © Los autores, 2006; © Edicions UPC, 2006 106 Problemas de electrotecnia 2 Transformador A: ⎛ 310,23 ⎞ ⎟⎟ = 889,42W PCuA = 1000 ⋅ ⎜⎜ ⎝ 328,95 ⎠ 2 ⎛ 6022,78 ⎞ PFeA = 400 ⋅ ⎜ ⎟ = 403,04W ⎝ 6000 ⎠ ηA = 370 ⋅ 310,23 ⋅ cos 37,6º 370 ⋅ 310,23 ⋅ cos 37,6º +889,42 + 403,04 η A = 98,6% 2 Transformador B: ⎛ 365,19 ⎞ PCuB = 1200 ⋅ ⎜⎜ ⎟⎟ = 1179,05W ⎝ 368,42 ⎠ 2 ⎛ 6022,78 ⎞ PFeB = 500 ⋅ ⎜ ⎟ = 503,80W ⎝ 6000 ⎠ ηB = 370 ⋅ 365,19 ⋅ cos 36,25º 370 ⋅ 365,19 ⋅ cos 36,25º +1179,05 + 503,80 © Los autores, 2006; © Edicions UPC, 2006 η B = 98,5% 107 Transformadores monofásicos 2.12 Problema 12 Un transformador monofásico de 10 kVA, 3000 V/220 V presenta unas pérdidas en el ensayo de vacío cuando se alimenta el lado de alta tensión a 2500 V de 160,616 W. Se sabe que εcc = 5 % i εXcc = 4 %. Se quiere alimentar por el lado de baja tensión una carga de 6,6 kW y cosφ = 0,8 (i) a la tensión de 220 V. Se pide: a) La tensión de alimentación del transformador b) El rendimiento del transformador en estas condiciones de carga Se quiere conectar en paralelo con la carga anterior una nueva carga de 8,8 kW y cos φ = 0,9 (i) por el lado de baja tensión. Para poder garantizar el suministro de potencia, se conecta en paralelo con el transformador anterior un nuevo transformador de 10 kVA, 3000 V/220 V y εcc = 4,5 %. c) Se pide el índice de carga de cada transformador cuando la carga total queda alimentada a 220 V por el lado de baja tensión Resolución: a) 2 ε Rcc = ε cc2 − ε Xcc = 5 2 − 4 2 = 3% rt = 3000 220 I 1n = Sn 10000 = = 3,333 A U 1n 3000 ε Rcc = X 1cc = I 2n = R1cc ·I 1n U 1n ε Xcc · U 1n I 1n Æ 4 · 3000 = 100 = 36 Ω 3,333 Sn = 45,45 A U 2n R1cc = ε Rcc · U 1n I1n Z 1cc = 27 + j 36 = 45 ∠ 53,13º Ω Carga I2 = P2 6600 = = 37,5 A U 2 · cos ϕ 220 · 0,8 cos ϕ c = 0,8 I 2/ = ϕ c = −36,87º I2 37,5 = = 2,75 A 3000 rt 220 I 2/ = 2,75 ∠ − 36,87º A U 2/ = U 2 · rt = 220 · rt = 220 · 3 · 3000 = 100 = 27 Ω 3,333 3000 = 3000 V 220 © Los autores, 2006; © Edicions UPC, 2006 108 Problemas de electrotecnia U 2/ = 3000 ∠ 0º V Si I 2/ = 2,75 ∠ − 36,87º A y U 1 = U 2/ + Z 1cc · I 2/ = 3000 ∠ 0º + 45 ∠ 53,13º · 2,75 ∠ − 36,87º = 3119 ∠ 0,63º V U1 = 3119 V b) η= η= P2 = P2 + PFe + PCu P2 2 ⎛V ⎞ P2 + Po ⎜⎜ 1 ⎟⎟ + I ' 22 ⋅R1CC ⎝ V1n ⎠ 6600 2 ⎛ 3119 ⎞ 2 6600 + 160,616 · ⎜ ⎟ + 27 · 2,75 ⎝ 2500 ⎠ = 6600 = 0,9356 7054,187 η % = 93,56% c) Condición que debe cumplirse en los transformadores en paralelo: C I · ε cc I = C II · ε cc II ε cc II 0,045 CI = = = 0,9 C II ε cc I 0,050 Æ C I = 0,9 · C II Carga total S T = S I + S II cos ϕ I = 0,8 Æ ϕ I = 36,87 º cosϕ II = 0,9 Æ ϕ II = 25,84º SI = S II = PI 6600 = = 8250 VA cos ϕ I 0,8 PII 8800 = = 9777,77 VA cos ϕ II 0,9 Æ S I = 8250 ∠ 36,87 º VA Æ S II = 9777,77 ∠ 25,84º VA S T = S I + S II = 17944,8 ∠ 30,88º VA Æ C I · S N I + C II · S N II = S T C I = 0,9 · C II ⎫ ⎬ C I · 10000 + C II · 10000 = 17944,8⎭ C I · 10000 + C II · 10000 = 17944,8 Æ C I = 0 ,850 C II = 0 ,944 Por lo tanto, resulta que las potencias aparentes aportadas por cada transformador son: S I = 8500 VA S II = 9444,63 VA © Los autores, 2006; © Edicions UPC, 2006 109 Transformadores monofásicos 2.13 Problema 13 Se somete un transformador monofásico al ensayo de estándar de vacío, aplicando 9120 V por el lado de alta tensión, absorbiendo de la red una potencia de 624,4 W y una intensidad de 0,975 A, siendo la tensión en el lado de baja tensión de 570 V. A continuación se realiza el ensayo estándar de corto circuito, alimentando el primario (bobinado de alta tensión) a 218,4 V, absorbiendo de la red una potencia de 1284 W y una intensidad de 9,483 A. Se pide: a) Valores de los parámetros del circuito equivalente: R1Fe y X1µ (valores reducidos al primario). b) Cuando el transformador se alimenta por el lado de alta tensión a 9200 V, determinar la tensión que llegará a una carga conectada al lado de baja tensión, la cual absorbe 100 kVA y presenta un factor de potencia 0,85 (i). c) Valor de la impedancia Z c de la carga d) Corriente absorbida por la carga e) Rendimiento del transformador Resolución: a) V1n = 9120 V V2n = 570 V I1n = 9,483 A I2n = rt.I1n = 151,73 A Po = U o ⋅ I o ⋅ cos ϕo Resultando: Po = U o2 RFe1 X 1µ = cos ϕo = → ϕo = 85,97 º → rt = → R1Fe = 9120 = 16 570 Po 624,4 = = 0,07 U o ⋅ I o 9120 ⋅ 0,975 tgϕo = 14,2 U o 2 9120 2 = = 133207 Ω 624,4 Po Uo2 Uo2 9120 2 = = = 9377 Ω Qo Po ⋅ tgϕ o 624,4 ⋅ 14,2 b) De la prueba de cortocircuito resulta: Z1CC = U 1CC 218,4 = = 23,03 Ω I1 9,483 cos ϕCC = 1284 PCC = = 0,62 U CC ⋅ I1 2184 ⋅ 9,483 → sin ϕCC = 0,7846 Z 1CC = Z 1CC ⋅ cos ϕ CC + Z 1CC ⋅ sin ϕ CC = 14,28 + j18,07 Ω Cuando está en carga resulta: S C = V ' 2 ⋅I ' 2 → I '2 = S C 10 5 = V '2 V '2 © Los autores, 2006; © Edicions UPC, 2006 110 Problemas de electrotecnia → V1 = V ' 2 + I ' 2 .Z1cc 9200∠ϕ º = V ' 2 ∠0º + 10 5 ∠ − 31,79º.23,03∠51,69º V '2 9200 .V ' 2 ∠ϕ º = V ' 2 ∠0º +23,03.10 5 ∠19,90 º 2 Resultando: ⎧⎪9200.V ' 2 . cos ϕ = V ' 22 +2165483,56 ⎨ ⎪⎩ 9200.V ' 2 . sin ϕ = 783894,10 8464.104.V ' 22 = V ' 42 +4330967,12.V ' 22 +4,6893.1012 + 6,1499.1011 Resultando: V’2 = 8957,84 V y V’2 = 257,07 V V’2 = 8957,84 V y La segunda solución no puede ser válida, por lo que resulta: V’2 = 8957,84 V → V2 = V '2 / rt = 559,87 V También se puede solucionar aplicando el método aproximado de Kapp: C = I2’/I2n’ = 11,16/9,483 = 1,177 ε Rcc = I1n .R1cc V1n = 9,483.14,28 = 0,01485 9120 ε Xcc = I1n . X1cc V1n = 9,483.18,07 = 0,01879 9120 V1 V2 − = C ⋅ (ε Rcc . cos ϕ + ε Xcc . sin ϕ ) V1n V2n 9200 V2 − = 1,177 ⋅ (0,01485.0,85 + 0,01879.0,527) 9120 570 → V2 = 559,88 V c) I2 = S C 100000 = = 178,61 A V2 559,865 ZC = V2 559,865 = = 3,134 Ω 178,61 I2 Z C = 3,134∠ arccos 0,85 = 3,134∠31,788º Ω d) I 2 = 178,61 A e) Como I1 = I2’ = 11,16 A, resulta: η= η= P2 S 2 . cos ϕ = P2 + PFe + PCu S 2 . cos ϕ + Po ⋅ (V1 / V1n ) 2 + C 2 .Pcc 10 5 ⋅ 0,85 2 ⎛ 9200 ⎞ 2 10 ⋅ 0,85 + 624 ⋅ ⎜ ⎟ + 1,177 .1284 ⋅ ⎝ 9120 ⎠ 5 = 0,9724 η = 97,24 % © Los autores, 2006; © Edicions UPC, 2006 I2’ = 11,16 A 111 Transformadores monofásicos 2.14 Problema 14 Se dispone de un transformador monofásico con las características nominales siguientes: 250 kVA, 15000 V/250 V, 50 Hz, PO = 4 kW, PCC = 5 kW, R1Fe = 56520 Ω, X1 = 11482 Ω, R1cc = 18 Ω, X1cc = 31,18 Ω. Tener en cuenta el circuito equivalente simplificado de la figura siguiente: X1cc R1cc RFe ZC’ Xµ Figura 2.14.1 Determinar el rendimiento en función del índice de carga cuando el secundario alimenta a tensión nominal una carga con un factor de potencia 0,8 (i). Resolución: Cálculo del rendimiento: η = 100 ⋅ η = 100 ⋅ η = 100 ⋅ Psalida V2n .I 2 . cos ϕ 2 = 100 ⋅ Pabsorbida V2n .I 2 . cos ϕ 2 + PFe + PCu C.V2n .I 2n . cos ϕ 2 C.S n . cos ϕ 2 = 100 ⋅ 2 C.V2 n .I 2n . cos ϕ 2 + PO + C .PCC C.S n . cos ϕ 2 + PO + C 2 .PCC C.250.0,8 → 2 η= C.250.0,8 + 4 + C .5 20000 200 + 4 / C + 5.C El valor máximo del rendimiento se producirá cuando se cumpla: d (4 / C + 5.C ) = 0 dC -4/C2 + 5 = 0 → → El rendimiento en función del índice de carga C, resulta: Cmáximo = η= 4 / 5 = 0,894 20000 200 + 4 / C + 5.C 100 90 95.719 80 95.718 Rendimiento Rendimiento 70 60 50 40 30 95.717 95.716 95.715 20 95.714 10 0 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 95.713 0.84 0.85 0.86 0.87 0.88 0.89 0.90 0.91 Índice de carga (C) Índice de carga (C) Figura 2.14.2 © Los autores, 2006; © Edicions UPC, 2006 0.92 0.93 0.94 0.95 112 Problemas de electrotecnia 2.15 Problema 15 Un alto horno eléctrico para a la producción de hierro absorbe 175 kW y 300 kVAr de un transformador monofásico a través de una línea monofásica de impedancia total 0,52 + j1,04 Ω. Esta se halla conectada a la red a través del transformador con les características siguientes: 500 kVA, 50000 V/3000 V, εcc = 10%, Pcc = 25 kW (se puede despreciar la rama en paralelo del circuito equivalente del transformador). El transformador está alimentado por el generador monofásico a través de una línea monofásica de impedancia total 1,04 + j2,08 Ω. Sabiendo que la tensión en el secundario del transformador es de 2900 V se pide: a) La corriente que circula por la línea entre el transformador y el horno. b) La tensión en bornes del generador. Resolución: ZLA X1CC R1CC Z’LB Transformador Figura 2.15.1 a ) Se trabaja con el circuito equivalente del transformador reducido al primario: U '2 = 2900 ⋅ 50000 = 48333,33 V 3000 2 ⎛ 50000 ⎞ Z ' LB = (0 ,52 + j1,04 ) ⋅ ⎜ ⎟ = (144 ,44 + j 288,89 ) Ω ⎝ 3000 ⎠ S 2 = P 2 + Q2 (conjunto línea – carga) (U '2 ⋅I '2 )2 = (144,44 ⋅ I '2 +175000)2 + (288,89 ⋅ I '2 +300000)2 (48333,33 ⋅ I '2 )2 = (144,44 ⋅ I '2 +175000)2 + (288,89 ⋅ I '2 +300000)2 Ecuación bicuadrada: I '2 2 = 20190,2 I '2 = 142,09 A I '2 2 = 57,2701 I '2 = 7,57 A I1n = 50000 SN = = 10 A U1N 3000 La solución válida es: I '2 = 7,57 A ⎛ 50000 ⎞ I 2 = I ' 2 ⋅⎜ ⎟ = 126,17 A ⎝ 3000 ⎠ b ) Ensayo de cortocircuito: © Los autores, 2006; © Edicions UPC, 2006 Z’C 113 Transformadores monofásicos RCC = PCC I 1n 2 = 25000 = 250 Ω 10 2 ε CC = 10% U CC = 0,1 ⋅ 50000 = 5000 V Z 1CC = U CC 5000 = = 500 Ω I 1n 10 X 1CC = Z 21CC − R 21CC = 433 Ω Origen de fases: 48333,33∠0º V (288,89 ⋅ I ' tgϕ = (144,44 ⋅ I ' 2 2 ) ) +300000 = 1,727 2 +175000 2 ϕ = 59,93º I ' 2 = 7,57∠ − 59,93º U G = U ' 2 +(R1CC + jX 1CC ) ⋅ I ' 2 + Z LA ⋅ I ' 2 U G = 48333,33∠0º +(250 + j 433) ⋅ 7,57∠ − 59,93º + + (1,04 + j 2,08) ⋅ 7,57∠ − 59,93º = 48333,33∠0º +502,31∠60º⋅7,57∠ − 59,93º = = 48333,33∠0º +3802,49∠0,07 º = 48333,33 + 3802,487 + j 4,64 = = 52135,82 + j 4,64 = 52135,82∠0º U G = 52135 ,82∠0º V © Los autores, 2006; © Edicions UPC, 2006 114 Problemas de electrotecnia 2.16 Problema 16 Una carga monofásica consume una potencia de 400 kW y 300 kVAr. La carga está conectada a un centro de transformación a través de una línea monofásica que presenta una impedancia total de valor 0,1 + j.0,2 Ω. El centro de transformación consta de dos transformadores monofásicos conectados en paralelo de las características siguientes: -Transformador A: 50000/3000 V, 400 kVA, εcc = 8%, Pcc = 18000 W. -Transformador B: 50000/3000 V, 300 kVA. Ensayo de cortocircuito del transformador B: 2500 V, 5 A, 6250 W (datos medidos en el lado AT). Sabiendo que la tensión a la salida de los transformadores es de 2900 V, se pide: a) Tensión en bornes de la carga. b) Tensión en el primario de los transformadores. c) Corriente a la salida de cada transformador. Resolución: a ) Transformador A InA = 400000 =8 A 50000 R1 CC A = Z 1 CC A = PCC A I 2 = 1n A 18000 = 281,25 Ω 82 ε CC A ⋅ U 1n A I 1n A = 0,08 ⋅ 50000 = 500 Ω 8 X 1CC A = Z 21CC A − R 2 1CC A = 413,398 Ω Z 1 CC A = 500∠55,77º Ω Transformador B Z 1 CC B = R1 CC B = 2500 = 500 Ω 5 PCu I 2 1B = 6250 = 250 Ω 52 X 1CC B = Z 21CC B − R 21CC B = 433,01 Ω Z 1 CC B = 500∠60º Ω © Los autores, 2006; © Edicions UPC, 2006 115 Transformadores monofásicos Zl = 0,1 + j0,2 2900 V carga U2C 400000 W 300000 VAr S C = 500000∠36,87 º VA Figura 2.16.1 U 2C = U 2C ∠0º Se toma como origen de fases 2900∠∂ = U 2C ∠0º +(0,1 + j 0,2 ) ⋅ I 2∠ − 36,87º 500000 = U 2 C ⋅ I 2 Resulta: U 2C = ±2865,04 V U 2 C = ±39,02 V (sin sentido físico) U 2C = 2865,04 V I2 = 500000 = 174,58 A 2865,04 ∂ = 0,3448 º I 2 = 174,58∠ − 36,87 º A b) Circuito equivalente reducido al lado de alta tensión: Z1CCA 0,1+j0,2 · (50000/3000)2 Z1CCB Càrrega G U1 U’2 = 2900·(5000/3000) 2865,01·(5000/3000) Figura 2.16.2 Z 1CC A − B = Z 1CC A ⋅ Z 1CC B Z 1CC A + Z 1CC B = 250,17∠57,89º Ω © Los autores, 2006; © Edicions UPC, 2006 116 Problemas de electrotecnia ⎛ 50000 ⎞ U 1 = U 2 '+ I 2 '⋅Z 1CC A− B = 2900 ⋅ ⎜ ⎟∠0,3448º + ⎝ 3000 ⎠ ⎛ 3000 ⎞ + 174,58 ⋅ ⎜ ⎟∠ − 36,87 º⋅250,17∠57,88º = 50792,78∠1,39º V ⎝ 50000 ⎠ c) I 2 A ⋅ Z 2CC A = I 2 ⋅ Z 2CC A− B I 2 A ⋅ Z 1CC A ⋅ I 2A = 1 rt 2 = I 2 ⋅ Z 2CC A− B ⋅ I 2 ⋅ Z 2CC A− B Z 1CC A = 1 rt 2 174,58∠ − 36,87 º +250,17∠57,89º 500∠55,77 º I 2 A = 87,32 A I 2 A = 87,32∠ − 34,76º A I 2B = I 2 ⋅ Z 1CC A− B = 87,32∠ − 38,99º A Z 1CC B I 2 B = 87,32 A © Los autores, 2006; © Edicions UPC, 2006 117 Transformadores trifásicos 3 Transformadores trifásicos © Los autores, 2006; © Edicions UPC, 2006 118 Problemas de electrotecnia 3.1 Problema 1 Un transformador trifásico de 320 kVA, 10,8 kV/0,4 kV, εcc = 4%, Pcc = 3584 W y conexión estrellatriangulo, alimenta una carga trifásica equilibrada por su secundario que absorbe 300 A con un factor de potencia de 0,8 inductivo, siendo la tensión aplicada al primario del transformador de 11,1 kV. Se pide la tensión en bornes de la carga. Resolución: I1n = rt = Sn 3 · U 1n = 320000 3 · 10800 = 17,1066 A I2n = Sn 3 · U 2n 10800 = 27 400 Referido al primario: PCC = 3 · R1 CC λ · I 12n λ Æ R1 CC λ = 3584 PCC = = 4,082 Ω 2 3 · I1 n λ 3 · 17,10662 U 1CC = ε cc .V1n = 0,04 · 10800 = 432 V Z1ccλ U1CCλ = 432 17,1066 =I’2λ 3 Figura 3.1.1 Z1cc λ = U 1ccλ 432 / 3 = = 14,58 Ω Z1ccλ 17,1066 X 1cc λ = Z12cc λ − R12cc λ = 14,58 2 − 4,08 2 = 13,997 Ω ϕ CC = arctg X 1CC λ R1CC λ = 73,74º 4,08 + j 13,997 U 1λ = 11000 3 ∠α º 11,11 A U 2/ λ Figura 3.1.2 © Los autores, 2006; © Edicions UPC, 2006 = 320000 3 · 400 = 461,88 A 119 Transformadores trifásicos En carga, la corriente del secundario vale I2λ = 300 A: I 2/ λ = I 2λ 300 = = 11,11 A rt 27 cos ϕ C = 0,8 ϕ C = 36,87 º → 11100 U 1 λ = U ' 2 λ + I ' 2 λ ⋅Z 1CC λ 3 11100 cos α = U ' 2λ +129,58 3 11100 3 U ' 2λ = 6278,28 V α = 0,87º sin α = 97,19 → U 2/ λ = 6278,28 V U2 = ∠α º = U ' 2 ∠0º +11,11∠ − 36,87 º⋅14,58∠73,74º U 2/ = 3 · 6278,28 = 10874,30 V 10874,30 = 402,75 V 27 Aplicando el método aproximado de Kapp, resulta: PCC = ε Rcc · Sn → ε Rcc = PCC 3584 = = 0,0112 Sn 320000 2 ε Xcc = ε cc2 − ε Rcc = 0,04 2 − 0,0112 2 = 0,0384 FP = cos ϕ = 0,8 C= → sin ϕ = 0,6 I2 300 = = 0,6495 I 2n 461,88 U1 U = 2 + C · [ε Rcc · cos ϕ c + ε Xcc · sin ϕ c ] U1n U 2 n 11100 U 2 = + 0,6495 · [0,0112 · 0,8 + 0,0384 · 0,6] 10800 400 → U 2 = 402,79 V © Los autores, 2006; © Edicions UPC, 2006 120 Problemas de electrotecnia 3.2 Problema 2 El transformador de la figura alimenta una carga según el circuito indicado: R2 A=C' R1 W1 a V1 B=A' S1 a’= b’= c’ W2 c T1 V2 S2 Carga equilibrada b T2 C=B' Figura 3.2.1 Las características del transformador son: 24000 V/380 V, Sn = 125 kVA, εcc = 4%, Po = 480 W, Pcc = 2530 W. Las lecturas de los vatímetros W1 y W2 son, respectivamente, 60186,56 W y 23813,44 W, mientras que el voltímetro V2 indica 368,6 V. Se sabe que el bobinado del secundario presenta una resistencia por fase de 0,01 Ω. Se pide: a) La resistencia por fase del bobinado del primario b) La lectura del voltímetro V1. c) El rendimiento del transformador. d) El índice horario del transformador Resolución: a) I2n = 125000 3 · 380 = 189,9178 A Esquema equivalente reducido al secundario, PCC = 3 · R 2 cc λ · I 22n λ Z 2 cc λ = U 2 cc λ I 2n λ Æ R2 ccλ = PCC 2530 = = 0,02338 Ω 2 3 · I 2 n λ 3 · 189,91782 4 380 · 100 3 = = 0,0462 Ω 189,9178 X 2 ccλ = Z 22ccλ − R22ccλ = 0,04622 − 0,023382 = 0,03985 Ω tg ϕ cc = 0,03985 0,02338 Æ ϕ cc = 59,6º Z 2 ccλ = (0,02338 + j 0,03985) Ω © Los autores, 2006; © Edicions UPC, 2006 121 Transformadores trifásicos R1λ rt2 0,02338 = R2 λ + Æ rt = R1 λ 0,02338 = 0,01 + 24000 = 63,16 380 Æ R1 λ = 53,37 63,16 2 Æ R1 ∆ = 3 ⋅ R1 λ = 160,11Ω b) W1 = 60186,56 W ⎫ ⎬ W2 = 23813,44 W ⎭ Æ tg ϕ T = 0,75 I 2λ = PT = W1 + W2 = 84000 QT = 3 · (W1 − W2 ) = 63000 84000 3 · 368,6 · 0,8 ϕ T = 36,87º = 164,465 A Æ cos ϕ T = 0,8 Æ I 2 λ = 164,465 ∠ − 36,87º A U 2λ = 368,6 ∠ 0º V 3 I 2λ = 164,465 ∠ − 36,87 º A U 1/λ = U 2λ + I 2λ ⋅ Z 2CCλ U 1/λ = 368,6 3 ∠ 0º + (0,02338 + j 0,03985) · 164,465 ∠ − 36,87 º U 1/λ = 219,839 ∠ 0,72 V U 1 = U '1 .rt = 219,839 · 3 · U 1/ = 219,839 · 3 V Æ 24000 = 24048,8 V 380 Æ U 1 = 24048,8 V c) η= P2 P2 = P2 + PFe + PCu P2 + Po ⋅ ( U1 / U1n )2 + PCu C= I 2 164,46 = = 0,866 I 2 n 189,91 η= 84000 2 ⎛ 24048,8 ⎞ 2 84000 + 480 · ⎜ ⎟ + 2530 · C ⎝ 24000 ⎠ = 84000 = 0,972 86379,34 η = 97,2 % © Los autores, 2006; © Edicions UPC, 2006 122 Problemas de electrotecnia d) Para determinar el índice horario, se deben hacer los diagramas siguientes: S1 R1 A B T1 C A=C’ A’ a R2 a’ B’ b b’ a C’ S2 c N T2 C=B’ c c’ Resulta un índice horario 11, siendo por lo tanto un transformador tipo Dy11 © Los autores, 2006; © Edicions UPC, 2006 b B=A’ 123 Transformadores trifásicos 3.3 Problema 3 Se dispone de un transformador trifásico Dy de características nominales 11 kV/380 V, 50 kVA. Se efectúa el ensayo de cortocircuito del transformador, alimentándolo por el lado de baja tensión a 15 V y absorbiendo 60 A y 1500 W. Por el lado de alta se encuentra conectado a la red, mientras que por el lado de baja tiene conectadas las cargas siguientes: Un motor trifásico de 9 kW, de 380 V entre fases con un rendimiento del 90% y un factor de potencia de 0,85. Un motor trifásico que absorbe 25 kW, de 380 V entre fases con un factor de potencia de 0,9. Una instalación de alumbrado formada por 90 lámparas de incandescencia de factor de potencia unidad, de 100 W a 220 V, repartidas equilibradamente entre les tres fases. Se pide: a ) Si en el lado de baja hay una tensión de 380 V, ¿cuál es la tensión de la red? b ) Calcular la potencia activa y la reactiva absorbida por el transformador de la red. c ) Determinar las pérdidas por efecto Joule en el transformador. NOTA: Menospreciar la rama en paralelo del circuito equivalente. Resolución: a) rt = U 1n = 28,9474 U 2n Ensayo de c.c. Z 2 cc λ = V 2 cc λ 15 / 3 = = 0,1443 Ω I2 60 Pcc = 3 · R 2 cc λ · I 22cc λ Æ (valor reducido al secundario) R 2 cc λ = X 2 cc λ = Z 22cc λ − R 22cc λ = 0,0395 Ω Pcc 3 · I 22cc λ Æ = 1500 3 · 60 2 = 0 ,1388 Ω Z 2 ccλ = 0 ,1443 ∠ 15,793º Ω Consumos Consumo 1 I1 = 9000 3 · 380 · 0,85 · 0,9 = 17,875 A Æ cos ϕ1 = 0,85 I 1 = 17,875 ∠ − 31,788º A © Los autores, 2006; © Edicions UPC, 2006 Æ ϕ1 = 31,778º 124 Problemas de electrotecnia Consumo 2 I2 = 25000 3 · 380 · 0,9 = 42,203 A Æ cos ϕ 2 = 0,9 Æ ϕ 2 = 31,778º cos ϕ 3 = 0,9 Æ ϕ 3 = 31,778º I 2 = 42,203 ∠ − 25,842º A Consumo 3 I3 = 90 · 100 3 · 380 · 1 = 13,674 A Æ I 3 = 13,674 ∠ 0º A I = I 1 + I 2 + I 3 = 72,406∠ − 22,58º A Z 2 ccλ = 0,1443 ∠ 15,793º Ω U '1λ I 2λ Zc 380 3 ∠ 0º = U 2 λ Figura 3.3.1 / U 1 λ = U 2λ + I 2λ ⋅ Z 2CCλ / U1 λ = 380 3 ∠ 0º + 0,1443 ∠ 15,793º · 72,406 ∠ − 22,58º = 229,771 ∠ − 0,308º V U '1λ = U 1λ · rt = 229,771 · 11000 = 6651,27 V 380 Æ U 1 = 3 ⋅ U 1 λ = 11520,33 V b) I1 = I 2 72,406∠ − 22,58º = = 2,5∠ − 22,58º A 11000 rt 380 S 1 = 3 ⋅ U 1 ⋅ I *1 = 3 ⋅ 11520,33∠ − 0,308º⋅2,5∠22,588º = 46184,20 + j 18922,69 VA P1 = 46184,20 W Q1 = 18922,69 VAr c) Pcu = 3 · I 2 2λ · R 2 cc λ = 3 · 72,406 2 · 0,1388 = 2184,43 W Æ © Los autores, 2006; © Edicions UPC, 2006 Pcu = 2184,43 W 125 Transformadores trifásicos 3.4 Problema 4 Un generador trifásico de 13,2 kV entre fases alimenta, a través de un transformador trifásico ideal, una carga trifásica conectada en estrella que absorbe una potencia de 1 MVA. Determinar las tensiones y las intensidades de corriente de línea y de fase en el transformador si está conectado: a) Estrella / estrella b) Estrella / triángulo c) Triángulo / estrella d) Triángulo / triángulo Suponer en todos los casos una tensión a la salida del transformador de 2,3 kV. Resolución: a) La conexión estrella / estrella corresponde al esquema siguiente: I1 I2 U2 U1 2300V 13200V Figura 3.4.1 en el cual se conocen las tensiones de línea del primario y del secundario. Las tensiones de fase o tensiones simples son respectivamente: U 1λ = 13200 = 7621 V 3 U 2λ = 2300 = 1328 V 3 La relación de transformación nominal puede hallarse indistintamente a partir del cociente entre las tensiones compuestas de ambos devanados o del cociente de las tensiones simples (la recomendación CEI 76, Transformadores de potencia, 4.4.5 que estipula que rt será la relación entre la tensión más elevada y la menor). En este último caso resulta: al ser ideal se cumple: rt = U 1n U 2n = U1 U2 rt = 13200 2300 = 5,7391 La intensidad de corriente en el secundario se puede determinar a partir de la potencia absorbida por la carga: S C = 3 ⋅U 2 A ⋅ I 2 A © Los autores, 2006; © Edicions UPC, 2006 126 Problemas de electrotecnia Despejando I 2 , se obtiene la intensidad de la corriente de línea, que coincide, al estar el secundario del transformador conectado en estrella, con la intensidad de corriente de fase secundaria del transformador: SC I 2l = = 3 .U 2 n 10 6 3 .2300 = 251 A Por tratarse de un transformador ideal, es decir, sin pérdidas, se verifica para cualquier carga: U1 I 2 = = rt U 2 I1 Por tanto: I 2A 251 = = 43,74 A 5,7391 rt I 1A = La intensidad de la corriente de línea primaria I1 coincide, al estar el primario del transformador conectado en estrella, con la intensidad de corriente de fase primaria del transformador. También se puede determinar la corriente absorbida por el primario del transformador para alimentar a la carga conectada en su secundario como: SC I 1A = 3 ⋅ U 1A = 1000000 = 43,74 A 3 ⋅13200 Como era de esperar, el resultado obtenido coincide con el anteriormente hallado. b) La conexión estrella / triángulo corresponde al siguiente esquema: I1 U1 I’2 13200V U2 I2 2300V Figura 3.4.2 Como las tensiones terminales son las mismas, se tiene: rt = 5,7391 La intensidad de corriente de línea en el lado del secundario del transformador vale: I 2A = SC 3 ⋅U 2n = 1000000 3 ⋅ 2300 = 251 A Y la intensidad de corriente secundaria por fase: I2 = I 2A 3 = 251 = 145 A 3 © Los autores, 2006; © Edicions UPC, 2006 127 Transformadores trifásicos Al estar el primario en estrella, se cumple: I I 1A = 2A rt = 251 5,7391 = 43,74 A = I 1 fase c) La conexión triángulo /estrella corresponde al siguiente esquema: U2 I’1 I2 2300V I1 13200V Figura 3.4.3 La relación de transformación sigue siendo la misma: rt = 5,7391 La intensidad de corriente de línea en el lado del secundario del transformador vale: I 2A = 1000000 = 251 A = I 2 fase por estar el secundario en estrella 3 ⋅ 2300 Teniendo en cuenta la relación entre las tensiones y corrientes de fase, se puede determinar la intensidad de corriente en el devanado primario: I1A = I 2A rt = 251 = 43,74 A 5,7391 Al estar el primario en triángulo resulta: I1 fase = I1A 3 = 25,25 A d ) La conexión triángulo / triángulo corresponde al siguiente esquema: I’2 I1 I2 U1=13200V U2=2300V Figura 3.4.4 rt = U1n 13200 = = 5,7391 U 2n 2300 © Los autores, 2006; © Edicions UPC, 2006 128 Problemas de electrotecnia La intensidad de corriente de línea en el lado del secundario del transformador vale: I 2A = 1000000 = 251 A 3 ⋅ 2300 Y la intensidad de corriente de fase correspondiente: I 2 fase = I 2A 251 = = 145 A 3 3 es decir, I 1A = I 2A 251 = = 43,74 A rt 5,7391 Determinada la intensidad de corriente de fase del primario, la intensidad de corriente de línea se calcula como: I1 fase = I1A 3 = 25,25 A © Los autores, 2006; © Edicions UPC, 2006 129 Transformadores trifásicos 3.5 Problema 5 Un transformador trifásico de 2 MVA, 33 kV/7,2 kV, grupo de conexión Dy5, tiene una resistencia y una reactancia por fase de 4,5 Ω y 22 Ω en el devanado primario, así como 0,6 Ω y 2,8 Ω en el devanado secundario. Este transformador alimenta una carga con una factor de potencia 0,8 inductivo que absorbe exactamente la intensidad de corriente nominal del transformador cuando la tensión de alimentación del primario es de 33 kV. Despreciando las pérdidas en el núcleo magnético del transformador, calcular: a) El circuito equivalente del transformador reducido al primario b) El circuito equivalente del transformador reducido al secundario c) La tensión en bornes de la carga, calculándola a partir del circuito equivalente del transformador reducido al primario. d) La tensión en bornes de la carga, calculándola a partir del circuito equivalente del transformador reducido al secundario. Resolución a) El grupo de conexión del transformador es Dy5, por lo que se verifica: rt = respiras U 1n N1 = = U 2n N 2 ⋅ 3 3 I1 → rt = 33000 = 4,5833 7200 UP IF1 U2 I2 US Figura 3.5.1 Se sabe que: R1∆ = 4,5 Ω X 1∆ = 22 Ω R2λ = 0 ,6 Ω X 2λ = 2 ,8 Ω La resistencia y la reactancia del secundario reducidas al primario valen respectivamente: R1CC∆ = R1∆ + R' 2∆ = R1∆ + 3 ⋅ R' 2λ = R1∆ + 3 ⋅ R2λ ⋅ rt 2 = 4,5 + 3 ⋅ 0,6 ⋅ 4,5833 2 = 42,31 Ω X1CC∆ = X1∆ + X '2∆ = X1∆ + 3 ⋅ X '2λ = X1∆ + 3 ⋅ X 2λ ⋅ rt 2 = 22 + 3 ⋅ 2,8 ⋅ 4,58332 = 198,45 Ω © Los autores, 2006; © Edicions UPC, 2006 130 Problemas de electrotecnia Z1CC∆ = R1CC∆ + jX 1CC∆ = 42,31 + j.198,45 Ω El circuito equivalente reducido al primario es: X 1CC∆ = j198,45Ω R1CC∆ = 42,31Ω I ' 2∆ U 1∆ U ' 2∆ Figura 3.5.2 b ) La resistencia y la reactancia del primario reducidas al secundario valen respectivamente: R2CCλ = R'1λ + R2λ = R'1∆ + R2λ = R1∆ 3 3 ⋅ rt 2 + R2λ = 4 ,5 3 ⋅ 4 ,58332 + 0 ,6 = 0 ,671 Ω X 2CCλ = X '1λ + X 2λ = X '1∆ + X 2λ = X 1∆ + X 2λ = 22 + 2 ,8 = 3,15 Ω 3 3 ⋅ 4 ,5833 2 3 ⋅ rt 2 Z 2CCλ = R2CCλ + jX 2CCλ = 0,671 + j .3,15 Ω El circuito equivalente del transformador reducido al secundario (esquema monofásico fase-neutro) es: Ρ2CCλ = 0,671Ω X2CCλ = j 3,15Ω U’1 U2 Figura 3.5.3 © Los autores, 2006; © Edicions UPC, 2006 131 Transformadores trifásicos c) La intensidad de corriente nominal primaria del transformador es: I1n = 2000000 = 35 A 33000 ⋅ 3 y la corriente de fase correspondiente: I1∆ = I1n 3 = 35 = 20,2 A 3 que coincide con la intensidad de corriente que absorbe la carga reducida al primario, puesto que, según el enunciado, el transformador no tiene pérdidas en el núcleo magnético. Por ser el factor de potencia de la carga 0,8 (cosφC = 0,8) inductivo, la intensidad de corriente que ésta absorbe por fase está desfasada en retraso un ángulo de 36,87º respecto a la tensión simple secundaria de la misma fase. Y para lo que sigue se debe recordar que la reducción de magnitudes de un devanado al otro es una transformación conforme, es decir, que se conservan los ángulos. I1∆ = 20,2∠ − 36,87º A Y teniendo en cuenta lo anteriormente expuesto, el circuito equivalente del transformador reducido al primario (esquema monofásico fase-neutro) cuando alimenta a la carga es: j 198,45Ω 42,31Ω I ∆1 U1∆ U’2∆ Figura 3.5.4 Tomando como origen de ángulos U’2, se tiene: U1 α IF1 φC U’2 XCC IF1 RCC IF1 Figura 3.5.5 U1∆ = U'2∆ +I 1∆ ⋅ Z1CC∆ © Los autores, 2006; © Edicions UPC, 2006 132 Problemas de electrotecnia y sustituyendo valores: 33000∠α º = U ' 2 ∆ ∠0º +( 42 ,31 + j198,45 ) ⋅ 20 ,2∠ − 36 ,87º Igualando partes real e imaginaria: ⎧33000 ⋅ cos α = U ' 2 ∆ + 4098,78 ⋅ cos 41,09º ⎨ ⎩ 33000 ⋅ senα = 4098,78 ⋅ sen 41,09º De donde se obtienen α = 4,68º U '2∆ = 29800,81 V y que, reducida al secundario, resulta: U 2∆ = U ' 2 ∆ 29800,81 = = 6502 V rt 4,5833 d) La intensidad de corriente nominal secundaria del transformador es: I 2n = Sn 3 ⋅ U 2n = 2000000 3 ⋅ 7200 = 160,37 A que coincide, según el enunciado, con la intensidad de corriente que absorbe la carga. A un factor de potencia inductivo 0,8 (cos φC = 0,8) le corresponde, tal como hemos visto anteriormente, un desfase en retraso de la intensidad de corriente secundaria respecto de la tensión de 36,87º. Por tanto: I 2λ = 160 ,37∠ − 36 ,87º A El circuito equivalente del transformador reducido al secundario (esquema monofásico fase-neutro) cuando alimenta a la carga es: 0,671Ω j 3,15Ω U2λ U’1λ Figura 3.5.6 Y el diagrama vectorial es: U’1 α I2n φC U2 XCC I2n RCC I2n Figura 3.5.7 © Los autores, 2006; © Edicions UPC, 2006 133 Transformadores trifásicos U '1 λ = U 2 λ + ( R2CC λ + jX 2CC λ ) ⋅ I 2 λ En el cual: U '1λ = U1λ 33000 = = 4156 ,95 V rt 7 ,9385 Resulta, por tanto: 4156 ,95∠α º = U 2λ ∠0º +( 0 ,671 + j 3,15 ) ⋅ 160 ,37 ∠ − 36 ,87º igualando partes real e imaginaria: ⎧4156 ,95 ⋅ cos α = U 2 λ + 516 ,39 ⋅ cos 41,09º ⎨ ⎩ 4156 ,95 ⋅ senα = 516 ,39 ⋅ sen 41,09º De donde se obtiene: α = 4,68º U 2λ = 3753,96 V → U 2 = 3 ⋅ U 2λ = 3 ⋅ 3753,96 = 6502 V © Los autores, 2006; © Edicions UPC, 2006 134 Problemas de electrotecnia 3.6 Problema 6 Se dispone de un transformador trifásico Yd de las características siguientes: S n = 20 MVA U1n = 128kV PCC = 30kW ε CC = 0,06 U 2 n = 24kV Se conecta al devanado de tensión inferior una carga trifásica equilibrada de 15 MW, con un factor de potencia de 0,8 inductivo y a una tensión de 23 kV. Calcular: a) Los valores de la resistencia, inductancia e impedancia de cortocircuito del transformador reducida al devanado de tensión superior b) La impedancia de la carga c) La tensión de línea existente en el devanado de tensión superior antes de producirse el cortocircuito d) Trabajando en las anteriores condiciones, en un momento determinado, se produce un cortocircuito en bornes de la carga, reduciéndose la tensión de alimentación del transformador a un 80% del valor que tenía anteriormente. Determinar las intensidades de las corrientes de línea en ambos lados del transformador en esta nueva situación. Resolución: a) Las intensidades de corriente nominales primaria y secundaria del transformador son respectivamente: I1n = I 2n = Sn 3 ⋅ U1n = Sn 3 ⋅ U 2n 20000000 3 ⋅ 128000 = 90,21A 20000000 = = 481,125 A 3 ⋅ 24000 La relación de transformación nominal: rt = U1n 128000 = = 5,333 U 2n 24000 Como se conocen las pérdidas en el ensayo de cortocircuito, se puede determinar el valor de la resistencia de cortocircuito reducida al devanado de tensión superior (en este caso, devanado primario) R1CCy: PCC = 3 ⋅ R1CCλ ⋅ I 21nλ R1CCy = PCC 3⋅ I 2 1nλ = 30000 3 ⋅ 90,212 = 1,229 Ω Y a partir de la tensión de cortocircuito, expresada en tanto por uno, se puede determinar la impedancia de cortocircuito reducida al primario, Z1CC , como: ε CC = Z1CCλ ⋅ I1nλ U1nλ © Los autores, 2006; © Edicions UPC, 2006 135 Transformadores trifásicos Z1CCλ = ε CC ⋅ U1nλ I1nλ = 0 ,06 ⋅ 128000 / 3 = 49 ,15 Ω 90 ,21 X1CCλ = Z 21CCλ − R 21CCλ = 49 ,137 Ω Z1CC λ = 1,229 + 49 ,137 j = 49 ,15∠88 ,567º Ω b) La intensidad de corriente en el secundario del transformador para la carga se obtiene de: PC = 3 ⋅ U 2 ⋅ I 2A ⋅ cos ϕ C PC I 2A = 3 ⋅ U 2 ⋅ cos ϕ C = 15.10 6 = 470 ,665 A = I 2 λ 3 ⋅ 23000 ⋅ 0 ,8 De donde la impedancia de carga por fase tiene un valor de: Z Cλ = U 2λ 23000 / 3 = = 28,21 Ω I 2λ 470 ,665 Y como se conoce el factor de potencia de la carga (cos φC = 0,8) y el tipo de carga (inductiva), se puede hallar en ángulo φC: ϕ C = 36,87º Por tanto: Z Cλ = 28,21∠36 ,87º Ω y reducida al primario vale: Z'Cλ = Z'Cλ ⋅ rt 2 = 28,21∠36 ,87º ⋅5,3332 = 802 ,42∠36 ,87º Ω c) El circuito equivalente del transformador reducido al primario (esquema monofásico fase-neutro) es: Z1CCλ U1λ ~ U’2λ Z’C I’2λ Figura 3.6.1 Tomando como origen de ángulos la tensión simple U 2λ reducida al primario, U ' 2λ : U ' 2λ = rt ⋅ U 2λ © Los autores, 2006; © Edicions UPC, 2006 136 Problemas de electrotecnia U ' 2λ = 5,333 ⋅ 23000 3 ∠0º = 70817 ,2∠0º V La intensidad de corriente de la carga en forma fasorial, tomando el anterior origen de ángulos, es: I 2λ = 470 ,665∠ − 36 ,87º A Y reducida al primario: I ' 2λ = I 2λ I ' 2λ = 470,665∠ − 36,87º = 88,255∠ − 36,87º A 5,333 rt A partir de los valores anteriormente calculados se puede calcular la tensión simple de alimentación del primario: U 1λ = U ' 2λ + I' 2 y λ ⋅ Z 1CCλ U1λ = 78817 ,2∠0º +88 ,255 ∠ − 36 ,87º ⋅49 ,15∠88 ,567º = 73584 ,720 ∠ 2 ,651º V Y la tensión de línea es: U1 = 3 ⋅ U1λ = 3 ⋅ 73584 ,72 = 127452 ,47 V U1 = 127452,47 V d) El circuito equivalente del transformador reducido al primario (esquema monofásico fase-neutro), cuando se produce un cortocircuito tripolar en el secundario y está alimentado a un 80% de la tensión del apartado anterior, es: Z1CCλ ~ 0,8 U1λ I1λ Figura 3.6.2 La corriente primaria del transformador en este caso vale: I1 = I1λ = 0,8 ⋅ U1λ 0 ,8 ⋅ 73584,720 = = 1197 ,668 A Z1CCλ 49,15 Y la corriente secundaria del transformador en este caso vale: I 2 = I 1 ⋅ rt I 2 = 1197,668 ⋅ 5,333 = 6387,163 A © Los autores, 2006; © Edicions UPC, 2006 137 Transformadores trifásicos 3.7 Problema 7 De un transformador trifásico de 124,7 kVA, relación de transformación 8250 V/500 V, grupo de conexión Dy5, se han realizado los siguientes ensayos: 1. Ensayo de vacío: Alimentando el transformador por el devanado de baja tensión a 400 V, la potencia absorbida es de 1300 W. 2. Ensayo de cortocircuito: Alimentando el transformador por el devanado de alta tensión a 314 V, circula la corriente nominal y la potencia absorbida es de 3000 W. Calcular: a) El rendimiento del transformador a plena carga cuando alimenta una carga inductiva de factor de potencia 0,9 a la tensión nominal conectada en el devanado de alta tensión. b) El rendimiento del transformador cuando trabaja a media carga, tensión nominal y el factor de potencia es la unidad. c) El rendimiento máximo del transformador y carga para la que se produce, cuando el factor de potencia es la unidad a la tensión nominal. d) Caídas de tensión relativa en la resistencia, reactancia e impedancia de cortocircuito a plena carga. e) Tensión necesaria en el primario para poder alimentar la carga del apartado a) cuando la tensión del secundario es de 8250 V. Resolución: a) El rendimiento del transformador se obtiene como: η= P2 P2 + PCu + PFe Siendo: P2 = Potencia activa suministrada a la carga PFe = Potencia activa que se disipa en el núcleo magnético del transformador (pérdidas en el hierro) PCu = Potencia activa que se disipa por efecto Joule en los devanados del transformador (pérdidas en el cobre) Cuando se efectuó el ensayo del transformador en vacío, la tensión de alimentación no era la nominal, por lo que la potencia absorbida, P’o, no corresponde a la potencia que absorbe el transformador en vacío a tensión nominal, valor designado normalmente por Po. La relación entre ambas potencias viene dada por: ⎛U Po = P' o ⋅⎜⎜ 1n ⎝ U1 2 2 ⎞ ⎛ 500 ⎞ ⎟⎟ = 1300 ⋅ ⎜ ⎟ = 2031 W ⎝ 400 ⎠ ⎠ Por tanto, las pérdidas en el hierro en este caso valen: PFe = Po = 2031 W Al trabajar el transformador a plena carga, la corriente por él suministrada es la nominal, por lo que las pérdidas en el cobre coinciden con las medidas en el ensayo de cortocircuito, es decir: © Los autores, 2006; © Edicions UPC, 2006 138 Problemas de electrotecnia PCu = 3000 W La potencia suministrada a la carga en estas condiciones es: P2 = 3 ⋅ U 2 n ⋅ I 2 n ⋅ cos ϕ C = S n ⋅ cos ϕ C Por lo que el rendimiento es: η= 124700 ⋅ 0,9 = 0,9571 124700 ⋅ 0,9 + 2031 + 3000 η = 95,71 % b) En este caso, se ha de tener presente que la potencia suministrada es la mitad de la nominal y que, por lo tanto, las pérdidas en el cobre son diferentes de las del ensayo de cortocircuito: PCu = C 2 ⋅ PCC = 0 ,5 2 ⋅ 3000 = 750 W P2 = 3 ⋅ U 2n ⋅ I 2 ⋅ cos ϕ C = 3 ⋅ U 2n ⋅ C ⋅ I 2n ⋅ cos ϕ C = S n ⋅ C ⋅ cos ϕ C η= 124700 ⋅ 0 ,5 ⋅1 124700 ⋅ 0 ,5 ⋅1 + 2031 + 3000 ⋅ 0,5 2 = 0,9573 η = 95,73 % c) El rendimiento máximo, par un factor de potencia dado, se consigue cuando se verifica: PFe = PCu PFe = C 2 ⋅ PCC Cη máx = PFe = PCC 2031 = 0 ,8228 3000 Por tanto, el rendimiento máximo vale: η máx = 124700 ⋅ 0,8228 124700 ⋅ 0,8228 + 3000 + 2 ⋅ 0,8228 2 = 0,9619 η = 96,19 % d) Previamente se calcularán los valores de las resistencias y reactancias de cortocircuito del transformador, suponiendo: 1: BT en Y 2: AT en ∆ La relación de transformación es: I1n = rt = 124700 Sn = = 144 A 3 ⋅ U1n 3 ⋅ 500 500 = 0,06 8250 I 2n = Sn 124700 = = 8,734 A 3 ⋅ U 2n 3 ⋅ 8250 El valor de la tensión de cortocircuito reducida al devanado de baja tensión vale: U 1CC = U 2CC ⋅ rt = 314 ⋅ 500 = 19,03 V 8250 y, teniendo presente que la conexión es en estrella, la tensión por fase correspondiente es: U1CCλ = 19,03 / 3 = 10,987 V Por lo tanto: © Los autores, 2006; © Edicions UPC, 2006 139 Transformadores trifásicos PCC = 3 ⋅ R1CCλ ⋅ I 21n → R1CCλ = PCC 3⋅ I 2 = 1n 3000 3 ⋅144 2 = 0,0482 Ω Y la impedancia de cortocircuito vale: 10 ,987 U Z1CCλ = 1CCλ = = 0 ,0762Ω I1n 144 X1CCλ = Z 21CCλ − R 21CCλ = 0 ,059 Ω De donde: Cálculo de las caídas de tensión relativa en la resistencia, reactancia e impedancia de cortocircuito a plena carga: ε RCC = R1CCλ ⋅ I1nλ 0 ,0482 ⋅ 144 = = 0 ,024 500 U1nλ 3 ε XCC = X1CCλ ⋅ I1nλ 0,059 ⋅ 144 = = 0 ,0295 500 U1nλ 3 ε CC = Z1CCλ ⋅ I1nλ 0 ,0762 ⋅ 144 = = 0 ,038 500 U1nλ 3 También se puede calcular ε CC como: ε CC = ε 2 RCC + ε 2 XCC e) A continuación calcularemos, utilizando el método aproximado Kapp, la tensión que hay que aplicar al devanado de baja tensión para poder alimentar una carga de las características especificadas en el enunciado a 8250 V. U1λ = U '2λ + R1CCλ ⋅ I1nκ ⋅ cos ϕC + X1CCλ ⋅ I1nλ ⋅ senϕC U 1λ = 8250 ⎛ 500 ⎞ ⋅⎜ ⎟ + 0,0482 ⋅144 ⋅ 0 ,9 + 0 ,059 ⋅144 ⋅ 0 ,436 = 299,63 V 3 ⎝ 8250 ⎠ La tensión que hay que aplicar es: U1 = 3 ⋅ U1λ = 3 ⋅ 298,63 = 517,23 V © Los autores, 2006; © Edicions UPC, 2006 140 Problemas de electrotecnia 3.8 Problema 8 Se conecta una carga de 150 kVA, con un factor de potencia de 0,96 inductiva, en el devanado de tensión inferior de un transformador trifásico. La tensión de alimentación de la carga es de 1000 3 V . En estas condiciones, la potencia absorbida por el transformador es de 157,5 kW, con un factor de potencia de 0,934 inductivo. Las características del transformador son: - Grupo de conexión Yy - Tensión nominal del devanado de tensión más elevada: 1900 3V - Tensión nominal del devanado de tensión inferior: 1100 3 V - Potencia nominal: 375 kVA - Potencia reactiva absorbida por el transformador en el ensayo estándar de vacío: 15 kVAr - Pérdidas del transformador en el ensayo estándar de vacío: 11250 W. Calcular: a) Los valores de la resistencia y reactancia de cortocircuito referidas al devanado de tensión superior (primario) b) La tensión que se ha de aplicar al primario del transformador para poder alimentar la carga en las condiciones indicadas c) La tensión de cortocircuito en valor relativo, ε CC d) La intensidad de la corriente de vacío del transformador Io aplicando en el primario la tensión del apartado b) Resolución: a) Las intensidades de corrientes nominales en ambos devanados del transformador valen respectivamente: I 1n = I 2n = Sn 3 ⋅ U 1n Sn 3 ⋅U 2n = = 375 ⋅10 3 3 ⋅1900 3 375 ⋅10 3 3 ⋅1100 3 = 65,79 A = 113,36 A Como se conocen las potencias activa y reactiva del transformador cuando trabaja en vacío, se puede determinar el factor de potencia en vacío: tgϕ o = Qo 15000 = = 1,33 Po 11250 → ϕ o = 53,13º → cos ϕ o = 0,6 Las pérdidas de potencia en vacío, activa y reactiva, cuando el transformador no trabaja a la tensión nominal, son: © Los autores, 2006; © Edicions UPC, 2006 141 Transformadores trifásicos 2 ⎛ U1 f P' o = Po ⎜ ⎜ U 1nf ⎝ 2 ⎞ ⎟ = 11250⎛⎜ 1000 ⎞⎟ = 9297 ,52 W ⎟ ⎝ 1100 ⎠ ⎠ ⎛ U1 f Q' o = Qo ⎜ ⎜ U 1nf ⎝ 2 ⎞ ⎟ = 15000⎛⎜ 1000 ⎞⎟ = 12396 ,7 VAr ⎟ ⎝ 1100 ⎠ ⎠ 2 Siendo U1f la tensión de alimentación de la carga por fase, y U1nf la tensión nominal por fase. A continuación, como ya se conocen la potencia absorbida por el transformador y las potencias cedidas a la carga y al núcleo ferromagnético del transformador, se pueden determinar las pérdidas en el cobre. Potencias cedidas a la carga: ( cosϕ C = 0,96 ϕ C = 16,26º senϕ C = 0,28 ) P2 = S C ⋅ cosϕ C = 150 ⋅ 0 ,96 = 144 kW Q 2 = S C ⋅ senϕ C = 150 ⋅ 0 ,28 = 42 kVAr La intensidad de corriente que circula por el secundario del transformador es: I2 = SC 3 ⋅U 2 150 ⋅10 3 = 3 ⋅1000 3 = 50A y que, reducida al primario del transformador, es: I' 2 = I2 50 = = 28,95 A rt ⎛ 1900 3 ⎞ ⎜ ⎟ ⎜ 1100 3 ⎟ ⎝ ⎠ El índice de carga es: C= I2 50 = = 0,44 I 2 n 113,96 Las pérdidas en el cobre valen: ( cosϕ 1= 0,934 ϕ 1= 20,93º tgϕ 1= 0,3825 ) PCu = P1 − P2 − P' o = 157 ,5 ⋅10 3 − 144 ⋅10 3 − 9297 ,52 = 4202 ,48 W QCu = Q1 − Q 2 − Q' o = P1tgϕ1 − Q 2 − Q' o = 60246 ,78 − 42000 − 12396 ,7 = 5850 ,08 VAr A partir de los resultados anteriores, se pueden calcular los valores de R1CCy y X1CCy referidos al primario: PCu = 3 ⋅ R1CCλ ⋅ I'2λ 2 R1CCλ = X 1CCλ = PCu 3 ⋅ I ' 2λ 2 = 2 = QCu 3 ⋅ I ' 2λ 4202,48 3 ⋅ 28,95 2 5850,08 3 ⋅ 28,95 2 = 1,67Ω = 2 ,32Ω Z 1CCλ = 1,67 + j 2 ,32 Ω © Los autores, 2006; © Edicions UPC, 2006 142 Problemas de electrotecnia b) A partir de los valores anteriores, se puede calcular la tensión que se ha de aplicar al primario del transformador, a partir del circuito equivalente fase-neutro, en el caso indicado: cos ϕ C = 0,96(i ) ϕ C = 16,26º → ⎛ 1900 ⎞ U 1λ = U ' 2λ + I' 2λ ⋅Z 1CCλ = U 2λ ⋅ rt + I' 2λ ⋅Z 1CCλ = 1000∠0º ⋅⎜ ⎟ + 28,95∠ − 16 ,26º ⋅(1,67 + j 2 ,32 ) ⎝ 1100 ⎠ Resultando: U 1λ = 1793,24∠1,63º V La tensión de línea que se ha de aplicar es: U1 = 3 ⋅ U1λ = 3105,98 V → U 1 ≅ 3106 V c) La tensión de cortocircuito en valor relativo es: ε CC = Z1CCλ ⋅ I1nλ = U1nλ ε CC = 0,0989 R1CCλ 2 + X1CCλ 2 ⋅ I1nλ → U1nλ = 1,67 2 + 2 ,322 ⋅ 65,79 1900 εCC = 9,89 % d) La pérdida de potencia en el ensayo de vacío Po es: Po = 3 ⋅ U 1 f ⋅ I 1o ⋅ cos ϕ o De aquí se puede hallar Io: I 1o = Po 9297 ,52 = = 2,88 A 3 ⋅U 1 f ⋅ cos ϕ o 3 ⋅1793,24 ⋅ 0,6 © Los autores, 2006; © Edicions UPC, 2006 143 Transformadores trifásicos 3.9 Problema 9 Desde las barras de una subestación reductora, se alimenta una carga trifásica equilibrada de 16 MW, con un factor de potencia 0,8 inductivo a una tensión de 25 kV. El transformador instalado en la subestación tiene las siguientes características nominales: S n = 25 MVA U1n = 220 kV ε CC = 0,1 (10%) PCC = 700 kW U 2 n = 25 kV La subestación se alimenta mediante una línea trifásica de 500 km de longitud, cuya impedancia unitaria por fase es Z1 = (0,14 + 0,48 j ) Ω/km según el esquema unifilar que se representa en la figura: TR L G ~ CARGA UG U1 U2 Figura 3.9.1 Despreciando la rama en paralelo del circuito equivalente del transformador, determinar: a) La tensión proporcionada por el alternador. b) La potencia aparente en forma compleja que suministra el alternador. c) El rendimiento de la transmisión. Resolución: Características del transformador: Intensidad de corriente nominal primaria del transformador: I 1n = Sn 3 ⋅U 1n = 25000 3 ⋅ 220 = 65,6 A Intensidad de corriente nominal secundaria: I 2n = Sn 3 ⋅ U 2n = 25000 3 ⋅ 25 = 577 ,35 A Relación de transformación: rt = U 1n 220 = = 8,8 U 2n 25 Componente real de la caída relativa de tensión en el transformador: ε RCC = PCC 700 = = 0,028 25000 Sn [2,8%] © Los autores, 2006; © Edicions UPC, 2006 144 Problemas de electrotecnia Componente imaginaria de la tensión de cortocircuito del transformador: [9,6%] ε XCC = ε 2 CC − ε 2 RCC = 0,12 − 0,0282 = 0,096 Por lo tanto: tgϕ CC = ε XCC 0,096 = = 3,4286 ε RCC 0,028 ϕ CC = 73,74º → senϕ CC = 0,96 → cos ϕ CC = 0,28 Por lo que: ε CC = 0,1∠73,74º = 0,028 + 0,096 j Características de la carga: SC = PC 16 = = 20 MVA cos ϕ C 0 ,8 SC = 20000∠36,87º kVA = [16000 + 12000 j ] kVA Que absorbe una intensidad de corriente del secundario del transformador que vale: I *2 = SC con 3 ⋅U 2 U 2 = U 2n = 25 kV Si tiene: I *2 = SC 3 ⋅ U 2n = 20000∠36 ,87º 3 ⋅ 25∠0º = 462∠36 ,87º A I 2 = 462∠ − 36,87º A = [369,6 − 277 j ] A Con lo cual, el índice de carga del transformador vale para esta carga conectada en el secundario: C= I2 462∠ − 36,87 º = = 0,8∠ − 36,87 º 577,35 I 2n Por lo tanto: C = 0,8∠ − 36,87º = 0,64 − 0,48 j Y la intensidad de corriente primaria del transformador, en estas condiciones, es: I 462∠ − 36 ,87º I1 = 2 = = 52,5∠ − 36 ,87º A rt 8,8 Características de la línea: Para una longitud de 500 km, la impedancia por fase de la línea vale: Z l = l ⋅ Z 1 = 500 ⋅ [0,14 + 0 ,48 j ] = [70 + 240 j ] = 250∠73,74º Ω © Los autores, 2006; © Edicions UPC, 2006 145 Transformadores trifásicos a) La caída de tensión del transformador se podrá calcular a partir de la expresión (método vectorial exacto): U 1 f = U ' 2 f + I ' 2 f ⋅Z 1CCf Z 1CCf = V1nf I 1nf ⋅ ε CC = 220 ⋅10 3 / 3 ⋅ 0 ,1∠73,74º = 193,60∠73,74º Ω 65,6 U ' 2 f = U 2 f ⋅ rt = 220 ⋅10 U 1 f = 220 ⋅10 3 3 3 3 ∠0º V I I' 2 f = 2 f rt = 52 ,5∠ − 36 ,87º A ∠0º +52 ,5∠ − 36,87º ⋅193,60∠73,74º = 135285,77∠2 ,58º V U 1 = 3 ⋅ U 1 f = 234,322 kV La tensión simple proporcionada por el alternador será: U Gf = Z l ⋅ I 1 + U 1 f U Gf = 250∠73,74º ⋅52 ,5∠ − 36 ,87º +135285,77∠2 ,58º = 146316,58∠5,48º V U G = 3 ⋅ U Gf = 253,428 kV b) La potencia aparente, en forma compleja, proporcionada por el alternador será: S G = 3 ⋅ U Gf ⋅ I *Gf = 3 ⋅ U Gf ⋅ I *1 S G = 3 ⋅146,316∠5,477º ⋅52,5∠36,87º = 23044,77∠42,347º kVA = [17,034 + j ⋅15,525] MVA c) El rendimiento de la transmisión vale: η = 100 ⋅ PC 16 = 100 ⋅ = 93,93% PG 17 ,034 © Los autores, 2006; © Edicions UPC, 2006 146 Problemas de electrotecnia 3.10 Problema 10 Un transformador trifásico, conexión estrella-triángulo, alimenta dos cargas, como se indica en el esquema de la figura adjunta. La relación de transformación del transformador es: 10 kV/4 kV. Cuando la tensión aplicada al primario es de 3108 V, la corriente de cortocircuito medida en el primario vale ICC = 2300 A y el factor de potencia en el ensayo de cortocircuito es cos φCC = 0,65 La impedancia por fase de la línea entre B y C es de (0,1+0,25j) Ω, mientras que entre C y D vale (0,35+0,45j) Ω. La frecuencia de la red es de 50 Hz. Se desprecian las pérdidas en vacío. Calcular: a) Valores de la resistencia y de la reactancia de cortocircuito b) Tensión a aplicar en el primario del transformador para que la carga 2 esté alimentada a 2900V c) Indicación del amperímetro AG d) Rendimiento del transformador e) Capacidad por fase de la batería de condensadores, conectados en estrella, en la parte de alta tensión, para que mejore el factor de potencia de la instalación hasta un valor de 0,95. A B C AG D λ /∆ Carga 1 I1 = 1000 A cos φ1 = 0,8 (i) Conexión λ Carga 2 I2 = 600 A cos φ2 = 0,6 (i) Conexión ∆ Figura 3.10.1 Resolución: a) En el ensayo de cortocircuito resulta: Z1CCλ = R1CCλ + jX 1CCλ La tensión aplicada por fase es 3108 / 3 V y, en consecuencia: Z1CCλ = U1ccλ 3108 / 3 = = 0 ,78 Ω I1CCλ 2300 Ya que: ϕ CC = arccos0 ,65 = 49,46º Z 1CCλ = 0 ,78∠49 ,46º Ω © Los autores, 2006; © Edicions UPC, 2006 147 Transformadores trifásicos R1CCλ = Z1CCλ ⋅ cos ϕCC = 0,78 ⋅ 0,65 = 0,507 Ω X1CCλ = Z1CCλ ⋅ sin ϕCC = 0,593 Ω b) Para calcular la tensión en el punto B, dibujemos previamente el circuito monofásico correspondiente: B Zl1 = (0,1+0,25j) Ω Zl2 = (0,35+0,45j) Ω C I1 CARGA 1 I2 CARGA 2 N N N D Figura 3.10.2 La tensión que se quiere obtener en bornes de la carga 2, en valor simple, es de un consumo de 600 A y un factor de potencia 0,6 inductivo. 2900 / 3 = 1674,31 V , con Determinada la tensión en el punto D, se puede calcular la tensión en el punto C. Si se toma como origen de fases: U D = 1674,31∠0º V , y teniendo en cuenta que el factor de potencia de la carga 2 es de 0,6 inductivo, ϕ 2 = 53,13º y en consecuencia, I 2 = 600∠ − 53,13º A . El diagrama vectorial es: UC I2 53,13º UD X12 I2 R12 I2 Figura 3.10.3 U Cλ = U Dλ + Z l 2 ⋅ I 2λ U Cλ = 1674,31∠0º +0,35 ⋅ 600∠ − 53,13º +0,45∠90º ⋅600∠ − 53,13º V U Cλ = 2016,31 − 6 j = 2016,32∠ − 0,17º V © Los autores, 2006; © Edicions UPC, 2006 148 Problemas de electrotecnia En el punto C, además del consumo de la carga 2, existe el correspondiente de la carga 1, que es de 1000 A, con un cos φ1 = 0,8 inductivo. Lo que significa que el ángulo formado por el vector U Cλ con el vector I1λ es φ1 = 36,87º, y con respecto al origen de ángulos elegido, es: I 1λ = 1000∠ − 0,17º −36 ,87º = 1000∠ − 37 ,04º A La corriente I que circula entre B y C es: I λ = I 1λ + I 2 λ = 1000∠ − 37 ,04º +600∠ − 53,13º A I λ = 1158,22 − 1082,37 j = 1585,24∠ − 43,06º A La tensión de fase en el punto B vale: U B λ = U C λ + Z l1 ⋅ I λ U B λ = 2016,32∠ − 0,17º +(0,1 + 0,25 j ) ⋅1585,2∠ − 43,06º V U B λ = 2402 ,35 + 175,18 j = 2408,73∠4,17º V R1CCλ X1CCλ I ' 2λ U Aλ U ' Bλ Figura 3.10.4 ( ) U Aλ = U ' Bλ + R1CCλ + j X1CCλ ⋅ I '2λ U Aλ = 6020 ,26∠4 ,17º + (0 ,507 + j 0 ,593) ⋅ 634 ,26∠ − 43,06º V U Aλ = 6495,95 + 493 j = 6514 ,63∠4,34º V La tensión que se ha de aplicar en el punto A es: U A = 6514,63 ⋅ 3 = 11283,67 V c) El amperímetro AG indica una lectura, que ya se calculó anteriormente y que vale: 1585,24 A. d) El rendimiento del transformador se puede determinar como la relación existente entre la potencia suministrada a la salida y la potencia absorbida de la red de alta tensión. Psuministrada = 3 ⋅ U Bλ ⋅ I' 2λ ⋅ cos(ϕ'UBλ −ϕ' I ' 2λ ) Psuministrada = 3 ⋅ 2408,73 ⋅ 1585,24 ⋅ cos( 4,17º +43,06º ) = 7778,8 kW © Los autores, 2006; © Edicions UPC, 2006 149 Transformadores trifásicos Pabsorbida = 3 ⋅ U Aλ ⋅ I 2λ ⋅ cos(ϕUAλ − ϕ I 2λ ) Siendo I2λ = I’2 λ /rt =1585,25/2,5 = 634,1 A Pabsorbida = 3 ⋅ 6514,63 ⋅ 634,1 ⋅ cos(4,34º +43,06º ) = 8388,4 kW η= Psu min istrada 7778,8 ⋅100 = ⋅100 = 92 ,73% Pabsorbida 8388,4 e) El circuito equivalente por fase es: A I’2λ ITλ UAλ ICλ N Figura 3.10.5 El ángulo que forman los vectores U Aλ e I' 2λ es: 4,34º +43,06º = 47,4º Lo que representa un factor de potencia de cos φ = 0,6768, que se quiere mejorar hasta cosφT = 0,95, es decir: φT = 18,195º. Si se elige como origen de ángulos, la tensión U A , el diagrama vectorial es: QC = Pabs ⋅ (tgϕ − tgϕ ') QC = 8388400 ⋅ (tg 47 ,4º −tg18,195º ) QC = 6365162,0 VAr V 2 6514 ,632 = 6365162 ,0 VAr QC = 3 ⋅ Aλ = 3 ⋅ XC XC X C = 20 Ω C= 1 1 = = 159,2 µF X C ⋅ ω 20 ⋅ 2π ⋅ 50 © Los autores, 2006; © Edicions UPC, 2006 150 Problemas de electrotecnia 3.11 Problema 11 Se quiere hacer trabajar dos transformadores trifásicos en paralelo, cuyas características se resumen en la tabla siguiente: Sn U1n U2n εCC Io PCC Po (kVA) (kV) (kV) (%) (%) (W) (W) A 250 15 0,4 4 1,7 4010 675 B 400 15 0,4 4,5 1,7 5780 990 TRANSFORMADOR Calcular: a) Características nominales del conjunto de los dos transformadores con el fin de poder obtener un funcionamiento óptimo. b) La relación en que se reparten las corrientes de una carga alimentada a la salida del conjunto de los dos transformadores conectados en paralelo. Resolución: a) La condición indispensable para un funcionamiento óptimo de los dos transformadores viene dada por la relación: C A ⋅ ε CCA = C B ⋅ ε CCB siendo C A y C B los índices de carga de los transformadores A y B, respectivamente, y ε CCA y ε CCB las tensiones en valores relativos obtenidas en el ensayo de cortocircuito. El transformador de menor tensión de cortocircuito relativa ε CCA es el que se sobrecargará: ε CCA = 0,04 < ε CCB = 0,045 Por lo tanto, si se quiere que el transformador A no se sobrecargue, el máximo índice de carga C A ha de ser igual a la unidad como máximo ( C A = 1). En consecuencia: C A ⋅ ε CCA = C B ⋅ ε CCB CB = C A ⋅ ε CCA 0,040 = 1⋅ = 0,888 0,045 ε CCB (88,8%) Por lo tanto, la potencia que puede dar el transformador B es: S *nB = C B ⋅ S nB = 0,888 ⋅ 400 = 355,55 kVA El conjunto del grupo de los dos transformadores da una potencia aparente total de: Sn = SnA + S *nB = 250 + 355,55 = 605,55 kVA © Los autores, 2006; © Edicions UPC, 2006 151 Transformadores trifásicos Como el transformador B, en estas condiciones trabaja con una potencia de 355,55 kVA, la corriente nominal también baja a un 88,8% y, en consecuencia, también baja la tensión ε CCB de cortocircuito en valor relativo. ε *CCB = 0,888 ⋅ 0,045 = 0,04 (4%) Pérdidas en vacío Puesto que la tensión de alimentación no varía U 1nA = U 1nB = 10kV y U 2 nA = U 2 nB = 400V , las pérdidas de cada transformador continúan siendo las mismas: Po = PoA + PoB = 675 + 990 = 1665 W Pérdidas en cortocircuito Las pérdidas en cortocircuito son proporcionales al cuadrado del índice de carga: PCC = C 2 A ⋅ PCCA + C 2 B ⋅ PCCB = 1 ⋅ 4010 + 0,8882 ⋅ 5780 = 8576 W Corriente de vacío del conjunto Las corrientes de vacío de los transformadores A y B son: I 1oA = i oA ⋅ I 1nA = i oA ⋅ I 1oB = ioB ⋅ I 1nB = i oB ⋅ S nA 3 ⋅ U 1nA = 0,017 ⋅ S nB = 0,017 ⋅ 3 ⋅ U 1nB 250000 3 ⋅15000 400000 3 ⋅15000 = 0,1635 A = 0,2617 A siendo la corriente total de vacío: I o1 = I1oA + I1oB = 0,1635 + 0,2617 = 0,4252 A Las corrientes nominales para los transformadores A y B, en las nuevas condiciones (C A = 1, C B = 0,8888) , son: S nA I1nA = 3 ⋅ U 1nA I *1nB = 250000 = 9,62 A 3 ⋅ 15000 = S *nB 3 ⋅ U 1nB = 355555 = 13,66 A 3 ⋅ 15000 La corriente total es: I1n = I1nA + I *1nB = 9,62 + 13,66 = 23,28 A Por lo tanto, la corriente relativa de vacío para el conjunto es: io = I 1o 0,4252 = = 0,018 I 1n 23,28 → io = 1,8 % b) Cuando el conjunto trabaja a potencia máxima, el transformador A aporta S nA= 250 kVA y el transformador B, S* nB = 355,55 kVA , siendo la aportación total de S n = 605,55 kVA . © Los autores, 2006; © Edicions UPC, 2006 152 Problemas de electrotecnia En consecuencia, la proporción de carga es: Transformador A: 250/605,55 = 0,4128 Transformador B: 355,55/605,55 = 0,5872 Por lo tanto, el transformador A aporta el 41,28 % de al corriente total de la carga y el transformador B el 58,72 %. © Los autores, 2006; © Edicions UPC, 2006 153 Transformadores trifásicos 3.12 Problema 12 Dos transformadores trifásicos conectados en paralelo alimentan a una carga inductiva de las siguientes características: cos ϕ C = 0,8 S C = 200 kVA El esquema de alimentación es el siguiente: TR 1 K1 200 kVA cos φC = 0,8 (i) TR 2 K2 Figura 3.12.1 Las características de los transformadores se resumen en la tabla siguiente: Grupo Transformado r Sn U1n U2n εCC PCC Po (kVA) (kV) (kV) (%) (W) (W) conexió n 1 250 6 0,38 4,5 2000 150 Yy0 2 100 6 0,38 4,5 800 60 Yy0 Se cierra el interruptor K1. Con el interruptor K2 abierto, se pide: a) Tensión a que debe alimentarse el transformador 1 para que en bornes de la carga se tengan 380 V b) Corriente que circula por el bobinado secundario c) Rendimiento del transformador A continuación se cierra el interruptor K2, de manera que la carga queda alimentada simultáneamente por ambos transformadores. Calcular: d) La tensión a que habrán de alimentarse los primarios de los transformadores para conseguir una tensión secundaria de 380 V e) Corrientes que circularán por cada uno de los secundarios de los transformadores f) Rendimiento del conjunto de los transformadores g) Indicar qué sucedería si, es estas últimas condiciones, el transformador 2 tuviera una εCC = 3%. © Los autores, 2006; © Edicions UPC, 2006 154 Problemas de electrotecnia Resolución: a) Si la carga está alimentada exclusivamente por el transformador 1, el índice de carga, al ser UC=U2n, vale: C= I2 = I 2n 3 ⋅ I 2 ⋅V2n 3 ⋅ I 2n ⋅V2n = S C 200 = = 0,8 S n 250 por otro lado: ε RCC = 3 ⋅ RCC ⋅ I 21n 2000 I1nλ 2 ⋅ R1CCλ 3 ⋅ I1nλ 2 ⋅ R1CCλ P = = = 0 ,008 (0,8%) = CC = 3 ⋅ I1nλ ⋅ V1nλ I1nλ ⋅ V1nλ Sn 3 ⋅ U1n ⋅ I1n 250000 ε XCC = ε 2 CC − ε 2 RCC = 0,045 2 − 0,008 2 = 0,0443 (4,43%) Para calcular la caída de tensión que se produce en el transformador, se utiliza la fórmula aproximada de Kapp: U1 U − 2 = C ⋅ [ε RCC ⋅ cos ϕ + ε XCC ⋅ sin ϕ ] U 1n U 2 n U1 380 − = 0,8 ⋅ [0,008 ⋅ 0,8 + 0,0443 ⋅ 0,6] 6000 380 U 1 = 6158,26 V b) La corriente que circula por el bobinado secundario es: I2 = SC 3 ⋅U 2 = 200000 = 303,9 A 3 ⋅ 380 c) Al ser U 1 = 6158,26 V resultará: η= S 2 ⋅ cosϕ2 S 2 ⋅ cosϕ2 + Po .(U1 / U1n ) 2 + C 2 PCC η = 100 ⋅ 200000 ⋅ 0,8 = 99,11 % 200000 ⋅ 0,8 + 150.(6158,26 / 6000) 2 + 2000 ⋅ 0,82 d) Si los dos transformadores trabajan en paralelo para poder conseguir un buen funcionamiento, se ha de cumplir que: ε CC1 ⋅ C1 = ε CC 2 ⋅ C 2 y como en este caso ε CC1 = ε CC 2 = 4,5% , se cumple que C1 = C 2 , es decir: 3 ⋅ U1n ⋅ I1 3 ⋅U1n ⋅ I 2 I1 I = 2 = = I1n I 2 n 3 ⋅ U 1n ⋅ I1n 3 ⋅U 1n ⋅ I 2 n En consecuencia: S1 S = 2 S1n S 2 n → S1 S1n 250 ⋅ 10 3 = 2,5 = = S 2 S 2 n 100 ⋅ 10 3 © Los autores, 2006; © Edicions UPC, 2006 155 Transformadores trifásicos Como S1 + S 2 = 200000 VA Resulta S1 = 142857 VA C1 = S 2 = 57143 VA S1 142857 = = 0,5714 = C 2 S1n 250000 Para el transformador 2: ε RCC 2 = PCC 2 800 = = 0,008 S n2 100000 (0,8%) ε XCC 2 = ε 2 CC 2 − ε 2 RCC 2 = 0,045 2 − 0,008 2 = 0,0444 (4,44%) Estos valores coinciden con los del transformador 1. Para el cálculo de U1 podemos aplicar la aproximación de Kapp en cualquiera de los dos transformadores: U1 U − 2 = C ⋅ [ε RCC ⋅ cos ϕ 2 + ε XCC ⋅ sin ϕ 2 ] U 1n U 2 n U1 380 − = 0,5714 ⋅ [0,008 ⋅ 0,8 + 0,0443 ⋅ 0,6] 6000 380 U 1 = 6113,07 V e) Las corrientes que recorren los secundarios de cada transformador valen, respectivamente: Transformador 1: I2 = S1 3 ⋅U n 2 = 142857 3 ⋅ 380 = 217,05 A Transformador 2: I2 = S2 3 ⋅U n 2 = 57143 3 ⋅ 380 = 86,82 A f) El rendimiento del conjunto vale: η= η= P2 S 2 ⋅ cos ϕ 2 = P2 + PFe + PCu S 2 ⋅ cos ϕ 2 + ( Po + Potrafo 2 ) + ( PCCtrafo1 + PCCtrafo 2 ) ⋅ C 2 trafo1 200000 ⋅ 0,8 200000 ⋅ 0,8 + (150 + 60) + (2000 + 800) ⋅ 0,5712 η = 99,30 % g) Si ε CC1 = 0,045 y ε CC 2 = 0,03 , resulta: 0,045 ⋅ C1 = 0,03 ⋅ C 2 → C1 = 0,6 ⋅ C 2 © Los autores, 2006; © Edicions UPC, 2006 156 Problemas de electrotecnia Para que no haya sobrecarga, C 2 = 1 (ya que es el transformador con ε CC menor) y C1 = 0,6 . Por lo que la carga máxima del conjunto será: S máx = S1 máx + S2 = C1 S1n + C 2 S 2 n = 0,6 ⋅ 250 + 1 ⋅ 100 = 266,6 kVA máx de los que 100 kVA corresponden al transformador 2 y el resto de 166,6 kVA al transformador 1. Como la carga actual conectada es de 200 kVA, la aportación del transformador 2 será: 266,6 200 = 100 S2 → S 2 = 75 kVA y la aportación del transformador 1 vale: S1 = 200 − 75 = 125 kVA Y los índices de carga son: C1 = S1 125 = = 0,5 S1n 250 C2 = S2 75 = = 0,75 S 2 n 100 Se calculan a continuación las tensiones relativas de cortocircuito para cada transformador: Transformador 1: ε CC = 4,5% ε RCC = 0,8% ε XCC = 4,43% ε CC = 0,045∠79,76º Transformador 2: ε CC = 3% ε RCC = PCC 800 = = 0,008 Sn 100000 ε XCC = ε 2 CC − ε 2 RCC = 0,0289 ε CC = 0,03∠74,53º Con lo datos anteriores se puede calcular la caída de tensión relativa para cada transformador, por el método aproximado de Kapp, a partir del transformador 1: Trafo 1: Sn I 1nλ = 3 ⋅ U 1n Z (1CCλ ) = 1 = 24 ,056 A U 1nλ ⋅ ε CC 6000 / 3 = ⋅ 0,045∠79,76º = 6,48∠79,76º = 1,152 + j 6,377 Ω I1nλ 24,056 Trafo 2: I1nλ = Sn 3 ⋅ U 2n Z (1CCλ ) = 2 Z (1CCλ )eq = = 24,056 A U 1n ⋅ ε CC 6000 / 3 = ⋅ 0,03∠74,53º = 10,80∠74,53º = 2,881 + j10,409 Ω I1nλ 9,623 Z (1CCλ )1 ⋅ Z (1CCλ )2 Z (1CCλ )1 + Z (1CCλ )2 U ' 2λ = U 2λ ⋅ rt = 380 3 ∠0 º ⋅ = 69,98∠154,29º = 4,05∠77,80º = 0,86 + j 3,96 Ω 17,264∠76,49º 6000 6000 = ∠0 º V 380 3 © Los autores, 2006; © Edicions UPC, 2006 157 Transformadores trifásicos I ' 2λ = I 2λ rt = 303,9 ∠ − 36,87º = 19,25∠ − 36,87º A 600 380 U 1λ = U ' 2λ + I ' 2λ ⋅Z (1CCλ )eq = 6000 3 ∠0º +19,25∠ − 36,87 º⋅4,07∠77,80º U 1λ = 3523,67∠0,83º V U 1 = 3 ⋅ U 1λ = 6103,18 V η= η= P2 S 2 ⋅ cos ϕ ⋅100 = ⋅100 P2 + PFe + PCu S 2 ⋅ cos ϕ + (Po1 + Po 2 ) + 3 ⋅ I ' 2λ 2 ⋅R1CCλ eq 200000 ⋅ 0,8 200000 ⋅ 0,8 + (150 + 60) + 3 ⋅19,25 2 ⋅ 0,86 ⋅100 = 99,28% © Los autores, 2006; © Edicions UPC, 2006 158 Problemas de electrotecnia 3.13 Problema 13 Un transformador trifásico Dy11 tiene Sn = 1000 kVA, 24 kV/380 V, Po = 2,15 kW, Pcc = 13,3 kW. Alimentando el lado de alta tensión a 720 V, se produce un cortocircuito en el lado de baja tensión, circulando 12 A por el lado de alta tensión. Este transformador se utiliza para alimentar por el lado de baja tensión a 344 V una carga de 850 kVA i cos φ = 0,8 (i). Se pide: a) La tensión de alimentación del transformador b) El rendimiento del transformador c) Si el transformador se alimenta a la tensión encontrada anteriormente y se produce un cortocircuito en el lado de baja tensión, determinar la corriente que circula por la línea en el lado de alta tensión. Resolución: I 1n = Sn 3V1n = 24,056 A I 2n = Sn 3 ⋅V2n = 1519,343 A rt = V1n = 63,158 V2n Del ensayo de cortocircuito no estándar resulta: Z1CCλ = V1CCλ = I1CC λ 720 3 = 34 ,64 Ω 12 Del ensayo de cortocircuito estándar: R1CCλ = PCC 3I 1n 2 = 13300 3 ⋅ 24 ,056 2 = 7 ,661Ω X 1CCλ = Z 1CCλ 2 − R1CCλ 2 = 33,78Ω → Z 1CCλ = 34,64∠77 ,22º Ω a) V1λ = I 2λ ' ⋅ Z1CCλ + V2λ ' cos ϕ = 0,8 → S = 3 ⋅ V 2λ ⋅ I 2λ V2λ = 344 3 ∠0º V ϕ = 36,87 º → I 2λ = 1426 ,59∠ − 36 ,87º A V2λ ' = rt ⋅ V2λ = 12543,69∠0º V → I 2λ = 1426 ,59∠ − 36 ,87º A → I 2λ ' = I 2λ / rt = 22,59∠ − 36,87º A V1λ = 22 ,59∠ − 36 ,87º ⋅34 ,64∠77 ,22º +12543,69∠0º = 13149 ,81∠2 ,21º V V1 = 3 ⋅ V1λ = 22776 ,14 V © Los autores, 2006; © Edicions UPC, 2006 159 Transformadores trifásicos b) η % = 100 ⋅ P2 = 100 ⋅ P2 + PFe + PCu 850 ⋅ 10 3 ⋅ 0,8 2 ⎛ 22,59 ⎞ ⎛ 22776,14 ⎞ 850 ⋅ 10 3 ⋅ 0,8 + 2150 ⋅ ⎜ ⎟ ⎟ + 13300⎜ ⎝ 24000 ⎠ ⎝ 24,05 ⎠ 2 η = 98,03 % Donde se ha aplicado: P2 = S2.cosφ2 c) En este caso, se alimenta el transformador por el lado A.T. con una tensión V1 = 22776,14 V. Al producirse un cortocircuito en el lado B.T. resulta: V1λ = I1λ.Z1ccλ I1λ = I1,línea = V1λ 22776,14 = = 657 ,5 1 A Z1ccλ 34,64 © Los autores, 2006; © Edicions UPC, 2006 161 Máquinas de corriente continua 4 Máquinas de corriente continua © Los autores, 2006; © Edicions UPC, 2006 162 Problemas de electrotecnia 4.1 Problema 1 Un telesilla está accionado por un motor serie de corriente continua, a través de un reductor. El motor serie, compensado y no saturado, está alimentado a 220 V y presenta una resistencia en el circuito inductor de 0,2 Ω. La resistencia del rotor es de 0,05 Ω. Para una determinada carga, el motor gira a 600 rpm y absorbe una potencia de 8800 W. En un momento determinado, la carga que arrastra aumenta en un 50% y se requiere que el motor continúe girando a la misma velocidad. Se pide: a) Par del motor antes de variar la carga b) Tensión a la que se tiene que alimentar el motor en las nuevas condiciones de carga Resolución: a) P =U · I Æ I= 8800 = 40 A 220 I M = 0,2 220 0,05 6000 rpm Figura 4.1.1 U = Em + RT · I Æ E m = 220 − (0,2 + 0,05) · 40 M · ω = Em · I Æ M = Resultando que el par motor vale: Æ E m = 210 V Em · I E ·I 210 · 40 = m = = 133,69 N·m 2 · π · n 2 · π · 600 ω 60 60 M = 133,69 N·m b) La carga mecánica aumenta en un 50% © Los autores, 2006; © Edicions UPC, 2006 163 Máquinas de corriente continua Em · I ⎫ ⎪⎪ n / /⎬ E ·I ⎪ M'= k m n' ⎪⎭ M =k Pero n = n/ Em · I ⎫ ⎪ M E m/ · I / ⎬ M / = 1,5 · M ⎪⎭ M Æ / = 210 · 40 1 = / 1,5 E m · I / Æ E ·I M = m 1,5 · M E m/ · I / Æ (1) E = k ⋅ w ⋅ φ = k m .I .n Em = km · I · n ⎫ / ⎬ (n = n ) Em/ = km · I / · n / ⎭ Æ Em I = / Em/ I Æ E m/ = 210 · I / = 5,25 ⋅ I ' 40 De las ecuaciones 1 y 2 resulta 1 210 · 40 Æ = 1,5 5,25 · ( I / ) 2 ( I / ) 2 = 2400 Æ I / = 48,989 A Æ E m/ = 257,196 V U ' = E m/ + RT · I / = 257,196 + (0,2 + 0,05) · 48,989 = 269,44 V U '= 269,44 V © Los autores, 2006; © Edicions UPC, 2006 (2) 164 Problemas de electrotecnia 4.2 Problema 2 La tabla siguiente muestra la característica de vacío de un generador de corriente continua con excitación independiente que gira a 4000 rpm: Ie (A) 0 1 2 3 4 5 6 Eo (V) 2 16 30,4 39,2 44,8 49,6 52 Las resistencias del inductor y del inducido son, respectivamente de 9,8 Ω y 0,02 Ω. El generador no dispone de bobinado compensador de la reacción del inducido. Se quiere alimentar una carga de 8 kW a la tensión de 40 V, necesitando una corriente en el bobinado inductor de 5 A, que lo proporcionada por una batería de V voltios (valor constante para los tres apartados). Se pide: a) El valor, en voltios, de la reacción del inducido. b) Si el generador trabajase a 3200 rpm, ¿a qué tensión quedaría alimentada la carga anterior suponiendo constante la reacción del inducido? c) Si en el apartado anterior se quiere alimentar la carga a 40 V, ¿cuánto tendría que valer la corriente del inductor y la resistencia inductora? Nota: Menospreciar la caída de tensión en las escobillas. Resolución: a) I Re = 9,8 Ω G 40 V Ri = 0,02 Ω Figura 4.2.1 I= 8000 = 200 A , 40 P= U2 RC Æ RC = (Eo − Vri ) − Ri · Ii = 40 V De la tabla del enunciado resulta: n = 4000 rpm⎫ ⎬ Ie = 5 A ⎭ Æ E o = 49,6 V © Los autores, 2006; © Edicions UPC, 2006 402 U2 = = 0,2 Ω 8000 P 165 Máquinas de corriente continua Vri = 49,6 − 40 − 0,02 · 200 = 5,6 V Æ Vri = 5,6 V b) Eo E o/ = kE · n · φ kE · n/ · φ = n n/ E o/ − Vri = (Ri + RC ) · I Æ E o/ = E o · Æ I= V = RC · I = 154,95 · 0,20 = 30,99 V n/ 3200 = 49,6 · = 39,69 V n 4000 39,69 − 5,6 34,09 = = 154,95 A 0,02 + 0,2 0,22 V = 30,99 V Æ c) Del apartado anterior se tiene que: E o/ = 39,69 V a 3200 rpm ⇒ I e/ = 5 A Eo// = 49,6 V a 3200 rpm ⇒ I e// = ? Eo/ k · n / · I e/ = Eo// k · n // · I e// ( Eo// = 49,6 V igual que en apartado a) ) n / = n // = 3200 rpm Æ I e// = E o// E o/ · I e/ = 49,6 · 5 = 6,24 A 39,69 I e// = 6,24 A Suponiendo constante la tensión de excitación, resulta: Ve = Re ⋅ I e = Re ' '⋅I e ' ' Æ Re// = Re · Ie 5 = 9,8 · = 7,85 Ω Æ // 6,24 Ie © Los autores, 2006; © Edicions UPC, 2006 Re// = 7,85 Ω 166 Problemas de electrotecnia 4.3 Problema 3 Se dispone de un motor de corriente continua con excitación serie y características: tensión nominal 240 V, potencia nominal absorbida 9600 W, resistencia de excitación 0’15 Ω, resistencia del inducido 0’2 Ω, velocidad nominal 500 rpm. El motor trabaja en unas condiciones en las cuales absorbe una quinta parte de la corriente nominal y la f.e.m. es la mitad de la que habría en condiciones nominales. Se pide para estas condiciones: a) La velocidad de giro del motor expresada en rpm b) La tensión de alimentación del motor c) El par electromagnético generado por el motor Resolución: a) 240 V M Rex = 0,15 Ω Ri = 0,2 Ω Figura 4.3.1 Pabs = 9600 W In = 240 = En + (0,2 + 0,15) · 40 E/ = En E / 9600 = 40 A 240 Æ E n 226 = = 113 V 2 2 = In · n / I ·n / Æ E n = 226 V I/ = 226 40 · 500 = 113 8 · n/ Æ I n 40 = =8A 5 5 n / = 1250 rpm b) U / = E / + (0,15 + 0,2) · I / = 113 + 0,35 · 8 = 115,8 V Æ U / = 115,8 V © Los autores, 2006; © Edicions UPC, 2006 167 Máquinas de corriente continua c) Pi ' = E '⋅I ' = M i '⋅ω ' Mi ' = E/ · I / E/ · I / = = 6,9 N·m / 2·π·n ω 60 → M i ' = 6,9 N·m © Los autores, 2006; © Edicions UPC, 2006 168 Problemas de electrotecnia 4.4 Problema 4 Un generador excitación derivación, de 100 kW de potencia nominal y tensión 232 V, presenta una resistencia total del inducido de 0,05 Ω y un bobinado inductor con una resistencia de 58 Ω. La caída de tensión en las escobillas es de 2 V/línea. a) Calcular la f.e.m inducida a plena carga y a media carga. b) Determinar la inducción en el entrehierro sabiendo que la máquina tiene 4 polos, que el inducido es del tipo imbricado y que dispone de 326 conductores activos en total, girando a 650 rpm a carga nominal. También se sabe que el diámetro del rotor es de 42 cm, la longitud del núcleo, en sentido axial, es de 28 cm, y que cada polo cubre un ángulo de 60º. c) Sabiendo que las pérdidas mecánicas y en el núcleo son de 1800 W, determinar el rendimiento del generador a carga nominal, así como la potencia que se tiene que suministrar desde el exterior para poder funcionar en estas condiciones. d) Índice de carga que hace que el rendimiento de la dinamo sea máximo y hallar el mismo. Se considerará que la reacción de inducido está compensada por un bobinado de compensación, la resistencia del cual está incluida y es de 0,05 Ω. Resolución: I Ie Ii Re = 58 Ω + E G U = 232 V Ri = 0,05 Ω Figura 4.4.1 a) In = Pn 100000 = = 431,034 A 232 Un Ie = U e 232 = = 4A Re 58 I (C =0,5) = 431,034 ⋅ 0,5 = 215,52 A Iin = 431,034 + 4 = 435,034 A I i (C =0,5) = 215,52 + 4 = 219,52 A E = U + ∆Uesc + I i ⋅ Ri E n = 232 + 2 + 0,05 ⋅ 435,034 = 255,752 V E(C = 0,5) = 232 + 2 + 0,05 ⋅ 219 ,52 = 244 ,976 V © Los autores, 2006; © Edicions UPC, 2006 169 Máquinas de corriente continua b) E= n p ⋅ z ⋅φ ⋅ 60 c En = 255,725 = B= φ s = ya que p = 2 y al ser imbricado p = c, resulta: 650 2 ⋅ 326 ⋅ φ ⋅ 60 2 → φ ángulo _ polar L ⋅ π ⋅ diámetro ⋅ 360º = φ = 72,417 mWb 0,072417 0,28 ⋅ 0,42 ⋅ π ⋅ 60 360 = 1,17 T c) Pgenerada = E n ⋅ I in + Pmec +núcleo = 255,752 ⋅ 435,034 + 1800 = 113060,816 W η= U ⋅I Pgenerada = 232 ⋅ 431,034 = 0,88447 113060,816 → η = 88,447 % d) η= U ⋅I Pgenerada = U ⋅I E ⋅ I + Pmec + núcleo 232 ⋅ I 232 ⋅ I 232 Será = = 2 2736,8 1800 + (4 + I )[232 + 2 + 0,05(4 + I )] 234,4 I + 2736,8 + 0,05I + 0,05I 234,4 + I 2736 , 8 2736 , 8 d ⎛ ⎞ máximo cuando + 0,05 I sea mínimo, es decir: + 0,05.I ⎟ = 0 ⎜ I dI ⎝ I ⎠ η= Resultando: I= 2736,8 = 233,96 A 0,05 η máximo = 0,899937 → → C= I 233,96 = = 0 ,54278 I n 431,034 ηmáximo = 89,9937 % © Los autores, 2006; © Edicions UPC, 2006 170 Problemas de electrotecnia 4.5 Problema 5 La característica de vacío a 600 rpm de un generador de corriente continua excitación derivación es la siguiente: Ie ( A ) 1 2 3 4 5 6 7 8 Eo ( V ) 23 45 67 85 100 112 121 126 La resistencia del devanado de la armadura es 0,03 Ω y la del devanado de excitación 17,6 Ω, siendo la tensión de bornes 114,4 V. Determinar: a) La corriente de carga con la que está funcionando. b) Si la resistencia de excitación se reduce hasta un valor de 15 Ω, sin que varíen la velocidad ni la intensidad de carga, ¿cuál sería la f.e.m. inducida, la tensión en bornes de la máquina y la corriente de excitación? c) En ambos casos calcular el rendimiento eléctrico de la máquina. Se despreciaran la caída de tensión en las escobillas y la reacción del inducido. Resolución: Ie I Ii + E G U Re Ri = 0,03 Ω Figura 4.5.1 a) Ie = U 114,4 = = 6,5 A Re 17,6 De la curva de magnetización: E = 112 + 121 = 116,5V 2 E = U + Ri ⋅ I i = 114,4 + 0,03 ⋅ Ii 116,5 = 114,4 + 0,03 ⋅ I i (interpolando) (Uesc = 0) I i = 70 A → I = I i − I e = 70 − 6 ,5 = 63,5 A © Los autores, 2006; © Edicions UPC, 2006 171 Máquinas de corriente continua b) Ii ' = I + Ie ' E '−U ' = 0,03 ⋅ ( I + I ' e ) E '−U ' = 1,905 + 0,03 ⋅ I ' e U ' = 15 ⋅ I ' e U ' = 15 ⋅ I ' e I ' −7 E '−121 (interpolación) = e 126 − 121 8 − 7 E '−121 = 5 ⋅ I 'e −35 Siendo I = 63,5 A, del sistema anterior de ecuaciones resulta: I ' e = 8,3843 A U ' = 125,765 V E ' = 127,922 V I 'i = 8,3843 + 63,5 = 71,884 A c) η e1 = U ⋅I 114,4 ⋅ 63,5 = = 0 ,8905 E ⋅ I i 116,5 ⋅ ( 63,5 + 6 ,5 ) → ηe1 = 89,05 % ηe2 = 125,765 ⋅ 63,5 = 0,8685 127,922 ⋅ 71,884 → ηe2 = 86,85 % © Los autores, 2006; © Edicions UPC, 2006 172 Problemas de electrotecnia 4.6 Problema 6 Dos generadores de corriente continua de excitación independiente deben funcionar en paralelo suministrando corriente a una carga de 1,4711 Ω. De cada generador se conocen los datos siguientes: Generador A: f.e.m. = 308,5 V Generador B: Ri = 0,1 Ω f.e.m. = 302 V Ri = 0,08 Ω ∆Uesc = 1,5 V P = 40 kW ∆Uesc = 2 V P = 30 kW Determinar la intensidad que aportará cada generador, la tensión en bornes de la carga y el índice de carga de cada máquina, así como su rendimiento, prescindiendo de las pérdidas de excitación y de las que no se conocen datos. Resolución: IA + - EA RC = 1,4711 Ω RiA = 0,1 Ω EB + - IB RiB = 0,08 Ω Figura 4.6.1 E A = ∆Uesc A + RiA ⋅ I A + U EB = ∆UescB + RiB ⋅ I B + U U = 1,411( I A + I B ) E A = ∆Uesc A + RiA ⋅ I A + 1,4711 ⋅ ( I A + I B ) EB = ∆UescB + RiB ⋅ I B + 1,4711 ⋅ ( I A + I B ) 308,5 = 1,5 + 0,1 ⋅ I A + 1,4711( I A + I B ) 302 = 2 + 0,08 ⋅ I B + 1,4711( I A + I B ) © Los autores, 2006; © Edicions UPC, 2006 173 Máquinas de corriente continua Del sistema de ecuaciones anterior resulta: I A = 127,778 A I B = 72,22 A U = 294,22 V I A + I B = 200 A CA = PA I .U 127,778 ⋅ 294,22 = A = = 0,93987 PAn PAn 40000 ηA = U .I A 294 ,22 = = 0 ,95371 E A .I A 308,5 CB = PB I .U 77,22 ⋅ 294,22 = B = = 0,70828 PBn PBn 30000 ηB = U .I B 294,22 = = 0,97424 → EB .I B 302 → η = 95,371 % ηB=97,424% © Los autores, 2006; © Edicions UPC, 2006 174 Problemas de electrotecnia 4.7 Problema 7 Una dinamo excitación shunt suministra en condiciones normales 80 A bajo una diferencia de potencial de 200 V y tiene un rendimiento del 94 %. Sus pérdidas se descomponen en: - 3 % en el inducido - 2 % en el inductor - 1 % por histéresis y corrientes de Foucault Calcular los valores de las diferentes pérdidas en las resistencias del inductor y del inducido, así como los valores de estas resistencias y la f.e.m. de la dinamo. Determinar asimismo, para qué índice de carga se obtendrá un rendimiento de la dinamo máximo. No se tendrán en cuenta la reacción del inducido ni caída de tensión alguna en las escobillas. Resolución: Ie I Ii Re G Ri Figura 4.7.1 Potencia útil suministrada por la dinamo: Potencia absorbida: Pu = 80 ⋅ 200 = 16000 W Pabs = Pérdidas totales: 16000 = 17021,3 W 0,94 17021,3 − 16000 = 1021,3 W Pérdidas en el inducido: Pi = 3 ⋅ 1021,3 = 510,65 W 3 + 2 +1 Pérdidas en el inductor: Pe = Pérdidas en el núcleo: PFe = 2 ⋅ 1021,3 = 340,4 W 3 + 2 +1 1 ⋅ 1021,3 = 170,2 W 3 + 2 +1 También se cumple: Pe = U2 Re Ie = 200 = 1,702 A 117,5 → 340,4 = 200 2 Re → Re = 117,5 Ω © Los autores, 2006; © Edicions UPC, 2006 175 Máquinas de corriente continua I i = I + I e = 80 + 1,702 = 81,702 A Pi = Ri ⋅ I i 2 → E = U + I i ⋅ Ri → 510,65 = Ri ⋅ 81,702 2 → Ri = 0,0765 Ω E = 200 + 0,0765 ⋅ 81,702 = 206 ,25 V Y el rendimiento será: η= η= Pu ,n ⋅ C Pu Pu = = Pabs Pu + PFe + Pe + Pi Pu ,n ⋅ C + PFe + Pe + C 2 ⋅ Pi ,n 16000 ⋅ C 16000 = 16000 ⋅ C + 170,2 + 340,4 + 510,65 ⋅ C 2 16000 + 510,6 + 510,65 ⋅ C C Para que el resultado se máximo, el denominador debe ser mínimo: d ⎛ 510,6 ⎞ + 510,65 ⋅ C ⎟ = 0 ⎜ dC ⎝ C ⎠ Resultando: C= 510,6 ≅1 510,65 © Los autores, 2006; © Edicions UPC, 2006 176 Problemas de electrotecnia 4.8 Problema 8 La característica de vacío a 750 rpm de un generador de corriente continua con excitación en derivación es: Iexc ( A ) 1 2 4 6 8 10 12 Eo ( V ) 25 49 97 142 175 205 225 La resistencia del circuito de excitación vale 24 Ω y la del inducido 0,04 Ω. Despreciando la caída de tensión en las escobillas, calcular: a) La corriente en la carga cuando la tensión en bornes de ésta es de 120 V. b) Si Re disminuye hasta 20 Ω sin variar la velocidad ni la corriente de la carga, calcular la corriente en el inductor, la f.e.m y la tensión en bornes de la carga. Iexc I - G Rexc U Ri + Figura 4.8.1 Resolución: a) I exc = U 120 = =5 A Rexc 24 Interpolando en la tabla del enunciado resulta: E5 A = 97 + 142 = 119,5 A 2 E = U + I i ⋅ Ri → 119,5 = 120 + I i ⋅ 0,04 → I = I i − I exc = 12,5 − 4 = 7,5 A b) E ' = U '+ I i '⋅Ri © Los autores, 2006; © Edicions UPC, 2006 I i = 12,5 A 177 Máquinas de corriente continua U ' = I exc '⋅Rexc ' I = cte y si Rexc ↓ implica que Iexc ↑; por lo tanto, en la característica de vacío debemos interpolar más a la derecha de la tabla del enunciado. Interpolando, resulta: I '−10 E '−205 = exc 225 − 205 12 − 10 E '−U ' = 0,3 + 0,04 ⋅ I exc ' E ' = 0,3 + 20,04 ⋅ I exc ' U ' = 20 ⋅ I exc ' E ' = 105 + 10 ⋅ I exc ' E '−205 = 10 ⋅ I exc '−100 Del sistema de ecuaciones anterior, resulta: I exc ' = 10,43 A E '= 209,28 V U ' = 208,6 V © Los autores, 2006; © Edicions UPC, 2006 178 Problemas de electrotecnia 4.9 Problema 9 Un motor con excitación en derivación consume en vacío 5 A cuando se encuentra conectado a una fuente de tensión continua de 600 V. La resistencia conjunta del devanado inducido y las escobillas es de 0,25 Ω y la Rexc = 300 Ω. Calcular la potencia útil y el rendimiento total cuando la intensidad que absorbe la fuente es: a) 20 A b) 50 A c) La relación de velocidades en las situaciones anteriores Resolución: Vacío Po = U ⋅ I o = 600 ⋅ 5 = 3000 W Pabs PRexc PRi Pi = E·Ii Pmec PFe Pu U = I exc ⋅ Rexc 600 = I exc ⋅ 300 → I exc = 2 A I io = I o − I exc = 5 − 2 = 3 A Po = PRe xc + PRi + Pmec + Fe + Pu Pero en vacío Pu = 0 , resultando: 3000 = U ⋅ I exco + I io 2 ⋅ Ri + Pmec + Fe → 3000 = 600 ⋅ 2 + 32 ⋅ 0,25 + Pmec + Fe Resultando: Pmec + PFe = 179775 W Las pérdidas anteriores son constantes, ya que al ser un motor derivación la velocidad de giro n ≅ cte a cualquier carga si U = cte. © Los autores, 2006; © Edicions UPC, 2006 179 Máquinas de corriente continua a) I = 20 A I = 20 A Iexc = 2 A Ii = I - Iexc = 18 A E = U − I i ⋅ Ri = 600 − 18 ⋅ 0,25 = 595,5 V Pi = E ⋅ I i = 10719 W Pu = Pi − Pmec+ Fe = 8921,25 W Pabs = U ⋅ I = 600 ⋅ 20 = 1200 W η= Pu 8921,25 ⋅100 = ⋅100 = 74,34% Pabs 12000 b) I = 50 A I = 50 A Iexc = 2 A Ii = I - Iexc = 48 A E = U − I i ⋅ Ri = 600 − 48 ⋅ 0,25 = 588 V Pi = E ⋅ I i = 28224 W Pu = Pi − Pmec+ Fe = 26426,25 W Pabs = U ⋅ I = 30000 W η= Pu 26426,25 ⋅100 = ⋅100 = 88,09% Pabs 30000 c) E = K ⋅ ω ⋅ φ = K '⋅n ⋅ φ = K ' '⋅n ⋅ I exc E ' = K ' '⋅n'⋅I ' exc E K ' '⋅n ⋅ I exc n = = E ' K ' '⋅n'⋅I ' exc n' n' = n ⋅ E' 588 = n⋅ = 0,9874.n E 595,5 → n' = 0,9874.n Por lo tanto se comprueba que n ≅ cte . © Los autores, 2006; © Edicions UPC, 2006 180 Problemas de electrotecnia 4.10 Problema 10 Dos generadores de corriente continua de excitación independiente tienen que funcionar conectados en paralelo para alimentar a una carga común de 1,2 Ω. Sus características son: Generador A EAn = 310 V RiA = 0,10 Ω ∆VescAn = 1,8 V PAn = 45kW Generador B EBn = 305 V RiB = 0,08 Ω ∆VescBn = 1,9 V PBn = 35kW Calcular la intensidad de corriente total en la carga, la que aporta cada generador, la tensión y la potencia en la carga, el índice de carga de cada máquina y el rendimiento de cada una, suponiendo que la f.e.m. de cada generador es la nominal. IB IA 0,10 Ω 310 V + - 0,08 Ω I U + GA + - 305 V GB 1,2 Ω Figura 4.10.1 E A = U + I A ⋅ RiA + ∆VescA 310 = (I A + I B ) ⋅1,2 + I A ⋅ 0,1 + 1,8 E B = U + I B ⋅ RiB + ∆VescB 305 = (I A + I B ) ⋅1,2 + I A ⋅ 0,08 + 1,9 U = (I A + I B ) ⋅ Rc arg a 308,2 = 1,3 ⋅ I A + 1,2 ⋅ I B IA = 308,2 1,2 303,1 1,28 1,3 1,2 1,2 1,28 = 137,39 A 1,32 308,2 1,2 303,1 IB = = 107,99 A 1,3 1,2 1,2 1,28 303,1 = 1,2 ⋅ I A + 1,28 ⋅ I B I = I A + I B = 245,38 A U = I ⋅1,2 = 245,38 ⋅1,2 = 294,46 V Pc arg a = U ⋅ I = 72253,6 W © Los autores, 2006; © Edicions UPC, 2006 181 Máquinas de corriente continua CA = PA U ⋅ I A 294,46 ⋅ 137,39 = = = 0,899 45000 PAn PAn ηA = U ⋅IA 294,46 = = 0,950 310 EA ⋅I A CB = PB U ⋅ I B 294,46 ⋅ 107,99 = = = 0,909 PBn PBn 35000 ηB = U ⋅IB 294,46 = = 0,965 EB ⋅ I B 305 © Los autores, 2006; © Edicions UPC, 2006 182 Problemas de electrotecnia 4.11 Problema 11 Un motor de corriente continua con excitación en paralelo absorbe 15 kW cuando se encuentra conectado a una red de corriente continua de 150 V y gira a 500 rpm. Se sabe que la tensión baja a 100 V manteniéndose constante la potencia que éste absorbe de la red de corriente continua. Calcular la velocidad en la nueva situación despreciando la caída de tensión en las escobillas. Iexc I Ii Rexc + E M U Ri Figura 4.11.1 Pabs = U ⋅ I → 15000 = 150 ⋅ I → I = 100 A U = I exc ⋅ Rexc → 150 = I exc ⋅150 → I exc = 1 A I i = I − I exc = 99 A U = E + I i ⋅ Ri → 150 = E + 99 ⋅ 0,03 → E = 147,03 V P' = U '⋅I ' → 15000 = 100 ⋅ I ' → I '= 150 A U' 100 = = 0,6 A Rexc 150 I ' i = I '− I ' exc = 149,3 A I ' exc = E ' = U '− I i '⋅Ri ' = 100 − 149,3 ⋅ 0,03 E = K ⋅ ω ⋅ φ = K '⋅n ⋅ φ = K ' '⋅n ⋅ I exc → → E ' = 95,52 V E K ' '⋅n ⋅ I exc = E ' K ' '⋅n'⋅I exc ' → Resultando n’ = 487,25 rpm © Los autores, 2006; © Edicions UPC, 2006 147,03 500 ⋅1 = 95,52 n'⋅0,6 183 Máquinas de corriente continua 4.12 Problema 12 Un motor con excitación serie se alimenta a 250 V a tensión constante y absorbe 25 A cuando gira a 800 rpm. Se sabe que Rexc = 0,25 Ω y Ri = 0,35 Ω. Si el par motor aumenta un 40 %, calcular: a) La corriente absorbida y la velocidad en esta nueva situación. b) La corriente absorbida y la velocidad si el par motor se reduce en un 25 % respecto a la situación inicial. I M U Rexc Ri Figura 4.12.1 U = E + (Ri + Rexc ) ⋅ I I = I i = I exc = 25 A Situación inicial: 250 = E + (0,25 + 0,35) ⋅ 25 → E = 235V E ⋅ Ii = M i ⋅ w → Mi = E ⋅ Ii 235 ⋅ 25 = = 70,13 Nm 2π 2π ⋅n ⋅ 800 60 60 a) M i ' = 1,4 ⋅ M i = 98,18 N.m E ' = K ⋅ n'⋅φ ' = K '⋅n'⋅I exc ' = K '⋅n'⋅I ' M i ' = K ⋅ I i '⋅φ ' = K '⋅I i '⋅I exc ' = K '⋅I ' 2 Mi K '⋅I 2 = M i ' K '⋅I ' 2 → 70,13 25 2 = 98,18 I ' 2 → I ' = 29,58 A E ' = U '− I '⋅(Ri + Rexc ) = 250 − 29,58 ⋅ 0,6 = 232,25 V E K '⋅n ⋅ I 800 ⋅ 25 235 = = = E ' K '⋅n'⋅I ' n'⋅29,58 232,25 → n' = 668,22 rpm © Los autores, 2006; © Edicions UPC, 2006 184 Problemas de electrotecnia b) M i ' ' = 0,75 ⋅ M i = 52,60 Nm Mi I2 = M i ' ' I ' '2 → 70,13 25 2 = 52,60 I ' ' 2 → I ' ' = 21,65 A E ' ' = U ' '− I ' '⋅(Ri + Rexc ) = 250 − 21,65 ⋅ 0,6 = 237 V E K '⋅n ⋅ I 800 ⋅ 25 235 = = = E ' ' K '⋅n' '⋅I ' ' n' '⋅21,65 237 → n' ' = 931,69 rpm © Los autores, 2006; © Edicions UPC, 2006 185 Máquinas de corriente continua 4.13 Problema 13 Una máquina de corriente continua tiene Ri = 0,5 Ω y Rexc regulable entre 100 y 400 Ω. La curva de vacío a 100 rpm es: Eo ( V ) 30 110 195 270 340 410 Iexc ( A ) 0,1 0,3 0,5 0,7 1,9 2 Región lineal Codo de saturación a) Funcionando como generador derivación que gira a 750 rpm y con Rexc = 300 Ω, suministra 39 A y 300 V. Calcular: 1. Par resistente ofrecido por la carga en estas condiciones 2. Curva de vacío a esta velocidad b) Funcionando como motor derivación alimentado a 250V y con Rexc = 210 Ω absorbe 15 kW, calcular la velocidad, el par electromagnético y el rendimiento suponiendo Pmec+Fe = 0. Iexc = 1A I = 39 A Ii G 300 Ω U = 300 V Ri Figura 4.13.1 a) 1. I exc = U 300 = =1 A Rexc 300 I i = I + I exc = 39 + 1 = 40 A E = U + I i ⋅ Ri + ∆Vesc → E = 300 + 40 ⋅ 0,5 + 0 = 320 V © Los autores, 2006; © Edicions UPC, 2006 186 Problemas de electrotecnia Pi = E ⋅ I i = M i ⋅ w → Mi = E ⋅ Ii 320 ⋅ 40 = 162,97 N.m = 2π 2π ⋅ 750 ⋅n 60 60 2. E K ⋅ n ⋅ φ n ⋅ I exc = = E ' K ⋅ n'⋅φ ' n'⋅I exc ' E' = E ⋅ (I exc = I exc ') 750 n = E⋅ = 0,75 ⋅ E 1000 n' La curva de vacío es entonces: E’o ( V ) 22,5 82,5 166,25 202,5 255 307,5 I’exc ( A ) 0,1 0,3 0,5 0,7 0,9 2 I exc = 250 = 1A 250 b) I= 15000 = 60 A 250 En el caso de trabajar como motor se tiene: I i = I − I exc = 59 A E mot = U − I i ⋅ Ri − ∆Vesc = 250 − 59 ⋅ 0,5 − 0 = 220,5 V E mot K ⋅ n mot ⋅ cte ⋅ I exc mot = E gen K ⋅ n gen ⋅ cte ⋅ I exc gen → 220,5 K ⋅ n mot ⋅ cte ⋅1 = 320 K ⋅ 750 ⋅ cte ⋅1 Resultando nmot = 516,80 rpm Mi = E ⋅ Ii 220,5 ⋅ 59 = = 240,4 N.m 2π 2π ⋅n ⋅ 516,80 60 60 η = 100 ⋅ Pu P − Pmec+ Fe E ⋅ Ii 220,5 ⋅ 59 = 100 ⋅ i = 100 ⋅ = 100 ⋅ = 86,73 % 15000 15000 Pabs Pabs © Los autores, 2006; © Edicions UPC, 2006 187 Máquinas de corriente continua 4.14 Problema 14 Un generador con excitación mixta corta alimenta a 100 V una carga que a esta tensión consume 12500 W. Se sabe que Ri = 0,04 Ω, Rexc serie = 0,06 Ω y Rexc derivación = 75 Ω. Suponiendo constantes las pérdidas mecánicas del generador y la potencia mecánica absorbida por éste, calcular el nuevo valor de la tensión de alimentación si la resistencia de la carga pasa a ser de 1 Ω y la intensidad del inducido vale 120 A. Suponer que la máquina dispone de devanado de compensación de la reacción del inducido, que ∆Vesc = 0 y que el núcleo magnético no se encuentra saturado. Id A Rexc d G I Ii + Rexc s Rcarga Ri - B Figura 4.14.1 Situación inicial: I= Pc arg a U = 12500 = 125 A 100 U AB = U + I ⋅ Rexc s = 100 + 125 ⋅ 0,06 = 107,5 V Id = U AB 107,5 = = 1,43 A Rexc d 75 I i = I + I d = 126,43 A E = U AB + I i ⋅ Ri = 107,5 + 126,43 ⋅ 0,04 = 112,56 V Pi = E ⋅I i = 112,56 ⋅ 126,43 = 14231 W Pabs = P i + P mec = cte → P i = cte = 14231 = E '⋅I i ' 14231 = E '⋅120 → E '= 118,59 V U ' AB = E ' − I i '⋅Ri ' = 118,59 − 0,04 ⋅120 = 113,79 V Resultando I d'= Por lo tanto, U AB ' 113,79 = = 1'52 A 75 Rexcd I'= U' R' c arg a U U ' = I '⋅R'c arg a = (I i '− I d ') ⋅ R'c arg a = (120 − 1,52) ⋅ 1 = 118,48 V © Los autores, 2006; © Edicions UPC, 2006 189 Máquinas asíncronas 5 Máquinas asíncronas © Los autores, 2006; © Edicions UPC, 2006 190 Problemas de electrotecnia 5.1 Problema 1 Un motor asíncrono gira a una velocidad de 465 rpm con carga nominal y a 497 rpm en vacío, estando alimentado a una tensión cuya frecuencia es de 50 Hz. Determinar: a) Velocidad de sincronismo b) Deslizamiento en vacío c) Deslizamiento a plena carga d) Frecuencia de las corrientes del estator en vacío y a plena carga e) Frecuencia de las corrientes del rotor en vacío y a plena carga Resolución: a) n= 60 ⋅ f 60 ⋅ 50 3000 = = p p p Siendo p = 1, 2, 3, …… Para distintos valores de p tenemos: n p =1 = 3000 rpm n p = 2 = 1500 rpm n p =3 = 1000 rpm n p = 4 = 750 rpm n p =5 = 600 rpm n p =6 = 500 rpm n p = 7 = 428,57 rpm En vacío se tiene n = 497 rpm. El valor que más se acerca es ns =500 rpm, es decir, p = 6. b) n − n 500 − 497 = = 0,006 s vacío = s 500 ns (0,6 %) c) s plena c arg a = 500 − 465 = 0,07 500 (7 %) d) f estator = 50 Hz en vacío y a plena carga. © Los autores, 2006; © Edicions UPC, 2006 191 Máquinas asíncronas e) f 2vacío = svacío ⋅ f1 = 0,006 ⋅ 50 = 0,3 Hz f 2 plena c arg a = s pc ⋅ f1 = 0 ,07 ⋅ 50 = 3,5 Hz © Los autores, 2006; © Edicions UPC, 2006 192 Problemas de electrotecnia 5.2 Problema 2 Un motor trifásico AEG de rotor bobinado, 380 V/600 V, 6,3 A/3,64 A, está alimentado por una línea de 380 V. Determinar los parámetros del circuito equivalente y las pérdidas mecánicas, si se conocen los resultados de los ensayos de vacío y de rotor bloqueado. a) Ensayo de rotor bloqueado: 60 V, 385 W, 544 VAr, 6,30 A b) Ensayos de vacío: 380 V, 2 A, 302 W, 1291 VAr 302 V, 1,5 A, 200 W 257 V, 1,2 A, 157 W 228 V, 1,1 A, 130 W 191 V, 0,9 A, 103 W La resistencia por fase del estator es de 4,8 Ω. El motor tiene un diseño que cumple la norma NEMA B, es decir, que X1/X2’ = 4/6. Resolución: Dado que el motor trabaja a 380 V, debe estar alimentado en triángulo. Circuito equivalente en triángulo por fase: R1 X2' X1 R2 ' ⎛1 ⎞ R 2 ' ⎜ −1⎟ ⎝s ⎠ Xµ R Fe Figura 5.2.1 Ensayo con rotor bloqueado ( ensayo de cortocircuito): La corriente por fase es de 6,30 / 3 A al estar conectado el motor en triángulo. PCC = 3 ⋅ I 1n 2 ⋅ ( R1 + R 2 ' ) 2 ⎛ 6,30 ⎞ ⎟ ⋅ (4,8 + R 2 ' ) 385 = 3 ⋅ ⎜⎜ ⎟ ⎝ 3 ⎠ → R 2 ' = 4,90Ω 2 2 QCC = 3 ⋅ I 1n ⋅ X 1CC → ⎛ 6,3 ⎞ ⎟ ⋅ X 1CC 544 = 3 ⋅ ⎜⎜ ⎟ ⎝ 3⎠ → © Los autores, 2006; © Edicions UPC, 2006 X 1CC = 13,71Ω 193 Máquinas asíncronas Al ser X 1CC = X 1 + X 2 ' = 13,71 = 4 X 2 '+ X 2 ' , resulta: 6 4 X 2 '+ X 2 ' 6 → → X 2 ' = 8,23 Ω X 1 = 5,48 Ω Ensayo de vacío: R1 X2' X1 R2 ' Xµ R Fe E ≈ U1 Figura 5.2.2 Q = QX 1 + QXµ 2 ⎛ 2 ⎞ 380 2 ⎟⎟ ⋅ 5,48 1291 = 3 ⋅ + 3 ⋅ ⎜⎜ Xµ ⎝ 3⎠ X µ = 341,35 Ω → P1o = PR1 + PRFe + Pmec P1o − 3 ⋅ R1 ⋅ I1o 2 = Pmec + 3 ⋅ U1o 2 RFe → P1o − 3 ⋅ 4,8 ⋅ I1o 2 = Pmec + 3 ⋅ U 1o 2 R Fe Equivalente a la siguiente ecuación: y = b + ax , siendo: x = U1o 2 y = Po − 3 ⋅ R1 ⋅ I1o 2 a= 3 RFe b = Pmec U1o Io Po x = U 1o 2 y = Po − 3 ⋅ R1 ⋅ I1o 2 380 2/ 3 302 144400 282,80 302 1,5 / 3 200 91204 189,20 257 1,2 / 3 157 66049 150,09 228 1,1 / 3 130 51984 124,19 191 0,9 / 3 103 36481 99,11 Realizada la regresión resulta: a = 1,7 ⋅ 10 −3 = b = 36,43 3 RFe → RFe = 1764,7Ω → Pmec = 36,43 W © Los autores, 2006; © Edicions UPC, 2006 194 Problemas de electrotecnia 5.3 Problema 3 De un motor asíncrono trifásico, alimentado a 230 V, 50 Hz y 8 polos, cuando gira a 720 rpm se han podido determinar las potencias siguientes: Potencia absorbida de la red: 3000 W Pérdidas en el cobre del estator: 120 W Pérdidas en el circuito magnético: 110 W Pérdidas mecánicas: 50 W Calcular el par útil desarrollado por el motor en las condiciones anteriores. Resolución: Pa: Potencia transferida del estator al rotor. Pa = Pabs − PFe1 − PCu1 = 3000 − 110 − 120 = 2770 W s= n s − n 750 − 720 = = 0,04 750 ns Se cumple: PCu 2 = s ⋅ Pa → PCu 2 = 0,04 ⋅ 2770 = 110,8 W Pu = Pa − PFe 2 − PCu 2 − Pmec Pu = 2770 − 0 − 110,8 − 50 = 2609,2 W Pu = Mu.W = M u . 2π ⋅ n 60 → Mu = Pu 2609,2 = = 34,6 N.m 2 ⋅ π ⋅ n 2 ⋅ π ⋅ 720 60 60 © Los autores, 2006; © Edicions UPC, 2006 195 Máquinas asíncronas 5.4 Problema 4 Se ensaya en vacío un motor asíncrono trifásico de 380 V/660 V dos veces. Cuando está conectado en triángulo, resulta: 380 V, 7 A y 900 W. Cuando está conectado en estrella, resulta: 380 V, 2,4 A y 454,2 W (no es su tensión normal de trabajo). Se sabe que la resistencia por fase del bobinado vale 0,8 Ω. Finalmente se conocen de este motor unas curvas de par y de rendimiento: Velocidad (rpm) 1500 1488 1474 1455 1431 1400 Par (N.m) 0 25 50 75 100 125 Rendimiento 0 0,45 0,68 0,88 0,86 0,81 Funcionando con una carga determinada y conectado en triángulo a 380 V, se miden con el tacómetro 1443 rpm y con la pinza amperimétrica 27 A. Determinar en este régimen la potencia útil desarrollada por el motor, el rendimiento y hacer una separación completa de todas las pérdidas. Resolución: A 1443 rpm, resulta: s= 1500 − 1443 ⋅100 = 3,8% 1500 Interpolando en las curvas de Par – velocidad, resulta: 75 + (100 − 75) ⋅ (1455 − 1443) = 87,5 N.m (1455 − 1431) Pu = M u ⋅ ω = 87,5 ⋅ 2π ⋅ 1443 = 13222,2 W 60 Interpolando en las curvas de rendimiento – velocidad: η = 0,88 − η= Pu Pabs (0,88 − 0,86) ⋅ (1455 − 1443) = 0,87% (1455 − 1431) → Pabs = 13222 ,2 = 15197 ,9 W 0 ,87 Pérdidas totales = Pabs – Pu = 15197,9 – 13222,2 = 1975,7 W De las pruebas de vacío, resulta: Po = PFe + PCu1 + Pmec → Po = PFe + 3.I12, fase .R1 + Pmec © Los autores, 2006; © Edicions UPC, 2006 196 Problemas de electrotecnia 2 Triángulo: ⎛ 7 ⎞ ⎟ + Pmec + PFe 900 = 3 ⋅ 0 ,8 ⋅ ⎜⎜ ⎟ ⎝ 3⎠ Estrella: ⎛ 380 / 3 ⎞ ⎟ 454 ,2 = 3 ⋅ 0 ,8 ⋅ 2 ,4 2 + Pmec + PFe ⋅ ⎜ ⎜ 380 ⎟ ⎝ ⎠ Del sistema anterior, resulta: 2 Pmec = 230,2 W PFe = 630,6 W Cuando trabaja en carga, resulta: Pérdidas en el estator por efecto Joule: 2 ⎛ 27 ⎞ ⎟⎟ = 583,2 W PCu1 = 3.I12, fase .R1 = 3 ⋅ 0 ,8 ⋅ ⎜⎜ ⎝ 3⎠ Potencia en el entrehierro: Pa = Pabs − PFe − PCu1 = 15197,9 − 630,6 − 583,2 = 13984,1 W Pérdidas en el rotor por efecto Joule: PCu2 = s ⋅ Pa = 0,038 ⋅ 13984,1 = 531,4 W Potencia mecánica interna: Pi = Pa − PCu 2 = 13452,7 W Potencia útil: Pu = Pi − Pm = 13452,7 − 230,2 = 13222,5 W Pérdidas adicionales: Padicionales = 13222,5 − 13222,2 = 0,3 W Factor de potencia: cos ϕ = Pabs 3 ⋅ U lin ⋅ I lin = 15197 ,9 3 ⋅ 380 ⋅ 27 = 0 ,8552 © Los autores, 2006; © Edicions UPC, 2006 197 Máquinas asíncronas 5.5 Problema 5 Hacer la separación de pérdidas de un motor asíncrono de 7,5 kW, 4 polos, 50 Hz, 400 V/693 V con los datos siguientes obtenidos en el laboratorio: Temperatura interna de trabajo = 65 ºC Resistencia por fase a esta temperatura = 0,8 Ω Pruebas en vacío y caliente Prueba en carga y caliente 400 V 400 V 6A Po = 1470 W 231 V 3,2 A Po = 595 W 116 V 1,6 A Po = 270 W 18 A Pabs = 11432 W 1420 rpm Mu = 61,5 N.m Determinar también el rendimiento y el factor de potencia de la prueba de carga, así como los parámetros aproximados del circuito equivalente por fase, suponiendo que el motor tiene un diseño que cumple la norma NEMA A, es decir, que X1 =1. X2' Resolución: Ya que la tensión es de 400 V, el motor se debe conectar triángulo. Po = PCu1 + PFe + Pmec → Po - PCu1 = PFe + Pmec 2 ⎛ 6 ⎞ ⎟ = Pmec + PFe 1470 − 3 ⋅ 0,8 ⋅ ⎜⎜ ⎟ ⎝ 3⎠ 2 2 ⎛ 3,2 ⎞ 231 ⎞ ⎟ = Pmec + PFe ⋅ ⎛⎜ 595 − 3 ⋅ 0,8 ⋅ ⎜⎜ ⎟ ⎟ ⎝ 400 ⎠ ⎝ 3⎠ 2 2 ⎛ 1,6 ⎞ 116 ⎞ ⎟ = Pmec + PFe ⋅ ⎛⎜ 270 − 3 ⋅ 0,8 ⋅ ⎜⎜ ⎟ ⎟ ⎝ 400 ⎠ ⎝ 3⎠ Tenemos un sistema de tres ecuaciones con dos incógnitas, entonces, resolvemos dos y comprobamos la tercera. Resulta: Pmec = 160 W PFe = 1280 W En carga, resulta: s= 1500 − 1420 = 0,053 1500 Pabs = 11432 W → 2 ⎛ 18 ⎞ ⎟⎟ = 259,2 W PCu1 = 3 ⋅ 0,8 ⋅ ⎜⎜ ⎝ 3⎠ Pa = Pabs − PCu1 − PFe = 11432 − 259,2 − 1280 = 9892,8 W © Los autores, 2006; © Edicions UPC, 2006 198 Problemas de electrotecnia Pi = Pa ⋅ (1 − s ) = 9892 ,8 ⋅ (1 − 0 ,053) = 9365 ,2 W Pu = Mu .w = 61,5 ⋅ 1420 ⋅ 2π = 9145 ,2 W 60 PCu 2 = Pa ⋅ s = 9892,8 ⋅ 0,053 = 527,6 W PTOT = Pabs − Pu = 11432 − 9145,2 = 2286,8 W Pérdidas totales: Pérdidas adicionales: Padicionales = 2286,8 − PCu1 − PCu 2 − PFe − Pmec = 60,0 W Factor de potencia: cos ϕ = Rendimiento: η= Pabs 3 ⋅ U lin ⋅ I lin = 11432 3 ⋅ 400 ⋅ 18 = 0 ,9167 Putil 9145 ,2 = = 0 ,8 Pabs 11432 Circuito equivalente: Il Rl Xl R2’ X2’ ⎛1 ⎞ R2' ⋅⎜ − 1⎟ ⎝s ⎠ Xµ RFe → En vacío: PFe = 1280 W 1280 = 3 ⋅ 4002 RFe → R Fe = 375 Ω So = 3 ⋅ 400 ⋅ 6 = 4156 ,92 VA 2 2 Qo = S o − Po = 3888,33 VAr → 3888,33 = 3 ⋅ 400 Xµ 2 → X µ = 123,45 Ω Suponiendo U l = 400∠0º V , resulta: Iµ = U1 400∠0º = = 3,24∠ − 90º A X µ 123,45∠90º Pabs = 11432 = 3 ⋅ 400 ⋅18 ⋅ cos ϕ I Fe = U1 400∠0º = 1,067∠0º A = RFe 375∠0º ϕ = 23,55º © Los autores, 2006; © Edicions UPC, 2006 199 Máquinas asíncronas I1, fase = 18 ∠ − 23,55º A 3 I 1, fase = I µ + I Fe + I ' 2 → I'2 = 8,51∠ − 6,13º A PCu 2 = 527 ,589 = 3.8,512 ⋅ R2 ' → R2' = 2,43 Ω R1 = 0 ,8 Ω ( X 1 + X 2' )2 + (R1 + R2' / s )2 = 400 8,51 ( X 1 + X 2' )2 + (0,8 + 2 ,43 / 0,053)2 = 400 → 8,51 ( X 1 + X 2' )2 = 59 ,85 Ω Si el motor es del tipo NEMA A, se cumple: X 1 = X 2' → X 1 = X 2' = 3,87 Ω © Los autores, 2006; © Edicions UPC, 2006 200 Problemas de electrotecnia 5.6 Problema 6 De un motor asíncrono trifásico de seis polos, 380 V conexión estrella y 50 Hz se conocen los resultados de las pruebas siguientes: Prueba de vacío a plena tensión: I 01 = 12,4 A P01 = 2733 W U 01 = 380 V Prueba de vacío a baja tensión: I 02 = 6,5 A P02 = 1855,7 W U 02 = 220 V Prueba de corriente continua: I CC = 50 A U CC = 12 V Prueba a plena carga: I n = 46,2 A U n = 380 V n = 955 rpm M = 2250 cm ⋅ kg Pn = 26701 W Hacer una separación completa de pérdidas en condiciones nominales, determinando incluso las pérdidas adicionales, y calcular también el rendimiento. Resolución: 12 Vcc = 0,5. = 0,12 Ω 50 I cc Corriente continua: R1 = 0,5. Vacío: Po = PCu1 + PFe + Pmec PFe = 1258,8 W 2733 = 3 ⋅ 0,12 ⋅ 12,4 2 + PFe + Pmec 2 ⎛ 220 ⎞ 1855,7 = 3 ⋅ 0,12 ⋅ 6,5 2 + PFe ⋅ ⎜ ⎟ + Pmec ⎝ 380 ⎠ Pmec = 1418,8 W Plena carga: Pabs = 26701 = 3 ⋅ 380 ⋅ 46,2 ⋅ cos ϕ cos ϕ = 0,8781 PCu1 = 3 ⋅ 0,12 ⋅ 46,22 = 768,4 W Pa = Pabs − PCu1 − PFe = 26701 − 768,4 − 1258,8 = 24673,8 W s= (en el entrehierro) 1000 − 955 = 0,045 1000 PCu 2 = s ⋅ Pa = 0,045 ⋅ 24673,8 = 1110,3 W Pi = Pa − PCu 2 = 24673 ,8 − 1110 ,3 = 23563 ,5 W Pi − Pmec = 23563 ,5 − 1418 ,8 = 22144 ,7 © Los autores, 2006; © Edicions UPC, 2006 201 Máquinas asíncronas Pu = M u .w = M u . 9,8N 1m 2π 2π ⋅ n = 955 ⋅ ⋅ 2250cm ⋅ Kg ⋅ ⋅ = 22051,6 W 1Kg 100cm 60 60 Padicional = 22144,7 − 22051,6 = 93,08 W Pérdidas totales = PCu1 + PCu 2 + PFe + Pmi + Padicionale s = 4649 ,4 W Y el rendimiento vale: η = Pútil 22051,6 = = 0 ,8259 Pabs 26701 (82,59 %) © Los autores, 2006; © Edicions UPC, 2006 202 Problemas de electrotecnia 5.7 Problema 7 Un motor asíncrono trifásico conectado en triángulo a una red de 230 V absorbe una potencia de 65 kW, con un factor de potencia de 0,87 inductivo. Por otra parte, se sabe que R1 = R2 ' y que cuando gira a 1410 rpm, el par generado por el motor es máximo. Si se deprecian la rama en paralelo del circuito equivalente y las pérdidas mecánicas, determinar: a) Corriente absorbida, rendimiento del motor y par mecánico interno a 1450 rpm b) Corriente absorbida y par durante el arranque c) Velocidad de giro cuando arrastra un par resistente de 40 N.m Resolución: En las condiciones del enunciado y teniendo en cuenta que el estator está conectado en triángulo: Pabs = 3 ⋅ U fase ⋅ I fase ⋅ cos ϕ 65000 = 3 ⋅ 230 ⋅ I linea ⋅ 0,87 3 I fase = Ilinea = 187,55 A 187 ,55 3 = 108,28 A I fase = 108 ,28∠ − ar cos 0 ,87 = 108 ,28∠ − 29 ,54º A Circuito equivalente triángulo por fase: R1 Ufase X1 R2’ X’2 Ifase R2’(1/s -1) Figura 5.7.1 Z eq = Donde: 230∠0º = 2 ,124∠29 ,54º = 1,848 + j1,047 Ω 108,28∠ − 29 ,54º 1,848 = R1 + R2 ' s Siendo s desconocido 1,047 = X 1 + X 2 ' = X 1CC © Los autores, 2006; © Edicions UPC, 2006 203 Máquinas asíncronas Por otra parte, según el enunciado, se obtiene el par máximo para una velocidad de 1410 rpm, es decir (ns = 1500 rpm ): s max = 1500 − 1410 = 0,06 1500 Según el enunciado: R1 = R2 ' R2 ' s max = R1 2 + X 1CC 2 → = 0,06 De aquí resulta: R2 ' = 0,06 ⋅ R12 + X 1CC 2 = 0,06 ⋅ R2 '2 +1,047 2 R 2 ' = 0,063 Ω = R1 a) Para 1450 rpm Z T = R1 + I fase = U → s= 1500 − 1450 = 0 ,0333 1500 0 ,063 R2 ' + j ⋅ X 1CC = 0 ,063 + + j ⋅ 1,047 Ω 0 ,0333 s fase ZT = → Z T = 2,227∠28,72º Ω 230∠0º = 103,28∠ − 28,72 A 2,227∠28,72º I linea = 3 ⋅ I fase = 178,88 A Pabs = 3 ⋅ U linea ⋅ I linea ⋅ cosϕ = 3 ⋅ 230 ⋅ 178,88 ⋅ cos 28,72 = 62495,05 W Putil = Pabs − PFe − PCu1 − PCu 2 − Pmec Al ser, según el enunciado, PFe = Pmec = 0 , resulta: Putil = 62495,05 − 3 ⋅103,28 2 ⋅ (0,063 + 0 ,063) = 58463,02 W El rendimiento será: η = 100 ⋅ Putil 58463,02 = 100 ⋅ = 93,55% Pabs 62495,05 P 58463,02 = 385,02 N.m Mi = i = ω 2π ⋅1450 60 b) En el arranque se tiene n = 0 y s = 1: R '⎞ ⎛ Z arranque = ⎜ R1 + 2 ⎟ + j ⋅ X 1CC = (0,063 + 0,063) + j ⋅ 1,047 = 1,077∠83,28º Ω s ⎠ ⎝ I fase arr = 230 = 213,56 A 1,077 © Los autores, 2006; © Edicions UPC, 2006 204 Problemas de electrotecnia I abs arr = 3 ⋅ 213,56 = 369,89 A 2 M i arr = 3 ⋅ U 1, fase ⋅ R2 ' [ 2π 2 2 ⋅ n s ⋅ (R1 + R2 ') + X 1CC 60 ] = 57,23 N ⋅ m c) Si M i = 40 N ⋅ m 40 = 3 ⋅ 230 2 ⋅ 0,063 / s 2 ⎡⎛ ⎤ 0 ,063 ⎞ 2π 2 ⋅1500 ⋅ ⎢⎜ 0,063 + ⎟ + 1,047 ⎥ 60 s ⎠ ⎢⎣⎝ ⎥⎦ Ecuación que, una vez resuelta, resulta: s = 0,0987 0,0987 = s = −0,0826 1500 − n 1500 → (sin sentido físico) n = 1351,95 rpm © Los autores, 2006; © Edicions UPC, 2006 205 Máquinas asíncronas 5.8 Problema 8 Se dispone de un motor asíncrono trifásico de 3 pares de polos, conectado en triángulo a una red de 400 V. 1. Condiciones a plena carga: 400 V, 35 A, 50 Hz, cos φ = 0,85 inductivo. 2. En el arranque a 400 V: Iarranque = 3,5 In, cos φarranque = 0,3, Marranque = 190 N·m Despreciando la rama en paralelo del circuito equivalente, calcular: a) Circuito equivalente b) El motor acciona un carga mecánica que presenta un par resistente de giro MR = 0,15.n+19,1 N.m, estando expresada la velocidad en rpm. En estas condiciones, determinar el rendimiento del motor, la potencia absorbida, la velocidad de giro y el factor de potencia. Resolución: ns = 60. f 60.50 = = 1000 rpm 3 p En el arranque se tiene s = 1: R '⎞ ⎛ Z arr = ⎜ R1 + 2 ⎟ + j ⋅ X1CC = (R1 + R2' ) + j ⋅ X1CC s ⎠ ⎝ U fase 400∠0º arr = Z arr = = 5,656∠72,54º = 1,697 + j 5,395 = (R1 + R2 ') + j ⋅ X1CC 35 I fase ∠ − ar cos 0,3 3,5 ⋅ arr 3 Resulta: R1 + R2’ = 1,697 Ω X1CC = 5,395 Ω R' 3 ⋅ U1, fase 2 ⋅ 2 3 ⋅ U1, fase 2 ⋅ R2' s M arr = = 2 ⎤ 2π ⋅ n ⋅ (R + R ' )2 + X ⎡⎛ 2 R '⎞ 2π 1 2 1CC s ⋅ ns ⋅ ⎢⎜ R1 + 2 ⎟ + X1CC 2 ⎥ 60 s ⎠ 60 ⎥⎦ ⎢⎣⎝ [ 190 = 3 ⋅ 400 2 ⋅ R2 ' ( 2π ⋅ 1000 ⋅ 1,697 2 + 5,395 2 60 ) → R2 ' = 1,326 Ω b) M = MR 3 ⋅ 400 2 ⋅ 1,326 s 2 ⎡⎛ ⎤ 2π 1,326 ⎞ 2 ⋅1000 ⋅ ⎢⎜ 0,371 + ⎟ + 5,395 ⎥ s ⎠ 60 ⎢⎣⎝ ⎥⎦ = 0,15 ⋅ n + 19,10 © Los autores, 2006; © Edicions UPC, 2006 ] → R1 = 0,371 Ω 206 Pero Problemas de electrotecnia s= ns − n 1000 − n = ns 1000 n = 1000 ⋅ (1 − s ) → Sustituyendo en la anterior ecuación, resulta: 0,05 s= 0,522 ± j1,049 sin sentido físico n = 1000 ⋅ (1 − s ) = 1000 ⋅ (1 − 0,05) = 950 rpm 1,326 ⎞ ⎛ Z = ⎜ 0,371 + ⎟ + j 5,395 = 27,427∠11,34º Ω 0,05 ⎠ ⎝ cosϕ = cos11,34º = 0,98 I fase = 400 = 14,58 A 27,427 → I linea = 3 ⋅ 14,58 = 25,26 A Pabs = 3 ⋅ U linea ⋅ I linea ⋅ cos ϕ = 3 ⋅ 400 ⋅ 25,26 ⋅ 0,98 = 17150,63 W Pu = M u ⋅ ω = M u ⋅ 2 ⋅π ⋅ n 2 ⋅ π ⋅ 950 = (0,15 ⋅ 950 + 19,10) ⋅ = 16076,57 W 60 60 Y el rendimiento será: η= Pu 16076,57 ⋅ 100 = ⋅ 100 = 93,74% Pabs 17150,63 © Los autores, 2006; © Edicions UPC, 2006 207 Máquinas asíncronas 5.9 Problema 9 Un motor trifásico, asíncrono de 400 V/690 V, 50 Hz, 4 polos, presenta los parámetros siguientes: R1 = R2 ' = 1 Ω X1 = X 2 ' = 6,6 Ω Se suponen unas pérdidas mecánicas de 250 W y se desprecia la rama en paralelo del circuito equivalente. El motor se conecta a una red de 400 V, 50 Hz. Se pide: a) Tipo de conexión del bobinado del estator para poder conectarlo a la red de 400 V b) Corriente de línea en el arranque c) Corriente absorbida a plena carga para un deslizamiento del 5 %. Calcular también las potencias absorbida, útil, y el rendimiento del motor d) Par mecánico interno a plena carga e) Velocidad para la cual se obtiene el par máximo, así como el valor del mismo Resolución: a) La conexión del bobinado del estator debe ser triángulo, a fin que a cada bobinado le llegue la tensión más pequeña de 400 V/690 V. b) En el arranque se tiene s = 1 y por lo tanto resulta, Z arr = (R1 + R2 ') + j ⋅ ( X1 + X 2 ') = (1 + 1) + j ⋅ (6,6 + 6,6 ) = 13,35∠81,38º Ω I arrlinea = 3 ⋅ I arr fase = 3 ⋅ U fase Z arranque = 3⋅ 400 = 51,90 A 13,35 c) R '⎞ 1 ⎞ ⎛ ⎛ Z = ⎜ R1 + 2 ⎟ + j ⋅ ( X1 + X 2' ) = ⎜1 + ⎟ + j ⋅ (6 ,6 + 6,6 ) Ω s ⎠ ⎝ ⎝ 0 ,05 ⎠ Ilinea = 3 ⋅ I fase = 3 ⋅ U fase Z fase = 3⋅ → Z = 24,80∠32,15º Ω 400 = 27 ,94 A 24,80 Pabs = 3 ⋅ U linea ⋅ I linea ⋅ cos ϕ = 3 ⋅ 400 ⋅ 27,94 ⋅ cos 32,15º → 2 Pabs = 16389,09 W ⎛ 1 ⎞ ⎛ 27 ,94 ⎞ ⎛1 ⎞ 2 − 1⎟ − 250 = 14582,23 W Pu = Pi − Pmec = 3 ⋅ I fase ⋅ R2' ⋅⎜ − 1⎟ − Pmec = 3 ⋅ ⎜ ⎟ ⋅1⋅ ⎜ s 0 , 05 3 ⎝ ⎠ ⎝ ⎠ ⎝ ⎠ Y el rendimiento resulta: η= Pu 14582 ,23 ⋅100 = ⋅100 = 88,99% Pabs 16389 ,09 © Los autores, 2006; © Edicions UPC, 2006 208 Problemas de electrotecnia d) n −n s= s ns → Pi = Mi.ω = Mi. 0,05 = 2π ⋅n 60 → 1500 − n → 1500 14832 ,23 = Mi. n = 1425 rpm 2π ⋅ 1425 60 → Mi = 99,39 N.m El par interno también se puede calcular a partir de la expresión: Mi = 3 ⋅ U1, fase 2 ⋅ R2' s 3 ⋅ 4002 ⋅ 2 ⎤ ⎡⎛ R '⎞ 2π ⋅ ns ⋅ ⎢⎜ R1 + 2 ⎟ + X1CC 2 ⎥ s ⎠ 60 ⎥⎦ ⎢⎣⎝ = 1 0,05 2 ⎤ ⎡⎛ 2π 1 ⎞ ⋅ 1500 ⋅ ⎢⎜1 + ⎟ + 13,22 ⎥ 60 ⎥⎦ ⎢⎣⎝ 0,05 ⎠ = 99 ,39 N.m e) smax = R2' R12 n −n s= s ns + X1CC 2 → = 0 ,07554 0 ,07554 = 3 ⋅ U1, fase 2 ⋅ M i ,max = 1500 − n max 1500 R2' smax 2 ⎤ ⎡⎛ 2π R2' ⎞ ⎢ ⎜ ⎟ ⋅ ns ⋅ ⎜ R1 + + X1CC 2 ⎥ ⎟ ⎥ ⎢⎝ 60 smax ⎠ ⎦ ⎣ → nmax = 1386,69 rpm = 107 ,31 N.m © Los autores, 2006; © Edicions UPC, 2006 209 Máquinas asíncronas 5.10 Problema 10 La máquina eléctrica del ejercicio anterior, conectada a la misma red, es impulsada por un motor auxiliar que le obliga a girar a 1575 rpm. Calcular: a) Corriente absorbida por la máquina b) Potencia mecánica que la máquina eléctrica absorbe del motor auxiliar c) Potencia, activa y reactiva que la máquina eléctrica entrega a la red d) Pérdidas por efecto Joule en la máquina eléctrica e) Rendimiento de la máquina eléctrica Resolución: a) s= ns − n 1500 − 1575 = = −0,05 ns 1500 La máquina eléctrica actúa como generador, al ser s < 0 . R1 X1 R’2 X’2 ⎛1 ⎞ R'2 ⋅⎜ − 1⎟ ⎝s ⎠ Figura 5.10.1 R '⎞ 1 ⎞ ⎛ ⎛ Z T = ⎜ R1 + 2 ⎟ + j ⋅ ( X1 + X 2' ) = ⎜1 + ⎟ + j ⋅ (6 ,6 + 6 ,6 ) = −19 + j13,2 Ω s ⎠ ⎝ ⎝ − 0 ,05 ⎠ Z T = 23,14∠145,21º Ω Cabe destacar que: ⎛1 ⎞ R2 ' ⎜ − 1⎟ < 0 ⎝s ⎠ Lo que indica que no es una verdadera resistencia, es una estrategia para poder simular mediante un circuito eléctrico la potencia mecánica de la máquina. © Los autores, 2006; © Edicions UPC, 2006 210 Problemas de electrotecnia I 1linea = 3 ⋅ U fase ZT = 3⋅ 400∠0º = 29 ,94∠ − 145,21º A 23,14∠145,21º I 1linea( entregado a la red ) = − I 1linea = 29,94∠( −145,21 + 180º ) = 29,94∠134,79º A I1línea = 29,94 A b) Para un generador: 2 ⎛ 29 ,94 ⎞ 1 ⎞ ⎛1 ⎞ ⎟ ⋅1 ⋅ ⎛⎜ Pi = 3 ⋅ I 1' 2 ⋅R 2 ' ⋅⎜ − 1⎟ = 3 ⋅ ⎜⎜ − 1⎟ = −18824 ,48 W ⎟ s − 0 , 05 ⎝ ⎠ ⎝ ⎠ ⎝ 3 ⎠ Pmec abs = − Pi = 18824,48 W c) Pabsorbida = 3 ⋅ U linea ⋅ Ilinea ⋅ cosϕ = 3 ⋅ 400 ⋅ 29,94 ⋅ cos145,21º = −17035,20 W Pentregada = − Pabsorbida = 17035,20 W Qabsorbida = 3 ⋅ U linea ⋅ Ilinea ⋅ sinϕ = 3 ⋅ 400 ⋅ 29,94 ⋅ sin145,21º = +11835,36 VAr Qentregada = −Qabsorbida = −11835,36 VAr d) 2 ⎛ 29,94 ⎞ ⎟⎟ ⋅ ( 1 + 1 ) = 1792,81 W PJoule = 3.I 2fase .( R1 + R2' ) = 3.⎜⎜ ⎝ 3 ⎠ e) η= Peléctrica entregada Pentregada por el motor auxiliar ⋅ 100 = 17035,20 ⋅ 100 = 90,5% 18824,48 © Los autores, 2006; © Edicions UPC, 2006 211 Máquinas asíncronas 5.11 Problema 11 La máquina eléctrica del ejercicio 9 actúa como motor, girando a plena carga, con un deslizamiento del 5 %. De forma instantánea se permuta la conexión de dos fases de la red. Calcular en este instante: a) Corriente absorbida por la máquina b) Potencia mecánica absorbida a través del eje del motor c) Par interno, desarrollado como freno d) Potencia absorbida de la red e) Pérdidas por efecto Joule, que tienen lugar en el motor Resolución: a) Antes de permutar las fases: s = 0,05, resultando n = 1425 rpm Al permutar la conexión de dos fases el campo gira en sentido contrario al rotor y resulta: ns = −1500 rpm s= ns − n −1500 − 1425 = = 1,95 ns − 1500 Al ser s > 1, el motor actúa como freno: 1 ⎞ R '⎞ ⎛ ⎛ Z T = ⎜ R1 + 2 ⎟ + j ⋅ ( X1 + X 2' ) = ⎜1 + ⎟ + j ⋅ (6 ,6 + 6 ,6 ) = 13,29∠83,46º Ω 1 95 ⎠ s , ⎠ ⎝ ⎝ I línea= 3 ⋅ I fase = 3 ⋅ U fase ZT = 3⋅ 400 = 52,13 A 13,29 b) R1 X1 R’2 X’2 P eléctrica ⎛1 ⎞ R'2 ⋅⎜ − 1⎟ ⎝s ⎠ Figura 5.11.1 © Los autores, 2006; © Edicions UPC, 2006 P mecánica 212 Problemas de electrotecnia 2 ⎛ 52,13 ⎞ 1 ⎞ ⎛1 ⎞ ⎟ ⋅1 ⋅ ⎛⎜ Pi = 3 ⋅ I 2 ' 2 ⋅R 2 ' ⎜ − 1⎟ = 3 ⋅ ⎜⎜ − 1⎟ ⎟ s , 1 95 ⎝ ⎠ ⎝ ⎠ ⎝ 3 ⎠ Pi = −1323,93 W < 0 Lo cual indica que el motor absorbe potencia de la carga que arrastra. Pmec abs = 1323,93 W c) P − 1323,93 = −8,87 N.m Mi = i = ω 2π ⋅1425 60 El par va en sentido contrario al movimiento, es un par de frenado. d) ⎛ 52 ,13 ⎞ ⎟.cos83,46º = 4113,58 W Pelect abs = 3 ⋅ U fase ⋅ I fase ⋅ cos ϕ = 3 ⋅ 400 ⋅ ⎜⎜ ⎟ ⎝ 3 ⎠ e) Las pérdidas por efecto Joule se pueden calcular de dos formas: 2 ⎛ 52,13 ⎞ ⎟⎟ ⋅ ( 1 + 1 ) = 5435,07 W PJoule = 3.I'22 .( R1 + R2' ) = 3 ⋅ ⎜⎜ ⎝ 3 ⎠ PJoule = Pelectr ,abs + Pmec ,abs = 4113,58 + 1323,93 = 5437,51 W © Los autores, 2006; © Edicions UPC, 2006 213 Máquinas asíncronas 5.12 Problema 12 Se dispone de un motor trifásico, asíncrono, 400 V/690 V, 50 Hz, 11 kW, 6 polos, factor de potencia 0,78 y par mecánico interno 109 N.m a 970 rpm. a plena carga. La resistencia por fase que presenta el estator es de 0,27 Ω. Efectuando el ensayo de vacío, el motor consume 10 A y absorbe una potencia de 900 W. Se conecta el motor a una red de 400 V. Calcular: a) Las pérdidas que tiene lugar en el motor cuando trabaja a plena carga b) Potencia absorbida por el motor a plena carga c) Rendimiento a plena carga Resolución: a) El motor se debe conectar en estrella. Pabs = PFe1 + PCu1 + Pa = PFe1 + PCu1 + PFe 2 + PCu 2 + Pi = PFe1 + PCu1 + PFe 2 + PCu 2 + Pmec + Putil Siendo PFe2 = 0, al ser la frecuencia de las corrientes del rotor muy baja. A plena carga: s= ns − n 1000 − 970 = = 0,03 1000 ns Pi = M i ⋅ ω = 109 ⋅ 2π ⋅ 970 = 11072 ,02 W 60 Pa = Pi + PCu 2 = Pi + s ⋅ Pa Pa = Pi 11072 ,02 = = 11414,45 W 1− s 1 − 0 ,03 PCu 2 = Pa − Pi = 342,43 W Pu = 11000 W (segun enunciado) Pmec = Pi − Pu = 11072,02 − 11000 = 72,02 W Del ensayo en vacío, y suponiendo PCu 2 ≅ 0 al ser la corriente del rotor muy baja y Puo = 0: Po = PCu 10 + PFe10 + Pmec 2 ⎛ 10 ⎞ 900 = 3 ⋅ ⎜ ⎟ ⋅ 0 ,27 + PFe 10 + 72 ,02 ⎝ 3⎠ → PFe10 ≈ PFe1 = 800 ,98 W © Los autores, 2006; © Edicions UPC, 2006 214 Problemas de electrotecnia b) Pabs = 3 ⋅ U fase ⋅ I fase ⋅ cos ϕ = Pa + PCu1 + PFe1 2 3 ⋅ 400 ⋅ I fase ⋅ 0 ,78 = 11414 ,45 + 3 ⋅ I fase ⋅ 0 ,27 + 800 ,98 I fase = 1142 ,4 A (sin sentido fisico) 13,20 A Ilinea = 3 ⋅ I fase = 3 ⋅13,20 = 22,86 A Pabs = 3 ⋅ 400 ⋅13,20 ⋅ 0,78 = 12358,7 W c) η= Pu 11000 ⋅ 100 = ⋅ 100 = 89 ,06 % Pabs 12358,7 © Los autores, 2006; © Edicions UPC, 2006 215 Máquinas asíncronas 5.13 Problema 13 Un motor asíncrono trifásico de jaula de ardilla mueve la cabina de un ascensor. Las características del motor son: 230 V/400 V, 50 Hz, 120 polos. Dicho motor se conecta a una red trifásica de 400 V y 50 Hz. La resistencia del estator por fase vale 1 Ω. Efectuando las pruebas de vacío y cortocircuito, han dado los siguientes resultados: Ensayo de vacío: 230 V, 4,4 A, 800 W, 49,8 rpm (considerar el circuito equivalente completo) Ensayo de cortocircuito (rotor bloqueado): 36 V, 10,1 A, 550 W Considerando que el par de pérdidas mecánicas de la máquina permanece constante, determinar: a) Tipo de conexión del estator del motor. b) Circuito equivalente aproximado por fase. c) Velocidad de ascenso de la cabina, sabiendo que el peso total es de 350 Kg y el radio de la polea de 0,15 m. Resolución: a) Dado que el motor es de 230 V/400 V y la red es de 400 V, la conexión debe ser en estrella. R S T Figura 5.13.1 b) El circuito equivalente estrella aproximado por fase es: X1 R1 RFe R’2 X’2 ⎛1 ⎞ R '2 ⋅⎜ − 1⎟ ⎝s ⎠ Xµ Figura 5.13.2 © Los autores, 2006; © Edicions UPC, 2006 216 Problemas de electrotecnia Ensayo rotor bloqueado: → n=0 s=1 Pcc = 3 ⋅ I 1cc , fase 2 ⋅ R1cc Al ser R1 = 1 Ω → I1cc = 550 = 3 ⋅10 ,12 ⋅ R1cc → → R1cc = 1,80 Ω → Z1cc = 2,057 Ω R'2 = R1cc − R1 = 1,8 − 1 = 0,8 Ω Vcc ,linea / 3 → Z1cc 10,1 = 36 / 3 Z 1cc X 1cc = Z 1cc 2 − R1cc 2 = 2 ,057 2 − 1,8 2 = 0,997 Ω Ensayo de vacío: ns = 60 ⋅ f 60 ⋅ 50 = = 50 rpm p 60 → n −n 50 − 49 ,8 so = s o = = 0,004 ns 50 2 ⎛ R' ⎞ Vo = I 1o ⋅ ⎜⎜ R1 + 2 ⎟⎟ + X 1cc 2 so ⎠ ⎝ 2 ⎛ 0,8 ⎞ = I1o ⋅ ⎜⎜1 + ⎟⎟ + 0,997 2 0 , 004 3 ⎝ ⎠ 230 PR1 cc o → I 1o = 0,661 A = PCu1 + PCu 2 = 3 ⋅ I1o 2 ⋅ R1cc = 3 ⋅ 0,6612 ⋅ 1,80 = 2 ,36 W Dado que no hay potencia útil al trabajar el motor en vacío, se cumple: Pi = Pmec ⎞ ⎛1 ⎞ ⎛ 1 Pi = Pmec = 3 ⋅ I1o 2 ⋅ R'2 ⋅⎜⎜ − 1⎟⎟ = 3 ⋅ 0 ,6612 ⋅ 0 ,8 ⋅ ⎜ − 1⎟ = 261,04 W s 0 , 004 ⎠ ⎝ ⎝ o ⎠ → Po = 3 ⋅ Vlinea o ⋅ I linea o ⋅ cos ϕo 800 = 3 ⋅ 230 ⋅ 4 ,4 ⋅ cos ϕ o Resulta: cos ϕo = 0,456 y sin ϕo = 0,890 PFe = Po − PR1CCo − Pmec = 800 − 2,36 − 261,04 = 536,54 W RFe = 3 ⋅ U fase o 2 PFe (230 3 ) 2 = 3⋅ 536,54 → RFe = 98,59 Ω Qo = 3 ⋅ U lineao ⋅ Ilineao ⋅ sin ϕo = 3 ⋅ 230 ⋅ 4,4 ⋅ 0,890 = 1559,63 VAr Por otra parte: Qo = 3 ⋅ U 2 linea o 2 + 3.I 1o .X 1cc Xµ → 1559 ,63 = 3 ⋅ ( 230 / 3 ) 2 + 3.0 ,6612 .0 ,997 Xµ X µ = 33,95 Ω © Los autores, 2006; © Edicions UPC, 2006 217 Máquinas asíncronas c) MOTOR Mmotor Mpérdidas Mresistente CABINA Figura 5.13.3 Cabe recordar que, según el enunciado, las pérdidas mecánicas son constantes e independientes de la velocidad. M motor = M resist + M pérdidas mecánicas 3 ⋅ U 21, fase ⋅ R'2 s 2 ⎤ ⎡⎛ R '⎞ 2π ⋅ ns ⎢⎜ R1 + 2 ⎟ + X1CC 2 ⎥ s ⎠ 60 ⎥⎦ ⎢⎣⎝ P = m ⋅ g ⋅ R + mec 2π .n 60 2 ⎛ 400 ⎞ 0 ,8 3⋅⎜ ⎟ ⋅ s 261,1 ⎝ 3⎠ = 350 ⋅ 9 ,8 ⋅ 0 ,15 + 2 2π ⎤ ⎡⎛ 0 ,8 ⎞ 2π 2 ⋅ 49 ,8 ⋅ n s ⋅ ⎢⎜1 + ⎟ + 0 ,997 ⎥ 60 60 s ⎠ ⎥⎦ ⎢⎣⎝ De la ecuación anterior resulta: 2040 (sin sentido físico) s= 0,0154 s= ns − n ns ω= 2π .n 2π = ⋅ 49 ,23 = 5,155 rad/s 60 60 → 0,0154 = 50 − n 50 → n = 49,23 rpm v = ω ⋅ R = 5,155 ⋅ 0,15 = 0,773 m/s © Los autores, 2006; © Edicions UPC, 2006 218 Problemas de electrotecnia 5.14 Problema 14 Un motor asíncrono trifásico 400 V/690 V, 37 kW, 6 polos, 50 Hz, rendimiento del 92,5 % y factor de potencia 0,85 inductivo. Cuando se conecta a una red de 400 V presenta un par de arranque igual a 1,7 veces el par nominal, siendo la corriente en este instante igual a 6 veces la corriente nominal. Se pretende arrancar el motor mediante un autotransformador para poder conseguir reducir la corriente de arranque, siendo el par de arranque mínimo requerido de 1,1 veces el par nominal. Calcular: a) Tensión que se debería aplicar al motor durante el arranque b) Corriente de arranque del motor c) Corriente absorbida de la red por el autotransformador Resolución: a) Dado que: Mi = 3⋅ R2 ' ⋅ U 1, fase 2 s 2 ⎡⎛ ⎤ R '⎞ 2π ⋅ n s .⎢⎜⎜ R1 + 2 ⎟⎟ + X 1CC 2 ⎥ 60 s ⎠ ⎢⎝ ⎥ ⎣ ⎦ M arr directo = M arr autotrafo M arr = k ⋅ U 1 2 → En el arranque: s = 1 U 2 directo 1,7 ⋅ Mn = 1 1,1 ⋅ Mn U 1 2 autotrafo 1,7 400 2 = 1,1 U 1 2 autotrafo → Resultando: U 1 autotrafo = 321,76 V b) Pabs = In = Pu η = 37000 = 40000 W 0 ,925 Pabs 3 ⋅ U n ⋅ cos ϕ = 40000 3 ⋅ 400 ⋅ 0 ,85 = 67 ,9235 A Durante el arranque directo la corriente es: U1directo U1autotrafo = I1directo / 3 I1autotrafo / 3 → I arr = 6.I n = 6 ⋅ 67,9235 = 407,541 A 400 6 ⋅ 67 ,9235 = 321,76 I 1 autotrafo → I1autotrafo = 327 ,826 A c) El autotransformador empleado debe tener una relación de transformación de: © Los autores, 2006; © Edicions UPC, 2006 219 Máquinas asíncronas rt = 400 321,76 Luego la corriente del autotransformador será: 327,826 = 263,70 A rt © Los autores, 2006; © Edicions UPC, 2006 220 Problemas de electrotecnia 5.15 Problema 15 Un motor trifásico asíncrono 230 V/400 V, 50 Hz, 3 kW, η = 72 %, cosφ = 0,67 (i), se conecta a una línea monofásica de 230 V y 50 Hz. a) Dibujar un esquema para poder conectar el motor a la línea monofásica. b) Explicar cómo se puede invertir el sentido de giro. c) Determinar el valor del condensador a utilizar. d) Desfase entre flujos que se consigue mediante la utilización del condensador del apartado c). Resolución: a) y b) L N Sentido de giro 230 V 50 Hz Placa de conexión Sentido de giro Figura 5.15.1 Si se tuviera que conectar a 400 V L N Sentido de giro 400 V 50 Hz Placa de conexión Sentido de giro Figura 5.15.2 © Los autores, 2006; © Edicions UPC, 2006 221 Máquinas asíncronas El condensador debe soportar como mínimo una tensión de 1,25 Un debido a las sobretensiones que se pueden producir por efectos de resonancia. Los flujos de las bobinas se han de desfasar 90º (condición óptima). c) Cálculo del valor del condensador: Zϕ Z -j.XC ϕ I1 Zϕ Z1 I2 Z2 Figura 5.15.3 Z1 = Zϕ Z 2 = Zϕ + I1 = I2 = Z ϕ (− jXc ) ⎡ Z ϕ − 2. jXc ⎤ ⎡ − jXc ⎤ ϕ −θ = Zϕ ⎢ = Z ϕ ⎢1 + ⎥ = Z2 ⎥ ϕ ϕ ϕ Z − jXc ⎣⎢ Z − jXc ⎦⎥ ⎣⎢ Z − jXc ⎦⎥ I2 V 0º Zϕ V ϕ 0º Z 2ϕ −θ V θ I1 El desfase entre las corrientes I2 e I1 se calcula como: ⎛ Z . sin ϕ − X C ⎝ Z . cos ϕ θ = arctg⎜⎜ tgθ = tg( β − α ) = ⎛ Z . sin ϕ − 2.X C ⎞ ⎟⎟ − arctg⎜⎜ Z . cos ϕ ⎝ ⎠ ⎞ ⎟⎟ = β − α ⎠ Z .X C . cos ϕ tgβ − tgα Z . cos ϕ = = 1 + tgβ .tgα Z 2 − 3.Z .X C . sin ϕ + 2.X C2 Z 2 / X C − 3.Z . sin ϕ + 2.X C Para que el desfase θ entre I2 y I1 sea máximo, se debe cumplir (maximizar θ equivale a maximizar tg θ): d ( tgθ ) =0 dX C → −Z2 +2=0 X C2 → XC = Z 2 siendo Z la impedancia por fase del motor. Supondremos el motor conectado en triángulo a una línea de 230 V: I fase = Pabs Pu / η 3000 / 0,72 = = = 9,01 A 3.U fase . cos ϕ 3.U fase . cos ϕ 3.230.0,67 El resultado anterior es congruente con los datos de partida del enunciado. © Los autores, 2006; © Edicions UPC, 2006 222 Problemas de electrotecnia Z= V fase = I fase XC = 230 = 25,52 Ω → 9,01 1 → ω .C XC = 18,05 = Z 2 1 2.π .50.C = 25,52 2 = 18,05 Ω → C = 176,4 µF Un método práctico aproximado es suponer 60-70 µF/1 kW. d) tgθ = Z . cos ϕ 2 Z / X C − 3.Z . sin ϕ + 2.X C 0,67 2. 2 − 3.0,742 cos ϕ = Z / X C − 3. sin ϕ + 2.X C / Z → FP = cosφ = 0,67 (i) tgθ = = = 1,114 → φ = 47,93º → cos ϕ 2 − 3. sin ϕ + 2 / 2 sinφ = 0,742 θ = 48,09º Aunque sería óptimo θ ≈ 90º, con el desfase obtenido es suficiente para que el motor gire sin problemas. © Los autores, 2006; © Edicions UPC, 2006 223 Máquinas asíncronas 5.16 Problema 16 Un motor asíncrono trifásico con el estator conectado en triángulo se alimenta de una línea de 380 V y 50 Hz. Absorbe 13953,94 W cuando tiene un par de salida de 122,13 N.m y un rendimiento del 87,092%. Les pérdidas mecánicas del motor son Pmec = n/2 W, siendo n la velocidad expresada en rpm. Se sabe que R1 = R2’ = R Ω, X1 = X2’ = 6,2.R Ω. Se pide: a) La velocidad y el número de pares de polos del motor b) Las pérdidas por efecto Joule en el rotor c) El valor de R d) El par de arranque del motor Nota: despreciar la rama en paralelo del circuito equivalente Resolución: a) Pu = η .Pabs = 0,87092.13953,54 = 12152,41 W P 12152,41 = 99,484 rad/s ω= u = Mu 122,13 → n= ω ⋅ 60 = 950 rpm 2π Por lo tanto tiene que ser p = 3 b) Pmec = s= n = 475 W 2 1000 − 950 = 0 ,05 1000 Pi = Pu + Pmec = 12150 + 475 = 12625 W Pi = ( 1 − s )Pa → 12625 = ( 1 − 0 ,05 )Pa → Pa = 13289 ,47 W Pcu2 = s ⋅ Pa = 664,47 W c) Pi = M i ⋅ ω 126,9 = → 12625 = M i ⋅ 99 ,484 3 ⋅ V1, fase 2 ⋅ → M i = 126 ,9 Nm R2' s 2 ⎡⎛ ⎤ R '⎞ 2π ⋅ ns ⎢⎜ R1 + 2 ⎟ + ( X1 + X 2' )2 ⎥ s ⎠ 60 ⎢⎣⎝ ⎥⎦ © Los autores, 2006; © Edicions UPC, 2006 224 Problemas de electrotecnia 3 ⋅ 380 2 ⋅ 126 ,9 = d) [( R 0,05 2π .1000 ⋅ 212 ⋅ R 2 + 12 ,4 2 ⋅ R 2 60 → )] R = 1,096 Ω Durante el arranque se cumple que s = 1 M arr = [ 3 ⋅ 380 2 ⋅1,096 2π ⋅1000 ⋅ (2 ⋅1,096 )2 + (2 ⋅ 6 ,2 ⋅1,096 )2 60 ] → M arr = 23,93 Nm © Los autores, 2006; © Edicions UPC, 2006 225 Máquinas asíncronas 5.17 Problema 17 Un motor asíncrono trifásico de rotor bobinado tiene los bobinados del estator y del rotor conectados en estrella. Se alimenta a su tensión nominal de 400 V y 50 Hz. A plena carga gira a 1440 rpm. Se sabe que R1 = 1 Ω, R2’ = 0,8 Ω, X1cc = 5 Ω y que las relaciones de transformación de tensión y de corriente son idénticas y de valor 2. Despreciando las pérdidas mecánicas y la rama en paralelo del circuito equivalente, calcular: a) La intensidad de corriente absorbida por el motor y el par interno a plena carga b) La corriente absorbida y el par de arranque con los anillos en cortocircuito c) La resistencia por fase que se debe conectar en serie con el rotor para que desarrolle el par máximo durante el arranque Resolución: a) R1 X1 R’2 X’2 ⎛1 ⎞ R' 2 ⋅⎜ − 1⎟ ⎝s ⎠ Figura 5.17.1 s= ns − n 1500 − 1440 = = 0 ,04 ns 1500 I1,línea = I1, fase = V1, fase Z1, fase (4%) V1, fase = ( R1 + R2' / s )2 + X12cc = 400 / 3 ( 1 + 0,8 / 0,04 )2 + 52 = 10,70 A ⎞ ⎛ 1 ⎛1 ⎞ ⎛1 ⎞ Pi = 3.I' 22 .R 2 '.⎜ − 1⎟ = 3.I 12, fase .R 2 '.⎜ − 1⎟ = 3.10 ,70 2 .0 ,8.⎜ − 1⎟ = 6594,6 W ⎝s ⎠ ⎝s ⎠ ⎝ 0,04 ⎠ Pi = M i .ω = M i . 2.π ⋅n 60 → Mi = 60.Pi 60.6594 ,6 = = 43,73 N.m 2.π .n 2.π .1440 b) En el momento del arranque se tiene s = 1: I arr = V1, fase Z 1,arr = V1, fase 2 ( R1 + R2 ' / 1 ) + X 12cc = 400 / 3 ( 1 + 0,8 ) 2 + 5 2 = 43,46 A © Los autores, 2006; © Edicions UPC, 2006 226 Problemas de electrotecnia R ' 0,8 3 ⋅ V1, fase 2 ⋅ 2 3 ⋅ ( 400 / 3 ) 2 ⋅ s 1 M i ,arr = = = 28,86 N.m 2 2 ⎡ ⎤ ⎡ ⎤ 2π .n s ⎛ 2π .1500 ⎛ 0 ,8 ⎞ R2 ' ⎞ 2 2 ⋅ ⎢⎜1 + ⋅ ⎢⎜ R1 + ⎟ + X 1cc ⎥ ⎟ +5 ⎥ 60 1 ⎠ 60 ⎢⎜⎝ s ⎟⎠ ⎥ ⎢⎣⎝ ⎥⎦ ⎣ ⎦ c) sM max = M i ,max = R2' R12 + X12cc 0 ,8 = 2 1 + 52 3 ⋅ V1, fase 2 ⋅ R2' s = 0 ,157 2 ⎤ ⎡⎛ R '⎞ 2π ⋅ ns ⋅ ⎢⎜ R1 + 2 ⎟ + X12cc ⎥ s ⎠ 60 ⎥⎦ ⎢⎣⎝ = 3 ⋅ ( 400 / 3 )2 ⋅ 0,8 0,157 2 ⎤ ⎡⎛ 0,8 ⎞ 2π ⋅ 1500 ⋅ ⎢⎜1 + ⎟ + 52 ⎥ 60 ⎥⎦ ⎢⎣⎝ 0,157 ⎠ = 83,50 N.m Para obtener el par máximo durante el arranque: R ' + R'2 ,añadida 0 ,8 + R'2 ,añadida sarr = 1 = 2 = R12 + X12cc 12 + 52 R2 ,añadida = R'2 ,añadida rtV .rt I = → 4,30 = 1,075 Ω 2.2 © Los autores, 2006; © Edicions UPC, 2006 R’2,añadida = 4,30 Ω 227 Máquinas asíncronas 5.18 Problema 18 Se dispone de un motor asíncrono trifásico de 230 V/400V, 50 Hz, 100 polos y rotor de jaula. A continuación se exponen los resultados de los diversos ensayos a los que se le ha sometido: - Ensayo de corriente continua: 12 V, 19,8 A (con el estator conectado en triángulo) - Ensayo de rotor bloqueado: 21,1 V, 16,25 A y 530 W (Despreciar la rama en paralelo del circuito equivalente.) - Ensayo de vacío: 230 V, 7,27 A, 750 W, 59,82 rpm (Se debe contemplar el circuito equivalente en su totalidad.) Se conecta a una red de 230 V y 50 Hz. Las pérdidas mecánicas se consideran constantes e independientes de la velocidad. Utilizar el circuito equivalente simplificado de la figura. Determinar: a) Las pérdidas mecánicas b) Los parámetros del circuito equivalente R1 RFe X1,cc R2’ RC’ = R2’(1/s-1) Xµ Figura 5.18.1 Resolución: a) y b) Al ser la red de 230 V, el motor se debe conectar en triángulo. Ensayo de corriente continua: 12 V R1∆ R1∆ R1∆ Figura 5.18.2 Req = V 12 = = 0 ,606 Ω I 19 ,8 © Los autores, 2006; © Edicions UPC, 2006 228 Problemas de electrotecnia Req = 0 ,606 = (R1∆ + R1∆ )⋅ R1∆ (R1∆ + R1∆ ) + R1∆ = 2 ⋅ R1∆ 3 → R∆ = 0,909 ∆ Ensayo de rotor bloqueado: R1CC∆ X1CC∆ 16,25 21,1 V A 3 Figura 5.18.3 PCC R1CC∆ = 3 ⋅ I1CC∆ 2 = 530 ⎛ 16,25 ⎞ ⎟⎟ 3 ⋅ ⎜⎜ ⎝ 3 ⎠ =2 Ω 2 R' 2∆ = R1CC∆ − R1 = 2 − 0,909 = 1,091 Ω Z 1CC∆ = V1CC∆ 21,1 = = 2,249 Ω I 1CC∆ 16 ,25 X 1CC∆ = 2,249 2 − 1,0912 = 1,0286 Ω → 3 Ensayo de vacío: R1∆ X1CC∆ R’2∆ I’2∆ X 1µ∆ R1Fe∆ V1 = 230 ⎛1 ⎞ R ' C = R ' 2 ⋅⎜ − 1⎟ ⎝s ⎠ Figura 5.18.4 n1 = 60 ⋅ f 60 ⋅ 50 = = 60 rpm p 50 s= 60 − 59,82 = 0,003 60 ⎞ ⎛ 1 ⎛1 ⎞ R' C = R' 2 ∆ ⋅⎜ − 1⎟ = 1,091 ⋅ ⎜ − 1⎟ = 362 ,5756 Ω ⎝s ⎠ ⎝ 0 ,003 ⎠ I' 2∆ = V1∆ ( R1CC∆ + Rc ' ) 2 + X 12CC∆ = 230 (2 + 362,5756)2 + 1,0282 2 © Los autores, 2006; © Edicions UPC, 2006 = 0,631 A 229 Máquinas asíncronas PR1 = 3 ⋅ R1∆ ⋅ I' 2 ∆ 2 = 3 ⋅ 0,909 ⋅ 0,6312 = 1,0857 W PR'2 = 3 ⋅ R' 2∆ ⋅I' 2∆ 2 = 3 ⋅1,091 ⋅ 0 ,6312 = 1,3031 W En vacío se cumple Pi = Pmec: Pi = Pmec = 3 ⋅ R' C ⋅I' 2∆ 2 = 3 ⋅ 362,5756 ⋅ 0,6312 = 433,09 W PFe = Po − PR1 − PR' 2 − Pi = 750 − 1,0857 − 1,3031 − 433,09 = 314,52 W R1Fe∆ = V12 230 2 = = 504,58 Ω 314,52 PFe 3 3 Po = 3 ⋅ V1o ⋅ I 1o ⋅ cos ϕ o → cos ϕ o = 750 3 ⋅ 230 ⋅ 7 ,27 / 3 = 0 ,259 → ϕ o = 74,95º tgϕ o = 3,723º Qo = Po ⋅ tgϕ o = 2797,37 kVAr Q µ = 2797,37 − 3 ⋅ X 1CC∆ ⋅ I 2∆ ' 2 = 2797,37 − 3 ⋅1,0286 ⋅ 0,6312 X 1µ∆ = → Q µ = 2796,14 VAr V12 230 2 = = 56,76 Ω Q µ 3 2796,14 3 © Los autores, 2006; © Edicions UPC, 2006 230 Problemas de electrotecnia 5.19 Problema 19 Se dispone de un motor trifásico asíncrono con rotor de jaula y las características siguientes: 15 CV, 220 V/380 V, 50 Hz, 4 polos, RFe = 330,91 Ω, Xµ = 74,99 Ω, R1 = R2’ = 0,5 Ω, X1+X2’ = 2,71 Ω. La red es de 380 V y 50 Hz. El circuito equivalente a tener en cuenta será: R1 RFe R2’ X1,cc RC’ = R2’(1/s-1) Xµ Figura 5.19.1 Determinar: a) El par motor en función del deslizamiento. b) El factor de potencia del motor en función del deslizamiento. c) El rendimiento eléctrico del motor en función del deslizamiento. Resolución: Al conectar el motor a una red de 380 V, el estator se debe conectar en estrella. a) Expresión del par motor: 3. Mi = Mi = 2.π . [ [ R' 2 ⋅ V12 s 3. n1 ⋅ ( R1 + R' 2 / s ) 2 + X 12cc 60 459,64 s ⋅ (0.5 + 0.5 / s ) 2 + 2.712 ] = 2.π . 0.5 ⋅ ( 380 / 3 ) 2 s [ 1500 ⋅ ( 0.5 + 0.5 / s ) 2 + 2.712 60 ] ] Representando el par interno Mi en función del deslizamiento s, resulta el gráfico de la figura siguiente: © Los autores, 2006; © Edicions UPC, 2006 231 Máquinas asíncronas 160 140 120 Par (N.m) 100 80 60 40 20 0 1,0 0,8 0,6 0,4 0,2 0,0 Deslizamiento (s) Figura 5.19.2 b) Del circuito equivalente simplificado se calcula la fase de la impedancia total, resultando: R1 RFe X1,cc R2’ RC’ = R2’(1/s-1) Xµ ZFe Zderecha Figura 5.19.3 Z Fe = 90º − arctg ( Xµ / RFe ) RFe .X µ 2 RFe 2 + Xµ = 73.1355577.23º Ω = 16.166 + j .71.327 Ω Z derecha = ( R1 + R' 2 / s ) + j .X 1cc = ( 0.5 + 0.5 / s ) + j .2.71 Haciendo el paralelo de las dos impedancias anteriores, resulta un ángulo de fase: ϕ = 77.23º +arctg( 2.71 74.037 ) − arctg( ) 0.5 + 0.5 / s ) 16.666 + 0.5 / s Representando gráficamente el factor de potencia del motor (cosφ) en función del deslizamiento, resulta el gráfico de la figura siguiente: © Los autores, 2006; © Edicions UPC, 2006 232 Problemas de electrotecnia 1.0 0.9 Factor de potencia 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 1.0 0.8 0.6 0.4 0.2 0.0 Deslizamiento (s) Figura 5.19.4 c) Para calcular el rendimiento eléctrico se debe hacer: η = 100 ⋅ Pi Pabsorbida 3. η = 100 ⋅ = 100 ⋅ V12 2 Z derecha 3.I'22 .R'c ⎡V2 3.⎢ 1 + I'22 .( R1 + R'2 + R'c ⎢⎣ RFe .R ' 2 ⋅(1 / s − 1) ⎡V2 V12 3.⎢ 1 + .( R1 + R ' 2 + R ' c 2 ⎢⎣ R Fe Z derecha ⎤ )⎥ ⎥⎦ = 100 ⋅ ⎤ )⎥ ⎥⎦ 0.5 ⋅ (1 / s − 1) 0.501511 0.0007555 0.52295 + + s s2 Representando gráficamente el rendimiento eléctrico del motor en función del deslizamiento, resulta: 100 90 80 Rendimiento 70 60 50 40 30 20 10 0 1.0 0.8 0.6 0.4 0.2 Deslizamiento (s) Figura 5.19.5 © Los autores, 2006; © Edicions UPC, 2006 0.0 233 Máquinas asíncronas 5.20 Problema 20 Un transformador trifásico de 50 kVA, 11000 V/400 V, 50 Hz, Dy11, εcc = 6%, εXcc = 4,8%, alimenta mediante una línea de 0,2 Ω/fase una estación de bombeo de agua donde hay instalada una bomba centrífuga accionada por un motor asíncrono de 11 kW, 230/400 V, 50 Hz, In = 21 A, nn = 480 rpm, FP = 0,95 (i) y Pmec = 225 W = constantes. Despreciar la rama en paralelo del circuito equivalente del motor. Se pide: a) Los parámetros del circuito equivalente del transformador reducidos al secundario (R2,cc,trafo, X2,cc,trafo) y los parámetros del circuito equivalente del motor reducidos al estator (R1,motor, R’2,motor, X1,cc,motor) b) La tensión de alimentación del transformador cuando el motor trabaja bajo condiciones nominales. c) El par interno que suministra el motor cuando gira a 490 rpm y está alimentado a tensión nominal. Resolución a ) Transformador Sn I 2n = ε CC = 3 ⋅U 2 n = 50000 3 ⋅ 400 = 72,168 A Z 2CC ⋅ I 2 nf Z 2CC = X 2CC = U 2 nf 0,06 ⋅ 400 72,168 0,048 ⋅ 400 3 = 0,192 Ω 3 72,168 = 0,1536 Ω R2CC = Z 2 2CC − X 2 2CC = 0,11519 Ω Motor (trabaja a 400 V, conexión estrella) Pmi = Pn + Pmec = 11000 + 225 = 11225 W R CC = R1 + R 2 ' XCC ⎛1 ⎞ R C ' = R 2 '⋅⎜ − 1⎟ ⎝s ⎠ I2nmotor Figura 5.20.1 Pmi = 3 ⋅ R C '⋅I 2 2 n motor I 2 n motor = 21 A © Los autores, 2006; © Edicions UPC, 2006 234 Problemas de electrotecnia RC ' = s= Pmi 11225 = = 8,4845 Ω 3 ⋅ I 2 n motor 3 ⋅ 212 n1 − n 500 − 480 = = 0,04 n1 500 ⎛1 ⎞ R C ' = R2 '⋅⎜ − 1⎟ ⎝s ⎠ → R2 ' = RC ' ⎛1 ⎞ ⎜ − 1⎟ ⎝s ⎠ = 8,4845 = 0,3535 Ω ⎛ 1 ⎞ − 1⎟ ⎜ ⎝ 0,04 ⎠ S motor = 3 ⋅ U n motor ⋅ I n motor = 3 ⋅ 400 ⋅ 21 = 14549,22 VA Pmotor = S motor ⋅ cos ϕ motor = 14549,22 ⋅ 0,95 = 13821,76 W Qmotor = S 2 motor − P 2 motor = 4543 VAr Pmotor = 3 ⋅ (RC '+ RCC ) ⋅ I 2 n motor (RC '+ RCC ) = 13821,276 = 10,447 3 ⋅ 21 Ω RCC = 10,447 − 8,4845 = 1,9627 Ω R1 = RCC − R 2 ' = 1,9627 − 0,3535 = 1,9627 − 0,3535 = 1,6092 Ω X CC = Qmotor 4543 = = 3,434 Ω 2 3 ⋅ I 2 n motor 3 ⋅ 212 b) 0,2 Ω Z 2CC = 0,11519 + j0,1536 XCCmotor R1’+R2’=1,96277 U'1f R’C = R2’ · (1/s – 1) = 8,4845 Ω U2f Línea Transformador Motor Figura 5.20.2 ( ) U 1 f = U 2 f + Z 2CC + Z l ⋅ I 2 nf = 400 3 ∠0º +21∠ − 18,1º⋅(0,11519 + j 0,1536 + 0,2) = 238,24∠0,24º V ⎛ 11000 ⎞ U 1 = 3 ⋅ 238,24 ⋅ ⎜ ⎟ = 11347,70 V ⎝ 400 ⎠ © Los autores, 2006; © Edicions UPC, 2006 235 Máquinas síncronas 6 Máquinas síncronas © Los autores, 2006; © Edicions UPC, 2006 236 Problemas de electrotecnia 6.1 Problema 1 Un generador síncrono de 4 polos alimenta una instalación a 380 V, 50 Hz, alimentando una carga resistiva pura. La carga consume una corriente de 100 A. El generador está conectado en estrella, presentando una reactancia síncrona por fase de 1 Ω, y una resistencia por fase despreciable. Determinar: a) Ángulo de potencia a que está funcionando b) Potencia suministrada por el generador Si se hiciera funcionar el generador anterior como motor síncrono, conectándolo a un sistema trifásico a 380 V, 50 Hz, con la misma excitación y proporcionando una potencia de 52 kW, determinar: c) Corriente absorbida por el motor síncrono d) Factor de potencia que presenta el motor Resolución: a) Al ser la carga resistiva pura, se cumple: EO φ= 0 → I = 100∠0º A j ⋅ X S ⋅ I G = j ⋅ 1⋅ 100 ∂G IG U= 380 ∠0 º 3 EoG , f = U G , f + I f ⋅ ( Rs + j .X s ) = 380 3 ∠0º +100∠0º.( 0 + j .1 ) = 241,108∠24,504º V Por lo tanto, resulta que el ángulo de potencia vale: δ = 24,504º b) 3 ⋅E O ⋅U G P= ⋅ sin δ G = XS 3 ⋅ 241,108 ⋅ 380 1 3 ⋅ sin 24,504º = 65817,9 W Dado que la potencia que proporciona el generador es consumida exclusivamente por la carga, también se podría haber calculado de esta forma: P = 3 ⋅ U G ⋅ I G ⋅ cos ϕ = 3 ⋅ 380 ⋅ 100 ⋅ 1 = 65817 ,9 W c) Al trabajar como motor resulta: PM = − 3 ⋅E O ⋅U G ⋅ sin δ M XS © Los autores, 2006; © Edicions UPC, 2006 237 Máquinas síncronas Teniendo en cuenta que al mantener la excitación y al conectarlo a un sistema trifásico (a una tensión por fase de 380 V ), la Eo se conserva. 3 Sustituyendo valores resulta: − 52000 = 3 ⋅ 241,108 ⋅ 380 1 3 ⋅ sin δ U M , f = EoM , f + I f . j. X s → M → δ M = −19,1279 º 380 ∠0º = 241,108∠ − 19,1279º + I M .1∠90º 3 Resultando: I M = 79,452∠6,072 º A d) De la expresión de la corriente del motor se obtiene: φM = -6,072º → cosφM = 0,9944 (c) También se podría calcular el factor de potencia del motor a partir de: PM = 3.U l .I l . cos ϕ M → 52000 = 3.380.79,452. cos ϕ M Resultando: cos ϕ M = 0,9944 © Los autores, 2006; © Edicions UPC, 2006 238 Problemas de electrotecnia 6.2 Problema 2 Se dispone de un motor síncrono, tetrapolar, a 380 V, 50 Hz, conectado en estrella, acoplado a una red para compensar el factor de potencia de la instalación. El motor proporciona una potencia de 45809,28 W, siendo su factor de potencia capacitivo de 0,87. El valor de la reactancia síncrona es de 1,2 Ω. Si el motor se hiciera trabajar como generador, sin modificar su excitación, acoplando a una turbina de gas y trabajando en un sistema eléctrico aislado, se pide: a) Tensión de vacío b) Tensión en bornes de una carga resistiva pura que consume 160 A c) Potencia consumida por al carga Resolución: a) El factor de potencia del motor vale: cos ϕ M = 0,87 (c) PM = 3.U l .I l . cos ϕ M → 45809,28 = 3 ⋅ 380 3 → ϕ M = −29,5413 º ⋅ I M ⋅ 0,87 resultando I M = 80 A EoM , f = U M , f − I f . j. X s → EoM , f ∠δ M = 380 ∠0º − 80∠29,5413º.1,2∠90º 3 De la expresión anterior resulta: EoM , f = 279,49∠ − 17,39º V Por lo tanto, la tensión de vacío por fase resulta ser: EoM , f = 279,49 V b) Si la carga es resistiva pura y consume 160 A, se cumple: EoG , f = U f + I f . j. X s → 279,49∠δ G = U f ∠0º + 160∠0º.1,2∠90º De la expresión anterior resulta: Uf = 203,10 V c) → Ul = Pc = 3.U l .I l . cos ϕ c → 3 .Uf = 351,78 V P = 3 ⋅ 351,78 ⋅ 160 ⋅ 1 = 97488 W También se puede calcular a partir de la expresión: PG = 3 ⋅E O ⋅U G ⋅ sin δ G XS QG = 3 ⋅UG ⋅ ( Eo . cos δ G − U G ) XS © Los autores, 2006; © Edicions UPC, 2006 239 Máquinas síncronas siendo QG = 0 = 3 ⋅UG ⋅ ( Eo . cos δ G − U G ) → XS cos δ G = U G 203,10 = = 0,727 Eo 279,49 resultando, δG = 43,39º PG = 3 ⋅ 279,49 ⋅ 203,10 ⋅ sin 43,39 º = 97489 ,4 W 1,2 La potencia que nos piden, es decir, la consumida por la carga, coincide con la subministrada por el generador. © Los autores, 2006; © Edicions UPC, 2006 240 Problemas de electrotecnia 6.3 Problema 3 Dos generadores trifásicos iguales entre sí, conectados en estrella, trabajan en paralelo formando un sistema aislado, y alimentan una carga de 2000 kW, factor de potencia 0,8 inductivo a 6600 V. La reactancia síncrona para cada generador es de 10 Ω por fase, pudiéndose despreciar el valor de la resistencia inducida. Se conoce además que la potencia suministrada por cada generador es la misma. Si uno de los generadores tiene su excitación de campo ajustada para proporcionar una corriente inductiva de 116 A, se pide: a) Corriente suministrada por el otro generador b) Ángulo de potencia de cada generador Resolución: a) I j10 j10 2000 kW Uf = G1 I1 6600 ∠0 º 3 Z cos φ = 0,8 φ = 36,87º G2 I2 Figura 6.3.1 cosφ = 0,8 (i) I = → P = 3.Vl . cos ϕ φ = 38,87º 2000000 = 218,693 A 3 ⋅ 6600 ⋅ 0,8 → I = 218,693∠ − 36,87º A Dado que a cada generador se le proporciona externamente potencia idéntica, deberán alimentar a la carga con una potencia igual a 2000000 = 1000000 W individualmente. 2 P = 3.Vl .I l . cos ϕ1 → 1000000 = 3 ⋅ 6600 ⋅ 116 ⋅ cos ϕ1 Resultando cos ϕ1 = 0,754 → ϕ1 = 41,05º → I 1 = 116∠ − 41,05º A © Los autores, 2006; © Edicions UPC, 2006 241 Máquinas síncronas El diagrama vectorial correspondiente por fase es: Uf = 6600 3 φ I 1 = 116∠ − 41,05º φ1 I = 218,693∠ − 36,87 º φ2 I2 Figura 6.3.2 Dado que I = I1 + I 2 , se tiene: 218,693∠ − 36,87 º = 116∠ - 41,05º + I 2 → I 2 = 103,346 ∠ − 32,18º A b) Para el generador G1 se tiene por fase: E 01 X S I1 Uf I1 Figura 6.3.3 E O ,G 1 = U E O ,G1 = f + X S ⋅ I1 6600 ∠0º + j10 ⋅ 116∠ − 41,05º = 3810,511∠0º +1160∠48,95º = 4655,23∠10,83º A 3 Ángulo de potencia del generador G1: δ 1 = 10,83º Igualmente: E O,G 2 = U E O ,G 2 = f + X S ⋅I2 6600 ∠0 º + j10 ⋅ 103,346 ∠ − 32,18º = 3810 ,511∠0º +1033,48∠57,823º = 4447 ,73∠11,34 º A 3 Ángulo de potencia del generador G2: δ 2 = 11,34º © Los autores, 2006; © Edicions UPC, 2006 242 Problemas de electrotecnia Como comprobación, se calcula la potencia que suministra cada generador: PG1 = 3 ⋅ PG 2 = 3 ⋅ Eo,G1 ⋅ U f X S1 E o ,G 2 ⋅ U f X S2 ⋅ sin δ1 ≅ 1000000 W ⋅ sin δ 2 ≅ 1000000 W © Los autores, 2006; © Edicions UPC, 2006 243 Máquinas síncronas 6.4 Problema 4 Un generador trifásico de 100 kVA, 400 V, 50 Hz, conectado en estrella, presenta una resistencia de inducido de 0,1 Ω y una reactancia sincrona de 1 Ω por fase. La característica de magnetización del generador es la siguiente: Eo ( V ) 136,4 267,3 394,6 469,2 538,3 600,2 Iex ( V ) 1 2 3 4 5 6 Se pide: a) Corriente de excitación para alimentar una carga inductiva a 380 V, que consume una potencia de 75000 W y presenta un factor de potencia 0,8. b) Corriente de excitación para poder efectuar la prueba de cortocircuito a la corriente nominal. Se pretende conseguir que la tensión inducida coincida con la tensión nominal del generador cuando se alimenta una carga que consume la corriente nominal. Se pide: c) Factor de potencia que debería presentar la carga d) Corriente de excitación para este caso Resolución: a) Ic = P = 3.Vl . cos ϕ 75000 = 142,43 A 3 ⋅ 380 ⋅ 0,8 ϕa =36,87º Ya que cosϕa = 0,8 (i) → → I c = 142,43∠ − 36,87º A El diagrama vectorial por fase es el siguiente: E of ϕ Ic E Of = U f X S ⋅Ic Uf R ⋅ IC + I C .( R + X S ) = 380 ∠0º +142,43∠ − 36,87º.(0,1 + j ⋅ 1) = 333,346∠18,43º V 3 EO = 3 ⋅ 333,346 = 571,58 V Se debe buscar, interpolando en la curva característica de magnetización, el valor correspondiente de magnetización: © Los autores, 2006; © Edicions UPC, 2006 244 Problemas de electrotecnia I ex = 5 + (6 − 5) ⋅ 571,58 − 538,3 = 5,54 A 600,2 − 538,3 b) In = Sn 3.Vn = 100000 = 144,337 A 3 ⋅ 400 U bf = 0 ( prueba de cortocircuito ) E of = U f + I n .( R + j. X S ) = 0 + 144,337∠0º.(0,1 + j.1) = 145,05∠84,29º V E o = 3 ⋅ 145,05 = 251,234 V Interpolando en la curva característica, resulta: I ex = 1 + (2 − 1) ⋅ (251,23 − 136,4) = 1,877 (267,3 − 136,4) A c) U = E o = 400 V (según el enunciado) U f = E of = 400 V 3 → E of = U f + I c .( R + j. X S ) 400 400 ∠δ º = ∠0º + 144,37 ∠ - ϕ º.(0,1 + j.1) 3 3 De la expresión anterior resulta: 400 400 ∠δ º = ∠0º + 145,06 ∠84,29º −ϕ º 3 3 Separando parte real e imaginaria, se tiene: 145,06. cos(84,29º −ϕ º ) = 400 ⋅ (cos δ − 1) 3 145,06. sin(84,29º −ϕ º ) = 400 ⋅ sin δ 3 Elevando al cuadrado y sumando las expresiones anteriores, resulta: δ = 36,61º 84,29º - φ = 108,30º → φ = -24,01º Por lo tanto, el factor de potencia de la carga resulta ser cosφ = cos(-24,01º) = 0,913 (c) d) En este caso se tiene que: EO = 400 V Interpolando en la curva característica se obtiene: I ex = 3 + (4 − 3) ⋅ (400 − 394,6) (469,2 − 394,6) = 3,0723 A © Los autores, 2006; © Edicions UPC, 2006 245 Máquinas síncronas 6.5 Problema 5 Un motor síncrono trifásico, conexión en estrella, tetrapolar, de potencia nominal 20 kW, 400 V, 50 Hz, rendimiento a plena carga 0,95, presenta una resistencia por fase en el inducido de 0,1 Ω y una reactancia síncrona de 1,5 Ω por fase. La curva característica de vacío es la siguiente: Eo ( V ) 173,2 294,5 346,4 435 474,5 Iex ( V ) 2 3,4 4,5 7,2 9,2 Se pide: a) Velocidad del motor Si el motor absorbe la corriente nominal con un factor de potencia de 0,8 capacitivo, calcular: b) Corriente de excitación c) Ángulo de potencia δ Cuando el motor absorbe de la red a la que está conectado 60 A, la corriente de excitación del inductor es de 10 A. Se pide: d) Potencia absorbida por el motor e) Factor de potencia que presenta en estas condiciones f) Ángulo de potencia δ Resolución: a) n= 60 ⋅ f 60 ⋅ 50 = = 1500 rpm p 2 b) Uf = 400 = 230,94 V 3 cos ϕ = 0,8 (c) In = → ϕ = −36,87º 20000 P = = 37,983 A 3 ⋅ Vl ⋅ cos ϕ ⋅ η 3 ⋅ 400 ⋅ 0,8 ⋅ 0,95 El diagrama vectorial correspondiente del motor es el siguiente: © Los autores, 2006; © Edicions UPC, 2006 246 Problemas de electrotecnia In ϕ = 36,87º U bf = 230,94 δ X S ⋅ In R ⋅ In Eof Figura 6.5.1 → U f = E of + I c .( R + j. X S ) 400 3 ∠0º = Eof + 37,983∠36 ,87º .(0,1 + j.1,5) Resultando: Eof = 266,42∠ − 10,34º V Interpolando en la curva característica, resulta: I ex = 4,5 + (7,2 − 4,5) ⋅ (355,838 − 346,4) = 4,7876 (435 − 346,4 ) A c) Ya que Eof = 266,42∠ − 10,34º V , el ángulo de potencia vale: δm = -10,34º d) A partir de la curva característica y de una corriente de excitación de 10 A, se calcula el valor de EO: E O = 474,5 + (474,5 − 435 ) ⋅ (10 − 7,2) = 529,8 V (9,2 − 7,2) E O f = 529,8 / 3 = 305,88 V E of = U f − I .( R + j. X S ) → 305,88∠δ m = 400 ∠0º - 60∠ - ϕ º.(0,1 + j.1,5) 3 Separando parte real y parte imaginaria, resulta: 305,88. cos δ m = 400 − 90,198. cos(86,19 º −ϕ ) 3 305,88.sin δ m = −90,198.sin(86,19º −ϕ ) Elevando al cuadrado y sumando, resulta: δm = -10,84º φ = -54,20º Por lo tanto, la potencia activa absorbida por el motor resulta ser: P = 3.U .I . cos ϕ = 3.400.60. cos(−54,20º ) = 24316,2 W © Los autores, 2006; © Edicions UPC, 2006 247 Máquinas síncronas e) cos ϕ = cos( −54,20º ) = 0,585 (c) f) δ m = −10,84º © Los autores, 2006; © Edicions UPC, 2006 248 Problemas de electrotecnia 6.6 Problema 6 Un motor trifásico, síncrono, conexión estrella, 400 V, trabaja con un factor de potencia igual a la unidad y desarrolla una potencia de 65000 W. Si la reactancia síncrona es de 1,2 Ω y la resistencia se considera despreciable, determinar: a) Tensión inducida por fase b) Ángulo de potencia c) Tensión inducida para que el motor desarrolle la misma potencia con un cos ϕ = 0,8 capacitivo Resolución: a) P = 3.U .I . cos ϕ → 65000 = 3 ⋅ 400 ⋅ I ⋅ 1 I → I = 93,819 A Uf δm XS ⋅I EO Figura 6.6.1 tgδ = X S ⋅ I 1,2 ⋅ 93,819 = = 0,487 400 Uf 3 → δ m = −25,989º 2 ⎛ 400 ⎞ ⎟⎟ + (1,2 ⋅ 93,819)2 = 256,92 V Eof = U 2f + ( X s .I )2 = ⎜⎜ 3 ⎠ ⎝ b) δ m = −25,989º c) P = 3.U .I . cos ϕ → cosφ = 0,8 (c) → φ = -36,87º 65000 = 3 ⋅ 400 ⋅ I ⋅ 0,8 → U f = E of + I c .( R + j. X S ) → → I = 117,27∠36,87º A 400 ∠0º = E 0 f + 117,27∠36,87 º.(0 + j.1,2) 3 Resultando E of = 334,86∠ − 19,65º V → I = 117,27 A E o = 3.E of = 580 V © Los autores, 2006; © Edicions UPC, 2006 249 Máquinas síncronas 6.7 Problema 7 Un motor síncrono trifásico conectado en estrella a 2300 V y 50 Hz, sobreexcitado, trabaja con un ángulo de potencia de -15º. La impedancia síncrona por fase es de (0,1 + j.1) Ω. Si el motor consume una corriente de 400 A, determinar el factor de potencia del motor. Resolución: El enunciado dice que el motor está sobreexcitado. Esto significa que tiene un factor de potencia capacitivo (φ < 0), es decir, que absorbe una Q < 0: Qm = 3 ⋅ U .(U − E of . cos δ m ) Xs → <0 Eof . cos δ m > U Por otra parte, debe cumplirse: U f = E of + I c .( R + j. X S ) → 2300 ∠0º = E of ∠ − 15º +400∠ − ϕ .(0,1 + j.1) 3 Separando las partes real e imaginaria resulta, 2300 = E of . cos( −15º ) + 401,995. cos(84,29 − ϕ ) 3 0 = Eof . sin( −15º ) + 401,995.sin(84,29 − ϕ ) Elevando al cuadrado y sumando, resultan dos soluciones posibles: Solución 1. Eof = 1074,14 V, φ = +40,54º Solución 2. Eof = 1491,17 V, φ = -21,96º La primera solución corresponde al caso de un motor subexcitado, mientras que la segunda corresponde al motor sobreexcitado, que es la premisa del enunciado. Por lo tanto resulta, Eof = 1491,17 V, cosφ = cos(-21,96º) = 0,927 (c) © Los autores, 2006; © Edicions UPC, 2006 250 Problemas de electrotecnia 6.8 Problema 8 La potencia eléctrica consumida por una empresa es en término medio de 150 kW, presentando un factor de potencia de 0,6 inductivo. La red de alimentación es de 400 V, 50 Hz. Se desea compensar el factor de potencia hasta la unidad instalando un motor síncrono que a su vez impulse una nueva central de aire acondicionado, cuya potencia necesaria prevista sea del orden de 21150 W. El motor síncrono a utilizar se le asigna un rendimiento 0,94. Se pide: a) Potencia aparente del motor a instalar b) Factor de potencia que presenta el motor Si el motor elegido es de 4 polos y presenta una impedancia síncrona por fase de (0 + j.1) Ω, calcular: c) Corriente consumida por el motor d) Velocidad de giro del motor e) Ángulo de potencia del motor f) Par útil desarrollado por el motor. Resolución: a) El diagrama vectorial de potencia es el siguiente: Q Q1 ϕ1 P ϕ2 ' Q2 Figura 6.8.1 cos ϕ1 = 0,6 (i) → ϕ1 = 53,13º → tgϕ1 = 1,3333 Q1 = P1 ⋅ tgϕ1 = 150000 ⋅ 1,3333 = 200000 VA El motor síncrono debe proporcionar una potencia útil de 21150 W, según el enunciado, con un rendimiento de 0,94: © Los autores, 2006; © Edicions UPC, 2006 251 Máquinas síncronas Pm = 21150 = 22500 W 0,94 Por otra parte, para conseguir un factor de potencia unidad, la potencia reactiva del motor debe ser: Qm = −Q1 = −200000 VA Luego S m = 22500 − j 200000 = 201261,64∠ − 83,58º VA S m = 201261,64 VA b) cos ϕ m = 0,11 (c) → ϕ m = −83,58º c) Im = Sm = 3 ⋅Ul 201261,64 = 290,496 A 3 ⋅ 400 → I m = 290,46∠ + 83,58º A d) → 2⋅ p = 4 p=2 n= 60 ⋅ f 60 ⋅ 50 = = 1500 rpm p 2 U = E Of + I m .( R + j. X s ) e) f E Of = U bf − j. X S ⋅ I m = 400 ∠0º − j ⋅ 1 ⋅ 290,496 ∠83,58º = 520,628∠ − 3,57 º V 3 Resultando δ m = −3,57º f) Mu = Pu ω = Pu 2π ⋅ n 60 = 21150 = 134,64 N ⋅ m 1500 2π ⋅ 60 © Los autores, 2006; © Edicions UPC, 2006 252 Problemas de electrotecnia 6.9 Problema 9 El motor síncrono de la figura está conectado en triángulo a la red eléctrica de la figura. El motor está sobreexcitado. A V W1 M ˜ W2 Figura 6.9.1 Las lecturas de los aparatos de medida son las siguientes: W1 = 20697,6 W, W2 = 22909,2 W, A = 66,52 A, V = 380 V La frecuencia de la red es de 50 Hz, y se sabe que el motor gira a 600 rpm. La medición de la resistencia del inducido por fase ha dado una lectura por fase de 0,1 Ω y la reactancia síncrona, en las condiciones de funcionamiento, es de 3 Ω por fase. Se pide: a) Número de polos del motor b) Potencia absorbida de la red c) Factor de potencia del motor d) Lectura del amperímetro A e) Rendimiento del motor en el supuesto de que las pérdidas rotaciones sean del orden de 3600 W f) Par útil desarrollado Se sabe además que el nivel de excitación con el que funciona el motor, en la característica de vacío, le corresponde una tensión por fase de 400 V. g) Calcular el ángulo de potencia. Resolución: a) n= 60 ⋅ f p Número de polos: → p= 60 ⋅ 50 =5 600 5 × 2 = 10 polos © Los autores, 2006; © Edicions UPC, 2006 253 Máquinas síncronas b) Al estar los vatímetros conectados según la conexión Aron: P = (W1 + W2 ) = 20697,6 + 22902,2 = 43599,8 W Q = 3 ⋅ (W1 − W2 ) = 3 ⋅ (20697,6 − 22902,2) = −3818,45 VAr c) tgϕ = Q −3818,45 = = −0,08373 P 43599,8 → ϕ = −4,7867 º cos ϕ = 0,9965 (c) d) P = 3 ⋅ U l ⋅ I l ⋅ cos ϕ P 43599,8 = = 66,475 A 3 ⋅ U l ⋅ cos ϕ 3 ⋅ 380 ⋅ 0,9965 Il = e) Pu = Pabs − Prot − 3 ⋅ R ⋅ I f 2 2 ⎛ 66,475 ⎞ Pu = 43599,8 − 3600 − 3 ⋅ 0,1 ⋅ ⎜ ⎟ = 39557,90 W 3 ⎠ ⎝ η= Pu 39557,9 = = 0,907 P 43599,8 → η % = 90,7% f) Mu = Pu n 2π ⋅ 60 = 39557 ,9 = 629 ,58 N ⋅ m 600 2π ⋅ 60 g) E of = U f − ( R + j .X S ) ⋅ I f 400∠δ m = U f ∠0º −(0,1 + j.3). 66,475 ∠4,7867 º 3 Separando las partes real e imaginaria de la expresión anterior, resulta: 400.cosδm = U + 5,78 400. sinδm = -115,07 Resultando δm = -16,72º, U = 377,31 V © Los autores, 2006; © Edicions UPC, 2006 254 Problemas de electrotecnia 6.10 Problema 10 El generador trifásico síncrono de la figura conectado en estrella alimenta a través de una línea, cuya impedancia se desprecia, dos cargas conectadas en paralelo según la figura adjunta. G A2 A1 W1 V W2 ˜ M ˜ Figura 6.10.1 El voltímetro V indica 380 V. Los vatímetros W1 y W2 indican respectivamente 12950,69 W y 5124,91 W. La carga en triángulo está formada por una impedancia por fase de valor 6 + j.8 Ω. El motor asíncrono gira a una velocidad de 1440 rpm, con un rendimiento del 80 %. Se sabe que la reactancia síncrona por fase del generador es de 0,1 Ω, siendo la resistencia despreciable. Se pide: a) Potencia útil del motor asíncrono b) Par útil del motor asíncrono c) Número de polos del motor d) Factor de potencia del motor e) Lectura del amperímetro A2 f) Lectura del amperímetro A1 g) Factor de potencia del conjunto carga – motor h) Valor de la tensión inducida en el generador i) Ángulo de potencia del generador Resolución: a) Pmotor = (W1 + W2 ) = 12950,69 + 5124,91 = 18075,6 W Q motor = 3 ⋅ (W1 − W 2 ) = 3 ⋅ (12950 ,69 − 5124 ,91) = 13554 ,64 VAr Pu = Pmotor ⋅η = 18075,6 ⋅ 0,8 = 14460,48 W © Los autores, 2006; © Edicions UPC, 2006 255 Máquinas síncronas b) Mu = Pu n 2π ⋅ 60 = 14400,48 = 95,894 N ⋅ m 1440 2π ⋅ 60 c) Al ser la velocidad de 1440 rpm, se tiene: 1440 ≅ 60 ⋅ f p → p= 60 ⋅ 50 = 2,08 1440 → 4 polos d) tgϕ motor = Qmotor 13554,64 = = 0,7498 Pmotor 18075,6 → ϕ motor = 36,865º Resultando cos ϕ motor = 0,8 (i) e) Pmotor = 3 ⋅ U l ⋅ I l ,motor ⋅ cos ϕ motor I l ,motor = Pmotor 3 ⋅ U l ⋅ cos ϕ motor = 18075,6 = 34,328 A 3 ⋅ 380 ⋅ 0,8 Resultando → I l ,motor = 34,328∠ − 36,87 º A A2 = 34,328 A f) La carga en triángulo consume por fase una intensidad: I f ,c arg a = 380∠0º = 38∠ − 53,13º A 6 + j.8 La corriente de línea en la carga en triángulo será: I l ,c arg a = 3 ⋅ 38∠ − 53,13º = 65,8179∠ − 53,13º A La lectura del amperímetro vendrá como resultado de la suma vectorial de las dos corrientes: I TOTAL = I l , motor + I l ,c arg a = 34,328∠ − 36,87º +65,8179∠ − 53,13º = 99,239∠ − 47,57º A Por lo tanto, resulta A1 = 99,239 A. g) Ya que I TOTAL = 99,239∠ − 47,57º A , resulta: ϕTOTAL = +47,57º → cosϕTOTAL = 0,6746 (i) También se podía haber calculado a partir de las potencias: © Los autores, 2006; © Edicions UPC, 2006 256 Problemas de electrotecnia PTOTAL = Pmotor + Pc arg a = 18075 ,6 + 3 ⋅ 6 ⋅ 38 2 = 44067 ,6 W QTOTAL = Q motor + Qc arg a = 13554,64 + 3 ⋅ 8 ⋅ 38 2 = 48210,64 VAr tgϕTOTAL = QTOTAL = 1,094 PTOTAL → ϕ TOTAL = +47,57º Resultando cos ϕTOTAL = 0,6746 (i) Que coincide con el hallado anteriormente. h) E of Uf X S .I TOTAL ϕTOTAL .I TOTAL Figura 6.10.2 E of = U f + ( R + j. X s ) ⋅ I TOTAL = 380 ∠0º +0,1∠90 º⋅99,239∠ − 47,57 º = 226,81∠1,69º V 3 E o = 3.E of = 392,848 V i) El ángulo de potencia del generador vale δ g = 1,69º © Los autores, 2006; © Edicions UPC, 2006 257 Máquinas síncronas 6.11 Problema 11 Se dispone de una instalación formada por un generador trifásico síncrono conectado en estrella que alimenta a través de una línea de impedancia despreciable un motor asíncrono. Para compensar el factor de potencia hasta la unidad, se ha colocado un motor síncrono según el esquema adjunto. El voltímetro indica una lectura de 380 V. La frecuencia de la red es de 50 Hz. G V ˜ M1 ASÍNCRONO M2 SÍNCRONO Figura 6.11.1 El motor M1 asíncrono es de potencia nominal 35 kW y trabaja con un rendimiento del 80%, sobre un par resistente de 175,3 N.m a una velocidad de 1415 rpm, absorbiendo una corriente de 57 A. El motor M2 síncrono es de 6 polos y absorbe la potencia de 32475 W, siendo su resistencia de inducido despreciable. Calcular: a) Potencia absorbida por el motor síncrono b) Factor de potencia que presenta el motor asíncrono c) Deslizamiento del motor asíncrono d) Potencia reactiva absorbida por el motor síncrono e) Factor de potencia del motor síncrono f) Corriente absorbida por el motor síncrono g) Valor de la reactancia síncrona del motor síncrono si el ángulo de potencia es de -25º h) Valor de la reactancia síncrona del generador síncrono si el ángulo de potencia es de +20º © Los autores, 2006; © Edicions UPC, 2006 258 Problemas de electrotecnia Resolución: a) Pu , M1 = M u ⋅ ω = 175,3 ⋅ PM1 = Pu , M1 = η 2π ⋅1415 = 25975,68 W 60 25975,68 = 32469,6 W 0,8 b) PM1 = 3 ⋅ U l ⋅ I M1 ⋅ cos ϕ M1 cos ϕ M1 = 32469,6 = 0,865 3 ⋅ 380 ⋅ 57 → ϕ M1 = 30º c) nS = s= 60 ⋅ f 60 ⋅ 50 = ≅ 1500 p p → p=2 1500 − 1415 = 0,056 = 5,6% 1500 d) tgϕ M1 = Q M1 PM1 QM1 = PM1 ⋅ tgϕ M1 = 32469,6 ⋅ tg 30º = 18746,23 VAr (inductiva) e) Al estar el factor del conjunto compensado hasta la unidad: Q M 2 = −QM 1 = −18746,23 VAr (capacitiva) PM2 = 32475, según el enunciado. tgϕ M 1 = QM 2 PM 2 = − 18746,23 = 0,577 32475 → ϕ M 2 = −30º cos ϕ M 2 = 0,866 (c) f) PM 2 = 3 ⋅ U l ⋅ I M 2 ⋅ cos ϕ M 2 IM2 = 32475 = 56,97 A 3 ⋅ 380 ⋅ 0,866 © Los autores, 2006; © Edicions UPC, 2006 259 Máquinas síncronas g) U f = E Of , M 2 + ( R + j. X S ) ⋅ I f , M 2 380 ∠0º = E of , M 2 ∠ − 25º + 56,97 ∠30 º. X s , M 2 ∠90 º 3 Separando partes real e imaginaria, resulta: 380 3 = Eof .cos( −25º ) − 28,485.X s ,M 2 0 = Eof .sin( −25º ) + 49 ,337.X s ,M 2 Del sistema anterior, resulta Xs,M2 = 2,85 Ω, Eof,M2 = 332,82 V h) Al estar compensado el factor de potencia total, la tensión y la corriente están en fase: I X smM 2 ⋅ I δG Uf I = I M1 + I M 2 = 57∠ − 30º + 56,97∠30º = 98,72∠0º A tgδ G = X s ,M 2 ⋅ I Uf → X s ,M 2 = U bf ⋅ tgδ G It 380 = ⋅ tg 20º 3 = 0,81 Ω 98,72 © Los autores, 2006; © Edicions UPC, 2006 260 Problemas de electrotecnia 6.12 Problema 12 Un motor asíncrono, trifásico, conexión estrella, acciona una carga resistente cuyo par obedece la siguiente expresión: 94,744 · M = w2, siendo w su velocidad de giro en rad/s. El rendimiento del motor es del 70%. La potencia nominal del motor es 75 CV, 50 Hz, y está alimentado a 500 V a través de una línea de impedancia despreciable por un generador de las siguientes características: - Potencia: 100 CV - Número de polos: 8 - Frecuencia: 50 Hz - Ángulo de potencia en que trabaja: 11º - Corriente de excitación: 1,5 A - Reactancia síncrona por fase: 1,1 Ω - Resistencia inducido despreciable La curva de magnetización del generador responde a los siguientes datos: Eo ( V ) 273,6 362 450,3 515,3 571,5 621,9 666,5 Iex ( V ) 0,6 0,8 1 1,2 1,4 1,6 1,8 Calcular: a) Corriente absorbida por el motor b) Factor de potencia que presenta el motor c) potencia absorbida por el motor d) Potencia útil desarrollada por el motor e) Par desarrollado por el motor f) Velocidad de giro del motor g) Número de polos del motor Resolución: a) Para una corriente de excitación de 1,5 A, se puede encontrar la tensión inducida de la curva de magnetización: E o = 571,5 + (621,9 − 571,5) ⋅ (1,5 − 1,4) = 596,7 V (1,6 − 1,4) © Los autores, 2006; © Edicions UPC, 2006 261 Máquinas síncronas El diagrama vectorial por fase del generador es el siguiente: E of = 596,7 3 B = 344,5 XS ⋅I δ = 11º O A ϕ I U bf = 500 3 = 288,67 Figura 6.12.1 Aplicando el teorema del coseno al triángulo OAB se puede calcular el valor de XsI: ( X s I ) 2 = 344,5 2 + 288,67 2 − 2 ⋅ 344,5 ⋅ 288,67 ⋅ cos 11º X s I = 82,287 V I= 82 ,287 = 74 ,81 A 1,1 b) Del triángulo anterior: Aplicando el teorema del seno: 344,5 82,285 = sin α sin 11º α = 53,02º sin α = 0,7988 α = 180º −53,02º = 126,98º El ángulo correcto es α = 126,98º , dado que es superior a 90º. β = 180º −126,98º = 53,02º Por otra parte: β + ϕ + 90º = 180º ϕ = 180º −90º − β = 180 − 90 − 53,02 = 36,98º → cos ϕ = 0,798 c) P = 3 ⋅ U ⋅ I ⋅ cos ϕ = 3 ⋅ 500 ⋅ 74,81 ⋅ 0,798 P = 5170 W d) Putil = P ⋅η = 51700 ⋅ 0,7 = 36190,2 W © Los autores, 2006; © Edicions UPC, 2006 262 Problemas de electrotecnia e) Putil = M u ⋅ ω 94,744 ⋅ M u = ω 2 Siendo Putil = 36190,2 W : ⎛ 36190,2 ⎞ ⎟ 94,744 ⋅ M u = ⎜⎜ ⎟ ⎝ Mu ⎠ 2 M u = 240 N·m f) w= Putil 36190,2 = = 150,79 rad/s 240 Mu n = 150 ,79 ⋅ 60 = 1439,96 rpm 2π g) n≅ 60 f p p= Número de polos: 60 f 60 ⋅ 50 = n n p=2 2p = 4 © Los autores, 2006; © Edicions UPC, 2006