¡(x) .dx) g(y) dY) - Agrupación 15 de Junio – MNR
Anuncio

ANÁLISIS MATEMÁTICO 111
LCC-LF
Primer Cuatrimestre 2010
Eduardo Santillán Marcus
Luciana Talarn - Gerardo Sbérgamo
Práctica
4: Integrales Múltiples
1. Evaluar las siguient es int egrales iterad as , integrando en y y después en x, y luego
primero en x y después en y:
1
Jo (y cos (x) + 2) dyd x ;
1
Jo (3x 2y - 2x y 2) dyd x ;
a)
c)
b)
d)
)
4
J0
dydx.
2. Calcul ar cada una de las siguientes integr ales.
JJR( X3 + y3) dxdy,
donde R = [0,1] x [0,1].
donde R = [-1 ,1] x [-1 ,1] .
JJRyexp( xy) dxdy ,
JJRln(X
.
3. Sea
R.
4. Sea
+ l)(y + 1)
dxdy, donde R
JJR Iyl cos
f cont inua, f
f
[0,1] x [0,1].
donde R = [0, 2] x [-1 , O].
° en el rectángulo R. Si JJR f dA
continua en [a, b] y
J(x)g(y) dA
=
=
O, mostrar que
f
=
° en
9 continua en [e, d]. Mostrar que:
¡(x)
.dx)
g(y) dY)
1
donde
R = [a , b] x [e, d]
5. Sea
J
cont inua en R = [a, b] x [e, d]; para a < x < b, e < y < d definir
l
F( x , y) =
x
J(u , v )dvdu.
Mostrar que D 12F (x , y) = D 2l F (x , y) = J( x, y).
(En base a este ejemplo se pu ede dar un a prueba de la inver tibilidad del orden de
deri vación) .
6. Evaluar las sigui ent es integrales iterad as y bosquejar las regiones D determinad as por
los lími t es de integración. Decir si las regiones son de tipo 1 , 2 , o de ambos tipos.
) J12 dx
r 3x+l
dy.
ex
l
Jo dx Jl (x + y)dy.
l
r
Jo
dx lx
x3 ydy.
2
ex p(x + y) dy.
dx
rl dx Jorx 2
dy.
Jo
En b) Y e), cambiar el orden de int egr ación. (¡Con los ext remos apropiados!).
x 2 + y2
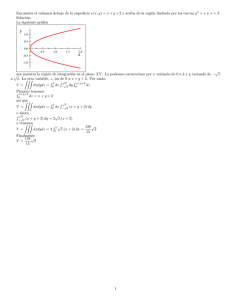
7. Sea D la región de los (x , y) t ales que 1
elemental? Evaluar JDJdA con J (x , y) = 1 + x y.
8. Encontrar el volumen limitado por la gráfica de
x = b, y = e, y = d, siendo:
J (x , y)
=
1 + 2x
2 e y
J (x , y)
o.
¿Es D un a región
y los planos z = O, x = a,
+ 3y, a = 1, b = 2, e = O Y d = 1.
J( x ,Y)= X4+y2,
a=-l , b=l , e=-3yd=-2.
9. Usar integrales dobles para calcular:
el volumen de un a esfera de radio
T.
el volumen limitado por un elipsoide de semiejes a, b, e.
c) el volumen de un cono circular recto de bas e de radio
T
y alt ur a h.
10. Sea D una región del tipo {( x , y) / y
,
x b} donde sp es un a
función no negativa y continua en el intervalo [a, b] . Sea J un a fun ción definid a en D
tal que J(x , -y) = - J (x , y)
y) E D . Mostrar que JJ f dA = o.
D
11. Utiliz ando el teorema del valor medio mostrar qu e:
-1 <
6-
dA
< ­1
Dy- x+3-4
donde D es el triángulo de vértices (O , O) , (1,1) , (1, O).
12. Dibujar la región plana limitad a por las rect as x = -1 , x
= -1 , x + y = 1, Y = -1.
Hallar las coordenadas del centro de graveda d, supuesta la densidad constante.
2
13. Calcular el momento de inercia respect o del eje x de una placa plan a del plano xy
limitada por las cur vas y =
y = 0,
= 2 con densidad superficial de masa
p(x , y) = Ix - vl
14. Una placa de oro ti ene la form a y tamaño del rect án gulo [0,
x [0,
(en centímetros ).
2(4
Su densid ad de masa es p(x , y ) = y2 sin x) + 2 (en gramos por centímetro cuadrado).
Si el oro cuesta $ 7 por gr amo, ¿cuánto vale la placa?
15. Transformar la siguiente int egral a coordenadas po lares y calcularla:
r dx
Jo Jx
(x 2 +
2
16. Sea S el paralelogramo con vérti ces
t ransformación lineal para calcular
J
°<
y
<x y
°
x
zr} ,
2(
(x -
17. Si D es el disco unitario, evaluar IID
coordenadas polares.
18. Sea D la región
O) ,
sin x
2
e- (x
(O,
Usar una adecuada
+ y)dxdy.
y2
+ )dx dy medi ante un cambio de vari abl es a
1. Calcular I I D (x
+ y) dx dy haci endo el cambio
de variables { x = u + v . Corroborar la respuesta evaluando la int egral direct amente
y=u-v
un a integral it erada.
19. Sea T(u , v ) = (x (u,v ), y(u, v )) la transformad a definida por T(u ,v) = (4u,3u
Sea D* el rectángulo [0,1] x [1 ,2]. Encontrar D = T(D*) y evaluar:
+ 3v) .
IID x y dx : dy .
IID( x - y) dx : dy.
20. Evaluar la integral llevando a cabo un cambio de variables apropiado
x+2y d d
cos(x _ y) x y,
R
donde R es la región acotad a por las rect as 2x - y
= 1, x -
Y = -3, 3x
+ y = 1.
21. Calcular las siguient es integr ales triples:
I I I v (1 + x + y + z )- 3 dxd ydz donde V es el tetraedro definido por los tres planos
coordenados y el plano x + y + z = 1.
IIIv
+ y2dxdydz , donde V es el sólido limitado por la hoj a superior del
cono z2 = x 2 + y2 y el plan o z = 1.
22. Calcular, pasando a coordenadas cilíndricas :
III( x 2 + y2 )dx dydz, siendo S el sólid o limi t ad o por la superficie x 2 + y2
s
el plano z = 2.
3
=
2z y
JJJ dxdydz, siendo S el sólido limit ad o por los tres planos coordenados, la super­
s
ficie z
= x 2 + y2 y el plan o x + y =
1.
23. Sea B la bola unitaria. Evaluar :
dxdydz
+ x 2 + y2 + z2 '
JJB
haciendo un cambio de variables apropiado
24. Calcular el volumen del sólido V limit ad o por el paraboloide z =
parte superior de la superficie esférica x 2 + y2 + z 2 = 5.
25. Sea
f
continua en un entorno del punto (a, b, e). Sea
en (a,b, c) y radio e. Demostrar que: lím
\
JJJB
+ y2)
y por la
la esfera(sólida) con cent ro
f(x,y ,z)dxdydz
=
f(a ,b , c).
Sug.: Demostrar primero un t eorem a del valor medio análogo al de las integrales dobles.
26. Calcular la masa y el cent ro de gravedad del sólido limitado por dos semiesferas con­
céntricas de radios a, b con O < a < b si:
la densidad de masa es constante;
b) la densidad en cada punto es igual al cuadrado de su distancia al centro.
27. Un cono circular recto homogéneo tiene alt ura h. Demostrar que la distancia del centro
de masa a la base es h/4.
28. Calcular el momento de inerci a de un a esfera de radio A respecto de un diámetro si su
densidad volumétrica de masa es constante.
29. Calcular el momento de inercia de un cilindro de radio A y masa
resp ecto de su eje
si la densidad en cada punt o es proporcional a la distancia del punto al eje del cilind ro .
30. El t allo de un hongo es un cilindro recto de diámetro 1 y de altura 2. Su sombrero es
un hemisferio de radi o R . El hongo es homogéneo y con simetría axial. Además, R es
t al que el centro de masa está situado en el plano en el cual el t allo se une al sombrero.
Calcular R.
Solución: R =
4