El Arte de Escher, la Gráfica Smith y la Geometría Hiperbólica

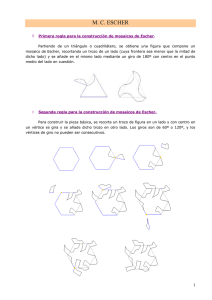
El Arte de Escher, la Gráfica Smith y la Geometría Hiperbólica
Madhu S. Gupta
Traducción: Dr. Roberto S. Murphy Arteaga
E
l propósito de este artículo es señalar
un enlace conceptual entre la creación
artística del bien conocido artista
holandés M.C. Escher (1898-1972),
llamada Círculo Límite IV (grabado en
madera, 1960), y la más conocida ayuda gráfica en
ingeniería de microondas, llamada Gráfica Smith
(1939-1944), creada por el ingeniero estadounidense
P.H. Smith (1905-1987). El fundamento del arte de
Escher y de la gráfica Smith se puede atribuir a la
invariancia de la razón cruzada de cuatro números
complejos sujetos a una transformación de Möbius en
el dominio de los números complejos. Al ser medidas
usando una métrica de distancia hiperbólica inducida
por la razón cruzada invariante con el modelo de
disco abierto del espacio hiperbólico de Poincare, las
figuras geométricas visualmente diferentes del trabajo
de Escher muestran periodicidad y forman un mosaico
de tamaño fijo. La Gráfica Smith se puede usar como
una herramienta para construir otros dibujos
parecidos a los de Escher, que presentan patrones en
mosaico periódicos y a la vez se perciben como una
progresión infinita en el círculo unitario.
A pesar de la imagen pública del ingeniero
transmitida por los medios,
los ingenieros se
involucran, disfrutan, contribuyen, hacen posible e
inspiran las bellas artes, tanto personal como
profesionalmente. Esto es de esperarse, ya que la
ingeniería, como el arte, requiere creatividad,
disciplina, atención al detalle, y sensibilidad a la
percepción humana.
La vibrante frontera entre
tecnología y arte ha sido ejemplificada por una gran
variedad de trabajos, aparatos y exhibiciones
creativas de varias formas de arte, como son la
música, el drama, la fotografía, la escultura y la
pintura [1]-[3]. Este artículo destaca otra frontera,
aunque poco conocida, entre el arte y las
herramientas tecnológicas, específicamente aquella
que enlaza ciertos grabados en madera de Escher y
la gráfica Smith, que permea la ingeniería de
microondas.
Los lectores lo pueden usar para
aumentar su apreciación de ese arte, para estimular el
interés en microondas entre los no-profesionales, o
para crear arte similar a la de Escher ellos mismos.
Madhu S. Gupta está en la Universidad Estatal de San
Diego, San Diego, CA 92182 EUA, 1 619 594 7015,
mgupta@mail.sdsu.edu.
Este artículo es una versión aumentada de la plática
invitada dada por el autor en MIKON-2006, Cracovia,
Polonia, en mayo de 2006.
Más información sobre MIKON-2006 se puede encontrar en
“Transnational News”, en la p. 94.
66 IEEE microwave magazine
Escher y su arte
Un artista apreciado por los tecnólogos
Han existido varios artistas, como sería Leonardo da
Vinci, cuyo trabajo tiene un cierto atractivo y ofrece un
nivel de apreciación más profundo entre el público
orientado a la tecnología. Entre este tipo de artistas,
uno de los favoritos del Siglo XX es Escher, cuyos
trabajos han fascinado a los científicos y a los
ingenieros por cerca de medio siglo. Sus trabajos han
sido reproducidos en publicaciones científicas,
revistas y monografías, y en las cubiertas de libros de
texto, pósteres, calendarios, y en los medios
populares. Una razón de su atractivo se debe al uso
de Escher de figuras como poliedros regulares,
diseños periódicos, imágenes en espejo, y objetos
como la banda de Möbius, que son conocidos por los
tecnólogos y que proporcionan un sentido de armonía
y orden. Una segunda razón de su popularidad es la
forma poco usual en que maneja el espacio en sus
trabajos,
con
reflexiones,
estiramiento,
deformaciones,
proyecciones
y
otras
transformaciones similares, que le llaman la atención
al público orientado a la tecnología. Esto es de
especial importancia si consideramos que Escher no
fue un matemático profesional, y ni siquiera tenía
algún entrenamiento en matemáticas. Sin embargo,
su manipulación intuitiva de regiones espaciales,
derivada
de
principios
estéticos,
representa
herramientas matemáticas sofisticadas, tales como el
mapeo conformal y la geometría hiperbólica, lo que
sugiere que estas operaciones no son enteramente
arbitrarias en un modo abstracto, sino que están
relacionadas a la percepción humana.
La vida de Escher
Maurits Cornelis Escher nació en Leeuwarden,
Holanda, el 17 de junio de 1898, y creció con sus
cuatro hermanos en Arnhem. A pesar de que su
padre era un ingeniero civil, y tres de sus hermanos
siguieron carreras en los campos de la ciencia y la
ingeniería, él no tenía inclinaciones hacia las
matemáticas y orientó sus intereses a las artes
gráficas. Estudió en la Escuela de Arquitectura y
Artes Decorativas de Haarlem, en donde aprendió la
técnica de madera de Samuel de Mesquita. En 1922
emigró a Italia, estableciéndose en Roma, donde vivió
hasta 1934. En este tiempo, produjo una gran
cantidad de bocetos de paisajes y edificios del sur de
Italia. En 1935 viajó a Suiza, donde vivió por dos
años, seguidos de tres años en Bélgica, y finalmente
en 1941, se estableció en Baarn, Holanda, donde
vivió las siguientes tres décadas hasta su muerte en
Octubre 2006
1972. Un autorretrato de Escher en 1935 se aprecia
en la Figura 1.
Simetrías y Periodicidades
Los teselados son formas de arreglos de adornos
periódicos en forma de mosaico. Una gran cantidad
de los trabajos de Escher se inspiraron en el arte de
los moros, quienes ocuparon España de 711 a 1492,
y decoraron pisos y paredes con mosaicos
multicolores que cubrían la superficie en su totalidad.
Sin embargo, mientras que los moros tenían prohibido
representar objetos animados por razones religiosas,
Escher lo hizo su marca distintiva. Sus dibujos
ilustran muchos tipos de simetrías, que han deleitado
a cristalógrafos y especialistas de teoría de grupos [5],
[6].
Transmutaciones graduales
Un motivo distintivo en muchas de las creaciones de
Escher, especialmente en sus obras más conocidas,
es la transformación gradual de una figura o teselado
a otra en piezas consecutivas de dibujos de mosaicos
periódicos.
Combinadas con perspectivas poco
usuales, brindan un efecto impresionante.
Ilusiones en dos y tres dimensiones
La representación de un objeto tridimensional (3-D) en
un
dibujo
bidimensional
(2-D)
resulta
en
ambigüedades de observación que proporcionan
muchas oportunidades para ilusiones ópticas. Escher
fue un maestro en este arte de engañar al ojo humano
en formas encantadoras.
Figura 1.
Autorretrato de M.C. Escher (1898-1972)
en espejo esférico, fechado en 1935, titulado Mano con
Globo Reflector.
La Obra de Escher
Las creaciones de Escher, producidas a lo largo de
cuatro décadas, incluyen unos 450 trabajos de arte,
que incluyen grabados en madera, litografías y
dibujos [4]. Aunque existe una gran variedad en el
trabajo de Escher, se pueden identificar temas
recurrentes en sus creaciones, de los cuales los
siguientes seis son los principales. Un ejemplo
ilustrativo de cada uno se muestra en la Figura 2.
Paisajes
Durante sus años inciales en Italia, Escher produjo
dibujos de paisajes, tanto reales como imaginarios,
con un impacto visual importante debido a su
selección de punto de referencia o el uso de luz,
sombras y color.
Perspectivas inusuales
Escher produjo una variedad de dibujos mostrando
detalles finos en las cosas, desde objetos cotidianos o
escenas de la vida diaria hasta los detalles
arquitectónicos de majestuosos edificios, pero desde
puntos de referencia ventajosos para producir
resultados cautivantes.
Octubre 2006
Representaciones del Infinito
Muchas de la obras de Escher transmiten una
impresión gráfica del infinito dentro de fronteras
finitas, al sugerir una continuación indefinida de
teselados en el espacio. Los trabajos de este tipo son
los que se examinarán en este artículo.
Representación del Infinito con Teselados
El concepto del infinito siempre ha tenido un aura de
misterio entre los matemáticos y aún entre quines no
tienen experiencia en este campo [7]-[8]. Muchos de
los trabajos tipo mosaico de Escher dan una
sensación de infinito debido a su periodicidad y
capacidad de extensión indefinida [8], pero en la
práctica, tienen que llegar a un paro brusco en el
borde de la obra. Es evidente que se necesita más
para verdaderamente transmitir el sentido de
extensión infinita, y Escher estaba fascinado con la
representación del infinito en un espacio finito. En los
últimos años de su carrera, empezando en la década
de los 50, Escher hizo varios intentos de representar
un mosaico infinito dentro de una frontera circular o
cuadrada, como se ilustra en la Figura 3.
Escher trató de capturar la percepción de un continuo
infinito con la reducción progresiva del tamaño de
cada pieza, ya sea hacia el centro o hacia el borde del
dibujo. En uno de sus primeros intentos [Figura 3(a)],
el acercamiento al infinito ocurre en el centro del
IEEE microwave magazine 67
(a)
(b)
(c)
(d)
(f)
(e)
Figura 2.
Ejemplos representativos del arte de Escher, ilustrando los principales temas de su obra. (a) Paisajes
inusuales. Goriano Sicoli, Abruzzi (1929). (b) Perspectivas inusuales. Dentro de San Pedro (1935). (c) Teselado.
Divisiones Regulares del Plano III (1957). (d) Transformaciones graduales. Cielo y Agua I (1938). (e) Ilusiones en dos y
tres dimensiones.
Cascada (1961).
(f) Representaciones del infinito.
Viñeta de Peces (1956).
68 IEEE microwave magazine
Octubre 2006
dibujo con la reducción del tamaño de las piezas. En
trabajos subsecuentes usó la técnica inversa [Figuras
3(b) y 3(c)], en los que busca alcanzar el infinito
presentando la reducción de tamaño hacia el
perímetro del dibujo. El mismo Escher no estuvo
satisfecho con estos intentos iniciales, y siempre
buscó formas de mejorarlos. Sus trabajos posteriores
incluyen dos grabados en madera, titulados Círculo
Límite III [Figura 3(d)] y Círculo Límite IV [Figura 3(e)],
que son sus trabajos en este género mejor conocidos.
El procedimiento para la construcción de teselados
con una figura fija, de cualquier contorno deseado, ha
sido descrito en la literatura [9], [10], como también ha
sido el análisis de la estructura geométrica de Círculo
Límite III [11], [12]. En este artículo se analiza en
detalle la estructura del Círculo Límite IV.
La Estructura de Círculo Límite IV
Teselados Construidos con Transformaciones
Círculo Límite IV, también conocida como Cielo e
Infierno, completada en julio de 1960 (Figura 4), es
considerada una de las obras maestras de Escher. El
original es un grabado en madera, impreso en negro y
ocre, mide 416 mm de diámetro, y muestra ángeles y
demonios en un teselado que llena por completo el
plano.
El tamaño de estas figuras decrece
paulatinamente del centro al perímetro, con más de
dos docenas de tamaños identificables, hasta que se
pierden en el límite visual identificable en un grabado
en madera. A pesar de que las figuras son de tamaño
diferente en el sentido euclidiano, demostraremos que
son de hecho congruentes bajo una métrica
hiperbólica de distancia; visto de esta manera, la obra
es simplemente un mosaico periódico con piezas de
tamaño constante y periodicidad uniforme en el
espacio hiperbólico.
El primer requisito, y la característica determinante
para un teselado, es la apariencia repetitiva del
elemento unitario en desplazamientos espaciales
periódicos. La especialidad de Escher era introducir
una transformación gradual del elemento base con
cada repetición sucesiva.
Para que la figura
transformada se siga reconociendo como una
transformación de la figura previa, es necesario que
ciertas características básicas de la figura no sufran
cambios. La transformación aplicada al elemento
base debe por lo tanto presentar algunas invariantes,
y esas invariantes deben tener una manifestación
geométrica agradable a la vista. Ésta es la base de
muchos de los teselados de Escher que usan este
cambio gradual.
Un segundo requisito impuesto aquí es la necesidad
de incluir una red infinita en un lienzo finito, lo que
implica que el tamaño y los desplazamientos
espaciales del elemento base no pueden ser
constantes. Por lo tanto, se requiere de una segunda
transformación en el tamaño y el desplazamiento del
elemento base en cada réplica. Como resultado de
esta transformación, el tamaño de las piezas debe
Octubre 2006
tender a cero, transmitiendo la sensación de infinito
deseada.
El grabado Círculo Límite IV (Figura 4) y otras obras
en esta categoría presentan ambas características —
un patrón repetido sujeto a una continua alteración y
una periodicidad con menor distancia en cada
repetición de la pieza. Por lo tanto, estas obras deben
emplear dos transformaciones simultáneas. En el
caso del Círculo Límite IV, la única transformación
aplicada al elemento base, la figura del ángel, es una
rotación. La transformación aplicada al tamaño y
distancia del elemento base es mucho más
complicada, y es sujeta a escrutinio en lo que sigue.
El Círculo Límite IV de Escher y la Gráfica Smith
La clave que nos dice que la gráfica Smith es
relevante en el entendimiento del arte gráfico de
Escher está en las escalas radiales tradicionalmente
provistas en la gráfica Smith. Entre las varias escalas
provistas para leer los coeficientes de reflexión, las
pérdidas por retorno, y la razón de voltaje de onda
estacionaria en diversas unidades, existe una que
expresa la razón de voltaje de onda estacionaria
(VSWR) en decibeles, que se extiende desde cero en
el centro de la gráfica a ∞ en el perímetro de la
gráfica. Este rango corresponde al que Escher
necesita para tratar de representar al infinito
gráficamente.
Como una prueba preliminar de esta idea, las
siguientes mediciones simples se pueden hacer en el
Círculo Límite IV. Aunque la mayoría de los ángeles
del dibujo son asimétricos, los que presentan simetría
bilateral tienen un eje de simetría que pasa por el
centro del círculo.
La altura de los ángeles
bilateralmente simétricos (definida en la dirección
radial como la distancia de cabeza a pie) se puede
por lo tanto obtener al medir, para cada uno de los
dos extremos, la distancia radial desde el origen, y
tomar su magnitud de la diferencia entre sus
coordenadas radiales. Si el Círculo Límite IV se
escala para caber exactamente dentro del círculo
unitario de la gráfica Smith, y la distancia radial de un
punto se mide con la escala para el VSWR en
decibeles, se obtienen los resultados listados en la
Tabla 1. Se encuentra que la altura de los ángeles
bilateralmente simétricos es de aproximadamente 8
dB. Este resultado acrecenta la conjetura de que las
figuras en el Círculo Límite IV son congruentes una
con otra, y abre la esperanza de que una herramienta
de la ingeniería como es la gráfica Smith pueda ser
relevante para entender una obra de arte estética. El
demostrar que los ángeles sin simetría bilateral
también son congruentes requiere de un análisis más
detallado.
La escala de VSWR nos permite únicamente medir la
distancia a lo largo de la dirección radial en el círculo
unitario. Para medir la distancia entre pares de
puntos arbitrarios Γ1 y Γ2 dentro del círculo unitario,
debemos examinar el origen geométrico de la escala
para el VSWR usada en la gráfica Smith. Estas
IEEE microwave magazine 69
(a)
(c)
(e)
(b)
(d)
(f)
Figura 3.
Intentos de Escher de representar el infinito de varias maneras. (a) Más Pequeño y Más Pequeño (1956).
(b) Círculo Límite I (1958). (c) Círculo Límite II (1959). (d) Círculo Límite III (1959). (e) Círculo Límite IV (1960). (f)
Cuadrado Límite (1964).
70 IEEE microwave magazine
Octubre 2006
mediciones generalizadas de distancia ya han sido
usadas en trabajos de microondas en una variedad de
contextos, y serán señaladas más adelante.
La Gráfica Smith y las Transformaciones
de Möbius
La Gráfica Smith como una Ayuda Gráfica
La Gráfica Smith (Figura 5) se ha convertido en un
icono de la ingeniería de microondas. Por ejemplo, se
usa frecuentemente en el diseño de logotipos, y es la
parte más recordada de los cursos de ingeniería de
microondas décadas después, cuando todo lo demás
que se aprendió en el salón de clases se ha olvidado.
La gráfica Smith tenía inicialmente la intención de ser
una herramienta gráfica para eliminar el tedio del
cómputo con números complejos [13], [14]. Aún
cuando esto ya no es una necesidad desde el
advenimiento de las calculadoras electrónicas en la
década de los 60, la gráfica Smith sigue siendo
altamente útil como una representación visual para el
entendimiento de la información.
cómputo, tanto en modernos programas de diseño
ayudado por computadora como en equipo de
medición de microondas controlado por computadora,
se sigue presentando la información en formato de
gráfica Smith.
La gráfica Smith se construye esencialmente para
realizar dos tareas básicas:
1)
La transformación entre un coeficiente de
reflexión Γ definido con respecto a una impedancia de
referencia Z0 y la correspondiente impedancia
normalizada Z/Z0:
Γ=
Z − Z0
Z + Z0
y Z=
Z0 + Z0 Γ
1− Γ
(1)
2)
La transformación, ya sea de Γ o Z, al
cambiar el plano de referencia en el que están
definidos, por una distancia l12 a lo largo de una línea
de transmisión uniforme con impedancia característica
Z0 y constante de propagación γ=jβ:
Z + Z0 tanh γl12
Z 2 = Z0 1
y Γ2 = Γ1 e−2γl12
Z1 tanh γl12 + Z0
(2)
Tabla 1. Medidas de las alturas de las figuras en
Círculo Límite IV.
Coordenada
Coordenada
Altura
Figura
Radial de la
Radial dl pie,
de la
Cabeza, H
F
Figura,
|H-F|
Ángel #1 8.3 dB
0 dB
8.3 dB
Ángel #2 7.2 dB
15.5 dB
8.3 dB
Ángel #3 23.5 dB
15.3 dB
8.2 dB
Ángel #4 22 dB
30.2 dB
8.2 dB
Ángel #5 39 dB
31 dB
8.0 dB
Mediciones limitadas a los ángeles con simetría bilateral.
Círculo Límite IV está sobrepuesto a la gráfica Smith, y las
distancias radiales desde el centro se toman con la escala
para el VSWR (en decibeles) provista con la gráfica Smith.
Figura 4.
El grabado en madera de Escher titulado
Cielo e Infierno, también conocido como Círculo Límite IV
(julio 1960), colocado en el círculo unitario con la escala del
VSWR de la gráfica Smith.
De entre las numerosas extensiones y aplicaciones de
la gráfica que se han propuesto a lo largo de los años
[15], aquellas que ayudan a pensar (más que sólo
calcular) continúan
siendo útiles
para
los
profesionales que han desarrollado la apreciación
intuitiva de ésta. La gráfica Smith está tan inmersa en
la conceptualización de los ingenieros de microondas
que a pesar de la muy sofisticada capacidad de
Octubre 2006
La gráfica de Smith cumple con la primera tarea al 1)
dibujar las escalas de las coordenadas polares en el
plano para graficar Γ, restringida al círculo unitario (es
decir, para valores de Γ de una red pasiva de un
puerto); 2) dibujar las líneas de las coordenadas
cartesianas
rectangulares
en
otro
plano,
distorsionable, para graficar Z/Z0, limitándose al
semiplano derecho (también para una red pasiva de
un puerto), y 3) distorsionando el sistema coordenado
cartesiano a manera que cuando ambos sistemas se
sobreponen, cada punto en un sistema coincide
exactamente con su mapa en el otro sistema
coordenado. La segunda tarea se realiza fácilmente
al rotar Γ por un ángulo de 2Im[γ]*l12, y sólo requiere
que se rotule la escala angular en el sistema
coordenado polar en unidades de 1/λ. Ya que cada
IEEE microwave magazine 71
una de estas dos tareas es sencillamente un ejemplo
de una transformación bilineal de Möbius de un
número complejo, podemos afirmar que la gráfica
Smith es una ayuda gráfica para realizar
transformaciones de Möbius.
Γin =
O
( S11S22 − S12S21 ) ΓL + S11
S22 ΓL + 1
Z Z − ( Z11Z22 − Z12 Z21 )
Zin = 11 L
ZL + Z22
(3)
Y cada una de éstas es un ejemplo de la
transformación de Möbius de un número complejo.
La transformación bilineal (lineal fraccional) de Möbius
de un número complejo está definida por
M( Z) ≡ W ≡
AZ + B
CZ + D
(4)
Donde A, B, C, y D son constantes complejas (es
decir, independientes de Z). Las propiedades de esta
transformación se pueden expresar de manera más
compacta añadiendo a esta definición algunos
requisitos adicionales, como los siguientes:
1) M ( ∞ ) ≡ A / C , y M ( −D / C ) ≡ ∞ , lo que nos
Figura 5.
La Gráfica Smith, con sus
radiales. (Cortesía de Analog Instrument Co.)
escalas
Transformaciones Bilineales de Möbius
Las transformaciones de Möbius son ubicuas en el
trabajo de microondas por razones prácticas. El plano
de referencia deseado o requerido para definir Γ o Z
es muy frecuentemente distinto al que se tiene para
llevar a cabo las mediciones o los cálculos exacta y
convenientemente;
las razones incluyen la
imposibilidad de acceder al plano para las
mediciones, la falta de disponibilidad de estándares
de referencia útiles en el plano, y la complejidad
estructural que crea campos multimodo o
acoplamientos en el plano.
Por lo tanto, muy
frecuentemente es necesario transformar, o extraer,
impedancias o coeficientes de reflexión entre dos
planos de referencia. La estructura electromagnética
que interviene entre estos dos planos muy
frecuentemente se puede representar adecuadamente
por una red lineal de dos puertos, caracterizada en el
dominio de la frecuencia por una matriz de
impedancia [Z] o una matriz de dispersión [S]. La
transformación de una función de respuesta (como
sería un coeficiente de reflexión o una impedancia)
por una red lineal de dos puertos arbitraria está dada
por
72 IEEE microwave magazine
permite extender el plano complejo al incluir el
punto Z = ∞ al especificar el dominio y el
rango de la transformación, haciendo así la
transformación de Möbius homomórfica.
2) AD − BC ≠ 0 , lo que nos permite normalizar la
transformación al dividir cada una de las
constantes A, B, C, y D por la cantidad AD-BC
sin
alterar
de
ninguna
manera
la
transformación.
La transformación de Möbius en el plano complejo
tiene varias propiedades útiles [16], prácticas tanto en
el arte como en la ingeniería de microondas [17], [18].
Estas propiedades se pueden describir en varios
lenguajes, es decir, algebraicamente, en forma de
matrices, geométricamente y topológicamente. El
enfoque geométrico es el más útil aquí, en vista de la
necesidad de relacionarlas a la obra gráfica de
Escher.
Propiedades
Geométricas
de
las
Transformaciones de Möbius
La transformación de Möbius mapea un número
complejo Z a otro número complejo W, cada uno de
los cuales requiere de un plano bidimensional para su
representación geométrica, en la cual es representado
por un punto. Una curva CZ en el plano Z es por lo
tanto una sucesión de puntos, cada uno de los cuales
se mapea a otro punto en el plano W, cuya sucesión
define otra curva CW; este proceso se puede llamar
la transformación de la curva. Esta transformación
conserva ciertas propiedades de la curva, y son estas
invariantes, compartidas por CZ y CW, las que nos
interesan aquí.
Para visualizar el efecto de esta transformación en el
plano complejo, nos ayuda considerar algunos casos
especiales de la transformación de Möbius dada en
(4).
Octubre 2006
•
•
•
Translación: W=Z+B (cuando A=D=1; C=0).
Escalamiento: W=|A|Z (cuando B=C=0; D=1,
A es real y positiva)
Rotación: W = Z exp ( j∠A ) (cuando B=C=0;
D=1; |A|=1)
•
Inversión: W=1/Z (cuando A=0; B=C=1; D=0)
El efecto geométrico de las primeras tres en una
curva se puede visualizar directamente; la última
operación puede ser vista como una reflexión en el
círculo unitario. La utilidad de estos casos especiales
reside en que sirven de bloques básicos para
cualquier transformación de Möbius, que se puede
expresar como la concatenación de estas operaciones
elementales; así se puede llegar a W en (4) siguiendo
la secuencia de transformaciones:
Z → CZ → CZ + D → 1/ ( CZ + D )
→ (BC − AD ) / C  / ( CZ + D )
→ (BC − AD ) / C  / ( CZ + D ) + ( A / C )
= ( AZ + B ) / ( CZ + D ) = W.
La transformación de Möbius de una curva en el plano
complejo tiene varias propiedades útiles, de entre las
cuales las tres siguientes son particularmente
relevantes aquí:
• La transformación mapea círculos (y por lo tanto
líneas rectas, que son un caso especial de los
círculos) en el plano Z a círculos en el plano W.
[De aquí la forma de las líneas en la gráfica Smith,
representando la transformación de las curvas
Re[Z] e Im[Z] por la transformación de Möbius de
(1)].
• La transformación es conformal, en el sentido de
que el ángulo formado por las curvas CZ1 y CZ2
(definido como el ángulo entre las tangentes a
estas curvas en su punto de intersección) en el
plano Z permanece sin alteración, tanto en
magnitud como en signo, después de una
transformación al plano W.
• Con la selección adecuada de una métrica de
distancia, la longitud de la curva geodésica entre
dos puntos Z1 y Z2 en el plano Z, es la misma que
entre sus imágenes W1 y W2;
la métrica
euclidiana no es adecuada.
Las demostraciones, ejemplos y aplicaciones de estas
propiedades se pueden encontrar en la literatura [16]
y [19] y en otras fuentes.
Es evidente que las dos primeras propiedades pueden
ayudar a conservar la forma de una figura reconocible
después de una transformación, mientras que la
tercera proporciona el escalamiento en el plano
euclidiano donde la distancia no es invariante. Estos
son los dos requisitos esenciales mencionados en
“Teselados Construidas por Transformaciones” para
la construcción de teselados que representan el
infinito. Nos enfocamos a la tercera propiedad y la
Octubre 2006
métrica de distancia requerida para invariancia a
manera de entender el escalamiento en distancia y
tamaño en la obras de Escher.
Métrica de Distancia Hiperbólica
Definición de una Métrica de Distancia
La distancia d(Z1,Z2) entre dos puntos Z1 y Z2 se
define como la trayectoria o curva más corta entre los
dos puntos. La curva con la longitud más corta entre
dos puntos es una geodésica, que es la
generalización de la línea recta de la geometría
euclidiana. A su vez, la longitud de una curva se
define como la integral (es decir, la suma) de
longitudes elementales entre puntos sucesivos a lo
largo de la curva, cada uno separado del otro por una
distancia infinitesimal.
Finalmente, la distancia
infinitesimal entre dos puntos se puede definir de la
manera euclidiana, ya que en el límite infinitesimal,
todos los espacios son esencialmente euclidianos
[20]. La métrica de distancia resultante tiene las
propiedades que esperaríamos intuitivamente de una
distancia, que son:
•
No negatividad: d ( Z1,Z2 ) ≥ 0 para toda Z1,
•
Z2.
Identidad: d ( Z1,Z2 ) = 0 si y sólo si Z1=Z2.
•
Simetría Bilateral: d ( Z1,Z2 ) = d ( Z2 ,Z1 ) para
•
toda Z1, Z2.
Desigualdad
del
Triángulo:
d ( Z1,Z3 ) ≤ d ( Z1,Z2 ) + d ( Z2 ,Z3 ) para toda Z1,
•
Z2 y Z3.
Continuidad de d ( Z1,Z2 ) , garantizada por su
correspondencia uno a uno con números
reales.
Es fácil ver que la métrica de distancia euclidiana
permanece invariante a las operaciones de
desplazamiento y rotación;
también permanece
invariante a la operación del complejo conjugado
( W = Z* ), que se puede interpretar como una
reflexión sobre el eje real. En contraste, como se ha
demostrado antes, una transformación de Möbius se
compone de escalamiento e inversión además de
translación y rotación, y en consecuencia, en general
no permite que la distancia euclidiana entre dos
puntos sea invariante. En su lugar, una de las
invariantes de la transformación de Möbius es su
razón cruzada, definida por:
( W1 − W3 ) ( W2 − W4 ) ( Z1 − Z3 ) ( Z2 − Z4 )
=
( W1 − W4 ) ( W2 − W3 ) ( Z1 − Z4 ) ( Z2 − Z3 )
(5)
Donde W1, W2, W3 y W4 son las imágenes de Z1, Z2,
Z3, y Z4 respectivamente, bajo la transformación. Por
lo tanto, una métrica de distancia basada en la razón
cruzada, o una función monotónica de ésta, sería
invariante a la transformación de Möbius. Lo que es
IEEE microwave magazine 73
más, ya que la métrica de distancia es dependiente de
la geodésica, que a su vez es determinada por las
reglas de geometría del espacio, es necesario
introducir un espacio diferente en el cual las reglas
geométricas son distintas a las euclidianas. De aquí
la necesidad de un espacio no-euclidiano.
Geometría No-Euclidiana
La geometría de la escuela de educación primaria es
llamada Geometría Euclidiana, en honor de Euclides
de Alejandría (alrededor de 300 AC), quien fue el
autor de Elementos de Geometría, un tratado sobre
geometría, que es aparentemente el libro más leído
en todas las ciencias, matemáticas y tecnología, en la
historia de la humanidad. Muy poco se puede decir
con certeza de Euclides, ya que la versión más
antigua de su libro, escrita en latín por Plono, data de
900 DC, 12 siglos después de Euclides (de hecho, de
los 15 libros o capítulos contenidos en los Elementos,
los dos últimos parecen ser adiciones posteriores, no
escritos por Euclides).
Euclides consolidó el
conocimiento de geometría de su tiempo al darle una
estructura axiomática, por medio de la cual todos los
resultados pueden ser deducidos del conjunto más
pequeño posible de postulados a priori. Este conjunto
mínimo consiste de cinco axiomas euclidianos, que
básicamente postulan la existencia de una línea recta,
continuidad, una métrica de distancia, la congruencia
de los ángulos, y las líneas paralelas. El quinto
postulado, el postulado de las paralelas, puede ser
escrito en una variedad de formas alternas pero
equivalentes (es decir, deducibles unas de otras), en
que especifica que existe una sola línea que pasa por
un punto P y es paralela a una línea L dada.
Después de Euclides, en un período de más de 2,000
años, existe una larga historia de esfuerzos por
matemáticos desde Arquímedes hasta Legendre, para
tratar de reducir el conjunto de postulados
euclidianos, siendo el quinto postulado el que ha
recibido el mayor escrutinio en intentos de deducirlo
de los otros cuatro. Fue hasta el Siglo XIX cuando
quedó claro que 1) el quinto postulado no es
consecuencia de los otros cuatro, 2) no es esencial en
la consistencia interna de la geometría, y 3) su
reemplazo por postulados alternativos puede resultar
en una geometría perfectamente auto consistente.
Estas geometrías son llamadas no-euclidianas, y hay
dos claras variedades de ellas, dependiendo del
reemplazo seleccionado para el quinto postulado. Si
el número de líneas pasando por P y paralelas a L es
cero, la geometría es elíptica (o de Riemann), en la
cual la suma de los ángulos internos de un triángulo
es mayor a 180°. Si el número es dos o más, la
geometría es hiperbólica, y en ésta la suma de los
ángulos internos de un triángulo es menor a 180°.
Posiblemente, la manera más sencilla de ilustrar y
entender la geometría no-euclidiana, y al mismo
tiempo demostrar la existencia y consistencia de sus
axiomas, es el construir un modelo de geometría no
euclidiana que se basa en la ya conocida geometría
74 IEEE microwave magazine
euclidiana. En lo que sigue, presentamos únicamente
un modelo de entre los muchos posibles, y sólo para
la variedad hiperbólica de la geometría no euclidiana,
que será requerido para la discusión posterior.
El Modelo del Disco Abierto de Poincaré para el
Espacio Hiperbólico
Para construir la nueva geometría, necesitamos
objetos que puedan englobar los conceptos de
puntos, líneas y planos, y a los cuales se puedan
aplicar un conjunto de postulados consistentes; un
conjunto mínimo consiste, por ejemplo, de los
axiomas euclidianos, que básicamente postulan la
existencia de una línea recta, continuidad, una métrica
para distancia, la congruencia de los ángulos, y líneas
paralelas. Sin embargo, el último postulado, el
postulado de las paralelas, no es esencial para autoconsistencia, y por lo tanto puede ser violado para
obtener una nueva geometría. Estos objetos pueden
ser seleccionados del mundo euclidiano en sí, y hay
muchas alternativas disponibles.
Una de las
selecciones es aquella de los puntos en el interior de
un círculo unitario, llevando al llamado Modelo de
Disco Abierto de Poincaré para la geometría
hiperbólica.
En el plano euclidiano, en el que cualquier punto
puede ser especificado por un número complejo Γ,
considere un círculo de radio unitario con su centro en
el origen. Designamos el interior de este círculo como
el plano hiperbólico, y el conjunto de todos los puntos
con |Γ|<1 en el círculo unitario abierto como puntos
hiperbólicos (puntos h). En seguida, considere un
círculo euclidiano (con centro C y radio R) que es
perpendicular al círculo unitario, es decir, intersecta el
círculo unitario en ángulos rectos en P y Q, que son
los puntos de intersección (por simetría, si los círculos
son mutualmente ortogonales en P, también serán
ortogonales en Q). Una línea hiperbólica (línea h) se
define como el conjunto de todos los puntos h en el
segmento interior de cualquier círculo ortogonal, como
se muestra en la Figura 6; cada selección de la
localización de C y la magnitud de R proporciona una
línea h diferente. Dados dos puntos h Γ1 y Γ2, existe
un círculo euclidiano único que pasa por ellos y es a
la vez normal al círculo unitario; por lo tanto, existe
una línea h única a través de dos puntos h dados. El
postulado euclidiano de congruencia de ángulos es
asegurado al conservar la medida euclidiana del
ángulo entre dos líneas. Estas definiciones cumplen
con los cuatro primeros postulados euclidianos,
incluyendo la existencia, continuidad y extensión
ilimitada, de una línea (hacia P y Q, que no son parte
de la línea al no ser puntos h).
Finalmente, consideramos un quinto postulado en
relación a las líneas paralelas. Dos líneas h son
paralelas entre sí si no se cruzan, es decir, no tienen
un punto h en común. Ya que más de una línea h se
puede dibujar pasando por un punto h dado Γ3, cada
una de ellas sin intersección con una línea h que pasa
Octubre 2006
por Γ1 y Γ2, es claro que en este modelo el número de
líneas paralelas que pasan por un punto dado, que
son paralelas a una línea dada, es mayor a uno, que
es la característica distintiva de las geometrías
hiperbólicas.
El probar la congruencia de segmentos de línea
requiere tener una métrica de distancia. En el espacio
hiperbólico, el requerir que la métrica de distancia
satisfaga las condiciones listadas en la sección
anterior, conlleva a una métrica natural, que se define
en lo siguiente.
el origen, la distancia radial al otro punto desde el
origen está dada por:
 1+ Γ 
dH ( 0, Γ ) = 2 tanh−1 Γ = loge 
 1 − Γ 


(8)
La Métrica de Distancia Hiperbólica
La distancia hiperbólica dH ( Γ1, Γ2 ) entre dos puntos h
Γ1 y Γ2 (es decir, la longitud de la línea h que los une)
es diferente de la distancia euclidiana dE entre dos
puntos euclidianos Γ1 y Γ2. De hecho, dH puede ser
definida en función de las distancias euclidianas de
cada uno de los puntos Γ1 y Γ2 desde los puntos de
intersección P y Q del círculo euclidiano ortogonal
mencionado antes (precaución: P es el punto límite al
que se aproxima la línea h Γ1Γ2 al extenderse hacia
Γ1, mientras que Q es el punto límite al extenderse
hacia Γ2);
entonces, la métrica de distancia
hiperbólica, obtenida del procedimiento detallado
arriba, es la siguiente:
 d ( Γ ,Q )   dE ( Γ2 ,P )  
dH ( Γ1, Γ 2 ) = loge  E 1

  (6)
 dE ( Γ2 ,Q )   dE ( Γ1,P )  
Donde dE denota la conocida distancia euclidiana
entre dos números complejos, definida por
dE ( Γ1,Q ) = Γ1 − Q . Estas distancias euclidianas se
pueden evaluar explícitamente en el modelo del disco
abierto, y después de su substitución, la distancia
hiperbólica entre dos puntos Γ1 y Γ2 se puede
expresar únicamente en función de los puntos por:
dH ( Γ1, Γ2 ) = 2 tanh−1
Γ1 − Γ2
1 − Γ1Γ2*
(7)
Esta definición de la distancia hiperbólica entre dos
puntos satisface todas las propiedades esperadas de
una métrica de distancia, listadas anteriormente.
Adicionalmente, es invariante ante una transformación
de Möbius, ya que la distancia en (6) es una función
monotónica de la razón cruzada, como se define en
(5).
En la gráfica Smith, esta misma invariancia de la
razón cruzada y la métrica de distancia se manifiestan
de muchas maneras, como es en la escala radial
usada para el VSWR, y son usadas en ciertas
construcciones geométricas, y en la definición de la
medida de variación entre dos impedancias distintas.
En el caso especial cuando uno de los puntos está en
Octubre 2006
Figura 6.
unitario.
Una
línea
hiperbólica
en
el
círculo
Esto es idéntico, considerando el factor de
escalamiento, con la definición del VSWR (en
decibeles) en una línea de transmisión sin pérdidas y
uniforme, terminada en una carga con coeficiente de
reflexión Γ. Como resultado, la escala para el VSWR
en decibeles, provista en la gráfica Smith, es
esencialmente una escala para la medición de la
distancia radial desde el origen usando la métrica
hiperbólica. Adicionalmente, (7) se puede ver como la
generalización de la definición del VSWR, y cuantifica
la distancia entre dos coeficientes de reflexión
cualquiera. Esta medición de distancia ha sido usada
en la ingeniería de microondas para una gran
variedad de situaciones, como sería medir la distancia
entre dos valores de impedancia en un diodo
conmutado [21] o para definir la ganancia de potencia
unilateral de un dispositivo activo inmerso en una red
sin pérdidas [18].
El Círculo Límite IV Analizado con la Métrica
Hiperbólica de Distancia
Regresando al Círculo Límite IV, ahora ya podemos
medir todas las figuras que aparecen en el dibujo,
incluyendo aquellas que no presentan simetría
bilateral. Cuando las figuras individuales son rotadas,
las partes más alejadas del origen sufren una
reducción en tamaño más severa a consecuencia de
la reducción de la escala hiperbólica cerca del
perímetro, y esto causa la aparente asimetría de las
figuras.
Con el objetivo de ilustrar esto, seleccionaremos sólo
una característica, la envergadura de las alas de los
ángeles con motivo de comparación. La Tabla 2
IEEE microwave magazine 75
muestra las coordenadas polares de las puntas de las
alas para un número de figuras de ángel, medidas en
referencia a otra. La envergadura se calcula entonces
de la métrica hiperbólica en (7), y también se lista en
la tabla.
Los resultados muestran que las
dimensiones son idénticas considerando la exactitud
que se puede obtener en un grabado en madera, y
nos permite concluir que en verdad las figuras son
congruentes. El Círculo Límite IV es por lo tanto sólo
un teselado regular cuando se mide con la métrica
hiperbólica, en la cual las piezas individuales han sido
rotadas.
Tabla 2. Medidas de las características de las
figuras en Círculo Límite IV.
Coordenadas de los
Extremos de las Alas
Ala
Ala
EnverFigura
Izquierda
Derecha
gadura,
en dB
Ángel #1
10.0 dB
0.515 ∠ 0°
0.515 ∠ 60°
Ángel #2
10.5 dB
0.515 ∠ 0°
0.81 ∠ 13°
Ángel #3
9.5 dB
0.815 ∠ 0°
0.87 ∠ 11°
Ángel #4
9.5 dB
∠
∠
0.887 0°
0.887 9°
Ángel #5
10.5 dB
0.815 ∠ 0°
0.91 ∠ 8°
Distancias en la métrica hiperbólica deducidas de las
coordenadas polares en el círculo unitario y cerradas al
medio decibel más próximo.
Agradecimientos
Debo hacer patente mi agradecimiento al finado Prof.
Robert L. Kyhl (1918-2003) del Instituto Tecnológico
de Massachussets (MIT), Cambridge, quien me
introdujo a este tema a través de un curso corto,
impartido durante el “Período de Actividades
Independientes” del MIT. Mi agradecimiento también
a la Compañía M.C. Escher (Baarn, Holanda),
propietaria de los derechos de autor, por su permiso
para reproducir los trabajos de Escher en este
artículo. Las obras de M.C. Escher Mano con Globo
Reflector, Gorianno Sicoli, Abruzzi, Dentro de San
Pedro, Divisiones Regulares del Plano III, Cielo y
Agua I, Cascada, Viñeta de Peces, Más Pequeño y
Más Pequeño, Círculo Límite I, Círculo Límite II,
Círculo Límite III, Círculo Límite IV, y Cuadrado Límite
están registradas (© 2006) por M.C. Escher
Company-Holland. Todos los derechos reservados.
www.mcescher.com.
[M.C. Escher’s Hand with Reflecting Globe, Gorianno
Sicoli, Abruzzi, Inside St. Peter’s, Regular Division of
Plane III, Sky and Water I, Waterfall, Fish Vignette,
Smaller and Smaller, Circle Limit I, Circle Limit II,
Circle Limit III, Circle Limit IV, and Square Limit ©
2006 The M.C. Escher Company-Holland. All rights
reserved. www.mcescher.com]
Referencias
76 IEEE microwave magazine
[1] E. Strosberg, Art and Science. Paris: Unesco,
1999 (también New York: Abbeville Press, 2001).
[2] S. Ede, Art and Science. London, U.K.: L.B.
Tauris, 2005.
[3] S. Wilson, Information Arts: Intersection of Arts,
Science, and Technology. Cambridge, MA: MIT
Press, 2002.
[4] M.C. Escher, M.C. Escher, His Life and Complete
Graphic Works (traducción del holandés por F.H.
Bool). New York: Abradale Press/Harry N.
Abrams, 1992.
[5] D. Schattschneider, Visions of Symmetry:
Notebooks, Periodic Drawings, and Related
Works of M.C. Escher. San Francisco, CA:
Freeman, 1990.
[6] C.H. MacGillavry, Fantasy and Symmetry: The
Periodic Drawings of M.C. Escher. New York:
Harry N. Abrams, 1976.
[7] E. Maor, To Infinity and Beyond. Cambridge, MA:
Birkhauser, 1987.
[8] M.C. Escher, Escher on Escher: Exploring the
Infinite (traducción del holandés por K. Ford).
New York: Abrams, 1989.
[9] E.R. Ranucci, “Master of tessellations: M.C.
Escher, 1898–1972,” Math. Teacher, vol. 67, pp.
299–306, abril 1974.
[10] J.L. Teeters, “How to draw tessellations of the
Escher type,” Math. Teacher, vol. 67, pp. 307–
310, abril 1974.
[11] H.S.M. Coxeter, “The non-Euclidean symmetry of
Escher’s picture Circle Limit III,” Leonardo, vol. 12,
no. 1, pp. 19–25, invierno 1979.
[12] H.S.M. Coxeter, “The trigonometry of Escher’s
woodcut Circle Limit III,” Math. Intell., vol. 18, no.
4, pp. 42–46, 1996.
[13] P.H. Smith, “Transmission line calculator,”
Electronics, vol. 12, no. 1, p. 29, enero 1939.
[14] P.H. Smith, “An improved transmission line
calculator,” Electronics, vol. 17, no. 1, pp. 130–
133, enero 1944.
[15] P.H. Smith, Electronic Applications of the Smith
Chart. New York: McGraw-Hill, 1969.
[16] F.J. Flanigan, Complex Variables. Harmonic and
Analytical Functions. Boston: Allyn and Bacon,
1972, pp. 304–324.
[17] G.F. Engen, Microwave Circuit Theory and
Foundations of Microwave Metrology. Stevenage,
U.K.: Peregrinus, 1992.
[18] M.S. Gupta, “Power gain in feedback amplifiers, a
classic revisited,” IEEE Trans. Microwave Theory
Tech., vol. 40, no. 5, pp. 864–879, mayo 1992.
[19] A. Ramsay and R.D. Richtmyer, Introduction to
Hyperbolic Geometry. New York: Springer-Verlag,
1995.
[20] H.S.M. Coxeter, Non-Euclidean Geometry.
Toronto, Canada: Univ. Toronto Press, 1942.
[21] K. Kurokawa and W.O. Schlosser, “Quality factor
of switching diodes for digital modulation,” Proc.
IEEE, vol. 58, no. 1, pp. 180–181, enero 1970.
Octubre 2006