Document

Análisis estocástico de una economía pequeña y abierta
21
eseconomía , vol. ix, 41, segundo semestre de 2014, pp. 21-52
Análisis estocástico de una economía
pequeña y abierta: políticas
fiscal y monetaria
(Recibido: noviembre 2013/Aprobado: abril 2014)
Diana Carmen Segura Rodríguez*
Francisco Venegas Martínez**
Héctor Allier Campuzano***
Resumen. En esta investigación se desarrolla un modelo macroeconómico
estocástico cuya característica principal es que los precios son conducidos
por procesos de difusión con saltos. La economía en cuestión es pequeña
(tomadora de precios) y abierta (no hay barreras arancelarias al intercambio
de bienes con el exterior) y está poblada por consumidores (con vida infinita) que también son productores con preferencias, dotaciones y tecnologías
idénticas. Cabe añadir que el modelo propuesto incorpora la exposición de
los agentes (consumidores, empresas y gobierno) a los distintos riesgos financieros que afectan día a día su toma de decisiones. En el equilibrio se
determinan en forma endógena los procesos estocásticos que conducen a
la tasa de inflación, la tasa de acumulación del capital, la tasa impositiva
a la riqueza y los rendimientos de los distintos activos disponibles en la
economía.
Palabras clave: modelo macroeconómico estocástico, administración de riesgos, política fiscal y monetaria.
Clasificación JEL: E52, E61.
Estudiante de Maestría en Ciencias Económicas de la ESE-IPN. Correo electrónico: <diana.segurar@
hotmail.com>.
**
Profesor-Investigador de la Sección de Estudios de Posgrado e Investigación de la Escuela Superior
de Economía del Instituto Politécnico Nacional. Correo electrónico: <fvenegas1111@yahoo.com.mx>.
***
Profesor de la Sección de Estudios de Posgrado e Investigación de la Escuela Superior de Economía
del Instituto Politécnico Nacional.
*
22
Diana C. Segura Rodríguez, Francisco Venegas Martínez y Héctor Allier Campuzano
Abstract. This paper develops a stochastic macroeconomic model whose
main feature is that prices are driven by diffusion processes with jumps.
The economy in question is small (price taker) and open (no barriers to
trade with identical goods) and is populated by infinite-lived consumers
who are also producers with identical preferences, endowments and technologies. Moreover the proposed model incorporates the exposure of the
agents (consumers, firms and government) to various financial risks that
affect their day-to-day decision making. In the equilibrium are endogenously determined the stochastic processes leading the inflation rate, the
rate of accumulation of capital, the tax rate on wealth and income from
the different assets available in the economy.
Keywords: stochastic macroeconomic model, risk management, fiscal and
monetary policy.
JEL classification: E52, E61
1. Introducción
En los últimos años, la teoría económica ha experimentado una serie de
cambios en el diseño y la instrumentación de la política económica, ya sea
política económica o fiscal. En el campo de la teoría macroeconómica, uno
de los cambios más importantes es el abandono del marco determinista;
no sólo por la inclusión de activos financieros riesgosos a la economía, sino
también como una necesidad para explicar y describir los procesos de decisión de los agentes económicos (consumidores, empresas, gobierno, intermediarios financieros, etcétera).
Estos cambios le dan una mayor importancia a los diferentes tipos de
riesgos (financiero, crédito, liquidez, operacional, económico, legal, etc.) a
que se exponen los agentes económicos, lo que ha conducido a una mayor
utilización de matemáticas más sofisticadas que permitan una óptima comprensión de los fenómenos de comportamiento aleatorio; evidentemente,
todos los fenómenos económicos son fenómenos estocásticos, porque se encuentran en un ambiente de riesgo e incertidumbre.
En consecuencia, el ambiente de riesgo e incertidumbre en el que actualmente vivimos, afectan las decisiones de los agentes sobre consumo,
Análisis estocástico de una economía pequeña y abierta
23
inversión y producción. Por ello, la importancia de una adecuada y
oportuna administración de riesgos por parte de los encargados de
diseñar la política económica (fiscal y monetaria), la cual radica en la
creación de dispositivos congruentes, eficaces y creíbles que minimicen el impacto esperado de los choques exógenos sobre las principales
variables económicas.
El objetivo de esta investigación, consiste en desarrollar un modelo macroeconómico estocástico que permita analizar en el equilibrio el
comportamiento de los agentes económicos (consumidores, empresas y gobierno) en condiciones de riesgo e incertidumbre, en una economía pequeña, abierta y estocástica.
Por lo anterior, la hipótesis a probar es que, una adecuada y oportuna administración de riesgos financieros y económicos en una economía pequeña
y abierta por parte de los encargados del diseño y la instrumentación de la
política económica reduce el efecto de los choques externos sobre variables
financieras (precios y rendimientos de activos) y económicas (producción,
consumo, inversión, empleo, gasto y deuda del Gobierno) relevantes.
Las justificaciones de la investigación se centran en modelar las variables
financieras de tal manera que ocasionalmente presentan movimientos bruscos e inesperados. Por ejemplo, los saltos bruscos en variables financieras
y económicas durante la crisis 2007-2009 en Estados Unidos y sus secuelas
en México. Dichos saltos ocasionaron en nuestro país que el PIB nacional
cayera hasta 6.1%, derivado de que Estados Unidos tuvo una contracción
de 3.5%.
El presente trabajo es importante para la economía mexicana, ya que
plantea la necesidad de un marco de análisis exhaustivo que incorpore saltos aleatorios en las variables económicas, por ello el periodo de análisis
de esta investigación comprende del año 1990 al 2011, se elige este marco
temporal por dos razones: la primera por abarcar dos periodos de crisis en
los que se presentan debacles financieras, siendo 1994-1995 y 2007-2009, la
segunda razón radica en los datos disponibles con los que se cuenta. Estos
hechos son sumamente importantes para la teoría y la investigación empírica en el desarrollo teórico de modelos de equilibrio general.
24
Diana C. Segura Rodríguez, Francisco Venegas Martínez y Héctor Allier Campuzano
El trabajo se divide en cuatro secciones. En la sección 2 se describe cómo
se lleva a cabo el modelado del comportamiento de variables económicas y
financieras cuando presentan saltos bruscos e inesperados; en la sección 3
se da una explicación de los activos disponibles con los que cuenta el consumidor, la empresa y el gobierno en el modelo. En la sección 4 se establece
el comportamiento de los agentes, se desarrolla la dinámica estocástica que
conduce al nivel general de precios, además se plantea el problema de decisión de los consumidores, empresas y gobierno, así como; en la sección
5 se especifica el equilibrio macroeconómico. Por último se presentan las
conclusiones y recomendaciones del modelo propuesto.
2. Modelado
del comportamiento de variables económicas y financieras
con saltos bruscos e inesperados
Las variables económicas y financieras se distinguen porque ocasionalmente
presentan movimientos imprevistos (auges o caídas). Estos movimientos se
presentan con más frecuencia de lo que se esperaría.
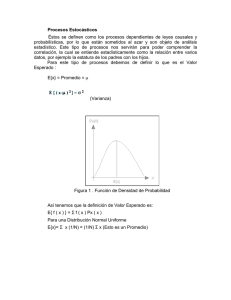
En la literatura económica y financiera, el supuesto de que los precios siguen una distribución lognormal,1 o que las tasas de crecimiento
de variables siguen una distribución normal, es muy común. En particular,
es usual suponer que los precios de los activos subyacentes siguen un
movimiento geométrico Browniano, en cuyo caso el rendimiento logarítmico es normal. Sin embargo, existe evidencia empírica (Venegas-Martínez, 2001) de que, en la mayoría de los casos, los precios de los activos,
sobre todo cuando se trata de datos diarios o intradía, no se comportan de
acuerdo a una distribución lognormal. De hecho dichos precios casi nunca se
comportan de acuerdo a distribuciones teóricas comúnmente conocidas (Venegas-Martínez, 2009).
Asimismo, se observa a menudeo que las distribuciones empíricas de
los rendimientos logarítmicos intradía estandarizados, de muy numerosos
1
Constituye el supuesto básico del modelo de Black-Sholes. Bajo este proceso, la rentabilidad del activo
subyacente tiene una trayectoria constante, que se recogen en la tendencia, con pequeñas modificaciones en intervalos de tiempo relativamente cortos, que se modelizan por un proceso de Wiener.
Análisis estocástico de una economía pequeña y abierta
25
activos subyacentes, presentan exceso de curtosis y sesgo (al compararse
con una distribución normal), y no siempre es permisible ajustar una distribución teórica simple.
La presencia de colas gordas o pesadas es debido al exceso de curtosis de
una distribución empírica con relación a la supuesta por una normal teórica.
Este exceso incrementa la probabilidad de presenciar valores grandes y
pequeños a costa de disminuir la probabilidad de ocurrencia de los valores
moderados.
En este caso, si la distribución normal se mezcla con una distribución
que genere movimientos extremos o saltos en el valor del rendimiento del
título, se producirían colas más pesadas y se tendría una aproximación más
realista del comportamiento del rendimiento del activo.
Lo que hace la distribución de Poisson es modelar los movimientos extremos
e inesperados que, ocasionalmente, ocurren en los rendimientos. Sin embargo
este problema ha llevado a algunos autores a explorar algunos instrumentos
analíticos que enfrente este problema, tal es la adopción del proceso de Itô.
De acuerdo con Baxter y Rennie (1996), hay dos características que distinguen el uso de proceso de Itô. La primera de esas características es que
la cualidad de modelar series con parámetros cambiantes, es inherente a su
definición. Como se sabe, un proceso de Itô es la suma de un valor inicial,
una integral de tiempo y una integral estocástica.
Las integrales tienen incrementos instantáneos cuyas medias (en el caso
de la integral de tiempo), varianzas y covarianzas (en el caso de la integral
estocástica) pueden fluctuar estocásticamente en el tiempo. De aquí que si
se desea atacar el problema de colas gordas ocasionado, digamos, por una
mayor volatilidad de los rendimientos, una solución posible es adaptar un
proceso de Itô a las series históricas mediante la manipulación de la integral
del tiempo, llamada drift, o de la integral estocástica, llamada dispersión o
coeficiente del proceso de Wiener. La manipulación puede abarcar desde un
cambio del drift hasta una mezcla de procesos de Poisson. La segunda característica que ha hecho atractivo el uso de los procesos de Itô es igualmente
importante, pues permite simular los precios de una obligación contingente
26
Diana C. Segura Rodríguez, Francisco Venegas Martínez y Héctor Allier Campuzano
a partir de una estrategia de negociación cuyos valores iniciales y de dispersión
sean iguales a los de un proceso de Itô. En presencia de mercados dinámicamente completos, el precio de cualquier obligación contingente puede ser replicado con la información generada por el proceso de Wiener. Éste es un resultado
que se desprende del hecho de que el supuesto de mercados completos es válido
si y sólo si los precios de las obligaciones son procesos de Itô (Nielsen, 1999). Las
fluctuaciones extremas de los precios pueden ser, entonces, modeladas a discreción buscando que el proceso de Wiener simule, por ejemplo, la trayectoria
leptocúrtica o de colas grandes de los datos originales.
Las fluctuaciones extremas de los precios pueden ser, entonces, modeladas a discreción buscando que el proceso de Wiener simule, por ejemplo, la
trayectoria leptocúrtica o de colas grandes de los datos originales.
3. Activos disponibles en la economía
El sistema financiero en la actualidad es de vital importancia para la
economía de cualquier país, ya que a través de éste se canaliza el dinero de
los ahorradores a los inversionistas quienes lo utilizan para generar mayor
producción en los distintos sectores de la economía y así poder realizar todas las actividades financieras existentes. Los sistemas financieros abarcan,
empresas, bancos e instituciones que satisfacen las decisiones financieras de
las familias, las empresas, los gobiernos locales y del exterior. Hay dos tipos
de mercado: mercado de deuda y mercado accionario o de capitales.
Los instrumentos del mercado de deuda comúnmente se clasifican según:
i) Su cotización. Los instrumentos se dividen en los que se cotizan “a
descuento” y los que se cotizan “a precio”.
ii) Su colocación. Hay dos maneras de ofrecer instrumentos de deuda al público inversionista: mediante colocación pública y colocación privada.
iii) El tipo de tasa.
iv) El riesgo del emisor.
Es un mercado donde se negocian acciones (shares en inglés) y otros valores, como los certificados o recibos que representan el capital social de las
empresas en función de:
Análisis estocástico de una economía pequeña y abierta
27
El mercado de capitales sirve para que las empresas consigan recursos
para crecer y para que los que ya no desean ser socios puedan vender su
participación a otros que sí desean serlo en función de:
• lo que se negocia:
mercados de valores
instrumentos de renta fija
instrumentos de renta variable
mercado de crédito a largo plazo (préstamos y créditos bancarios)
• su estructura:
mercados organizados
mercados no-organizados (over the counter)
• los activos:
mercado primario
mercado secundario
• él rendimiento para el inversionista se presenta de dos formas:
dividendos que genera la empresa
ganancias de capital.
4. Comportamiento de los agentes económicos
Supuestos del modelo
Con el propósito de obtener soluciones analíticas en el siguiente modelo estocástico, la estructura de la economía se plantea de la siguiente forma: una
economía poblada por consumidores que también son productores con
preferencias, dotaciones y tecnologías idénticas. Estos individuos viven para
siempre y desean maximizar su satisfacción por un bien genérico de consumo (el
supuesto de vida infinita se puede reemplazar por un padre que se interesa por
maximizar la satisfacción de sus hijos, nietos, bisnietos y demás descendientes).
La economía en cuestión es la de un país que no puede influir en los precios externos y que se mantendrá, por siempre, en esta condición, es decir, una economía
tomadora de precios.
Pt = Pt * Et
28
Diana C. Segura Rodríguez, Francisco Venegas Martínez y Héctor Allier Campuzano
El precio del bien en la economía doméstica, Pt satisface la condición de poder
de paridad de compra (PPE):
Pt = Pt * Et
En donde Pt * es el precio (en dólares) del bien en cuestión en el resto del
mundo y Et , es el tipo de cambio nominal. Por simplicidad, se supone que
Pt * ≡ 1, en cuyo caso el nivel general de precios, Pt es igual al tipo de cambio, Et .
De esta manera, se tiene que:
dPt dEt
=
, Pt
Et
Es decir, la tasa de inflación es igual a la tasa de depreciación del tipo de
cambio. Posteriormente se supondrá que la tasa de depreciación del tipo
de cambio tiene un comportamiento estocástico. De hecho se supondrá
que el tipo de cambio sigue un movimiento geométrico browniano combinado con un proceso de Poisson.
En esta economía los residentes pueden tener dos tipos de activos: moneda doméstica y bonos internacionalmente negociables denominados en
moneda extranjera (por ejemplo, dólar).
Bajo condiciones de arbitraje internacional se supone también que se satisface la paridad de tasas de interés, esto es:
rt = rt * +ε t , donde rt es la tasa de interés real doméstica y rt * es la tasa de interés real
internacional, la cual, sin menoscabo de generalidad, se supone constante,
rt * = rt .
Dinámica del nivel general de precios
Un supuesto de trabajo que se retoma de (Venegas-Martínez, 2009) es que
los agentes económicos que se desenvuelven en una economía producen
un solo bien y está poblada por consumidores idénticos, con vida infinita,
que maximizan su satisfacción por el bien en cuestión y que perciben que el
Análisis estocástico de una economía pequeña y abierta
29
precio del bien, Pt es conducido por un proceso estocástico de difusión con
saltos:
dPt = πPt dt + σ P Pt dWP ,t + vP Pt dQP ,t (1)
donde π es parámetro de tendencia que representa la tasa de inflación
media esperada condicional de que ningún salto ocurra, σP es la volatilidad
esperada de la tasa de inflación y 1+vP es el tamaño promedio esperado de
posibles saltos en el nivel general de precios. El proceso WP, t es un proceso
de Wiener estandarizado y distribuido N(0,dt), es decir, distribuido normalmente con media cero y varianza dt, más precisamente, la media y la varianza
son expresadas como E ⎣⎡dWP,t ⎦⎤ = 0 y Var ⎡⎣dWP,t ⎤⎦ = dt. Los saltos, en el nivel general de precios, siguen una distribución del tipo
Poisson, Qp,t con parámetro de intensidad λp , de tal manera que:
Ρ {un salto de tamaño 1 durante dt} = P {dQ p,t =1} = λdt + o(dt ). (2)
P {ningún salto durante dt} = P {dQ p ,t = 0} = 1 − λdt + o(dt ).
(3)
mientras que:
De aquí que E[dqp,t]=Var[dQp,t]= λPdt. El número inicial de saltos es igual a
cero, es decir, Qp,t = 0. Además se supone que Wp,t y Qp,t no están correlacionados entre sí.
La tendencia π, así como los componentes de difusión y el salto σpPtdWp,t
y vpPtdQp,t , se determinarán endógenamente.
Consumidores
El consumidor representativo posee tres diferentes activos: dinero, Mt ; títulos de deuda pública, Bt , y títulos de capital (acciones), Kt . En consecuencia,
la riqueza real, zt , del individuo viene expresada por:
zt = mt + bt + kt (4)
30
Diana C. Segura Rodríguez, Francisco Venegas Martínez y Héctor Allier Campuzano
donde mt =Mt / Pt representa los saldos monetarios reales y bt =Bt / Pt
son la tenencia de bonos del sector público en términos reales. Este consumidor obtiene su satisfacción por el consumo del bien que produce
la economía y por la tenencia de saldos reales debido a sus servicios de
liquidez.
Se trabajará con una función de utilidad esperada, tipo Von Neumann-Morgenstern. Específicamente, la función de utilidad total descontada al tiempo
t=0, V0 , nos muestra la situación de un agente económico representativo, competitivo y adverso al riesgo, que se puede representar en forma separable:
⎧∞
⎫
V0 = E0 ⎨ ∫ ⎡⎣u ( ct ) + v ( mt )⎤⎦ e dt ⎬ ⎩0
−δt
⎭
(5)
donde E0 es la esperanza condicional al conjunto de información disponible,
información relevante disponible al tiempo t=0; u(ct )es el índice de satisfacción
por el consumo; v(mt ) es la utilidad por mantener saldos reales; δ es la tasa subjetiva de descuento, también llamada tasa subjetiva intertemporal.
En particular, se eligen las variables: u(ct ) = θ log(ct ) y v(mt ) = log(mt) a fin
de generar soluciones que faciliten el análisis.
Por otra parte, la evolución de la acumulación de la riqueza real sigue
una distribución que se representa por una función diferencial estocástica:
dzt = zt ⎡⎣ Nm,t dRm,t + Nb,t dRb,t + Nk ,t dRk ,t ⎤⎦ − ct (1 − τc ) dt − dτt
(6)
donde:
N j ,t ≡
dRj,t :
dτt :
dτc :
jt
: proporción del portafolio en el activo j, j = m,b,k
zt
tasa de rendimiento real después de impuestos sobre el activo
impuestos sobre la riqueza
impuesto sobre el consumo
Rendimiento de los activos
A continuación se especifica la dinámica del rendimiento de los activos.
Análisis estocástico de una economía pequeña y abierta
31
Se supone que las tasa nominal de rendimiento que paga el dinero es
cero y los bonos un rendimiento i. El rendimiento estocástico por la tenencia
de saldos reales al tiempo t, dRm,t , es el cambio porcentual en el precio del
dinero, en términos de bienes.
En este escenario se hace indispensable utilizar el cálculo estocástico,
cuyo objeto de estudio es la integral estocástica, con el cual se analizan, actualmente, toda la teoría económica en tiempo continuo y estocástico.
La aplicación del lema de Itô al cambio porcentual del inverso del nivel
de precios, tomando (1) como proceso subyacente, conduce a:3
⎛
⎞
P
⎝ t⎠
⎛ 1
⎞
1
− 1⎟ dQP ,t
dR m,t = Pt d ⎜ ⎟ = rmdt − σ P dWP ,t + ⎜
⎝ 1 + vP
⎠
(7)
donde
Rm = −π + σ 2P Ahora el rendimiento estocástico por la tenencia de bonos se obtiene:
⎛ 1
⎝ 1 + vP
⎞
− 1⎟ dQ P ,t dR b,t = rb dt − σ P dWP ,t + ⎜
donde
⎠
(8)
Rb = i (1 − τ y ) − π + σ2P
Aquí τy es la tasa de impuesto sobre ingresos por intereses realizados. Es
importante observar que los rendimientos del dinero y de los bonos se ven
afectados por la volatilidad y posibles saltos en el nivel general de precios.
Con respecto a la tasa de rendimiento de las acciones después de impuestos será denotada por el momento, mediante:
dR k ,t = rk dt+σk dWk ,t + vk dQk ,t
3
(9)
Para un mayor entendimiento consultarse las derivaciones y demostraciones de los resultados analíticos de las ecuaciones (apéndice C).
32
Diana C. Segura Rodríguez, Francisco Venegas Martínez y Héctor Allier Campuzano
donde los procesos dQk,t y dQk,t tienen características similares a los procesos
definidos en (1).
Además de los impuestos τy y τc que se pagan sobre el ingreso por intereses y por el consumo, respectivamente, el consumidor paga un impuesto
sobre la riqueza de la forma:
dτt = zt τdt+x t σ τdWτ,t + xt vτdQ τ,t (10)
donde, τ es la tasa de impuesto media esperada de la riqueza real. Al igual
que antes στdWτ,t y dQk, t comparten las mismas características que los procesos
de Wiener y de Poisson definidos anteriormente en (1). La tendencia τ , así
como los componentes de difusión y salto στdWτ,t y vτdQτ,t se determinan en
forma endógena.
Decisiones óptimas de los consumidores
El objetivo del consumidor es elegir, en cada momento, el portafolio de activos y la cantidad de consumo que maximicen (5) sujeto a (6). Nótese que
después de sustituir las expresiones (7)-(10) en la ecuación estocástica de
acumulación de la riqueza (6), ésta se transforma en:
c (1 + τc )
⎤
dzt ⎡
= ⎢ N m ,t rm + N b ,t rb + N k ,t rk − t
− τ ⎥ dt
zt ⎣
zt
⎦
+ ⎡ N σ dW − N + N σ dW − σ dW ⎤
τ
τ ,t ⎦
b ,t ) P
P ,t
⎣ k ,t k k ,t ( m ,t
⎡
⎤
⎛ 1
⎞
− 1⎟ dQ P ,t + N k ,t vk dQ k ,t − vτdQ τ,t ⎥
+ ⎢ ( N m ,t + N b ,t ) ⎜
⎜
⎟
⎢⎣
⎥⎦
⎝ 1− vp ⎠
(11)
La solución del problema de optimización total descontada sujeto a (11)
y a la restricción de normalización:
N m,t + N b ,t + N k ,t = 1 Están dadas por:4
4
Para una mejor comprensión de las ecuaciones 13-16 consultar apéndice A.
(12)
Análisis estocástico de una economía pequeña y abierta
33
δθ
z
(1 + θ)(1 + τc ) t
ct =
(13)
(1 + θ ) r − N + N σ2 + N σ − σ −
λ P vP
1
0=⎜
⎢ m ( m ,t
⎥ -φ (14)
⎟+
b ,t ) P
k ,t Pk
Pτ
⎛
⎞
⎜N ⎟
⎝ m ,t ⎠
δ
⎡
⎤
⎢⎣
1 + (1 − N m,t − N b ,t ) vP ⎥⎦
(1 + θ ) ⎡
⎤
λ v
1 + (1 − N m,t − Nb ,t ) vP ⎥⎦
(15)
⎤
λ P vk
1 + (1 − N m,t − N b ,t ) vk ⎦⎥
(16)
P P
0=
⎢ rb − ( N m,t + Nb ,t ) σ P + N k ,t σ Pk − σ Pτ −
⎥ -φ
δ
2
⎢⎣
y
(1 + θ ) ⎡
0=
⎢ rk − N k ,t σk + ( N m ,t + N b ,t ) σ Pk + σk τ −
⎥ -φ δ
2
⎣⎢
donde ϕ es el multiplicador de Lagrange asociado a la restricción (12).
Después de restar (14) de (15), se encuentra la proporción óptima de la
riqueza asignada a la tenencia de saldos reales:
δ
Nˆ m ,t =
i (1 − τ y ) (1 + θ )
(17)
Así mismo, después de restar (15) de (16), se tiene que:
λ v
1 + Nk ,t vP
λv
1 + Nk ,t vk
k k
P P
N k ,t B − A −
−
=0
(18)
donde:
B ≡ σ 2P + 2σ Pk + σ k2 > 0 A ≡ rk − rb + σ2P + σPk + σPτ + σk ,τ .
(19)
(20)
Claramente, la ecuación (18) es cúbica y, por tanto, se tiene al menos una
solución real, la cual denotaremos mediante Nˆ k ,t = Nˆ k ,t (i ) . En particular, si se
supone que vP y vk son cero, equivalentemente λP =λk = 0 se tiene como única
solución (cf . Turnovsky, 1993):
34
Diana C. Segura Rodríguez, Francisco Venegas Martínez y Héctor Allier Campuzano
A
Nˆ k ,t
vP vk =0
=
B
(21)
Si los parámetros de intensidad λP y λk se ajustan de tal maneta que
vP y vk sean de la misma magnitud, entonces (26) se transforma en una
ecuación cuyas soluciones están dadas por:
AvP − B ± ( AvP + B ) + 4 BvP ( λ P + λ k )
ˆ
2
N k ,t
vP vk =
2
(22)
2 BvP
Observamos que el discriminante es positivo y, en consecuencia, ambas
raíces son reales. Nótese también que en ningún caso se han impuesto restricciones para que las proporciones de riqueza asignadas a la tenencia de activos
sean estrictamente positivas y menores que la unidad. Por tanto, las ventas
en corto de activos son permitidas en todo momento.
Definitivamente, el portafolio óptimo queda entonces completamente
determinado con Nˆ b,t el cual se obtiene a partir de (12) como:
δ
Nˆ = 1 −
− Nˆ b ,t
i (1 − τ y ) (1 − θ )
k ,t
(23)
Comportamiento de las empresas
Los activos en la economía, en especial la empresa, constituyen los recursos
asignados a la producción de un bien o servicio. Si la empresa no posee activos, por tanto, no puede producir bienes o prestar servicios.
Especificación de la tecnología
La producción sigue una trayectoria estocástica definida por:
dyt = γ kt dt + γ ktσ y dWt y ,t + γ kt v y dQy ,t
(24)
donde g representa el producto marginal promedio esperado del capital. Aquí
como en el caso del consumidor, dWty, t es un proceso de Wiener y dQy, t es un
proceso de Poisson.
Análisis estocástico de una economía pequeña y abierta
35
4.4.2 Rendimiento de las acciones
En términos generales, el rendimiento que paga la empresa sobre las acciones emitidas se puede definir como:
dv du
dRk ,t = (1 − τ y ) t + t
kt
ut
(25)
donde dvt son los dividendos y ut es el precio de las acciones, en términos
del producto. Se supone que no hay impuestos sobre ganancias del capital.
De esta forma, el rendimiento de las acciones tiene dos componentes: los
dividendos que se pagan por acción y las ganancias (o pérdidas) de capital
que resultan de diferencias en el precio de los títulos de capital. A continuación
se examina cada componente por separado.
Primero, para conocer la trayectoria que sigue dut /ut es necesario analizar el comportamiento de la producción, el stock de acciones, el capital
disponible y la política de inversión de la empresa. Todas estas variables
determinan la posible existencia de ganancias de capital. Ahora bien, si se
supone que el stock de acciones en cualquier tiempo, t, permanece constante
(digamos igual a N) entonces se cumple que Nut=kt . Por lo tanto:
dkt = Ndut (26)
(1 −τ P ) dyt =dvt +dkt (27)
Segundo, la producción después de impuesto puede tener dos usos: el
pago de dividendos, dvt , o el financiamiento de nueva inversión, dkt , entendida como la adquisición de capital nuevo. De esta forma, la trayectoria que
sigue la producción después de impuestos está dada por:5
donde τP es el impuesto sobre ingresos corporativos y vt representa el pago
de dividendos.
Después de combinar las ecuaciones (26) y (27), se obtiene:
5
En el caso mexicano, no hay impuestos sobre ganancias de capital cuando las operaciones se llevan a cabo
en mercados reconocidos por las instituciones financieras, tal es el caso de la Bolsa Mexicana de Valores.
36
Diana C. Segura Rodríguez, Francisco Venegas Martínez y Héctor Allier Campuzano
dut (1 − τ P ) dyt - dvt
=
u
k
(28)
dv
dy
dRk ,t = −τ y t + (1 − τ P ) t
kt
kt
(29)
t
t
Sustituyendo esta función en la del rendimiento de las acciones (25), tenemos
Los dividendos
La médula de la política de dividendos es el porcentaje de las utilidades que
se pagará en forma de dividendos. Se conoce también como tasa de distribución o de reparto de utilidades. El porcentaje que se paga tiene efectos en
el precio de las acciones de la empresa y en sus perspectivas de crecimiento.
El consejo de administración decreta una cantidad específica que se pagará
en dividendos en una determinada fecha futura a los accionistas registrados
hasta cierta fecha anterior.
Los principales objetivos de la política de dividendos consisten en evitar
las disminuciones del dividendo y avanzar hacia una tasa de distribución
determinada previamente.
La política de dividendos influye en el precio de las acciones de la empresa y en sus perspectivas de crecimiento, esto se debe a que el precio de
las acciones pueda resultar afectado por el contenido informativo del dividendo. Si un dividendo aumentado hace pensar a los accionistas que la
empresa ha entrado a una etapa de mejores perspectivas en cuanto a utilidades, el precio de las acciones puede reaccionar favorablemente.
En el modelo se supondrá que los dividendos que pagan las empresas
son una fracción constante α del ingreso corporativo después de impuestos.
Es decir, los dividendos tienen la forma:
dvt = α (1 − τ P ) dyt ,
0 ≤ α ≤ 1 (30)
Después de sustituir la expresión anterior en la ecuación (29) se obtiene
la trayectoria estocástica del rendimiento de las acciones en términos del
proceso que sigue la producción de bienes:
Análisis estocástico de una economía pequeña y abierta
dy
dRk ,t = (1 − τ P ) (1 − ατ y ) t kt
37
(31)
Es importante observar en esta ecuación que el componente estocástico
está determinado por dyt , ya que el resto de las variables son deterministas.
Finalmente, de la ecuación (9), se sigue que:
(
)
(32)
(
)
(33)
(
)
(34)
rk = (1 −τ P ) 1 − ατ y γ
y
! k dWk ,t = (1" # P ) 1" $# y %! y dWy,t vk dQk ,t = (1 −τ P ) 1 − ατ y γ vy dQy ,t
De esta forma, la tasa de rendimiento de las acciones está en función de
la tasa del producto marginal del capital. Similarmente, el componente estocástico dRk,t depende de los shocks de productividad derivados de cambios
en γ y el comportamiento exógeno de dWy,t , además de los posibles saltos dQy,t .
Acciones del gobierno y restricción presupuestal
A fin de completar el análisis macroeconómico de equilibrio general, se
describen las acciones del gobierno.
Cabe mencionar que en este apartado se analizan los tres principales instrumentos de política económica que emplea el gobierno: Gasto público, oferta
monetaria y emisión de deuda, interna o externa, o ambas.
El gobierno tiene el monopolio de la emisión de dinero y, a la vez, emite
deuda para financiar su gasto.
La restricción presupuestal que enfrenta el gobierno en términos reales,
está dada por:
dgt − dτ 1t − dτ 2t + mt dRm,t + bt dRb ,t = dmt + dbt (35)
donde dgt es el cambio en gasto público del gobierno en términos reales; dτ1t
es el cambio en el impuesto total recaudado proveniente de los consumidores,
38
Diana C. Segura Rodríguez, Francisco Venegas Martínez y Héctor Allier Campuzano
en términos reales, dτ2t es el cambio en el impuesto total recaudado proveniente de las empresas, también en términos reales.
En este modelo se supone que el gasto que realiza el gobierno sigue un
proceso estocástico definido por:
dgt = g γ kt dt + γ ktσ g dWg ,t + γ kt vg dQg ,t
(36)
Al igual que en los casos anteriores, dWg,t es un proceso estocástico con
una distribución normal con media cero y varianza dt y dQg,t es un proceso
de salto de Poisson.
De esta forma, el gasto de gobierno está definido como una fracción
dgt del producto real. Habrá que señalar que, en este caso, el factor estocástico del gasto es proporcional al producto.
La oferta monetaria
La oferta monetaria en esta economía tiene asociada una regla de expansión
que es conducida por un proceso estocástico de difusión con saltos de la
forma:
dM t = µ M t dt + σ M M t dWM ,t + vM dQM ,t
(37)
donde μ es la tasa de expansión monetaria media esperada, dWM,t es el componente de difusión y dQM,t es el componente de saltos en la tasa de expansión monetaria.
La deuda pública
La política de deuda que sigue el gobierno se hace vía emisión de bonos.
En este caso la política de endeudamiento se fija de forma tal que la razón
entre el stock de bonos y el stock monetario se mantenga constante, es decir,
se supone que:
Bt
= k = constante
Mt
(38)
Análisis estocástico de una economía pequeña y abierta
39
De esta forma se obtiene la expresión:
dBt dM t
=
Bt
Mt
(39)
Lo anterior significa que en operaciones de mercado abierto, el cambio
porcentual de deuda emitida o equivalentemente, al cambio porcentual en
la cantidad que crece la oferta monetaria es igual al cambio porcentual de la
deuda gubernamental que se salda.
Impuestos directos e indirectos
De acuerdo a Stiglitz (2000), se acepta que un “buen” sistema tributario
debe tener cinco propiedades:
1. Eficiencia económica: no interfiere en la asignación eficiente de los recursos.
2. Sencillez administrativa: será fácil y relativamente barato de administrar.
3. Flexibilidad: debe ser capaz de responder fácilmente (en algunos casos
automáticamente) a los cambios de las circunstancias económicas.
4. Responsabilidad política: debe diseñarse de tal forma que cada individuo pueda averiguar qué está pagando y saber en qué medida el
sistema refleja sus preferencias.
5. Justicia: será justo en su manera de tratar a los diferentes individuos.
Recuérdese que si no hubiera fallos en el mercado, la economía asignaría
automáticamente los recursos de una manera eficiente. La información
transmitida por los precios de mercado haría que la producción, el intercambio y la combinación de productos fabricados y vendidos fueran eficientes;
y no sería posible mejorar el bienestar de ninguna persona sin empeorar el
de alguna otra. La mayoría de los impuestos alteran los precios relativos,
por lo que distorsionan las señales de los precios y, en consecuencia, alteran
la asignación de los recursos.
Con respecto al modelo los cambios en las cantidades reales de tributación, dτ1t y dτ1t , que provienen de los consumidores y de las empresas,
respectivamente, se describen a continuación. Todas las tasas τy , τP y τc son
40
Diana C. Segura Rodríguez, Francisco Venegas Martínez y Héctor Allier Campuzano
exógenas en nuestro modelo. En el caso de los consumidores, el impuesto total
tiene cuatro componentes: el gravado sobre los intereses, ganancias de capital, nivel de riqueza y consumo. De esta forma, las cantidades respectivas se
agregan como sigue:
(
)
!
d! 1,t = i! y N b,t at dt + "! y (1# ! P )$ kt dt + % y dWy,t + v y dQ y,t
!
+ a ! dt + a % dW + a v dQ + ! c dt
t
t
!
! ,t
t !
! ,t
c t
(40)
Para las empresas, los impuestos se gravan sobre los ingresos corporativos, es decir:
(41)
dyt = ct dt + dkt + dgt
5. Equilibrio general
En esta sección se determinan endógenamente, en equilibrio, la tasa de inflación, la tasa de acumulación de capital, la tasa impositiva a la riqueza y
los rendimientos de los activos disponibles en la economía.
Para encontrar la trayectoria que sigue la acumulación de capital en esta
economía, dkt /kt , se parte de la identidad del ingreso nacional:
dyt = ct dt + dkt + dgt
(42)
Al sustituir en (42), las ecuaciones (13), (24) y (36), que corresponden a la
trayectoria óptima del consumo, a la dinámica de producción y a la política
de gasto del sector público, respectivamente, se obtiene:
)
dk t &
#$
!
=
!
1"
g
"
+ dt + ! , y dWt y,t " , g dWg,t
(
(
)
k t ('
(1+ $ )(1+ % c ) N k ,t +*
(
(
+ ! v y dQ y,t " vg dQg,t
)
(43)
)
De esta forma, la acumulación de capital sigue una trayectoria estocástica derivada de la diferencia entre la producción menos el consumo y el
gasto del gobierno. Consecuentemente, el componente no estocástico de esta
ecuación, está determinado por:
Análisis estocástico de una economía pequeña y abierta
41
" dk %
*+
! ! = E $ t ' = ( (1) g ) )
(1+ + )(1+ , c ) N k ,t
# kt &
(44)
lo que define la tasa esperada de acumulación de capital.
Finalmente, se puede concluir que:
*
=E #
)" kt &% ,
+
(
'
2
(.
)
! dkt $
2
2
2
2
2
2
,
)
y
+.g +-
(v /
y
y
+ vg / g
) (45)
Este resultado será utilizado en la determinación del equilibrio general.
Una vez determinadas las decisiones óptimas de los agentes, el comportamiento de las empresas y las acciones del gobierno, así como el establecimiento de las variables exógenas, lo que resta es obtener el equilibrio macroeconómico general.
Dado que en esta economía los saldos monetarios reales y los bonos en
términos reales están ligados a los movimientos en el nivel general de precios, es necesario, en primer instancia, especificar el comportamiento que
sigue la inflación y como es generada endógenamente por el modelo mismo.
Las cantidades
endógenas.
!
N j,t , j = m,b,k,
así como la tasa de interés nominal son variables
El nivel de precios se puede expresar en la forma:
!
N k ,t M t
Pt = !
N m,t kt
(46)
!
Dado que los valores óptimos de N j,t , j = m,b,k, son constantes, al derivar
estocásticamente la razón entre el dinero y capital f ( M t , kt ) = M t kt se obtiene:
2
dPt dM t dk t ⎛ dM t ⎞⎛ dk t ⎞ ⎛ dk t ⎞
=
−
−
+
dM t
Mkt
kt
⎜
⎟⎜
⎟ ⎜
⎟
⎝ M t ⎠⎝ kt ⎠ ⎝ kt ⎠
(47)
La condición de primer orden del consumo conduce a:
ct
!"
!
=
kt (1+ " ) (1+ # c ) N k ,t ( i *)
(48)
42
Diana C. Segura Rodríguez, Francisco Venegas Martínez y Héctor Allier Campuzano
donde, la i* (tasa de interés nominal de equilibrio) se determinará posteriormente.
Después de sustituir (1), (37), (43), (45) y (48) en la expresión (47), se tiene que:
%
c (
! dt + " PdWP,t + v PdQP,t = µdt + " M dWM ,t + v M dQM ,t # '$ (1# g ) # t * dt
kt )
&
# $ " y dWt y,t # " g dWg ,t # $ v y dQ y,t # v g dQg,t
(
(
) (
) (
)
)
# $" My dt + $ 2 " 2 + " 2 + $ 2 v 2y + y + v 2 + g dt
y
g
g
(49)
Por lo tanto, la tasa esperada de inflación en el equilibrio satisface:
(
)
*
'
$%
, +# 2 - 2 + - 2 + v 2 . y + v 2 . g " #- M y
!
! * = µ " )# (1" g )
y
g
y
g
(50)
(1+ % )(1+ & c ) N k,t ( i *) ,+
)(
Los componentes estocásticos de difusión y saltos satisfacen, respectivamente, las siguientes condiciones:
σ PdWP,t = σ M dWM ,t − γ (σ y dWt y ,t − σ g dWg ,t )
(51)
vPdQP,t = vM dQM ,t − γ (vy dQy ,t − vg dQg ,t ) (52)
Las ecuaciones anteriores, (50)-(52), determinan endógenamente la
tasa de inflación esperada consistente con un portafolio cuya integración
constante en el tiempo. Se puede observar en (50) que la inflación media
esperada de equilibrio depende positivamente de la tasa de crecimiento
de la oferta monetaria y negativamente de la tasa de acumulación de
capital, así como positivamente de las varianzas de los shocks fiscales y
productivos. Por otra parte, las ecuaciones (51) y (52) determinan endógenamente los componentes estocásticos de difusión y saltos, respectivamente, en la tasa de inflación.
Es importante destacar que la componente de saltos en la tasa de inflación está en función de las componentes estocásticas de los saltos en las
tasas de expansión monetaria, la producción y el gasto del gobierno.
Análisis estocástico de una economía pequeña y abierta
43
Relaciones de equilibrio
Para encontrar la tasa de rendimiento de equilibrio de los saldos monetarios
y bonos en términos reales, es necesario sustituir las expresiones anteriores
en los rendimientos dados en (7) y (8), respectivamente, de tal forma que el
rendimiento de los saldos reales está dada por:
(
)
rm* = !" + # 2M + $ 2 # 2y + # 2g ! 2$# My (53)
Obsérvese también que la siguiente identidad es válida en todo tiempo t,
(1 + k ) δ N k ,t = 1 −
i (1 − τ y ) (1 + θ )
Después de sustituir el valor óptimo de la proporción de la riqueza asignada a la tenencia de títulos de capital, se obtiene la tasa de interés de equilibrio, es decir:
(1+ k )!
i* =
1" # y (1+ $ ) 1" N k ,t ( i *)
(
)
(
)
(54)
De esta forma, la ecuación anterior determina el valor de equilibrio de
la tasa de interés nominal implícitamente. Por tanto, el rendimiento de los
bonos está dado por:
(
)
(
)
r * = i * 1! " y ! # + $ 2M + % 2 $ 2y + $ g2 ! 2%$ M ,y b
(55)
En este caso, la tasa rk está dada por la ecuación (32). Finalmente, de la
ecuación (48) se sigue que:
ct
!"
=
kt
(
%
1+ k !
(1+ " )(1+ # c ) ''1$ i * 1$( # )1+ " **
))
y (
&
(
)
(56)
Lo que conjuntamente con la ecuación (44), conduce a la tasa esperada de
crecimiento del capital:
44
Diana C. Segura Rodríguez, Francisco Venegas Martínez y Héctor Allier Campuzano
*
'
,
)
,
)
$%
! = " )1#
# g , '
)
(1+ k )$ *, ,,
) " (1+ & c ) (1+ % ) )1#
) i * 1# & y (1+ % ) ,
,
)
+
(
+
(
(
(57)
)
6. Conclusiones y recomendaciones
En esta investigación se desarrolló un modelo de equilibrio macroeconómico
en un ambiente estocástico. Las variables exógenas incluyen los parámetros de
política económica (crecimiento monetario, μ ; gasto público, g ; política
de deuda, f, y las tasa de impuesto τy , τc y τP ). De igual forma los procesos estocásticos exógenos son los respectivos a crecimiento monetario, dWM,t ; gasto
público, dWg,t , y la producción dWM,t . El resto de los procesos estocásticos son
endógenos y pueden ser explicados como funciones simples de los choques
exógenos. Asimismo, se determinó el equilibrio macroeconómico en donde
las varianzas de los choques exógenos, tanto para difusiones como para saltos, desempeñan un papel importante en la administración de riesgos.
La actitud del consumidor hacia el riesgo de los instrumentos de inversión es independiente del nivel de su riqueza, es decir, que el nivel
resultante de riqueza en cualquier instante no tiene efecto alguno sobre las
decisiones en la integración del portafolio. Sería interesante posteriormente
el efecto resultante de comparar sujetos adversos o no al riesgo por medio
de sus tasas subjetivas de descuento.
El costo de oportunidad, que representa una forma de sacrificio, de mantener saldos reales es positivo. Esta situación es importante ya que el dinero
entra directamente en la función de utilidad, el signo en el costo de oportunidad de mantener saldos monetarios reales es irrelevante, contrario a lo
que se tendría en el caso de una economía con una restricción en donde un
costo de oportunidad positivo obligaría a los consumidores a mantener el
mínimo posible de saldos reales para financiar su consumo.
Es necesario señalar que todos los participantes del mercado financiero tienen alguna expectativa sobre el comportamiento del precio de
Análisis estocástico de una economía pequeña y abierta
45
sus activos. Y la forma en que cada individuo conforma sus expectativas es
muy variada, dependiendo de la información disponible, y, lo más importante, la capacidad de procesarla e interpretarla. Ya que aun cuando todos
los agentes contarán con la misma información, la valuación de cada uno
sería distinta, puesto que utilizan herramientas diferentes para realizar el
análisis y sus respectivas predicciones. También intervienen algunos factores psicológicos como el optimismo pesimismo sobre el futuro y las preferencias al riesgo.
Respecto al gobierno éste maneja monopólicamente la emisión de dinero para financiar, entre otros objetivos, su déficit presupuestal junto con la
emisión de deuda y la creación de impuestos. La inclusión de un proceso
estocástico con saltos refleja la regla de crecimiento de la oferta monetaria.
Por lo anterior se concluye que un buen desempeño de nuestra economía
requiere de un crecimiento sostenido, acompañado de un desarrollo
económico y social que permita incrementar los niveles y la calidad de vida
de toda la población con más y mejores oportunidades. Para ello, la estrategia de política económica que debe seguir México tiene que enfocarse hacia
la consideración de los factores de riesgo, a través de modelos estocásticos,
para planear, gradualmente, un incremento en la eficiencia de los mercados
de bienes, factores e instrumentos financieros a fin de contribuir con el potencial de crecimiento y la generación de mejores condiciones económicas y
sociales para nuestro país.
La política económica puede influir en el funcionamiento del sistema,
no sin vaivenes y contradicciones, mediante la aplicación de instrumentos,
imponiéndole cierto dinamismo, reduciendo los efectos de fenómenos
negativos, y promoviendo o desestimulando ciertos sectores y grupos.
La función clásica que se atribuye al Estado es asignar recursos para lograr
la máxima eficiencia económica, y la justicia social, mediante el manejo del
presupuesto público (gasto e ingreso) y en el marco jurídico e institucional
que el Estado fija. Esta función básica tiene como gran objetivo alcanzar los
beneficios que se derivan de la cooperación económica. Sin embargo, también es cierto que cumplir esta función encierra una disyuntiva entre eficiencia y equidad (trade off), en la medida que no siempre es fácil determinar la
46
Diana C. Segura Rodríguez, Francisco Venegas Martínez y Héctor Allier Campuzano
línea fronteriza entre el dominio del Estado y del mercado en la asignación
de recursos entre usos alternativos. Esta función del Estado da cuenta de la
complejidad y extensión de su papel en la economía. Sin embargo, al parecer no basta con aplicar reformas al mercado y crear políticas macroeconómicas para alcanzar un crecimiento económico sostenido; se requiere contar con
nuevas y más eficientes instituciones para enfrentar los nuevos retos de la
globalización, y al mismo tiempo contar con mecanismos para hacer eficiente
la distribución de los recursos.
Referencias
Baxter M. y A. Rennie (1996). “Financial Calculus. An Introduction to derivate Pricing”.
Cambridge University Press, Cambridge, pp. 62.
Nielsen, L. (1999). Princing and Hedging of Derivate Securities. Oxford University
Press, New York.
Stiglitz, J. (2006). El malestar en la globalización. Taurus, México.
Turnovsky, S. (1993). “Macroeconomic policies, growth, and welfare in a stochastic
economy”, Vol. 34, No. 4, pp. 953-981.
Venegas, F. (2001). “Temporary stabilization: a stochastic analysis”, Journal of Economics Dynamics and Control, vol 25, núm. 9, pp. 1429-1449.
___ (2009). “Un modelo estocástico de equilibrio macroeconómico: acomulación de
capital, inflación y política fiscal”, Centro de Investigación Económica, vol. lxxviii,
núm. 268, pp. 69-114.
Análisis estocástico de una economía pequeña y abierta
47
Apéndices
Apéndice A
Para resolver un problema de control estocástico del tipo:
%' #
)'
máxE & $ F x,u e!"t dt * u
(' 0
+'
donde u es un vector de controles y x es una variable de estado, sujeto a
( )
dx
= µdt + σ P dW + vdQ
x
(A.1)
(A.2)
donde dW y dQ son procesos de Wiener y de Poisson respectivamente, se utiliza la
ecuación de Hamilton-Jacobi-Bellman (H-J-B) de la programación dinámica continua:
$
1
0 = máx % F ( x,u ) ! "V ( x ) + xV´( x ) µ + x 2 #V´´( x )
u
2
&
(
*
+' )V x (1+ v ) ! V ( x ) +
donde
⎧∞
⎫
V ( x ) e−δt = sup ⎨∫ F ( x, u ) e−δt ds ⎬
u ⎩0
⎭
(
(A.3)
}
)
En el modelo planteado se desea resolver
*, (
.,
máx
V0 =
máx
E0 + ) "!log ( ct ) + log N m,t zt $ e&'t dt / (A.4)
%
ct ,N m,t ,N ,N
ct ,N m,t ,N b,t ,N k ,t
b,t k ,t
,- 0 #
,0
(
)
sujeto a
&
c (1+ " c )
dz t #
= % N m,t rm + N b,t rb + N k ,t rk ! t
! "(
zt $%
zt
('
+ # N k ,t ) k dWt ! N m,t + N b,t ) PdWP,t ! ) "dW",t &
$
'
y
(A.5)
N + N + N =1
(A.6)
(
m,t
b,t
)
k ,t
donde i, π, πc , πy , y τ , junto con las varianzas y covarianzas correspondientes, se
toman como dadas. En este caso, la ecuación de Hamilton-Jacobi-Bellman (H-J-B)
conduce a:
48
Diana C. Segura Rodríguez, Francisco Venegas Martínez y Héctor Allier Campuzano
(
)
z ) # $V ( z )
máx
H ct , N m,t , N b,t , N k ,t ; zt !
máx
{" log ( c ) + log ( N
ct ,N m,t ,N b,t ,N k ,t
ct ,N m,t ,N b,t ,N k ,t
t
m,t t
t
)
&
c (1+ % c )
+z tV´( zt ) ( N m,t rm + N b,t rb + N k ,t rk # t
# %+
zt
+*
('
2
1
+ z 2V´´( zt ) & N m,t + N b,t , 2P + N 2 , 2 + , 2
(
k ,t k
%
2
'
(
)N
(
#2 N m,t + N b,t
)
k ,t
,
Pk
(
(
)) # V ( z ))* # N )=0
+ - k &V zt 1+ N k ,t vk
'
(
+ 4 1# N m,t # N b,t
)
}
# 2N k ,t , kt )+ *
1
VP ) 1
+3 # V ( zt )3
1+ VP *2
2
+ 2 N m,t + N b,t ,
. . &
+ - P 0 V 0 zt (1# N m,t + N b,t
/ / '
( (
)
(A.7)
t
%
Pt
(
)
&V zt (1+ vt ) # V ( zt ) )
'
*
k ,t
Esta condición evaluada en el máximo es una ecuación diferencial (determinista)
de segundo orden en V(zt ). Para resolver esta ecuación diferencial, se postula V(zt )
de la forma V(zt ) = β0+β1 log (zt). Consecuentemente, las dos primeras derivadas son:
β
β
V ´( zt ) = 1 y V ´´( zt ) = − 12 zt
zt
(A.8)
Después de sustituir estas expresiones en la condición H-J-B, se sigue
máx
ct ,N m,t ,N b,t ,N k ,t
máx
ct ,N m,t ,N b,t ,N k ,t
(
)
{"log (c ) + log ( N z ) # $ &'%
H ct , N m,t , N b,t , N k ,t ; zt !
t
&
m,t t
(
2
((
)
0
+ %1 log ( zt ) ()
)
2
)
ct (1+ , c )
(
t
.)
+%1 - N m,t #* + + P + N b,t i 1# , y # * + + P + N k ,t rk #
# ,.
z
-'
(
1 &
# %1 - N m,t + N b,t
2 '
(
)
)+
2
#2 N m,t + N b,t N +
k ,t
2
P
Pk
+ N 2 +2 + +2
k ,t
(
k
,
)
+ 2 N m,t + N b,t +
Pt
# 2N k ,t + (
.
kt )
}
& & 0
VP 3 (
+ %1 - / P - log 2 1# N m,t + N b,t
. + / k &' log 1+ N k ,t vk ()
1+
VP 54 .)
-' -' 1
+/ , &' log (1+ vt ) () + 6 1# N m,t # N b,t # N k ,t ( = 0
)
(
)
(
(
)
)
(A.9)
Análisis estocástico de una economía pequeña y abierta
49
Las condiciones de primer orden (necesarias) para una solución interior son:
∂H
∂ct
∂H
∂Nm,t
∂H
∂Nb,t
∂H
∂Nk ,t
∂H
∂φ
= 0,
= 0,
= 0,
=0 y
=0
(A.10)
Estas condiciones conducen en forma inmediata a las ecuaciones:
∂H
∂ct
θ
ct
β (1 + τ
zt
)
c
(A.11)
0=
= − 1
(
)
!H
1
0=
=
+ "1 % rm,t # N m,t + N b,t $ 2P + N k ,t $ Pk
&
!N m,t N m,t
(A.12)
#$ P' #
0=
(
( PVP
1+ 1# N m,t # N b,t
(
)
)
+#,
vP +
*
)
!H
= "1 % rb,t # N m,t + N b,t $ 2P + N k ,t $ Pk
&
!N b,t
)
( PVP
(A.13)
+#,
#$ P' #
+
1+ 1# N m,t # N b,t v P
*
!H
2
(A.14)
0=
= "1 % rk ,t # N k ,t $ k + N m,t + N b,t $ Pk
&
!N k ,t
(
)
(
+$ k' +
(
)
( kVk
1+ 1# N m,t # N b,t
)
)
+#,
vk +
*
!H
0=
= 1# N m,t + N b,t + N k ,t !"
(
)
(A.15)
Las cuales coinciden con (13)-(16)
Apéndice B
Derivación y demostración de los resultados analíticos
Derivación de la ecuación (7)
Retomando en cuenta que el lema de Itô extiende la diferencial de una función del
proceso subyacente hasta el segundo orden a fin de conservar términos en dt. En lo que
respecta al proceso de Poisson, la diferencial incluye el salto en f (Pt ) inducido por el
salto en Pt .
50
Diana C. Segura Rodríguez, Francisco Venegas Martínez y Héctor Allier Campuzano
# ! f (P )
!2 f ( P )
! f (P )
&
1
t
t
t
df ( Pt ) = %
µ P Pt +
" 2P P 2 ( d t +
" P PdWP,t
2
(
%$ !( Pt )
2
!P
)
+ *+ f Pt (1+ v P ) ) f ( Pt ) ,- dQP,t
t
t
!( Pt )
('
(C.1)
Si se denota f (Pt ) = 1/Pt , entonces
! 1
$
! 1$ 1 *
d # & = , '( + ) 2P d t ' ) PdWP,t + #
' 1& dQP,t /
" 1+ v P %
" Pt % Pt +,
./
(
)
(C.2)
Si se divide (A.2) entre 1/Pt , el resultado coincide con la ecuación (7)
! 1$
! 1
$
dR m,t = Pt d # & = rmd t ' ( PdWP,t + #
' 1& dQP,t " Pt %
" 1+ v P %
Derivación de la ecuación (18)
Para obtener la ecuación (18) basta restar la ecuación (15) de la (16), de tal manera que
& PvP
(1+ !) ')r # N + N $ 2 + N $ # $ #
0=
b
m,t
b,t
P
k ,t Pk
P%
" )
1+ 1# N m,t # N b,t v P
(
*
!
!
!
&
v
P k
,
#rk # N k ,t $ 2k + N m,t + N b,t $ Pk + $ k% #
1+ 1# N m,t # N b,t vk ,
+
(
)
(
(
)
(
)
(C.3)
)
Se utiliza la ecuación (12) dada por
N m,t + N b,t + N k ,t = 1
Entonces la ecuación (A.3) toma la forma
& PvP
(1+ !) ')r # N + N $ 2 + N $ # $ #
0=
b
m,t
b,t
P
k ,t Pk
P%
"
)
1+ 1# N m,t # N b,t v P
(
*
!
!
!
&
v
P k
!
#rk # N k ,t $ 2k + N m,t + N b,t $ Pk + $ k% #
,
1+ N k ,t vk ,+
(
)
(
(
)
)
(C.4)
Análisis estocástico de una economía pequeña y abierta
51
A partir de la cual se obtiene
(1+ ") & r ! r + $ 2 + $ + $ + $ ( + * N! & $ 2 + $ + $ 2 (
0=!
P
Pk
P%
k% )
1 k ,t ' P
Pk
k)
# 'k b
(1+ ") &, + P!v p + + !k vk (!
# ,' 1+ N k ,t v P 1+ N k ,t vk -)
(C.5)
Si ahora se denotan
2
2
B = σ P + 2σ Pk + σ k > 0 (30)
A = r − r + σ2 + σ + σ + σ (31)
k
b
P
Pk
Pτ
kτ
La ecuación (A.5) se transforma en (1+ !) % !
$ Pv p
$ v (
1+ N k ,t vk *)
!
!k k * = 0
+
' N k ,t B # A #
"
'&
1+ N k ,t v P
(26)