NOCIONES SOBRE ESTRUCTURAS ALGEBRÁICAS modificada

ALGUNAS NOCIONES SOBRE ESTRUCTURAS ALGEBRÁICAS
1. Operación
1.1 Definición: Sea A, B dos conjuntos no vacíos, f una relación de de A
en B , decimos que f es una operación cuando a cada elemento del
conjunto A le corresponde un único elemento del conjunto B
la cual se representa por.
f :A→B
x → f ( x) = y; donde x ∈ A; y ∈ B.
Son sinónimos: Función, Relación Operacional, Trasformación, Ley de
composición.
1.2 Clases de Operaciones: Éstas se clasifican de acuerdo a la forma
que tenga el conjunto de partida. Es decir si
A = A1 × A2 × A3 × .... × An ; ∀Ai ≠ φ llamamos a
f :A→B
x → f ( x) = y; donde x ∈ A; y ∈ B.
a. Operación Unitaria: si A = A1 simbólicamente sería
f : A1 → B
x → f ( x) = y; donde x ∈ A1 ; y ∈ B.
b. Operación Binaria: Si A = A1 × A2 . Simbólicamente
f : A1 × A2 → B
x → f ( x) = y; donde x ∈ A1 × A2 ; y ∈ B.
Donde la forma de x es un par ordenado de la forma
x = (a1 , a2 ) donde a1 ∈ A1 ; a2 ∈ A2 .
c. Operación n − aria : Si A = A1 × A2 × A3 × .... × An . simbólicamente sería
f : A1 × A2 × A3 × .... × An → B
x → f ( x) = y; donde x ∈ A1 × A2 × A3 × .... × An ; y ∈ B.
Donde la forma de x es una n − ada de la forma
x = (a1 , a2 ,..., an ) Donde ai ∈ Ai .
1.3 Clases de Operaciones Binarias.
a. Operación Binaria Interna (OBI): Si f es una operación binaria
(como se definió arriba) y se cumple que A1 = A2 simbólicamente
f : A1 × A1 → A1
x → f ( x) = y; donde x ∈ A1 × A1 ; y ∈ B.
Obvio que es lo mismo si el subíndice hubiese sido 2.
b. Operación Binaria Externa (OBE): Si f es una operación binaria
(como se definió arriba) y se cumple que B = A1 en tal caso se dirá
que f es una operación binaria externa definida en A1 por medio de
A2 a derecha, simbólicamente
f : A1 × A2 → A1
x → f ( x) = y; donde x ∈ A1 × A2 ; y ∈ A1.
en forma análoga si B = A2 en tal caso se dirá que f es una
operación binaria externa definida
en A2 por medio de A1 a izquierda, simbólicamente
f : A1 × A2 → A2
x → f ( x) = y; donde x ∈ A1 × A2 ; y ∈ A2 .
1.4 Propiedades de las OBI.
Por comodidad y para que el lector no se confunda representaremos
la operación OBI por ” ∗ “ y por “ ∆ ”
Sean ∗ : A × A → A; ∆ : A × A → A; dos OBI, donde en A se ha definido al
menos una relación de equivalencia que para nuestro caso será la
igualdad; “ = “ entonces se dice que “ ∗ “ cumple con la propiedad:
A. Interna o clausurativa si solo si para todo a, b ∈ A se cumple que
a ∗ b = c donde c ∈ A (Toda OBI es clausurativa)
B. Asociativa si y solo si para todo a, b, c ∈ A se cumple que
a ∗ (b ∗ c ) = ( a ∗ b ) ∗ c
C. Existencia de elemento Neutro si y solo si para todo a ∈ A se
cumple que existe un único elemento e ∈ A que cumple con
a ∗ e = a (llamado Neutro a derecha ) y que además debe cumplirse
que e ∗ a = a (llamado neutro a izquierda).
D. Tiene la propiedad de la existencia del elemento inverso si y
solo si ∗ cumple la propiedad del elemento neutro e ∈ A y que para
todo a ∈ A se cumple que existe un único elemento a , ∈ A llamado
elemento inverso de a que tiene la característica que
a ∗ a , = e (Inverso a derecha) y además a , ∗ a = e (Inverso a
izquierda)
E. Conmutativa si y solo si para todo a, b ∈ A; a ∗ b = b ∗ a .
F. Distributiva: se dice que ∆ distribuye a ∗ si se cumple que para
todo a, b, c ∈ A; a∆ ( b ∗ c ) = ( a∆b ) ∗ ( a∆c )
1.5 ESTRUCTURA ALGEBRAÍCA
Un conjunto A se dice que es una Estructura Algebraica si A ≠ φ y en A
se define un conjunto no vacío de operaciones {∗, ⊗, ⊕, , ∆,....} y un
conjunto no vacío de relaciones {=, ≤, ≥, ∼, ≅, ≠, ,...}
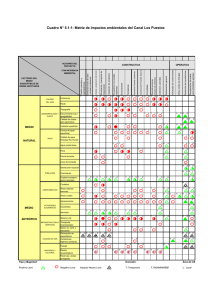
1.6 PRINCIPALES ESTRUCTURAS ALGEBRAICAS
Las principales Estructuras Algebraicas que se pueden definir en el
conjunto A ≠ φ en el cual se han definido al menos las operaciones (PO),
llamada primera y (SO) llamada segunda operación, y al menos una
relación como la igualdad son:
El Grupo, A; PO ; El anillo A; PO; SO ; El anillo Unitario A; PO; SO ;
El anillo Conmutativo A; PO; SO ; Cuerpo A; PO; SO ; Campo
PROPIEDADES
Primera Operación (PO)
GRUPO
GRUPO ABELIANO
ANILLO
ANILLO CONMUTATIVO
ANILLO UNITARIO
CUERPO
CAMPO
A; PO; SO las cuales deben de cumplir las propiedades que se muestran
en la tabla de abajo
x
(PO) es Interna x
(PO) cumple con asociativa x
(PO) cumple con elemento Neutro x
(PO) cumple propiedad de elementos inversos x
(PO) cumple conmutativa
x
x
x
x
x
x
segunda Operación (SO)
(SO) es Interna
(SO) cumple con asociativa
(SO) cumple con elemento Neutro
(SO) cumple propiedad de elementos inversos en el conjuno menos el neutro de la (PO)
(SO) cumple conmutativa
(SO) distribuye a (PO)
ESPACIOS LINEALES SOBRE UN CAMPO
La principal estructura que trabaja el curso de Álgebra Lineal es la de
Espacio Lineal sobre un Campo, regularmente este campo será los
Reales y en tal caso lo llamaremos ESPACIOS LINEALES REALES o
también puede ser que el capo sea los complejos tal caso lo llamaremos
ESPACIOS LINEALES SOBRE LOS COMPLEJOS.
Definición: El conjunto A ≠ φ en el cual se define una relación de
equivalencia como la igualdad se dice que conforma un Espacio Lineal
sobre el Campo K (Los Reales o los Complejos con la suma y el
producto) si se cumple lo siguiente
En A se define una OBI que en nuestro caso será “ + ” que cumple que
A; + es un Grupo Abeliano
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x x x x x
En A se define una OBE que en nuestro caso será “ i ” en A por medio
de K tal que en A; +,i se cumple que si α , β ∈ K y que u , v ∈ A
entonces
1. (α + β )i u = (α i u ) + ( β i u )
2. α i ( u + v ) = (α i u ) + (α i v )
3.
(α i β )
i u = α i (β i u
)
4. Si 1 es el neutro de “ i ” en el campo K ; +,i entonces 1 i u = u
Regularmente para nosotros en el curso de Álgebra Lineal OBI es la operación
“+“
y OBE es la operación “ i ” tal cual como están definidas en el conjunto A .