TEMA 33: POTENCIA, EJE Y CENTRO RADICAL 1 La potencia
Anuncio
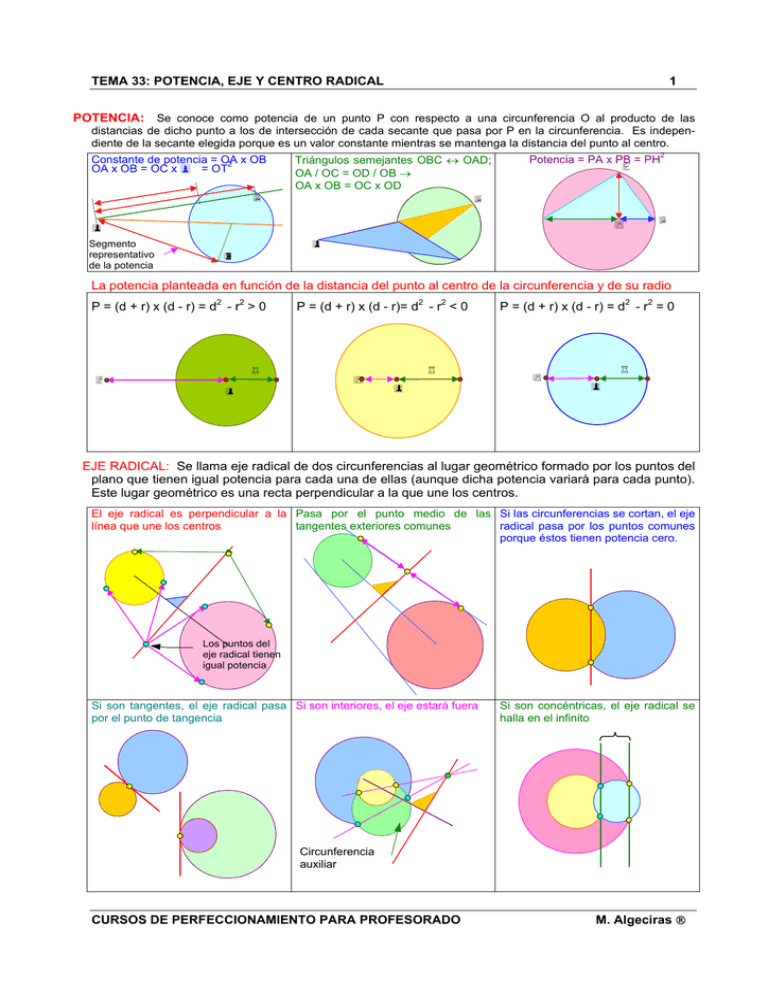
TEMA 33: POTENCIA, EJE Y CENTRO RADICAL 1 POTENCIA: Se conoce como potencia de un punto P con respecto a una circunferencia O al producto de las distancias de dicho punto a los de intersección de cada secante que pasa por P en la circunferencia. Es independiente de la secante elegida porque es un valor constante mientras se mantenga la distancia del punto al centro. Triángulos semejantes OBC ↔ OAD; OA / OC = OD / OB → OA x OB = OC x OD Constante de potencia = OA x OB 2 OA x OB = OC x = OT Segmento representativo de la potencia 2 Potencia = PA x PB = PH W La potencia planteada en función de la distancia del punto al centro de la circunferencia y de su radio P = (d + r) x (d - r) = d2 - r2 > 0 P = (d + r) x (d - r)= d2 - r2 < 0 P = (d + r) x (d - r) = d2 - r2 = 0 EJE RADICAL: Se llama eje radical de dos circunferencias al lugar geométrico formado por los puntos del plano que tienen igual potencia para cada una de ellas (aunque dicha potencia variará para cada punto). Este lugar geométrico es una recta perpendicular a la que une los centros. El eje radical es perpendicular a la Pasa por el punto medio de las Si las circunferencias se cortan, el eje línea que une los centros tangentes exteriores comunes radical pasa por los puntos comunes porque éstos tienen potencia cero. Los puntos del eje radical tienen igual potencia Si son tangentes, el eje radical pasa Si son interiores, el eje estará fuera por el punto de tangencia Si son concéntricas, el eje radical se halla en el infinito Circunferencia auxiliar CURSOS DE PERFECCIONAMIENTO PARA PROFESORADO M. Algeciras TEMA 33: POTENCIA, EJE Y CENTRO RADICAL 2 CENTRO RADICAL: Es el punto de igual potencia con respecto a tres circunferencias. La intersección de los ejes radicales de cada pareja de circunferencias tiene la misma potencia con respecto a las tres dadas. Eje radical HACES DE CIRCUNFERENCIAS CORRADICALES Si se cuenta con dos circunferencias y su eje radical, se denominan circunferencias corradicales con las primeras a aquellas que tienen el mismo eje radical. Existe un conjunto Eje radical indefinido de ellas. Si las dos circunferencias definidoras del haz son tangentes exteriores, formarán parte del haz todas aquellas que pasen por el punto de tangencia y tengan su centro en la misma recta que las dos iniciales. Si las dos circunferencias que definen el haz son secantes, todas las demás también pasarán por los dos puntos de corte. Si las dos circunferencias son exteriores pueden hallarse las demás a partir de la definición de los polos. Para ello, dadas las dos circunferencias y su eje radical, trazar una tangente a una de ellas desde el punto O en que se corta el eje radical con la línea de los centros CC´. Con centro en O y radio OT (tangente anterior), dibujar una circunferencia que cortará a la línea de los centros CC´ en los puntos M y N (denominados polos del haz). Las circunferencias buscadas del haz serán aquellas con centro en la misma línea de los centros CC´ (exterior al diámetro MN) y radio la tangente desde el centro elegido a la circunferencia de diámetro MN. Cómo trazar las circunferencias corradicales de un haz Los haces ortogonales tienen su centro en los ejes radic. POLAR RESPECTO A UN POLO Y UN CIRCULO DIRECTOR: Se denomina polar respecto a un punto fijo P, llamado polo y un círculo director dado de centro O, a la recta que como lugar geométrico es el eje radical de dos circunferencias, la del círculo director y la trazada con diámetro OP. polar P P polar CURSOS DE PERFECCIONAMIENTO PARA PROFESORADO M. Algeciras