REPÚBICA DE PANAMÁ UNIVERSIDAD TECOLÓGICA DE
Anuncio

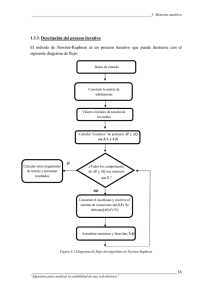
REPÚBICA DE PANAMÁ UNIVERSIDAD TECOLÓGICA DE PANAMÁ CENTRO REGIONAL DE AZUERO FACULTAD DE INGENIERÍA CIVIL MÉTODOS NUMÉRICOS LABORATORIO #2 “PROGRAMA DE NEWTON-RAPHSON” PROFESORA: MARQUELA DE COHEN PREPARADO POR: Batista, Didio 7-706-4 Batista, Edison 6-713-1645 Díaz, Eduardo 7-706-1995 Durán, María 7-706-1657 González, Librada 7-706-1764 Osorio, Dionel Rodríguez, Roderick 8-826-1775 7-707-287 II SEMESTRE FECHA DE ENTREGA JUEVES, 8 DE OCTUBRE DE 2009. INTRODUCCCIÓN El Método de Newton-Raphson es ampliamente utilizado para encontrar las raíces de la ecuación f(x)=0, ya que converge rápidamente, la contra es que uno debe conocer la derivada de f(x) y se necesita una aproximación inicial a la raíz. El método de Newton es conocido en análisis numérico, como el método de Newton-Raphson o el método de Newton-Fourier; el cual es un algoritmo eficiente para encontrar aproximaciones de los ceros o raíces de una función real. También puede ser usado para encontrar el máximo o mínimo de una función, encontrando los ceros de su primera derivada. La idea de este método es la siguiente: se comienza con un valor razonablemente cercano al cero (denominado punto de arranque), entonces se reemplaza la función por la recta tangente en ese valor, se iguala a cero y se despeja (fácilmente, por ser una ecuación lineal). Este cero será, generalmente, una aproximación mejor a la raíz de la función. Luego, se aplican tantas iteraciones como se deseen. Supóngase f : [a, b] -> R función derivable definida en el intervalo real [a, b]. Empezamos con un valor inicial x0 y definimos para cada número natural n Donde f ' denota la derivada de f. CONTENIDO El método fue diseñado para realizar los cálculos con la siguiente ecuación: F(X) = e-x-x Declaración de las variables: Ea = error aproximado I = términos Fx = primera derivada de la función Fx2= segunda derivada de la función Eti2 = error E = cuadrado del error Xi = valor inicial n = cifras significativas X = raíz de la ecuación Ecuación = tolerancia El este programa elaborado en visual Basic, calcularemos las raíces de la ecuación, la mas aproximada, los errores normalizados de cada iteración, los errores y el cuadrado del error. Todo esto dándole un valor inicial xi = 0 con cierta cantidad de cifras significativas. PANTALLA DEL PROGRAMA DESARROLLO DEL PROGRAMA CODIGO DEL PROGRAMA SEGUNDA PARTE DEL CODIGO CONCLUSION Este método, el cual es iterativo, es uno de los más usados y efectivos. A diferencia de los métodos anteriores, el método de Newton-Raphson no trabaja sobre un intervalo sino que basa su fórmula en un proceso iterativo. Con este método comprobamos que hay convergencia en el mismo, ya que el error es aproximadamente igual al cuadrado del error. BIBLIOGRAFIA http://www.google.com/search?hl=es&source=hp&q=metodo+de +newton+raphson&lr=&aq=1&oq=METODO+DE+N http://noosfera.indivia.net/metodos/newtonRaphson.html Programa Visual Basic y apuntes de la materia.