See discussions, stats, and author profiles for this publication at: https://www.researchgate.net/publication/305852121
Una Introducci�on al M�etodo de Newton para resolver ecuaciones no
lineales.
Book · April 2009
CITATIONS
READS
0
6,486
1 author:
Manuel Aurelio Diloné
Universidad de La Rioja (Spain)
8 PUBLICATIONS 6 CITATIONS
SEE PROFILE
Some of the authors of this publication are also working on these related projects:
Dinámica del método de Halley View project
Construcción de un modelo matemático para la solución óptima del problema de localización de los sistemas de distribución de gas natural para abastecimiento del
parque de generación de energía eléctrica. View project
All content following this page was uploaded by Manuel Aurelio Diloné on 09 August 2016.
The user has requested enhancement of the downloaded file.
Una introducción al método de Newton-Raphson
para resolver ecuaciones no lineales
Manuel Aurelio Diloné Alvarado
13 de julio de 2009
2
Una introducción al método de Newton-Raphson
para resolver ecuaciones no lineales.
3
Una introducción al método de Newton-Raphson
para resolver ecuaciones no lineales
Manuel Aurelio Diloné Alvarado. M.A
Impresión: Impresora ServiCentro. C/ Progreso, Nagua, Provincia María Trinidad
Sánchez. República Dominicana.
Impreso en la República Dominicana.
Printed in Dominican republic.
ISBN: 978-9945-00-206-5.
4
Dedicación
A mi esposa Jocelyn Espinal, gracias por brindarme en todo momento el apoyo,
el ánimo y el amor que he necesitado para terminar este proyecto. En gran medida
a ti debo el honor de haber finalizado este trabajo.
A mis hijos Anneuri Manuel y Manuel Aurelio Jr. Por ser ellos la fuente de mi
mayor inspiración.
5
6
Prólogo
Este documento es fruto del trabajo realizado por D. Manuel Aurelio Diloné Alvarado durante su estancia de investigación en la Universidad de La Rioja, en los
cursos 2006–07, 2007–08 y 2008–09. Dicha estancia fue motivada por el convenio
firmado por la Universidad de La Rioja y la Secretaría de Estado de Educación Superior, Ciencia y Tecnología de la República Dominicana con el objetivo de impulsar
los estudios de doctorado científico técnicos en dicho país.
Una de las primeras acciones que impulsó el citado convenio fue la llegada a la
Universidad de La Rioja, a comienzos del curso 2006–07, de dos profesores dominicanos para la realización de los cursos de doctorado en dicha Universidad, uno de
los cuales era D. Manuel Aurelio Diloné Alvarado. En concreto, el profesor Diloné
se inscribió en el programa de doctorado que se imparte de forma conjunta entre
los departamentos de Matemáticas y Computación e Ingeniería Eléctrica de la Universidad de La Rioja, cursando con éxito las asignaturas en las que se matriculó.
Además de los conocimientos adquiridos en estas asignaturas, el profesor Diloné ha
complementado su formación con el manejo de algunas herramientas que en la actualidad resultan imprescindibles para cualquier investigador en Matemáticas, tales
como el procesador de textos científicos LATEX o el programa de cálculo simbólico
Mathematica.
Una vez superado el periodo de docencia, tuvo que afrontar la realización de un
trabajo de investigación, optando para ello por alguna de las líneas que se ofertaban desde el departamento de Matemáticas y Computación de la Universidad de La
Rioja. En concreto, la línea de investigación elegida fue Procesos iterativos para la
resolución de ecuaciones no lineales. Aplicaciones. Para ayudarle a llevar a cabo su
cometido al profesor Diloné se le asignó un tutor académico, que es quien subscribe
estas líneas. Recuerdo con cariño la primera entrevista que tuve como tutor de Diloné, en la cual se me presentó como un «soldado disciplinado» dispuesto a conseguir
todas aquellas metas académicas que se le propongan.
Dentro de la línea de investigación elegida, el trabajo del profesor Diloné se centra
en el estudio del método de Newton y su aplicación a la ecuación de Kepler. Este
tema combina a la perfección dos de los tópicos más clásicos en el Análisis Numérico
y la Matemática Aplicada en general. Por una parte, el estudio de procesos iterativos
para resolver ecuaciones no lineales y, en particular el método de Newton, es un tema
de incuestionable actualidad, a tenor de las publicaciones al respecto que aparecen
en diversas revistas científicas. Por otra parte, la ecuación de Kepler es, sin duda, una
de las ecuaciones más estudiadas en la bibliografía matemática. La combinación de
ambos tópicos ofrece unas enormes posibilidades investigadoras, como lo demuestran
los logros alcanzados hasta el momento. En concreto, además de la publicación de
esta monografía, se ha presentado una comunicación en las III Jornadas de Análisis
Numérico y Aplicaciones, celebradas en la Universidad de La Rioja en noviembre
de 2008 y se tiene admitido un capítulo en el libro Computational Mathematics:
Theory, Methods and Application que publicará a finales de 2009 la editorial Nova
Science Publishers, Inc., con sede en Nueva York.
La tarea investigadora del profesor Diloné en la Universidad de La Rioja culminará a finales del presente curso 2008–09, con la defensa de su trabajo de investigación
y la obtención del Diploma de Estudios Avanzados. Pero es en ese momento, cuando
vuelva a su República Dominicana natal, cuando dará comienzo la etapa más apa7
8
PRÓLOGO
sionante de su labor investigadora: la realización de una tesis doctoral, su defensa
y la obtención del correspondiente título de doctor. Sin duda, con la estancia realizada en la Universidad de La Rioja y los logros alcanzados durante esta época, el
profesor Diloné ha iniciado con paso firme su andadura hacia el título de doctor.
Pero aún queda mucho camino por recorrer, mucho que investigar, redactar y publicar. Además habrá que salvar las dificultades añadidas que motivan el tener que
trabajar a distancia y el tener que «abrir huella» a la hora de realizar las gestiones
administrativas y burocráticas generadas al coordinar las distintas instituciones que
se puedan ver involucradas en este camino al doctorado.
Así, nos gustaría emular al insigne matemático riojano Julio Rey Pastor (Logroño, 1888 – Buenos Aires, 1962), que con su vida y su obra mostró cómo el poder de
las Matemáticas permite cruzar fronteras y unir a pueblos y generaciones distintas.
Nos disponemos a cruzar el «río Océanos» (así es como Rey Pastor denominaba
coloquialmente al Océano Atlántico), tendiendo en este caso un puente entre las
orillas del río Ebro y las cálidas aguas caribeñas por el que las Matemáticas puedan
caminar a sus anchas. Es posible que el profesor Diloné sea el primero en cruzar este
puente pero, sin duda, no será el último ya que nos encontramos ante el inicio de
una colaboración a la que se la augura un gran futuro.
Logroño, abril de 2009
Dr. José Manuel Gutiérrez Jiménez
Profesor del Departamento de Matemáticas y Computación
de la Universidad de La Rioja
Nota preliminar del autor
Es bien sabido que la resolución de ecuaciones no lineales constituyen un aspecto
fundamental en el estudio de cualquier disciplina matemática. Con el texto que el
lector tiene en sus manos pretendemos completar la información que el discente de la
carrera de matemática posee de dicho aspecto para abordar con éxito un primer curso
de Análisis Matemático. Su contenido recoge una colección de teoremas y ejercicios,
quizás no tratados lo suficientemente aquí, concernientes al método de NewtonRaphson, y otro adicional en donde se aplican las condiciones de la convergencia
semilocal del método anterior mencionado a la ecuación de Kepler.
El libro se estructura en tres capítulos: Resolución numérica de ecuaciones no
lineales, El método de Newton-Raphson y El método de Newton-Raphson aplicado
a la ecuación de Kepler. En el primer capítulo se trata de ofrecer una visión teórica
de los conceptos, que a nuestro parecer, son necesarios para lograr entender todos
los factores que se involucran en el proceso de solución de una ecuación no lineal a
partir de un método iterativo. El segundo capítulo se centra en el método de NewtonRaphson y en el mismo se presenta la descripción del mismo a partir de tres puntos
de vistas: el desarrollo de Taylor, su construcción geométrica y como iteración de
punto fijo. También se presenta un estudio referido a la convergencia local, global y
semilocal de dicho método, así como un análisis de su orden de convergencia e índice
de eficiencia. Finalizamos este segundo capítulo con una serie de ejemplos numéricos
en los cuales se puede apreciar las fortalezas y debilidades que presenta el método de
Newton-Raphson. El tercer capítulo está dedicado al análisis del método de NewtonRaphson aplicado a la ecuación de Kepler. En concreto, hacemos un estudio de las
condiciones de convergencia semilocal presentadas por Kantorovich y Smale, y de sus
variante, Gutiérrez y Wang-Zhao. Hemos querido abordar cada capítulo con ciertos
detalles, de manera que su lectura permitan al discente la mejor comprensión en
todos los pasos de las demostraciones de los teoremas y ejercicios resueltos que se
presentan en los mismos.
Deseo manifestar mi agradecimiento al Dr. José Manuel Gutiérrez Jiménez, Guti.
Por todas las cosas en que me ha ayudado me ha demostrado que, además de ser un
excelente matemático, es también mi amigo. Gracias Guti por estar siempre presente
en todos aquellos momentos en que las dudas parecían hacer naufragar esta investigación, sin tus consejos este libro nunca hubiese sido posible. Por último, también
quiero agradecer al personal del Departamento de Matemática y Computación de la
Universidad de La Rioja, y de manera muy especial al Dr. Juan Luis Varona, Dr.
Oscar Ciaurri, Dr. Manuel Bello y a la Dra. Natalia Romero. Gracias por vuestras
continuas muestras de solidaridad para conmigo.
Nagua, abril de 2009
Manuel Aurelio Diloné Alvarado
Miembro del Instituto Nacional de Formación y Capacitación del Magisterio
INAFOCAM
9
10
NOTA PRELIMINAR DEL AUTOR
Índice general
1. Resolución numérica de ecuaciones no lineales
1.1. Introducción . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2. Clasificación de los métodos iterativos. . . . . . . . . . . . . . . . . .
2. El Método de Newton-Raphson
2.1. Introducción . . . . . . . . . . . . . . . . . . . . . . . . .
2.2. Descripción del método . . . . . . . . . . . . . . . . . .
2.2.1. A partir del desarrollo de Taylor . . . . . . . . .
2.2.2. Construcción geométrica: método de la tangente.
2.2.3. Iteración del punto fijo. . . . . . . . . . . . . . .
2.3. Estudio de convergencia . . . . . . . . . . . . . . . . . .
2.3.1. Convergencia Local. . . . . . . . . . . . . . . . .
2.3.2. Convergencia Global. . . . . . . . . . . . . . . . .
2.3.3. Convergencia Semilocal. . . . . . . . . . . . . . .
2.4. Orden de convergencia y eficiencia . . . . . . . . . . . .
2.4.1. Orden de convergencia . . . . . . . . . . . . . . .
2.4.2. Índice de eficiencia . . . . . . . . . . . . . . . . .
2.4.3. Orden de convergencia computacional . . . . . .
2.5. Ejemplos numéricos . . . . . . . . . . . . . . . . . . . .
2.5.1. Ecuaciones no lineales resueltos por el método de
2.5.2. Ejemplos patológicos . . . . . . . . . . . . . . . .
3. El método de Newton aplicado a la
3.1. Introducción histórica . . . . . . .
3.2. El teorema de Kantorovich . . . .
3.3. El teorema de Gutiérrez . . . . . .
3.4. La α-teoría de Smale . . . . . . . .
3.5. La α-teoría de Wang-Zhao . . . . .
3.6. Ejemplos numéricos . . . . . . . .
Bibliografía
ecuación
. . . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
de
. .
. .
. .
. .
. .
. .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
Newton.
. . . . .
Kepler
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1
1
5
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
7
7
9
9
9
10
11
11
12
16
25
25
25
26
27
27
32
.
.
.
.
.
.
.
.
.
.
.
.
43
43
45
46
49
51
54
57
11
12
ÍNDICE GENERAL
Capítulo 1
Resolución numérica de
ecuaciones no lineales
1.1.
Introducción
Muchos problemas relacionados con las Matemáticas se reducen a resolver una
ecuación
f (x) = 0,
(1.1)
donde, en principio, supondremos que f es una función real de variable real. Pese
a su sencillez de planteamiento, éste ha sido un problema complicado que ha sido
tratado por numerosos matemáticos célebres: Cardano, Newton, Ruffini, Galois, etc.
Incluso para funciones «sencillas» como son los polinomios, el cálculo de sus raíces es
un tema complicado. En un principio, se intentó encontrar dichas raíces en función
de los coeficientes del polinomio, como ocurre con la ecuación de segundo grado:
√
−b ± b2 − 4ac
2
ax + bx + c = 0 ⇐⇒ x =
.
2a
También se conocen fórmulas para polinomios de grados 3 y 4 aunque, debido a su
complejidad, no se suelen usar en la práctica. A principios del s. XIX, Galois probó
que no existen este tipo de fórmulas para polinomios de grado mayor o igual que 5.
El problema de no poder encontrar de forma exacta las soluciones de una ecuación
surgía también al trabajar con ecuaciones trascendentes, como la ecuación de Kepler,
relacionada con el cálculo de órbitas planetarias:
f (E) = E − e sen E − M
para distintos valores de E y de M .
Estas limitaciones obligan a buscar métodos para encontrar las soluciones de una
ecuación de forma aproximada. Básicamente, estos métodos generan una sucesión
{x1 , x2 , . . . , xn , . . . } que, en condiciones adecuadas, converge a una solución de la
ecuación (1.1). En muchas ocasiones, esta sucesión se genera de forma recursiva
xn+1 = F (xn , . . . , xn−p+1 ),
a partir de una función de iteración, F , que puede depender de uno o varios argumentos.
Los intentos por resolver estos tipos de ecuaciones se vienen reflejando desde
la antigüedad. Leyendo a Knill [50], nos damos cuenta que desde las civilizaciones
griegas, aproximadamente dos mil años antes de Cristo, ya se conocían algoritmos
iterativos, tal es el caso de la fórmula de Herón para
√ el cálculo de raíces cuadradas,
donde partiendo de una aproximación inicial s de S se propone como nueva aproximación (s + S/s)/2. Con esta fórmula, Herón podía aproximar el valor de la raíz
1
2
CAPÍTULO 1. RESOLUCIÓN NUMÉRICA DE ENL
cuadrada que aparece en la fórmula del área de un triángulo:
p
S = p(p − a)(p − b)(p − c),
donde p = (a + b + c)/2 es el semiperímetro del triángulo de lados a, b y c.
La utilización de un algoritmo iterativo conlleva el planteamiento de varios problemas teóricos ya que es básico examinar su velocidad de convergencia, determinar
el número de iteraciones necesarias para obtener la precisión acordada, estudiar los
efectos de la aritmética del computador sobre la sucesión, así como resolver el problema de buscar una buena aproximación inicial.
El problema de resolver una ecuación presenta aspectos muy diferentes. Por ejemplo, con respecto a la función que se presente, la misma puede ser polinomial, trascendental o no disponer de una expresión explícita de la misma, tal y como ocurre
cuando se trata de una ecuación diferencial. Por otra parte, está el problema que
presentan las soluciones, pues es sabido que una ecuación puede no tener solución,
tener una única solución, poseer soluciones múltiples o tener infinitas soluciones.
Definición 1 (Error Absoluto). Dada una sucesión {xn }∞
n=0 convergente a un
límite x∗ , definimos el error absoluto como la diferencia entre el valor exacto xn de
la sucesión y x∗ .
an = xn − x∗ .
En ocasiones se usa la expresión
|an | = |xn − x∗ |,
para referirse al módulo del error absoluto.
Definición 2 (Error Relativo). El error relativo del límite x∗ de una sucesión
{xn }∞
n=0 con respecto al valor exacto xn de la sucesión, es el cociente entre el módulo
del error absoluto y el valor absoluto del valor exacto.
rn =
|xn − x∗ |
.
|xn |
El error relativo y el módulo del error absoluto tienen un uso muy especial en
la determinación del criterio de parada y el orden de convergencia de un algoritmo
iterativo.
Definición 3 (Criterios de parada). Los criterios de parada son los que definen
el momento en que se detendrá el algoritmo que se está ejecutando, pues establecen
cuando se está lo suficientemente cerca del valor buscado.
El proceso habitual para fijar un criterio de parada consiste en fijar un parámetro
pequeño llamado tolerancia, denotado usualmente por T OL, deteniéndose el proceso
cuando se cumple una de las siguientes condiciones
1. |xn − xn−1 | < T OL.
2.
|xn −xn−1 |
|xn |
< T OL.
Estos criterios están justificados en el hecho de que para muchas sucesiones, las
expresiones 1 y 2 intervienen en las cotas del error, es decir
|xn − x∗ | ≤ Kn |xn − xn−1 |,
de esta manera se consigue que si |xn −xn−1 | es pequeño, entonces el error cometido,
cuando Kn sea de un tamaño moderado, también será pequeño. Un error muy a
menudo cometido cuando se resuelve una ecuación no lineal (1.1) es el hecho de
usar, como único criterio de parada, la expresión
|f (xn )| < T OL,
1.1. INTRODUCCIÓN
3
pues suponer siempre que xn es una buena aproximación de la raíz si se cumple que
f (xn ) es pequeño, puede resultar completamente incorrecto para algunas funciones.
Este tipo de caso luego se verá en los ejemplos que presentaremos.
Definición 4 (Orden de convergencia). El orden de convergencia nos indica la
velocidad con la cual una sucesión converge a su límite. En términos matemáticos
asume la siguiente expresión:
|xn+1 − x∗ |
= C,
n→∞ |xn − x∗ |p
lı́m
con C ∈ R+ y p ≥ 1,
donde {xn } es la sucesión, x∗ el número al que converge la sucesión, p es el orden
de convergencia y C es la constante asintótica de error.
Si p = 1, 2, 3, 4, 5, se dice que es de orden lineal, cuadrático, cúbico, cuártico y
quíntico respectivamente.
Se debe recalcar la importancia práctica que presenta el orden de convergencia.
En efecto, cuando xi+1 está lo suficientemente cerca de x∗ , se cumple
|xi+1 − x∗ | ≈ µ|xi − x∗ |p ,
y haciendo
Dn = − log |xi − x∗ |,
se obtiene
Dn+1 = pDn + r,
donde r = − log µ.
Esto significa que en cada iteración se multiplica aproximadamente por p, el
número de cifras exactas, de forma que, en general, un algoritmo con orden de
convergencia alto converge más rápidamente que un algoritmo de orden menor.
Cuando se verifica que
|xn+1 − x∗ |
=0
n→∞ |xn − x∗ |
lı́m
ó
|xn+1 − x∗ |
= 0,
n→∞ |xn − x∗ |2
lı́m
∗
el orden de convergencia de la sucesión {xn }∞
n=1 a x se llama superlineal o supercuadrático, respectivamente.
Una caracterización del orden del convergencia la encontramos en el teorema
de Schröder, cuya demostración damos a continuación. Parte de la demostración la
pueden encontrar en [48] y [82].
Teorema 1 (de Schröder). Consideremos un método iterativo
xn+1 = g(xn ),
(1.2)
en el que g es continua y q veces diferenciable en en entorno de x∗ , un punto fijo de
g, x∗ = g(x∗ ). Entonces la sucesión {xn } converge a x∗ con orden de convergencia
q si
dj g(x∗ )
dq g(x∗ )
= 0, j = 1, 2, . . . , q − 1,
6= 0.
j
dx
dxq
Demostración. Desarrollando (1.2) en serie de Taylor se obtiene
xn+1 = g(xn ) = x∗ + g 0 (x∗ )(xn − x∗ ) + · · · +
1 dq g(x)
(xn − x∗ )q ,
q! dxq
Luego, usando la condición del enunciado, se sigue
xn+1 − x∗ =
con lo que
1 dq g(x∗ )
(xn − x∗ )q ,
q! dxq
|xn+1 − x∗ |
1 dq g(x∗ )
=
6= 0.
∗
q
n→∞ |xn − x |
q! dxq
Por lo tanto el método tiene orden de convergencia q.
lı́m
x ∈ (xn , x∗ ).
4
CAPÍTULO 1. RESOLUCIÓN NUMÉRICA DE ENL
Otro importante aspecto que tiene que ver con la convergencia es el que se refiere
a la velocidad de convergencia de dos sucesiones, ya que ésta nos permitirá comparar
la velocidad de los diferentes algoritmos iterativos.
Definición 5 (Velocidad de convergencia de dos sucesiones). Dada una sucesión {xn } que converge a x y una sucesión {yn } que converge a y, se dice que {yn }
converge más rápidamente que {xn } si
y − yn
= 0.
n→∞ x − xn
lı́m
Otro elemento que también se emplea para comparar la velocidad de convergencia
de dos sucesiones es la constante asintótica del error. En efecto, dadas dos sucesiones
con el mismo orden de convergencia, la que tenga la constante asintótica del error más
pequeña convergerá más rápidamente que la otra. El recíproco de esta proposición no
es cierto, pues dos sucesiones del mismo orden y con la misma constante asintótica
de error no tienen por qué converger con la misma velocidad. En [21], se muestran
varios ejemplos que verifican la no reciprocidad de la proposición.
Ejemplo 1. Dadas yn = an /n2 y xn = an /n con 0 < a ≤ 1, el orden de convergencia
es 1 y a es, para ambos casos, la constante asintótica del error, pero {yn } converge
más rápidamente a cero.
Solución 1. Notemos que al sustituir cualquier valor de 0 < a < 1 y n ≥ 1 se
obtiene
0 < yn < xn , ∀n ≥ 1.
Para una mayor profundidad de los aspectos concernientes a orden y velocidad
de convergencia, ver a [4], [16], [52], [64] y [73] entre otros.
En la determinación de las raíces de una ecuación no lineal, el aumento del orden
de convergencia permite reducir el número de iteraciones. Pero el aumento en el
orden requiere una mayor cantidad de evaluaciones de funciones y sus derivadas,
aumentando el tiempo de cálculo en cada iteración. Esto podría significar que el
aumento del orden de convergencia del método lleva implícito que el mismo sea
menos eficiente, pero no siempre es así ya que en realidad lo que se establece es un
equilibrio entre el orden de convergencia y el coste operacional del algoritmo.
Desde el punto de vista práctico, lo realmente importante no es ni el orden de
una sucesión ni el número de iteraciones necesarias para llegar a la precisión deseada,
sino el tiempo que emplea el computador en alcanzar tal precisión, por lo tanto el
coste del cómputo de una iteración es fundamental. En otras palabras, el índice de
eficiencia del método iterativo es básico. Veamos su definición:
Definición 6 (Índice de eficiencia computacional de un método). De acuerdo
con [38], existen dos tipos de índice de eficiencia:
i) El de aritmética con precisión fija y pequeña. El índice de eficiencia viene
definido por la expresión
IEC(p, d) = p1/d ,
(1.3)
donde p > 1 es el orden de convergencia del método y d es el número de
evaluaciones de la función f o de sus derivadas.
ii) El de aritmética con múltiple precisión. En este caso el índice de eficiencia del
método se denota por la fórmula
1
IEC(d, p, α) = p C(d,p,α) = p
1−p−α
d
,
Donde p y d tienen el mismo significado que en la ecuación (1.3) y
d
es el coste total o tiempo computacional de evaluar a f , en donde.
1 − p−α
= logk+1 (2k + 1), para k ≥ 1.
C(d, p, α) =
α
1.2. CLASIFICACIÓN DE LOS MÉTODOS ITERATIVOS.
5
y k es una constante que indica el número de veces que se debe evaluar la
función f .
Computacionalmente hablando, cuanto mayor sea el índice de eficiencia mejor
es el método iterativo. Es importante señalar que una mejora en el orden de convergencia de un método iterativo, no siempre implica una mejora en la eficiencia
computacional del mismo. Generalmente estas mejoras traen como consecuencia el
incremento del coste de evaluar la función, en perjuicio de su eficiencia.
1.2.
Clasificación de los métodos iterativos.
Existen diferentes formas de clasificar los procesos iterativos, dependiendo de
los aspectos que se vayan a tener en cuenta. Por ejemplo, en función del número
de elementos de la sucesión {xn } que necesitamos para calcular xn+1 , los podemos
catalogar en dos grandes bloques
(i) Métodos de un punto. Aquellos en los que la sucesión de iteración es de la
forma
xn+1 = g(xn ).
Entre estos se encuentran el método de: Newton-Raphson, Halley, SuperHalley, Chebyshev, etc.
(ii) Métodos multipunto. En estos la función de iteración es de la forma
xn+1 = g(xn , xn−1 , . . . , xn−p+1 ),
con p ≥ 1.
Es decir, son métodos en los que el n-énesimo término viene dado en función de
los p términos anteriores. A este grupo pertenecen los métodos de: la Secante,
Steffensen, Falsa Posición o Regula Falsi, etc.
Pero ésta no es una clasificación única. Por ejemplo, Aubanell y Delshams [5]
presentan una clasificación de los métodos iterativos atendiendo a dos rasgos que los
caracterizan:
1. La herramienta que se emplea en el desarrollo de la función. De acuerdo a la
herramienta que se emplea en el desarrollo de la función, los métodos iterativos
se clasifican en:
Métodos de Taylor. Son aquéllos que utilizan el desarrollo de Taylor,
es decir, calculan a xn+1 a partir del conocimiento de la función y de sus
derivadas en un punto xn . Ejemplos: método de Euler, método de Punto
medio.
Métodos de Interpolación. En éstos se calcula xn+1 a partir del conocimiento de la función en xn , xn−1 , . . . . Ejemplos: método de Lagrange,
método de Hermite.
2. La función que se desarrolla o se interpola. Por la función que se desarrolla o
se interpola, es decir, si se emplea g = f −1 , que es equivalente a buscar a x∗
tal que f (x∗ ) = 0 a buscar x∗ tal que g(0) = x∗ , es posible dar dos enfoques
a los métodos que se aplicaran en la solución del problema según se emplee el
desarrollo de Taylor o la interpolación de la función f ó g:
Métodos Directos. Si usamos la función f . Ejemplos: método de NewtonRaphson, Método de Halley.
Métodos Inversos. Si empleamos la función g = f −1 . Ejemplo: método
de Chebyshev.
Además, teniendo en cuenta el comportamiento especial para raíces múltiples,
consideraremos un tercer bloque
6
CAPÍTULO 1. RESOLUCIÓN NUMÉRICA DE ENL
(iii) Métodos para raíces múltiples.
Es conocido que algunos métodos, i.e el método de Newton-Raphson y el método de la Secante, disminuyen su orden de convergencia cuando la ecuación
que intentan resolver tienen raíces múltiples. Para evitar esta consecuencia se
han creado una serie de métodos que introducen en el método original una
constante de multiplicidad que permite aumentar nuevamente el orden de convergencia.
Entre los métodos para encontrar raíces múltiples tenemos el de NewtonRaphson modificado, Newton Relajado, King-Van de Vel, etc.
Capítulo 2
El Método de
Newton-Raphson
2.1.
Introducción
La idea general de resolver una ecuación mediante un algoritmo iterativo o estimando la solución mediante la adicción de un término corrector ha sido empleada
por muchas culturas milenarias. Por ejemplo, en la antigua Grecia y Babilonia se
emplearon métodos parecidos a los utilizados por Newton, para aproximar la solución de radicales. Métodos algebraicamente equivalente al de Newton también fueron
aplicados en el siglo XII, por el algebrista Sharaf al-Din al-Tusi. En el siglo XV ,
el matemático árabe Al-Kashi empleó un algoritmo numérico para encontrar las
raíces p-ésimas de N en la ecuación xp = N . También Henry Briggs, en su obra
Trigonometria Britannica publicada en 1633, usó un método parecido al de Newton.
Leyendo a Tjalling J. Ypma [96] encontramos que
la primera formulación del método de Newton-Raphson
apareció en un tratado de Newton titulado De analysi per aequationes numero terminorum infinitas, el cual
fue, probablemente, presentado a mediados del año 1669
y publicado en 1711 por William Jones. Esta primera formulación es considerablemente diferente a la que conocemos hoy en día y estaba definida para resolver sólamente
ecuaciones polinómicas. Además la forma de realizar los
cálculos son mucho más tediosos que en la formulación
actual. En 1671 Newton dio a conocer un tratado, con
una versión ligeramente más comprensible, titulado De
Figura 2.1: Sir Isaac
methodis fluxionum et serierum infinitarum, la cual fue
Newton (1643–1727)
publicada por John Colson en 1736.
El proceso descrito por Newton requiere un cálculo explícito de una sucesión
polinómica de la forma g1 , g2 , . . . , que lo convierte en un método muy laborioso.
También se observa que la estimación final x∗ es calculada al final del proceso como
x∗ = x0 + c0 + c1 + . . . en vez de hacer las estimaciones sucesivas de xn , lo cual
evidencia que Newton no utilizó una técnica recursiva.
La primera vez que Newton publica su método aplicado a ecuaciones no polinómicas fue en la segunda y tercera edición de su obra Philosophiae Naturalis Principia
Mathematica, la cual fue presentada en 1687 en Londres. En ellas describe las técnicas para resolver la ecuación de Kepler
f (E) = E − e sen E − M,
(2.1)
donde M es la anomalía media, E es la anomalía excéntrica y e es la excentricidad
de la elipse.
7
8
CAPÍTULO 2. EL MÉTODO DE NEWTON-RAPHSON
La segunda formulación del método de Newton
se debe a Joseph Raphson, quien en 1690 publicó
un tratado titulado Analysis aequationum universalis en el cual se presentó un método nuevo para
resolver ecuaciones polinómicas. Una segunda edición de dicho tratado se publicó como libro en 1697,
con un apéndice que hace referencia a Newton. Se
comprueba que los dos métodos son matemáticamente equivalentes, la diferencia es que Raphson
no necesitó generar una sucesión de polinomios, como lo hacía Newton.
Figura 2.2: Thomas SimRaphson consideró una ecuación de la forma
pson (1710 − 1761)
a3 − ba − c = 0, donde a es una variable. Prosigue
indicando que si g es una estimación de la solución
x∗ , entonces, una mejor aproximación se consigue haciendo a g + x, donde
x=
c + bg − g 3
.
3g 2 − b
Formalmente esto es de la forma
g+x=g−
f (g)
,
f 0 (g)
con f (a) = a3 − ba − c,
pero como en el caso de Newton, Raphson también procedió de manera puramente
algebraica, aunque prefirió las reglas del cálculo al utilizar la forma de derivada,
pues en cada ejemplo escribió expresiones, tales como f (x) y f 0 (x), para referirse a
polinomios completos.
Los contactos entre Newton y Raphson parece que fueron muy limitados, aunque parece que Newton aprovechó las circunstancia de la muerte de Raphson para
adjuntar un apéndice al último libro de Raphson, titulado Historia fluxionum. En el
prefacio del tratado de 1690, Raphson se refiere a los trabajos de Newton, indicando
que su método no es único.
La tercera versión del método de Newton se
debe a Thomas Simpson y la misma está descrita
en un libro titulado Essays on Several Curious and
Useful Subjects in Speculative and Mixed Mathematicks, publicado en 1740 en Londres. En el ensayo
número seis, Simpson describe un nuevo método
para la solución de ecuaciones numéricas, sin hacer referencia a los trabajos de ningún predecesor.
En el prefacio de dicho ensayo, contrasta las técnicas de su método, las cuales estaban basadas en
el análisis matemático y cálculo numérico, con los
Figura 2.3: Joseph Louis
métodos algebraicos de entonces. En éste se dan
Lagrange
(1736 − 1813)
ejemplos de solución de ecuaciones polinómicas y
no polinómicas, con detalles para resolver ecuaciones en una o dos variables mediante instrucciones que involucran el signo ẋ, el cual
es equivalente a dx/dt. Además aparece la primera formulación de un método iterativo para resolver, en general, ecuaciones no lineales basados en el cálculo numérico.
Finalmente, fue Lagrange, en 1798, quien introdujo el método de Newton-Raphson
con la simbología que se emplea actualmente. La obra en que aparece esta notación
moderna se titula Sur la méthode d’Approximation donnée par Newton y en la misma no hace referencia a los trabajos de Simpson, aunque si menciona a Newton y
Raphson.
2.2. DESCRIPCIÓN DEL MÉTODO
2.2.
9
Descripción del método de Newton-Raphson
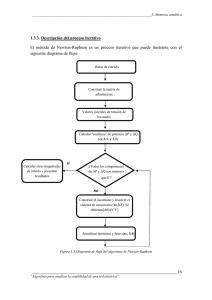
El método de Newton-Raphson es un proceso iterativo que, en condiciones adecuadas, permite aproximar una solución x∗ de una ecuación no lineal (1.1). Partiendo
de una aproximación inicial x0 de la raíz x∗ , el método de Newton-Raphson define
una sucesión
f (xn )
xn+1 = xn − 0
, n = 0, 1, 2, 3, . . . .
(2.2)
f (xn )
Existen varias formas de deducir la expresión (2.2). A continuación presentamos,
de forma reducida, algunas de ellas.
2.2.1.
A partir del desarrollo de Taylor
La técnica que explicaremos a continuación aparece en varios libros clásicos de
Análisis Numérico, entre ellos [16], [27], [48] y [53].
Sea x0 una aproximación de x∗ , la raíz de f (x) = 0. Buscamos un término
corrector h de forma que x + h sea la raíz buscada, es decir,
f (x0 + h) = f (x∗ ) = 0.
Si desarrollamos por la serie de Taylor f (x0 + h) se obtiene:
0 = f (x0 + h) = f (x0 ) + hf 0 (x0 ) +
h2 00
f (x0 ) + · · · .
2!
(2.3)
La solución exacta de esta ecuación nos daría el término corrector h tal que
x0 + h = x∗ .
Si en lugar de considerar la ecuación (2.3), tomamos su linealizada
f (x0 ) + hf 0 (x0 ) = 0,
obtenemos de forma sencilla su solución
h=−
f (x0 )
.
f 0 (x0 )
Si bien este valor no es la solución exacta de (2.3), en condiciones adecuadas
podría ser una buena aproximación. De esta forma
x0 + h = x0 −
f (x0 )
,
f 0 (x0 )
sería una mejor aproximación a x∗ que la dada inicialmente por x0 .
Si denotamos por
f (x0 )
x1 = x0 − 0
,
f (x0 )
y reiteramos el proceso obtenemos el método de Newton-Raphson: (2.2).
2.2.2.
Construcción geométrica: método de la tangente.
Esta técnica aparece en una inmensa bibliografía de Métodos Matemáticos y
Análisis Numérico, entre los que podemos citar los siguientes: [10], [13], [15], [52],
[55], [69], [65], [68], [69], [74] y muchísimos más.
La técnica de iteración de este método consiste en tomar un punto inicial x0 , véase
la figura (2.4), para luego trazar por el punto (x0 , f (x0 )) la tangente geométrica a la
gráfica de la función f (x). Luego, la intersección de dicha tangente con el eje X nos
da un nuevo punto x1 , por el cual trazamos una nueva recta tangente a la gráfica
de la función, pero esta vez por el punto (x1 , f (x1 )). En condiciones adecuadas la
sucesión así obtenida
x0 , x1 , x2 , . . . , xn−1 , xn , . . .
10
CAPÍTULO 2. EL MÉTODO DE NEWTON-RAPHSON
tiende a la raíz exacta x∗ .
y
f Hx0 L
f Hx1 L
f Hx2 L
x*
x2
x1
x0
x
Figura 2.4: Interpretación geométrica del método de Newton-Raphson
Por la ecuación de la recta tangente obtenemos
y − f (x0 ) = f 0 (x0 )(x1 − x0 ).
Luego, en la intersección con el eje X, (y = 0), se sigue
x1 = x0 −
f (x0 )
.
f 0 (x0 )
Reiterando el proceso se llega a la función iterativa (2.2) para el punto xn .
2.2.3.
Iteración del punto fijo.
El método de Newton-Raphson puede ser obtenido a partir de del método de
iteración del punto fijo. Para ello escribiremos la ecuación f (x) = 0 como
x = x − f (x),
(2.4)
luego introducimos en (2.4) un parámetro λ, con lo cual
x + λx = λx + x − f (x),
de donde
λ
1
x+
(x − f (x)) = G(x).
(2.5)
λ+1
1+λ
Si x∗ es una raíz de f (x), x∗ es un punto fijo de G(x). Si imponemos que G0 (x∗ ) =
0 es un punto fijo superatractor, entonces el parámetro λ debe cumplir
x=
λ
1
+
(1 − f 0 (x∗ ) = 0,
1+λ 1+λ
de donde se obtiene
λ = f 0 (x∗ ) − 1.
(2.6)
Sustituyendo (2.6) en (2.5) y utilizando la iteración del punto fijo, sigue
xn+1
=
=
=
G(xn )
1
f 0 (x∗ − 1)
xn + 0 ∗ (xn − f (xn ))
0
∗
f (x )
f (x )
f (xn )
xn − 0 ∗ .
f (x )
Pero como x∗ es, en principio desconocido, podemos usar la aproximación definida
por x∗ ∼ xn para llegar al siguiente método iterativo.
xn+1 = xn −
f (xn )
,
f 0 (xn )
que es, de nuevo, el método de Newton-Raphson.
2.3. ESTUDIO DE CONVERGENCIA
2.3.
11
Estudio de la convergencia del método de NewtonRaphson
En los apartados anteriores, hemos visto como definir una sucesión
xn+1 = xn −
f (xn )
f 0 (xn )
con el objetivo de aproximar la solución de x∗ de la ecuación f (x) = 0.
Tenemos que ser conscientes de que la convergencia de {xn } hacia x∗ no siempre
va a suceder. Para que esto ocurra, se tienen que dar una serie de condiciones sobre
la función f , el punto de partida x0 o la raíz x∗ . En concreto, distinguiremos 3 tipos
de resultados de convergencia:
1. Local: Se dan condiciones sobre la raíz x∗ .
2. Semilocal: Se dan condiciones sobre el punto de partida x0 .
3. Global: Se dan condiciones sobre un intervalo.
Existen una gran cantidad de publicaciones con diversos resultados de convergencia para el método de Newton-Raphson (véanse [4], [5], [7], [21], [28], [30], [47],
[52], [54], [55], [57],[60], [68], [73], [74], [78] y [82]). No es nuestro objetivo dar un
listado exhaustivo de todos ellos. No obstante, a modo de ejemplos, expondremos
uno o dos resultados de cada tipo de convergencia.
2.3.1.
Convergencia Local.
El teorema que presentamos a continuación ha sido elegido tomando en cuenta
la forma sencilla y poderosa de su demostración. En el mismo se introducen dos
elementos, la función de iteración del método de Newton-Raphson (Nf (x)) y su
derivada (Lf (x)), las cuales toman la forma siguiente:
f (x)
.
f 0 (x)
f (x)f 00 (x)
.
f 0 (x)2
Nf (x)
= x−
(2.7)
Lf (x)
=
(2.8)
Las funciones (2.7) y (2.8) son muy utilizadas en las demostraciones de la convergencia de muchos métodos iterativos, tales como el método de Halley y el método
de Chebyshev, así como en libros y artículos de Análisis Numérico, entre los que se
pueden citar a [2], [23], [40] y [84].
Es importante destacar que la expresión (2.8) es identificada como el Grado de
Convexidad Logarítmico de una función. Leyendo a [40] encontramos que el grado de
convexidad logarítmico de una función es una medida puntual de la convexidad, dada
por la resistencia de una función a ser «concavizada» por un operador logarítmico.
En otras palabras, es el numero de veces que hay que aplicar un operador logarítmico
a una función convexa para obtener como resultado una función cóncava.
Además, el grado de convexidad logarítmico está relacionado con la velocidad de
convergencia del método de Newton-Raphson. En efecto, leyendo a [24] encontramos
que a partir de la interpretación geométrica del método de Newton- Raphson se
verifica que a menor convexidad logarítmica de la función y = f (x), la sucesión de
Newton-Raphson presenta mayor velocidad de convergencia a la raíz de la ecuación
f (x) = 0, por lo que la convexidad logarítmica es aplicada para construir nuevas
variantes del método de Newton. Para un estudio profundo de las variaciones del
método de Newton a partir de la aplicación del grado de convexidad logarítmico,
consúltese nuevamente [24] y [36].
12
CAPÍTULO 2. EL MÉTODO DE NEWTON-RAPHSON
Teorema 2. Sea f una función dos veces diferenciable en un entorno I de una
solución x∗ de f (x) = 0. Supongamos que f 0 (x∗ ) 6= 0. Entonces existe un r > 0 tal
que si x0 ∈ (x∗ − r, x∗ + r) la sucesión
xn+1 = xn −
f (xn )
,
f 0 (xn )
converge a x∗ .
Demostración. Como xn+1 = Nf (xn ), restando x∗ a ambos lados se sigue
Z
∗
∗
x − xn+1
∗
x∗
= x − Nf (xn ) = Nf (x ) − Nf (xn ) =
Z
xn
Nf0 (t)dt
x∗
=
Lf (t)dt.
xn
Como f (x∗ ) = 0 y f 0 (x∗ ) 6= 0, entonces Lf (x∗ ) = 0.
Por la continuidad de Lf (x), existe r ∈ R tal que si t ∈ (x∗ − r, x∗ + r), |Lf (t)| ≤
γ < 1.
De esta forma, si x0 ∈ (x∗ − r, x∗ + r), entonces
Z
∗
x∗
|x − x1 | ≤
Lf (t)dt ≤ γ|x∗ − x0 | < r,
luego x1 ∈ (x∗ − r, x∗ + r).
x0
Inductivamente, si xn ∈ (x∗ − r, x∗ + r), entonces
Z
|x∗ − xn+1 | ≤
x∗
Lf (t)dt ≤ γ|x∗ − xn | < r,
es decir xn+1 ∈ (x∗ − r, x∗ + r).
xn
Además
|x∗ − xn+1 | ≤ γ|x∗ − xn | ≤ γ 2 |x∗ − xn−1 | ≤ · · · ≤ γ n+1 |x∗ − x0 |.
Luego
lı́m xn+1 = x∗
n→∞
2.3.2.
para todo x0 ∈ (x∗ − r, x∗ + r).
Convergencia Global.
En el Análisis Numérico principalmente se emplean dos teoremas que permiten
conocer el comportamiento global de los métodos iterativos de un punto. Éstos son
1. El teorema del Punto Fijo.
2. El teorema de Fourier.
El teorema del Punto Fijo nos da las condiciones suficientes para la convergencia
de un algoritmo, a partir de un valor inicial tomado en un intervalo apropiado. Para
su demostración se hace necesario conocer de antemano el significado de función
contractiva.
Definición 7 (Función contractiva). Una función g(x) ∈ C 1 (I) es contractiva en
I, si existe 0 < L < 1 tal que para todo x, y ∈ I, se cumple
|g(x) − g(y)| ≤ L|x − y|.
A la condición |g(x) − g(y)| ≤ L|x − y| se le llama condición de Lipchitz y a L
constante de Lipchitz. Normalmente se dice que una función g(x) es contractiva si
su constante de Lipchitz es menor que la unidad.
2.3. ESTUDIO DE CONVERGENCIA
13
Teorema 3 (Punto Fijo). Sea I un intervalo cerrado y g : I → I una contracción
(L < 1). Bajo estas condiciones se cumple que:
i) La sucesión definida por xn+1 = g(xn ) converge para todo valor inicial x0 ∈ I.
ii) La sucesión converge a un punto fijo de g, es decir si x∗ = lı́mn→∞ xn ⇒ x∗ =
g(x∗ ).
iii) Este punto fijo es único en I, es decir, existe un único x∗ ∈ I
x∗ .
tal que
g(x∗ ) =
Demostración. Para demostrar i) probaremos que la sucesión {xn } es de Cauchy.
En efecto, consideremos la sucesión definida por el enunciado del teorema
xn+1 = g(xn ).
(2.9)
Como la diferencia entre dos términos cualesquiera de (2.9) cumple que
|xn+m − xn | = |xn+m − xn+m−1 + xn+m−1 − · · · + xn+1 − xn |.
De donde
|xn+m − xn | ≤ |xn+m − xn+m−1 | + · · · + |xn+1 − xn |.
(2.10)
Pero
|xn+m − xn+m−1 | ≤
Luego
Lm−1 |xn+1 − xn | + · · · + L2 |xn+1 − xn | +
L|xn+1 − xn | + |xn+1 − xn | = |xn+1 − xn |(1 + L + L2 + · · · + Lm−1 ).
|xn+m − xn+m−1 | ≤ |xn+1 − xn |(1 + L + L2 + · · · + Lm−1 ).
Ahora (1 + L + L2 + · · · + Lm−1 ) es la suma de los términos de una progresión
geométrica, por tanto
|xn+m − xn+m−1 | ≤ |xn+1 − xn |
1 − Lm
.
1−L
(2.11)
Asimismo
|xn+1 − xn | ≤ L|xn − xn−1 | ≤ L2 |xn−1 − xn−2 | ≤ · · · ≤ Ln |x1 − x0 |.
(2.12)
Sustituyendo (2.11) y (2.12) en (2.10) se sigue
|xn+m − xn | ≤ Ln
1 − Lm
|x1 − x0 |.
1−L
Esto nos garantiza que la sucesión es de Cauchy, ya que si L < 1 el término
1 − Lm
|x1 − x0 |,
1−L
está acotado y el término Ln puede ser todo lo pequeño posible sin más que tomar
un n suficientemente grande.
Por tanto, bajo estas condiciones, para todo ε > 0 podemos encontrar un k ∈ N
tal que ∀ n ≥ k, m ≥ 1 se cumple que
|xn+m − xn | < ε.
Es decir que la sucesión {xn } es de Cauchy, y por tanto convergente.
Para probar ii) es suficiente ver que al verificar la condición de Lipchitz, g es
continua y por tanto
g( lı́m xn ) = lı́m g(xn ) = lı́m xn+1 ⇒ x∗ = g(x∗ ).
n→∞
n→∞
n→∞
14
CAPÍTULO 2. EL MÉTODO DE NEWTON-RAPHSON
Para demostrar iii), supongamos que existen dos puntos fijos x∗ 6= x∗∗ con lo
que
|x∗ − x∗∗ | = |g(x∗ ) − g(x∗∗ )|.
Luego, por la condición de Lipchitz se sigue
|x∗ − x∗∗ | ≤ L|x∗ − x∗∗ |,
lo cual es un absurdo, ya que por hipótesis L < 1. Luego, x∗ = x∗∗ .
Teorema 4 (Condiciones de convergencia de Fourier). Sea f (x) : [a, b] → R
una función f ∈ C 2 [a, b] que cumple las siguientes condiciones:
i) f (a)f (b) < 0.
ii) f 0 (x) 6= 0, ∀x ∈ [a, b].
iii) f 00 (x) no cambia de signo en [a, b].
f (b)
iv) máx{| ff0(a)
(a) |, | f 0 (b) |} ≤ b − a.
Entonces existe una única raíz x∗ de (1.1) en [a, b] y la sucesión {xn }∞
n=0 , definida
por (2.2) converge hacia x∗ para cualquier valor inicial x0 ∈ [a, b].
Demostración. De acuerdo a las condiciones que se establecen en las hipótesis, pueden darse varias posibilidades. Para fijar ideas asumiremos que f 0 (x) < 0 y que
f 00 (x) ≥ 0 en [a, b], con lo cual se asegura que ii) y iii) se cumplan.
Notemos que en estas condiciones x∗ es la única raíz de f (x) = 0 en [a, b].
Además, al ser f 0 (x) < 0 y verificar i), se sigue que f (a) > 0 y f (b) < 0, tal y como
se muestra en la gráfica (2.5).
y
b
x
a
Figura 2.5: Interpretación geométrica del teorema de Fourier.
Visto esto, y asumiendo que x0 ∈ [a, x∗ ] demostraremos que:
{xn }∞
n=0 es una sucesión creciente.
∗
El límite de {xn }∞
n=0 es la raíz x
Veamos la primera parte. Si x0 ∈ [a, x∗ ] entonces xn < xn+1 < x∗ . La demostración será por inducción.
Para n = 0 verificaremos que x0 < x1 < x∗ .
Por (2.2) sabemos que
f (x0 )
x1 = x0 − 0
.
f (x0 )
2.3. ESTUDIO DE CONVERGENCIA
15
Pero f 0 (x0 ) < 0 y f (x0 ) > 0, luego
x1 − x0 = −
f (x0 )
> 0,
f 0 (x0 )
por tanto x0 < x1 .
Ahora demostraremos que x1 < x∗ , para esto comprobaremos que x∗ − x1 > 0.
Aplicando el teorema del valor medio, se sigue
x∗ − x1 = Nf (x∗ ) − Nf (x0 ) = Nf0 (γ)(x∗ − x0 ),
donde
Nf0 (γ) =
f (γ)f 00 (γ)
> 0,
f 0 (γ)2
Luego
para γ ∈ (x0 , x∗ ).
x∗ − x1 > 0.
Asumiendo que xk < xk+1 < x∗ demostraremos que xk+1 < xk+2 < x∗ . Lo
haremos aplicando un procedimiento análogo al anterior. Primero demostraremos
que xk+1 < xk+2 .
Nuevamente, por (2.2) se obtiene
xk+2 = xk+1 −
f (xk+1 )
.
f 0 (xk+1 )
Pero acá también se cumple que f 0 (xk+1 ) < 0 y f (xk+1 ) > 0, por tanto
xk+2 − xk+1 = −
f (xk+1 )
> 0,
f 0 (xk+1 )
luego
xk+1 < xk+2 .
Para demostrar que xk+2 < x∗ comprobaremos que x∗ − xk+2 > 0. Aplicando de
nuevo el teorema del valor medio, se sigue
x∗ − xk+2 = Nf (x∗ ) − Nf (xk+1 ) = Nf0 (θ)(x∗ − xk+1 ),
donde
Nf0 (θ) = Lf (θ) =
f (θ)f 00 (θ)
> 0,
f 0 (θ)2
para θ ∈ (xk+1 , x∗ ).
Por lo tanto x∗ − xk+2 > 0, xk+2 < x∗ . Así queda demostrado que {xn }∞
n=0 es
una sucesión creciente acotada superiormente por x∗ y, en consecuencia, {xn } es una
sucesión convergente.
∗
Veamos ahora que el límite de la sucesión {xn }∞
n=0 es la raíz x .
Aplicando límites a (2.2) se sigue
lı́m xn+1 = lı́m
n→∞
n→∞
xn −
f (xn ) .
f 0 (xn )
Pero
lı́m xn+1 = lı́m xn = L.
n→∞
n→∞
Además, como f y f 0 son funciones continuas en [a, b],
L=L−
f (L)
f (L)
=⇒ 0
= 0.
f 0 (L)
f (L)
Como f 0 (L) < 0 se sigue que f (L) = 0 y, por tanto, L = x∗ .
Quedan por comprobar los casos siguientes
16
CAPÍTULO 2. EL MÉTODO DE NEWTON-RAPHSON
1) f 0 (x) < 0,
f 00 (x) ≤ 0,
x ∈ [a, b].
2) f 0 (x) > 0,
f 00 (x) ≥ 0,
x ∈ [a, b].
3) f 0 (x) > 0,
f 00 (x) ≤ 0,
x ∈ [a, b].
Sin embargo, el caso 3) se reduce al caso estudiado cambiando a f por −f . A su
vez, el caso 1) se reduce al 2) de la misma forma. En ese sentido hagamos el siguiente
análisis.
Haciendo un cambio de variable z = −x y llamando q a la función resultante se
sigue
f (x) = f (−z) = q(z),
esta función está definida en [−b, −a] y se comprueba que
f 0 (x) =
dq(z) dz
= −q 0 (z).
dz dx
Análogamente se comprueba que f 00 (x) = q 00 (z). Esto significa que la raíz x∗ de
(1.1) en [a, b] se habrá transformado en la raíz −x∗ de q(z) = 0 en [−b, −a].
Entonces, el caso 2) se reduce también al que hemos estudiado, porque si f 0 (x) >
0 y f 00 (x) ≥ 0 en [a, b], q 0 (z) < 0 y q 00 (z) ≥ 0 en [−b, −a], luego el teorema será
válido para q. Deshaciendo el cambio, también será cierto para el caso 2) y para el
caso 1).
De acuerdo a [40], las condiciones de Fourier son insuficientes para asegurar la
convergencia del método de Newton-Raphson, pues tomando en cuenta la interpretación geométrica del método de Newton-Raphson, nos damos cuenta que su convergencia está asegurada siempre y cuando la segunda derivada de la función f 00 (x)
no cambie de signo en el intervalo [a, b] en que aparece la solución x∗ . Es decir,
cuando la función tenga un punto de inflexión en su dominio. En ese sentido, [40]
realiza un estudio del método de Newton-Raphson en función del grado de convexidad logarítmico (2.8). Para mayores detalles de este estudio refierase nuevamente a
[40].
2.3.3.
Convergencia Semilocal.
Históricamente hablando, en 1829, Cauchy presentó el primer resultado de convergencia semilocal
para el método de Newton-Raphson. Los detalles
de dicho teorema se encuentran en [12], mientras
que en [94] aparece un resumen parecido al que
presentamos a continuación.
Teorema 5 (Cauchy). Sea X = R,
0)
C2 , σ0 = − ff0(x
(x0 ) , η = |σ0 | y
I = hx0 , x0 +2σ0 i ≡
F = f ∈
[x0 , x0 + 2σ0 ],
si σ0 ≥ 0,
[x0 + 2σ0 , x0 ],
si σ0 < 0.
Asumamos que x0 ∈ X y además que
i) f 0 (x0 ) 6= 0.
iv) |f 00 (x0 )| ≤ K ∈ I.
v) 2Kη < |f 0 (x0 )|,
entonces F (x) tiene a x∗ como solución única en I.
Figura 2.6: Augustin Louis
Cauchy (1789 − 1857)
2.3. ESTUDIO DE CONVERGENCIA
17
Este resultado, inicialmente establecido para
funciones reales de variable real, fue generalizado
años más tarde por Kantorovich en su célebre teorema enunciado para operadores definidos en espacios de Banach.
Leyendo a [36], encontramos que fue a finales
del 1940 cuando L. V. Kantorovich y L. B. Rall introdujeron el método de Newton-Raphson en estos
tipos de espacios. Su planteamiento establece que
si F es un operador suficientemente diferenciable
definido entre dos espacios de Banach X e Y , a
partir de un punto x0 ∈ X se construye la sucesión
Figura 2.7: Leonid V. Kande Newton-Raphson
0
−1
xn+1 = xn − F (xn ) F (xn ), torovich (1912 − 1986)
(2.13)
donde F 0 (xn )−1 es el inverso del operador lineal F 0 (xn ).
A partir de ciertas condiciones, Kantorovich demostró que la sucesión {xn },
generada a partir de (2.13) está bien definida y es convergente a una solución de
F (x) = 0. Para una vision mas profunda del teorema de Kantorovich se puede
consultar a [44], [60] y [62].
A finales de los años 80, surgió una
nueva teoría sobre la convergencia semilocal de procesos iterativos. Esta teoría,
conocida como α- teoría fue introducida
por H. M. Kim y S. Smale [18]. Kim la
introdujo en su tesis doctoral titulada
Computational Complexity of the Euler
Type Algorithms for the Roots of Polynomials, publicada en febrero del 1986
y en un artículo publicado en 1988 bajo
el título On approximate zeroes and root
finding algorithms. En ambos trabajos
Figura 2.8: Stephen Smale (1930)
Kim aplicó la α-teoría a ecuaciones polinómicas de una variable. Por su parte,
Smale en un libro titulado New Directions in Pure, Applied and Computational Mathematics, publicado en 1986, introdujo la α-teoría para sistemas de ecuaciones, los
cuales tienen solución en base a tres invariantes de la forma
||DF (x)−1 F (x)||.
1
Dk F (x) (k−1)
,
γ(F, x) = sup ||DF (x)−1
||
k!
α(F, x) = β(F, x)γ(F, x).
β(F, x) =
k ≥ 2,
donde F es un un operador definido entre dos espacios de Banach.
En este trabajo demostraremos el teorema de Kantorovich y de la α teoría de
Smale como una versión en R que podrá ser extendida al caso general.
Teorema 6 (Teorema de Kantorovich en R). Sea f : I → R, en donde I es un
intervalo abierto en R, una función diferenciable en I. Asumamos, sin pérdida de
generalidad, que f (x0 ) 6= 0 y que
i) x0 ∈ I.
ii) f 0 (x0 ) 6= 0.
iii)
f (x0 )
f 0 (x0 )
iv)
f 0 (x)−f 0 (y)
f 0 (x0 )
≤ β.
≤ γ|x − y|,
∀x, y ∈ I.
18
CAPÍTULO 2. EL MÉTODO DE NEWTON-RAPHSON
v) h = γβ ≤ 1/2.
vi) t∗ =
√2β
1+ 1−2h
es tal que (x0 − t∗ , x0 + t∗ ) ⊂ I.
Entonces el método de Newton-Raphson
xn+1 = xn −
f (xn )
,
f 0 (xn )
n ≥ 0,
∗
∗
está bien definido y {xn }∞
n=0 converge a x ∈ I, donde f (x ) = 0.
Demostración. Para encontrar una sucesión que mayorice a {xn }∞
n=0 vamos a considerar el polinomio
p(t) =
1 2
γt − t + β,
2
cuyas raíces son
∗
t ,t
∗∗
=
1±
√
(2.14)
1 − 2γβ
,
γ
tal y como se muestra en la gráfica (2.9)
p HtL
t*
t*
*
Figura 2.9: Gráfica del polinomio mayorizante p(t) = 21 γt2 − t + β
Notemos que (2.14) tendrá solución en R cuando 1 − 2γβ ≥ 0, de donde γβ ≤ 12 .
Esto explica la condición v)
Aplicando el método de Newton-Raphson a (2.14) se sigue
"
#
−β+tn − 12 γt2n
p(tn )
t
.
n+1 = tn − p0 (tn ) = tn −
1−γtn
(2.15)
t0 = 0.
Notemos que el polinomio p(t) cumple las condiciones de Fourier. Así, tomando
a t0 = 0 se genera una sucesión monótona creciente cuyo límite es t∗ . Ahora, por
inducción probaremos que
|xn+1 − xn | ≤ tn+1 − tn ,
∀ n ≥ 0.
Sustituyendo a n = 0 en (2.15) se sigue
t1 − t0 = −
p(t0 )
p(0)
=− 0
= β,
p0 (t0 )
p (0)
Sustituyendo n = 0 en (2.2) y aplicando iii)
|x1 − x0 | ≤ β = t1 − t0 .
En consecuencia x1 ∈ I ya que |x1 − x0 | < t1 < t∗ .
t1 = β.
2.3. ESTUDIO DE CONVERGENCIA
19
Supongamos que x0 , x1 , . . . , xm ∈ I y además que |xi+1 − xi | ≤ ti+1 − ti para
i = 0, 1, . . . , m − 1, demostraremos que |xm+1 − xm | ≤ tm+1 − tm .
En efecto, como
|xm − x0 | ≤ |xm − xm−1 | + |xm−1 − xm−2 | + · · · + |x1 − x0 |.
≤ (tm − tm−1 ) + (tm−1 − tm−2 ) + · · · + (t1 − t0 ).
= tm − t0 = tm < t∗ ,
se tiene que xm ∈ I.
Por otra parte, notemos que
1 − γ|xm − x0 | ≥ 1 − γtm ⇒
Además
|xm+1 − xm | =
1
1
≤
.
1 − γ|xm − x0 |
1 − γtm
f (xm )
f (xm ) f 0 (x0 )
= 0
.
0
f (xm )
f (x0 ) f 0 (xm )
(2.16)
Aplicando la condición iv) se sigue
f 0 (xm ) − f 0 (x0 )
f 0 (xm )
≤ γ|xm −x0 | ⇒ 1− 0
≤ γ|xm −x0 | ≤ γ(tn −t0 ) < γt∗ < 1.
0
f (x0 )
f (x0 )
Luego
−γ|xm − x0 | ≤ 1 −
Entonces
−γ|xm − x0 | − 1 ≤ −
Luego
−1 < 1 −
Así
f 0 (xm )
≤ γ|xm − x0 |.
f 0 (x0 )
f 0 (xm )
≤ γ|xm − x0 | − 1.
f 0 (x0 )
f 0 (xm )
f 0 (xm )
⇒
−
< 0.
f 0 (x0 )
f 0 (x0 )
f 0 (xm )
f 0 (xm )
≥ 1 − γ|xm − x0 |.
= 0
0
f (x0 )
f (x0 )
De donde
f 0 (x0 )
1
≤
.
0
f (xm )
1 − γ|xm − x0 |
(2.17)
Ahora bien, de (2.2) se deduce
f (xm ) = f (xm ) − f (xm−1 ) − f 0 (xm−1 )(xm − xm−1 ).
Luego
f (xm )
f (xm ) − f (xm−1 ) − f 0 (xm−1 )(xm − xm−1 )
=
=
f 0 (x0 )
f 0 (x0 )
Z
xm
h f 0 (t) − f 0 (x
xm−1
m−1 )
f 0 (x0 )
Haciendo el cambio de variable t = xm−1 + s(xm − xm−1 ) se sigue
f (xm )
≤
f 0 (x0 )
Z
1
0
f 0 (xm−1 + s(xm − xm−1 )) − f 0 (xm−1 )
|(xm − xm−1 )|ds.
f 0 (x0 )
(2.18)
Aplicando la condición iv) a (2.18) se sigue
f (xm )
≤
f 0 (x0 )
Z
0
1
Z
γs|xm − xm−1 |2 ds = γ|xm − xm−1 |2
1
sds ≤
0
1
γ|xm − xm−1 |2 .
2
(2.19)
i
dt .
20
CAPÍTULO 2. EL MÉTODO DE NEWTON-RAPHSON
Sustituyendo (2.17) y (2.19) en (2.16) se sigue
1
2 γ(tm
|xm+1 − xm | ≤
− tm−1 )2
.
1 − γtm
(2.20)
p(tm )
.
p0 (tm )
(2.21)
Por otra parte
tm+1 − tm = −
De (2.14) se obtiene
p0 (t) = γt − 1.
p00 (t) = γ.
p(i) (t) = 0, i ≥ 3.
(2.22)
(2.23)
Aplicando el desarrollo de Taylor a (2.14) se sigue
1
p(tm ) = p(tm−1 ) + p0 (tm−1 )(tm − tm−1 ) + p00 (tm−1 )(tm − tm−1 )2 + 0.
2
Pero
tm − tm−1 = −
p(tm−1 )
.
p0 (tm−1 )
(2.24)
(2.25)
Luego, sustituyendo (2.23) y (2.25) en (2.24) se sigue
p(tm ) =
1
γ(tm − tm−1 )2 .
2
(2.26)
Sustituyendo (2.26) y (2.22) en (2.21)
tm+1 − tm =
1
2 γ(tm
− tm−1 )2
.
1 − γtm
(2.27)
Finalmente, sustituyendo (2.27) en (2.20)
|xm+1 − xm | ≤ tm+1 − tm .
El proceso inductivo queda probado. Como {tn }∞
n=0 es convergente, se sigue que
también
es
convergente.
{xn }∞
n=0
De (2.19) se deduce que cuando m → ∞, entonces f (xm ) → 0. Por tanto {xm }
converge a x∗ , la solución de f (x∗ ) = 0.
Teorema 7 (α-teoría de Smale en R.). Sea f : D ⊆ R → R una función continua
y diferenciable en un intervalo D en el que se cumplen las siguientes condiciones:
i)
ii)
f (x0 )
f 0 (x0 )
≤ β. f 0 (x0 ) 6= 0.
(k)
(x0 )
1 f
k! f 0 (x0 )
≤ γ k−1 ,
para k ≥ 2.
√
iii) α = βγ ≤ 3 − 2 2.
Entonces el método de Newton-Raphson definido por (2.2) converge a x∗ solución
de f (x) = 0.
Demostración. Dado {xn }, se demostrará que |xn+1 − xn | ≤ tn+1 − tn , donde {tn }
es una sucesión real obtenida al aplicar el método de Newton-Raphson a la función
mayorante φ(t).
Consideremos la función
φ(t) = β − t +
X
k≥2
γ k−1 tk = β − t +
γt2
,
1 − γt
para 0 ≤ t <
1
,
γ
(2.28)
2.3. ESTUDIO DE CONVERGENCIA
21
cuya gráfica es
Φ HtL
t*
t*
*
Figura 2.10: Gráfica de la función mayorizante φ(t) = β − t +
γt2
1−γt
Notemos que para φ(t) = 0 se debe cumplir
φ(t) = 2γt2 − t(α + 1) + β = 0,
de donde
∗
t ,t
∗∗
=
(α + 1) ±
p
(α + 1)2 − 8α
.
4γ
(2.29)
Luego, para que (2.29) tenga raíz en R se debe cumplir
(α + 1)2 − 8α ≥ 0,
√
de donde α2 − 6α + 1 ≥ 0, por tanto α ≤ 3 − 2 2.
Como vemos, este resultado se deduce directamente de la condición iii).
Ahora, sea {tn } la sucesión obtenida al aplicar el método de Newton-Raphson a
(2.28), es decir:
t
n+1
= tn −
φ(tn )
β(1 − γtn )2 − tn (1 − γtn )2 + γt2n (1 − γtn )
=
.
0
φ (tn )
−1 + 2γtn (2 − γtn )
(2.30)
t0 = 0.
Observemos que para n = 0, de (2.30) se obtiene
t1 − t0
φ(t0 )
φ0 (t0 )
φ(t0 )
φ0 (t0 )
φ(0)
− 0
φ (0)
= β,
≤ β,
= β,
= β.
Asimismo, si sustituimos n = 0 en (2.2) y aplicamos i) se sigue
|x1 − x0 | ≤
f (x0 )
f 0 (x0 )
≤
f (x0 )
≤ β = t1 − t0 .
f 0 (x0 )
φ(t0 )
.
β=− 0
φ (t0 )
Por otra parte, notemos que
X
kγ k−1 tk−1 ⇒ φ0 (t0 ) = φ0 (0) = −1.
φ0 (t) = −1 +
k≥2
(2.31)
(2.32)
(2.33)
22
CAPÍTULO 2. EL MÉTODO DE NEWTON-RAPHSON
Además
φ00 (t)
=
X
k(k − 1)γ k−1 tk−2 .
k≥2
000
φ (t)
=
X
k(k − 1)(k − 2)γ k−1 tk−3 .
k≥3
φ(j) (t)
..
.
X
=
k(k − 1) . . . (k − j + 1)γ k−1 tk−j .
k≥j
Entonces
φ(j) (t0 ) = φ(j) (0) = k!γ k−1 .
(2.34)
Luego, de (2.34) y (2.33) se obtiene
γ k−1 =
φ(j) (t0 )
1 φ(j) (t0 )
=−
.
k!
k! φ0 (t0 )
(2.35)
Aplicando ii) en (2.35) se sigue
1 f (k) (x0 )
1 φ(k) (t0 )
k−1
.
≤
γ
=
−
k! f 0 (x0 )
k! φ0 (t0 )
(2.36)
Probaremos que las desigualdades (2.31), (2.32) y (2.36) se cumplen siempre. En
otras palabras, demostraremos que si (2.31), (2.32) y (2.36), se cumplen, entonces
f (xj )
f 0 (xj )
≤ −
1 f (k) (xj )
k! f 0 (xj )
|xj+2 − xj+1 |
φ(tj )
,
φ0 (tj )
para j = 0, 1, 2, . . . .
1 φ(k) (tj )
,
k! φ0 (tj )
tj+2 − tj+1 .
≤ −
≤
(2.37)
para k ≥ 2 y j = 0, 1, 2, . . . .
La demostración será por inducción.
Para j = 0; (2.31), (2.32) y (2.36) son ciertas por hipótesis. Comprobaremos que
si son ciertas para j, también lo serán para j + 1.
Aplicando el desarrollo de Taylor a f (xj+1 ) se sigue
f (xj+1 ) = f (xj ) + f 0 (xj )(xj+1 − xj ) +
X 1
f (k) (xj )(xj+1 − xj )k .
k!
(2.38)
k≥2
Pero
(xj+1 − xj ) = −
f (xj )
.
f 0 (xj )
(2.39)
Sustituyendo (2.39) en (2.38) se sigue
f (xj+1 ) = f (xj ) − f 0 (xj )
f (xj ) X 1 (k)
+
f (xj )(xj+1 − xj )k .
f 0 (xj )
k!
k≥2
Así
f (xj+1 ) =
X 1
f (k) (xj )(xj+1 − xj )k .
k!
k≥2
Luego
X 1 f (k) (xj ) f (xj )
f (xj+1 )
≤
f 0 (xj )
k! f 0 (xj ) f 0 (xj )
k≥2
k
≤
Xh
k≥2
−
1 φ(k) (tj ) ih φ(tj ) ik
− 0
. (2.40)
k! φ0 (tj )
φ (tj )
2.3. ESTUDIO DE CONVERGENCIA
23
Si ahora aplicamos el desarrollo de Taylor a φ(tj+1 ) se sigue
φ(tj+1 ) = φ(tj ) + φ0 (tj )(tj+1 − tj ) +
X 1
φ(k) (tj )(tj+1 − tj )k .
k!
(2.41)
k≥2
Pero
(tj+1 − tj ) = −
φ(tj )
.
φ0 (tj )
(2.42)
Sustituyendo (2.42) en (2.41) sigue
φ(tj+1 ) = φ(tj ) − φ0 (tj )
φ(tj ) X 1 (k)
+
φ (tj )(tj+1 − tj )k .
φ0 (tj )
k!
k≥2
Así
φ(tj+1 ) =
X 1
φ(k) (tj )(tj+1 − tj )k .
k!
k≥2
Luego
−
Xh
1 φ(k) (tj ) ih φ(tj ) ik
φ(tj+1 ) X 1 φ(k) (tj )
k
=
−
(t
−
t
)
=
−
− 0
.
j+1
j
φ0 (tj )
k! φ0 (tj )
k! φ0 (tj )
φ (tj )
k≥2
k≥2
Entonces, (2.40) se transforma en
f (xj+1 )
φ(tj+1 )
.
≤− 0
f 0 (xj )
φ (tj )
(2.43)
Por otra parte, aplicando el desarrollo de Taylor a la derivada de (2.38) se sigue
f 0 (xj+1 ) =
X 1
f (k+1) (xj )(xj+1 − xj )k .
k!
k≥0
Luego
1−
X 1 f (k+1) (xj )
X
f 0 (xj+1 )
φ(k+1) (tj ) h φ(tj ) ik
k
≤
|x
−
x
|
≤
−(k
+
1)
.
j+1
j
f 0 (xj )
k
f 0 (xj )
φ0 (tj )
φ0 (tj )
k≥1
k≥1
(2.44)
Por otro lado
φ0 (tj+1 ) = φ0 (tj ) +
X
k≥1
h φ(t ) ik
j
(k + 1)φ(k+1) (tj ) 0
.
φ (tj )
De donde
φ0 (tj ) − φ0 (tj+1 ) =
X
−(k + 1)φ(k+1) (tj )
k≥1
0
0
φ (tj ) − φ (tj+1 )
φ0 (tj )
=
φ0 (tj+1 )
1− 0
φ (tj )
=
X
−(k + 1)
φ(k+1) (tj ) h φ(tj ) ik
.
φ0 (tj )
φ0 (tj )
−(k + 1)
φ(k+1) (tj ) h φ(tj ) ik
.
φ0 (tj )
φ0 (tj )
k≥1
X
k≥1
Sustituyendo (2.45) en (2.44) se sigue
1−
f 0 (xj+1 )
φ0 (tj+1 )
< 1,
≤
1
−
f 0 (xj )
φ0 (tj )
pues φ es de signo constante en (0, t∗ ).
h φ(t ) ik
j
.
φ0 (tj )
(2.45)
24
CAPÍTULO 2. EL MÉTODO DE NEWTON-RAPHSON
Así
f 0 (xj )
1
φ0 (tj )
h
i
≤
=
.
φ0 (t
)
f 0 (xj+1 )
φ0 (tj+1 )
1 − 1 − φ0 (tj+1
j)
(2.46)
Aplicando el desarrollo de Taylor a f (k) (xj+1 ) se sigue
f (k) (xj+1 ) =
X1
f (k+1) (xj )(xj+1 − xj )i .
i!
i≥0
Luego
1 f (k) (xj+1 )
k! f 0 (xj )
≤
X (k + 1)!
k! i!
X k + i −1 φ(k+1) (tj ) (tj+1 − tj )i =
i
(k + 1)! φ0 (tj )
i≥0
≤
1
f (k+1) (xj )
|xj+1 − xj |i ≤
(k + 1)! f 0 (xj )
i≥0
=
−
1 φ(k) (tj+1 )
1 X 1 φ(k+1) (tj )
(tj+1 − tj )i = −
.
0
k!
i! φ (tj )
k! φ0 (tj )
i≥0
Además
1 φ(k) (tj+1 )
1 X 1 φ(k+1) (tj )
=
(tj+1 − tj )i .
k! φ0 (tj )
k!
i! φ0 (tj )
1≥0
Así que
Entonces
1 φ(k) (tj+1 )
1 f (k) (xj+1 )
≤−
.
0
k! f (xj )
k! φ0 (tj )
(2.47)
f (xj+1 )
f 0 (xj ) f (xj+1 )
≤
.
f 0 (xj+1 )
f 0 (xj+1 ) f 0 (xj )
(2.48)
Sustituyendo (2.46) y (2.43) en (2.48) se sigue
f (xj+1 )
φ(tj+1 )
φ0 (tj ) φ(tj+1 )
=− 0
.
≤
−
0
0
0
f (xj+1 )
φ (tj+1 ) φ (tj )
φ (tj+1 )
Asimismo
1 f (k) (xj+1 )
1 f (k) (xj+1 ) f 0 (xj )
≤
.
k! f 0 (xj+1 )
k! f 0 (xj )
f 0 (xj+1 )
(2.49)
Sustituyendo (2.46) y (2.47) en (2.49) sigue
1 f (k) (xj+1 )
1 φ(k) (tj+1 ) φ0 (tj )
1 φ(k) (tj+1 )
≤−
=−
.
0
0
0
k! f (xj+1 )
k! φ (tj ) φ (tj+1 )
k! φ0 (tj+1 )
Por último
|xj+2 − xj+1 | ≤
f (xj+1 )
φ(tj+1 )
= tj+2 − tj+1 .
≤− 0
f 0 (xj+1 )
φ (tj+1 )
Luego, hemos probado que
|xk+1 − xk | ≤ tk+1 − tk .
Además {tk } es convergente a t∗ , por tanto {tk } es de Cauchy, lo cual implica
que {xk } también es de Cauchy y que {xk } converge a x∗ .
Por otra parte, notar que de (2.37) se deduce que
lı́m
j→∞
f (xj )
φ(t∗ )
φ(xj )
= − 0 ∗ = 0.
≤ lı́m − 0
0
j→∞
f (xj )
φ (xj )
φ (t )
Entonces f (x∗ ) = 0, luego x∗ es la solución de f (x).
2.4. ORDEN DE CONVERGENCIA Y EFICIENCIA
25
2.4.
Orden de convergencia y eficiencia del método
de Newton-Raphson
2.4.1.
Orden de convergencia
Como establecimos en la sección 1.1, el orden de convergencia de un método
iterativo nos indica la «velocidad» con la cual una sucesión converge a su límite. La
característica principal de esta «velocidad» se verifica en la proporción con que se
multiplican los dígitos significativos de la solución aproximada. Así, cuando el método iterativo posee convergencia lineal, los dígitos significativos se reproducen a la
misma escala, mientras que si la convergencia es cuadrática, los dígitos significativos
en cada iteración se van incrementando en potencia de dos y así sucesivamente.
El teorema que presentamos a continuación demuestra que para raíces simples el
método de Newton-Raphson posee un orden de convergencia cuadrático o de orden
dos.
Teorema 8. Sea x∗ una raíz simple de (1.1), es decir f (x∗ ) = 0 y f 0 (x∗ ) 6= 0.
Entonces el método de Newton-Raphson definido por (2.13) es de segundo orden o
de convergencia cuadrática.
Demostración. Para demostrar lo anteriormente indicado se comprobará que Nf0 (x∗ ) =
Lf (x∗ ) = 0 y Nf00 (x∗ ) = L0f (x∗ ) 6= 0.
En efecto
Nf0 (x∗ ) = Lf (x∗ ) =
f (x∗ )f 00 (x∗ )
= 0,
f 0 (x∗ )
pues f (x∗ ) = 0 y f 0 (x∗ ) 6= 0.
Además
Nf00 (x∗ ) = L0f (x∗ ) =
f 0 (x∗ )f 00 (x∗)
f 00 (x∗ )
=
6= 0,
f 0 (x∗ )2
f 0 (x∗ )
pues f 0 (x∗ ) 6= 0 y f 00 (x∗ ) 6= 0.
Luego, por el teorema de Schröder, el orden de convergencia de (2.13) es cuadrático.
Además, la constante del error asintótico es
C=
1 |f 00 (x∗ )|
.
2 |f 0 (x∗ )|
Como se ha demostrado, el orden de convergencia del método de Newton-Raphson
es, por lo menos, cuadrático, siempre y cuando las raíces de la función f (x) sean
simples. Es conocido que, para raíces múltiples, se pierde la convergencia cuadrática,
pasando a convergencia lineal.
2.4.2.
Índice de eficiencia
Es importante indicar que, al contrario del continente europeo, en el continente
americano, y en gran parte de las islas que conforman la cuenca del Caribe, se utiliza
la coma gramatical para separar las cantidades que representan miles de unidades.
Asimismo, se emplea el punto gramatical para separar las partes que representan
fracciones de unidades. En adelante usaremos la coma y el punto desde una visión
americana.
Tomando en cuenta a (1.3), sabemos que
IEC(p, d) = p1/d .
Considerando que p = 2, d = 2, luego
√
1
IEC(p, d) = 2 2 = 2 ≈ 1.414213562373095,
es el índice de eficiencia del método de Newton-Raphson.
26
CAPÍTULO 2. EL MÉTODO DE NEWTON-RAPHSON
2.4.3.
Orden de convergencia computacional
Recordemos que en la matemática computacional un método iterativo trata de
resolver una ecuación del tipo (1.1) mediante aproximaciones sucesivas a la solución.
Tomando esto en cuenta, Weerakoon y Fernando [90], Grau [38] y Grau y Gutiérrez
[39] han introducido formas diferentes de aproximar el orden de convergencia de un
método iterativo. En concreto, cada uno de ellos define lo que se llama el orden de
convergencia computacional OCC de un método iterativo. Nos encontramos, por
tanto, con tres definiciones del OCC, que denotaremos OCCW , OCCG y OCCGG .
De acuerdo a [90], el OCCW viene expresado por la fórmula
OCCW =
ln |(xn+1 − x∗ )/(xn − x∗ )|
,
ln |(xn − x∗ )/(xn−1 − x∗ )|
(2.50)
en donde x∗ es una raíz de la función f (x) y xn+1 , xn y xn−1 son tres iteraciones
consecutivas próximas a la raíz x∗ .
Por su parte [38] define el OCCG a partir de la expresión
OCCG =
ln |(xn+1 − xn )/(xn − xn−1 )|
,
ln |(xn − xn−1 )/(xn−1 − xn−2 )|
(2.51)
en donde xn+1 , xn , xn−1 y xn−2 son cuatro iteraciones consecutivas próximas a la
raíz x∗ .
Mientras que [39] definen el OCC a partir de la expresión
OCCGG =
ln |(xn − α
e/(xn−1 − α
e)|
,
ln |(xn−1 − α
e)/(xn−2 − α
e)|
(2.52)
en donde xn+1 , xn , xn−1 y xn−2 son cuatro iteraciones consecutivas próximas a la
raíz x∗ y
(xn+1 − xn )2
α
e = xn+1 −
xn+1 − 2xn + xn−1
Notemos que en (2.50) es necesario conocer la solución de la ecuación, mientras
que en (2.51) y (2.52) no es necesario conocer dicha solución, esto implica que la
aplicación de la ecuación (2.50) podría tener inconvenientes cuando una iteración
xn está muy próxima a la solución x∗ . En ese caso, aparecerían dos iteraciones
sucesivas con el mismo valor. Es importante señalar que la suceción de iteraciones
que se apliquen tanto en (2.50) como en (2.51) y (2.52) deben estar lo mas próximas
posibles a x∗ .
A continuación se va a calcular el OCCG , OCCW y el OCCGG para un conjunto
de funciones test. Las funciones que se presentan en la siguiente tabla fueron tomadas
de [63], [83] y [90]. En la siguiente tabla se comprueba que el OCCG , OCCW y el
OCCGG promedio del método de Newton-Raphson es 2.02298, 1.99904 y 1.96442
respectivamente, lo cual significa que, computacionalmente hablando, el orden del
método de Newton-Raphson también es cuadrático. Los valores que se presentan se
obtuvieron mediante el siguiendo procedimiento:
1. La solución aproximada de cada ecuación se encontró utilizando el código para
implementar el método de Newton-Raphson con el paquete Mathematica.
2. Los valores iniciales se tomaron de forma optimizada, es decir, lo más próximo
a la solución.
3. Para aplicar a (2.50) se tomo la solución apróximada generada por cada ecuación y se tomaron las tres soluciones sucesivas más próximas a dicha solución
apróximada.
4. Para aplicar a (2.51) y (2.52) se tomaron las cuatro soluciones sucesivas más
próximas a la supuesta solución generadas por cada ecuación.
2.5. EJEMPLOS NUMÉRICOS
Función f (x)
x3 + 4x2 − 10
sen2 (x) − x2 + 1
x2 − ex − 3x + 2
cos(x) − x
(x − 1)3 − 1
x3 − 10
x2
xe − sen2 (x) + cos(x) + 5
x3 + log(x)
1
x − sen(x) + 1
2
2
2
x sen (x) + ex cos(x) sen(x) − 28
Promedio
27
x0
1.0
1.0
1.0
1.0
1.8
1.5
-1.0
0.5
-1.0
4.4
OCCG
2.00564
2.00155
1.99794
1.93728
2.0099
2.00299
2.0438
2.00087
2.36985
1.85999
2.02298
OCCW
1.99957
1.99966
1.99825
1.99803
1.99939
1.99916
1.99968
2.00067
2.00013
1.9959
1.99904
OCCGG
1.9804
1.98758
1.94079
1.91155
1.97686
1.9937
1.98951
2.00067
2.00326
1.85991
1.96442
Raíz (x∗ )
1.365230
1.404491
0.257530
0.739085
2.000000
2.154434
-1.166495
0.704709
-0.629446
4.622104
Cuadro 2.1: OCC promedio del método de Newton.
2.5.
Ejemplos numéricos
En esta sección aplicaremos el método de Newton-Raphson a partir de dos momentos. En un primer momento se presentan una serie de problemas en los cuales
el método de Newton-Raphson funciona perfectamente. En el segundo momento se
presentan los ejemplos patológicos, es decir, aquellas situaciones en los cuales el
método de Newton-Raphson no arroja los resultados esperados.
2.5.1.
Ecuaciones no lineales resueltos por el método de Newton.
Los ejemplos presentados a continuación han sido diseñados y codificados en el
lenguaje del paquete Mathematica. Para un estudio más profundo de este acápite,
véase [8], [28], [47],[55], [57], [66], [69], [91], [113], [114], [116] y [120].
Ejemplo 2. Al principio de cada año un banco deposita v euros en un fondo de
inversión y retira un capital de M euros al final del n− ésimo año. Mediante el
método de Newton-Raphson se pretende calcular el tipo medio de interés anual r de
esta inversión, sabiendo que M está relacionada con r por la siguiente ecuación.
M =v
n
X
(1 + r)k = v
k=1
1+r
[(1 + r)n − 1].
r
Solución 2. Observando la ecuación anterior, se deduce que r es la solución de la
ecuación
f (r) = M − v
1+r
[(1 + r)n − 1],
r
f (r) = 0.
Para la construcción de la gráfica, vamos a suponer que v es 10, 000 euros y que
después de 5 años M es igual a 60, 000 euros. Bajo estas condiciones se obtiene la
gráfica (2.11)
28
CAPÍTULO 2. EL MÉTODO DE NEWTON-RAPHSON
30 000
20 000
10 000
-0.2
0.1
-0.1
0.2
-10 000
-20 000
-30 000
n
Figura 2.11: Gráfica de la función f (r) = M − v 1+r
r [(1 + r) − 1]
1. Se observa que f (r) tiene solución única en el intervalo [0.0, 0.1]
2. Construcción de la función de iteración.
f (r)
=
60, 000 − 10, 000
rn+1
=
rn −
rn+1
=
r
0
1
2
3
4
5
1+r
[(1 + r)5 − 1].
r
f (rn )
.
f 0 (rn )
1 + 20rn2 + 30rn3 + 18rn4 + 4rn5
.
15 + 40rn + 45rn2 + 24rn3 + 5rn4
(2.53)
rn
0.1
0.06325399881896841
0.06140685508980816
0.06140241156217179
0.0614024115365252
0.0614024115365252
Cuadro 2.2: Valores obtenidos a partir de (2.53)
3. Resultado.
Después de 4 iteraciones el método converge a la raíz aproximada x4 = 0.0614024115365252.
Luego, el tipo de interés es aproximadamente igual a 6.14 %
Ejemplo 3. En cursos de física avanzada se sabe que la posición en función del
tiempo para un tiro parabólico viene dada por la forma
2
v0
x(t) = x0 + 2x (1 − e−w t ),
w
i
2
1 h
g y(t) = y0 + 2 v0y + 2 1 − e−w t − gt ,
w
w
k
donde w2 = m
, x(t): alcance con respecto al tiempo, y(t): altura con respecto al
tiempo, x0 : distancia inicial con respecto a la tierra, y0 : altura inicial con respecto
a tierra, v0x : velocidad inicial con respecto a la tierra, v0y : velocidad inicial con
respecto a la altura, t: tiempo, g: gravedad, k: constante de proporcionalidad, m:
masa.
Supongamos que un proyectil
√ de masa m = 4 Kg es lanzado desde la tierra con
π
una velocidad inicial k~v0 k = 2 m
s , formando con la horizontal un ángulo de θ = 4 .
m
Si la constante de proporcionalidad k = 2 Kg
s y tomamos la gravedad g = 9.8 s2 ,
aproximaremos el alcance del proyectil aplicando el método de Newton-Raphson.
2.5. EJEMPLOS NUMÉRICOS
29
Solución 3. Por los datos suministrados en el enunciado, sabemos que k~v0 k =
y θ = π4 , luego
√
√
2
√
2
= 1.
√2
√ 2
= k~v0 k sen(θ) = 2
= 1.
2
v 0x
= k~v0 k cos(θ) =
v0y
2
Notemos que w2 = 12 . Tomando el origen de referencia en el punto de lanzamiento, se tiene que (x0 , y0 ) = (0, 0), luego, la posición en función del tiempo del
proyectil es
x(t)
=
y(t)
=
1
2 1 − e− 2 t .
h
i
1
2 (1 − 2g) 1 − e− 2 t − gt .
(2.54)
(2.55)
El plan ahora es determinar la solución t∗ de y(t) = 0, luego x(t∗ ) sería el alcance
del proyectil. Así
tn+1
=
=
y(tn )
.
y 0 (tn )
[20.6(1 − e−0.5tn ) − 9.8tn ]
tn −
.
10.3e−0.5tn − 9.8
tn −
(2.56)
En adelante hay que tener cuidado en seleccionar a t0 , pues una mala elección
puede hacer que se obtenga una solución que no nos interese. Por ejemplo, si tomamos t0 = 0.03, la solución que se obtiene tiende a t∗ = 0, que al ser sustituida en
(2.54), nos daría una falso alcance.
La razón de la convergencia anterior es que la función y(t) corta al eje de las
abscisa en t = 0 y además tiene un máximo relativo en t = 0.099523, luego, al ser
y(t) una función creciente en el intervalo I = (0, 0.099523), si tomamos un t0 ∈ I,
la sucesión que se obtiene converge a t = 0.
-0.4
0.2
-0.2
0.4
-0.2
-0.4
-0.6
-0.8
i
h
1
Figura 2.12: Gráfica de la función y(t) = 2 (1 − 2g) 1 − e− 2 t − gt
Este problema se resuelve tomando un valor t0 > 0.099523. Si tomemos a t0 = 0.4
se genera la siguiente tabla
30
CAPÍTULO 2. EL MÉTODO DE NEWTON-RAPHSON
n
0
1
2
3
4
5
6
7
8
tn
0.4
0.26405006877449
0.21254143019785
0.20132631548484
0.20072639679455
0.20072466363483
0.20072466362036
0.20072466362036
0.20072466362036
Cuadro 2.3: Valores obtenidos a partir de (2.56).
Así, t6 ≈ 0.20072466362036 es una aproximación de la solución t∗ . Sustituyendo
este valor en (2.54), se obtiene que el alcance del proyectil sería x(t6 ) = 2(1 −
e−0.5t6 ) ≈ 0.190981 metros.
Ejemplo 4. Aplicando el procedimiento que desarrolló F. Vieta, a finales del siglo
XVI, calcularemos las dos primeras aproximaciones del polinomio x3 − 2x − 5 = 0.
Verificaremos que este procedimiento coincide con el método de Newton-Raphson.
Solución 4. De los datos del problema se obtiene que el polinomio a considerar es
P (x) = x3 − 2x − 5. Notemos que P (2) = −1 < 0 y P (3) = 16 > 0, luego, por el
teorema de Bolzano, existe una raíz x∗ del polinomio P (x) tal que x∗ ∈ (2, 3). Luego,
el valor entero x0 más próximo e inferior a la raíz es x0 = 2, el cual tomaremos
como una primera raíz, es decir x∗ ≈ x0 = 2.
Realizando el cambio de variable x = x0 + s = 2 + s, el polinomio P (x) se
transforma en
P (2 + s) = −1 + 10s + 6s2 + s3 .
(2.57)
Despreciando los términos de grado superior a uno de (2.55) sigue
P (2 + s) = −1 + 10s.
Cuya raíz es s = 1/10. Luego, la nueva aproximación de la raíz del polinomio
original es
x∗ ≈ x1 = x0 + s = 2 + 0.1 = 2.1.
Realizando el cambio de variable x = x1 + s el polinomio P (x) ahora es
P (2.1 + s) = 0.061 + 11.23s + 6.3s2 + s3 .
(2.58)
Nuevamente despreciando, de (2.58), los términos de grado superior a uno, obtenemos que
P (2.1 + s) = 0.061 + 11.23s,
cuya raíz es s = −0.00543188. Luego, la nueva aproximación de la raíz x∗ del polinomio P (x) es
x∗ ≈ x2 = x1 − 0.00543188 = 2.1 − 0.00543188 = 2.09457.
Aplicando el método de Newton-Raphson para aproximar la raíz de P (x) sigue
xn+1
=
=
P (xn )
,
P 0 (xn )
x3 − 2xn − 5
xn − n 2
.
3xn − 2
xn −
Tomando a x0 = 2, obtenemos la siguiente tabla
(2.59)
2.5. EJEMPLOS NUMÉRICOS
n
xn
0
2.000000
31
1
2.100000
2
2.094568
3
2.094551
4
2.094551
Cuadro 2.4: Valores obtenidos a partir de (2.59).
En la tabla se verifica que las dos primeras iteraciones coinciden con el método
aplicado por Vieta.
Ejemplo 5. Aplicaremos el método de Newton-Raphson para encontrar la solución
aproximada de la ecuación
f (x) = 6x3 − 39x2 + 45x = 0,
comenzando a partir de la solución inicial x0 = 4.
Solución 5.
1. Gráfica de la función.
100
50
-2
4
2
6
8
-50
-100
-150
Figura 2.13: Gráfica de la función f (x) = 6x3 − 39x2 + 45x
La gráfica muestra la existencia de tres raíces, aproximaremos la mayor de
ellas, tomando un x0 = 4.
2. Construcción de la función de iteración.
xn+1
n
xn
0
4.000000
1
6.857143
f (xn )
.
f 0 (xn )
45xn − 39x2n + 6x3n
= xn −
.
45 − 26xn + 6x2n
−13x2n + 4x3n
=
.
6x2n − 26xn + 15
= xn −
2
5.708987
3
5.160504
4
5.011191
(2.60)
5
5.000060
6
5.000000
Cuadro 2.5: Valores obtenidos a partir de (2.60).
3. Resultado.
La raíz aproximada es x6 = 5.
Ejemplo 6. Comprobaremos que la ecuación
f (x) = ex + x,
tiene una única raíz real y aproximaremos dicha raíz por el método de NewtonRaphson. Detendremos el proceso de iteración cuando se verifique que |xn − xn−1 | ≤
0.5 × 10−3 .
32
CAPÍTULO 2. EL MÉTODO DE NEWTON-RAPHSON
Solución 6.
1. Gráfica de la función.
20
15
10
5
-3
-1
-2
1
2
3
Figura 2.14: Gráfica de la función f (x) = ex + x
Se verifica que la función f (x) = ex + x, es continua y derivable en el intervalo
[−1, 0]. Como
f (−1) = −0.632121 < 0,
f (0) = 1 > 0.
Además se verifica que f 0 (x) = ex +1 > 0 en todo el intervalo, luego f (x) tiene
a lo sumo una solución en [−1, 0]. Tomemos x0 = −1
2. Construcción de la función de iteración.
n
xn
xn
=
xn
=
xn
=
0
-1.000000
f (xn−1 )
, n ≥ 1,
f 0 (xn−1 )
exn−1 + xn−1
xn−1 −
,
1 + exn−1
exn−1 (−1 + xn−1 )
.
1 + exn−1
xn−1 −
1
-0.537883
2
-0.566987
(2.61)
3
-0.567143
Cuadro 2.6: Valores obtenidos a partir de (2.61).
3. Resultado.
La raíz aproximada es x3 = −0.567143.
2.5.2.
Ejemplos patológicos
Entenderemos por ejemplos patológicos, como aquellos ejemplos en los cuales el
método de Newton-Raphson falla o converge a una solución no esperada. Son diversas
las razones que permiten el desarrollo de estos casos, pero las más importantes son:
Cuando la sucesión diverge lentamente a +∞.
Cuando la sucesión de puntos generada por la función oscila sin converger.
En caso de que se presente el fenómeno de la periodicidad, es decir, cuando
los resultados de la función generan una sucesión de puntos que tienden a
repetirse. Es lo que se conoce como la presencia de ciclos atractores.
2.5. EJEMPLOS NUMÉRICOS
33
En caso de que se presente el fenómeno de repulsión, es decir, cuando los valores
de la función de iteración se alejan de la posible solución.
Antes de iniciar con dichos ejemplos, recordemos las condiciones típicas para la
convergencia de (2.2), dichas condiciones fueron tomadas de ([8]).
0)
Sea f (x) una función, x0 un punto inicial e I0 = [x0 , 2µ0 ], donde µo = ff0(x
(x0 ) , un
intervalo en el cual la función es dos veces diferenciable, entonces las condiciones
sup |f 00 (x)| = M,
x∈I0
|f 0 (x0 )| ≥ 2|µ0 |M,
(2.62)
son suficientes para asegurar la existencia de una solución x∗ de f (x) en I0 , y para
la convergencia de (2.2) a esa solución.
De forma general, la condición (2.62) se cumple para
|f 00 (xn )| ≤ M,
|f 0 (xn )| ≥ 2|µn |M,
n = 1, 2, · · ·
Recordemos también que en la solución de una ecuación mediante métodos numéricos, comúnmente se aplica el siguiente criterio de parada
|xn+1 − xn | < ε,
ε > 0.
(2.63)
Donde xn es el n−ésimo termino de la sucesión generada y ε > 0 es la tolerancia.
Veamos algunos ejemplos que demuestran lo anteriormente señalado. Para un
análisis más profundo de estos de ejemplos ver [8], [19], [28], [42], [47] y [57].
Ejemplo 7. Parte del ejemplo que detallamos a continuación aparece en [8]. En el
mismo se presenta un caso de repulsión. Dada la función
f (x) = x1/3 ,
(2.64)
demostraremos que para cualquier valor inicial diferente de cero, el método de NewtonRaphson diverge.
Solución 7. Notemos que la función dada posee solución única en x∗ = 0. Aplicando
el método de Newton-Raphson a (2.64) sigue
xn+1
=
xn −
=
xn −
f (xn )
,
f 0 (xn )
1/3
xn
−2
1/3xn 3
= −2xn ,
luego, para cualquier punto de partida distinto de cero, el método de Newton-Raphson
se aleja de la solución x∗ = 0. En efecto, dado x0 se sigue
x1
x2
xn
= −2x0
= 2 2 x0
..
.
= (−1)n 2n x0 .
Luego si x0 > 0 se tiene que
lı́m xn = ∞,
n→∞
n par
lı́m xn = −∞.
n→∞
n impar
Si x0 < 0 se obtiene
lı́m xn = −∞,
n→∞
n par
lı́m xn = ∞.
n→∞
n impar
En ambos casos el método de Newton-Raphson presentará una divergencia oscilatoria.
34
CAPÍTULO 2. EL MÉTODO DE NEWTON-RAPHSON
Ejemplo 8. El siguiente ejemplo aparece en [19]. En el mismo se presenta una
función que posee falsa convergencia.
Buscaremos una función h(x) en la que el método de Newton-Raphson genere
una sucesión {xn } divergente, pero que cumpla la condición (2.63).
Solución 8. Notemos que para valores pequeños de x, la función del ejemplo 7
√
f (x) = 3 x,
(2.65)
posee un punto fijo repulsor en cero. También observemos que para valores grandes
de x, la función
2
ψ(x) = e−x ,
(2.66)
tendrá un comportamiento semejante. Por consiguiente, tomaremos a la función h
como el producto de (2.65) y (2.66). Así
h(x) =
√
3
2
xe−x .
(2.67)
La función (2.67) tiene una solución trivial en x = 0, pero como demostraremos,
la iteración bajo el método de Newton-Raphson nunca converge a este cero, a menos
que no se escoja a x0 = 0. Sin embargo, si aplicamos (2.63) como criterio de convergencia y si ninguna de las iteraciones es un punto crítico de h(x), el método de
Newton-Raphson tendría convergencia en una zona en la cual no hay ceros.
Aplicando el método de Newton-Raphson a (2.67) sigue
xn+1 = xn −
h(xn )
= xn −
h0 (xn )
1
3
h
xn
=
x
1−
n
− 2x2n
1
3
i
1
2xn (1 + 3x2n )
. (2.68)
=
−
1 − 6x2n
− 2x2n
Analicemos a (2.68) y caractericemos su punto fijo.
xn+1 = f (xn ), donde f (x) = −
2(−1 − 9x2 + 36x3 )
2xn (1 + 3x2n )
0
y
f
(x)
=
.
1 − 6x2n
(1 − 6x)2
Como
f (0) = 0 y f 0 (0) = −2, entonces para x = 0 existe un punto fijo repulsor.
Analicemos su comportamiento. Supongamos
√ que xn no pertenece al intervalo
(− √16 , √16 ). Asumamos también que xn 6= 1/ 6, porque la derivada de h(x) en ese
punto se hace cero, aún así, el método de Newton-Raphson diverge. En efecto, si
xn > √16 entonces
xn+1 − xn = f (xn ) − xn = −xn
2 + 6x2 + 1 − 6x2 −3xn
n
n
=
> 0.
2
1 − 6xn
1 − 6x2n
Es decir xn+1 > xn , luego xn → ∞.
Análogamente, si xn < − √16 , entonces
xn+1 − xn =
−3xn
< 0, luego xn+1 < xn , por tanto xn → −∞.
1 − 6x2n
Para xn 6= 0 y xn ∈ (− √16 , √16 ) se obtiene
xn+1
1 + 3x2n
1 + 3x2n
=2
=
2
> 2.
xn
1 − 6x2n
1 − 6x2n
Entonces
1
|xn+1 | > 2|xn |, luego, en algun momento xn+1 > √ , por tanto xn → ∞.
6
2.5. EJEMPLOS NUMÉRICOS
35
Si para algún n se obtiene que f (xn ) = ± √16 , entonces xn+1 → ±∞.
Por tanto, en todos los casos la sucesión diverge a ±∞.
0.6
0.4
0.2
-3
-2
1
-1
2
3
-0.2
-0.4
-0.6
Figura 2.15: Gráfica de la función h(x) =
√
3
xe−x
2
5
-2
1
-1
2
-5
Figura 2.16: Gráfica de la función f (x) =
−2x(1+3x2 )
.
1−6x2
Ejemplo 9. La siguiente función ha sido considerada en [42]. Su gráfica puede verse
en la figura 2.17. Dada la función
π
π − 2x sen( x ), si x 6= 0,
f (x) =
(2.69)
π, si x = 0.
Demostraremos que la sucesión generada a partir de aplicar el método de NewtonRaphson a (2.69), converge a un límite que no es solución de (2.69).
Solución 9. Notemos que lı́mx→0 f (x) = π, luego f (x) es continua en todo punto.
Aplicando el método de Newton-Raphson a (2.69) se sigue
xn+1 = xn −
πxn − 2πxn cos( xπn )
f (xn )
=
−
.
f 0 (xn )
2[π cos( xπn ) − xn sen( xπn )]
Notemos que (2.70), a partir de x0 = 0,5 genera la sucesión xn =
1
efecto, se prueba por inducción que si xn = 2n+1
, entonces
xn+1 = −
(2.70)
1
2n+1 .
En
1
1
π 2n+1
− 2π 2n+1
cos(2n π)
1
π
1
=
( n+1 ) = n+2 .
2π
2π 2
2
Luego
lı́m xn = lı́m
x→∞
x→∞
1
= 0.
2n+1
(2.71)
36
CAPÍTULO 2. EL MÉTODO DE NEWTON-RAPHSON
y
4
3
2
1
x3x2 x1
-1.5
-1.0
x0
0.5
-0.5
1.0
1.5
x
Figura 2.17: Gráfica de la función f (x) = π − 2x sen( πx ) y de las iteraciones del
método de Newton-Raphson.
Sin embargo, de (2.69) se sigue que f (0) = π, luego, el límite de (2.71) no es
solución de (2.69).
En el siguiente ejemplo, el método de Newton-Raphson da como resultado una
sucesión oscilante divergente.
Ejemplo 10. Dada la función f (x) = arctan(x) aplicaremos el método de NewtonRaphson empleando un x0 = 1,45. Comprobaremos que los resultados obtenidos representan una sucesión oscilante divergente.
Solución 10.
1. Construcción de la función de iteración.
xn+1
= xn −
f (xn )
.
f 0 (xn )
= xn − (1 + x2n ) arctan(xn ).
(2.72)
Estudiemos la sucesión (2.72) y caractericemos el punto fijo. Sea
xn+1 = f (xn ),
donde
f (x) = x − (1 + x2 ) arctan x,
(2.73)
f 0 (x) = −2x arctan x.
(2.74)
y
Para f (x) = x, se sigue que x∗ = 0 es un punto fijo de (2.73). Sustituyendo
dicho punto fijo en (2.74) se obtiene que f 0 (x∗ ) = 0, por tanto, el cero es un
punto fijo superatractor de (2.72).
Notar que
|f 0 (x)| < 1 ⇔ |x arctan x| <
1
,
2
pero
x arctan x − 0.5 = 0 ⇔ x = 0.765378926665789 = a,
por lo tanto
|f 0 (x)| < 1 ⇔ |x| < a,
luego, para todo x0 ∈ (−a, a) se asegura la convergencia de (2.72).
2.5. EJEMPLOS NUMÉRICOS
37
y
x
a
-a
Figura 2.18: Gráfica de f (x) = x arctan x
Para x0 ∈
/ (−a, a), el método de Newton-Raphson puede converger o presentar
una divergencia oscilatoria.
y
1.0
0.5
-4
2
-2
4
x
-0.5
-1.0
Figura 2.19: Gráfica de la función f (x) = arctan(x) y de las iteraciones del método
de Newton-Raphson.
La gráfica (2.19), para un x0 = 1.45 muestra la presencia de una sucesión
oscilatoria alrededor de la solución única x = 0.
n
0
1
2
3
4
5
6
7
8
9
10
11
xn
1.4500
-1.55026
1.84593
-2.88911
8.67845
-102.443
16281.4
−4,16358 × 108
2,72305 × 1017
−1,16474 × 1035
2,13099 × 1070
−7,13317 × 10140
Cuadro 2.7: Valores obtenidos a partir de (2.72).
El próximo ejemplo prueba que el método de Newton-Raphson produce una
sucesión que tiende casi a repetirse (esto es lo que se llama un ciclo atractor).
Ejemplo 11. Aplicaremos el método de Newton-Raphson a la ecuación x3 −x−3 = 0
iniciando el proceso para x0 = 0.
38
CAPÍTULO 2. EL MÉTODO DE NEWTON-RAPHSON
Solución 11.
1. Construcción de la función de iteración.
xn+1 = xn −
x3n − xn − 3
2x3 + 3
= n2
.
2
3xn − 1
3xn − 1
(2.75)
Realicemos un análisis de la función de iteración (2.75).
2. Determinemos y caractericemos sus puntos fijos.
xn+1 = g(x)
donde
g(x) =
2x3 + 3
,
3x2 − 1
(2.76)
si g(x) = x, se sigue
2x3 + 3
= x ⇔ x∗ = 1.6717.
3x2 − 1
Luego, sustituyendo x∗ = 1.6717 en la derivada de (2.76) se obtiene que
g 0 (x∗ ) < 1, es decir, (2.75) posee un punto fijo atractor.
Veamos ahora la monotonía de (2.76).
Notemos que a partir del denominador
√
de (2.76) se obtiene que x = ±1/ 3.
10
5
-3
-2
1
-1
2
3
-5
-10
Figura 2.20: Gráfica de la función asociada al método de Newton, g(x) =
2x3 +3
3x2 −1
Observando la gráfica (2.20) se verifica que (2.76) es monótona creciente en los
intervalos (−∞, − √13 ), (− √13 , 0) y (x∗ , +∞).
Analicemos el comportamiento de (2.76) cuando x0 ≥ x∗ . En efecto, si
x0 ≥ x∗
entonces xn → x∗ de forma decreciente, es decir
xn+1 < xn ,
∀n ≥ 0
y
5
4
3
2
x*
2
3
4
5
x
Figura 2.21: Comportamiento de (2.76) cuando x0 ≥ x∗
2.5. EJEMPLOS NUMÉRICOS
39
Si x0 ∈ ( √13 , x∗ ), entonces x1 > x∗ , luego, por el caso anterior también convergerá
a x∗ , pues
xn+1 < xn ,
∀n ≥ 1
y
6
4
2
1
x*
2
3
4
5
x
-2
Figura 2.22: Comportamiento de (2.76) cuando x0 ∈ ( √13 , x∗ )
En un entorno de cero (−, ), si x0 ∈ (−, ), entonces xn presentará ciclos.
Experimentalmente se ha comprobado que ≈ 0.058.
y
-3
-2
1
-1
2
x
-5
-10
-15
-20
-25
Figura 2.23: Iteraciones del método de Newton-Raphson para f (x) = x3 − x − 3
En cualquier otro caso, se tiene convergencia, ya que
Si x0 > x∗ , entonces xn converge monótonamente a x∗ .
Si x0 < x∗ y x0 6= (−, ) llega el momento en el que xn > x∗ , luego también
converge.
Ejemplo 12. Dada la ecuación f (x) = cos(x) aplicaremos el método de NewtonRaphson, utilizando una aproximación inicial x0 = 3,0. Comprobaremos que el método de Newton-Raphson produce una sucesión que converge a una solución no esperada.
Solución 12.
1. Gráfica de la función.
40
CAPÍTULO 2. EL MÉTODO DE NEWTON-RAPHSON
y
1.0
0.5
-6
-4
2
-2
4
6
x
-0.5
-1.0
Figura 2.24: Iteraciones del método de Newton-Raphson para f (x) = cos(x)
Se observa que existen infinitas raíces: (2k + 1)π/2, k ∈ Z. Tomando una
aproximación inicial x0 = 3, se espera que converja a una de las soluciones
más próximas: π/2 ó 3π/2. Sin embargo, converge a −3π/2, como se ve en el
cuadro (2.8).
n
0
1
2
3
4
5
6
xn
3.00000
-4.01525
-4.85266
-4.71146
-4.71239
-4.71239
-4.71239
Cuadro 2.8: Valores obtenidos al aplicar el método de Newton-Raphson a f (x) =
cos(x)
La tabla muestra que el método de Newton-Raphson no converge a la solución
esperada, esto es debido a que la pendiente de la derivada de la función es muy
pequeña y la recta tangente a la función es casi horizontal. Además, se tomó una
aproximación inicial que coincidía con el punto de inflexión de la curva que representa
la función.
El ejemplo siguiente muestra una ecuación cuyas raíces son complejas.
Ejemplo 13. Dada la ecuación x2 − 2x + 5 = 0, aplicaremos el método de NewtonRaphson tomando a x0 = 3,5 como la aproximación inicial.
Solución 13.
1. Construcción de la función de iteración.
xn+1
=
=
5 − 2xn + x2
,
−2 + 2xn
−5 + x2n
.
2(−1 + xn )
xn −
(2.77)
Análicemos a 2.77. Veamos si tiene puntos fijos.
xn+1 = h(xn )
donde
h(x) =
−5 + x2
,
2(−1 + x)
(2.78)
2.5. EJEMPLOS NUMÉRICOS
41
pero h(x) = x ⇔ x = 1 ± 2i, luego (2.77) tampoco tiene puntos fijos.
6
4
2
-4
2
-2
4
-2
-4
-6
Figura 2.25: Gráfica de la función h(x) =
−5+x2
2(−1+x)
Luego, véase Figura (2.26), para cualquier x0 , la función (2.78) presentará una
divergencia oscilatoria.
y
x0
x
Figura 2.26: Comportamiento de (2.78)cuando x0 < 0
y
50
40
30
20
10
-6
-4
-2
2
4
6
x
Figura 2.27: Iteraciones del método de Newton-Raphson para f (x) = x2 − 2x + 5
La gráfica comprueba que no existe solución real, pues la curva no corta al eje
0X.
42
CAPÍTULO 2. EL MÉTODO DE NEWTON-RAPHSON
x0
x1
x2
x3
x4
x5
..
.
x10
x11
..
.
x40
-4
-1.1
0.9023
21.4389
11.1216
5.8632
..
.
-23.6247
-11.2311
..
.
-10.5682
-0.7
1.3264
-4.9628
-1.6460
0.4328
4.2426
..
.
0.1392
2.8932
..
.
-2.4868
0.5
4.75
2.3416
0.1801
3.0295
1.0293
..
.
-2.9444
-0.4652
..
.
-1.3910
6.5
3.3863
1.3550
-4.4548
-1.3607
0.6667
..
.
-0.2840
1.9155
..
.
8.2370
10
5.2777
2.6713
0.6390
6.3603
3.3070
..
.
2.7082
0.6832
..
.
6.0321
Cuadro 2.9: Valores obtenidos al aplicar el método de Newton a f (x) = x2 − 2x + 5
La tabla muestra las sucesiones originadas a partir de diferentes valores iniciales,
las mismas oscilan de izquierda a derecha sin converger, por lo tanto ninguna de las
aproximaciones que se verifican son un valor aproximado de la raíz.
Capítulo 3
El método de Newton
aplicado a la ecuación de
Kepler
3.1.
Introducción histórica a la ecuación de Kepler.
Johannes Kepler (1571 − 1630) fue un astrólogo alemán nacido en Württemberg. Realizó sus estudios en la
Universidad de Tübingen, donde su maestro M. Mästlin
le inició en el sistema heliocéntrico de Copérnico. Enseñó matemática en Heidelberg y Tubinga. En su obra
Materium Cosmographicum mostró que los planos de las
órbitas planetarias son próximos entre sí, pero diferentes, y que las mismas pasan, no por el centro de la órbita
terrestre, como lo había establecido Copérnico, sino por
el sol. En 1600, un edicto de la iglesia católica le obliga
a renunciar a su cátedra en la universidad de Graz; emigrando a Dinamarca, donde inicia a trabajar con Tycho
Brahe. Kepler, a la muerte de Tycho Brahe, quedo en
Figura 3.1: Johannes
posesión de sus datos astronómicos, los cuales eran para
Kepler (1571 − 1630)
su época, los más precisos.
Fue alrededor del año 1609, cuando Kepler, en su libro Astronomia Nova, enunció
la ley de las órbitas, cuya expresión analítica es una ecuación algebraica no lineal de
la forma
f (E) = E − e sen E − M.
(3.1)
Para la solución de la ecuación de Kepler es necesario conocer los valores de la
anomalía media, M , y de la excentricidad, e, de la órbita. La ecuación de Kepler fue
una de las primeras ecuaciones que mediante métodos numéricos se le dio solución.
Desde los días de Newton este problema a sido extensamente estudiado y su solución
se a conseguido de diversas maneras. Esto, como lo establece Danby, [17] , demuestra
que el tema es abierto y existen muchas posibilidades para promover la invención de
nuevas alternativas de solución.
Veamos algunos momentos importantes en la solución de (3.1).
Jacques Cassini, [11], publicó un artículo en el cual emplea un método geométrico
para dar solución a la ecuación de Kepler. Para la anomalía excéntrica obtuvo la
expresión
1
1
EC = M + .
(3.2)
2
2
Jeremiah Horrocks, en 1638, describe un método basado en diferencias apróxi43
44
CAPÍTULO 3. EL MÉTODO DE NEWTON APLICADO A LA EK
madas, para tal caso emplea la fórmula
EH − M = e sen EH = sen(EH − M ).
(3.3)
Donde
1 3
e sen3 M + E.
6
Peder Horrebow, en 1717, obtuvo una solución de la ecuación de Kepler que está
estrechamente relacionada a la solución de Horrocks. Los detalles de la solución están
contenidos en unos artículos publicados en 1717 y 1718, los cuales fueron compilados
en 1742 en un manuscrito titulado Adytum Astronomiae.
EH ≈
E = M − e sen(∠BCF ).
(3.4)
Donde ∠BCF es E0 .
Cristopher Wren, en 1658, ofrece una solución de la ecuación de Kepler basada
en las cicloides, la misma aparece en un tratado publicado por John Wallis, [89]. La
solución que aparece en la sección De problemate Kepleriano per cycloidem solvendo
es
E = M − e sen E = |OH| + |HF | = |OF |.
(3.5)
Isaac Newton, en el Libro I, proposición 31 de la Principia de 1686, emplea la
construcción de Wren para ubicar la posición de un planeta en una órbita elíptica,
pero luego, en el Scholium, presenta una forma más práctica de resolver ese problema.
John Couch Adams, en [1], presenta un método basado en la curva de los senos.
E = M − e sen E.
(3.6)
T. Levi-Civita, [51], presenta una interesante solución a la ecuación de Kepler en
forma de series infinitas. Su trabajo fue puramente analítico. Demostró que si
√
e exp( 1 − e2 )
√
z=
, 0 ≤ e < 1,
(3.7)
1 + 1 − e2
entonces la ecuación de Kepler tendrá por solución a
E=
∞
X
Ln (M )z n ,
0 ≤ z < 1.
(3.8)
n=0
K. Stumpff, [80], aplicó las series de Lie a algunos problemas de la mecánica
celeste, obteniendo una solución en series de Lie para la ecuación de Kepler.
∞
h
i X
(M − M0 )n n
E = exp (M − M0 )D(x)|x=E0 =
D (x)|x=E0 ,
n!
n=0
(3.9)
donde D(x) es un operador lineal de la forma
D(x) =
1
.
1 − e cos x
(3.10)
En este acápite se considera la famosa ecuación de Kepler, consúltese (2.1), donde
e y M son conocidos, como función test para analizar diversos resultados de convergencia semilocal para el método de Newton-Raphson. En concreto, se estudian
los resultados dados por Kantorovich ([46]) y Smale ([77], [87]) y algunas de sus
variantes ([35], [88]). Dichos resultados, además de garantizar la convergencia del
método de Newton-Raphson a una solución de (2.1), pueden verse también como
unos resultados de existencia y unicidad de solución para la ecuación de Kepler.
Así, y generalizando el trabajo realizado en [97], obtendremos distintos dominios de
existencia y unicidad de la forma
[M − t∗ , M + t∗ ]
y (M − t∗∗ , M + t∗∗ ), respectivamente.
3.2. EL TEOREMA DE KANTOROVICH
45
Los valores de t∗ y t∗∗ están dados en función de la excentricidad e de la órbita.
Tanto en la teoría de Kantorovich como en la de Smale (α-teoría), la idea de
la demostración consiste en construir una función mayorizante de la cual obtener
información sobre la convergencia del método de Newton-Raphson.
Así, sea φ(t) una función mayorizante obtenida por alguna de las teorías consideradas. Se comprobará que φ(t) tiene dos raíces: t∗ y t∗∗ que son las que proporcionan
los dominios de existencia y unicidad buscados.
Aunque la idea que presentamos se aplica a la ecuación de Kepler, se podría
seguir el mismo esquema para otros tipos de ecuaciones: Complejas, sistemas de
ecuaciones, ecuaciones funcionales, etc.
En lo que sigue:
1. Vamos a construir la función mayorizante para la ecuación de Kepler siguiendo
4 teorías:
i) Kantorovich, ([46]).
ii) Gutiérrez, ([35]).
iii) α-teoría de Smale (artículo de Zhen-Shi-Ming), ([97]).
iv) α-teoría de Wang-Zhao, ([87]).
2. Vamos a ver bajo qué condiciones la correspondiente función mayorizante tiene
raíces reales. Esto nos va a dar un resultado que garantiza la existencia de
solución para la ecuación de Kepler en términos de la excentricidad e.
3. Vamos a determinar los correspondientes dominios de existencia y unicidad en
cada caso.
3.2.
El teorema de Kantorovich
Teorema 9. Si e ≤ 0.4142, entonces la ecuación de Kepler tiene solución. Dicha
solución está localizada en el intervalo
y es única en
[M − t∗ , M + t∗ ].
(3.11)
(M − t∗∗ , M + t∗∗ ),
(3.12)
donde
∗
=
t∗∗
=
t
1−
√
1 − 2δ
.
√δ
1 + 1 − 2δ
,
δ
son las raíces del polinomio mayorizante
p(t) =
1 2
δt − t + δ,
2
con δ =
e
.
1−e
Además, el método de Newton-Raphson, definido por
En+1 = En −
f (En )
,
f 0 (En )
n ≥ 0,
(3.13)
iniciando en E0 = M , converge a dicha solución.
Demostración. Tomemos E0 = M en el teorema de Kantorovich. Luego se deben
cumplir las siguientes condiciones:
i) f 0 (E0 ) 6= 0.
46
CAPÍTULO 3. EL MÉTODO DE NEWTON APLICADO A LA EK
ii)
iii)
f (E0 )
f 0 (E0 )
≤ β.
f (E)−f (y)
f 0 (E0 )
≤ γ(E − y),
∀E, y ∈ I.
iv) h = γβ ≤ 12 .
Para ello, calcularemos los parámetros β y γ.
Notemos que
f 0 (E) = 1 − e cos E ⇒ |f 0 (E0 )| ≥ 1 − e.
f 0 (y) = 1 − e cos y.
|f (E0 )| ≤ |e sen E0 | ≤ e.
0
|f (E) − f 0 (y)| = e| cos E − cos y| ≤ e|E − y|.
Así
f (E0 )
e
≤
= β = δ.
0
f (E0 )
1−e
Además
f (E) − f (y)
e
≤
|E − y|,
f 0 (E0 )
1−e
Luego
h = γβ = δ 2 =
por lo que γ = δ.
e 2
1
≤ .
1−e
2
Y por tanto
2e2 ≤ (1 − e)2 ⇔ 2e2 ≤ 1 − 2e + e2 ⇔ 0 ≤ 1 − 2e − e2 ⇔ 0 ≤ 2 − (1 − 2e + e2 ).
Luego
√
√
0 < 2 − (1 + e2 ) ⇔ (1 + e)2 ≤ 2 ⇔ − 2 ≤ 1 + e ≤ 2.
(3.14)
Tomando la parte positiva de (3.14) se sigue
√
√
1 + e ≤ 2 ⇔ e ≤ 2 − 1 ≈ 0.4142.
Notemos que la condición e ≤ 0.4142 garantiza tres cosas:
1. La ecuación de Kepler tiene solución: E ∗ .
2. El polinomio mayorizante p(t) = 1/2δt2 − t + δ tiene soluciones reales: t∗ y t∗∗ .
3. E ∗ está localizada en el intervalo [M − t∗ , M + t∗ ] y es la única solución en
(M − t∗∗ , M + t∗∗ ).
Por último, el método de Newton-Raphson definido por (3.13), iniciando en E0 =
M , converge a E ∗ .
3.3.
El teorema de Gutiérrez
Como vimos en el acápite anterior, el teorema de Kantorovich presenta las siguientes condiciones:
i) x0 ∈ I.
ii) f 0 (x0 ) 6= 0.
iii)
f (x0 )
f 0 (x0 )
iv)
f 0 (x)−f 0 (y)
f 0 (x0 )
≤ β.
≤ γ|x − y|,
∀x, y ∈ I.
3.3. EL TEOREMA DE GUTIÉRREZ
47
v) h = γβ ≤ 1/2.
En 1997, José Manuel Gutiérrez presentó un nuevo teorema de convergencia
semilocal para el método de Newton-Raphson. En dicho teorema Gutiérrez no toma
en cuenta la condición v) de Kantorovich, sino que la sustituye por dos expresiones
en que se aplica la derivada segunda de la función en x
1.
f 00 (x0 )
f 0 (x0 )
2.
f 00 (x)−f 00 (x0 )
f 0 (x0 )
≤ b.
≤ K|x − x0 |.
Además, aplica la condición iii) en la forma
f (x0 )
≤ a,
f 0 (x0 )
con lo que se obtiene el nuevo polinomio mayorizante
b
K
p(t) = a − t + t2 + t3 .
2
6
(3.15)
Los detalles de la demostración de éste teorema se encuentran en [35]. A continuación analizaremos su aplicación al caso de la ecuación de Kepler.
Teorema 10. Si e ≤ 0.3759, entonces la ecuación de Kepler tiene solución. Dicha
solución está localizada en el intervalo (3.11) y es única en (3.12) donde t∗ y t∗∗
son las raíces del polinomio mayorizante
1
1
p(t) = δ − t + δt2 + δt3 ,
2
6
con δ =
e
.
1−e
Además, el método de Newton-Raphson, definido por (3.13), iniciando en E0 =
M , converge a dicha solución.
Demostración. Tomemos a E0 = M en el teorema de Gutiérrez. Luego se deben
cumplir las siguientes condiciones:
i)
f (E0 )
f 0 (E0 )
≤ a.
ii)
f 00 (E0 )
f 0 (E0 )
≤ b.
iii)
f 00 (E)−f 00 (E0 )
f 0 (E0 )
≤ K|E − E0 |.
Ahora calcularemos los parámetros a, b y K. Observemos que
f 0 (E) = 1 − e cos E ⇒ |f 0 (E0 )| = |1 − e cos E| ≥ 1 − e.
f 00 (E) = e sen E ⇒ |f 00 (E0 )| = |e sen E0 | ≤ e.
|f 00 (E) − f 00 (E0 )| =
e| sen E − sen E0 | ≤ e|E − E0 |.
luego
f (E0 )
f 0 (E0 )
f 00 (E0 )
f 0 (E0 )
00
f (E) − f 00 (E0 )
f 0 (E0 )
≤
≤
≤
e
= a.
1−e
e
= b.
1−e
e
e
|E − E0 | ⇒ K =
.
1−e
1−e
Así
a=b=K=
e
= δ.
1−e
(3.16)
48
CAPÍTULO 3. EL MÉTODO DE NEWTON APLICADO A LA EK
Sustituyendo (3.16) en (3.15) se obtiene
δ
δ
p(t) = δ − t + t2 + t3 .
2
6
(3.17)
cuya gráfica es
p HtL
m
t*
M
t*
*
Figura 3.2: Gráfica del polinomio mayorizante p(t) = δ − t + 2δ t2 + 6δ t3
En donde M y m representan el máximo y el mínimo de la función p(t) respectivamente, analicemos a (3.17).
p0 (t) =
p00 (t) =
1
−1 + δt + δt2 ⇒ p0 (0) = −1 < 0.
2
δ + δt > 0, ∀δ > 0.
Entonces existe un único mínimo t̂ tal que p0 (t̂) = 0. Luego
r
√
−δ ± δ 2 + 2δ
2
0
p (t̂) = 0 ⇔ t̂ =
= −1 ± 1 + .
δ
δ
Tomando la raíz positiva se sigue
r
2
1+ .
δ
t̂ = −1 +
Notemos que haciendo
∆ = 1/δ,
t̂ = −1 +
y
p(t̂) =
se sigue
√
(3.18)
1 + 2∆.
1
1
1
(1 − ∆t̂ + t̂2 + t̂3 ).
∆
2
6
(3.19)
Apliquemos la condición de convergencia a (3.19). Sea p(t̂) < 0, luego
p(t̂) =
=
=
1
1
1
(1 − ∆t̂ + t̂2 + t̂3 ).
∆
2
6
√
√
1
(4 − 1 + 2∆ + ∆(3 − 2 1 + 2∆)) < 0.
3∆
1√
2 √
1 4
( +∆−
1 + 2∆ − ∆ 1 + 2∆) < 0.
∆ 3
3
3
(3.20)
Recordemos que ∆ > 0, luego (3.20) será cierto si y solo si
1√
2 √
4
+∆−
1 + 2∆ − ∆ 1 + 2∆ < 0.
3
3
3
(3.21)
3.4. LA α-TEORÍA DE SMALE
49
De (3.21) se sigue
4 + 3∆
(4 + 3∆)2
16 + 24∆ + 9∆2
<
<
<
√
√
√
3
1 + 2∆ + ∆ 1 + 2∆ = 1 + 2∆(1 + 2∆) = (1 + 2∆) 2 .
(1 + 2∆)3 .
1 + 6∆ + 12∆2 + 8∆3 .
Luego
8∆3 + 3∆2 − 18∆ − 15 > 0 ⇔ ∆ ≈ 1.66032.
(3.22)
Sustituyendo (3.22) en (3.18) se sigue
δ<
1
.
∆
(3.23)
Sustituyendo (3.23) en (3.16)
e
1
1
<
⇔e<
≈ 0.3759.
1−e
∆
1+∆
Notemos que la condición e ≤ 0.3759 también nos garantiza tres cosas:
1. La ecuación de Kepler tiene solución: E ∗ .
2. El polinomio mayorizante p(t) = δ − t + 12 δt2 + 16 δt3 tiene dos soluciones reales:
t∗ y t∗∗ .
3. E ∗ está localizada en el intervalo [M − t∗ , M + t∗ ] y es la única solución en
(M − t∗∗ , M + t∗∗ ).
Por último, el método de Newton-Raphson definido por (3.13), iniciando en E0 =
M , converge a E ∗ .
3.4.
La α-teoría de Smale
Teorema 11. Si e ≤ 0.3594, entonces la ecuación de Kepler tiene solución. Dicha
solución está localizada en el intervalo (3.11) y es única en (3.12) donde t∗ y t∗∗
son las raíces de la función mayorizante
φ(t) = δ − t +
γt2
.
1 − γt
Con δ definido en 3.16 y
γ = sup(
k≥2
1
δ k−1
)
.
k!
Además, el método de Newton-Raphson, definido por (3.13), iniciando en E0 =
M , converge a dicha solución.
Demostración. Tomemos a E0 = M en el teorema de la α-teoría de Smale. Luego
se deben cumplir las siguientes condiciones:
i) f 0 (E0 ) 6= 0.
ii) β(E0 , f ) =
iii)
(k)(E0 )
1 f
k! f 0 (E0 )
f (E0 )
f 0 (E0 )
.
≤ γ k−1 ,
√
iv) α = βγ ≤ 3 − 2 2.
k ≥ 2.
50
CAPÍTULO 3. EL MÉTODO DE NEWTON APLICADO A LA EK
Calculemos los parámetros β, γ y α.
Notemos que
f 0 (E) = 1 − e cos E
00
f (E) = e sen E
f 000 (E) = e cos E
|f 0 (E0 )| ≥ 1 − e.
⇒
⇒
⇒
..
.
|f k (E0 )| ≤ e,
|f 00 (E0 )| ≤ e.
|f 000 (E0 )| ≤ e.
k ≥ 2.
Así
β(E0 , f )
=
γ(E0 , f )
=
α
f (E0 )
e
≤
.
0
f (E0 )
1−e
1
1
h
i k−1
1 f (k) (E0 ) k−1
e
≤
, k ≥ 2.
k! f 0 (E0 )
k!(1 − e)
"
# 1
e k 1 k−1
√
= βγ ≤
≤ 3 − 2 2.
1 − e k!
Consideremos a (3.24)
Sea
"
e k 1
α≤
1 − e k!
1
# k−1
√
≤ α0 ≤ 3 − 2 2.
(3.24)
(3.25)
Luego, de (3.25) se sigue
e k 1
1 − e k!
e k
1−e
e 1−e
Ahora, sea
≤ α0k−1 .
≤ α0k−1 k!.
1
≤ (α0k−1 k!) k .
1
δk = (α0k−1 k!) k ,
(3.26)
k ≥ 2.
(3.27)
Necesitamos conocer el mínimo valor de δk .
De (3.27) se sigue
1
δk+1 = [α0k (k + 1)!] k+1 .
y
δkk = (α0k−1 k!),
k ≥ 2.
Por tanto
δk+1
δk
1
h
i k+1
α0k (k + 1)!
=
h
i k1
α0k−1 k!
=
=
α0
k
1
1
k+1
k+1
− k−1
−k
1
k
k!
(k + 1) k+1 .
1
h α (k + 1)k i k(k+1)
0
,
k!
k ≥ 2.
(3.28)
Ahora utilizaremos (3.28) para hallar el mínimo de δk . Lo haremos por inducción.
Si k = 2, luego
h 9α i 16
h 9(3 − 2√2) i 16
δ3
0
=
=
= 0,772 . . . < 1.
δ2
2
2
Entonces δ3 < δ2 .
3.5. LA α-TEORÍA DE WANG-ZHAO
51
Para k = 3 se sigue
1
1
h 64α i 12
h 64(3 − 2√2) i 12
δ4
0
=
=
= 1,83 . . . > 1.
δ3
9
9
Por tanto δ4 > δ3
Luego, si k ≥ 3, entonces
k+1
k+2
k+1 !
k
=
k + 2 k+1
k+1
k+1
> 1.
k!
Por tanto δk+1 > δk , ∀k ≥ 3.
Así, el mínimo corresponde a k = 3, luego
1
δ3 = [6α02 ] 3 = 0.5610688.
Conocido el ínfimo de δk , inmediatamente de (3.26) podemos conocer el mínimo
valor de e. Así
e
δ3
≤ δ3 ⇔ e ≤ (1 − e)δ3 ⇔ e(1 + δ3 ) ≤ δ3 ⇔ e ≤
≈ 0.3594.
1−e
1 + δ3
Notemos que la condición e ≤ 0.3594. otra vez nos garantiza tres cosas:
1. La ecuación de Kepler tiene solución: E ∗ .
2. La función mayorizante φ(t) = δ − t +
δ 2 t2
1−δt
tiene soluciones reales: t∗ y t∗∗ .
3. E ∗ está localizada en el intervalo [M − t∗ , M + t∗ ] y es la única solución en
(M − t∗∗ , M + t∗∗ ).
Por último, el método de Newton-Raphson definido por (3.13), iniciando en E0 =
M , converge a E ∗ .
3.5.
La α-teoría de Wang-Zhao
Como hemos visto, la α-teoría de Smale es una técnica muy conocida para estudiar la convergencia semilocal del método de Newton-Raphson, esto es, establece
sobre un punto inicial x0 y una función f ciertas condiciones que permiten al método
de Newton-Raphson converger.
Recordemos que las condiciones impuestas por la α-teoría son:
i) f 0 (x0 ) 6= 0.
ii)
iii)
f (x0 )
f 0 (x0 )
≤ β.
(k)
(x0 )
1 f
k! f 0 (x0 )
≤ γ k−1 ,
k ≥ 2.
√
iv) α = βγ ≤ 3 − 2 2.
También recordemos que que los resultados de la convergencia son probados a
partir de de la siguiente función mayorizante
φS (t) = β − t +
X
k≥2
γ k−1 tk = β − t +
γt2
.
1 − γt
52
CAPÍTULO 3. EL MÉTODO DE NEWTON APLICADO A LA EK
Wang y Zhao,[87], consideraron que la condición iv) es muy restrictiva y demostraron que la convergencia del método de Newton-Raphson se puede obtener,
además de las dos primeras condiciones, a partir de las condiciones del tipo
1 f (k) (x0 )
≤ γk ,
k! f 0 (x0 )
k ≥ 2,
y la función mayorizante
φW (t) = β − t +
X
γk tk .
(3.29)
k≥2
Notemos que γk ≤ γ k−1 , para k ≥ 2. Luego φW (t) ≤ φS (t), para t ≥ 0. En
consecuencia φS (t) mayoriza a φW (t), por tanto φS (t) = 0 implica que φW (t) = 0,
pero no lo contrario.
El trabajo de Wang y Zhao tiene un gran significado teórico, pues los mismos pueden ser aplicados a situaciones donde la α-teoría de Smale falla. En [34] encontramos
un ejemplo que ilustra éste caso.
A continuación presentamos un teorema en el que se aplica la α-teoía de WangZhao a la ecuación de Kepler.
Teorema 12. Si e ≤ 0.3678, entonces la ecuación de Kepler tiene solución. Dicha
solución está localizada en el intervalo (3.11) y es única en (3.12) donde t∗ y t∗∗
son las raíces de la función mayorizante
φ(t) = δ exp(t) − (1 + δ)t,
con δ =
e
.
1−e
Además, el método de Newton-Raphson, definido por (3.13), iniciando en E0 =
M , converge a dicha solución.
Demostración. Tomemos a E0 = M en el teorema de la α-teoría de Wang-Zhao.
Luego se deben cumplir las siguientes condiciones:
i) f 0 (E0 ) 6= 0.
ii) β(E0 , f ) =
iii)
(k)
(E0 )
1 f
k! f 0 (E0 )
f (E0 )
f 0 (E0 )
.
≤ γk ,
k ≥ 2.
Para ello calcularemos los parámetros β y γ.
Observar que
f 0 (E) = 1 − e cos E
f 00 (E) = e sen E
⇒
⇒
|f 0 (E0 )| ≥ 1 − e.
|f 00 (E0 )| ≤ e.
f 000 (E) = e cos E
⇒
..
.
|f 000 (E0 )| ≤ e.
|f k (E0 )| ≤ e,
k ≥ 2.
Así
β(E0 , f ) =
1 f (k) (E0 )
k! f 0 (E0 )
≤
f (E0 )
e
, por tanto β = δ.
≤
f 0 (E0 )
1−e
δ
1 e = γk , por lo que γk = .
k! 1 − e
k!
(3.30)
(3.31)
3.5. LA α-TEORÍA DE WANG-ZHAO
53
Sustituyendo (3.30) y (3.31) en (3.29) se sigue
X
X 1
δ−t+
γk tk = δ − t +
δtk .
k!
k≥2
k≥2
=
δ−t+δ
X tk
k≥2
=
=
k!
.
δ − t + δ[exp(t) − 1 − t].
δ exp(t) − (1 + δ)t = p(t).
(3.32)
Cuya gráfica es
p HtL
m
Figura 3.3: Gráfica del polinomio mayorizante p(t) = δ exp(t) − (1 + δ)t
En donde m también representa el mínimo de la función p(t), analicemos a (3.32)
p0 (t) =
p00 (t) =
δ[exp(t)] − (1 + δ) ⇒ p0 (0) = δ − 1 − δ = −1 < 0.
δ[exp(t)] ⇒ f 00 (t) > 0, ∀t > 0.
Luego, existe un único mínimo t̂ tal que p0 (t̂) = 0. Notar que
p0 (t̂) = δ[exp(t̂)] − (1 + β) = 0.
Por tanto
δ[exp(t̂)] = 1 + δ ⇔ exp(t̂) =
1+δ
1
⇔ exp(t̂) = 1 + .
δ
δ
Luego
1
t̂ = ln(1 + ).
(3.33)
δ
Ahora analicemos la condición de convergencia de p(t̂). Sea p(t̂) < 0, luego
p(t̂) = δ[exp(t̂)] − (1 + δ)t̂ < 0.
Sustituyendo (3.33) en (3.34) se sigue
h
1
1 i
− (1 + δ) ln 1 +
< 0.
p(t̂) = δ exp ln 1 +
δ
δ
1
1
− (1 + δ) ln 1 +
< 0.
= δ 1+
δ
δ
1
= (1 + δ) − (1 + δ) ln 1 +
< 0.
δ
i
h
1
< 0.
= (1 + δ) 1 − ln 1 +
δ
Recordemos que (1 + δ) > 0, luego (3.35) será cierto si y sólo si
1
1 − ln 1 +
< 0.
δ
(3.34)
(3.35)
(3.36)
54
CAPÍTULO 3. EL MÉTODO DE NEWTON APLICADO A LA EK
De (3.36) sigue
1
1
1
1 < ln 1 +
⇔ exp(1) < 1 + ⇔ exp(1) − 1 < .
δ
δ
δ
Luego
δ=
1
.
exp(1) − 1
(3.37)
Sustituyendo (3.30) en (3.37)
e
1
1
<
⇔ e exp(1) − e < 1 − e ⇔ e <
≈ 0.3678.
1−e
exp(1) − 1
exp(1)
Notemos que la condición e ≤ 0.3678. también nos garantiza tres cosas:
1. La ecuación de Kepler tiene solución: E ∗ .
2. La función mayorizante φ(t) = δ exp(t) − (1 + δ)t tiene soluciones reales: t∗ y
t∗∗ .
3. E ∗ está localizada en el intervalo [M − t∗ , M + t∗ ] y es la única solución en
(M − t∗∗ , M + t∗∗ ).
Por último, el método de Newton-Raphson definido por (3.13), iniciando en E0 =
M , converge a E ∗ .
3.6.
Ejemplos numéricos.
En esta sección describiremos el comportamiento de los radios de existencia, t∗ ,
y de los radios de unicidad, t∗∗ , bajo las diferentes teorías estudiadas. Así, t∗K , t∗G ,
t∗S and t∗W −Z , serán los radios de existencia obtenidos bajos las condiciones de las
teorás de Kantorovich, Gutiérrez, Smale y wang-Zhao respectivamente. Asimismo,
∗∗ ∗∗
∗∗
t∗∗
K , tG , tS and tW −Z serán los radios de unicidad.
Condición
Kantorovich
Gutiérrez
α-teoría de Smale
α-teoría de Wang-Zhao
t∗
√
1− 1−2δ 2
δ
t∗∗
√
1+ 1−2δ 2
δ
Menor raíz√positiva de p(t)
3
3 2
3
Mayor raíz√positiva de p(t)
3
3 2
3
Menor raíz positiva de φ(t)
Mayor raíz positiva de φ(t)
(1+δ )−
(1+δ ) −8δ
4δ 2
(1+δ )+
(1+δ ) −8δ
4δ 2
Cuadro 3.1: Radios de existencia, t∗ , y de unicidad, t∗∗ , en función del parámetro
δ.
En concreto, véase el Cuadro 3.1, si tomamos E0 = M e introducimos el parámee
tro δ = 1−e
, siendo e la excentricidad de la elipse, podemos ver en qué condiciones
se asegura la existencia y unicidad de solución para la ecuación de Kepler.
Condición
Kantorovich
Gutiérrez
α-teoría de Smale
α-teoría de Wang-Zhao
Función mayorizante
p(t) = 12 δt2 − t + δ
p(t) = δ − t + 21 δt2 + 16 δt3
γt2
φ(t) = δ − t + 1−γt
, γ = supk≥2 (δ/k!)1/(k−1)
φ(t) = δ exp(t) − (1 + δ)t
e
e ≤ 0.4142
e ≤ 0.3759
e ≤ 0.3594
e ≤ 0.3678
Cuadro 3.2: Funciones mayorizantes en función del parámetro δ y valores de e para
los cuales existe solución
Comparando los dominios de existencia y unicidad de solución obtenidos según
las distintas técnicas, véase el Cuadro 3.2. Se observa que, bajo las condiciones
3.6. EJEMPLOS NUMÉRICOS
55
de Cauchy-Kantorovich, la ecuación de Kepler posee el mayor rango de solución
(e ≤ 0.4142).
La comparación, véase nuevamente el Cuadro 3.2, también nos permite verificar
que bajo las condiciones del teorema de Gutiérrez, la ecuación de Kepler posee un
rango de solución, (e < 0.3759), mayor que bajo las condiciones de la α-teoría de
Wang-Zhao, (e < 0.3678), y de la α-teoría de Smale (e ≤ 0.3594).
t∗K
0.269
[-0.24, 0.29]
0.079
[2.08, 2.24]
Casos
Mercurio
Hungaria
t∗G
0.268
[-0.24, 0.29]
0.079
[2.08, 2.24]
t∗S
0.267
[-0.24, 0.29]
0.079
[2.08, 2.24]
t∗W −Z
0.263
[-0.24, 0.28]
0.079
[2.08, 2.24]
Cuadro 3.3: Dominios de existencia de solución, según las teorías en dos casos reales.
Aplicando los resultados obtenidos a dos casos reales, en concreto, se analizan los
caso del planeta Mercurio, cuya e = 0.205 y M = 0.0067π, y del asteroide Hungaria,
para el cual e = 0.073 y M = 0.69π, e comprueba que los dominios de existencia de
solución, véase Cuadro 3.3, para las diferentes técnicas aplicadas, son prácticamente
iguales.
Casos
Mercurio
Hungaria
t∗∗
K
7.459
(-7.43, 7.48)
25.09
(-22.9, 27.2)
t∗∗
G
3.363
(-3.34, 3.38)
7.271
(-5.10, 9.43)
t∗∗
S
3.739
(-3.719, 3.761)
12.659
(-10.4, 14.8)
t∗∗
W −Z
7.330
(-7.31, 7.35)
79.166
(-77.0, 81.3)
Cuadro 3.4: Dominios de unicidad de solución, según las teorías en dos casos reales.
En cuanto a los dominios de unicidad de solución, consúltese el cuadro 3.4, se verifica que bajo las condiciones de la Gutiérrez y de Kantorovich, el planeta Mercurio
posee el menor y mayor dominio de unicidad respectivamente. Asimismo, para las
condiciones de Gutiérrez y la α-teoría de Wang-Zhao, el asteroide Hungaria posee
el menor y mayor dominio de unicidad respectivamente.
Finalmente, hacemos un estudio comparativo de cómo se comportan los radios
de existencia y unicidad de solución para la ecuación de Kepler, obtenidos a partir
de los diferentes resultados de convergencia semilocal estudiados. Analizamos su
comportamiento en función de la excentricidad e.
e
0,05
0,1
0,15
0,2
0,25
0,3
0,35
t∗K
0.0527047
0.111806
0.179307
0.258343
0.354249
0.477412
0.653407
t∗G
0.052706
0.111832
0.179483
0.259118
0.357119
0.487869
0.702381
t∗S
0.0530554
0.113400
0.183295
0.266465
0.369312
0.505545
0.724562
t∗W −Z
0.052706
0.111833
0.179491
0.259171
0.357403
0.489402
0.716639
Cuadro 3.5: Dominios de existencia.
Entre el dominio de existencia y la excentricidad, consúltese el cuadro 3.5, existe
una relación directamente proporcional.
Para una misma excentricidad, véase nuevamente el cuadro 3.5, los dominios
de existencia que representan cada una de las teorías estudiadas son prácticamente
iguales.
56
CAPÍTULO 3. EL MÉTODO DE NEWTON APLICADO A LA EK
e
0,05
0,1
0,15
0,2
0,25
0,3
0,35
t∗∗
K
37.9473
17.8882
11.154
7.74166
5.64575
4.18925
3.06088
t∗∗
G
9.25181
5.93227
4.40664
3.45089
2.75074
2.17266
1.60847
t∗∗
S
3.33209
2.80848
2.45821
2.14796
1.87743
1.62167
1.31745
t∗∗
W −Z
4.49976
3.57715
2.99359
2.54264
2.15329
1.78134
1.34972
Cuadro 3.6: Dominios de unicidad.
Entre el dominio de unicidad y la excentricidad, véase el cuadro 3.6, existe una
relación inversamente proporcional.
Con la misma excentricidad, consúltese nuevamente el cuadro 3.6, en cada teoría
se obtienen dominios de unicidad completamente diferentes.
Bibliografía
[1] J. C. Adams: On Newton’s solution of Kepler’s problem. Monthly Notices of
Royal Astronomical Society, Vol. 43, (1882) pp. 43–49.
[2] S. Amat, S. Busquier, J. M. Gutiérrez, Geometric constructions of iterative
functions to solve nonlinear equations, Journal of Computational and Applied
Mathematics, 157 (2003) 197–205.
[3] S. Amat, S. Busquier, D. El Kebir, J. Molina, A fast Chebyshev’s method for
quadratic equations, Applied Mathematics and Computation, 148 (2004) 461–
474.
[4] I. K. Argyros, Newton methods. Nova Science Publisher, Inc, New York, 2004.
[5] A. Aubanell. A. Benseny y A. Delshams, Útiles básicos de cálculo numérico,
Editorial Labor, S. A, Barcelona, España, 1993.
[6] D. K. R. Babajee and M. Z. Dauhoo, An analysis of the properties of the variants
of Newton’s method wiht third order convergence, Applied Mathematics and
Computation, 183, Issue 1 (2006) 659–684.
[7] R. G. Bartle, Introducción al análisis matemático, Editorial Limusa, S. A, México. 1980.
[8] A. Ben-Israel, Newton’s Method with modified funtions, Contemporary Mathematics, 204 (1997) 39–50.
[9] R. Burden and D. Faires, Análisis Numérico, Grupo Editorial Iberoamérica,
España, 1985.
[10] B. Carnahan and H. A. Luther, Applied Numerical Method, John Wiley and
Sons, New York, 1969.
[11] J. D. Cassini: Nouvelle manière géometrique et directe de trauver les apogées,
les excentricités, et les anomalies du mouvement des planètes. Memoires de l’
Académie Royale des Science, Vol. 10, (1669) pp. 488–491.
[12] A. L. Cauchy, Leçons sur le Calcul Differentiel, Sur la détermination approximative des racines d’une équation algébrique ou transcendante, París, 1829.
[13] S. C. Chapra and R. P. Canale, Numerical methods for engineers, McGrau-Hill,
1998.
[14] J. Chavarriga, I. A. García, J. Giné, Manual de métodos numéricos, Ediciones
de la Universidad de Lleida, 1998.
[15] A. M. Cohen, Análisis Numérico, Editora Reverté, S.A, 1977.
[16] D. Conte y C. De Boor, Análisis Numérico elemental, McGrau-Hill. Inc, USA,
1972.
[17] J. M. A. Danby and T. M. Burkardt: The solution of Kepler equation I. Celestial
Mechanics, Vol. 31, (1983) pp. 95–107.
57
58
BIBLIOGRAFÍA
[18] J. P. Dedieu and M. H. Kim, Newton’s method for analytic system of equations
with constant rank derivatives, Journal of Complexity, 18 (2002) 187–209.
[19] G. C. Donovan, A. R. Miller and T. J. Moreland, Pathological functions for
Newton’s method, American Mathematical Monthly, 100 (1993) 53–58.
[20] N. L. De la Caille, Sur les éléments de la théorie du soleil, Premier Mémoire,
Mémoires de l’Académie Royale des Sciences, A2 (1750) 166–178.
[21] J. M. Díaz y F. B. Trujillo, Introducción a los métodos numéricos para la resolución de ecuaciones, Servicio de publicaciones de la Universidad de Cádiz,
1998.
[22] P. Díez, A note on the convergence of the Secant Method for simple and multiple
roots, Applied Mathematics Letters, 16 (2003) 1211–1215.
[23] J. A. Ezquerro, J. M. Gutiérrez, M. A. Hernández y M. A. Salanova, El método de Halley: Posiblemente, el método más redescubierto del mundo,Margarita
Mathematica, Servicio de Publicaciones de la Universidad de la Rioja, Logroño,
2001.
[24] J. A. Ezquerro, Construcción de procesos iterativos mediante aceleración del
método de Newton, Tesis Doctoral, Servicio de Publicaciones de la Universidad
de la Rioja, Logroño, 1996.
[25] W. F. Ford and J. A. Pennline, Accelerate convergence in Newton’s method,
SIAM Review, 38 (1996) 658–659.
[26] J. S. Frame, A variation of Newton’s method. American Mathematical Monthly,
51 (1944) 36–38.
[27] C. E. Froberg, Introduction to numerical analysis, Addison-Wesley, Second edition, 1970.
[28] F. García y A. Nevot, Métodos numéricos en forma de ejercicios resueltos,
UPCU Departamento Publicaciones, Madrid, 1997.
[29] B. García, I. Higueras y T. Roldán, Análisis Matemático y Métodos Numéricos,
Universidad Pública de Navarra, Campus de Arrosadia, Pamplona, España,
2005.
[30] M. Gasca, Cálculo Numérico. Resolución de ecuaciones y sistemas, Editora
Librería Central, Zaragoza, 1987.
[31] E. Gaughan, Introducción al análisis, Editorial Alhambra S. A, Madrid, 1972.
[32] W. Gautschi, Numerical Analysis. An introduction, Birkhäuser Boston, USA,
1997.
[33] J. Gerlach, Accelerated convergence in Newton’s Method, SIAM Review, 36
(1994) 272–276.
[34] J. M. Gutiérrez, M. A. Hernández y M. Amparo Salanova, α-theory for nonlinear
Fredholm integral equations, Grazer Mathematische Berrichte, 346 (2004) 187–
196.
[35] J. M. Gutiérrez, A new semilocal convergence theorem for Newton’s method,
Journal of Computational and Applied Mathematics, 79 (1997) 131–145.
[36] J. M. Gutiérrez, El método de Newton en espacios de Banach, Tesis doctoral,
Universidad de La Rioja, Servicio de Publicaciones, Logroño, 1995.
[37] J. M. Gutiérrez y M. A. Hernández, A family of Chebyshev-Halley type method
in Banach spaces, Austral. Math. Soc. 55 (1997) 113–130.
BIBLIOGRAFÍA
59
[38] M. Grau: Eficiencia computacional de métodos iterativos con multiprescisión,
Comunicación particular.
[39] M. Grau and J. M. Gutiérez: Some family of zero-finder methods derive from
Obreshkov’s techiques, Comunicación particular.
[40] M. A. Hernández y M. A. Salanova, La convexidad en la resolución de ecuaciones escalares no lineales, Servicio de Publicaciones de la Universidad de la
Rioja, Logroño, 1996.
[41] F. H. Hildebrand, Introduction to Numerical Analysis, Dover Publications, Inc,
New York, 1974.
[42] P. Horton, No Fooling! Newton’s Method Can Be Fooled, Mathematics Magazine, 80 (2007) 383–387.
[43] J. A. Infante y J. M. Rey, Métodos numéricos. Teoría, problemas y prácticas
con MATLAB, Ediciones Pirámide, tercera edición, Madrid, 2007.
[44] L. V. Kantorovich, On Newton’s method for functional equations, Dokl. Akad.
Nauk, SSRR 59 (1948) 1237–1240.
[45] L. V. Kantorovich, The majorant principle and Newton’s method. Dokl. Akad.
Nauk, SSRR 76 (1951) 17–20.
[46] L. V. Kantorovich and G. P. Akilov, Functional Analysis, Pergamom, Oxford,
(1982).
[47] A. Kharab and R. B. Guen, An introduction to numerical methods. A MATLAB
approach, Chapman and Hall/ CRC, Florida, 2002.
[48] D. Kincaid, Análisis Numérico, Addison-Wesley Iberoamericana, 1991.
[49] E. Kobal, Notice concerned with the calculation of roots of numerical equations,
Monatsh. Math. 02 (2002) 331–332.
[50] R. J. Knill, A modified Babylonian algorithm, Amer. Math. Monthly, 99 (1997)
734–737.
[51] T. Levi-Civita: Sopra la equazione di Kepler. Astronomische Nachrichten, Vol.
164, (1904) pp. 313–314.
[52] O. M. López, Métodos iterativos de resolución de ecuaciones, Editorial Alhambra, S. A, Madrid, 1986.
[53] R. Lozada, Análisis Matemático, Ediciones Pirámide, Madrid, 1978.
[54] I. Martín. y V. M. Pérez, Cálculo numérico para computación en ciencia e
ingeniería. MATLAB, Editora Síntesis S.A, Madrid, 1998.
[55] V. Muto, Curso de métodos numéricos, Servicio editorial de la Universidad del
Pais Vasco, 1998.
[56] S. Nakamura, Análisis numérico y visualización gráfica con MATLAB, PrenticeHill Inc, A Simon y Schuster Company, Mexico, 1997.
[57] C. Neuhauser, Matemática para ciencias, Pearson Educación, S. A, Madrid,
2004.
[58] I. Newton, Sir Isaac Newton Mathematical Principles of Ntural Philosophy and
his System of the World, University of California Press, Berkeley, 1934.
[59] A. Newmaier, Introduction to numerical analysis, Cambridge University Press,
UK, 2001.
60
BIBLIOGRAFÍA
[60] J. M. Ortega and W. C. Rheinbolt, Iterative Solution of Nonlinear Equations
in Several Variables, SIAM, Philadelphia, 2000.
[61] M. A. Ostrowski, Solution of Equations and Sistems of Equations, Academic
Press, New York, 1966.
[62] M. A. Ostrowski, Solution of Equations in Euclidean and Banach Spaces, Academic Press, New York, 1976.
[63] A. Y. Özban, Some new variants of Newton’s method, Applied Mathematics
Letters, 17 (2004) 667–682.
[64] J. R. Pastor, P. Callejas y C. Trejo, Análisis Matemático, Editora Kapeluz,
Argentina, 1969.
[65] M. Pal, Numerical analysis for scientists and engineers, Alpha Science International Ltd, United Kingdom, 2007.
[66] A. Quarteroni y F. Saleri, Cálculo científico con MATLAB y Octave, SpringerVerlag, Roma, 2006.
[67] V. Ramírez, D. Barrera, M. Pasadas y P. González, Cálculo numérico con Mathematica, Editora Ariel, Barcelona, 2001.
[68] A. Ralston, Introducción al análisis numérico, Editora Limusa, México, 1978.
[69] F. J. Rodríguez, Cálculo y Métodos Numéricos. Teoría, Algoritmos y Problemas resueltos, Universidad Pontificia de Comillas, Colección Ingeniería, Madrid,
España, 2003.
[70] T. R. Scavo and J. B. Thoo, On the geometry of Halley’s method, American
Mathematical Monthly, 102 (2002) 417–426.
[71] F. Scheid, Análisis Numérico, McGrau-Hill, México, 1998.
[72] E. Schröder, On infinitely many algorithms for solving equations, Math. Ann.
02 (1870) 317–365.
[73] R. E. Scraton, Métodos numéricos básicos, McGrau-Hill, México, 1987.
[74] J. N. Sharma, Numerical methods for engineers and scientists, Alpha Science
International LTD, Second edition, 2007.
[75] W. T. Shaw, Complex analysis with Mathematica, Cambridge University Press,
United Kingdom, 2006.
[76] S. Smale, The fundamental theory for solving equations, The international congress of mathematicians, Providence, USA, 1987.
[77] S. Smale, Newton’s method estimates from data at one point, The Merging of
Disciplines: New Directions in Pure Applied and Computational Mathematics,
R. Ewing, K. Gross and C. Martin (eds.), pp 185–196, Springer-Verlag, USA,
1986.
[78] M. Spivac, Calculus. Cálculo infinitesimal, Editora Reverté, S. A, Segunda edición, Barcelona, 1992.
[79] G. W. Steward, Afternotes on numerical analysis, SIAM, Philadelphia, 1996.
[80] K. Stumpff: On the application of Lie-series to problems of celestial mechanics.
National Aeronautics and Space Administration. Tecnical notes. USA. 1986.
[81] E. Süli and D. Mayers, An introduction to numerical analysis, Cambridge University Press, UK, 2003.
BIBLIOGRAFÍA
61
[82] J. F. Traub, Iterative methods for the solution of equations, Prentice -Hall,
Englewood Cliffs, N.J, 1964.
[83] N. Ujeviéc, An iterative method for solving nonlinear equations, Journal of
Computational and Applied Mathematics, 2 (2006) 1–9.
[84] J. L. Varona, Graphic and numerical comparisons between iterative methods,
Math. Intelligencer, 24 (2002) 37–46.
[85] J. L. Varona, Representación gráfica de fractales mediante un programa de cálculo numérico simbólico, La Gaceta de la RSME, 6 (2003) 214–230.
[86] O. Vaarmann, High order iterative methods for decomposition-coordination problems, Technological and economic development of economy, XII (2006) 56–61.
[87] D. Wang y F. Zhao, The Theory of Smale’s Point Estimation and its Applications, Journal of Computational and Applied Mathematics, 60 (1995) 253–269.
[88] X. H. Wang, Convergence of Newton’s method and uniqueness of the solution
of equations in Banach space, IMA J. Numer. Anal. 20 (2000) 123–134.
[89] J. Wallis: Problematis Kepleriani per cycloidem solutio. Opera Mathematica,
Vol.1, (1695) pp. 540 − −541.
[90] S. Weerakoon and T. G. I. Fernando, A variant of Newton’s method with accelerated third-order convergence, Applied Mathematics Letters, 13 (2000) 87–93.
[91] S. Wolfram, The Mathematica Book, Cambridge University Press, U. K, 1996.
[92] C. Woodford and C. Phillips, Numerical methods with worked examples,
Chapman-Hall, U. K, 1997.
[93] D. T. Whiteside, The mathematical papers of Isaac Newton, Cambridge University Press. 06 (1974) 308–323.
[94] T. Yamamoto, Historical development in convergence analysis for Newton’s and
Newton-like methods, Journal of Computational and Applied Mathematics, 124
(2000) 1–23.
[95] D. M. Young. and R. G. Todd, A Survey of Numerical Mathematics, Dover
Publications, Inc, New York, 1973.
[96] T. J. Ypma, Historical Developmente of Newton-Raphson Method, SIAM Review, 37 (1965) 531–551.
[97] Zhen Shi-Ming, Point estimates for Halley’s iteration, Acta Mathematicae Aplicate Sinica, 14 (1991) 381–383.
[98] http://www.uv.es/diazj/cn_tema2.pdf
[99] http://www.wikipedia.org/wiki/Metodo_de_Newton.html
[100] http://www.uam.es/personalpdi/ciencias/barcelo/cnumerico.html
[101] http://www.neoparaiso.com/logo/metodo-newton.html
[102] http://www.numericalmethods.eng.usf.edu/mws/gen/03n/e/mws.pdf
[103] http://www.descartes.cnice.mecd.es/materialesdidacticos.html
[104] http://www.cidse.itcr.ac.cr/revistamate/HERRAmInternet/ecuaexcl/lnode5.html
[105] http://www.docentes.uacj.mx/gtapia/AN/Unidad21/Newton.html
[106] http://www.numbers.computation.free.fr/Constant/Algoritms/newton.html
62
BIBLIOGRAFÍA
[107] http://www.allege.com/artigos/newtoncas.pdf
[108] http://www.pgrafica.webideas4a11.com/newton_raphson.html
[109] http://www.mathword.wolfram.com/NewtonMethod.html
[110] http://www.ugrad.math.ubc.ca/coursedoc/math100/notes/approx/newton.html
[111] http://www.sosmath.com/calculus/diff/der07/der07.html
[112] http://www.dailnet.unirioja.es/servlet/articulo?codigo=2159507
[113] http://www.mathumn.edu/~garrett/qr/Newton.html
[114] http://www.dedekind.mit.edu/18.013A/HTML/chapter13/section01.html
[115] http://www.ies.co.jp/math/java/cal/roota/roota.html
[116] www.alepho.clarku.edu/~djoyce/newton/method.html
[117] http://www.Shodor.org/UNChen/math/newton/index.html
[118] http://www.reserch.microsotf.com/~minka/papers/newton.html
[119] http:/www.planemath.org/encyclopedia/NewtonRaphsonMethod.html
[120] http://www.math.fullerton.edu/mathews/n2003/Newton’sMethodMod.html
[121] http://www.math.heldermann.de/JAA/JAA09/jaa0919.html
[122] http://numbers.computation.free.fr/Constants/Algorithms/Newton.html
View publication stats
BIBLIOGRAFÍA
63
Este libro se termino de imprimir en el mes de mayo del año 2009 en los talleres
gráficos de ServiCentro
C/ Progreso, Nagua, República Dominicana.