Fundamentos Físicos de la Ingeniería
Anuncio
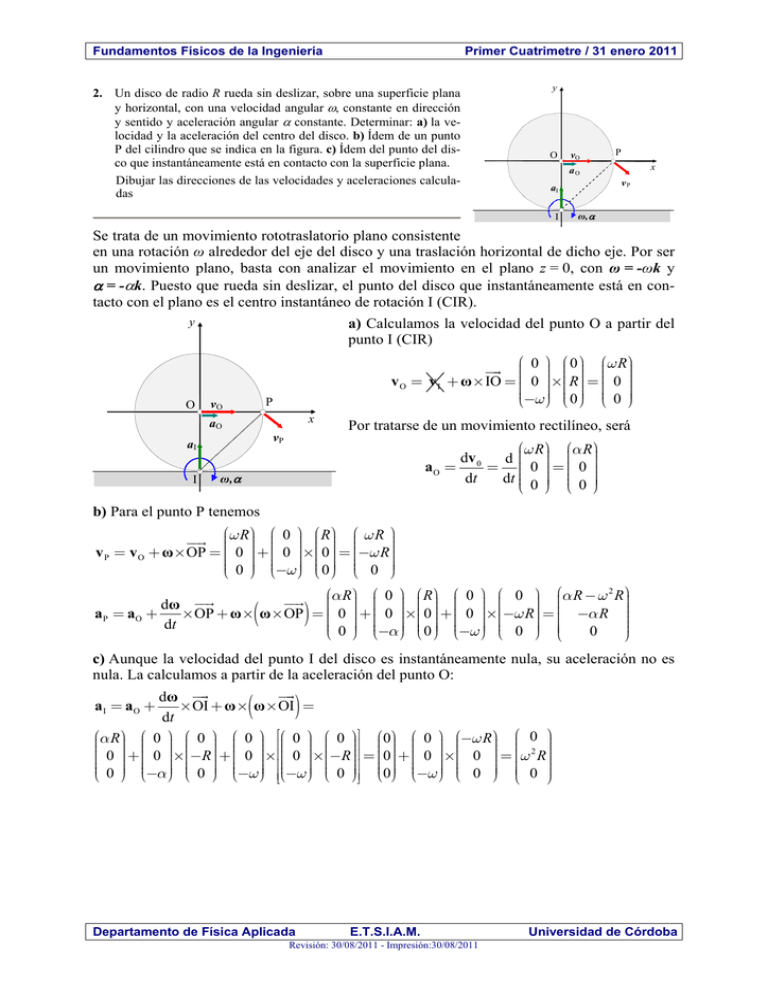
Fundamentos Físicos de la Ingeniería Primer Cuatrimetre / 31 enero 2011 2. Un disco de radio R rueda sin deslizar, sobre una superficie plana y horizontal, con una velocidad angular , constante en dirección y sentido y aceleración angular constante. Determinar: a) la velocidad y la aceleración del centro del disco. b) Ídem de un punto P del cilindro que se indica en la figura. c) Ídem del punto del disco que instantáneamente está en contacto con la superficie plana. Dibujar las direcciones de las velocidades y aceleraciones calculadas y O vO P x aO vP aI I ω, Se trata de un movimiento rototraslatorio plano consistente en una rotación ω alrededor del eje del disco y una traslación horizontal de dicho eje. Por ser un movimiento plano, basta con analizar el movimiento en el plano z = 0, con ω = -ωk y = -k. Puesto que rueda sin deslizar, el punto del disco que instantáneamente está en contacto con el plano es el centro instantáneo de rotación I (CIR). a) Calculamos la velocidad del punto O a partir del punto I (CIR) y O æç 0 ö÷÷ çæ 0 ö÷÷ çæw Rö÷÷ v O = v I + ω ´ IO = ççç 0 ÷÷´ççç R÷÷ = ççç 0 ÷÷ çèç-w ø÷÷ ççè 0 ø÷÷ ççè 0 ÷÷ ø P vO x aO vP aI I Por tratarse de un movimiento rectilíneo, será æw Rö æa Rö dv 0 d çç ÷÷÷ çç ÷÷÷ aO = = çç 0 ÷ = çç 0 ÷ dt dt çç 0 ÷÷ çç 0 ÷÷ è ø è ø ω, b) Para el punto P tenemos æçw Rö÷÷ çæ 0 ÷÷ö çæ R÷÷ö çæ w R ÷÷ö v P = v O + ω ´ OP = ççç 0 ÷÷ + ççç 0 ÷÷´ççç 0 ÷÷ = ççç-w R÷÷ ççè 0 ÷÷ø ççè-w ÷÷ø ççè 0 ÷÷ø ççè 0 ÷÷ø æa Rö÷ æ 0 ö÷ æ Rö÷ æ 0 ö÷ æ 0 ö÷ æça R - w 2 Rö÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ dω ÷ ç a P = aO + ´ OP + ω ´ ω ´ OP = ççç 0 ÷÷ + ççç 0 ÷÷´ççç 0 ÷÷ + ççç 0 ÷÷´ççç-w R÷÷ = çç -a R ÷÷÷ ÷ ÷ ÷ ÷ ÷ dt ÷÷ ççè 0 ÷ø çèç-aø÷ çèç 0 ø÷ ççè-w ÷ø çèç 0 ÷ø çç 0 è ø ( ) c) Aunque la velocidad del punto I del disco es instantáneamente nula, su aceleración no es nula. La calculamos a partir de la aceleración del punto O: dω a I = aO + ´ OI + ω ´ ω ´ OI = dt æa Rö÷ æ 0 ö÷ æ 0 ö÷ æ 0 ö÷ éæ 0 ö÷ æ 0 ÷öù æ0÷ö æ 0 ö÷ æ-w Rö÷ æç 0 ö÷ çç ÷ çç ÷ çç ÷ çç ÷ êçç ÷ çç ÷ú çç ÷ çç ÷ çç ÷ ÷ ç çç 0 ÷÷ + çç 0 ÷÷´çç-R÷÷ + çç 0 ÷÷´ êçç 0 ÷÷´çç-R÷÷ú = çç0÷÷ + çç 0 ÷÷´çç 0 ÷÷ = ççw 2 R÷÷÷ ÷ ÷ ÷ ÷ ÷ ÷ ÷ ÷ ÷ ççè 0 ÷ø ççè-a÷ø èçç 0 ÷ø èçç-w ÷ø êèçç-w ÷ø èçç 0 ÷øú ççè0÷ø ççè-w ÷ø ççè 0 ÷ø çç 0 ÷÷ êë úû è ø ( ) Departamento de Física Aplicada E.T.S.I.A.M. Revisión: 30/08/2011 - Impresión:30/08/2011 Universidad de Córdoba Fundamentos Físicos de la Ingeniería Primer Cuatrimetre / 31 enero 2011 3. Un hombre que pesa 80 kg permanece de pie sobre la parte trasera de una gran balsa de 400 kg de peso y 20 m de longitud que se está moviendo con una velocidad de 4 m/s sin rozamiento sobre la superficie de un lago de aguas tranquilas. El hombre empieza a caminar sobre la balsa hacia la parte delantera de ésta, con una velocidad de 2 m/s respecto a la balsa. a) Calcular la velocidad de la balsa mientras el hombre está caminando. b) ¿Que distancia habrá recorrido la balsa sobre el lago antes de que el hombre llegue a la parte delantera de la balsa? m v M V L a) Por no existir rozamiento ni ninguna otra fuerza exterior al sistema hombre-balsa, la cantidad de movimiento de éste se conserva. Para un observador exterior, la cantidad de movimiento del sistema antes de que el hombre comience a caminar es: (m + M )V0 Durante el intervalo de tiempo en que el hombre está andando sobre la balsa, su velocidad absoluta será la suma de su velocidad relativa a la balsa (vrel) y de la velocidad de la balsa (V) y la cantidad de movimiento del sistema es: MV + m (vrel + V ) Igualando y despejando V se obtiene (m + M )V0 = MV + m (vrel + V ) (m + M )V0 = MV + mvrel + mV = (m + M )V + mvrel V= (m + M )V0 - mvrel m+M = V0 - m 80 vrel = 4 2 = 4 - 0.33 = 3.67 m/s m+M 80 + 400 b) Como el hombre se mueve con una velocidad de 2 m/s respecto a la balsa, resulta obvio que empleará 10 s en recorrerla. Por lo tanto el trayecto recorrido por la balsa durante los 10 s que emplea el hombre en recorrerla hasta llegar a su parte delantera será: x = Vt = 3.67´10 = 36.7 m Otro planteamiento: Por no existir rozamiento ni ninguna otra fuerza exterior al sistema hombre-balsa, la cantidad de movimiento de éste se conserva: Δp = Δph + Δpb = 0 Durante el intervalo de tiempo en que el hombre está andando sobre la balsa, su velocidad absoluta será la suma de su velocidad relativa a la balsa (vrel) y de la velocidad de la balsa (V), de modo que la expresión anterior nos conduce a: m (vrel + V -V0 ) + M (V -V0 ) = 0 V = V0 - Departamento de Física Aplicada E.T.S.I.A.M. Revisión: 30/08/2011 - Impresión:30/08/2011 m vrel m+M Universidad de Córdoba Fundamentos Físicos de la Ingeniería Primer Cuatrimetre / 31 enero 2011 4. Dos bloques de madera, de 10 kg y 15 kg de masa, se encuentran sobre un plano inclinado y están unidos entre sí por una cuerda ligera que pasa por una polea de rozamiento e inercia despreciables, como se indica en la figura. El coeficiente de rozamiento entre todas las superficies en contacto vale 0.30. Determinar el valor crítico del ángulo de inclinación del plano que impide el deslizamiento de los bloques. m1 θ m2 Comenzamos estableciendo el esquema de fuerzas o diagrama de cuerpo libre correspondiente a cada uno de los bloques, tal como se muestra en la figura, en la que hemos indicado también el sentido de movimiento posible para cada uno de los bloques, teniendo en cuenta que las únicas fuerzas activas son los pesos de los mismos. En las condiciones críticas de movimiento inminente, la resultante de todas las fuerzas actuantes sobre cada bloque será nula, de modo que: ì(1) ï [1] ï í ï ï î(2) ì ï(3) [2] ï í ï ï î(4) N1 = m1 g cos q T = m1 g sen q + f1 = m1 g sen q + m N1 N 2 = N1 + m2 g cos q m2 g sen q = T + f1 + f 2 = T + m N1 + m N 2 Donde hemos tenido en cuenta que f1 = m N1 y f2 = mN2 . De modo que disponemos de 4 ecuaciones con cuatro incógnitas (T , N1 , N 2 , q ). Sustituyendo las expresiones de N1 y N 2 en las expresiones (2) y (4) tenemos: ïìïT = m1 g sen q + m N1 = m1 g sen q + mm1 g cos q í ïïm2 g sen q = T + m N1 + m ( N1 + m2 g cos q ) = T + 2mm1 g cos q + mm2 g cos q î Y sustituyendo la primera en la segunda, para eliminar la tensión T, tenemos: m2 g sen q = m1 g sen q + 3mm1 g cos q + mm2 g cos q (m2 - m1 ) sen q = m cos q (3m1 + m2 ) De modo que tg q = m 3m1 + m2 3´10 + 15 = 0.3´ = 0.3´9 = 2.7 q = 69.7º m2 - m1 15 -10 Planteamiento rápido: (m2 - m1 ) g sen q = 2 f1 + f 2 = 2mm1 g cos q + m (m1 + m2 ) g cos q = m (3m1 + m2 ) g cos q tg q = m 3m1 + m2 3´10 + 15 = 0.3´ = 0.3´9 = 2.7 q = 69.7º m2 - m1 15 -10 Departamento de Física Aplicada E.T.S.I.A.M. Revisión: 30/08/2011 - Impresión:30/08/2011 Universidad de Córdoba Fundamentos Físicos de la Ingeniería Primer Cuatrimetre / 31 enero 2011 5. Una masa puntual m está colgada de un punto fijo mediante un hilo inextensible de masa despreciable y longitud l. Cuando la masa cuelga verticalmente, recibe una impulsión horizontal, como se indica en la figura. Determinar: a) la velocidad inicial que adquiere la masa.; b) la velocidad de la masa en función del ángulo θ que en un instante dado forma el hilo con la vertical; c) la aceleración tangencial, la aceleración normal y la tensión del hilo. l Π θ m a) Comenzamos determinando la velocidad inicial que adquiere la masa como resultado de la impulsión que recibe: P = Δp = mv0 v0 = P m b) Podemos determinar la velocidad en cualquier otro instante expresando la conservación de la energía: 1 2 1 mv0 - mgl = mv 2 - mgl cos q v 2 = v02 - 2 gl (1- cos q ) 2 2 c) La componente normal de la aceleración se calcula fácilmente a partir de la velocidad, ya que al tratarse de una trayectoria circular será: v2 v2 an = = 0 - 2 g (1- cos q ) l l l T v Para determinar la componente tangencial de la aceleración y la tensión del hilo, aplicamos la ecuación del movimiento en el instante genérico representado en la figura: ïìï-mg sen q = mat í ïïîT - mg cos q = man Π m mg v0 De la primera ecuación se obtiene la aceleración tangencial: at = -g sen q Y de la segunda ecuación se obtiene la tensión del hilo: T = mg cos q + man = mg cos q + m Departamento de Física Aplicada v02 v2 - 2mg (1- cos q ) = m 0 - mg (2 - 3cos q ) l l E.T.S.I.A.M. Revisión: 30/08/2011 - Impresión:30/08/2011 Universidad de Córdoba








