centro educativo paulo freire centro educativo paulo freire taller

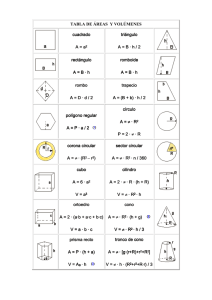
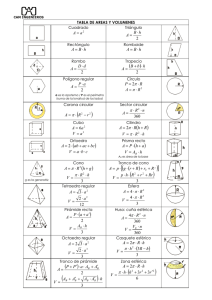
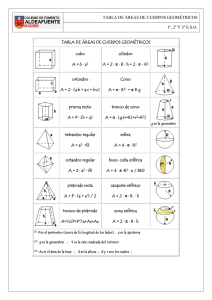
CENTRO EDUCATIVO PAULO FREIRE
TALLER
EJERCICIOS:
1: Una plaza circular está limitada por una circunferencia de
longitud 188,4m. Determinar el diámetro y el área de la plaza.
2: Si el área de un círculo es 144࣊ cm2, determinar la longitud
de la circunferencia que limita al círculo.
3: Calcular el área de las regiones sombreadas de las
siguientes figuras (a, b, c y d).
a)
b)
c)
d)
4: Una mesa circular de 2m de diámetro debe ser cubierta por
un mantel, de tal manera que cuelguen del borde de la mesa
40cm del mantel: ¿Cuántos m2 debe tener el mantel?
PROBLEMAS:
1: Calcular el área de un triángulo si las longitudes de su base
y de su altura son 12m y 15m respectivamente.
2: ¿Cuántas hectáreas tienen un terreno rectangular de 170m
de frente por 110m de fondo?
3: Se desea cubrir con un tapete el piso de una alcoba de 8m
de largo por 5,5m de ancho. ¿Cuánto vale entapizarlo si el
precio por m2 es $800?
4: ¿Qué superficie se puede cubrir con 24 hojas de un
periódico de 80cm de largo por 50cm de ancho?
5: El perímetro de un rectángulo es 48cm y la longitud de la
base es el doble de la altura. ¿Cuál es el área del rectángulo?
6: Se desea construir una carretera de 22Km de largo por una
faja de 8m de ancho. Determinar el precio del terreno que
ocupa la carretera si se compra a $20.000 cada Dm2.
7: Calcular el área de un cuadrado de 80dm de lado.
EJERCICIOS:
1: Determinar el área de la región del plano limitada por un
trapecio, si sus bases miden 40m y 30m, y su altura 10m.
2: El área de un rombo es 54m y la longitud de una de sus
diagonales es 12. ¿Cuál es la longitud de la otra área del
rombo?
3: Calcular el área de un rombo si las longitudes de sus
diagonales son 20cm y 8cm.
4: Hallar el área de un rombo equilátero si su perímetro es
24m.
5: Si el perímetro de un triángulo equilátero es 27m, hallar su
altura y su área.
EJERCICIOS:
1: Dados los cuerpos geométricos de las siguientes figuras,
indicar cuáles son poliedros y cuales son cuerpos redondos.
2: De los poliedros de las figuras ¿Cuáles son prismas?,
¿cuáles son pirámides?
EJERCICIOS: A los cuerpos redondos se les da también el
nombre de cuerpos de revolución, ya que se pueden obtener al
girar figuras planas de una recta en el espacio.
Indicar el nombre de la región del espacio que se obtiene al
girar las siguientes figuras un ángulo de 360º (una vuelta en
el espacio).
a) Un rectángulo
b) Un triángulo rectángulo
- 2 -
c)
Una
semicircunferencia
d) Un semicírculo
PROBLEMAS:
FIGURA
1: El ortoedro ABCDFGHE de la figura,
indicar todos los vértices, las aristas y las
caras.
2: Dos caras de un ortoedro que no tienen
punto común alguno se llaman caras
opuestas del ortoedro. Indicar dos pares
de caras opuestas en el ortoedro
ABCDFGHE de la figura.
3: Dos vértices de un ortoedro que no
pertenecen a una misma cara se llaman
vértices opuestos del ortoedro ABCDFGHE de la figura.
4: Dos aristas paralelas en un ortoedro que no están sobre una
misma cara se llaman aristas opuestas del ortoedro. Indicar
tres partes de aristas opuestas en el ortoedro ABCDFGHE de la
figura.
5: Cada par de vértices opuestos determinan una diagonal del
ortoedro. Indicar dos diagonales en el ortoedro ABCDFGHE de
la figura.
EJERCICIOS:
1: La suma de las medidas de todas las aristas de un cubo es
80cm. ¿Cuál es el volumen del cubo? (12 aristas)
2: Una caja de 3cm de altura tiene por base un cuadrilátero
regular (cuadrado). Si el volumen es 75cm3, determinar la
longitud del lado del cuadrilátero.
- 3 -
3: El volumen de una caja cúbica es 5.832cm3. Determinar el
número de cubos de 6cm de aristas que se pueden incluir en la
caja.
PROBLEMAS:
1: El área de la base de una pirámide cuadrangular es 40dm2 y
su volumen 200dm3. ¿Cuál es la longitud de la altura de la
pirámide?
2: Calcular el volumen de una pirámide recta si se sabe que
tiene por base un triángulo rectángulo de catetos 8cm y 4cm, y
que la altura es la tercera parte de la suma de las medidas de
los catetos de la base.
3: La carpa de un circo tiene forma de una pirámide regular
cuadrangular (base un cuadrado). Si la altura de la carpa es
30m y el lado de la base mide 20m, ¿Cuál es el volumen de la
región del espacio que encierra la carpa?
4: La torre de una iglesia se compone de un ortoedro de 20m
de altura y de base un rectángulo de lados 5m y 4m, y de
pirámide recta de igual base y de altura 6m, colocada sobre el
ortoedro.
¿Cuál es el volumen de la torre?
EJERCICIOS:
1: Calcular el volumen de un cono si tiene 24cm de altura y si
de longitud de la circunferencia de la base es 56,52cm.
2: El volumen de un cilindro es 780cm3. Si su altura es
12,56cm, ¿Cuál es la longitud de la circunferencia de la base?
3: Calcular los volúmenes de un cilindro y de un cono que
tienen igual altura (12cm) e igual base (6cm de diámetro).
¿Cómo están relacionados estos dos volúmenes?
4: Un pozo, de forma cilíndrica, tiene un orificio de longitud 4m
y una profundidad de 8m. ¿Cuántos días duro su perforación si
se sabe que por días se extraen 10m3 de tierra?
5: Un cigarrillo tiene 0,8cm de longitud. ¿Se pueden empacar
20 de estos cigarrillos en una caja en forma de ortoedro de
aristas 8cm, 5,6cm y 2,4cm?
EJERCICIOS:
1: Un jardinero ha dado a un pino la forma que
ilustra en la figura. El volumen del espacio que
ocupa el pino es:
- 4 -
2: El volumen del cuerpo geométrico de la figura:
3: El carro tanque de la figura siguiente cobra cada dm de
combustible que movilice, a razón $ a por kilómetro. El precio
por trasporte t kilómetros el tanque complemento lleno es:
MODELACIÓN: Encerrar las figuras que no son polígonos.
1:
4:
2:
5:
3:
6:
RAZONAMIENTO: Resolver a partir de la figura.
1: ¿Cuántos triángulos hay?
2: ¿Todos los triángulos son regulares?
3: ¿TZKYWS es un polígono?
4: ¿AZKD es un polígono? ¿Por qué?
5: Suponer que TZKYWS es un hexágono,
¿Qué medida tienen los ángulos T, Z, K, Y, W
y S?
6: ¿Qué segmentos se deben eliminar de la
- 5 -
estrella para que la figura nombrada en el punto 5 sea
polígono?
EJERCITACIÓN: Utilizar las propiedades de los triángulos para
determinar la medida del ángulo que falta:
1:
3:
2:
4:
EJERCITACIÓN: Clasificar los siguientes triángulos según la
medida de sus lado y sus ángulos.
1:
2:
3:
4:
RAZONAMIENTO: Encontrar la medida de los ángulos dadas las
condiciones.
1:
2:
3:
- 6 -