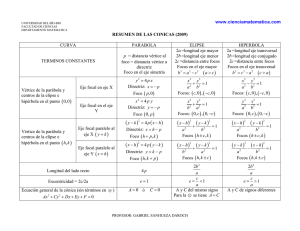
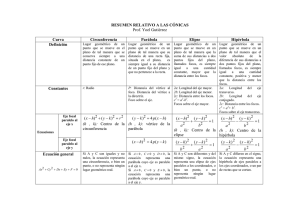
Profesor: Carlos Landero H. Cónicas de la forma
Anuncio
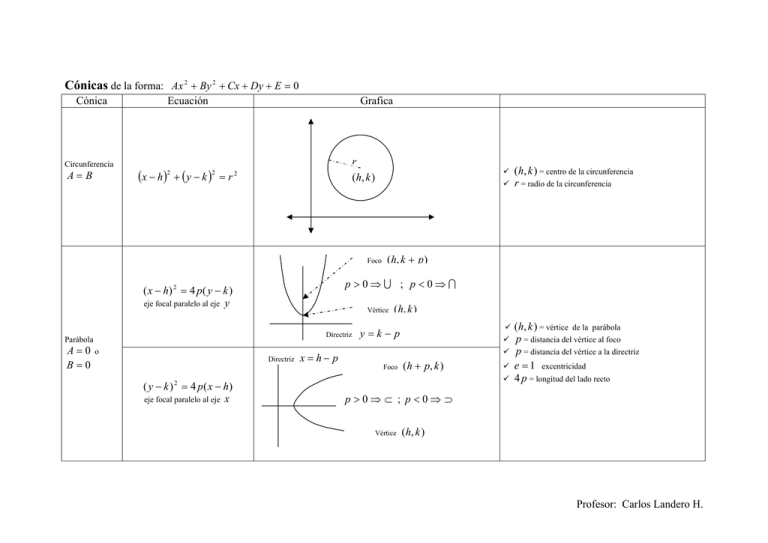
Cónicas de la forma: Ax 2 By 2 Cx Dy E 0 Cónica Circunferencia A B Ecuación x h 2 Grafica y k r 2 r ( h, k ) 2 Foco Directriz Directriz ( y k ) 2 4 p ( x h) eje focal paralelo al eje x (h, k ) = vértice de la parábola p = distancia del vértice al foco p = distancia del vértice a la directriz e 1 excentricidad 4 p = longitud del lado recto ( h, k p ) Vértice Parábola o (h, k ) = centro de la circunferencia r = radio de la circunferencia p0 ; p0 ( x h) 2 4 p ( y k ) eje focal paralelo al eje y A0 B0 x h p ( h, k ) ykp Foco ( h p, k ) p0 ; p0 Vértice ( h, k ) Profesor: Carlos Landero H. Centro A B Vértices ( h a, k ) ( h a, k ) Focos ( h c, k ) ( h c, k ) igual signo ( h, k a ) ( h, k a ) Vértices ( y k) ( x h) 1 2 a b2 eje focal paralelo al eje y 2 2 Centro Focos ( x h) 2 ( y k ) 2 1 a2 b2 eje focal paralelo al eje x Focos Centro A B distinto signo ( h c, k ) ( h c, k ) ( h, k a ) ( h, k a ) ( y k) ( x h) 1 2 a b2 eje focal paralelo al eje y 2 Centro Focos 2 ( h a, k ) ( h a, k ) ( h, k ) Vértices 2 ( h, k ) 2 ( h, k c ) ( h, k c ) Vértices Hipérbola ab c a b2 (h, k ) = centro de la elipse 2a = longitud del eje mayor 2b =longitud del eje menor 2c = distancia entre los focos e c / a 1 excentricidad 2b 2 / a = longitud del lado recto Siempre ( x h) 2 ( y k ) 2 1 a2 b2 eje focal paralelo al eje x Elipse ( h, k ) ( h, k ) c2 a2 b2 (h, k ) = centro de la hipérbola 2a = longitud del eje transverso 2b = longitud del eje conjugado 2c = distancia entre los focos e c / a 1 excentricidad 2b 2 / a = longitud del lado recto ( h, k c ) ( h, k c ) Profesor: Carlos Landero H.