Análisis de vibraciones de una reductora industrial - e
Anuncio

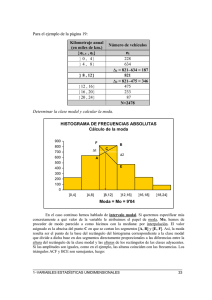
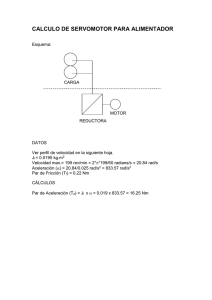
Análisis de vibraciones de una reductora industrial Autor: Pedro Manuel Carrión Abengózar Tutores: Cristina Castejón Sisamón Juan Carlos García Prada Índice Introducción a los engranajes Utilidades de las reductoras de velocidad Modelado con Solid Edge Análisis modal con Femap/Nx Nastran Resultados: Cálculos de las frecuencias de trabajo • Conclusiones • Futuros desarrollos • • • • • Introducción: Objetivos del proyecto Índice: 1.‐ Introducción. 2.‐ Reductoras de velocidad. 3.‐ Modelado 3D 4.‐ Análisis modal. • Planos de una reductora industrial de la marca Belga Hansen Transmission que está en servicio en la fábrica de Alcalá de Henares de la empresa ROCA S.A. 5.‐ Resultados. 6.‐ Conclusiones. 7.‐ Futuros desarrollos. • El objetivo es modelar la reductora en un programa de diseño 3D y realizar estudios estáticos mediante métodos numéricos. Introducción: Evolución de los engranajes Índice: 1.‐ Introducción. 2.‐ Reductora de velocidad. 3.‐ Modelado 3D 4.‐ Análisis modal. 5.‐ Resultados. 6.‐ Conclusiones. 7.‐ Futuros desarrollos. • Anticitera (100 a. C.). • Engranajes helicoidales y epicicloidales, China (50 d. C.). • Engranajes epicíclicos, mundo islámico (S. XI). • Leonardo da Vinci dejo numerosos esquemas de engranajes tipo helicoidal. • Evolución de la envolvente de los dientes. Reductora de velocidad Índice: 1.‐ Introducción. 2.‐ Reductora de velocidad. 3.‐ Modelado 3D 4.‐ Análisis modal. 5.‐ Resultados. Motor eléctrico 4 polos (n=1500rpm) Reductora de velocidad Ortogonal (iT=23,68) 6.‐ Conclusiones. 7.‐ Futuros desarrollos. Montaje del conjunto Cinta transportadora (n=62,08rpm) Reductora de velocidad: Datos técnicos de la reductora ortogonal Reductor Hansen Power Plus RNG34S‐BNN‐23: Índice: 1.‐ Introducción. 2.‐ Reductora de velocidad. Relación de reducción 3.‐ Modelado 3D 4.‐ Análisis modal. 5.‐ Resultados. 6.‐ Conclusiones. 7.‐ Futuros desarrollos. Etapa 1 2 Etapa 2 3,2 Etapa 3 3,7 Total 23,68 Datos de entrada Datos de salida Velocidad [rpm] 1480 62,08 Potencia [kW] 75 70,5 Par [Nm] 483,1 10844,5 Modelado 3D Índice: 1.‐ Introducción. 2.‐ Reductora de velocidad. 3.‐ Modelado 3D 4.‐ Análisis modal. 5.‐ Resultados. 6.‐ Conclusiones. 7.‐ Futuros desarrollos. Modelado de las piezas que componen la reductora de velocidad con Solid Edge: • • • • Engranajes – Ejes de transmisión. Rodamientos. Carcasas y tapas. Ensamblaje. Modelado 3D: Engranajes – Ejes de transmisión Índice: 1.‐ Introducción. 2.‐ Reductora de velocidad. Diseñador de engranajes rectos y cónicos de SE Coronas dentadas 3.‐ Modelado 3D 4.‐ Análisis modal. 5.‐ Resultados. 6.‐ Conclusiones. 7.‐ Futuros desarrollos. Piñones Engranajes Modelado 3D: Rodamientos Índice: 1.‐ Introducción. 2.‐ Reductora de velocidad. Base de datos de rodamientos de SKF: 3.‐ Modelado 3D 4.‐ Análisis modal. 5.‐ Resultados. 6.‐ Conclusiones. 7.‐ Futuros desarrollos. Rodamiento de rodillos a rótula: Modelado 3D: Carcasas y tapas. Índice: 1.‐ Introducción. 2.‐ Reductora de velocidad. 3.‐ Modelado 3D 4.‐ Análisis modal. 5.‐ Resultados. 6.‐ Conclusiones. 7.‐ Futuros desarrollos. Carcasas Tapas Modelado 3D: Ensamblaje Índice: Modelo ensamblado: 1.‐ Introducción. 2.‐ Reductora de velocidad. 3.‐ Modelado 3D 4.‐ Análisis modal. 5.‐ Resultados. 6.‐ Conclusiones. 7.‐ Futuros desarrollos. Animación del modelo: Modelado 3D: Ensamblaje Índice: Imagen renderizada de la reductora: 1.‐ Introducción. 2.‐ Reductora de velocidad. 3.‐ Modelado 3D 4.‐ Análisis modal. 5.‐ Resultados. 6.‐ Conclusiones. 7.‐ Futuros desarrollos. Detalle del engranaje Análisis modal con Femap y NX/Nastran Índice: 1.‐ Introducción. 2.‐ Reductora de velocidad. 3.‐ Modelado 3D 4.‐ Análisis modal. 5.‐ Resultados. 6.‐ Conclusiones. 7.‐ Futuros desarrollos. • Un modo normal de un sistema oscilatorio es la frecuencia a la cual la estructura deformable oscilará al ser perturbada. Los modos normales son también llamados frecuencias naturales o frecuencias resonantes. Para cada estructura existe un conjunto de estas frecuencias que es único. Ecuación diferencial del movimiento ondulatorio v2 ∂ 2ψ ∂ 2ψ = 2 ∂x 2 ∂t fn = ωn n = 2π 2 L n = 1, 2,3,... ⎛ nπ yn ( x ) = A sin ⎜ ⎝ L • Femap y Nx/Nastran ⎞ x⎟ ⎠ Análisis modal con Femap y NX/Nastran Índice: 1.‐ Introducción. 2.‐ Reductora de velocidad. 3.‐ Modelado 3D 4.‐ Análisis modal. Mallado de la estructura 1.‐ Análisis de modos normales de vibración del conjunto reductora de velocidad. 5.‐ Resultados. 6.‐ Conclusiones. 7.‐ Futuros desarrollos. 2.‐ Análisis de modos normales de vibración del mecanismo interior de la reductora de velocidad. Análisis modal ¡Error! La memoria virtual esta completa, se necesita una ampliación Análisis modal con Femap y NX/Nastran Análisis Modal Índice: 1.‐ Introducción. 2.‐ Reductora de velocidad. Primer modo de vibración Eje 3 1751,619 Hz Eje 2 1858,318Hz Eje 1 2160,629 Hz 3.‐ Modelado 3D 4.‐ Análisis modal. 5.‐ Resultados. 6.‐ Conclusiones. 7.‐ Futuros desarrollos. Análisis modal con Femap y NX/Nastran Análisis Modal Índice: 1.‐ Introducción. 2.‐ Reductora de velocidad. 3.‐ Modelado 3D 4.‐ Análisis modal. Primer modo de vibración Carcasa 285,3538 Hz Eje Piñón Cónico 3636,189 Hz 5.‐ Resultados. 6.‐ Conclusiones. 7.‐ Futuros desarrollos. Resultados: Cálculos de las frecuencias de trabajo Datos técnicos de la reductora de velocidad Índice: 1.‐ Introducción. 2.‐ Reductora de velocidad. 3.‐ Modelado 3D 4.‐ Análisis modal. 5.‐ Resultados. 6.‐ Conclusiones. 7.‐ Futuros desarrollos. Potencia (kW) 90 Velocidad (min-1) 1480 Relación de transmisión engranaje cónico i1 2 Relación de transmisión primer 3,2 engranaje recto i2 Relación de transmisión segundo 3,7 engranaje recto i3 Relación de reducción total iT 23,68 Frecuencias de trabajo de los ejes: ω = 2π f nejepiñóncónico = n1 = 153,93 rad ⇒ f ejepiñóncónico = 24, 49 Hz n1 = 76,97 rad s i1 ⇒ f eje1 = 12, 25Hz n1 = 24,05 rad s i1 ⋅ i2 ⇒ f eje 2 = 3,83Hz n1 = n2 = 6,5 rad s i1 ⋅ i2 ⋅ i3 ⇒ feje3 = 1,03Hz neje1 = neje 2 = neje3 = s Resultados: Cálculos de las frecuencias de trabajo Índice: Composición de ondas: 1.‐ Introducción. 2.‐ Reductora de velocidad. 3.‐ Modelado 3D 4.‐ Análisis modal. 5.‐ Resultados. 6.‐ Conclusiones. 7.‐ Futuros desarrollos. Frecuencias de trabajo de la carcasa: Frecuencias (Hz) Ejes del reductor Eje Piñón Cónico 24,49 Hz Eje 1 12,25 Hz Eje 2 3,83 Hz Eje 3 1,03 Hz Carcasa principal 122,5 Hz Conclusiones Índice: 1.‐ Introducción. 2.‐ Reductora de velocidad. 3.‐ Modelado 3D 4.‐ Análisis modal. 5.‐ Resultados. 6.‐ Conclusiones. 7.‐ Futuros desarrollos. • Modelo 3D de una reductora industrial real, para su estudio. • Análisis de vibraciones de cada elemento de la misma, comprobando las frecuencias de trabajo características para estudiar su integridad. • Se han utilizado y probado los programas de modelado y simulación SE y FEMAP comprando que son buenos sistemas de análisis de elementos mecánicos Conclusiones ¡Peligro de daño estructural! Índice: 1.‐ Introducción. 2.‐ Reductora de velocidad. Frecuencia de trabajo Modo de vibración n 3.‐ Modelado 3D 4.‐ Análisis modal. ¡RESONANCIA! 5.‐ Resultados. 6.‐ Conclusiones. 7.‐ Futuros desarrollos. Frecuencias de trabajo (Hz) Primer modo de vibración (Hz) Eje Piñón Cónico 24,49 Hz 3636,189 Hz Eje 1 12,25 Hz 2160,629 Hz Eje 2 3,83 Hz 1858,318Hz Eje 3 1,03 Hz 1751,619 Hz Carcasa 122,5 Hz 285,3538 Hz Conclusiones Índice: 1.‐ Introducción. 2.‐ Reductora de velocidad. 3.‐ Modelado 3D 4.‐ Análisis modal. 5.‐ Resultados. 6.‐ Conclusiones. 7.‐ Futuros desarrollos. • Efecto de la resonancia. Copa de cristal Puente de Tacoma Futuros desarrollos Índice: 1.‐ Introducción. 2.‐ Reductora de velocidad. 3.‐ Modelado 3D 4.‐ Análisis modal. 5.‐ Resultados. 6.‐ Conclusiones. 7.‐ Futuros desarrollos. • Realizar estudios de defectos típicos en este sistema mecánico para su inclusión en el estudio de vibraciones. Para mejorar el mantenimiento predictivo que se ha iniciado. •Utilizar otros software de elementos mecánicos que permitan realizar el análisis del conjunto completo, e incluso análisis de vibraciones dinámicos (Abaqus, Cosmos). Análisis de vibraciones de una reductora industrial Autor: Pedro Manuel Carrión Abengózar Tutores: Cristina Castejón Sisamón Juan Carlos García Prada GRACIAS POR SU ATENCIÓN