Detector de secuencia
Anuncio

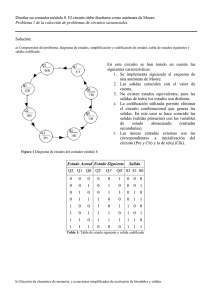
Problema de circuito secuencial. Se trata de diseñar un circuito con una única entrada y una única salida que detecte la presencia de cualquiera de las dos secuencias siguientes: a) 010 b) 111. La salida se debe activar al recibir el último digito de la secuencia y situar el circuito en disposición de detectar una nueva secuencia. ___________________________________________________________________________ Solución: a) Diagrama de estados Figura 1: Diagrama de estados inicial b) Tabla de estados siguientes y salida Estado Actual Estado Siguiente Salida E=0 E=1 E=0 E=1 S0 S1 S2 0 0 S1 S3 S4 0 0 S2 S5 S6 0 0 S3 S0 S0 0 0 S4 S0 S0 1 0 S5 S0 S0 0 0 S6 S0 S0 0 1 Tabla 1: Tabla de estados siguientes y salida c) Simplificación de estados S1 S2 S3 S4 S5 S6 S1- S3 S2- S4 S1- S5 S2- S6 S1- S0 S2- S0 X S1- S0 S2- S0 X S0 S3- S5 S4- S6 S3- S0 S4- S0 X S3- S0 S4- S0 X S1 S5- S0 S6- S0 X S5- S0 S6- S0 X S2 X X X S3 X S4 X S5 Tabla 2: Tabla de implicaciones. Introducción de datos. Recorremos ahora la tabla de implicaciones para ver si se cumplen las condiciones. Así en la primera celda que analiza si S1 y S2 son equivalentes vemos que lo deben ser S2 y S4 y estos no lo son (en su casilla tienen una cruz). Por tanto no son equivalentes y así lo marcamos. Hacemos lo mismo con las restantes. S1 S2 S3 S4 X X X X X X X X X S5 X X X S6 X S0 X S1 X S2 X X X S3 X S4 X S5 Tabla 3: Primera revisión Finalmente observamos que los estados S3 y S5 son los únicos estados equivalentes, con lo que el diagrama de estados simplificado es el siguiente. Figura 2: Diagrama de estados simplificado d) Tabla de estados siguientes y salida codificados. Estado Actual Estado Siguiente E=0 Salida E=1 E=0 E=1 Q2 Q1 Q0 Q2' Q1' Q0' Q2' Q1' Q0' S0 0 0 0 1 1 0 0 1 1 0 0 S1 1 1 0 0 1 0 1 0 0 0 0 S2 0 1 1 0 1 0 0 0 1 0 0 S3 0 1 0 0 0 0 0 0 0 0 0 S4 1 0 0 0 0 0 0 0 0 1 0 S6 0 0 1 0 0 0 0 0 0 0 1 - 1 0 1 X X X X X X X X - 1 1 1 X X X X X X X X Tabla 4: Tabla de estado siguiente y salida codificada e) Elección de los elementos de memoria y tablas de excitación Biestables D Estado Actual Estado Siguiente E=0 Salida E=1 E=0 E=1 Q2 Q1 Q0 D2 D1 D0 D2 D1 D0 0 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 0 1 0 0 0 0 0 1 1 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 1 1 0 1 X X X X X X X X 1 1 1 X X X X X X X X Tabla 5: Tabla de excitación de biestables D Biestables SR Estado Actual Estado Siguiente E=0 Salida E=1 E=0 E=1 Q2 Q1 Q0 S2 R2 S1 R1 S0 R0 S2 R2 S1 R1 S0 R0 0 0 0 1 0 1 0 0 X 0 X 1 0 1 0 0 0 1 1 0 0 1 X 0 0 X X 0 0 1 0 X 0 0 0 1 1 0 X X 0 0 1 0 X 0 1 X 0 0 0 0 1 0 0 X 0 1 0 X 0 X 0 1 0 X 0 0 1 0 0 0 1 0 X 0 X 0 1 0 X 0 X 1 0 0 0 1 0 X 0 X O 1 0 X 0 X 0 1 0 1 1 0 1 X X X X X X X X X X X X X X 1 1 1 X X X X X X X X X X X X X X Tabla 6: Tabla de excitación de biestables SR f) Simplificación de variables de estado y de salida Tabla 7: Q 2′ = D 2 = Q 2 Q1Q0 E + Q Q1 E Tabla 8: Q1′ = D1 = Q 2 Q1Q0 + Q 2 Q1 E + Q1Q0 E Tabla 9: Q0′ = D0 = Q2 Q1Q0 E + Q1Q0 E Tabla 10: Z = Q 2 Q1 E + Q1Q0 E g) Circuito secuencial global Figura 3: Circuito secuencial del detector de secuencia. Implementación de tipo Mealy. h) Circuito combinacional Figura 4: Circuitos combinacionales del detector de secuencia i) Simulaciones Figura 5: Cronograma con todas las posibles combinaciones de entrada. Figura 6: Cronograma con entrada no sincronizada con el circuito.