plan de mate discreta sabatino
Anuncio

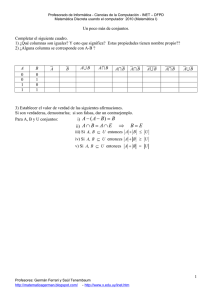
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA ESCUELA DE FORMACIO DE PROFESORES DE ENSEÑANZA MEDIA –EFPEMCATEDRA DE MATEMATICA MATEMATICA DISCRETA Y TEORIA AXIOMATICA CODIGO: M10-31 LICENCIATURA EN LA ENSEÑANZA DE LA MATEMATICA Y LA FISICA PLAN SABATINO CATEDRÁTICO: Lic. Leonel Humberto Ajanel Torres. I. DESCRIPCIÓN DEL CURSO El estudiante de la Licenciatura de la Enseñanza de Matemática y la Física ha adquirido un amplio conjunto de conocimientos en el área de la Matemática. Sin embargo aún no se ha hecho énfasis en el carácter formal que reviste las distintas áreas de esta disciplina. Sin pretender que adquiera las competencias de un profesional de la matemática pura, por la necesidad de una adecuada comprensión de los conceptos matemáticos, es vital que se nutra de la esencia de la metodología de la Matemática, y ésta es, sin duda, el sistema axiomático que está a la base de toda construcción matemática. De ahí que, aunque varios temas ya han sido discutidos en cursos del profesorado, se abordan, ahora desde un punto de vista más formal, de cara a entender la Matemática como un cuerpo de conocimientos construidos lógicamente y con una estructura que permita la continuación de ese cuerpo. Especial énfasis se hará en la comprensión de las demostraciones. II. Competencias Pensamiento lógico, Resolución de problemas, Lectura comprensiva y Escritura Madura. III. Habilidades: Identificar, Diferenciar, Relacionar, Operar, Resolver, Argumentar, Comparar. Demostrar, Inferir. IV. Contenidos 1. Conceptuales 1.1. Fundamentos de Lógica. 1.1.1. Conectivos lógicos y tablas de verdad. 1.1.2. Equivalencia lógica: las leyes de la lógica. 1.1.3. Implicación lógica: Reglas de inferencia. 1.1.4. Cuantificadores. Cuantificadores y demostración de teoremas. 1.2. Teoría de Conjuntos. 1.2.1. Conjuntos y subconjuntos. 1.2.2. Operaciones entre conjuntos y las leyes de la teoría de conjuntos. 1.2.3. Técnicas de conteo y diagramas de Venn. 1.3. Inducción matemática. 1.3.1. El principio del buen orden. 1.3.2. Demostración de teoremas. 2. Procedimentales Identifica los diferentes procesos para resolver problemas de lógica. 3. Actitudinales Trabajo cooperativo Analiza, explica y resuelve problemas de lógica. Actitud crítica Autonomía Creatividad Relaciona la lógica con la teoría de conjuntos. Aplica métodos para resolver problemas de lógica y de la teoría de conjuntos Actitud reflexiva Autorreflexión (metacognición) Revisión y autoevaluación (autorregulación) 1.4. Álgebra booleana. 1.4.1. Circuitos combinatorios. 1.4.2. Funciones booleanas y simplificación de circuitos. Aplica estrategias de lectura comprensiva y escritura madura en la resolución de problemas. Demuestra teoremas aplicando las reglas de inferencias. V. No. Evaluación Actividades Valoración (puntos) 1 Prueba corta 10 2. Prueba parcial 1 20 3 Prueba parcial 2 20 4 Hojas de trabajo cooperativo 10 5. Tareas 10 6. Evaluación final 30 Total 100 El curso se aprueba con una nota mínima de 61 puntos de 100. Fecha de realización o entrega 13/06 14/06 20/06 20/06 27/06 27/06 VI. Metodología En cada sesión, la clase se desarrollará en 4 momentos. 1. Introducción: En la que se indicará el tema a desarrollar, activación de pre saberes, desequilibrio cognitivo y modelaje. 2. Trabajo personal: lectura de texto y ejercitación, realización de pruebas. 3. Trabajo cooperativo: Realización de ejercicios cooperativos. 4. Puesta en común. VII. Recursos: Texto impreso, textos y revistas digitales, pizarra, marcadores y computadora. VIII. Bibliografía. 1. Bustamante Arias, Alfonso. (2009). Lógica y argumentación, de los argumentos inductivos a las álgegras de Boole. 1ª. ed. México: Pearson educación. 2. Grimaldi, R. (1998). Matemáticas discretas y Combinatoria. 3ª. ed. México: Pearson Prentice Hall. 3. Lipschutz, Seymour. (1991). Teoría de conjuntos y temas afines. México: McGraw-Hill Interamericana. 4. Rosen, Kenneth H. (2004). Matemática discreta y sus aplicacaciones. 5ª. ed. España: McGraw-Hill Interamericana. 5. Solow. Daniel. (1993). Cómo entender y hacer demostraciones en matemáticas. México: Limusa.