1. La expresión de 0.33 0.11 como porcentaje es

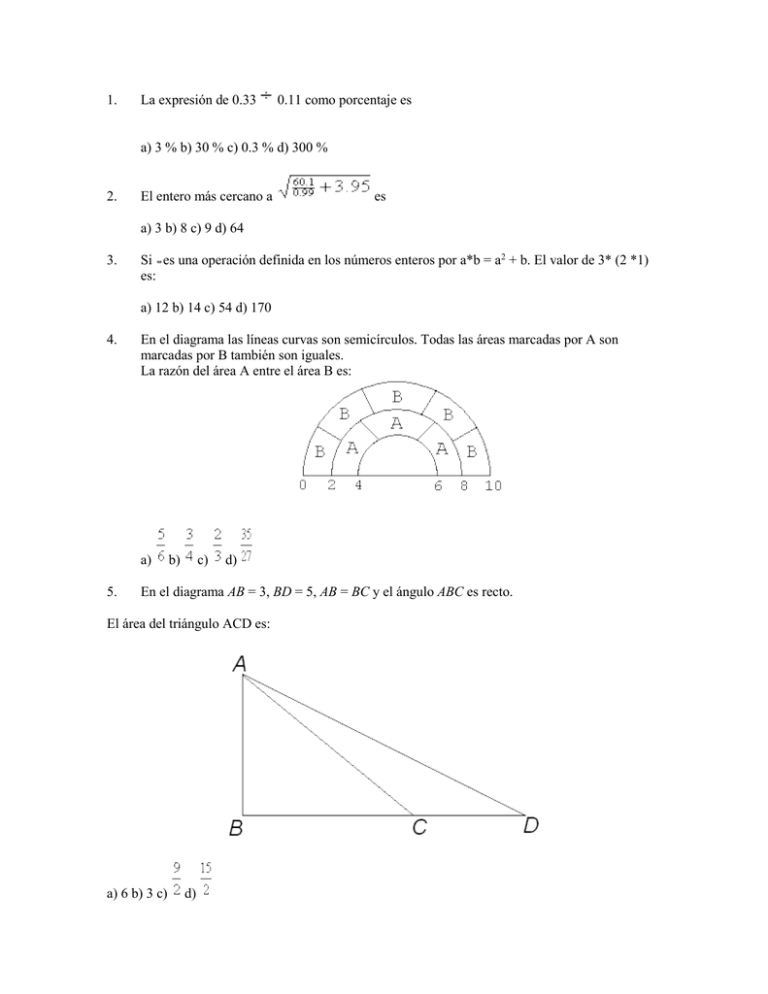
1.
La expresión de 0.33
0.11 como porcentaje es
a) 3 % b) 30 % c) 0.3 % d) 300 %
2.
El entero más cercano a
es
a) 3 b) 8 c) 9 d) 64
3.
Si es una operación definida en los números enteros por a*b = a2 + b. El valor de 3* (2 *1)
es:
a) 12 b) 14 c) 54 d) 170
4.
En el diagrama las líneas curvas son semicírculos. Todas las áreas marcadas por A son
marcadas por B también son iguales.
La razón del área A entre el área B es:
a)
5.
b)
c)
d)
En el diagrama AB = 3, BD = 5, AB = BC y el ángulo ABC es recto.
El área del triángulo ACD es:
a) 6 b) 3 c)
d)
6.
Los enteros mayores que uno se van colocando en las columnas P, Q, R, S y T como se
muestra. La columna en la cual se colocara el número 2002 es:
a) P b) R c) S d) T
7.
Se tiene cinco pedazos de cadena, cada uno con tres eslabones. Si cuesta $1 cortar un eslabón
y $2.50 soldarlo, el menor costo para hacer una cadena que ocupe los 15 eslabones es:
a) $10.50 b) $14 c) $19.50 d) $9.50
8.
Un solo pedazo de cuerda se pasa por los hoyos del cartón. La parte de arriba del cartón se
muestra en la figura.
De las siguientes figuras una de ellas no puede ser la parte de debajo del cartón, ésta es:
9.
La suma de dos enteros es -4 y su producto es -21. El mayor de esos enteros es:
a) -7 b) -3 c) 3 d) 7
10. En un año un equipo de básquetbol jugó 180 juegos. Nunca perdió más de 3 juegos seguidos
y nunca ganó más de 5 juegos seguidos. El número de juegos que ganó debió haber sido
a) No más de 45 b) No más de 150
c) No más de 135 d) exactamente 111
11.
Los números en las caras opuestas de un dado suman 7, así, 2 y 5, 4 y 3, 6 y1 están en caras
opuestas. Los cuatro dados de la siguiente figura están colocados de manera que las caras que
se tocan siempre suman 9. El número de juegos que ganó debió haber sido:
a) 4 b) 3 c) 1 d) 2
12.
En la siguiente figura las rectas AN, AM y BC son tangentes al círculo y la longitud de AN es
7. El perímetro del triángulo ABC es:
a) 12 b) 13 c) 14 d) 15
13.
Un número entero se llama número ascendente si cada uno de sus dígitos es mayor que el
dígito de la izquierda. Por ejemplo 2478 es un número ascendente. La cantidad de números
ascendentes entre 4 000 y 5 000 es:
a) 7 b) 8 c) 9 d) 10
14.
Si en el cuadrado ABCD el triangulo ABE es equilátero, el ángulo BFC mide
a) 120º b) 105º c) 90º d) 95º
15. Dos postes verticales de diferentes alturas están colocados a nivel del piso. Dos cuerdas
amarradas en la parte de arriba de cada poste se amarran también a la base del otro poste. Las
cuerdas se cruzan en un punto que está a 24 m de altura. Si el poste más bajo mide 40 m de
altura, la altura del otro poste es:
a) 48 m
b) 52 m
c) 56 m
d) 60 m
16.
a)
17.
Considerando la siguiente figura, la pendiente de O A es:
b)
d)
Si
a) 3 b)
18.
c)
, el valor de
c)
es:
d) 5
De un cubo de cinco unidades por lado se han quitado todos los cubitos para formar túneles
de un lado a otro con la forma que se indica. ¿Cuántos cubitos se han quitado?
a) 25 b) 45 c) 33 d) 31
19.
Las cifras 1, 2, 3, 4, 5 y 6 se usan para escribir un número abcdef de seis dígitos tal que abc es
divisible entre 4, bcd es divisible entre 5, cde divisible entre 3 y def es divisible entre11. El
digito a es:
a) 1 b) 2 c) 3 d) 4
20.
El promedio de n números positivos es 60. Después de quitar uno de los números, el
promedio de los n-1 restantes es 70. El máximo valor de n es:
a) 6 b) 7 c) 8 d) 12
21. Los de los ahorros de Pablo son 21 pesos ¿Cuánto dinero tiene ahorrado?
a) 147 b) 9 c) 49 d) 12
22. El ángulo C O B mide 120ْ, El ángulo C O D es la mitad del ángulo B O A.¿Cuánto mide el
ángulo B O A?
a) 90ْ b) 60ْ c) 20ْ d) 40ْْ
23. De 120 estudiantes de ingles o francés hay 100 que llevan clase de ingles y 50 clases de francés
¿Cuántos llevan francés nada más?
a) 20 b) 30 c) 25 d) 40
24. Sofía tendrá 21 en el año 2000 y en ese año tendrá el triple que su prima Isabel.¿En qué año
nació Isabel?
a) 1995 b) 1993 c) 1996 d) 1994
25. Una caja de manzanas se vende a 16 pesos, un árbol de manzanas en producción da
aproximadamente tres cajas al año. En una huerta con 144 árboles los de los árboles están en
producción ¿Qué cantidad de dinero daría la huerta si se vendiese la producción?
a) 4,382 b) 5,510 c) 5,760 d) 6,612
26. En la figura, ABEF es un rectángulo y el triángulo CDE es un triángulo isósceles, AB = 100cm;
AF es el triple de AB, BC es el doble de AB y el perímetro de la figura es 9.41 m.La longitud de CD
es:
a) 1.41 m b) 2.41 m c) o.41 m d) 3.41 m
27. Si N es un número con este aspecto 3a42b, con a y b dígitos. ¿De cuántas maneras puedo elegir
a y b para que N sea divisible por 6?
a) 2 b) 19 c) 17 d) 6
28. Sabiendo que BCDE es un cuadrado y que ABE es un triángulo equilátero con 18 cm. de
perímetro, calcula el perímetro del pentágono ABCDE
29 En la tienda puedo comprar por $1 un refresco o un chocolate o un paquete de galletas, por $2
una torta o un sándwich o un helado. Si quiero gastar exactamente $3 ¿De cuántas maneras puedo
hacerlo sin tener cosas repetidas?
a)6 b) 10 c) 9 d) 12
30. Ya completé los del álbum, para llenar
estampas, en total, llevan el álbum?
de lo que me falta necesito 36 estampas. ¿Cuántas
a) 76 b) 360 c) 136 d) 158
31. En un triángulo isósceles uno de los ángulos mide 22ْ ¿Cuántos grados puede medir otro de los
ángulos?
a) 78 b) 80 c) 136 d) 158
32. El perímetro de un cuadrado es 3 veces el perímetro de otro cuadrado. ¿Cuántas veces el área
del mayor es el área del cuadrado menor?
a) 9 b) 2 c) 3 d) 6
33. Si el camino sigue siempre el mismo patrón:
¿Cuál es la sucesión de flechas que van del punto 425 al punto 427?
34. El número que se encuentra a la mitad entre
a)
35. Si
b)
c)
y
es:
d)
A =60ْ
E = 40ْ y
C =30ْ entonces
BDC =
a) 60º b) 50º c) 30º d) 40º
36. La siguiente figura se puede doblar de manera que se forme un cubo, ¿Cuál es la letra que en la
cara opuesta a la cara marcada con x al formar el cubo?
a) B b) C c) D d) E
37. Un auto viaja del punto A al punto B. Si sólo puede viajar hacia el sur o hacia el este. ¿Cuántas
rutas distintas puede tomar?
a) 10 b) 9 c) 8 d) 12
38. ¿Cuántos números distintos pueden formarse al tomar dos o tres dígitos consecutivos del
número 123456789101112? Recuerda que 1 no es primo
a) 5 b) 6 c) 7 d) 8
39. El diagrama muestra las equivalencias entre las figuras. ¿Cuántas Y se necesitarían para
balancear una Z?
a) 4 b) 6 c) 3 d) 5
40. Los números 1, 2, 3, 4,5 se colocan en la figura de modo que solo aparezcan una vez en cada
renglón, una vez en cada columna y una vez en cada diagonal. El valor P + Q es:
a) 61 b) 8 c) 9 d) 7
41. ¿Cuántos es (1·9·9·9) – (1+9+9+9)?
a) 0
b) 701
c) 703
d) 702
42. Si Sofía le da a Pablo dos chocolates, éste le presta su bicicleta durante tres horas. Si le
da doce caramelos se la presta durante dos horas. Sofía le va a dar un chocolate y tres
caramelos. ¿Cuánto tiempo le va a prestar la bicicleta Pablo?
a) 30 minutos
b) 60 minutos
c) 120 minutos
d) 90 minutos
43. Uno de los siguientes números 25, 28, 29, 30, 37 es el promedio de los otros cuatro.
¿Qué número es?
a) 28
b) 29
c) 30
d) 37
44. Se tienen 97 cubos de1 cm. de lado Se fabrica con ellos el cubo más grande posible
pegando unos con otros. ¿Cuántos cubos quedarán inutilizados?
a) 81
b) 16
c) 33
d) 14
45. Si al dividir un entero a entre 10, el resto es igual al cociente. ¿Cuántos valores posibles
de a hay?
a) 0
b) 1
c) 9
d) 10
46. Si un cuadrado tiene área de 225 m2 y cada lado se aumenta 7 m, ¿cuál es el área en
m2 del nuevo cuadrado?
a) 232 m2
b) 274 m2
c) 1575 m2
d) 484 m2
47. Una bola de billar es lanzada desde la esquina de una mesa formando un ángulo de 45º
como se muestra en la figura, la bola siempre rebota formando un ángulo igual al de
llegada. El primer rebote de la bola es el punto O. ¿Qué punto toca en el séptimo rebote?
a) P
b) N
c) T
d) M
48. Un número x es la mitad de otro y el doble de un tercero. La suma de los otros es 917.
¿Cuál es el valor de x?
a) 425
b) 524
c) 262
d) 181
49. ¿Cuántas veces forman un ángulo recto las agujas de un reloj entre las 12 del mediodía
y las de la noche?
a) 24
b) 12
c) 22
d) 10
50. El largo y el lado de un terreno miden respectivamente 25 m y 12 m. En un dibujo a
escala del mismo el largo mide 10 cm. ¿Cuánto debe medir el ancho?
a) 2 cm
b) 2 cm
c) 4 cm
d) 4 cm
51. Pablo tiene dos veces más hermanos que hermanas, su hermana Sofía tiene cinco veces
más hermanos que hermanas ¿Cuántos hermanos y hermanas hay en esa familia?
a)
4 hermanos, 2 hermanas
b) 2 hermanos, 5 hermanas
c)
5 hermanos, 2 hermanas
d) 2 hermanos, 4 hermanas
52. En un segmento con extremos S (izquierdo) y D (derecho) se colocan los puntos: A tal
que S A = S D; L tal que S L = S D, y U tal que AU = AD. Entonces en le segmento las
letras están en le siguiente orden:
a) SALUD
b) SUALD
c) SAULD
d) SLAUD
53. ¿Cuál es el área de la parte cubierta por el triángulo, usado como unidad de medida un
cuadrito?
a) 15
b) 12
c) 9
d) 6
54. Un triángulo ABC está inscrito en una circunferencia de radio 5 cm. Se sabe que A y B son los
extremos de un diámetro y que la cuerda BC mide 6 cm. Entonces el área del triángulo ABC en
cm2 es:
a) 24
b) 6
c) 12
d) 2
55. Sofía y su papá corren dándole vueltas a la manzana. Si ella corre tres veces más que él y si
ambos empiezan al mismo tiempo en el punto A. ¿en qué punto de la manzana se van a volver a
encontrar?
a) A
b) E
c) G
d) C
56. Con una bomba de vació en cada golpe se puede sacar un tercio del aire de una botella. ¿Qué
fracción del aire original queda después de aplicarle cinco veces la bomba a la botella?
1
1
211
121
a) 243
b) 243
c) 243
d) 243
57.
Siguiendo la serie, ¿cuál será el perímetro de la figura que tenga 327 cuadros sombreados?
a) 668 u
b) 664 u
c) 654 u
d) 644 u
58. El reloj se ha vuelto loco: cada 3 segundos se atrasa un segundo, por eso cada 3 minutos se
atrasa un minuto y cada 3 horas se atrasa una hora. ¿Cuánto tiempo real debe pasar para que mi
reloj complete 24 horas?
a) 72 horas
b) 48 horas
c) 36 horas
d) 42 horas
59.
En un cajón hay 10 pares de calcetines de color rojo y 10 pares de calcetines negros, en otro
cajón hay 10 pares de guantes de color rojo y la misma cantidad de pares de guantes de color negro.
¿Cuántos calcetines y guantes será suficiente sacar de cada cajón para que con ellos se pueda formar
un par cualquiera de calcetines y un par de guantes?
a)
3 calcetines, 21 guantes
b)
11 calcetines, 21 guantes
c)
11 calcetines, 11 guantes
d)
3 calcetines,11 guantes
60. El cuadrado grande mide 169 u2 de superficie. ¿Cuánto mide de la superficie del cuadrado más
pequeño?
a)
169
16
b)
169
4
c)
169
8
d)
169
2
61. Un coche viaja a 90 km/hora. La distancia en metros que recorre en 10 segundos es:
a) 25 b) 1500 c) 250 d) 3240
62. Los números 1, 2, 3, y 4 se colocan en las casillas de cada uno de estas se encuentran
los cuatro números. La suma de los números de las casillas marcadas con * es:
a) 4 b) 7 c) 5 d) 6
63. En le diagrama el área sombreada vale:
a) 21 b) 20 c) 22 d) 19
64. Si
𝑥
a) 2 + 1
, entonces el valor de
𝑥
b) 2 − 1
c)
𝑥
4
+1
es:
𝑥
d) 4 − 1
65. Los lados de un cubo se duplican en longitud. El crecimiento del volumen del nuevo
cubo respecto al original es:
a) 900% b) 700% c) 600% d) 200%
66. A las 12 horas, la manecilla de las horas se mueve dos veces más rápido que
normalmente y la de los minutos a la mitad de su velocidad normal. Cuando las dos
manecillas coinciden por primera vez la hora real es:
a) 3:00 b) 3:30 c) 4.00 d) 6.00
67. Se necesitan 200 ml. De liquido para llenar un vaso a 0.8 de su capacidad. La capacidad
del vaso en ml. Es:
a) 220 b) 225 c) 240 d) 250
68. El ángulo más grande de un triángulo es 35º más que el menor y el menor es 10º menos
que el tercero. El número de grados del menor ángulo es:
a) 45 b) 50 c) 55 d) 60
69. Un cable esta formado al combinar 7 alambres circulares que se tocan como se muestra
en la figura. Para mantenerlos fijos se coloca una banda que los apriete. Si cada alambre
tiene 2 unidades de radio, la longitud de la banda es:
a)
b)
c)
d)
70. El primero de enero de 1986 fue un miércoles. El primero de enero de 1992 cayó en:
a) martes b) miércoles c) jueves d) viernes
71. Cada uno de los números 1, 2, 3, 4, 5, 6 se pinta en una de las caras de un cubo que se
coloca sobre una mesa. De tres posiciones distintas un observador ve la cara de arriba y dos
laterales adyacentes. Las sumas de los números de las caras que ve el observador en esas
tres posiciones son respectivamente 9, 14 y15. El número que se encuentra en la cara
cubierta por la mesa es:
a) 1 b) 2 c) 3 d) 4
72. Un rectángulo ABCD tiene un cuadrado AEFK de área 4 y otro de área 9, GHCJ. Si
EFGH están ubicados y FG = 5 el área sombreada es:
a) 31 b) 33 c) 35 d) 37
73. En el diagrama AD = DB = 5, EC = 2AE = 8 y la medida del ángulo AED es 90º. La
longitud de BC es:
a)
b)
c)
d)
74. Si a = 2b y b = 4c entonces a + 2b-8c vale.
a) 8c b) 4c c) 12c d) 16c
75. Si el número de cuatro dígitos 8mn9 es el cuadrado de un número entero, entonces m +
n vale:
a) 11 b) 4 c) 6 d) 10
76. Si 10 maquinas idénticas hacen que la producción de una fabrica pase de 1500 unidades por
hora a 2250 unidades por hora, ¿cuántas máquinas serán necesarias para aumentar la producción de
1500 unidades por hora a 2400 unidades por hora?
a) 14 b) 12 c) 18 d) 20
77. Si la longitud de la diagonal de un rectángulo es
entonces el área es:
a) 5
metros y un lado mide cinco metros,
m2 b) 29 m2 c) 10 m2 d) no se puede determinar
78. Al restar seis veces el reciproco de un número positivo a el mismo se obtiene uno, ¿cuál es ese
número?
a) 2 b) 3 c) 4 d) 6
79. Se tiene un cuadrado de 10 cm por 10 cm. Se quiere construir un rectángulo cuyos lados sean
enteros y su perímetro mida 20 cm de tal manera que su área sea el 16% del área del
cuadrado.¿Cuáles son las medidas de los lados del rectángulo?
a) 9 cm. y 1 cm. b) 8 cm. y 2 cm. c) 7 cm. y 3 cm. d) 6 cm. y 4 cm.
80. .El área de la estrella sombreada es: (Considera como unidad de área el cuadrito que se
encuentra en la parte superior.)
a)6 u2 b) 8 u2 c) 10 u2 d) 12 u2
81. ¿Qué porción de la figura está sombreada?
a)
b)
c)
d)
82. ¿Cuántos números telefónicos de siete cifras hay que sean capicúas y no empiecen con cero?
(Número capicúa es aquel que se lee igual de atrás para adelante que de adelante para atrás).
a) 9 999 b) 7 200 c) 10 000 d) 9 000
83. Considerando la siguiente figura, encuentra x:
a) 4 b) 5 c) 6 d) 7
84. El reloj se ha vuelto loco: cada 3 segundos se atrasa un segundo, por eso cada 3 minutos se
atrasa un minuto y cada 3 horas se atrasa una hora. ¿Cuánto tiempo real debe pasar para que
mi reloj complete 24 horas?
a) 72 horas b) 48 horas c) 36 horas d) 42 horas
85. Siguiendo la serie, ¿cuál será el perímetro de la figura que tenga 327 cuadros sombreados?
a) 668 u b) 664 u c) 654 u d) 644 u
86. Si A =
elementos de A es:
a) 10 b) 5 c) 8 d) 12
, entonces la cantidad de números pares de la forma a2 con a
b y a, b
87. C1es un circulo de diámetro 6 cm. y C 2 es un circulo de diámetro 10 cm. Renata quiere que
esos dos círculos sean tangentes, sabe que hay dos posibilidades para escoger la distancia
entre los centros, ¿Cuántos son esas dos posibilidades?
a) 3 y 5 b) 4 y 16 c) 2 y 8 d) 6 y 10
88. En un recipiente de forma cilíndrica, cuya base mide 8 cm. de diámetro y 10.5 cm. de altura, se
introduce una piedra. En seguida se vierte agua en el recipiente hasta cubrir la piedra. La altura que
alcanza el nivel del agua con la piedra adentro del recipiente es de 8cm. Cuando se saca la piedra el
nivel del agua baja 3 cm. Selecciona la opción que representa el volumen de la piedra (considera
=3.14)
a) 401.92 cm.3 b) 376.80 cm3 c) 276.32 cm3 d) 150.72 cm3
89. En un cajón hay 10 pares de calcetines de color rojo y 10 pares de calcetines negros, en otro
cajón hay 10 pares de guantes de color rojo y la misma cantidad de pares de guantes de color negro.
¿Cuántos calcetines y guantes será suficiente sacar de cada cajón para que con ellos se pueda formar
un par cualquiera de calcetines y un par de guantes?
a) 3 calcetines, 21 guantes
b) 11 calcetines, 21 guantes
c) 11 calcetines, 11 guantes
d) 3 calcetines, 11 guantes
90. Un ciudadano tenía siete amigos. El primero venia a visitarlo cada tarde, el segundo cada
segunda tarde, el tercero cada tercera tarde y así sucesivamente hasta el séptimo que venia cada
séptima tarde. ¿Con cuanta frecuencia se encontraban los siete amigos y el anfitrión la misma tarde?
a) 110 b) 420 c) 210 d) 5040
91. En dos triángulos isósceles rectángulo con hipotenusa 9 se inscriben los cuadrados sombreados
A Y A ¿Cuál es la razón de las áreas
1
a)
2
b)
c)
?
d)
92. ¿Cuál de los cuatro recipientes tiene menor capacidad?
a) 1 b) 2 c) 3 d) 4
93. El costo por noche de una habitación doble en un hotel es $420 con el 15% de IVA incluido.
Pedro y Pablo se hospedaron una noche en una habitación doble, acordando que Pablo pagaría sólo
el IVA. ¿Cuál de las siguientes opciones se aproxima más a la cantidad que pagó Pedro?
a) $365 b) $237 c) $179 d) $183
94. Un depósito tiene dos llaves para la entrada de agua. Si se abre sólo la llave A, el depósito se
llena en 5 minutos. Si se abre sólo la llave B, el depósito se llena en 10 minutos. ¿Cuál es el tiempo
aproximado si se abren las dos llaves al mismo tiempo?
b) Entre 3 y 4 minutos
c) Entre 4 y5 minutos
d) Entre 7 y10 minutos
e) Más de 10 minutos
95. Un coche con cinco ruedas (cuatro más la de repuesto) ha recorrido 30 000 Km., Las cinco
ruedas se han utilizado la misma cantidad de Kilómetros. ¿Cuántos Kilómetros ha recorrido cada
rueda?
a) 6 000 km.
b) 7 500 km.
c) 24 000 km.
d) 30 000 km.
96. Si al numerador y al denominador de
que se sumó es:
a) 2 b) 3 c) 10 d) 15
se les suma el mismo número, se obtiene,
.El número
97. Después de 4 exámenes mi promedio es 5. Para que mi promedio suba un punto, debo de sacar
en el siguiente examen:
a) 6 b) 8 c) 9 d) 10
98. Siete chicos, por turno, reciben un caramelo. Cuando cada uno tiene 17 caramelos ya no se
pueden seguir repartiendo equitativamente pero sobran caramelos. El número de caramelos que
había para repartir es mayor que 100. Entonces el número de caramelos puede ser:
a) 92 b) 112 c) 119 d) 125
99. Se sabe que el número A77C es divisible por 12.Si A y C son distintos A + C puede valer:
a) 3 b) 2 c) 7 d) 8
100. Si w, x, y y z son cuatro dígitos distintos del conjunto
+
a)
1, 2, 3, 4, 5, 5, 7, 8,9
y si la suma
es lo más pequeño posible entonces
b)
c)
d)
101. El digito de las unidades de un producto de seis números enteros consecutivos es
a) 0 b) 2 c) 4 d) 6
102. ¿Para cuántos valores positivos de n(n >0) la expresión
a)7 b) 8 c) 9 d) 10
es un entero?
103. Cien jóvenes fueron a un campamento de béisbol. De ellos, 52 eran derechos y 48 zurdos;40
provenían de las ligas menores del norte y 60 de las ligas del sur. Veinte zurdos eran de la
liga del norte. ¿Cuántos hombres derechos eran de la liga del sur?
a) 20 b) 32 c) 40 d) 48
104. Una maquina de chicles tiene 9 chicles rojos, 7 blancos y 8 verdes. ¿Cuál es el menor número
de chicles que hay que comprar para estar seguros de que se tienen 4 chicles del mismo color?
a) 8 b) 9 c) 10 d) 12
105. Si X, Y y Z son dígitos diferentes entonces la suma más grande posible que nos dé tres dígitos
tiene la forma:
a) XXY b) XYZ c) YYX d) YYZ
106. ¿Cuántas maneras hay de escribir el número 20 como suma exacta de tres números primos? (el
1 no lo consideramos primo)
a) 0 b) 1 c) 2 d) 3
107. En el diagrama el segmento BC une los centros de los círculos. AB es perpendicular a BC, BC
=8 Y AC =10. El perímetro del circulo pequeño es:
a) 2
b) 4
c) 6
d) 8
108. Un triangulo equilátero DEF está inscrito en otro equilátero ABC como se muestra en la
figura, con DE perpendicular a BC. La razón entre las áreas de los triángulos DEF y ABC
es:
a)
b)
c)
d)
109. Los lados de un triángulo tienen longitudes 11, 15 y k donde k es un entero ¿Para cuántos
valores de k el triángulo es obtuso?
a) 5 b) 12 c) 13 d)8
110. Si a, b y c son números enteros positivos tales que ab = c, bc =12 y b =3c ¿Cuánto vale abc?
a) 4 b) 36 c) 6 d) 12
111. Los puntos PQ y R dividen a la recta AC en cuatro partes iguales. ¿Cuál es la pendiente de BR?
a)
b)
c)
d)
112. Tres círculos son tangentes a la línea Q R y entre si como lo muestra la figura. Los círculos
grandes tienen el mismo radio. ¿Cuál es la razón entre el radio del circulo pequeño y el grande?
a) 1:3 b) 1:8 c) 1:6 d) 1:4
113. El área del triángulo determinado por las rectas cuyas ecuaciones son y = x, y = -x y y = 6 es:
a) 24
b) 12 c) 36 d) 24
114. La suma de los cuadrados de tres números consecutivos cualesquiera es:
a) Siempre impar b) Siempre par c) Nunca es divisible entre 3 d) Nunca es divisible entre 5
115. ¿Cuántos números de 10 dígitos que contienen sólo ceros y unos son divisibles entre 9? (El
primer digito tiene que ser uno).
a) 9 b) 10 c) 8 d) 11
116. Se colocan cada uno de los números 1, 2, 3, 4,5 en una de las casillas de la figura de manera
que la suma de los números en vertical es igual a la de los números en horizontal y esa suma es 8.
¿Qué número debe colocarse en el centro?
117. Dieciocho hombres pueden hacer una pared en 10 días. ¿Con cuántos hombres menos se haría
la obra en 30 días?
118. Si se dobla la figura siguiente y se construye un cubo, entonces en cada vértice se encontrarán
tres caras. Si multiplicamos los números que aparecen en las tres caras que se encuentran en cada
vértice, ¿cuál es el mayor producto que se obtiene?
119. Se colocan nueve paradas de autobús de manera que la distancia entre dos paradas
consecutivas sea siempre la misma. La distancia entre la primera parada y la tercera es de 600 m.
¿Qué distancia hay entre la primera y la última parada?
120. El ángulo a mide 162º. ¿Cuánto mide el ángulo b?
121. Los cuadrados de lado 6 se sobreponen de manera que forman un rectángulo de 6 por 10.
¿Cuál es el área de la región sobrepuesta?
122. El peso total de los que aparecen en los dos platillos de la balanza es de 4.9 kg. ¿Cuánto pesa
cada cuadrado?
123. A continuaciones se presentan tres vistas de un “castillo” hecho con cubos.
¿Cuál es el mínimo número de cubos necesario para construir este castillo?
124. ¿Cuántos polígonos regulares tienen ángulos internos cuya medida sea un número entero de
grados?
125. El rectángulo grande esta dividido en 8 rectángulos y un cuadrado como lo indica la figura.
Los lados de los rectángulos y del cuadrado son números enteros y el perímetro esta marcado dentro
de cada uno de ellos.
¿Cuál es el perímetro del rectángulo grande?
126. En el diagrama se muestra parte de una escala. La flecha indica:
a) 12.4 b) 12.3 c) 12.1 d) 12.2
127. Si m = 1 y n = 5, la expresión que indica un valor mayor es:
a) m + n b)
c) n – m d) m x n
128. Sofía tiene dos hermanos y cuatro hermanas. Pablo es su hermano. El producto del
numero de hermanas por el numero de hermanos de Pablo es:
a) 12 b) 9 c) 6 d) 8
129. De las cuatro figuras que se muestran indica la que tiene mayor perímetro
a) A b) B c) C d) D
130. Cada ladrillo mide 2 por 8 cm. La longitud del contorno marcado es:
a) 48 b) 80 c) 62 d) 64
131. Un vendedor reduce el precio de un artículo de 25.00 pesos en 35 por ciento. El precio
del artículo rebajado es:
a) 24.65 b) 8.75 c) 16.25 d) 17.25
132. Si 6 es un tercio de un número entonces el doble de ese número es:
a) 4 b) 12 c) 18 d) 36
133. Si se suma 7 a la mitad de un número se obtiene 21. El número es:
a) 7 b) 28 c) 14 d) 56
134. Un avión tiene 300 asientos y en un vuelo se tiene que por cada dos asientos ocupados,
hay uno vació. El número de asientos ocupados en ese vuelo es:
a) 100 b) 50 c) 150 d) 200
135. En un torneo de básquetbol hay16 equipos, si cada equipo juega hasta que pierde una
vez, cuántos juegos en total se llevaron para tener un campeón.
a) 15 b) 16 c) 4 d) 8
136. El número de líneas de simetría de la figura es:
a) 3 b) 1 c) 6 d) 12
137. En la figura los puntos ABCD son puntos medios del rectángulo. ¿Encuentra cuál es la
fracción del rectángulo que está sombreada?
a)
b)
c)
d)
138. Cuando se arma el desarrollo de la figura para obtener un cubo la letra W se encuentra
en una cara. La letra que está en la cara opuesta es:
a) S b) V c) K d) X
139. Un coche viaja a 90 km/hora. La distancia, en metros que recorre en 10 segundos es:
a) 25 b) 1500 c) 250 d) 3240
140. Los números 1, 2, 3 y 4 se colocan en las casillas de cada fila, columna y diagonal de
manera que en cada uno de estas se encuentran los cuatro números. La suma de los
números de las casillas marcadas con * es:
a) 4 b) 7 c) 5 d) 6