H+ - Biopent
Anuncio

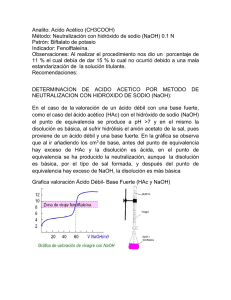
Laboratorio Química Física I Introducción teórica Prác7ca 1 LQF1 2014/15 Atkins, 8ª ed., tema 5 Roberto Tejero Levine, 5ª ed, tema 10 Conduc7vidad: aplicaciones – es la capacidad de una disolución de conducir la corriente eléctrica – es una medida de la concentración iónica total que 7ene una disolución – Se aplica en una gran variedad de industrias. Por ejemplo en la industria alimentaria se u7liza para determinar la salinidad de las muestras y se aplica como control de calidad – En general, la medida de conduc7vidad es una forma rápida y sencilla de determinar la fuerza iónica de una disolución. – la medida de conduc7vidad en aguas residuales, efluentes industriales etc. sirve para proporcionar lecturas de fuerza iónica total. Tipo de agua Conduc2vidad Agua ultrapura 0,055 µS/cm Agua des7lada 0,5 µS/cm Agua de montaña 1,0 µS/cm Agua domés7ca Máx. para agua potable 500 a 800 µS/cm 1055 µS/cm Agua de mar 56 mS/cm Agua salobre 100 mS/cm Conduc7vidad • Electrolito: sustancia que en disolución acuosa produce iones. – Fuertes (totalmente disociados): NaCl, MgSO4 – Débiles (parcialmente disociados): NH3, CH3COOH • Conductores – Electrónicos: la conducción de la corriente se debe al flujo de electrones – Electrolí7cos o iónicos: la conducción de la corriente eléctrica se debe al movimiento de los iones en el seno de la disolución • Conduc2vidad: medida de la facilidad con la que una corriente eléctrica pasa a través de un conductor • Conduc2vidad electrolí2ca: factores de los que depende – – – – Tamaño y carga de los iones Velocidad de los iones Viscosidad del medio temperatura Electrolitos: clasificación • Basándose en la estructura, los electrolitos se clasifican en – Verdaderos: están formados por iones en estado puro. La mayoría de las sales son de este 7po: NaCl, CuSO4, MgS están formados por iones posi7vos y nega7vos – Potenciales: están formados por moléculas sin carga en estado puro, pero cuando se disuelven reaccionan con el disolvente y producen iones. El ácido acé7co (CH3-­‐COOH), cloruro de hidrógeno (HCl), etc. • En estado líquido puro un electrolito verdadero es buen conductor de la electricidad (sales fundidas) • En estado líquido puro un electrolito potencial es mal conductor de la electricidad Electrolitos Cuando z+ = 1 y |z-­‐| = 1 electrolito 1:1 ej: NaCl Cuando z+ = 2 y |z-­‐| = 1 electrolito 2:1 ej: Ba(NO3)2 Cuando z+ = 1 y |z-­‐| = 2 electrolito 1:2 ej: Na2SO4 Cuando z+ = 2 y |z-­‐| = 2 electrolito 2:2 ej: MgSO4 • La presencia de iones hace que estas disoluciones presenten conduc2vidad eléctrica • Las interacciones entre los iones son tan fuertes que hacen que estas disoluciones se aparten de la idealidad incluso a muy bajas concentraciones y requieran tratamiento especial. Ac7vidad de los iones • No hay forma experimental de separar la contribución de cada ion (ca7ón o anión) al producto γ+γ-­‐ • Solución: asignar la “responsabilidad” por la “no idealidad” a ambos iones. Se introduce el coeficiente de ac2vidad iónico medio como – Electrolito 1:1 2 ± γ = γ +γ − – En general, para cualquier electrolito 1/2 γ ± = (γ +γ − ) ν − ν − 1/ν + − γ ± = (γ γ ) OBJETIVO DE LA PRÁCTICA HAc + H 2O ↔ Ac − + H 3O+ [Ac − ][H 3O+ ] coα 2 ' Ka = = [HAc] 1− α aAc− aH O+ γ − γ + [Ac − ][H 3O+ ] 2 ' Ka = = γ± Ka γ HAc [HAc] Ka = 3 aHAc γ − [Ac − ] γ + [H 3O+ ] = γ HAc [HAc] coα 2 Ka = γ 1− α 2 ± Teoría de Debye-­‐Hückel γ± En 1923 Debye y Hückel usan un modelo simplificado de una disolución de electrolitos y la mecánica estadís-ca para deducir expresiones teóricas de los coeficientes de ac7vidad en la escala de molalidades: 1. 2. 3. 4. 5. Iones: esferas rígidas de diámetro a Carga uniforme Disolvente medio sin estructura Disolución muy diluida con interacciones coulómbicas Cada ion rodeado de otros de signo contrario 1/2 z+2 A I m1/2 ln γ + = − 1+ BaI m1/2 z−2 A I m1/2 ln γ − = − 1+ BaI m1/2 " 2N A ρ A % B ≡ e$ ' # ε oε r kT & a ≡ diámetro 3/2 % 1/2 " e2 A ≡ ( 2π N A ρ A ) $ ' 4 πε ε kT # & o r Im ≡ 1 mi zi2 ∑ 2 i Fuerza iónica Teoría de Debye-­‐Hückel, γ± ln γ ± = −z+ z− A I m1/2 1+ BaI m1/2 log γ ± = −A z+ z− I m1/2 1+ 0, 328 a I m1/2 En disoluciones diluidas el denominador se hace 1 log γ ± = −A z+ z− I m1/2 Ley límite de Debye-­‐Hückel Para disoluciones acuosas diluidas a 25 oC y esferas de 3 Å log γ ± = −0, 510 z+ z− I 1/2 m Ley límite de Debye-­‐Hückel I m1/2 log γ ± = −0, 510 z+ z− 1+ I m1/2 Ley de Debye-­‐Hückel (ampliada) Fuerza iónica y coeficiente ac7vidad 1 I= ∑ mi zi2 2 i Disoluciones acuosas a 25 ˚C (ρ = 1 g/mL) 1 I= ∑ ci zi2 2 i Para el caso de la prác7ca: electrolito 1:1 y concentración coα 1 I= (coα + coα ) = coα 2 log γ ± = −A coα Magnitudes y unidades Símbolo Nombre R Resistencia ρ Resis7vidad L Conductancia 𝜅 Conduc7vidad específica Λ Conduc7vidad molar κ disolución = κ disolvente + κ soluto Expresión R =ρ l A Unidades Ω (ohm) Ω cm L= 1 R 1 1 l κ= = ρ RA κ Λ =1000 c Ω-­‐1 = S (siemens) S cm-­‐1 S cm2 M-­‐1 Medida de la conduc7vidad Un sistema completo para la medida de conduc7vidad está formado por los siguientes elementos básicos: – – – Células de dos electrodos y célula de dos electrodos con sensor de temperatura Célula de conduc7vidad. Sonda de temperatura. Instrumento de medida. El conducqmetro mide la conduc7vidad eléctrica de los iones en una disolución. – Para ello aplica un campo eléctrico entre dos electrodos y mide la resistencia eléctrica de la disolución. Para evitar cambios en las sustancias, efectos de capa sobre los electrodos, etc. Se aplica una corriente alterna. Imprescindible que el líquido llegue a cubrir el orificio de salida del aire Cálculo de la constante de célula: calibrado del conducqmetro. Se medirá la conduc7vidad específica de una disolución de KCl de concentración y conduc7vidad conocidas: KCl 0.01 M entre 20 y 30 °C κ = 1278 + (t -­‐ 20.0) 27 S cm-­‐1 donde t es la temperatura en °C Variación de κ con la concentración • Varía igual para todos los electrolitos • Primero aumenta con la concentración hasta un máximo: al aumentar c hay más iones • Luego disminuye: procesos de asociación entre los iones (interacciones asocia7vas) Variación de Λ con la concentración Λ = Λo – B c1/2 B = a + bΛo a = 60,2 S cm2 mol-­‐1 M-­‐1/2 b = 0,229 M-­‐1/2 Ley de la migración independiente de los iones de Kohlrausch ∞ ∞ + ∞ − Λ = ν +λ + ν −λ Λo = λo(+) + λo(–) Estrictamente correcto sólo si la disolución es infinitamente diluida Λo(AcH) = Λo(NaAc) + Λo(HCl) – Λo(NaCl) Λo(AcH) = λo(Ac–)+ λ o(Na+) + λo(Cl–) + λo(H+) – λo(Na+) – λo(Cl–) Λo(AcH) = λo(Ac–) + λo(H+) Grado de disociación (α) y Λ Λ α= Λo α= Ecuación a resolver Λ α= Λe Λ Λ Λ = = Λ e Λ o − Bc1/2 Λ o − B(coα )1/2 Λ α= Λ o − B(coα )1/2 Valoraciones conduc7métricas • Ácido fuerte con base débil • Ácido débil con base fuerte • ??? • ??? Ácido fuerte con NaOH HCl → H + + Cl − Cond (S) Na(OH ) → Na+ + OH − Inicial Final VNaOH (mL) H + , Cl − < H + , Cl − , Na+ Ácido fuerte con NaOH HCl → H + + Cl − Cond (S) Na(OH ) → Na+ + OH − Inicial Final VNaOH (mL) H + , Cl − < H + , Cl − , Na+ Balance: sus7tuimos un ion que conduce mucho (H+) por otro que conduce menos (Na+) por lo que la conduc7vidad disminuirá pronunciadamente Ácido fuerte con NaOH HCl → H + + Cl − Na(OH ) → Na+ + OH − Cond (S) Inicial Final H +, Cl − < H +, Cl −, Na+ Balance: sus7tuimos un ion que conduce mucho (H+) por otro que conduce menos (Na+) por lo que la conduc7vidad disminuirá pronunciadamente VNaOH (mL) Una vez se hayan agotado los H+ la siguiente adición de NaOH incrementará de forma notable la concentración de OH-­‐ por lo que la conduc7vidad aumentará de forma pronunciada Ácido fuerte con NaOH HCl → H + + Cl − Na(OH ) → Na+ + OH − Cond (S) Inicial Final H + , Cl − < H + , Cl − , Na+ Balance: sus7tuimos un ion que conduce mucho (H+) por otro que conduce menos (Na+) por lo que la conduc7vidad disminuirá Una vez se hayan agotado los H+ la siguiente adición de NaOH incrementará de forma notable la concentración de OH-­‐ por lo que la conduc7vidad aumentará de forma pronunciada VNaOH (mL) El volumen correspondiente al punto de corte de las rectas de ambos tramos será el resultado de la neutralización Ácido débil con NaOH HAc ↔ H + + Ac − Cond (S) Ac = CH 3COO - Na(OH ) → Na+ + OH − Inicial Final VNaOH (mL) H + , Ac − ~H + , >Ac− , Na+ Ácido débil con NaOH HAc ↔ H + + Ac − Cond (S) Ac = CH 3COO - Na(OH ) → Na+ + OH − Inicial Final VNaOH (mL) H + , Ac − ~H + , >Ac− , Na+ Balance: como si añadiéramos lentamente (Na+) por lo que la conduc7vidad aumentará suavemente (Na+ conduce menos que H+) Ácido débil con NaOH HAc ↔ H + + Ac − Ac = CH 3COO - Na(OH ) → Na + + OH − Cond (S) Inicial Final H + , Ac − H + , >Ac− , Na + Balance: como si añadiéramos lentamente (Na+) por lo que la conduc7vidad aumentará suavemente (Na+ conduce menos que H+) VNaOH (mL) Una vez agotado el equilibrio (la can7dad de HAc) la siguiente adición de NaOH incrementará de forma notable la concentración de OH-­‐ por lo que la conduc7vidad aumentará de forma pronunciada Ácido débil con NaOH HAc ↔ H + + Ac − Ac = CH 3COO - Na(OH ) → Na + + OH − Cond (S) Inicial Final H + , Ac − H + , >Ac− , Na + Balance: como si añadiéramos lentamente (Na+) por lo que la conduc7vidad aumentará Una vez agotado el equilibrio (la can7dad de HAc) la siguiente adición de NaOH incrementará de forma notable la concentración de OH-­‐ por lo que la conduc7vidad aumentará de forma pronunciada VNaOH (mL) El volumen correspondiente al punto de corte de las rectas de ambos tramos será el resultado de la neutralización Ácido fuerte + ácido débil con NaOH HCl → H + + Cl − Cond (S) HAc ← H + + Ac − Na(OH ) → Na+ + OH − Inicial Luego VNaOH (mL) HAc, H + , Cl − HAc, H + , Cl − , Na+ Ácido fuerte + ácido débil con NaOH HCl → H + + Cl − Cond (S) HAc ← H + + Ac − Na(OH ) → Na+ + OH − Inicial Luego VNaOH (mL) HAc, H + , Cl − HAc, < H + , Cl − , Na+ Ácido fuerte + ácido débil con NaOH HCl → H + + Cl − Cond (S) HAc ↔ H + + Ac − Na(OH ) → Na+ + OH − Inicial VNaOH (mL) HAc, H + , Cl − , Ac − , Na+ Luego HAc, ~H + , Cl − , >Ac − , >Na+ Ácido fuerte + ácido débil con NaOH HCl → H + + Cl − Cond (S) HAc ↔ H + + Ac − Na(OH ) → Na+ + OH − Inicial H + , Cl − , Ac − , Na+ + − − + − Luego H , Cl , Ac , Na , OH VNaOH (mL) Ácido fuerte + ácido débil con NaOH Cond (S) V1 V2 VNaOH (mL) V1 = volumen de valoración del ácido fuerte V2-­‐ V1= volumen de valoración del ácido débil Los puntos de corte de las rectas nos permi7rán calcular los valores de los volúmenes. Precauciones en la valoración Formación de burbuja El disolvente debe cubrir los orificios