Ver/Abrir
Anuncio

CENTRO DE NEUROCIENCIAS DE CUBA
DEPARTAMENTO DE NEUROINFORMÁTICA
FORMULACIÓN BAYESIANA DE LA REGRESIÓN LINEAL CON
RESTRICCIONES BASADAS EN LOS MODELOS DE NORMAMIXTA Y ELASTIC NET
Tesis presentada en opción al grado de
Master en Ciencias Matemáticas
Autor: Lic. Deirel Paz Linares
Tutores: Inv. Aux. Eduardo Martínez Montes, Dr. C.
Inv. Aux. Mayrim Vega Hernández, Ms. C.
La Habana, 2015
AGRADECIMIENTOS
La realización de este trabajo se debe fundamentalmente a las ideas y conocimiento
del estado del arte, sobre los temas de Análisis Bayesiano y Problema Inverso,
aportados por Mayrim Vega Hernández y Eduardo Martínez Montes.
Tampoco puedo dejar de mencionar que ningún resultado hubiese sido posible sin la
apertura a la investigación, en el Centro de Neurociencias de Cuba, bajo la dirección
de Pedro A. Valdés Sosa.
Quisiera dirigir un reconocimiento especial a Eduardo Martínez Montes por su
paciencia en todo momento, y guía en el desarrollo de la parte teórica del trabajo,
gracias a lo cual despejamos el camino hacia este corte de los resultados.
De gran importancia fue el conocimiento impartido, en las diferentes asignaturas
relacionadas con Teoría de Probabilidades, por el profesor José E. Valdés Castro.
De mucho peso también fue el apoyo de Pedro A. Rojas López en la implementación
del algoritmo y la discusión de diversos temas que permitieron hacer correcciones a la
teoría en este documento.
Y como siempre de inmenso valor ha sido el apoyo de la familia, en especial de mi
madre y mi esposa, y también de los amigos, de entre los cuales no puedo dejar de
mencionar a Marcos Verdugo Quero y Camilo Pérez Demydenko.
2
ÍNDICE
Introducción ....................................................................................................................................................... 4
Capítulo 1: Regresión lineal penalizada .......................................................................................................... 11
1.1 Enfoque clásico...................................................................................................................................... 11
1.2 Enfoque Bayesiano ................................................................................................................................ 14
Capítulo 2: Formulación de la regresión lineal con el modelo de Elastic Net en el contexto del Bayes
empírico ................................................................................................................................................................. 19
2.1 Transformación del Modelo Bayesiano jerárquico del Elastic Net........................................................ 19
2.2 Aprendizaje mediante el enfoque del Bayes Empírico en el modelo jerárquico del Elastic Net ........... 21
2.3. Aspectos computacionales del proceso de optimización y algoritmo ENET-RVM ............................. 27
Capítulo 3: Formulación bayesiana del modelo espacio-temporal con penalizadores basados en la normamixta ...................................................................................................................................................................... 30
3.1 Definición de norma-mixta .................................................................................................................... 30
3.2 El campo aleatorio de los parámetros en el modelo de la norma-mixta................................................. 33
3.3 Aprendizaje mediante el enfoque del Bayes Empírico en el modelo jerárquico de la norma-mixta...... 39
3.4 Aspectos computacionales del proceso de optimización y algoritmo MXN-RVM ............................... 41
Capítulo 4: Resultados y Discusión ................................................................................................................. 44
4.1 Estudio de simulaciones ........................................................................................................................ 44
4.2 Estudio de datos reales....................................................................................................................... 6564
Conclusiones................................................................................................................................................ 7675
Recomendaciones ........................................................................................................................................ 7978
Referencias .................................................................................................................................................. 8079
Anexos ......................................................................................................................................................... 8483
Prueba del Lema 2.1.1 ............................................................................................................................. 8483
Prueba de la Proposición 2.2.1 ................................................................................................................ 8584
Prueba de la Proposición 2.2.2 ................................................................................................................ 8685
Prueba de la Proposición 3.1.4 ................................................................................................................ 8786
Prueba del Lema 3.2.5 ............................................................................................................................. 8786
Prueba de la Proposición 3.3.1 ................................................................................................................ 8988
3
INTRODUCCIÓN
Los problemas inversos son especialmente comunes en Biofísica, donde usualmente una
cantidad pequeña de datos está disponible con respecto al gran número de parámetros
necesarios para modelar el sistema. Ejemplos clásicos de problemas inversos en las
neurociencias son los conocidos Problema Inverso de la Electroencefalografía (EEG) y
Problema Inverso de la Magnetoencefalografía (MEG). Estos consisten en la determinación
de la Densidad de Corriente Primaria (DCP), producida en el interior del cerebro a partir de la
medición del potencial eléctrico en un arreglo de electrodos distribuidos sobre la superficie
del cuero cabelludo, en el caso del EEG, o a partir de un arreglo de sensores de la intensidad
de campo magnético colocados a pocos centímetros de distancia de la cabeza, en el caso del
MEG. Aunque físicamente estos problemas son diferentes, ambos conllevan a un problema
inverso matemáticamente equivalente, de forma que los métodos para resolver uno son
extrapolables al otro problema. Por simplicidad, en esta tesis nos referiremos solamente al
problema inverso del EEG.
Para abordar la solución de este problema es necesario conocer la ecuación que relaciona el
potencial eléctrico ( ) y la DCP ( ), lo cual se denomina problema directo del EEG. Bajo
determinadas suposiciones sobre la geometría y propiedades eléctricas de la cabeza, y con el
uso de la aproximación cuasiestática, la solución del problema directo se expresa por la
ecuación
(
)
∫ (
)
(
)
, ver (Riera, 1999), donde (
DCP en el espacio de los generadores cerebrales y el tiempo, y
(
) representa la
) es el llamado Lead
Field Eléctrico (LFE), que depende también de las posiciones de los electrodos
, y que
contiene la información sobre las propiedades electromagnéticas y demás suposiciones físicas
del volumen conductor, o sea, de la cabeza. En este trabajo emplearemos el LFE calculado
4
con un modelo del volumen conductor conocido como modelo de las tres esferas concéntricas,
homogéneas e isotrópicas (Riera, 1999). De acuerdo a esta formulación, el problema inverso
consiste en resolver una ecuación integral de Fredholm de primer tipo, que comúnmente es
discretizada en un sistema de ecuaciones lineales:
Donde
,
y
son las versiones discretas del potencial eléctrico, el LFE y la DCP, y
es
un término de error que modela el ruido inevitable en las mediciones del EEG.
El EEG proporciona mediciones del potencial eléctrico en el cuero cabelludo, utilizando una
cantidad de electrodos distribuidos según un sistema estándar (Klem, 1999) que varía entre 19
y 256, aunque los más comunes actualmente son los montajes de 32, 64 y 128 canales.
Generalmente para tener una resolución espacial aceptable de la distribución de corriente, la
región del cerebro es discretizada en un arreglo de miles de unidades de volumen
(denominadas vóxeles). Esto implica que el sistema de ecuaciones lineales es indeterminado y
su solución no es única, por lo que la inferencia de los parámetros
es un problema mal
planteado en el sentido de Hadamard (Hadamard, 1923).
Uno de los enfoques más comunes para estimar una solución adecuada es el Método de
Regularización o Método de Mínimos Cuadrados Penalizados, establecido por (Tikhonov y
Arsenin, 1977), donde el estimador de los parámetros se obtiene a partir de la optimización de
cierta función de costo del problema, que generalmente es la suma del error de ajuste y una
función de restricción o penalización
. Este enfoque tiene una larga historia de desarrollo
teórico y ofrece ahora grandes ventajas en lo que respecta al tiempo de convergencia de los
algoritmos, para optimizar la función objetivo, cuando
es una función convexa y
diferenciable. El uso de penalizadores basados en la norma L2 de los parámetros, que es
5
clásico en la literatura estadística, se conoce como el método Rigde (Hoerl y Kennard, 1970) y
sus ventajas y desventajas han sido ampliamente estudiadas. Variantes de este método han
dado lugar a soluciones del problema inverso del EEG (o indistintamente, soluciones inversas)
muy reconocidas, como la Mínima Norma, Mínima Norma Pesada y LORETA (del inglés,
Low Resolution Electromagnetic Tomography) (Pascual-Marqui, 1999).
Otros métodos, basados en penalizadores convexos no diferenciables, como el Least Absolute
Shrinkage Selection Operator (LASSO) (Tibshirani, 1996), han mostrado buenos resultados
reconstruyendo DCPs con raleza en la distribución espacial. Una gran ventaja de los métodos
de regularización es la posibilidad de ser extendidos a múltiples restricciones, como es el caso
de Elastic Net (ENET) (Zou et al., 2005) y el LASSO-Fused (Tibshirani et al., 2005), en tanto
que el cálculo de los estimadores es realizado con los mismos algoritmos (Sanchez–Bornot et
al., 2008), como por ejemplo con el LQA (del inglés, Local Quadratic Aproximation, Fan et
al. 2001) y MM (del inglés, Majorization Minorization, Hunter et al. 2005). A pesar de que el
enfoque clásico permite tener en cuenta modelos muy complejos (múltiples funciones de
penalización) sin pérdida considerable de rapidez de cómputo, la estimación es poco robusta
debido a la sensibilidad de la solución al conjunto de restricciones seleccionadas para
regularizar el problema (dicha selección dependerá del escenario de la actividad eléctrica
cerebral presente), mientras que otra de sus desventajas la constituye la elección heurística de
los parámetros de regularización, los cuales reflejan el balance relativo de las restricciones
(Trujillo, 2006).
Una alternativa a los métodos de regularización es el enfoque Bayesiano (aprendizaje
Bayesiano), con el cual se obtiene una solución del problema de regresión, formulando la
función de densidad de probabilidad (pdf, del inglés probability density function) a posteriori,
6
a partir de la combinación de la verosimilitud con la pdf a priori de los parámetros, que
incorpora convenientemente las restricciones o penalizaciones deseadas. Esta variante también
permite tener en cuenta modelos complejos, pero debido a la naturaleza probabilística del
modelo la estimación de los parámetros es generalmente más robusta. Esto es posible gracias
a que los hiperparámetros del modelo, que actúan en el balance de propiedades de la solución
o seleccionando el conjunto activo (elementos no nulos) de los parámetros, se obtienen (o
aprenden) a través de sus estimadores maximum a posteriori (MAP) en un segundo nivel de
inferencia (MacKay, 2003). Un ejemplo es el Relevance Vector Machine (RVM) (Tipping,
2001), consistente en el aprendizaje Bayesiano de vectores ralos (pocas componentes activas)
empleando una pdf a priori Normal univariada para cada componente del vector de
parámetros, con varianzas que a su vez son hiperparámetros modelados con una pdf a priori
Gamma.
Aunque los métodos basados en el aprendizaje Bayesiano son teóricamente más robustos que
los clásicos en la estimación de soluciones inversas, solo se ha logrado hacer inferencia por
medio de algoritmos eficientes y rápidos con modelos sencillos. Mientras que otros métodos
basados en modelos complejos como el ENET Bayesiano (Li and Lin, 2010), o la formulación
Bayesiana de distintas variantes del LASSO (Kyung et al. 2010), involucran el uso algoritmos
de Expectation-Maximization (EM), o de los métodos de Monte Carlo, que implican cargas
computacionales altas y gran cantidad de iteraciones para obtener estimaciones confiables.
En el caso del PI del EEG, existen estudios que evidencian que las fuentes eléctricas pueden
tener propiedades tanto de suavidad como de raleza en diferentes estados cerebrales, incluso
coexistiendo en determinados casos. Importantes esfuerzos se han hecho en orden de
balancear raleza y suavidad combinando funciones de penalización basadas en normas L1 y
7
L2. Un ejemplo es el trabajo de Vega-Hernández et al. (2008), donde se realiza una
formulación general del PI en un modelo de regresión lineal de múltiple penalización y
evalúan modelos que combinan funciones basadas en ambas normas, con el objetivo de
recuperar una solución rala compuesta de parches suaves en el espacio. En otro ejemplo se
utiliza como función de penalización la combinación de normas L1/L2 para exigir una
solución rala solamente para la amplitud del vector de PCD, manteniendo suavidad entre las 3
componentes espaciales x, y, z, que definen la dirección espacial de esta magnitud física
(Haufe et al. 2008). Sin embargo en estos casos el grado de raleza/suavidad depende
fuertemente de los parámetros de regularización, para los cuales generalmente se utilizan
criterios de información heurísticos, como el AIC, BIC y la Validación Cruzada Generalizada
(GCV por sus siglas en inglés). Estos criterios no siempre son adecuados en las condiciones
de problemas mal planteados y no siempre ofrecen los valores óptimos de los parámetros por
lo que dan lugar a soluciones no del todo confiables.
Otra propiedad importante de la actividad cerebral, que no es tenida en cuenta en ninguno de
los modelos mencionados arriba, es la continuidad (suavidad) en el tiempo de las activaciones
de las fuentes generadoras. Para resolver este problema se han realizado propuestas, como son
por ejemplo los modelos de componentes espacio-temporales (Valdés-Sosa et al. 2009), o los
modelos basados en penalizadores de norma-mixta, que consiste en la formulación matricial
de la regresión lineal, con la aplicación de una norma L1 al vector formado por las normas L2
de las filas de la matriz de parámetros, buscando promover raleza en el espacio y suavidad en
el tiempo (Ou et al. 2009). Recientemente se ha popularizado la combinación normas L1, L2,
y de orden superior, conocida como función de penalización de norma-mixta (MXN), en sus
aplicaciones a la solución del problema inverso del EEG, gracias a los métodos basados en
8
operadores de proximidad, que permiten optimizar rápidamente la función de costo convexa
no diferenciable asociada (Gramfort et al. 2012), aunque se mantienen con la problemática de
la estimación de valores óptimos de los parámetros de regularización.
En este trabajo proponemos un formalismo Bayesiano para la mezcla de penalizaciones con
normas L1 y L2, en el caso de los modelos ENET, MXN, y también de sus combinaciones.
Con esta formulación perseguimos imponer, a la solución del problema inverso, diferentes
grados de raleza y suavidad tanto en la dimensión espacial como la temporal, con el
aprendizaje de los hiperparámetros del modelo que controlan dichas propiedades en un
segundo nivel de inferencia, por medio de algoritmos eficientes y rápidos, basados en el
procedimiento de Bayes Empírico, evitando el cómputo con los métodos de Monte Carlo o
algoritmos EM.
Hipótesis:
El uso del enfoque Bayesiano en modelos que mezclan raleza y suavidad por medio de
penalizaciones con normas L1 y L2, como Elastic Net, norma-mixta, y sus combinaciones,
permite desarrollar métodos para la solución del problema inverso espacio-temporal del EEG,
donde los parámetros y los hiperparámetros pueden ser estimados dentro de algoritmos
eficientes y rápidos, evitando el uso de algoritmos de Expectation-Maximization y métodos de
Monte Carlo poco prácticos computacionalmente dada la alta dimensionalidad del problema
en cuestión.
Objetivo General:
Desarrollar un modelo Bayesiano jerárquico para la solución del problema inverso espaciotemporal del EEG, con distribuciones de probabilidad a priori basadas en la combinación de
9
restricciones L1/L2, donde tanto los parámetros como los hiperparámetros se estimen a partir
de los datos por medio de algoritmos iterativos.
Objetivos Específicos:
1. Formular el modelo bayesiano de Elastic Net y derivar un algoritmo basado en el
procedimiento de la evidencia y del Bayes Empírico para la estimación de los
hiperparámetros.
2. Transformar el modelo Bayesiano no separable, de la a priori asociada a la normamixta, en un modelo jerárquico, en el nivel de los parámetros.
3. Desarrollar un algoritmo para la estimación de los parámetros y los hiperparámetros
del nuevo modelo jerárquico para la norma mixta, basado en el procedimiento de la
evidencia y del Bayes Empírico.
4. Comprobar preliminarmente la efectividad de ambos modelos con datos simulados.
Comparar entre ellos los resultados, en cuanto al aprendizaje de raleza o suavidad, y
también con métodos establecidos.
5.
Aplicación de los métodos obtenidos a la localización de las fuentes cerebrales en un
estudio real de potenciales evocados visuales.
10
CAPÍTULO 1: REGRESIÓN LINEAL PENALIZADA
1.1 Enfoque clásico
Una formulación más general del problema inverso del EEG, que permite tener en cuenta
restricciones espacio-temporales en la solución, es la regresión lineal matricial:
1-1
Donde los parámetros ( ) constituyen una matriz
( representa la cantidad de vóxeles y
T la cantidad de instantes de tiempo), los datos ( ) y el ruido ( ) son matrices
dónde (
,y
es
).
El enfoque clásico de la estadística para la estimación de los parámetros en la regresión lineal
se basa en la regularización de Tikhonov. De forma más general, este problema se planteó
formalmente como la regresión de mínimos cuadrados con múltiple penalización (VegaHernández et al., 2008):
̂
{‖
‖
∑
(
)}
1-2
Donde el primer término es el error de ajuste al dato y el segundo agrupa el conjunto de
restricciones (penalizaciones) impuestas, los
son los parámetros de regularización, que
asignan pesos a las restricciones. La matriz H representa un operador lineal que
convenientemente se utilice en determinadas aplicaciones, opciones bastante comunes son el
uso de la matriz identidad ( ) o del operador Laplaciano spacial discreto ( ), segundas
derivadas, ver Pascual-Marqui 1999. En el caso de que el penalizador se pueda descomponer
como una suma sobre las columnas de los parámetros (
(
)
∑
(
)) y si este no
representa ninguna restricción temporal, el parámetro de regularización podría ser distinto
11
para cada instante de tiempo (
(
)
∑
(
)), en lo adelante sin perder la
generalidad mantendremos la notación más abreviada.
Dentro de las formas de penalización más comunes se encuentran el RIDGE (
el LASSO (
( )
‖ ‖ ), el LASSO-FUSION (
conformado por la combinación ( ‖ ‖
( )
()
‖ ‖ ),
‖ ‖ ) mientras que el ENET está
‖ ‖ ).
Con el ENET se podrían obtener tanto soluciones tipo RIDGE, que son suaves en el espacio,
cuando
, o soluciones tipo LASSO, que son ralas en el espacio, cuando
La Figura 1 muestra varios casos, si
.
tendremos el LASSO, y se reforzará un mínimo
en cero, debido a que la variación del penalizador respecto al parámetro es un infinitesimal de
primer orden, mientras que si
tendremos el RIDGE y él mínimo no se reforzará de
manera singular en cero sino en un entorno incluyendo valores no cero, debido a que la
variación es un infinitesimal de segundo orden.
Figura 1: Forma del penalizador de ENET (eje Y), respecto a una componente de los
parámetros (eje X), para distintos valores de cuando
.
12
La complejidad del proceso de solución de la ecuación [1-2] depende de la forma de los
penalizadores, en particular de su diferenciabilidad. Por ejemplo para el RIDGE puede ser
obtenida analíticamente efectuando la derivada matricial e igualando a cero (Magnus and
Neudecker, 2007):
̂
(
)
1-3
Debido a este hecho los métodos de estimación basados en la penalización RIDGE son los
más eficientes y rápidos computacionalmente para un
dado. Por el contrario en los casos del
LASSO y ENET es imposible obtener estimadores explícitos, por lo que para optimizar la
función de costo se emplean algoritmos iterativos, como el LQA (Sanchez–Bornot et al.,
2008), que en general expresan el estimador ̂(
)
en una iteración
RIDGE que depende del estimador en la iteración
̂(
)
.
( ̂(
como una solución
:
)
)/
1-4
El cálculo de la solución depende de la elección del parámetro de regularización, que se puede
escoger a partir de un criterio de información que tenga en cuenta la varianza explicada por el
modelo y la complejidad del mismo, como por ejemplo Akaike Information Criterion (AIC),
Bayesian Information Criterion (BIC) y Generalized Cross-Validation (GCV), ver Hastie et
al, (2009). Con este enfoque se pueden incorporar múltiples penalizadores convexos, pero en
estos casos surgen complicaciones con la elección de varios parámetros de regularización. Por
ejemplo, el tiempo de cómputo aumenta considerablemente al tener que calcular la solución
del problema de optimización en la ecuación [1-2] para una gran cantidad de combinaciones
de los parámetros de regularización, cuando queremos seleccionar la combinación óptima.
Otra dificultad la constituye la fiabilidad de la elección, incluso aunque el tiempo de cómputo
13
pueda reducirse. Un ejemplo es el “problema del doble encogimiento” en el ENET, donde no
hay criterio para elegir la combinación óptima de (
), lo cual se ha tratado de resolver de
manera secuencial, seleccionando un intervalo de valores para
información para determinar
( ‖ ‖
fijar
(
y aplicando criterios de
O reparametrizando las penalizaciones de la forma
)‖ ‖ , que permite fijar el peso relativo de cada término a partir de
y estimando solamente
.
1.2 Enfoque Bayesiano
Otro enfoque para abordar el problema de la estimación de los parámetros en la regresión es el
Bayesiano, donde se modela la relación entre los datos con los parámetros como una pdf
condicional
( |
) (Verosimilitud), y el conocimiento a priori (información adicional)
sobre el problema como una pdf ( | ) (a priori de los parámetros), donde
y
pueden ser
magnitudes fijas o variables desconocidas, en cuyo caso son llamados hiperparámetros del
modelo y para ellos se establecen las correspondientes pdf a priori
( ) y
( ). A este
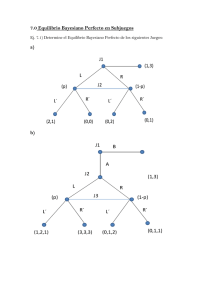
modelo se le puede asociar un diagrama plano, red Bayesiana (Figura 2a), donde la pdf
conjunta de los datos, los parámetros y los hiperparámetros, se puede descomponer en factores
que representan las pdf condicionales de los nodos en la red (Beal, 2000):
(
)
( |
) ( | ) ( ) ( )
1-5
Para la estimación de los parámetros es necesario conocer la pdf condicional de los parámetros
respecto a los datos (a posteriori), para la cual haciendo uso de la regla de Bayes para las
distribuciones de variables aleatorias continuas (Durrett, 1996), obtenemos:
( |
)
(
(
)
)
Si combinamos la ecuación [1-5] y [1-6] tenemos entonces:
14
1-6
( |
)
( |
) ( | )
1-7
Si son conocidos los hiperparámetros entonces el estimador de los parámetros ( ̂) se obtiene a
partir del maximum a posteriori (MAP):
̂
* ( |
)+
1-8
Desafortunadamente en la mayoría de los casos los hiperparámetros no son conocidos, y el
problema consiste en como inferirlos. Para ello existen vías como:
Joint maximum a posteriori (JMAP): Estimar los parámetros y los hiperparámetros
conjuntamente maximizando la a posteriori conjunta de los parámetros y los
hiperparámetros:
( ̂ ̂ ̂)
(
)*
(
| )
( |
(
| )+
1-9
) ( ) ( )
1-10
Marginalized maximum a posteriori I (MMAP de tipo I): Integrar la a posteriori
conjunta en la ecuación [1-10] respecto a los hiperparámetros, y maximizar respecto a
los parámetros:
̂
( | )
* ( | )+
∫ (
| )
1-11
1-12
Marginalized maximum a posteriori II (MMAP de tipo II o Bayes Empírico): Integrar
la a posteriori de la ecuación [1-10] respecto a los parámetros, y maximizar respecto a
los hiperparámetros. Luego substituir los valores estimados de los hiperparámetros en
[1-8].
( ̂ ̂)
(
)*
15
(
| )+
1-13
(
| )
∫ (
̂
{ ( |
| )
1-14
̂ ̂ )}
1-15
El problema de la regresión lineal penalizada puede ser abordado en general desde el enfoque
Bayesiano, si en el modelo lineal de la ecuación [1-1] asumimos que el término de error es un
ruido blanco de varianza
, consideramos que la a priori de los parámetros es una pdf
exponencial con cuyo argumento es el segundo término de la ecuación [1-2], y tenemos en
cuenta distribuciones a priori para los parámetros de regularización.
Bajo estas condiciones el modelo de regresión lineal se transforma en un modelo Bayesiano
jerárquico (Figura 2a), donde se cumple para las respectivas pdf:
1) Verosimilitud:
Donde
( |
)
( |
)
(
)) ⁄
(
( |
(
)
) (
)
1-16
(
)
.
2) A priori de los parámetros:
∑
( | )
Donde
(
)
1-17
es la constante de normalización.
3) A priori de los hiperparámetros: *
Cuando las columnas de
(
)+ , ( ).
son estocásticamente independientes (Figura 2b), tenemos un caso
especial de Modelo Bayesiano que se puede separar en T componentes independientes al nivel
de los parámetros:
(
|
)
(
|
16
)
1-18
(
∑
| )
(
)
1-19
1
…
…
1
…
…
(b)
(a)
Figura 2: Grafos orientados asociados al modelo Bayesiano de la regresión lineal (a), y el
caso particular de modelo Bayesiano separable en el tiempo (b).
Ambos enfoques (Mínimos Cuadrados Penalizados y Bayesiano) son equivalentes en la
estimación de los parámetros. Si en el modelo Bayesiano de la regresión lineal queremos
estimar los parámetros a través del MAP, por medio de la fórmulas [1-8], [1-16] y [1-17],
entonces después de algunas transformaciones algebraicas obtenemos:
̂
{‖
Si en la ecuación [1-20] substituimos
‖
∑
por
( )}
1-20
entonces obtenemos exactamente la
ecuación [1-2], que es la función de costo del problema de estimación de los parámetros en la
regresión lineal con múltiple penalización. De esta forma, la formulación bayesiana de la
regresión lineal de los modelos empleados en la estadística clásica correspondería a distintas
densidades de distribución, como se muestra en la siguiente tabla.
17
Modelo
Ridge
Ridge L
Lasso
Lasso Fusión
ENET
ENET L
Penalizador
‖ ‖
‖ ‖
‖ ‖
‖ ‖
‖ ‖
‖ ‖
pdf a priori asociada
Normal
Normal
Laplace
Laplace
‖ ‖
‖ ‖
Normal-Laplace
Normal - Laplace
Para el caso del ENET ha sido propuesta una formulación Bayesiana donde los parámetros y
los hiperparámetros se estiman por medio de un algoritmo que vincula tanto la vía de JMAP
como Bayes Empírico, pero de forma que para los parámetros se utiliza el muestreo de las
distribuciones a posteriori con métodos de Monte Carlo (MC), y para los hiperparámetros
métodos de EM-MC. Con esto se evita el “problema del doble encogimiento” que aparece en
el enfoque clásico, pero introduce un alto costo computacional.
18
CAPÍTULO 2: FORMULACIÓN DE LA REGRESIÓN LINEAL CON EL
MODELO DE ELASTIC NET EN EL CONTEXTO DEL BAYES EMPÍRICO
2.1 Transformación del Modelo Bayesiano jerárquico del Elastic Net
El ENET en la formulación Bayesiana puede interpretarse como una pdf que es la mezcla de
una distribución Normal y una de Laplace:
( |
∑.
)
‖
‖
‖
‖ /
2-1
Note que aquí para simplificar, sin perder generalidad, omitimos de la formulación el
operador de segundas derivadas.
Este modelo, debido a la separabilidad de la norma L2 al cuadrado y la norma L1, introduce a
priori independencia estocástica en los parámetros en las dimensiones espacio-temporal, lo
que matemáticamente se expresa con la siguiente descomposición de la pdf a priori:
( |
)
|
∏
Con la introducción de un nuevo hiperparámetro
|
2-2
(ver Lema 2.1.1), el cual posee una a
priori Gamma Truncada, se puede reorganizar el modelo de forma que el parámetro posee una
distribución Normal (Li and Lin 2010, Kyung et al. 2010). Esto permite transformar el modelo
Bayesiano jerárquico del ENET, en un modelo de Mezcla de Gaussianas Escaladas, ver Figura
3, donde la a priori de los nuevos hiperparámetros está parametrizada en (
Lema 2.1.1 (ver prueba en anexos): Sea que la variable aleatoria
|
|
, donde
|
|
).
tiene una pdf de la forma
es una constante de normalización. Entonces se cumple que:
∫
(
|
)
19
(
|
(
))
2-3
(
Donde
(
|
(
)
2-4
)) es una pdf Gamma Truncada, con corte en
.
Analíticamente el nuevo modelo se describe por el siguiente conjunto de distribuciones.
Verosimilitud:
(
|
)
2-5
A priori de los parámetros:
.
|
(
)/
2-6
A priori de los hiperparámetros:
∏
1
(
|
(
))
2-7
(
(
)
)
2-8
(
(
)
)
2-9
(
( )
…
…
…
…
)
1
1
1,1 ,
2,1
1,
,
2,
1,
,
2,
Figura 3: Representación gráfica del Modelo Bayesiano jerárquico del Elastic Net.
20
2-10
Este modelo puede ser interpretado como una extensión del RVM (Tipping, 2001) -que utiliza
solamente una a priori gaussiana- y del modelo de Babacan et al. (2010) -que utiliza
solamente una a priori de Laplace-, para incorporar la mezcla de ambas distribuciones,
respondiendo a como en un modelo con estructura RVM se le puede incorporar información a
priori que permita balancear la raleza/suavidad.
En el ENET original la raleza/suavidad es controlada en la a priori de los parámetros [2-2].
Cuando
( |
tenemos que
)
( |
( |
)
. |
/ y cuando
), mientras que para entender como en el ENET jerárquico la
raleza/suavidad es controlada, es suficiente con ver que si
implica por la fórmula [2-7] que los valores más probables de
fórmula [2-4] las varianzas a priori son cercanas a cero (
a soluciones muy ralas. En el caso
parámetros ( |
tenemos que
)
entonces
.|
entonces
están cercanos a
, esto
y por la
) en muchos casos, conllevando
, y por tanto la a priori de los
/, según [2-4] y [2-6].
2.2 Aprendizaje mediante el enfoque del Bayes Empírico en el modelo jerárquico del
Elastic Net
Debido a la independencia estocástica de los parámetros y los hiperparámetros en distintos
instantes de tiempo, el modelo de la Figura 3 admite la siguiente factorización, en lo que
llamaremos formulación instantánea, donde la pdf conjunta del dato los parámetros y los
hiperparámetros tiene la forma:
(
)
∏ (
)
21
2-11
Aplicando las fórmulas [1-5], [2-5], [2-6], esta probabilidad conjunta se puede descomponer
en un producto de pdf Normales que depende de los parámetros y la pdf conjunta de los
hiperparámetros.
(
)
(
|
) .
|
(
)/ (
)
2-12
De igual forma la pdf conjunta de los hiperparámetros, haciendo uso de la fórmula [2-7] y la
suposición de que son estocásticamente independientes, se puede factorizar sobre los nodos de
los hiperparámetros en la Figura 3.
(
)
∏
(
|
(
)) (
) ( )
) (
2-13
Para obtener el estimador de los parámetros ( ̂ ) es suficiente con reorganizar el producto de
normales en [2-12], que resulta en una nueva distribución Normal. El estimador puede
obtenerse automáticamente haciendo uso de [1-8], y del siguiente resultado.
( )
Proposición 2.2.1 (ver prueba en anexos): Si definimos
( )
(
.
(
|
) .
|
(
|
( )|
)/ )
(
.
entonces se cumple:
)/
|
( )/
.
|
(
)/ (
Teniendo en cuenta [1-7] puede deducirse que a la posteriori de
.
|
donde:
|
)
2-14
corresponde al término
( )/ en la ecuación [2-14], de donde el estimador MAP se obtiene como ̂
.
22
La descomposición en la Proposición 2.2.1 permite arribar a una forma ventajosa de la a
posteriori de los hiperparámetros, substituyendo [2-14] y [2-12] en [2-11] y luego integrando
sobre , de acuerdo a [1-14] en el MMAP de tipo II. De ahí obtenemos que:
(
| )
(
(
(
| )
)
(
( )
)
| )
∏|
( )|
.
|
(
)/ (
|
) (
)
2-15
En modelos que tienen una a posteriori similar, como en el LASSO Bayesiano y el RVM ya
mencionados, se han derivado algoritmos eficientes y rápidos, para obtener los estimadores en
el proceso de optimización de la función [2-15]. En este trabajo ateniéndonos al costo
computacional que involucra el uso de los métodos de Monte Carlo, justo como hemos
mencionado, seguimos la estrategia de optimización del RVM.
En lo adelante en vez de maximizar [2-15] lidiaremos con la función auxiliar , que es menos
(
el logaritmo de la a posteriori (
| )), y nos conduce a un problema de
optimización equivalente.
∑ ( )
2-16
( )
|
( )|
|
|
(
|
)|
.
‖
(
‖
23
)/
∑
∫
( ⁄
∑
)
⁄
(
)
2-17
(
Observe que
)
(
( )
)
contiene implícitamente los hiperparámetros. La función
es muy
multimodal (no convexa), pero por la convexidad respecto a cada uno de los argumentos
{
} individualmente y su forma diferenciable en [2-17] es posible un
proceso de optimización iterativa (ver Tipping, 2001 o Wipf and Nagarajan, 2009). La
optimización se realiza por el método de iteración de punto fijo, que es menos robusto
respecto a la variante de EM, como es discutido en Wipf and Nagarajan, 2009, pero que
conduce más rápidamente a la solución. Debido a que la experiencia nos indica que
alcanzamos más simplicidad en la formulación, realizaremos el siguiente cambio de variable
La siguiente proposición muestra las derivadas de la función [2-16], ver Magnus and
Neudecker, 2007.
Proposición 2.2.2 (ver prueba en anexos):
a)
.
(
(
(
2-19
)
∑ {
2-18
( )/
.
b)
c)
)/ )
(
(
)
)
( )/
.
(
)
24
∫
. ⁄
/
}
2-20
∑ {
d)
(
( )/
.
)
(
e)
∑
{
. ( )
)
/
. ⁄
∫
‖
/
‖ }
}
2-21
2-22
Note que al aplicar las derivadas quedan términos que contienen de forma implícita los
hiperparámetros, dado que la derivada de
con respecto a
posee una forma no lineal en el
( )/, por lo que fijamos el mismo del paso anterior para manejar una
término .
función más simple que es convexa como analizaremos más adelante. Observe que en esta
formulación Bayesiana establecemos a priori no informativas para
y .
Las derivadas en [2-18], [2-19] y [2-22] conducen fácilmente a las fórmulas de actualización
de los hiperparámetros igualando a cero:
( )
̂
̂
2-23
√
,
̂
∑
∑
.
‖
( )/
‖
( )
∑
2-24
2-25
Ahora tomaremos en consideración la función que es el argumento bajo el operador
diferencial en [2-20] y [2-21] debido a que por las particularidades del modelo, la a posteriori
posee otros términos que la distinguen respecto a los ejemplos de optimización encontrados en
la literatura del aprendizaje bayesiano con modelos semejantes.
25
(
)
∑
(
)
{
∫
( ⁄
.
( )/
(
)
)
2-26
}
El dominio de definición de la función en [2-26], respecto a los argumentos (
), es el
conjunto abierto del plano comprendido entre los ejes de coordenadas y la curva definida por
{
}
(Figura 4A), donde se preserva la no negatividad de las varianzas a priori
en la fórmula [2-4]. La función objetivo es continua diferenciable y acotada (Figura 4B) en
dicha región, por tanto tiene un mínimo en ella.
Figura 4: Aquí empleamos la función (
∫
. ⁄
/
)
.
/
⁄.
/
como una simplificación de [2-26] para representar la región del
) donde está definida (A), y el comportamiento de
plano (
sus argumentos individualmente (B).
26
respecto a cada uno de
No se puede encontrar una fórmula cerrada de actualización para (
) por la no linealidad
en [2-26], pero el procedimiento no conduce a más complicación que optimizar una función
explícita de dos variables. De ahí que:
̂
{
*
}
̂
{
[ √
}
{ (
)}
{ (
)}
+
2-27
2-28
]
2.3. Aspectos computacionales del proceso de optimización y algoritmo ENET-RVM
En el proceso de optimización a través de las fórmulas en la Proposición 2.2.2, la matriz de
varianzas
determina que parámetros del modelo son relevantes (explican el dato) y cuáles
van a cero. Véase en la fórmula de la matriz de covarianzas de la a posteriori de los
parámetros ( ), en la Proposición 2.2.1, que cuando
el elemento
de la matriz
argumento bajo la inversa, en la fórmula de ( ), tiende a infinito, llevando a cero todos
( ) y en la columna
aquellos elementos que caen en la fila
manera similar los parámetros que no explican el dato ( ̂
en la próxima iteración, a causa de que
. De
), reforzarán su desactivación
cuando sustituimos la fórmula [2-4] de los
hiperparámetros , que involucra los valores de
conjunto de las varianzas a priori
( ), de donde ̂
( ) y
, en [2-24]. Debido a que un
tienden a cero, la función [2-17] cae en un mínimo local
, y entonces no tiene sentido continuar el proceso de optimización de
manteniendo
aquellos términos no acotados. Por esta razón aquí asumimos la metodología de
redimensionar el modelo (Tipping 2001, Faul and Tipping 2003), donde evitamos la
complicación
del
mínimo
local,
eliminando
27
los
parámetros,
hiperparámetros
y
correspondientes columnas del Lead Field, en cada instante de tiempo, para un conjunto
índices tal que {
de
}
. Nos basamos en el conjunto activo
de
(complemento
) y reformulamos el modelo Bayesiano solo con los parámetros e hiperparámetros
relevantes, arribando a una nueva función objetivo para la estimación de los hiperparámetros,
que solo contiene términos acotados.
̂
{
[
∫
{∑ {
}
(
)
.
(
]
. ⁄
/
( )/
)
}}
2-
29
̂
̂
[ √
∫
{
}
{∑ {
(
)
.
(
]
. ⁄
/
}}
( )/
)
2-
30
El alto costo computacional en que se incurre para obtener ( ) por medio de la operación de
inversión en la Proposición 2.2.1, puede evitarse involucrando el procedimiento de
28
descomposición en valores singulares (SVD, siglas en inglés) y la identidad de Woodbury
(Magnus and Neudecker, 2007). En efecto, si tenemos que la SVD de
es:
2-31
Entonces substituyendo [2-31] en la fórmula para ( ) tenemos que:
( )
.
(
(
Multiplicando [2-32] por
( )
)/ )
.
(
(
)/ )
2-32
y aplicando la identidad de Woodbury obtenemos:
(
) (
(
)
)
2-33
Aquí proponemos un algoritmo, ver pseudocódigo en Algoritmo 1, que recibe como entradas
los valores de los hiperparámetros y que actualiza iterativamente ( )
̅̅̅̅̅, , ,
.
Algoritmo 1 (ENET-RVM)
ENTRADA:
,
SALIDA: , ,
,
,
Inicializa ( )
Inicializa
y
para
̅̅̅̅̅
[2-24]
Inicializa
Iterar hasta cumplir criterio de convergencia
Calcular
[2-4], ( )
̅̅̅̅̅ [2-33] y actualizar
Determinar el conjunto activo de
y actualizar
Finalizar
29
[2-23] y
[2-24].
[2-29],
[2-30] y
[2-25].
,
y
CAPÍTULO 3: FORMULACIÓN BAYESIANA DEL MODELO ESPACIOTEMPORAL CON PENALIZADORES BASADOS EN LA NORMA-MIXTA
3.1 Definición de norma-mixta
Definición 3.1.1: Sea
el espacio de las matrices reales de dimensión
Denominamos norma-mixta (MXN) a la función ‖ ‖
‖ ‖
(∑
(∑
|
.
:
| ) ) ,
3-1
,
De acuerdo con la definición anterior se pueden verificar algunas propiedades que son
heredadas por el espacio métrico (
), donde definimos la métrica (
)
‖
‖
a partir de la norma-mixta.
(
Proposición 3.1.2: Sean
* +
). Sean
/
* +
generados por la columna-t /fila-s de las matrices, y
* +
/
* +
subespacios de
:
* +
/
* +
operadores de proyección del espacio de las matrices en los respectivos subespacios. Entonces
* +
la distancia en los subespacios
asociadas a las normas
/
/
* +
está dada respectivamente por las métricas
.
La Proposición 3.1.2 puede demostrarse fácilmente chequeando que las siguientes igualdades
se cumplen:
* +
(
(
*+
* +,
, , -
*+
-)
‖
, -)
‖
* +
* +,
-‖
‖
‖
,
-‖
‖
‖
Note que la Definición 3.1.1, se puede escribir en función de la traspuesta de la matriz
, que ha sido utilizada en la literatura (Gramfort et al. 2012) y es de la forma:
30
‖ ‖
(∑
(∑
|
| ) ) ,
3-2
,
Aunque el valor de la norma es el mismo, al definir la norma mixta de una manera u otra se
obtiene la misma métrica en los subespacios
* +
* +
/
.
Definición 3.1.3: (Lehmann and Casella 1998) Un conjunto dado
convexo si para todo
este conjunto
y
, tenemos
(
(
) )
( )
(
. Una función sobre
) ( )
Proposición 3.1.4 (ver prueba en anexos): Las funciones
∑
)
es convexa si la siguiente desigualdad se cumple:
(
( )
, se dice que es
.∑
|
( )
3-3
.∑
(∑
|
|) / y
| / son convexas, y no diferenciables en el origen de coordenadas.
Pese a la convexidad de la función de costo del problema de regresión con penalización de
norma mixta, la no diferenciabilidad y la no separabilidad de la suma en las funciones
y
contribuyen a enlentecer los algoritmos de optimización (Beck and Teboulle 2009, Gramfort
et al. 2012), en casos de alta dimensionalidad. Aunque en la norma-mixta la no separabilidad
es una propiedad intrínseca, la ventaja de la variante en la Definición 3.1.1, radica en la
posibilidad de descomponerla como una suma de normas de las columnas de , permitiendo
independizar la regresión penalizada en los distintos instantes de tiempo. En el caso de
la irracionalidad puede ser fácilmente evitada tomando el cuadrado de
induciendo una norma
al cuadrado en
* +
y una norma
( ), pero esta vez
al cuadrado en
* +
, la cual
corresponde a la función de penalización del Elitist-Lasso (Kowalski and Torrésani, 2009).
31
( )
Si formulamos la regresión con la función de penalización
penalización sobre un elemento
admite la descomposición ∑ ‖
donde
∑
|
Figura 5: Forma de
(
( )), eje X (
( ) (ver Proposición 3.1.4) la
no puede ser separada del resto en
‖ , su comportamiento en
( )
. Dado que
tiene la forma (
|
|) ,
| será una magnitud que portará la dependencia con las otras variables.
( ) (ver Proposición 3.1.4) para distintos valores de
. Eje Y
).
Este penalizador puede adoptar ambas formas extremas del ENET, estilo LASSO cuando
delta es grande y estilo RIDGE cuando delta es muy pequeño (Figura 5), de forma que se
impone un balance pues delta será mayor mientras menos valores no nulos presente . En este
sentido, el modelo de la norma-mixta presenta una manera de controlar la raleza por medio de
los deltas, que son funciones de los parámetros.
El empleo de
( ) como función de penalización, la cual induce una norma
una norma
en
* +
en
* +
y
, se limita a los métodos de regularización, debido a que su
irracionalidad la convierte en prácticamente intratable en el enfoque Bayesiano.
32
3.2 El campo aleatorio de los parámetros en el modelo de la norma-mixta
Ahora tomaremos en consideración la teoría de los Campos Aleatorios de Markov (MRF,
siglas en inglés) para las pdf exponenciales, conocidas como pdf de Gibss (como en el enfoque
Bayesiano de la regresión lineal). Para hacer más interpretables los resultados (en cuanto al
enfoque Bayesiano de la regresión lineal penalizada) proponemos un tratamiento menos
general, a través de las definiciones y proposiciones básicas. Denominamos „cliqué‟ a los
pares de nodos en el MRF y los llamados „potenciales‟ en la teoría, corresponden a las
funciones de penalización, para una introducción al tema ver Kindermann and Snell (1980).
Definición 3.2.1: Sea
que representa un arreglo de variables aleatorias (vector aleatorio,
matriz aleatoria), el cual tiene una pdf conjunta de la forma ( )
admite la descomposición ∑(
(
)
);
(
( )
cumple: ‖
este
‖
)
caso
,
|
∑
‖
los
||
|
‖
,
es una
es un Campo Aleatorio de Markov (MRF,
que consiste en la columna-t de la matriz , la cual
, es un MRF.
La prueba de la Proposición 3.2.1 es obvia dado que el vector aleatorio
(
( )
)+ son llamadas potenciales.
Proposición 3.2.2: El vector aleatorio
tiene pdf conjunta ( )
, donde
es el conjunto de pares de índices y
constante de normalización. Entonces se dice que
siglas en inglés), y las funciones *
( )
tiene pdf conjunta
es la constante de normalización, y la siguiente descomposición se
∑
potenciales
,y
|
||
de
*(
|. De lo cual fácilmente se puede concluir que en
la
)(
Definición
)+
.
33
3.2.1
son
proporcionales
a
El MRF de la Proposición 3.2.2 admite una representación por medio de un grafo no orientado
(red de Markov) completamente conectado (Figura 6), donde los nodos corresponden a las
variables aleatorias {
} y los enlaces representan las relaciones funcionales entre los
elementos a través de los diferentes potenciales, tanto aquellos que dependen solo de los
propios nodos como los que vinculan todos los pares de nodos posibles.
11
…
1,
…
,
…
,
,
1
1
1
Figura 6: Red de Markov de los parámetros en el modelo Bayesiano de la norma-mixta.
La teoría de MRF ofrece una regla para establecer probabilidades condicionales en una red de
Markov, lo que permite derivar métodos de inferencia en Campos Aleatorios que se basan en
el paso del modelo de probabilidad de las variables aleatorias originales a las probabilidades
condicionales, lo cual contribuye a simplificar mucho los modelos, volviéndolos tratables
analíticamente o permitiendo acelerar algoritmos de muestreo de Gibbs (Murphy, 2012).
Definición 3.2.3: Sea
que representa un arreglo de variables aleatorias. Sea
subconjunto de elementos de
( )
+,
, donde
, con pdf conjunta condicional de la forma
( ) admite la descomposición ∑(
es el complemento de
dice que el par (
en , y
)
(
),
*(
(
|
un
)
)
es una constante de normalización. Entonces se
) es un Campo Aleatorio de Markov Condicional (CMRF, siglas en
inglés).
Proposición 3.2.4: Cualquier par (
) de un MRF constituye también un CMRF.
34
Para demostrar la Proposición 3.2.4 podemos aplicar la regla de Bayes a un par cualquiera
(
) del MRF de la Definición 3.2.1:
(
|
)
(
)⁄ (
)
∑
(
Luego empleando la siguiente descomposición:
( )
(
*(
(
∑
)
)
)
(
+,
)
)
{(
)
}, y
Podemos llegar a que:
(
(
) ∑(
(
)
(
)
)
∑(
∫
|
(
)
)
,
∑(
)
De ahí se obtiene que (
∑(
)
)
∑(
∑(
∫
)
(
)
(
)
(
)
.
)
)
, con lo cual quedan satisfechas
las condiciones de la Definición 3.2.3.
De la Proposición 3.2.4 puede deducirse que el vector aleatorio
(
| )
‖
‖
, con pdf de la forma
, es también un CMRF para cualquier partición en dos subconjuntos de
sus componentes. En particular se puede obtener la pdf condicional de la variable aleatoria
respecto a su complemento, el vector
,
.
El lema a continuación resume el resultado de la aplicación de las reglas de la Teoría de
Probabilidades, en el paso a las probabilidades condicionales en el MRF de la Proposición
3.2.2. Para una introducción a este tópico en la Teoría de Probabilidades moderna ver
(Durrett, 1996).
35
Lema 3.2.5 (ver demostración en anexos): Para la variable aleatoria
elementos del vector
cuya pdf es de la forma
(
, que constituyen los
‖
| )
‖
, se verifican las
propiedades a), b) y c).
a)
b)
(
|
|
)
Donde
∑
(
‖
)
Donde
|
(
‖
3-4
es cierta constante de normalización.
(
)
3-5
) es la función indicadora de la región
y
c) ∫ (
|y
|
| )
̅̅̅̅̅+,
*
es cierta constante de normalización.
∫
‖
‖
3-6
La importancia de lo señalado en Lema 3.2.5 a) reside en mostrar que tomar la pdf condicional
(
|
), en vez de la versión marginalizada
(
| )
∫
‖
‖
, que no
tiene una pdf en forma explícita, nos permite arribar a un modelo sencillo separable para los
parámetros. El costo de dicha transformación es la adición al modelo de las nuevas variables
aleatorias o hiperparámetros
, los cuales heredan el comportamiento multivariado de en el
modelo original, Lema 3.2.5 b), mientras que la identidad en Lema 3.2.5 c) valida la
formulación empleada en este trabajo, sin tener en cuenta resultados más generales.
En Lema 3.2.5 b) establecemos la pdf conjunta del vector aleatorio
, la cual no puede ser
descompuesta en potenciales que dependan de subconjuntos de elementos de menor tamaño
que el vector aleatorio completo. A este tipo de campo aleatorio le corresponde también una
red de Markov completamente conectada, con un potencial para los elementos
general
y otro
para la interacción entre todos los nodos, como se muestra en la Figura 7. La nueva
36
estructura de la red, al nivel de los hiperparámetros, nos fuerza a encarar un modelo no
separable justo como en el principio, pero en esta ocasión dicha dificultad se puede evadir
debido al origen de los hiperparámetros, como veremos más adelante. Otras complicaciones
aparecen dado que en el nuevo modelo el hiperparámetro
parámetros
y de los hiperparametros
aprendizaje de
conecta con el nivel de los
, lo cual complicará las ecuaciones para el
cuando aplicamos el método de la evidencia.
1,
…
1,
…
,
,
…
,
…
…
,
…
,
,
11
Figura 7: Nuevo modelo asociado a la norma-mixta, que consiste en una red Bayesiana
para los parámetros y una red de Markov para los hiperparámetros.
Ahora están dadas las condiciones para hacer una última transformación al modelo Bayesiano
de la norma-mixta combinando los resultados en el Lema 2.1.1 y Lema 3.2.5 a), observando la
correspondencia de
y
con
y
del ENET. Las respectivas pdf a priori de
y
en el nuevo modelo jerárquico serían las siguientes:
(
|
)
(
(
(
En este modelo
|
)
(
|
)
3-7
)
|
(
3-8
))
3-9
controla la raleza/suavidad en todos los parámetros de los niveles
superiores, mientras que los
actúan como pesos que balancean esta propiedad, sobre cada
37
nodo (parámetro) de forma individual (ver figura 8). Como en el ENET, los
relevancia de los parámetros en el modelo, de forma que si
de los parámetros
controlan la
las varianzas a priori
. Para realizar este control correctamente, los
se estiman por vía
del máximo a posteriori.
,
1,
1,
…
,
…
,
,
1,
,
,
,
…
,
,
11
Figura 8: Representación gráfica del nuevo modelo resultante de las transformaciones en
Lema 3.2.5 y Lema 2.1.1.
Para darle una solución práctica a este problema, observemos que en este nuevo modelo los
parámetros dependen de una nueva estructura de hiperparámetros, en la que ellos exhibirán un
comportamiento aleatorio similar a que si fueran generados aleatoriamente por el modelo
original, no solo en el sentido de las distribuciones a priori, sino que también son equivalentes
en el sentido de las distribuciones a posteriori (Beal, 2003). O sea, muestrear los parámetros y
el hiperparámetro
a partir de las distribuciones a posteriori del nuevo modelo es equivalente
estadísticamente a muestrear los parámetros de la a posteriori del modelo original mientras se
genera
a través de la expresión dada en el Lema 3.2.5 a). Por tanto, para el desarrollo de un
algoritmo que permita el aprendizaje de los hiperparámetros y la estimación de los parámetros
nosotros utilizaremos dicha expresión para la actualización de
38
en cada iteración.
3.3 Aprendizaje mediante el enfoque del Bayes Empírico en el modelo jerárquico de
la norma-mixta
Con las transformaciones al modelo Bayesiano jerárquico asociado a la función de
penalización de la norma mixta, llevadas a cabo en el Epígrafe 3.2, arribamos a un nuevo
modelo generativo probabilístico donde los parámetros tienen una pdf Normal, representado
en la Figura 9. La a posteriori conjunta, de forma similar al Epígrafe 2.2 empleando [2-5] y
[3-7], se puede escribir:
(
)
(
|
) (
|
(
)) (
)
3-10
La pdf conjunta de los hiperparámetros, de acuerdo al modelo, se puede factorizar sobre los
nodos de la red de la Figura 9, usando [3-9] y [3-5].
(
)
∏
.
1
|
(
‖
)/
‖
(
) ( ) ( )
3-11
…
…
1
1
…
…
1
Figura 9: Modelo generativo probabilístico del dato, asociado a la norma-mixta.
La función objetivo del problema de optimización será:
∑
( )
39
3-12
( )
|
( )|
|
∑
‖
. ⁄
∫
( )
(
)|
.
∑
/
(
)/
.
⁄
|
/
|
‖
‖
( )
‖
3-13
Observe que en [3-13] el término
es obtenido a partir de la constante de normalización
en el Lema 3.2.5 b).
Proposición 3.3.1 (ver prueba en anexos):
( )
a)
.
(
(
(
)
3-14
( )/
.
( )
b)
)/ )
(
)
.
( )/
3-15
c)
{∑ {
(
)
(
∑‖
d)
‖
∑
. ⁄
∫
/
}
)
3-16
}
. ( )
{
/
‖
‖ }
3-17
Las demás derivadas en [3-14], [3-15] y [3-17] conducen fácilmente a las fórmulas de
actualización de los hiperparámetros, de forma similar a las del Epígrafe 2.2.
̂
( )
;
( )
.
(
40
(
)/ )
3-18
̂
√
,
∑
̂
‖
∑
Donde
( )/
.
3-19
‖
3-20
( )
∑
está dado por la ecuación [3-8]. Para el estimador de
tendremos un problema de
optimización con una función objetivo similar a [2-26].
( )
∑ {
(
( )/
.
)
(
∑
∫
. ⁄
/
‖
3-21
‖
El dominio de definición de la función en [3-21] es el intervalo [
que la función objetivo es continua en el intervalo abierto (
tiende a infinito en los extremos
}
)
y
){
(
(
(
){
){
}], de forma
}), mientras que
}. Entonces el estimador del hiperparámetro
se representa por la expresión:
̂
*
(
),
-+
* ( )+
3-22
3.4 Aspectos computacionales del proceso de optimización y algoritmo MXN-RVM
De forma similar a lo explicado en el Epígrafe 2.3 aquí empleamos la estrategia de conjunto
activo y de redimensionar el modelo en cada iteración, borrando los parámetros y los
hiperparámetros cuyos índices (
partir del conjunto activo
) pertenecen al conjunto , tal que {
(complemento de
función objetivo para la estimación de
:
41
(
)
}. A
) se puede expresar de forma explícita la
̂
*
(
,
)
∑
-+
(
)
{
∫
( |
(
)
( )/
.
(
{
)
)
}
∑‖
(
)
(
(
‖
)
)
}
3-23
Pueden extraerse conclusiones, sobre el control de la raleza espacial y suavidad temporal, a
partir del comportamiento asintótico de la función objetivo en [3-21]. En el primer sumando,
el término ∑ {
decrece cuando
término cuando
valores de
grandes)
. ⁄
∫
/
} representa una función no lineal que rápidamente
crece, pero lo hace más lentamente que la tendencia al infinito del primer
(
)
{
}. Esto permite la adaptación del mínimo en [3-21] a los
(globalmente), tal que si la estimación en un paso no es rala (
tenderá a valores mayores (hacia
(
)
{
tiene valores
}), llevando más varianzas
a
valores pequeños y promoviendo mayor raleza en el próximo paso. Lo contrario pasa cuando
la estimación es demasiado rala (
de
(
)
{
tiene valores pequeños), entonces
será menor, alejado
} y será menos probable que se eliminen nuevos elementos del conjunto
activo. Aquí proponemos un algoritmo, ver pseudocódigo en Algoritmo 2, que recibe como
42
entradas los valores de los hiperparámetros y que actualiza iterativamente ( )
,
̅̅̅̅̅, , ,
y .
Algoritmo 2 (MXN-RVM)
ENTRADA:
,
SALIDA: , , , ,
Calcular los valores iniciales de
( )
Calcular valores iniciales de
[3-19].
y
y
para
Inicializa
Iterar hasta cumplir criterio de convergencia
Calcular
[3-8], ( )
̅̅̅̅̅ [2-33] y actualizar
Determinar el conjunto activo de
y actualizar
Finalizar
43
[3-18],
[3-23] y
y
[3-19]
[3-20].
̅̅̅̅̅
CAPÍTULO 4: RESULTADOS Y DISCUSIÓN
4.1 Estudio de simulaciones
Para validar la teoría estudiamos la habilidad de los métodos propuestos reconstruyendo la
Densidad de Corriente Primaria (DCP) a partir de datos simulados de EEG. Para una
simulación realista de baja dimensionalidad, empleamos como espacio de generadores un
anillo de 736 vóxeles en un plano axial de la corteza cerebral correspondiente al atlas cerebral
estándar del Instituto Neurológico de Montreal (MNI, http://www.bic.mni.mcgill.ca/).
Simulamos 3 fuentes activas (que llamaremos “parches” A, B y C), con distinta distribución
(raleza/suavidad) en el espacio, cuya amplitud varía en el tiempo siguiendo diferentes cursos
temporales (ver Figura 10). El “lead field” fue calculado como la matriz de transformación de
estas fuentes a 31 canales de registro, utilizando un modelo de 3 esferas homogéneo y suave a
pedazos, según se desarrolló en (Riera, 1999). El potencial eléctrico (EEG) se calculó a partir
Figura 10: Columna izquierda. Arriba: Espacio de los generadores (rojo) y los electrodos (amarillo). Centro:
corte axial con la distribución espacial de las fuentes simuladas, A (1 vóxel), B (5 vóxeles) and C (gaussiana
espacial). Abajo: Evolución temporal de las fuentes, A (gaussiana temporal), B (sinusoide temporal) and C
(sinusoide temporal). Columna derecha: Matriz que representa el mapa espacio-temporal de la simulación.
44
de la multiplicación del “lead field” por la DCP simulada y adicionando ruido blanco
(Relación Señal-Ruido (RSR) de 70db).
Estudio de las soluciones obtenidas con el modelo Elastic Net y el algoritmo ENET-RVM
La solución inversa se estimó con los algoritmos ENET-RVM y MXN-RVM, comparando los
resultados obtenidos tanto con el empleo de valores fijos de los parámetros de regularización,
como con el aprendizaje de los distintos grados de raleza/suavidad de las fuentes simuladas a
través de la estimación dentro del algoritmo de dichos parámetros. En el caso del ENET
calculamos las soluciones que utilizan las combinaciones de los parámetros (α1=1, α2=1) y
(α1=1, α2=100). De acuerdo con el modelo, la primera combinación conllevaría a obtener una
solución que explica el dato con igual peso relativo de suavidad y raleza, mientras que la
segunda debe llevar a soluciones de mayor raleza para tratar de explicar el dato. Por su parte,
la solución con aprendizaje se obtiene a partir de los valores iniciales α1 (0)=1 y α2 (0)=1.
Como se muestra en la Figura 11 (fila de abajo), las soluciones con los parámetros fijos se
comportan según lo esperado, mientras que la solución con aprendizaje de los hiperparámetros
encuentra un intermedio entre la solución más suave y la más rala en los distintos parches
simulados. En este modelo se estiman los valores de los hiperparámetros para cada instante de
tiempo independiente, lo cual hace más difícil que las soluciones muestren suavidad temporal,
al contrario de las soluciones en que se fijan estos parámetros para todos los instantes de
tiempo. En este caso, la relación entre los hiperparámetros estimados α2/α1 varió en el tiempo
en un rango entre 1 y 20, pero con un bajo coeficiente de variación, siendo la media y la
desviación estándar de 3.08±1.53.
45
Figura 11: Soluciones inversas obtenidas empleando el algoritmo ENET-RVM con valores
fijos de los parámetros de regularización (abajo), y con aprendizaje (derecha arriba).
La Tabla I muestra algunas medidas cuantitativas de la calidad de la estimación por estos tres
métodos. En particular, como medida de “distancia” de cada matriz estimada (Jest) a la matriz
solución simulada (Jsim) calculamos la diferencia entre 1 y la correlación de Pearson (valor
entre -1 y 1, donde 0 se interpreta como no correlación, que representa el grado de
dependencia lineal entre las matrices) entre las dos matrices vectorizadas, de forma que
menores valores implican mayor similitud de la solución estimada con la solución real. La
raleza de cada solución se calculó como el porcentaje de elementos nulos en la matriz (o sea, a
mayor cantidad de elementos nulos, mayor raleza, coincidiendo con el concepto intuitivo).
También, a partir de considerar a Jsim como una matriz binaria, donde dos clases se definen
46
por los elementos nulos y no nulos, es posible para cada Jest calcular el área bajo la curva
ROC (AUC, del inglés area under the curve, también llamada precisión o exactitud) y los
valores de sensibilidad y especificidad determinados por la idéntica binarización de las
soluciones estimadas. Esta tabla muestra que la distancia con respecto a la solución simulada
de la solución con el aprendizaje es intermedia con respecto a las otras dos soluciones con
valores fijos. Sin embargo el nivel de raleza en todo el mapa espacio-temporal es similar a la
de la solución más rala y el área bajo la curva ROC es la menor, debido a una baja
sensibilidad. Estos últimos resultados pueden explicarse precisamente por los diferentes
grados de raleza estimados independientemente para cada instante de tiempo, lo que conllevó
a soluciones con mayor raleza en la dimensión temporal.
En la Figura 12 mostramos un acercamiento de las fuentes estimadas y en la Tabla II las
correspondientes medidas cuantitativas en tres zonas espacio-temporales que denominamos
PARCHES A, B y C, respectivamente. Se puede observar el efecto de la estimación con
aprendizaje en las características de los parches, donde la distancia a la solución simulada
toma valores intermedios a las soluciones con los hiperparámetros fijos, así como raleza y
precisión (AUC), excepto en el parche C donde la mayor raleza de la Jsim con aprendizaje
conlleva a una mayor distancia y menor AUC.
ENET-MM ENET-RVM
Tabla I: Medidas cuantitativas de las soluciones ENET-RVM y ENET-MM en los datos simulados
Soluciones
1-corr
Raleza Jest (%)
Raleza Jsim (%)
α2/α1 = 1
0.156
96.28
97.01
71.96
98.38
85.59
α2/α1 Estimado
0.278
97.95
97.01
41.67
99.17
70.57
α2/α1 = 100
0.282
97.92
97.01
51.77
99.45
75.71
α2/α1 = 9
α2/α1 = 99
α2/α1 = 999
0.558
88.59
97.01
67.44
90.31
80.29
0.678
94.59
97.01
37.24
95.57
66.66
0.734
95.80
97.01
23.42
96.39
60.06
47
Sens(%) Espec(%) AUC(%)
Tabla II: Medidas cuantitativas calculadas en los 3 parches para las soluciones ENET-RVM
Soluciones
Parche A (Ral. Jsim=99.27%) Parche B (Ral. Jsim=40.60%)
Parche C (Ral. Jsim=0%)
1-corr Raleza(%) AUC(%) 1-corr Raleza(%) AUC(%)
1-corr Raleza(%) AUC(%)
1.005
α2/α1 = 1
α2/α1 Estim 1.004
α2/α1 = 100 0.916
98.70
49.34
0.139
29.15
80.08
0.167
45.75
77.07
99.01
49.50
0.224
56.32
78.71
0.372
75.75
64.61
99.08
57.47
0.313
65.08
79.4
0.336
58.49
67.78
48
Figura 12: Detalles en los distintos parches de la simulación de las soluciones inversas
estimadas empleando el algoritmo ENET-RVM con valores fijos de los parámetros de
regularización (filas 2 y 4), y con aprendizaje de los hiperparámetros (fila 3).
En un estudio no exhaustivo del proceso de aprendizaje de los hiperparámetros con el
algoritmo ENET-RVM, se encontró un patrón de convergencia monótono pero sensible a los
valores iniciales como se muestra en la Figura 13. Si iniciamos con la combinación α1=1 y
α2=10, α2 converge a valores más altos y se obtiene una solución del vector de parámetros más
49
rala (en los tres instantes de tiempo donde son máximos cada parche). ENET-RVM procesa
un instante de tiempo de la solución en 4.8s (150 iteraciones), de forma que la estimación
para todo el mapa espacio-temporal se toma unos 16 min.
50
Figura 13: Soluciones inversas estimadas con ENET-RVM con aprendizaje de los
hiperparámetros a partir de dos diferentes valores iniciales de los mismos. Las tres primeras
filas muestran la solución en los instantes de tiempo correspondientes a las columnas 1, 25 y
122 (o sea, en los picos del curso temporal de la amplitud de los parches C, A y B,
51
respectivamente). Las últimas tres filas muestran el correspondiente patrón de convergencia
de los valores de los hiperparámetros.
Se realizaron comparaciones entre las soluciones estimadas con el ENET-RVM y las
estimadas con el algoritmo MM (del inglés Majorization-Minorization), que utiliza una
aproximación cuadrática local y no un formalismo bayesiano completo (Sanchez–Bornot et
al., 2008)). En esta versión se utilizan los hiperparámetros de la forma
y
(
), donde se fija la razón entre los dos hiperparámetros (a través de fijar ) y se estima un
solo parámetro de regularización
como el que minimiza la función de validación cruzada
generalizada. En este caso calculamos las soluciones empleando tres diferentes valores para
(0,1; 0,01 y 0,001), que refuerzan distintos grados de raleza/suavidad en la solución al
proponer relaciones α2/α1 iguales a 9; 99 y 999. En la Figura 14 podemos observar que el
ENET-MM puede recuperar los parches B y C, pero introduciendo una gran cantidad de otras
activaciones “fantasma” en la solución (o sea, que no aparecen en la solución simulada), aún
en el caso en que la relación de los hiperparámetros conlleva a soluciones de alta raleza. En la
Figura 15 se muestran los detalles de las soluciones en los tres parches, donde aunque las
soluciones muestran el mismo efecto que la de ENET-RVM en cuanto a la dificultad en
recuperar la continuidad temporal (también aquí se estima independientemente en cada
instante de tiempo), se puede observar que tienen mayor dificultad para estimar la distribución
espacial en comparación con el ENET-RVM. En particular, cuando el conjunto de valores de
los hiperparámetros conduce a una solución más rala, esta muestra menos fantasmas, pero
tiende a deteriorar la recuperación de los parches. Esto se confirma con las medidas
cuantitativas que se muestran en la Tabla I, donde las soluciones de ENET-MM siempre
muestran mayores distancias a la solución simulada, menor raleza y menor AUC que las tres
soluciones obtenidas con el algoritmo ENET-RVM.
52
Figura 14: Comparación de las soluciones inversas estimadas por medio del algoritmo
ENET-RVM con las obtenidas por el ENET clásico (ENET-MM). En el primero los
hiperparámetros se aprenden dentro de la formulación bayesiana y en el segundo se fijan los
valores relativos (se muestran las diferentes combinaciones utilizadas) y se estima un solo
hiperparámetro como el que minimiza la función de crossvalidación generalizada.
53
Figura 15: Detalles de los parches espacio-temporales de las soluciones inversas obtenidas
empleando los algoritmos ENET-RVM y ENET-MM.
54
Estudio de las soluciones obtenidas con el modelo de Norma Mixta y el algoritmo MXNRVM
Para el caso del modelo que utiliza como a priori la norma mixta (MXN), comparamos las
soluciones inversas obtenidas con diferentes valores fijos del hiperparámetro que controla la
raleza (α=1 y α=10), con la solución obtenida con la estimación del mismo (aprendizaje)
partiendo de un valor inicial igual a 1 (Figura 16). Puede verse que la solución MXN-RVM es
capaz de estimar unas pocas fuentes en el espacio con suavidad a lo largo del intervalo de
tiempo en que estas están activas. En particular, las soluciones obtenidas con el
hiperparámetro fijo muestran mayor continuidad en los cursos temporales, aunque el aumento
de la raleza en la dimensión espacial no permite que se estimen bien las fuentes suaves y
aparecen activaciones “fantasmas” aisladas. Por otro lado, la solución con el aprendizaje del
hiperparámetro parece estimar mejor las activaciones espacialmente suaves, lo cual es
consistente con el hecho de que el valor estimado del hiperparámetro fue de 0.014, menor que
los utilizados en las otras dos soluciones. Sin embargo, esta solución mostró un efecto similar
al de la solución ENET-RVM, donde se subestimó la amplitud en algunos instantes de tiempo
y se pierde la suavidad temporal. Esto explica que en el análisis de las medidas cuantitativas
que aparecen en la Tabla III, aunque la solución aprendida tiene una distancia a la simulada
similar a las otras, su raleza general (espacio-temporal) es mayor que las otras y su
sensibilidad es manifiestamente más baja, llevándola a tener la menor AUC. En la Tabla III
también puede verse que en general, las soluciones MXN fueron más ralas que la solución
simulada, por lo que las distancias a esta fueron mayores y las AUC menores, en comparación
con las soluciones estimadas con el algoritmo ENET-RVM (Tabla I).
55
LASSO-MM MXN-RVM
Tabla III: Medidas cuantitativas de las soluciones MXN-RVM y LASSO-MM en los datos simulados
Soluciones
1-corr
Raleza Jest (%)
Raleza Jsim (%)
Sens(%) Espec(%) AUC(%)
α= 1
0.583
98.99
97.01
21.37
99.62
60.51
α Estimado
0.564
99.20
97.01
17.66
99.72
58.71
α = 10
0.562
98.93
97.01
21.52
99.56
60.56
α = 0,002
α = 1,187
α = 572
0.747
96.07
97.01
20.39
96.58
58.64
0.59
96.93
97.01
21.91
97.51
59.87
0.542
98.78
97.01
29.10
99.64
64.38
Figura 16: Soluciones inversas estimadas empleando el algoritmo MXN-RVM con valores
fijos del hiperparámetro (abajo), y con aprendizaje (derecha arriba).
Cuando miramos con más detalle las soluciones estimadas en las zonas de los 3 parches
espacio-temporales de interés (Figura 17), podemos confirmar que la solución que estima el
hiperparámetro es la que peor recupera la suavidad temporal pero es más efectiva para
56
recuperar las fuentes espaciales (parches B y C). Esto sugiere que en el modelo MXN donde
utilizamos un solo parámetro que controla la raleza espacial, la suavidad temporal puede
deteriorarse cuando hay activaciones que no son ralas y que obligan al parámetro a converger
a valores pequeños para poder recuperarlas. Cabe señalar que tanto las soluciones ENETRVM como las MXN-RVM fueron incapaces de localizar espacialmente la activación del
parche A, por lo que no se podría concluir que esto esté relacionado con la falta de suavidad y
extensión temporal de la misma, sino a la alta correlación que existe entre las columnas del
“lead field” alrededor de ese vóxel, llevando a que la activación máxima se estime en vóxeles
cercanos y no exactamente en el vóxel 100. Las medidas cuantitativas calculadas en los
parches se muestran en la Tabla IV. Consistentemente con nuestra discusión anterior, las tres
soluciones son muy similares en la estimación del parche A, pero la solución obtenida con el
aprendizaje del hiperparámetro muestra la mayor raleza en los otros dos parches. A pesar de
esto, en el parche C es la de menor distancia a la solución simulada y mayor AUC, debido a
que el bajo valor del hiperparámetro permitió estimar mejor la distribución espacial suave,
aunque a costa de deterioro en la suavidad temporal.
Tabla IV: Medidas cuantitativas calculadas en los 3 parches para las soluciones MXN-RVM
Parche A (Ral. Jsim=99.27%) Parche B (Ral. Jsim=40.60%)
Parche C (Ral. Jsim=0%)
Soluciones
1-corr Raleza(%) AUC(%) 1-corr Raleza(%) AUC(%)
1-corr Raleza(%) AUC(%)
α= 1
α Estimado
α = 10
1.004
99.39
49.69
0.494
77.21
69.18
0.737
81.40
49.15
1.004
99.39
49.69
0.499
79.06
67.63
0.698
90.09
52.32
1.003
99.46
49.73
0.506
77.66
68.8
0.734
81.92
51.49
57
Figura 17: Detalles en los distintos parches espacio-temporales de la simulación de las
soluciones inversas obtenidas con el algoritmo MXN-RVM, tanto con valores fijos del
hiperparámetro (filas 2 y 4), y con el aprendizaje bayesiano del mismo (fila 3).
En el estudio de la convergencia del hiperparámetro α con este algoritmo, observamos que hay
un patrón más robusto que en el caso del ENET-RVM, lográndose la convergencia al mismo
valor antes de las 150 iteraciones cuando se usaron valores iniciales de α=1 y α=10 (Figura
18). Las soluciones para las columnas donde cada activación simulada fue máxima mostraron
58
el mismo nivel de raleza en ambos casos. En nuestro estudio el algoritmo MXN-RVM, al
igual que el ENET-RVM, demoró 4.8 s en estimar la solución en un instante de tiempo (150
iteraciones como promedio), mientras que todo el mapa espacio-temporal se estimó en 16
min. Sin embargo, de la convergencia del hiperparámetro observada en la Figura 18,
podríamos decir que con la implementación de un criterio de parada adecuado, este algoritmo
pudiera utilizar alrededor de 100 iteraciones solamente para alcanzar la solución, por lo que
sería más rápido que el algoritmo de ENET-RVM.
De manera similar al caso del ENET-MM, exploramos las soluciones obtenidas con el modelo
LASSO y el algoritmo MM (LASSO-MM). La Figura 19 muestra estas soluciones junto con
la del MXN con el aprendizaje del hiperparámetro y la Tabla 3 muestra las correspondientes
medidas cualitativas. Aquí se destaca que el LASSO ofrece soluciones de alta raleza como era
de esperar, aunque en los casos en que la verdadera solución no lo es, o sea, donde existen
activación suave de muchos vóxeles vecinos o cercanos, el hiperparámetro óptimo debería
tomar valores muy pequeños. Estos valores pequeños conllevan a una solución que trata de
explicar estos parches con más activaciones no nulas pero a lo largo de todo el mapa espaciotemporal, conllevando a la aparición de más fuentes fantasmas que en el caso del MXN. Los
detalles de estas soluciones en los tres parches estudiados se muestran en la Figura 20, donde
se confirma la mayor raleza y la menor distancia a la solución simulada de la solución MXN
cuando el parámetro de regulación no es muy grande. Aunque este es un estudio exploratorio
con pocos valores del parámetro de regularización, estos resultados sugieren que la solución
MXN es más robusta ante los escenarios que no satisfacen las suposiciones de raleza de la
solución, ofreciendo soluciones más ralas que la real, pero con menos fantasmas que la
solución LASSO-MM.
59
Figura 18: Soluciones inversas estimadas con MXN-RVM con aprendizaje del
hiperparámetro a partir de dos diferentes valores iniciales del mismo. Las tres primeras
filas muestran la solución en los instantes de tiempo correspondientes a las columnas 1, 25
y 122 (o sea, en los picos del curso temporal de la amplitud de los parches C, A y B,
respectivamente). La última fila muestra los correspondientes patrones de convergencia
del hiperparámetro.
60
Figura 19: Comparación de las soluciones inversas estimadas por medio del algoritmo
MXN-RVM con las obtenidas por el LASSO (LASSO-MM). En el primero los
hiperparámetros se aprenden dentro de la formulación bayesiana y en el segundo se fijan
distintos valores para el correspondiente parámetro de regularización.
61
Figura 20: Detalles de los parches espacio-temporales de las soluciones inversas obtenidas
empleando los algoritmos MXN-RVM y LASSO-MM.
62
Por último, estudiamos la robustez del ENET-RVM y el MXN-RVM, utilizando el
aprendizaje de los hiperparámetros, ante diferentes niveles de ruido en la señal
(correspondientes a una relación señal-ruido RSR de 30db y 10db). En la Figura 21 se observa
que la solución con MXN-RVM es más robusta que la estimada por el ENET-RVM que
tiende a asimilar el ruido como parte de la solución, mostrando más fuentes activas que las
que realmente fueron simuladas (sobreajuste). Cuando fijamos los hiperparámetros en
combinaciones que imponen mayor raleza de las soluciones en ambos algoritmos, el ENETRVM puede manejar mejor el nivel de ruido sin la presencia de muchas activaciones
fantasmas, mientras que el MXN-RVM continúa siendo robusto al ruido pero puede mostrar
activaciones fantasmas con el exceso de raleza.
Figura 21: Comparación de las soluciones inversas estimadas por medio de los algoritmos
ENET-RVM y MXN-RVM para distintos niveles de ruido, con aprendizaje de los
hiperparámetros.
63
En resumen, este estudio con una simulación realista que no cumple estrictamente con las
suposiciones teóricas de los modelos nos permitió observar la relación existente entre la
estimación de los hiperparámetros y las propiedades de las soluciones en las dos dimensiones.
Al existir una sola fuente realmente rala (sólo un vóxel) que no tenía alta suavidad temporal y
otras dos fuentes con mayor distribución espacial, las soluciones con parámetros fijos que
imponían mayor raleza no fueron las mejores en sentido general. Sin embargo, el aprendizaje
de los hiperparámetros fue bastante efectivo en ambos casos para tratar de explicar
correctamente la distribución espacial de las fuentes. En el caso del ENET-RVM,
encontramos que es menos robusta al ruido, por lo que al hacer la estimación de la solución
espacial independientemente para cada instante de tiempo, la influencia del ruido conllevó a
que no se estimara correctamente la suavidad temporal. Por otro lado, en el caso del MXNRVM el deterioro de la suavidad temporal estuvo directamente relacionado con la estimación
de un hiperparámetro pequeño para lograr explicar la suavidad espacial. Igualmente se
encontró que a mayores valores del hiperparámetro, se estimaban soluciones de mayor raleza
espacial, alejándose de la solución simulada, pero garantizando mucho mejor la continuidad y
suavidad temporal de las activaciones estimadas. Esto sugiere en al tener un solo parámetro
para controlar la raleza este consistentemente garantiza la suavidad temporal solo cuando las
fuentes espaciales son realmente ralas. En general, el algoritmo MXN-RVM es propenso a
estimar soluciones de mayor raleza que la real y el ENET tiende a sobreajustar el dato,
mostrando más fuentes fantasmas, lo cual a su vez explica su menor robustez ante mayores
niveles de ruido en los datos. Estudios futuros pueden orientarse al desarrollo de modelos
espacio-temporales de ENET, modelos de MXN que permitan controlar por separado los
niveles de suavidad y raleza en las dimensiones temporal y espacial; y la posibilidad de
64
combinar estos modelos para tener mayor flexibilidad en la estimación de fuentes con
diferentes características espacio-temporales.
4.2 Estudio de datos reales
Como datos reales utilizamos registros de EEG de 30 electrodos, con una frecuencia de
muestreo de 128 Hz, en un experimento donde se presentaron estímulos visuales a sujetos
sanos (Makeig, 2002). A los sujetos se les pide discriminar, por medio de la acción física de
pulsar un botón, entre dos tipos de figuras geométricas que aparecen en una región de la
pantalla, donde se les ha indicado el lugar en que aparecerá el estímulo y bajo qué condiciones
debe efectuar la acción. Los registros del EEG en una ventana de tiempo de 3 s alrededor del
momento de presentación del estímulo (1 s pre-estímulo y 2 s post-estímulo) se repiten 80
veces (corridas para distintos sujetos) y se promedian para cancelar la actividad oscilatoria de
fondo que no está relacionada con el estímulo, obteniéndose lo que se conoce como Potencial
Evocado Visual. La señal temporal obtenida contiene 384 instantes de tiempo, donde el
estímulo ocurre en el instante 128. La Figura 22 muestra las series de tiempo de este Potencial
Evocado y señala los dos instantes de tiempo escogidos por nosotros para estimar la solución
inversa con los algoritmos propuestos: el instante 165 (281 ms post estímulo) donde se
encuentra el valor máximo negativo y el instante 179 (430 ms post estímulo) correspondiente
al valor máximo positivo del potencial eléctrico entre todos los electrodos. Para la solución
del problema inverso empleamos un cerebro promedio, definiendo un enrejado de generadores
sobre la sustancia gris de la corteza cerebral y del tallo cerebral y el tálamo, con un total de
3244 vóxeles.
65
Figura 22: Series de tiempo del Potencial Evocado Visual para todos los electrodos. A:
Instante en que ocurre el estímulo, empleado como instante de referencia (t = 0). B: Mínimo
global del voltaje en el tiempo (t = 281 ms). C: Máximo global del voltaje en el tiempo (t =
430 ms).
Calculamos las soluciones inversas con los métodos ENET-RVM, MXN-RVM y las
comparamos con una de las soluciones inversas más reconocidas y utilizadas en la literatura,
la Tomografía Eléctrica de Baja Resolución (LORETA). Para mostrar los resultados
presentamos las fuentes principales, donde ocurren los máximos de actividad, en los planos
ortogonales (occipital, sagital y coronal) donde mejor se observan, y la actividad secundaria
por medio de una imagen de la proyección de máxima intensidad de todas las activaciones del
espacio tridimensional a dichos planos, (conocido como “cerebro de cristal”). Empleamos una
escala de colores para representar la magnitud del módulo del vector de la DCP, y las
coordenadas x, y, z representan la localización del máximo con respecto al sistema de
coordenadas de los vóxeles de la imagen.
En el instante 165 el máximo de la actividad estimada con los tres métodos se encuentra en el
área de Brodmann 19, que corresponde a la corteza visual secundaria, del hemisferio derecho
66
(Figura 23). Como es esperado, la solución LORETA es la más suave, extendiendo la
activación principal no solo en las áreas visuales (occipital) de ambos hemisferios, sino
también en áreas temporales. La solución con el ENET-RVM es también suave en el espacio
pero posee menos dispersión espacial, mostrando también activaciones occipitales en ambos
hemisferios y otras activaciones pero como fuentes mejor diferenciadas. Con el método
MXN-RVM se obtiene una solución de mayor raleza, mostrando únicamente una fuente
principal en este plano bien localizada en el área visual derecha, lo cual es más consistente
con lo que se conoce sobre las áreas involucradas en el procesamiento visual (Guyton, 1970).
La Figura 24 muestra la proyección de máxima intensidad de estas mismas soluciones,
confirmando la gran dispersión espacial de la solución LORETA que muestra una activación
secundaria en el área temporal superior. La solución de ENET-RVM muestra las mismas
fuentes que LORETA pero con mayor raleza, de forma que activaciones secundarias
temporales, frontales y centro-parietales pueden distinguirse. A diferencia de LORETA, las
áreas temporales no aparecen con la mayor amplitud después del área visual, sino la
activación centro parietal (área de Brodmann 4) de la corteza motora, que puede estar
relacionada con la activación de las neuronas de esta área, al desencadenar la acción física en
respuesta al estímulo (Guyton, 1970). La solución MXN-RVM solo muestra esta activación
centro-parietal como la única fuente secundaria, lo cual ofrece una imagen más clara y más
consistente con la neurofisiología en este experimento visual.
67
Figura 23: Representación en los planos ortogonales del máximo de la DCP estimada por
medio de los tres métodos, en el instante 165, correspondiente al máximo valor negativo del
Potencial Evocado Visual.
68
Figura 24: Proyección de la máxima intensidad de la DCP estimada por medio de los tres
métodos, en el instante 165, correspondiente al máximo valor negativo del Potencial Evocado
Visual.
Es importante señalar las diferencias entre estas soluciones y las soluciones obtenidas con los
modelos Ridge L, ENET L y LASSO Fusión, para estos mismos datos, utilizando el algoritmo
MM, las cuales se muestran en la Figura 25. Esta figura corresponde a la Figura 3 de VegaHernández et al. 2008 y muestra la proyección de máxima intensidad de estas soluciones con
la orientación de los hemisferios contraria a las figuras 22 y 23. Puede observarse la gran
coincidencia de las soluciones LORETA y Ridge L, que son teóricamente equivalentes y de la
solución ENET-RVM con algunas de las soluciones de ENET L presentadas con diferentes
valores de la relación entre los parámetros que controlaban la raleza (λ1) y la suavidad (λ2)
69
respectivamente. En este último caso, los parámetros de regularización se estimaban
heurísticamente con la validación cruzada, lo que implicaba el cálculo de la solución inversa y
la evaluación de la función de validación cruzada para cada valor de los parámetros. Esto,
unido a la lenta convergencia del algoritmo MM, hizo imposible que se estimaran ambos
parámetros y se calcularan solamente las soluciones para un conjunto de razones entre ellos,
estimándose por validación cruzada un solo peso relativo para la penalización. Luego, fue
necesario el uso de métodos estadísticos para determinar cuál de las diferentes soluciones
ENET L era la óptima. En nuestro caso, es relevante el hecho de que se logra obtener una
única solución ENET con un juego de hiperparámetros que se estiman automáticamente
dentro del algoritmo, y esta solución es muy similar a las obtenidas con valores intermedios
de la relación entre suavidad y raleza con el MM.
Con respecto a la solución MXN-RVM, resalta que esta es esencialmente diferente de la
solución más rala de las obtenidas con el MM, el LASSO FUSION. Dicha solución en la
Figura 25 puede explicarse como el otro caso extremo de la solución ENET L donde las
mismas activaciones que aparecen en esta se mantienen pero mucho más concentradas,
mostrando incluso la subsistencia de puntos aislados con magnitudes altas. En el caso del
MXN-RVM solo subsisten dos activaciones y presentan cierto grado de suavidad espacial.
Como en este caso estamos calculando la solución para un solo instante de tiempo, no es
posible explicar esta diferencia por el hecho de ser un modelo espacio-temporal donde la
información temporal puede influir en una mejor estimación de las activaciones espaciales.
Por tanto, creemos que esto se debe esencialmente al proceso de aprendizaje del
hiperparámetro que controla la raleza dentro del formalismo bayesiano completo, a diferencia
de la optimización del parámetro de regularización por validación cruzada generalizada.
70
Figura 25: Versión en colores de la Figura 3 de Vega-Hernández et al. 2008. Para el mismo
dato utilizado aquí, en el instante 165 correspondiente al potencial máximo negativo del
Potencial Evocado Visual, se muestra la proyección de la máxima intensidad de la DCP
estimada por medio de los métodos Ridge L, Elastic Net L y Lasso Fusión, utilizando el
algoritmo MM y estimando los parámetros de regularización por Validación Cruzada
Generalizada. La primera solución es teóricamente equivalente a la solución LORETA y para
el ENET se utilizaron diferentes valores de la relación entre el parámetro que controla la
raleza y el que controla la suavidad. Nótese que la orientación de los hemisferios es contraria
a las figuras anteriores.
71
En el instante 179, que corresponde al máximo valor positivo del Potencial Evocado Visual,
las soluciones inversas muestran un comportamiento bastante similar al del instante 165 en
cuanto a la dispersión espacial de las fuentes y la aparición de fuentes secundarias espurias o
no, sin embargo, encontramos diferencias en cuanto a la localización de la máxima activación
(Figuras 26 y 27). A diferencia del instante analizado anteriormente, los tres métodos no
coincidieron en la localización de la máxima activación, de forma que con LORETA esta se
localizó en el área de Brodmann 43, mientras que ENET-RVM y MXN-RVM la mostraron en
el área de Brodmann 21. Este último resultado es más interpretable desde el punto de vista del
funcionamiento del sistema visual (Guyton, 1970), debido a que la información visual primero
es proyectada en la corteza visual (área de Brodmann 18 y 19) y luego pasa a las áreas 20 y
21, donde la información visual es integrada a un nivel más alto (rostros, palabras, etc.). La
solución LORETA es de nuevo demasiado dispersa y muestra además de la activación
principal, otras áreas occipitales frontales y parietales, haciendo muy difícil distinguir cual es
relevante o constituye una activación diferente y cual es solamente una extensión de la fuente
principal. Igualmente, ENET-RVM mostró soluciones con un compromiso entre raleza y
suavidad, que permite distinguir mejor las diferentes activaciones estimadas, aunque la gran
cantidad de ellas sigue haciendo difícil determinar cuáles son fisiológicamente factibles. Por
último la solución MXN-RVM vuelve a ser la solución de mayor raleza, mostrando el
máximo de activación en el área temporal superior y una pequeña activación residual en el
área visual occipital. Esta solución tiene mayor fundamento fisiológico, ya que en este
instante de tiempo se conoce que otros aspectos cognitivos (forma, color, movimiento) de la
información visual están siendo procesados/integrados en dichas áreas, aunque puede que
todavía queden activaciones en el área visual. Es importante recalcar que las activaciones
72
obtenidas con esta solución inversa no son puntuales sino que muestran cierto soporte espacial
también más cercano a las consideraciones fisiológicas de la conectividad entre áreas
cerebrales cercanas.
En sentido general, estos resultados muestran que tanto la solución ENET-RVM como la
MXN-RVM muestran ventajas con respecto a versiones reconocidas en la literatura en cuanto
a la estimación de localización y dispersión de las activaciones principales, pero sobre todo
con la ventaja metodológica de la estimación automática dentro de un formalismo bayesiano
de los hiperparámetros que controlan los niveles de raleza y suavidad espacio-temporal de la
solución. De todas formas, cabe señalar que según los resultados de las simulaciones, la
solución ENET-RVM puede estar sobreajustando el ruido presente en los datos de forma que
muestra más activaciones fantasmas y la solución MXN-RVM puede resultar en patrones
espaciales de mayor raleza que las activaciones reales. Sin embargo, si la localización de estas
pocas activaciones es cercana a la localización de las fuentes reales, esta propiedad puede ser
muy útil en el estudio de las fuentes electrofisiológicas de los diversos procesos cerebrales.
Estudios que involucren un conjunto de simulaciones exhaustivas variando las localizaciones
de las fuentes simuladas y la combinación de ellas deben desarrollarse en un futuro para la
validación de estas soluciones como una alternativa poco costosa en la detección de fuentes
cerebrales.
73
Figura 26: Representación en los planos ortogonales del máximo de la DCP estimada por
medio de los tres métodos, en el instante 179, correspondiente al máximo valor positivo del
Potencial Evocado Visual.
74
Figura 27: Proyección de la máxima intensidad de la DCP estimada por medio de los tres
métodos, en el instante 179, correspondiente al máximo valor positivo del Potencial Evocado
Visual.
75
CONCLUSIONES
En este trabajo propusimos métodos para la solución del problema inverso del EEG,
empleando la formulación Bayesiana para incorporar combinaciones de restricciones de tipo
L1/L2. Con respecto a los objetivos específicos que nos planteamos podemos concluir que:
-
La formulación bayesiana del ENET, extendida de forma similar al RVM, adicionando
un nuevo nivel de parámetros y empleando la herramienta del Bayes Empírico,
permite obtener una forma explícita de la verosimilitud de tipo II o evidencia de los
hiperparámetros, de donde se pueden derivar ecuaciones de actualización de los
mismos.
Con estas ecuaciones se pueden proponer diferentes algoritmos de optimización
iterativa para la estimación de parámetros e hiperparámetros. Nosotros desarrollamos
algoritmos directos MAP en un modo similar al RVM.
-
La formulación dentro del enfoque de aprendizaje Bayesiano nos permitió introducir
una a priori basada en la norma L1 en el espacio y otra basada en la norma L2 al
cuadrado en el tiempo. Con esto se logra obtener una pdf a priori que es separable en
cada instante de tiempo (columnas de la matriz de parámetros) y permite transformar
el Campo Aleatorio de Markov espacial (inducido por la a priori de la norma-mixta)
en un modelo jerárquico al nivel de los parámetros de tipo ENET.
El nuevo modelo de la norma-mixta contiene nuevos hiperparámetros (relacionados
con la a priori Normal - Laplace) que controlan localmente la raleza. Los mismos
heredan las conexiones entre los nodos del MRF original y pueden ser actualizados por
una regla simple, que tiene un sentido estadístico, mejorando la eficiencia del
76
algoritmo de inferencia. La equivalencia entre el modelo de partida y el modelo tipo
ENET se demuestra con el Lema 3.2.5.
-
La equivalencia entre los modelos de MXN y ENET permite aplicar el procedimiento
del Bayes Empírico de manera similar para ambos, obteniéndose fórmulas de
actualización semejantes e interpretables desde el punto de vista del grado de raleza y
suavidad impuestos en la estimación de los parámetros. Este resultado muestra la
extensibilidad del RVM a modelos más complicados como ENET y MXN.
-
En una validación preliminar de los métodos propuestos con datos simulados, estos se
comportaron de acuerdo a los supuestos teóricos del modelo, demostrando la utilidad
de los algoritmos desarrollados. El aprendizaje de los hiperparámetros en el caso de
ENET-RVM conlleva a soluciones más cercanas a las simuladas pero con niveles de
raleza altos por ser menos robusta ante el ruido y estimar independientemente las
soluciones para los distintos instantes de tiempo. El MXN-RVM tiende a estimar
soluciones más ralas que las simuladas pero con alta robustez al ruido. El
hiperparámetro que controla la raleza espacial también controla la suavidad temporal,
de forma que si se tratan de obtener soluciones suaves (no ralas) se pierde la
continuidad en el tiempo.
El ENET-RVM introduce menos activaciones fantasmas en la solución y recupera
mejor las fuentes que el ENET-MM con relación de parámetros similares. Además,
obtiene soluciones de raleza intermedia (mayor que la solución LORETA y menor que
la solución Lasso Fusión) con la estimación de los hiperparámetros sin necesidad de
post-procesamiento estadístico.
77
El MXN-RVM con el aprendizaje del hiperparámetro estima soluciones de alta raleza,
pero con menos activaciones fantasmas que la solución del LASSO-MM cuando se
estiman fuentes no ralas.
-
En el caso de los datos reales la solución inversa con el algoritmo ENET-RVM es
suave en el espacio pero mucho más localizadas, alrededor del máximo, que la
calculada con el método de LORETA. Las soluciones obtenidas con el MXN-RVM
fueron ralas, pero esencialmente diferentes a las soluciones de alta raleza conocidas en
la regresión penalizada como el Lasso Fusión. En particular, mostraron pocas
activaciones con cierto soporte espacial en lugar de muchas activaciones puntuales
aisladas. Con ambos, ENET-RVM y MXN-RVM, se logran estimar patrones de
fuentes cerebrales con mayor interpretación neurofisiológica.
78
RECOMENDACIONES
Este trabajo se dirigió fundamentalmente al desarrollo de nuevos modelos teóricos y su
validación y aplicación preliminar. Por tanto, los resultados presentados abren nuevas
preguntas y caminos de investigación para la búsqueda de versiones finales más adecuadas
para resolver los problemas planteados por el análisis de datos de EEG reales tanto en la
investigación como en la práctica clínica.
Como recomendaciones para las aplicaciones futuras de estos métodos, señalaremos la
utilización del algoritmo ENET-RVM con parámetros fijos de los hiperparámetros en caso de
que los datos sean muy ruidosos, y lo mismo puede hacerse con el uso del MXN-RVM si hay
fuentes muy suaves espacialmente, debido a que con este modelo solo es posible recuperar
fuentes ralas.
Para el trabajo futuro es recomendable trabajar sobre la convexidad de la función objetivo
(evidencia de tipo II) para reducir la sensibilidad a las condiciones iniciales.
También sugerimos explorar la habilidad de los métodos propuestos estimando fuentes
profundas o extenderlos a Promediación Bayesiana de Modelos. Desarrollar modelos que
extiendan los propuestos a incorporar restricciones en la dimensión temporal con
hiperparámetros que regulen la raleza y suavidad en esta dimensión, independientemente de la
suavidad o raleza espacial.
La equivalencia entre los dos modelos ENET y MXN, en la formulación Bayesiana, sugiere la
posibilidad de hacer un tratamiento semejante para distribuciones a priori basadas en
penalización múltiple, con modelos de norma-mixta, Elastic Net y también restricciones de
ortogonalidad, para agregar más flexibilidad a la estimación, ya sea con los parámetros de
regularización fijos o con aprendizaje.
79
REFERENCIAS
Alexander Schmolck and Richard Everson, 2007: Smooth relevance vector machine: a
smoothness priorextension of the RVM. Machine Learning, 68, 107-135.
Alexandre Gramfort, Matthieu Kowalski, Matti Hämaläinen, 2012: Mixed-norm
estimates for the M/EEG inverse problem using accelerated gradient methods. Physics
in Medicine and Biology 57, 1937-1961.
Andrews D. F. and Mallows C. L. 1974: Scale Mixtures of Normal Distributions.
Journal of the Royal Statistical Society. Series B (Methodological), 36(1), 99-102.
Bishop C. M. 2005: Pattern Recognition and Machine Learning.
Beal M. J. 2003: Variational Algorithms for Approximate Bayesian Inference. Thesis
submitted for the degree of PhD of the University of London.
Babacan S. D., Molina R. and Katsaggelos A. K. 2010: Bayesian Compressive
Sensing Using Laplace Priors. IEEE Transactions on image processing 19(1), 53-63.
Beck A and Teboulle M 2009: A fast iterative shrinkage-thresholding algorithm for
linear inverse problems SIAM Journal on Imaging Sciences 2(1), 183–202.
Faul A. C. and Tipping M. E. 2003: Fast Marginal Likelihood Maximization for
Sparse Bayesian Models. Proceedings of the ninth international workshop on artificial
intelligence and statistics1(3).
Fan, J. and Li, R. 2001: Variable Selection via Nonconcave Penalized Likelihood and
Its Oracle Properties. J. Amer. Statist. Assoc., 96, 1348-1360.
Hoerl A. E. and R. W. Kennard. 1970: “Ridge Regression: Biased Estimation for
Nonorthogonal Problems”. Technometrics, 12 (1), 55-67.
80
Hadamard J., (1923) Lecture on the Cauchy problem in linear partial differential
equations. New Haven, CT: Yale University Press.
Haufe S, Nikulin V V, Ziehe A, Müller K R and Nolte G 2008: Combining sparsity
and rotational invariance in EEG/MEG source reconstruction‟ NeuroImage 42(2),
726–38.
Hunter, D. R. and Li, R. 2005: Variable selection using MM algorithms. Ann.
Statist.,33,1617-1642.
Kindermann R. and Snell J. L. 1980: Markov Random Fields and Their Applications.
American Mathematical Society.
Kowalski M and Torrésani B 2009: Sparsity and persistence: mixed norms provide
simple signals models with dependent coefficients. Sig Imag Video Process 3(3), 251–
264.
Kevin P. Murphy, 2012: Machine Learning a Probabilistic Perspective. MIT Press.
George H. Klem, Hans Otto Luders, H.H. Jasper and C. Elger, 1999:
Recommendations for the Practice of Clinical Neurophysiology. Guidelines of the
International Federation of Clinical Physiology
MacKayD. J. C. 2003: Information Theory, Inference, and Learning Algorithms.
Cambridge University Press.
Magnus, J. R., and Neudecker H. 2007: Matrix Differential Calculus with Applications
in Statistics and Econometrics.
Ou W, Hämaläinen M and Golland P, 2009: A distributed spatio-temporal EEG/MEG
inverse solver NeuroImage 44(3), 932–946.
81
Park, T. and Casella, G. 2008: The Bayesian Lasso. Journal of the American
Statistical Association, 103, 681-686.
Pascual-Marqui R. D., (1999) Review of Methods for solving the EEG Inverse
Problem. International Journal of Biolectromagnetism. Volume 1, Number 1, pp: 7586.
Quing Li and Nan Lin, 2010: The Bayesian Elastic Net. Bayesian Analysis, 5(1), 151170.
Riera J. J. 1999: Physical Bases of Brain Tomography. Thesis submitted for the degree
of PhD on Physics of the Havana University.
Richard Durrett, 1996: Probability Theory and Examples, 2nd Edition, Daxbury Press.
Sanchez J. M., Martinez E., Lage A.,Vega M. and Valdes P. A. 2008: Uncovering
sparse brain effective connectivity: A voxel-based approach using penalized
regression. Statistica Sinica, 18, 1501-1518.
Tikhonov A. N. and Arsenin V. Y. 1977: Solution to ill posed problems. V. H.
Winston, Washington, DC.
Tibshirani R. 1996: Regression and Shrinkage via the LASSO. Journal of the Royal
Statistical Society. Series B (Methodological), 58(1), 267-288.
Tibshirani R., M. Saunders, S. Rosset, J. Zhu and K. Knight. 2005. Sparsity and
smoothness via the fused lasso. Journal of the Royal Statistical Society Series BStatistical Methodology, 67, 91-108.
Tipping M. E. 2001: Sparse Bayesian Learning and the Relevance Vector Machine.
Journal of Machine Learning Research 1, 211-244.
82
Lehmann, E. L. and Casella, G. 1998. Theory of Point Estimation, 2nd Edition, New
York: Springer-Verlag.
Minjung Kyung, Je Gilly, Malay Ghoshz and George Casella, 2010: Penalized
Regression, Standard Errors, and Bayesian Lassos. Bayesian Analysis, 5(2), 369-412.
Vega M., Martinez E., Sanchez J. M., Lage A. and Valdes P. A. 2008: Penalized least
squares methods for solving the EEG inverse problem. Stat Sin18:1535–1551.
Valdes P. A., Vega M., Sanchez J. M., Martınez E. and Bobes M. A. 2009: EEG
source
imaging
with
spatio-temporal
tomographic
nonnegative
independent
component analysis. Human Brain mapping, 30(6), 1898–910.
Wipf D. and Nagarajan S. 2009: A unified Bayesian framework for MEG/EEG source
imaging. Neuroimage 44, 974-966.
Zou H. and T. Hastie. 2005: Regularization and Variable Selection via the Elastic Net.
Journal of the Royal Statistical Society Series B, 67 (2), 301.
83
ANEXOS
Prueba del Lema 2.1.1
|
Aplicando la mezcla de gaussianas
|
|
∫
(
)
∫
(
|
(
(
∫
)
)
en la fórmula de arriba:
)
∫
(
√
̃ y poniendo
|
|
, nos queda:
̃
∫
̃
De nuevo cambiando las variables
)
√
Haciendo el cambio de variable
|
√
√̃ √
, y poniendo
|
√
̃
tendremos:
∫
√
√
∫
√
(
)
(
)
.
Entonces bajo la integral anterior tendremos un término que corresponde a una pdf Normal:
(
)
,
√
Y otro que corresponde a una Gamma Truncada en el intervalo .
(
).
/:
√
(
⁄
.
/)
(
84
)
(
).
Finalmente podemos llegar a qué:
|
|
(
∫
)
⁄
(
.
/)
.
Prueba de la Proposición 2.2.1
(
⁄
) .
(
)/
) (
(
|
| |
(
(
|
)
(
)
(
(
(
)/
)|
)
(
)
.
(
)/
)|
( )
|
.
)
|
(
|
)
| |
(
(
(
)
(
)
)|
(
|
)
| |
(
)
( )
(
(
)
)
( )
)|
Pero puede demostrarse que:
(
)
( )
‖
‖
.
(
)/
De donde:
(
⁄
) .
(
)/
(
|
|
| |
( )|
(
.
⁄
)
( )
(
)
‖
‖
.
)|
( )/
.
⁄
(
85
)/ (
⁄
).
(
)/
Prueba de la Proposición 2.2.2
(
.
a)
(
(
)/
.
(
)
‖
‖
)/ )
.
(
)/
.
b)
|
( )|
|
(
)|
.
(
)/
.
( )
(
( )/
.
(
)
(
( )
⁄
/
)
.
)
c)
|
{
( )|
( )
∑
|
(
)|
∑
.
(
)/
∑
∑
∑
∫
( ⁄
∫
)
( ⁄
}
)
=
( )/
.
∑{
∫
( ⁄
)
}
d)
{
|
( )|
|
(
)|
.
86
(
)/
∑
∫
( ⁄
)
}
( )
∑
∑
∑
∑
∫
( ⁄
)
=
∑
e)
‖
|
( )|
‖
∑ {
( )/
.
∑{
∑
|
|
∑
. ( )
/
∫
‖
( ⁄
∑
‖
‖
)
}
( ( )
)
‖ }.
Prueba de la Proposición 3.1.4
Sean
(
y
verificar que
( )
( )
Si analizamos las derivadas de
) ,
( )
,
-. Entonces debido a que
( )
y
(
) ( )
y
son normas fácilmente se puede
( ). Queda demostrada la convexidad.
:
(∑
.∑
|
|)
(∑
|
Es fácil ver que si
|
|
|) /
.∑
entonces
|
|
|
| /
, que esta indefinida en cero. Queda
demostrada la no diferenciabilidad.
Prueba del Lema 3.2.5
a)
Si en la Proposición 2.1.4 ponemos
para las pdf (
)
Proposición 2.1.2,
,
y
(
|
||
)⁄ (
b) Es fácil ver que se cumple
y
∑
)
∑
∫
∑
|
). Si además ponemos los potenciales igual que en la
, obtenemos que (
|
De donde podemos concluir que
entonces tenemos que, por la regla de Bayes
|
|y
∫
|, donde la matriz
es la identidad. Entonces la pdf de la variable
87
∑
|
||
,
|
|
|
||
||
|
|
.
.
es una matriz de unos
puede representarse
(
)
(
|
respecto a
|)
(
), donde
, (
)
es la función delta de Dirac. Para la pdf de
(
(
) (
)
marginalizamos
), nos queda que:
∫ (
|
|)
(
‖
)
Si en esta misma integral tenemos en cuenta la simetría respecto a
‖
.
y reorganizamos el argumento en
obtenemos:
(
)
(
| |
)∫ (
De donde, por las propiedades de la delta de Dirac, (
c)
Si en el nuevo modelo con las pdf de
marginalizamos respecto a
(
)
y
(
‖
)
‖
‖
)
)
‖
, donde (
y
(
(
|
),
|
.
|
∏
)
en la fórmula:
) (
)
|
∏
‖
|
‖
(
)
Obtenemos que:
∫ (
)
|
∫∏[
|
∫
|
Haciendo el cambio de variable
∫ (
‖
|
‖
]
‖
‖
(
(
)
)
|, entonces la integral anterior queda:
| |
)
Descomponiendo el término ‖
|
‖
(∑
∫
|
(∑
|)|
|
|
|)|
|
‖
‖
(∑
|
|) y substituyendo en la
expresión de arriba obtenemos:
∫ (
| |
)
| |
∫
(∑
|
|)|
∫
|
(∑
(∑
|
|
|
(∑
|
|)|
|
(∑
(∫
(∑
|
|)|
|
)
|)|
|)
88
|
|)
|
| |
(∑
∫
|
|)|
|
(∑
|
|)
De donde finalmente:
∫ (
)
(∑
∫
‖
∫
|
|)|
|
(∑
|
|)
‖
Prueba de la Proposición 3.3.1
a)
( )
.
(
b)
(
.
)/
‖
(
‖
)/ )
.
(
)/
.
( )
|
( )|
|
(
)|
.
(
)/
( )
.
(
( )/
.
.
/
.
/
)|
.
( )
⁄
/
)
.
c)
∑{
|
( )|
|
(
‖
∑
( )
(
)/
∑
∫
( ⁄
‖ }
∑
∑
∑
‖
89
∑
‖
∫
( ⁄
)
)
∑
d)
‖
( )/
.
,∑ ,
|
( )|
‖
∑ {
∑
. ⁄
∫
|
|
∑
. ( )
/
90
‖
/
-
∑‖
∑
‖
‖
‖ }.
‖
( ( )
-.
)