00 introduccion - Generando Conocimiento

APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
0. INTRODUCCIÓN
Se presenta de forma concisa y práctica la herramienta de minería de datos WEKA.
Estos apuntes son una recolección de información de muy variadas fuentes, páginas de Internet,
artículos etc., todas ellas aparecen citadas en las referencias. Esperamos que estos sean de utilidad
para los alumnos que se acerquen al análisis de datos y en particular para aquellos que tengan
interés en aplicar los conocimientos teóricos en el campo de la práctica.
Ésta, es una
herramienta de
aprendizaje
automático y data
mining, escrita en
lenguaje Java,
gratuita y
desarrollada en la
Universidad de
Waikato.
WEKA1 se
distribuye como
software de libre
distribución.
La primera sección tiene un enfoque teórico - práctico, pretendiendo servir de guía de utilización
de esta herramienta para ello se obviarán los detalles técnicos y específicos de los diferentes
algoritmos, que se presentan en una sección aparte, y se centrará en su aplicación, configuración y
análisis dentro de la herramienta. Por tanto, se remite al lector a la sección 2 con los detalles de las
técnicas y los algoritmos para conocer sus características, parámetros de configuración,
comparaciones, etc. Para reforzar el carácter práctico de la primera sección, además se adoptará un
formato de tipo tutorial, con un conjunto de datos disponibles sobre el que se irán aplicando las
diferentes facilidades de WEKA. Se han seleccionado algunas de las técnicas disponibles para
aplicarlas a ejemplos concretos, siguiendo el acceso desde la herramienta al resto de técnicas
implementadas, presentada a modo ilustrativo.
En un anexo electrónico (en disco) se adjuntará material oficial bajado de la página de Weka y
algunos artículos de interés, además de los “dataset” o ficheros de datos que se utilizaran tanto en
los ejemplos como en los ejercicios.
1
El programa WEKA se puede descargar desde: http://www.cs.waikato.ac.nz/ml/weka
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
A continuación se citan las principales referencias bibliográficas consultadas para armar estos
apuntes.
0.1. REFERENCIAS
DIEGO GARCÍA MORATE, Manual de Weka, (diego.garcia.morate(at)gmail.com)
JOSÉ ANTONIO GÁMEZ MARTÍN, apunte de cátedra Minería de Datos, Sistemas Informáticos Ingeniería Informática, Curso 2006/2007, Universidad de Castilla-La Mancha , Escuela Politécnica
Superior de Albacete (http://www.pol-ab.uclm.es/ )
JOSÉ MANUEL MOLINA LÓPEZ y JESÚS GARCÍA HERRERO, Técnicas de Análisis de Datos,
Aplicaciones Prácticas Utilizando Microsoft Excel y Weka, apuntes de la cátedra Técnicas de IA para
el Análisis de Datos, Actividad Docente, Grupo de Docencia Inteligencia Artificial, Informática Teórica
y Compiladores, (http://scalab.uc3m.es/~docweb/index.html)
JOSÉ HERNÁNDEZ ORALLO y CÈSAR FERRI RAMÍREZ, Práctica de minería de datos:
introducción a Weka , apuntes del Curso de Doctorado Extracción Automática de Conocimiento en
Bases de Datos e Ingeniería del Software, Universitat Politècnica de València, Marzo 2006
(jorallo@dsic.upv.es y cferri@dsic.upv.es).
LÓPEZ DE ULLIBARRI GALPARSORO I, PITA FERNÁNDEZ, S., Medidas de concordancia: el
índice de Kappa, Unidad de Epidemiología Clínica y Bioestadística. Complexo HospitalarioUniversitario Juan Canalejo., A Coruña (España) Cad Aten Primaria 1999; 6: 169-171.
M.ASUNCIÓN VICENTE, Inteligencia Artificial y Reconocimiento de Patrones, Departamento:
Ingeniería de Sistemas Industriales, Curso 5º, 2006-2007, (http://isa.umh.es/asignaturas/iarp/)
MIGUEL GARRE, JUÁN JOSÉ CUADRADO y MIGUEL ÁNGEL SICILIA, Comparación de
diferentes algoritmos de clustering en la estimación de coste en el desarrollo de software, Dept. de
Ciencias de la Computación - ETS Ingeniería Informática, Universidad de Alcalá, Ctra. Barcelona km
33.6 – 28871, Alcalá de Henares, Madrid.
WEKA. University of Waikato (http://www.cs.waikato.ac.nz/ml/weka)
WekaDOC, artículos sobre Weka,( http://weka.sourceforge.net/wekadoc/)
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
MANUAL DE WEKA
Se han seleccionado algunas de las técnicas disponibles para aplicarlas a ejemplos concretos,
siguiendo el acceso desde la herramienta al resto de técnicas implementadas, a continuación se
enunciará el ejemplo que se resolverá durante toda esta sección. Se sugiere que el lector aplique los
pasos indicados y realice los análisis sugeridos para cada técnica con objeto de familiarizarse y
mejorar su comprensión. Éste análisis tiene un enfoque introductorio e ilustrativo para acercarse a
las técnicas disponibles y su manipulación desde la herramienta, dejando abierto para el
investigador llevar el estudio de este dominio a resultados y conclusiones más elaboradas
Los principales 1ejemplos seleccionados contienen datos provenientes del campo de la enseñanza,
correspondientes a 2alumnos que realizaron las pruebas de selectividad en los años 1993-2003
procedentes de diferentes centros de enseñanza secundaria de la comunidad de Madrid. Por tanto,
en estos ejemplos se ilustra la aplicación y análisis de técnicas de extracción de conocimiento sobre
datos del campo de la enseñanza, aunque sería directa su traslación a cualquier otra disciplina
Datos de ejemplo (selectividad.arff):
El fichero de datos objeto de análisis en esta guía contiene muestras correspondientes a 18802 alumnos
presentados a las pruebas de selectividad y los resultados obtenidos en las pruebas. Los datos que describen
cada alumno contienen la siguiente información: año, convocatoria, localidad del centro, opción cursada (de
5 posibles), calificaciones parciales obtenidas en lengua, historia, idioma y las tres asignaturas opcionales,
así como la designación de las asignaturas de idioma y las 3 opcionales cursadas, calificación en el
bachillerato, calificación final y si el alumno se presentó o no a la prueba.
Los datos de entrada a la herramienta, sobre los que operarán las técnicas implementadas, deben estar
codificados en un formato específico, denominado Attribute-Relation File Format. Los datos deben estar
dispuestos en el fichero de la forma siguiente: cada instancia en una fila, y con los atributos separados por
comas. Por tanto, puede comprobarse que la cabecera del fichero de datos, "selectividad.arff", sigue el
formato mencionado anteriormente:
@relation selectividad
@attribute Año_académico real
@attribute convocatoria {J, S}
@attribute localidad {ALPEDRETE, ARANJUEZ, ... }
@attribute opcion1ª {1,2,3,4,5}
@attribute nota_Lengua real
@attribute nota_Historia real
@attribute nota_Idioma real
@attribute des_Idioma {INGLES, FRANCES, ALEMAN}
@attribute des_asig1 {BIOLOGIA, DIB.ARTISTICO_II,... }
@attribute calif_asig1 real
@attribute des_asig2 {BIOLOGIA, C.TIERRA, ...}
@attribute calif_asig2 real
@attribute des_asig3 {BIOLOGIA, C.TIERRA, ...}
@attribute calif_asig3 real
@attribute cal_prueba real
@attribute nota_bachi real
@attribute cal_final real
@attribute Presentado {SI, NO}
@data ...
1
2
Analizados con la interfaz Explorer (ver sección 1.4)
ACTIVIDAD DOCENTE, Grupo de Docencia Inteligencia Artificial, Informática Teórica y Compiladores,
Técnicas de IA para el Análisis de Datos - http://scalab.uc3m.es/~docweb/index.html
-1-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Objetivos del análisis
En nuestro caso, uno de los objetivos perseguidos podría ser el intentar relacionar los resultados obtenidos en
las pruebas con características o perfiles de los alumnos, si bien la descripción disponible no es muy rica y
habrá que atenerse a lo que está disponible. Algunas de las preguntas que podemos plantearnos a responder
como objetivos del análisis podrían ser las siguientes:
¿Qué características comunes tienen los alumnos que superan la prueba? ¿y los alumnos mejor
preparados que la superan sin perjudicar su expediente?
¿existen grupos de alumnos, no conocidos de antemano, con características similares?
¿hay diferencias significativas en los resultados obtenidos según las opciones, localidades, años, etc.?,
¿la opción seleccionada y el resultado está influida depende del entorno?
Como veremos, muchas veces el resultado alcanzado puede ser encontrar relaciones triviales o
conocidas previamente, o puede ocurrir que el hecho de no encontrar relaciones significativas, lo
puede ser muy relevante. Por ejemplo, saber después de un análisis exhaustivo que la opción o localidad
no condiciona significativamente la calificación, o que la prueba es homogénea a lo largo de los años, puede
ser una conclusión valiosa, y en este caso "tranquilizadora".
1. ENTORNO WEKA
Esta ave da nombre a una extensa colección de algoritmos de Máquinas de conocimiento desarrollados por la universidad de Waikato (Nueva Zelanda) implementados en Java; útiles para ser
aplicados sobre datos mediante los interfaces que ofrece o para embeberlos dentro de cualquier
aplicación. Weka contiene las herramientas necesarias para realizar transformaciones sobre los
datos, tareas de clasificación, regresión, clustering, asociación y visualización. Diseñado como una
herramienta orientada a la extensibilidad por lo que añadir nuevas funcionalidades es una tarea
sencilla.
Sin embargo, y pese a todas las cualidades que Weka posee, tiene un gran defecto y éste es la
escasa documentación orientada al usuario que tiene, junto a una usabilidad bastante pobre, lo
que la hace una herramienta díficil de comprender y manejar sin información adicional3.
3
WekaDOC, artículos sobre Weka, http://weka.sourceforge.net/wekadoc/
-2-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
La licencia de Weka es GPL4, lo que significa que este programa es de libre distribución y difusión. Además, ya que Weka está programado en Java, es independiente de la arquitectura, ya que
funciona en cualquier plataforma sobre la que haya una máquina virtual Java disponible.
Esta sección tiene por objetivo explicar el funcionamiento básico de este programa y sentar unas
bases para que el lector pueda ser autodidacta.
1.1. INSTALACIÓN Y EJECUCIÓN
WEKA se distribuye como un fichero ejecutable comprimido de java (fichero "jar"), que se invoca
directamente sobre la 5máquina virtual JVM.
Una vez descomprimido Weka y teniendo apropiadamente instalada la máquina de virtual Java,
para ejecutar Weka simplemente debemos ordenar dentro del directorio de la aplicación el mandato:
java -jar weka.jar
La herramienta se invoca desde el
intérprete de Java, en el caso de utilizar
un entorno windows, bastaría una
ventana de comandos para invocar al
intéprete Java:
No obstante, si estamos utilizando la máquina virtual de Java de Sun (que habitualmente es la más
corriente), este modo de ejecución no es el más apropiado, ya que, por defecto, asigna sólo 100
megas de memoria de acceso aleatorio para la máquina virtual, que muchas veces será insuficiente
para realizar ciertas operaciones con Weka (y obtendremos el consecuente error de insuficiencia de
memoria); por ello, es altamente recomendable ordenarlo con el mandato:
java -Xms<memoria-mínima-asignada>M
-Xmx<memoria-máxima-asignada>M -jar weka.jar
Dónde el parámetro -Xms indica la memoria RAM mínima asignada para la máquina virtual y Xmx la máxima memoria a utilizar, ambos elementos expresados en Megabytes si van
acompañados al final del modificador “M”. Una buena estrategia es asignar la mínima memoria a
utilizar alrededor de un 60% de la memoria disponible.
Para obtener la lista de opciones estándar, si usamos la máquina virtual de Sun, ordenamos el
mandato java -h, y para ver la lista de opciones adicionales java -x.
Una vez que Weka esté en ejecución aparecerá una ventana denominada selector de interfaces
(figura 1.1), que nos permite seleccionar la interfaz con la que deseemos comenzar a trabajar con
Weka. Nos ofrece cuatro opciones posibles de trabajo:
4
5
GNU Public License. http://www.gnu.org/copyleft/gpl.html
En las primeras versiones de WEKA se requería la máquina virtural Java 1.2 para invocar a la interfaz
gráfica, desarrollada con el paquete gráfico de Java Swing. A partir de la versión, Weka 3-4, se requiere
Java 1.3 o superior. La misma se puede bajar desde la Web: http://www.sun.com
-3-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Figura 1.1. Ventana de Selección
Las posibles interfaces a seleccionar son Sim ple Cli, Explorer, Experimenter y Knowledge flow que
se explica en la Figura 1.1, se explicarán detenidamente y de forma individual en secciones
siguientes.
1.2. FICHEROS .arff
Nativamente Weka trabaja con un formato denominado ARFF, acrónimo de Attribute-Relation File
Format. Es un 6archive de texto ASCII que describe una lista de instancias que comparten un
conjunto de atributos.
Un fichero con este formato, no sólo contiene los datos desde donde vamos a efectuar el
aprendizaje, además incluye meta-información sobre los propios datos, como por ejemplo el
nombre y tipo de cada atributo, así como una descripción textual del origen de los datos. Podemos
convertir ficheros en texto conteniendo un registro por línea y con los atributos separados con
comas (formato csv) a ficheror arff mediante el uso de un filtro convertidor.
6
Estos ficheros fueron desarrollados por el proyecto de aprendizaje de maquinas del departamento de
Ciencias de computación de la Universidad de Waikato para el uso con el software: Weka machine learning
software. (Mas información puede ser obtenida en http://www.cs.waikato.ac.nz/~ml/).
-4-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Estos ficheros tienen dos secciones distintas. La primera sección es la información de encabezado, a
la que le sucede la información de DATA o datos. El encabezado de los archivos ARFF contiene los
nombres de las relaciones, una lista de atributos (las columnas en los datos) y sus tipos.
1. Cabecera. Se define el nombre de la relación. Su formato es el siguiente:
@relation <nombre-de-la-relación>
Donde <nombre-de-la-relación> es de tipo String7. Si dicho nombre contiene algún espacio
será necesario expresarlo entrecomillado.
2. Declaraciones de atributos. En esta sección se declaran los atributos que compondrán
nuestro archivo junto a su tipo. La declaración de atributos toma la forma de una secuencia
ordenada. Cada atributo tiene su @attribute el cual define el nombre del atributo y el tipo de
dato. El orden que son declarados los atributos indican la columna en que se encuentras los
datos de dicho atributo en el @data. La sintaxis es la siguiente:
@attribute <nombre-del-atributo> <tipo> .
Donde <nombre-del-atributo> es de tipo String, debe comenzar con un carácter alfabético. El
nombre deberá llevar comillas si incluye espacios. El <tipo-dato> puede ser de cuatro tipos
para correr en WEKA: numérico, <nominal-specification>, string y date [<date-format>].
•
Atributos Numéricos. Pueden ser números real o integer (reales o enteros)
NUMERIC Expresa números reales8.
•
INTEGER Expresa números enteros.
Date (fecha) attributes. Los atributos de Fecha se declaran de la siguiente forma:
@attribute <nombre> date [<date-format>]
Donde <nombre> es el nombre del atributo y <date-format> es un string opcional que
especifica como se podrán imprimir los valores de fecha (son los mismos formatos simples
de fecha).
DATE Expresa fechas, para ello este tipo debe ir precedido de una etiqueta de formato entrecomillada. La etiqueta de formato está compuesta por caracteres separadores (guiones
y/o espacios) y unidades de tiempo, el formato por descarte es el combinado hora y fecha
de ISO-8601: "yyyy-MM-dd'T'HH:mm:ss":
dd Día. MM Mes. yyyy Año. HH Horas. mm Minutos. ss Segundos.
•
Atributos String. Sirven para crear atributos que tiene valores arbitrarios de texto, los
cuales son de mucho uso en aplicaciones de minería, (Weka Filters to manipulate strings
(like StringToWordVectorFilter)). Los atributos string se declaran de la siguiente forma:
@ATTRIBUTE LCC
string
STRING Expresa cadenas de texto, con las restricciones del tipo String comentadas
anteriormente.
•
Atributos Nominales. Los valores Nominales son definidos por medio de las listas de
posibles valores del <nominal-specification> de la siguiente forma:
{<nombre-nominal1>, <nominal nombre-nominal2>, < nombre-nominal3>, ...}
7
8
Entendiendo como tipo String el ofrecido por Java
Debido a que Weka es un programa Anglosajón la separación de la parte decimal y entera de los números
reales se realiza mediante un punto en vez de una coma.
-5-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
ENUMERADO El identificador de este tipo consiste en expresar entre llaves y separados
por comas los posibles valores (caracteres o cadenas de caracteres) que puede tomar el
atributo. Por ejemplo, si tenemos un atributo que indica el tiempo podría definirse:
@attribute tiempo {soleado,lluvioso,nublado}
3. Sección de datos. La declaración de @data es una línea simple que denota el comienzo del
segmento de datos del archivo. El formato es:
@data
Declaramos los datos que componen la relación separando entre comas los atributos y con
saltos de línea las relaciones. Cada instancia esta representada en una sola línea, que tiene
como final un fin de instancia. Los valores de cada instancia están delimitados por comas.
Deben aparecer en el orden que fueron declarados en la sección de cabecera.
@data 4,3.2
Aunque éste es el modo “completo" es posible definir los datos de una forma abreviada
(sparse data), formato que se explica más adelante.
En el caso de que algún dato sea desconocido se expresará con un símbolo de cerrar
interrogación (“?").
Como se ve a continuación:
@data
4.4,?,1.5,?,Iris-setosa
Es posible añadir comentarios con el símbolo “ %”, que indicará que desde ese símbolo hasta el
final de la línea es todo un comentario. Los comentarios pueden situarse en cualquier lugar del
fichero.
Ejemplo 1: Los valores nominales y de string son sensible a casos, por lo que si contienen cualquier
espacio deberán ir entre comillas como se ve:
@relation LCCvsLCSH
@attribute LCC string
@attribute LCSH string
@data
AG5,
'Encyclopedias and dictionaries.; Twentieth century.'
AS262, 'Science -- Soviet Union -- History.'
AE5,
'Encyclopedias and dictionaries.'
AS281, 'Astronomy, Assyro-Babylonian.;Moon -- Phases.'
AS281, 'Astronomy, Assyro-Babylonian.;Moon -- Tables.'
Ejemplo 2: Las fechas deberás ser especificadas en la sección data usando la representación
especificada de string en la declaración de atributos, como se ve:
@RELATION Timestamps
@ATTRIBUTE timestamp DATE "yyyy-MM-dd HH:mm:ss"
@DATA
"2001-04-03 12:12:12"
"2001-05-03 12:59:55"
-6-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Archivos Sparse ARFF (desparramados)
Si tenemos una muestra en la que hay muchos datos que sean 0 podemos expresar los datos
prescindiendo de los elementos que son nulos, rodeando cada una de las filas entre llaves y situando
delante de cada uno de los datos el número de atributo9.
Los archivos Sparse ARFF son muy similares a los ARFF normales, pero con los datos con valor 0
no serán representados. Tienen el mismo encabezado (i.e. @relation y @attribute) pero la sección
data es distinta, como se ve en ejemplo:
En vez de representar cada valor en este orden:
@data
0, X, 0, Y, "class A"
0, 0, W, 0, "class B"
Los atributos distintos de cero son identificados explícitamente por un numero de atributo y su valor
de la siguiente manera:
@data
{1 X, 3 Y, 4 "class A"}
{2 W, 4 "class B"}
Cada instancia esta rodeada por < >, y el formato de entrada para cada entrada es: <index> <space>
<value> donde index es el atributo índice (partiendo de 0).
Hay que notar que los valores omitidos en instancias sparse son 0, no son valores que faltan!. Si un
valor es desconocido se deberá representar con un signo de interrogación (?).
Nota: Existe un problema al guardar objetos de instancias Sparce (SparseInstance objects) de los datasets
que tienen atributos string. En Weka, los valores de datos string son guardados como números; estos
números actúan como índices en un arreglo de posibles valores de atributos. Entonces el primer valor string
es asignado con índice 0 lo que quiere decir que el valor se guardara como 0. Cuando la instancia Sparce es
escrita, la instancia string con valor interno 0 no saldrá, por lo tanto el valor se perderá y cambiarán los
valores de atributos. Para solucionar el problema, hay que agregar un valor “dummy string” en el índice 0
que nunca será usado.
1.3. SIMPLE CLI
Simple CLI es una abreviación de Simple Client. Esta interfaz (figura 1.3) proporciona una consola
para poder introducir mandatos. A pesar de ser en apariencia muy simple es extremadamente
potente porque permite realizar cualquier operación soportada por Weka de forma directa; no
obstante, es muy complicada de manejar ya que es necesario un conocimiento completo de la
aplicación.
Su utilidad es pequeña desde que se fue recubriendo Weka con interfaces. Actualmente ya prácticamente sólo es útil como una herramienta de ayuda a la fase de pruebas.
9
La numeración de atributos comienza desde el 0, por lo que primero es el 0 y no el 1
-7-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Figura 1.3: Interfaz de modo consola
Los mandatos soportados son los siguientes:
java <nombre-de-la-clase><args>
Ejecuta el método “main” de la clase dada con los argumentos especificados al ejecutar este
mandato (en el caso de que realmente se haya proporcionado alguno). Cada mandato es atendido en
un hilo independiente por lo que es posible ejecutar varias tareas concurrentemente.
Detiene la tarea actual.
“Mata” la tarea actual. Este comando es desaconsejable, sólo debe usarse
Hill
en el caso de que la tarea no pueda ser detenida con el mandato break.
cls (Clear Screen).
Limpia el contenido de la consola.
Exit
Sale de la aplicación.
help <mandato>
Proporciona una breve descripción de cada mandato.
Break
1.3.1 Utilización de WEKA desde la línea de comandos.
En ocasiones es más práctico utilizar los algoritmos de WEKA desde la línea de comandos. Por
ejemplo, si se quiere lanzar muchas veces un clasificador para obtener estadísticas de resultados, se
puede automatizar el proceso mediante un bucle.
Lanzamiento de un comando Weka desde MS-DOS
Como ejemplo, se generará desde MS-DOS un árbol de decisión a partir de un fichero de datos de
entrenamiento propio de WEKA. Para ello, en primer lugar abriremos una ventana de comandos de
MS-DOS. Dentro de esa ventana, nos situaremos en el directorio donde se encuentra instalado
WEKA. 10En la mayor parte de los ordenadores, este directorio será “…\data\”:
java weka.classifiers.trees.J48 –t data\weather.arff –C 0.30
Los comandos se ingresan de la misma manera si ingresamos a la interfaz Simple CLI, la carpeta por
defecto en la que trabaja es la de “…\data\...”.
10
-8-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Veamos en detalle la instrucción tecleada:
(lanza el intérprete java)
(elige un clasificador de entre todos los disponibles, en
weka.classifiers.trees.J48
este caso el generador de árboles de decisión J48)
–t data\weather.arff
(indica cuál es el fichero de datos de entrenamiento a utilizar).
(fija un parámetro del clasificador. En este caso es el umbral de confianza para
–C 0.30
la poda de los árboles).
Java
El resultado que aparecerá en pantalla será el siguiente:
Options: -C 0.30
J48 pruned tree
-----------------outlook = sunny
| humidity <= 75: yes (2.0)
| humidity > 75: no (3.0)
outlook = overcast: yes (4.0)
outlook = rainy
| windy = TRUE: no (2.0)
| windy = FALSE: yes (3.0)
Number of Leaves : 5
Size of the tree : 8
Time taken to build model: 0.02 seconds
Time taken to test model on training data: 0 seconds
=== Error on training data ===
Correctly Classified Instances 14 100 %
Incorrectly Classified Instances 0 0 %
Kappa statistic 1
Mean absolute error 0
Root mean squared error 0
Relative absolute error 0 %
Root relative squared error 0 %
Total Number of Instances 14
=== Confusion Matrix ===
a b <-- classified as
9 0 | a = yes
0 5 | b = no
=== Stratified cross-validation ===
Correctly Classified Instances 9 64.2857 %
Incorrectly Classified Instances 5 35.7143 %
Kappa statistic 0.186
Mean absolute error 0.2857
Root mean squared error 0.4818
Relative absolute error 60 %
Root relative squared error 97.6586 %
Total Number of Instances 14
=== Confusion Matrix ===
a b <-- classified as
7 2 | a = yes
3 2 | b = no
La forma de lanzar cualquier otro clasificador o cualquier otra función de WEKA es similar. Para
determinar el tipo de funciones disponibles, basta con comprobar los distintos directorios que
existen a partir de weka_java\weka\:
•
•
•
•
•
Associations: algoritmos para generar reglas a partir de datos.
AttributeSelection: selección de características.
Classifiers: clasificadores.
Clusterers: agrupación de datos.
Core: funciones núcleo de WEKA (no se usan directamente).
-9-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
•
•
•
•
•
Datagenerators: generación automática de datos (aleatorios).
Estimators: estimadores estadísticos.
Experiment: interfaz de usuario.
Filters: filtros de datos y de atributos.
Gui: interfaz de usuario.
Dentro de cada directorio existen múltiples subdirectorios, por lo tanto la cantidad de algoritmos
disponible en WEKA es muy elevada.
Lanzamiento de un Comando Weka desde Matlab
Es práctico lanzar los comandos de WEKA desde Matlab para poder incluir bucles y funciones de
lectura automática de resultados fácilmente.
Para lanzar WEKA desde Matlab se realiza una llamada al sistema (a MS-DOS) mediante el
comando !:
Desde la ventana de comandos de Matlab, nos situaremos en el directorio correcto mediante el
comando cd:
>> cd ‘c:\iarp\weka_java’
Una vez en el directorio correcto, teclearemos:
>> !java weka.classifiers.trees.J48 –t data\weather.arff –C 0.30
Y obtendremos el mismo resultado que el obtenido sobre la ventana de MS-DOS. Una ventaja
adicional de utilizar Matlab es que el comando se puede modificar a voluntad desde dentro del
programa, mediante la instrucción eval.
Por ejemplo, para generar un árbol de decisión con un umbral de confianza ajustable para la poda
podemos teclear las siguientes instrucciones de Matlab:
>> conf = 0.30;
>> orden = sprintf (‘!java weka.classifiers.trees.J48 –t data/weather.arff –C %f’,
conf);
>> eval(orden);
El resultado será similar al obtenido en el resto de pruebas Por último, será posible realizar un bucle para
distintos valores del parámetro del clasificador, de la forma siguiente:
>> cf = [0.05 0.10 0.15 0.20 0.25 0.30];
>> for i=1:6
>> orden = sprintf(‘!java weka.classifiers.trees.J48 –t data/weather.arff –C %f’,
cf(i));
>> eval(orden);
>> end;
Lectura automática de resultados de Weka
Comprobar los resultados de WEKA sobre la pantalla no es práctico cuando se realizan múltiples
experimentos dentro de un bucle. Desde Matlab es posible leer automáticamente los resultados,
siempre que éstos se hayan guardado anteriormente en un fichero.
Para guardar los resultados en un fichero, basta con utilizar el operador de redirección de MS-DOS
(símbolo >) que hace que los datos no se muestren en pantalla sino que se escriban en el fichero que
se indique.
-10-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Desde Matlab, bastaría con teclear un comando como el siguiente:
>> !java weka.classifiers.trees.J48 –t data\weather.arff > out.txt
La redirección hace que los resultados se guarden en el fichero ‘out.txt’ y que no aparezcan en
pantalla. Para comprobar que todo ha funcionado correctamente, se buscará el fichero anterior
desde el explorador de Windows y se abrirá con el programa Wordpad (el programa Notepad puede
mostrar incorrectamente los saltos de línea).
El último paso consiste en extraer automáticamente la información deseada del fichero de
resultados. Supongamos que los datos que nos interesan son los porcentajes de clasificaciones
correctas tanto sobre los datos de entrenamiento como en un experimento de validación cruzada.
Tales datos aparecen en el siguiente punto de los resultados:
1. Porcentaje de clasificaciones correctas sobre los datos de entrenamiento:
=== Error on training data ===
Correctly Classified Instances 14
100 %
2. Porcentaje de clasificaciones correctas en un experimento de validación cruzada:
=== Stratified cross-validation ===
Correctly Classified Instances 9 64.2857 %
Podemos escribir un programa Matlab que lea el fichero de resultados y busque precisamente esa
información. El programa es el siguiente:
% lee resultados de WEKA
function [porcent1, porcent2] = lee_weka (fichero)
% abre fichero de resultados
file = fopen(fichero, 'r');
% busca primer dato
cadena = busca_comienzo('=== Error on training data ===', file);
cadena = busca_comienzo('Correctly Classified Instances', file);
datos = sscanf(cadena(31:length(cadena)), '%f');
porcent1 = datos(2);
% busca segundo dato
cadena = busca_comienzo('=== Stratified cross-validation ===', file);
cadena = busca_comienzo('Correctly Classified Instances', file);
datos = sscanf(cadena(31:length(cadena)), '%f');
porcent2 = datos(2);
fclose(file);
return
% busca una cadena que comienza por unos ciertos caracteres
function cadena = busca_comienzo(comienzo, file);
carac = length(comienzo);
seguir=1;
while seguir==1
cadena = fgets(file);
if (length(cadena)>=carac)
if cadena(1:carac)==comienzo
seguir=0;
end
end
end
return
-11-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
La forma de utilizar el programa será la siguiente:
· En primer lugar, el programa se debe copiar en el directorio de la asignatura:
C:\iarp\weka_java
· En Segundo lugar, se lanzará el programa desde Matlab de la forma siguiente:
>> [porcent1, porcent2] = lee_weka('out.txt')
porcent1 = 100
porcent2 = 64.2857
Una vez que somos capaces de leer los resultados, es posible lanzar un clasificador con distintos
valores para sus parámetros en un bucle y almacenar todos los resultados. Se probará el siguiente
programa Matlab:
>> cf = [0.05 0.10 0.15 0.20 0.25 0.30];
>> for i=1:6
>> orden = sprintf
(‘!java weka.classifiers.trees.J48 –t data/weather.arff –C %f >
out.txt’, cf(i));
>> eval(orden);
>> [p1(i), p2(i)] = lee_weka(‘out.txt’);
>> end;
Una vez ejecutado el programa anterior, los resultados estarán disponibles en los vectores p1 y p2, y
podrán ser mostrados, por ejemplo, mediante un comando plot:
>> plot(p1,‘r*’);
>> plot(p2,‘go’);
1.4. EXPLORER
El modo Explorador es el modo más usado y más descriptivo11. Éste permite realizar operaciones
sobre un sólo archivo de datos. La ventana principal es la mostrada en la figura 1.4.
Es muy importante reseñar que Weka es un programa en continuo desarrollo y cada una de las 4
interfaces que posee evoluciona en separado por lo que actualmente no son equivalentes por completo, es
decir, hay ciertas funcionalidades sólo realizables por algunas de las interfaces y no por otras y viceversa
11
-12-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Figura 1.4: El modo explorador. Ventana inicial.
Como se puede observar existen 6 sub-entornos de ejecución. Una vez seleccionada la opción
Explorer, se crea una ventana con 6 pestañas en la parte superior que se corresponden con
diferentes tipos de operaciones, en etapas independientes, que se pueden realizar sobre los datos:
Además de estas pestañas de selección, en la parte inferior de la ventana aparecen dos elementos
comunes. Uno es el botón de “Log”, que al activarlo presenta una ventana textual donde se indica
la secuencia de todas las operaciones que se han llevado a cabo dentro del “Explorer”, sus tiempos
de inicio y fin, así como los mensajes de error más frecuentes. Junto al botón de log aparece un
icono de actividad (el pájaro WEKA, que se mueve cuando se está realizando alguna tarea) y un
indicador de status, que indica qué tarea se está realizando en este momento dentro del Explorer.
-13-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
1.4.1.
Preprocesado
Esta es la parte primera por la que se debe pasar antes de realizar ninguna otra
operación, ya que se precisan datos para poder llevar a cabo cualquier análisis. El primer
paso para comenzar a trabajar con el explorador es definir el origen de los datos. Weka soporta
diferentes fuentes que coinciden con los botones que están debajo de las pestañas superiores
mostrados en la ventana 1.5. La disposición de la parte de preprocesado del Explorer, Preprocess,
es la que se indica en la figura 1.5 siguiente.
Figura 1.5. Ventana de Preprocesamiento
Hay tres posibilidades para obtener los datos: un fichero de texto, una dirección URL o una base de
datos, dadas por las opciones: Open file, Open URL y Open DB, correspondientes a los primeros
tres botones en la parte superior de la sección de proceso:
La manera más fácil y más común de obtener la data para introducir en Weka es aquella con
formato ARFF y cargarla usando el botón Open File… (ARFF tienen extención “.arff”).
Entonces, para abrir ficheros en Weka, las diferentes posibilidades son las siguientes:
Open File
Al pulsar sobre este botón aparecerá una ventana de selección de fichero. Aunque el formato por
defecto de Weka es el arff eso no significa que sea el único que admita, para ello tiene
interpretadores de otros formatos. Éstos son:
-14-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
− CSV
Archivos separados por comas o tabuladores. La primera línea contiene los
atributos. Podemos convertir ficheros en texto conteniendo un registro por línea y con los
atributos separados con comas (formato csv) a ficheror arff mediante el uso de un filtro
convertidor, como se explicará más adelante.
− C4.5
Archivos codificados según el formato C4.5. Unos datos codificados según este
formato estarían agrupados de tal manera que en un fichero .names estarían los nombres de los
atributos y en un fichero .data estarían los datos en sí. Weka cuando lee ficheros codificados
según el formato C4.5 asume que ambos ficheros (el de definición de atributos y el de datos)
están en el mismo directorio, por lo que sólo es necesario especificar uno de los dos.
Instancias Serializadas
Weka internamente almacena cada muestra de los datos como una instancia de la clase instance.
Esta clase es serializable12 por lo que estos objetos pueden ser volcados directamente sobre un
fichero y también cargados de uno.
Para cargar un archivo arff simplemente debemos buscar la ruta donde se encuentra el fichero y
seleccionarlo. Si dicho fichero no tiene extensión arff, al abrirlo Weka intentará interpretarlo, si
no lo consigue aparecerá un mensaje de error como el de la figura 1.5.
Figura 1.5. Error al abrir un fichero.
Pulsando en Use converter nos dará la opción de usar un interpretador de ficheros de los tipos ya
expuestos.
Open Url
Con este botón se abrirá una ventana que nos permitirá introducir una dirección en la que definir
dónde se encuentra nuestro fichero. El tratamiento de los ficheros (restricciones de formato, etc.)
es el mismo que el apartado anterior.
Open DB
Con este botón se nos da la posibilidad de obtener los datos de una base de datos.
12
En Java un objeto es serializable cuando su contenido (datos) y su estructura se transforman en una
secuencia de bytes al ser almacenado. Esto hace que estos objetos puedan ser enviados por algún flujo de
datos con comodidad
-15-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Figura 1.6: Ventana para seleccionar una base de datos.
Para configurarla lo primero es definir la url por la cual es accesible la base de datos, la contraseña
para acceder, el nombre de usuario, la consulta que queremos realizar y si queremos o no usar el
modo de datos abreviado (sparse data). Así mismo los botones de la parte inferior dan posibilidad
de cargar y guardar esta configuración en un fichero.
Una vez seleccionado el origen de los datos podremos aplicar algún filtro sobre él o bien pasar a las
siguientes secciones y realizar otras tareas.
Los botones que acompañan a abrir el fichero: Undo y Save, nos permiten deshacer los cambios y
guardar los nuevos datos ya transformados (en formato arff). Además, se muestra en la ventana
(figura 1.7) una vez cargados los datos, un cuadro resumen, Current relation, con el nombre de la
relación que se indica en el fichero (en la línea @relation del fichero arff), el número de instancias
y el número de atributos, junto con un resumen con estadísticas de los mismos (media aritmética,
rango de los datos, desviación estándar, número de instancias distintas, de qué tipo son, etc.). de
modo que se pueden seleccionar para ver sus detalles y propiedades.
Figura 1.7: Modo explorador con un fichero de datos cargado.
-16-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
En la parte derecha aparecen las propiedades del atributo seleccionado. Si es un atributo simbólico,
se presenta la distribución de valores de ese atributo (número de instancias que tienen cada uno de
los valores). Si es numérico aparece los valores máximo, mínimo, valor medio y desviación
estándar.
Si seleccionamos cada uno de los atributos, conoceremos más información del atributo en cuestión:
tipo (Type) nominal o numérico, valores distintos (Distinct), número y porcentaje de instancias con
valor desconocido para el atributo (Missing codificado en el fichero arff con “?”) y valores de
atributo que solamente se dan en una instancia (Unique). Debajo de este resumen se muestra un
histograma con información sobre la distribución de los ejemplos para ese atributo, arriba de éste
hay un menú desplegable que permite variar el atributo de referencia que se representará en color
para contrastar ambos atributos. Pulsando en Visualize all se abre una ventana desplegable
mostrando todas las gráficas pertenecientes a todos los atributos.
En nuestro ejemplo (pruebas de selectividad), utilizaremos siempre los datos almacenados en un
fichero, que es lo más rápido y cómodo de utilizar. En el ejemplo que nos ocupa, abra el fichero
“selectividad.arff” con la opción Open File.
Siguiendo con el ejemplo, una vez cargado e fichero “selective.arff”, observamos la siguiente ventana:
En la parte inferior se presenta gráficamente el histograma con los valores que toma el atributo. Si es
simbólico, la distribución de frecuencia de los valores, si es numérico, un histograma con intervalos
uniformes. En el histograma se puede presentar además con colores distintos la distribución de un segundo
atributo para cada valor del atributo visualizado. A modo de ejemplo, a continuación mostramos el
histograma por localidades, indicando con colores la distribuciones por opciones elegidas.
-17-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Se ha seleccionado la columna de la localidad de Leganés, la que tiene más instancias, y donde puede verse
que la proporción de las opciones científicas (1 y 2) es superior a otras localidades, como Getafe, la segunda
localidad en número de alumnos presentados.
Ejercitación: Visualice los histogramas de las calificaciones de bachillerato y calificación final de
la prueba, indicando como segundo atributo la convocatoria en la que se presentan los alumnos
1.4.1.1.
Creación e Importación de ficheros CVS
Los ficheros de datos están habitualmente en formato ASCII (texto) delimitado por espacios en
blanco o en formato Excel. Weka no puede leer directamente ficheros Excel (de extensión .xls),
pero sí ficheros ASCII que usen como delimitador la coma, como los CSV (columnas separas por
coma).
Creación del fichero CSV
Tenemos un fichero de datos procedentes de MS Excel, la tabla de datos maquina.xls:
Figura 1.8. Hoja de Excel con la tabla “maquina”
-18-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Este fichero contiene 3 variables numéricas y 2 categórica. La primera fila contiene, además, las
etiquetas de las variables.
Generamos un fichero CVS desde Excel ingresando en Archivo, Guardar como...
Figura 1.9. Guardar Como desde Excel
Se abre una ventana (figura 1.10) en la que especificamos la carpeta o directorio de destino (P.ej.:
A:\, C:\Mis Documentos, ...) el nombre de fichero (en este caso, calidad maquina.cvs) y el tipo de
archivo como CSV (delimitado por comas):
Figura 1.10 Selección del destino y tipo de fichero a guardar
-19-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Pinchamos en Guardar y ya tenemos el fichero CSV que Weka puede leer.
Nota: la generación de ficheros delimitados por coma o por punto y coma depende de la configuración
regional del sistema operativo. Si tenemos configurado el signo decimal como “.” (punto), los archivos que
se creen bajo este sistema usaran como separador de columna (atributo) el “;” (punto y coma); cómo Weka
importa sólo los delimitados por coma y no por punto y coma, tendremos que reemplazar los “;” (punto y
coma) por “,” (comas) con la ayuda del Block de Nota de Windows.
Lectura de fichero CSV y creación del fichero ARFF
Como dijimos, Weka no trabaja directamente con ficheros de datos ASCII, sino que necesita
convertirlos a un formato propio de fichero, lo que se conoce como ficheros ARFF. Para realizar esa
conversión, por ejemplo, en el caso del fichero “maquina.csv” que hemos creado, pinchamos en
“Open File...”, indicamos en tipo de archivo “todos los archivos” y seleccionamos el fichero CSV
que creamos.
Figura 1.11. Cargar el fichero CSV desde Weka.
Weka detecta que no es un fichero ARFF y permite usar el conversor (figura 1.12). Pinchamos en
“User Conver” y luego “OK”.
Figura 1.12. Uso del conversor CSVLoader de Weka
-20-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Weka carga el fichero:
Fichero 1.13. Fichero cargado
Finalmente para guardar este archivo en el formato ARFF, incesamos en “Save”, donde indicamos
el destino, nombre y tipo de archivo (asegurarse de escribir la extensión “.arff” junto con el
nombre).
Figura 1.14. Guardar el fichero en el formato ARFF
-21-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
1.4.1.2.
Aplicación de filtros
Weka permite aplicar una gran diversidad de filtros sobre los datos, permitiendo realizar transformaciones sobre ellos de todo tipo. Al pulsar el botón Choose dentro del recuadro Filter se nos
despliega un árbol en el que seleccionar los atributos a escoger (figura 1.15). Permite escoger un
filtro y tener sus opciones de configuración.
Figura 2.15: Aplicando un filtro en el modo explorador.
WEKA tiene integrados filtros que permiten realizar manipulaciones sobre los datos en dos niveles:
atributos e instancias. Las operaciones de filtrado pueden aplicarse “en cascada”, de manera que
cada filtro toma como entrada el conjunto de datos resultante de haber aplicado un filtro anterior.
Una vez que se ha aplicado un filtro, la relación cambia ya para el resto de operaciones llevadas a
cabo, existiendo siempre la opción de deshacer la última operación de filtrado aplicada con el
botón Undo. Además, pueden guardarse los resultados de aplicar filtros en nuevos ficheros, que
también serán de tipo ARFF, para manipulaciones posteriores
Tendremos acceso a multitud de herramientas para el preprocesamiento de datos. Estas
herramientas permiten (entre otras muchas funcionalidades):
− Realizar un filtrado de atributos
− Cambiar el tipo de los atributos (discretizar o numerizar)
− Realizar muestreos sobre los datos
− Normalizar atributos numéricos
− Unificar valores de un mismo atributo
El mismo tipo de cuadro de diálogo es usado para otros objetos como clasificadores (classifiers) y
agrupadores (clusters), como se verá a continuación. Un simple click en el botón izquierdo del
Mouse en el nombre del filtro, en la parte superior de la ventana, genera un la lista (drop down list)
de todos los filtros, ahí se hace click en el requerido. Cuando es escogido un filtro, el campo en la
ventana cambia para reflejar las opciones disponibles. Haciendo click en cualquiera de éstas, da la
oportunidad de cambiar su configuración (settings).
Puede verse que los filtros de esta opción son de tipo no supervisado (unsupervised): son
operaciones independientes del algoritmo análisis posterior, a diferencia de los filtros supervisados
que se verán en la sección de “selección de atributos”, que operan en conjunción con algoritmos de
clasificación para analizar su efecto.
-22-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Están agrupados según modifiquen los atributos resultantes o seleccionen un subconjunto de
instancias (los filtros de atributos pueden verse como filtros "verticales" sobre la tabla de datos, y
los filtros de instancias como filtros "horizontales"). Como puede verse, hay más de 30
posibilidades, de las que destacaremos únicamente algunas de las más frecuentes. A continuación se
hace una breve descripción de cada uno de ellos13.
Attribute Los filtros agrupados en esta categoría son aplicados a atributos.
•
Add Añade un atributo más. Como parámetros debemos proporcionarle la posición que va a ocupar este
nuevo atributo (esta vez comenzando desde el 1), el nombre del atributo y los posibles valores de ese
atributo separados entre comas. Si no se especifican, se sobreentiende que el atributo es numérico.
•
AddExpression Este filtro es muy útil puesto que permite agregar al final un atributo que sea el valor de
una función. Es necesario especificarle la fórmula que describe este atributo, en donde podemos calcular
dicho atributo a partir de los valores de otro u otros, refiriéndonos a los otros atributos por “a” seguido del
número del atributo (comenzando por 1). Por ejemplo: (a3^3.4)*a1+sqrt(floor(tan(a4)))
Los operadores y funciones que soporta son +, —, *, /, ^, log, abs, cos, exp, sqrt, floor (función techo),
ceil (función suelo), rint (redondeo a entero), tan, sin, (,). Otro argumento de este filtro es el nombre del
nuevo atributo.
•
AddNoise Añade ruido a un determinado atributo que debe ser nominal. Podemos especificar el
porcentaje de ruido, la semilla para generarlo y si queremos que al introducir el ruido cuente o no con los
atributos que faltan.
•
ClusterMembership Filtro que dado un conjunto de atributos y el atributo que define la clase de los
mismos, devuelve la probabilidad de cada uno de los atributos de estar clasificados en una clase u otra.
Tiene por parámetro ignoredAttributeIndices que es el rango de atributos que deseamos excluir para
aplicar este filtro. Dicho intervalo podemos expresarlo por cada uno de los índices los atributos separados
por comas o definiendo rangos con el símbolo guión (“-”). Es posible denotar al primer y último atributo
con los identificadores first y last (en este caso la numeración de los atributos comienza en 1, por lo que
first corresponde al atributo número 1).
•
Copy Realiza una copia de un conjunto de atributos en los datos. Este filtro es útil en conjunción con
otros, ya que hay ciertos filtros (la mayoría) que destruyen los datos originales. Como argumentos toma un
conjunto de atributos expresados de la misma forma que el filtro anterior. También tiene una opción que es
invertSelection que invierte la selección realizada (útil para copiar, por ejemplo, todos los atributos menos
uno).
•
Discretize Discretiza un conjunto de valores numéricos en rangos de datos. Como parámetros toma los
índices de los atributos discretizar (attribute indices) y el número de particiones en que queremos que
divida los datos (bins). Si queremos que las particiones las realice por la frecuencia de los datos y no por el
tamaño de estas tenemos la opción useEqual-Frecuency. Si tenemos activa esta última opción podemos
variar el peso de las instancias para la definición de los intervalos con la opción
DesiredWeightOfInstancesPerInterval. Si, al contrario tenemos en cuenta el número de instancias para la
creación de intervalos podemos usar findNumBins que optimiza el procedimiento de confección de los
mismos. Otras opciones son makeBinary que convierte los atributos en binario e invertSelection que
invierte el rango de los atributos elegidos.
•
FistOrder Este filtro realiza una transformación de los datos obteniendo la diferencia de pares
consecutivos de datos, suponiendo un dato inicial adicional de valor 0 para conseguir que la cardinalidad
del grupo de datos resultante sea la misma que la de los datos origen.
Por ejemplo, si los datos son 1 5 4 6, el resultado al aplicar este filtro será 1 4 -1 2. Este filtro toma un
único parámetro que es el conjunto de atributos con el que obtener esta transformación.
13
Por una cuestión de organización interna Weka cataloga todos los filtros dentro de una categoría
denominada Unsu-pervised, en futuras versiones se espera que se habiliten filtros de clase Supervised.
-23-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
•
MakeIndicator Crea un nuevo conjunto de datos reemplazando un atributo nominal por uno booleano
(Asignará “1” si en una instancia se encuentra el atributo nominal seleccionado y “0” en caso contrario).
Como atributos este filtro toma el índice el atributo nominal que actuará como indicador, si se desea que la
salida del filtro sea numérica o nominal y los índices los atributos sobre los que queremos aplicar el filtro.
•
MergeTwoValues Fusiona dos atributos nominales en uno solo. Toma como argumentos la posición del
argumento resultado y la de los argumentos fuente.
•
NominalToBinary Transforma los valores nominales de un atributo en un vector cuyas coordenadas son
binarias.
•
Normalize Normaliza todos los datos de manera que el rango de los datos pase a ser X(i) =
[0,1]. Para normalizar un vector se utiliza la fórmula:
x (i)
n
∑ x(i)
2
i =1
•
NumericToBinary Convierte datos en formato numérico a binario. Si el valor de un
dato es 0 o desconocido, el valor en binario resultante será el 0.
•
NumericTransform Filtro similar a AddExpression pero mucho más potente. Permite aplicar un método
java sobre un conjunto de atributos dándole el nombre de una clase y un método.
•
Obfuscate Ofusca todas las cadenas de texto de los datos. Este filtro es muy útil si se desea compartir una
base de datos pero no se quiere compartir información privada.
•
PKIDiscretize Discretiza atributos numéricos (al igual que Discretize), pero el número de intervalos es
igual a la raíz cuadrada del número de valores definidos.
•
RandomProjection Reduce la dimensionalidad de los datos (útil cuando el conjunto de datos es muy
grande) proyectándola en un subespacio de menor dimensionalidad utilizando para ello una matriz
aleatoria. A pesar de reducir la dimensionalidad los datos resultantes se procura conservar la estructura y
propiedades fundamentales de los mismos.
El funcionamiento se basa en el siguiente producto de matrices: X(i×n)∗R(n×m) = Xrp(i×m)
Siendo X la matriz de datos original de dimensiones i (número de instancias) × n (número de atributos), R
la matriz aleatoria de dimensión n (número de atributos) × m (número de atributos reducidos) y Xrp la
matriz resultante siendo de dimensión i×m.
Como parámetros toma el número de parámetros en los que queremos aplicar este filtro
(numberOfAttributes) y el tipo de distribución de la matriz aleatoria que puede ser:
−
Sparse 1 − 3 con probabilidad
−
Sparse 3 -1 con probabilidad
−
Gaussian Utiliza una distribución gaussiana.
1
2
1
6
, 0 con probabilidad
2
1
.
y 1 con probabilidad
2
3
y
3 con probabilidad
1
6
.
Además de estos parámetros, pueden utilizarse también el número de atributos resultantes después de la
transformación expresado en porcentaje del número de atributos totales (percent), la semilla usada para la
generación de números aleatorios (seed), y si queremos que aplique antes de realizar la transformación el
filtro ReplaceMissingValues,
•
Remove Borra un conjunto de atributos del fichero de datos.
•
RemoveType Elimina el conjunto de atributos de un tipo determinado.
•
RemoveUseless Elimina atributos que oscilan menos que un nivel de variación. Es útil para eliminar
atributos constantes o con un rango muy pequeño. Como parámetro toma el máximo porcentaje de
variación permitido, si este valor obtenido es mayor que la variación obtenida la muestra es eliminada.
•
ReplaceMissingValues Reemplaza todos los valores indefinidos por la moda en el caso de que sea un
atributo nominal o la media aritmética si es un atributo numérico.
-24-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
•
Standarize Estandariza los datos numéricos de la muestra para que tengan de media 0 y la unidad de
varianza. Para estandarizar un vector x se aplica la siguiente fórmula:
x(i ) =
x(i ) − x
σ ( x)
•
StringToNominal Convierte un atributo de tipo cadena en un tipo nominal.
•
StringToWordVector Convierte los atributos de tipo String en un conjunto de atributos representando la
ocurrencia de las palabras del texto. Como atributos toma:
−
DFTranform que indica si queremos que las frecuencias de las palabras sean transformadas según la
regla:
− TFTransform Otra regla de transformación: log(1+frecuencia de la palabra i en la instancia j)
− attributeNamePrefix, prefijo para los nombres de atributos creados
− Delimitadores (delimiters), conjunto de caracteres escape usados para delimitar la unidad fundamental
(token). Esta opción se ignora si la opción onlyAlphabeticTokens está activada, ya que ésta, por
defecto, asigna los tokens a secuencias alfabéticas usando como delimitadores todos los caracteres
distintos a éstos.
− lowerCaseTokens convierte a minúsculas todos los tokens antes de ser añadidos al diccionario.
− normalizeDocLength selecciona si las frecuencias de las palabras en una instancia deben ser
normalizadas o no.
− outputWordCounts cuenta las ocurrencias de cada palabra en vez de mostrar únicamente si están o no
están en el diccionario.
− useStoplist si está activado ignora todas las palabras de una lista de palabras excluidas (stoplist).
− wordsToKeep determina el número de palabras (por clase si hay un asignador de clases) que se
intentarán guardar.
•
SwapValues Intercambia los valores de dos atributos nominales.
•
TimeSeriesDelta Filtro que asume que las instancias forman parte de una serie temporal y reemplaza los
valores de los atributos de forma que cada valor de una instancia es reemplazado con la diferencia entre
el valor actual y el valor pronosticado para dicha instancia. En los casos en los que la variación de tiempo
no se conozca puede ser que la instancia sea eliminada o completada con elementos desconocidos (símbolo
“?”). Opciones:
−
−
−
−
attributeIndices Especifica el rango de atributos en los que aplicar el filtro.
FillWithMissing Las instancias al principio o final del conjunto de datos, donde los valores calculados
son desconocidos, se completan con elementos desconocidos (símbolo “?”) en vez de eliminar dichas
instancias, que es el comportamiento por defecto.
InstanceRange Define el tamaño del rango de valores que se usará para realizar las restas. Si se usa un
valor negativo significa que realizarán los cálculos con valores anteriores.
invertSelection Invierte la selección realizada.
Instance Los filtros son aplicados a instancias concretas enteras.
•
NonSparseToSparse Convierte una muestra de modo completo a modo abreviado.
•
Randomize Modifica el orden de las instancias de forma aleatoria.
•
RemoveFolds Permite eliminar un conjunto de datos. Este filtro está pensado para eliminar una partición
en una validación cruzada.
-25-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
•
RemoveMisclassified Dado un método de clasificación lo aplica sobre la muestra y elimina aquellas
instancias mal clasificadas.
•
RemovePercentage Suprime un porcentaje de muestras.
•
RemoveRange Elimina un rango de instancias.
•
RemoveWithValues Elimina las instancias acordes a una determinada restricción.
•
Resample Obtiene un subconjunto del conjunto inicial de forma aleatoria.
•
SparseToNonSparse Convierte una muestra de modo abreviado a modo completo. Es la operación
complementaria a NonSparseToSparse.
Aplicando filtros
La configuración de un filtro sigue el esquema general de configuración de cualquier algoritmo
integrado en WEKA. Una vez seleccionado el filtro específico con el botón Choose, aparece su
nombre dentro del área de filtro (el lugar donde antes aparecía la palabra None). Se puede
configurar sus parámetros haciendo clic sobre esta área, momento en el que aparece la ventana de
configuración correspondiente a ese filtro particular. Si no se realiza esta operación se utilizarían los
valores por defecto del filtro seleccionado.
El 14proceso general de configuración, es elegir el filtro deseado y sus opciones, luego hacer click
en el botón “Add” para sumarlo a la lista. Los filtros solo serán aplicados cuando se hace click en el
botón “Apply Filters” y serán aplicadas en el orden que aparezcan en la lista.
- Se puede remover en cualquier filtro de la lista con el botón “Delete”.
- El botón “Replace” en la parte superior de la sección de pre proceso reemplaza la “Base
Relation” con el “Current Working Relation”, haciendo los cambios permanentes, al menos hasta
que un nuevo archivo es cargado.
- Finalmente, el botón “Save”… en la parte superior derecha de la pantalla, guarda el “Working
Relation” en archivo de extención ARFF, dejándolo habilitado para usos futuros.
1.4.1.2.1. Ejemplo de aplicación de filtros de atributos.
Vamos a indicar, de entre todas las posibilidades implementadas, la utilización de filtros para
eliminar atributos, para discretizar atributos numéricos, y para añadir nuevos atributos con
expresiones, por la frecuencia con la que se realizan estas operaciones.
Filtros de selección
Vamos a utilizar el filtro de atributos “Remove”, que permite eliminar una serie de atributos del
conjunto de entrada. En primer lugar procedemos a seleccionarlo desde el árbol desplegado con el
botón Choose de los filtros. A continuación lo configuraremos para determinar qué atributos
queremos filtrar.
Como primer filtro de selección, vamos a eliminar de los atributos de entrada todas las
calificaciones parciales de la prueba y la calificación final, quedando como únicas calificaciones la
nota de bachillerato y la calificación de la prueba. Por tanto tenemos que seleccionar los índices
5,6,7,10,12,14 y 17, indicándolo en el cuadro de configuración del filtro Remove:
14
Interfaz Experiemnter permite armar un listado de filtros a aplicar con las opciones Add
-26-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Como puede verse, en el conjunto de atributos a eliminar se pueden poner series de valores
contiguos delimitados por guión (5-7) o valores sueltos entre comas (10,12,14,17). Además, puede
usarse “first” y “last” para indicar el primer y último atributo, respectivamente.
La opción invertSelection es útil cuando realmente queremos seleccionar un pequeño subconjunto
de todos los atributos y eliminar el resto. Open y Save nos permiten guardar configuraciones de
interés en archivos. El botón More, que aparece opcionalmente en algunos elementos de WEKA,
muestra información de utilidad acerca de la configuración de los mismos. Estas convenciones
para designar y seleccionar atributos, ayudan, y para guardar y cargar configuraciones específicas es
común a otros elementos de WEKA.
Una vez configurado, al accionar el botón Apply del área de filtros se modifica el conjunto de datos
(se filtra) y se genera una relación transformada. Esto se hace indicar en la descripción “Current
Relation”, que pasa a ser la resultante de aplicar la operación correspondiente (esta información se
puede ver con más nitidez en la ventana de log, que además nos indicará la cascada de filtros
aplicados a la relación operativa). La relación transformada tras aplicar el filtro podría almacenarse
en un nuevo fichero ARFF con el botón Save, dentro de la ventana Preprocess.
Filtros de discretización
Estos filtros son muy útiles cuando se trabaja con atributos numéricos, puesto que muchas
herramientas de análisis requieren datos simbólicos, y por tanto se necesita aplicar esta
transformación antes. También son necesarios cuando queremos hacer una clasificación sobre un
atributo numérico, por ejemplo clasificar los alumnos aprobados y suspensos. Este filtrado
transforma los atributos numéricos seleccionados en atributos simbólicos, con una serie de
etiquetas resultantes de dividir la amplitud total del atributo en intervalos, con diferentes opciones
para seleccionar los límites.
Por defecto, se divide la amplitud del intervalo en tantas "cajas" como se indique en bins (por
defecto 10), todas ellas de la misma amplitud. Por ejemplo, para discretizar las calificaciones
numéricas en 4 categorías, todas de la misma amplitud, se configuraría así:
-27-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Observe el resultado después de aplicar el filtro y los límites elegidos para cada atributo. En este
caso se ha aplicado a todos los atributos numéricos con la misma configuración (los atributos
seleccionados son first-last, no considerando los atributos que antes del filtrado no eran numéricos).
Observe que la relación de trabajo ahora (“current relation”) ahora es el resultado de aplicar en
secuencia el filtro anterior y el actual.
A veces es más útil no fijar todas las cajas de la misma anchura sino forzar a una distribución
uniforme de instancias por categoría, con la opción useEqualFrequency. La opción findNumBins
permite opimizar el número de cajas (de la misma amplitud), con un criterio de clasificación de
mínimo error en función de las etiquetas.
Haga una nueva discretización de la relación (eliminando el efecto del filtro anterior y dejando la
relación original con el botón Undo) que divida las calificaciones en 4 intervalos de la misma
frecuencia, lo que permite determinar los cuatro cuartiles (intervalos al 25%) de la calificación en la
prueba: los intervalos delimitados por los valores {4, 4.8, 5.76}
Podemos ver que el 75% alcanza la nota de compensación (4). El 50% está entre 4 y 5.755, y el
25% restante a partir de 5.755.
-28-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Filtros de añadir expresiones
Muchas veces es interesante incluir nuevos atributos resultantes de aplicar expresiones a los
existentes, lo que puede traer información de interés o formular cuestiones interesantes sobre los
datos. Por ejemplo, vamos a añadir como atributo de interés la "mejora" sobre la nota de
bachillerato, lo que puede servir para calificar el "éxito" en la prueba. Seleccionamos el filtro de
atributos.
AddExpression, configurado para
obtener la diferencia entre los
atributos calificación en la prueba, y
nota de bachillerato, en las
posiciones15 y 16: después de
aplicarlo aparece este atributo en la
relación, sería el número 19, con el
histograma indicado en la figura.
Después de aplicarlo aparece este
atributo en la relación, sería el
número 19, con el histograma
indicado en la figura:
-29-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
1.4.1.2.2. Ejemplo de aplicación de filtros de instancias.
De entre todas las posibilidades implementadas para filtros de selección de instancias (selección de
rangos, muestreos, etc.), nos centraremos en la utilización de filtros para seleccionar instancias
cuyos atributos cumplen determinadas condiciones.
Selección de instancias con condiciones sobre atributos
Vamos a utilizar el filtro RemoveWithValues, que elimina las instancias de acuerdo a condiciones
definidas sobre uno de los atributos.
Las opciones que aparecen en la ventana de
configuración son las indicadas a continuación.
El atributo utilizado para filtrar se indica en
"attributeIndex". Si es un atributo nominal, se
indican los valores a filtrar en el último
parámetro, "nominalIndices". Si es numérico, se
filtran las instancias con un valor inferior al
punto de corte, "splitPoint". Se puede invertir el
criterio de filtrado mediante el campo
"invertSelection".
Este filtro permite verificar una condición
simple sobre un atributo. Sin embargo, es
posible hacer un filtrado más complejo sobre
varias condiciones aplicadas a uno o varios
atributos sin más que aplicar en cascada varios
filtros.
A modo de ejemplo, utilice tres filtros de este tipo para seleccionar los alumnos de Getafe y
Leganés con una calificación de la prueba entre 6.0 y 8.0. Compruebe el efecto de filtrado
visualizando los histogramas de los atributos correspondientes (localidad y calificación en la
prueba), tal y como se indica en la figura siguiente:
-30-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
1.4.2.
Clasificación
En esta sección abordamos el problema de la clasificación, que es el más frecuente en la práctica.
En ocasiones, el problema de clasificación se formula como un refinamiento en el análisis, una vez
que se han aplicado algoritmos no supervisados de agrupamiento y asociación para describir
relaciones de interés en los datos.
Se pretende construir un modelo que permita predecir la categoría de las instancias en función de
una serie de atributos de entrada. En el caso de WEKA, la clase es simplemente uno de los atributos
simbólicos disponibles, que se convierte en la variable objetivo a predecir. Por defecto, es el último
atributo (última columna) a no ser que se indique otro explícitamente
Pulsando en la segunda pestaña (zona superior) del explorador entramos en el modo clasificación
(figura 1.16). En la parte superior de la sección de clasificadores, está el cuadro “Cassifier”. Este
cuadro contiene un campo de texto que da el nombre de los clasificadores seleccionados por el
momento y sus opciones. Haciendo click en el cuadro de texto, muestra un cuadro de diálogo de un
editor genérico de objeto (generic object editor), al igual que los filtros. Esto permite elegir un
clasificador de los que están disponibles en la Weka y configurarlo.
Como podemos observar en la figura 1.16., el entorno cambia bastante con respecto a la ventana
anterior. La parte superior, como es habitual sirve para seleccionar el algoritmo de clasificación y
configurarlo. El resto de elementos a definir en esta ventana se describen a continuación
Figura 1.16: El modo clasificación dentro del explorador.
-31-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Si queremos realizar una clasificación lo primero será elegir un clasificador y configurarlo a nuestro gusto, para ello pulsaremos sobre el botón Choose dentro del área Classifier. Una vez pulsado se
desplegará un árbol que nos permitirá seleccionar el clasificador deseado. Una vez seleccionado
aparecerá, en la etiqueta contigua al botón Choose, el filtro seleccionado y los argumentos con los
que se ejecutará. Esta información es muy útil si queremos utilizar el interfaz de consola ya que
podremos configurar nuestro filtro con la interfaz y luego obtener el resultado apto para línea de
mandato.
Para poder acceder a las propiedades de cada clasificador deberemos hacer doble-click sobre la
etiqueta antes mencionada. Al darle aparecerá una nueva ventana con las propiedades junto a una
breve explicación del mismo.
Estos métodos se han agrupado a grandes rasgos en las siguientes familias15:
El resultado de aplicar el clasificador elegido será, probado según las opciones que serán
configuradas haciendo click en el cuadro “test options”. Podemos establecer como queremos
efectuar la validación del modelo aprendido. Entonces una vez elegido el clasificador y sus
características el próximo paso es la configuración del modo de entrenamiento (Test Options).
Weka proporciona 4 modos de prueba:
el clasificador es evaluado en torno a la calidad de predicción de la clase de las
instancias que fue entrenado.
Con esta opción Weka entrenará el método con todos los datos disponibles y luego lo aplicará otra
vez sobre los mismos; evalúa el clasificador sobre el mismo conjunto sobre el que se construye el
modelo predictivo para determinar el error, que en este caso se denomina "error de
resustitución". Por tanto, esta opción puede proporcionar una estimación demasiado optimista del
comportamiento del clasificador, al evaluarlo sobre el mismo conjunto sobre el que se hizo el
modelo
el clasificador es evaluado en torno a calidad de predicción de la clase de un set
de instancias cargadas de un archivo.
Marcando esta opción tendremos la oportunidad de seleccionar, pulsando el botón Set... , un
fichero de datos con el que se probará el clasificador obtenido con el método de clasificación
usado y los datos iniciales. Sobre cada dato se realizará una predicción de clase para contar los
errores.
15
Esta clasificación no es exhaustiva, ya que hay métodos de aprendizaje que caerían en más de uno de
estos grupos.
-32-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
el clasificador es evaluado por validación cruzadas.
Pulsando el botón Cross-validation Weka realizará una validación cruzada 16estratificada del número de particiones dado (Folds). La validación cruzada consiste en: dado un número n se divide
los datos en n partes y, por cada parte, se construye el clasificador con las n - 1 partes restantes y
se prueba con esa. Así por cada una de las n particiones. Esta opción es la más elaborada y
costosa.
Se dividen las instancias en tantas carpetas como se indica y en cada evaluación se toman las
instancias de cada carpeta como datos de test, y el resto como datos de entrenamiento para
construir el modelo. Los errores calculados son el promedio de todas las ejecuciones.
el clasificador es evaluado con respecto a la calidad de predicción de un cierto
porcentaje de datos (data), en los cuales están sustentadas las pruebas.
Se define un porcentaje con el que se construirá el clasificador y con la parte restante se probará.
La cantidad de datos (held) sustentada depende del valor ingresado en el campo “%”.El valor
indicado es el porcentaje de instancias para construir el modelo, que a continuación es evaluado
sobre las que se han dejado aparte. Cuando el número de instancias es suficientemente elevado,
esta opción es suficiente para estimar con precisión las prestaciones del clasificador en el dominio
Mayores alcances (opciones avanzadas) de opciones de prueba, pueden ser configuradas haciendo
click en botón “More options…”: (figura 2.17).
Figura 2.17: Ventana de opciones adicionales en el modo de clasificación.
Las opciones que se nos presentan son:
(salida del modelo): el modelo de clasificación del set de total entrenamiento,
puede ser visto, visualizado o tener otras salidas, permite visualizar (en modo
texto y, con algunos algoritmos, en modo gráfico) el modelo construido por el
clasificador (árbol, reglas, etc.). Una vez construido y probado el clasificador, nos
mostrará en la salida del clasificador (parte media derecha de la ventana 1.16) el
modelo que ha construido.
16
Una validación-cruzada es estratificada cuando cada una de las partes conserva las propiedades de la
muestra original (porcentaje de elementos de cada clase).
-33-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
(salida estadística por clase): las estadísticas precisión/rellanado
(precesion/recall) y verdadero/falso (true/false), para cada clase pueden
obtenerse. Obtiene estadísticas de los errores de clasificación por cada
uno de los valores que toma el atributo de clase
(salida medidas de evaluación de entropía): Muestra
información de mediciones de la entropía en la clasificación.
(matriz de confusión): la matriz de confusión de las predicciones de los
clasificadores están incluidas en las salidas. Esta tabla cuyo número de
columnas es el número de atributos muestra la clasificación de las
instancias. Da una información muy útil porque no sólo refleja los
errores producidos sino también informa del tipo de éstos.
Si tuviéramos el problema de clasificar un conjunto de vacas en dos clases gordas y flacas y aplicamos
un clasificador, obtendríamos una matriz de confusión como la siguiente.
Gordas Flacas
32
4
Gordas
4
43
Flacas
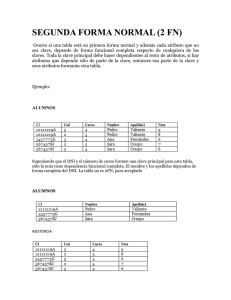
Tabla 2.1: Ejemplo de una matriz de confusión
Donde las columnas indican las categorías cllasificadas por el clasificador y las filas las categorías reales de los datos. Por lo que los elementos en la diagonal principal son los elementos que
ha acertado el clasificador y lo demás son los errores.
(guarda predicciones de visualización): las predicciones de los
clasificadores son recordados para poder ser visualizados.
(evaluación sensible de costo), los errores son evaluados con respecto
a matriz de costos. El botón “Set…”permite especificar la matriz de
costos usada.
especifica semilla al azar (random seed) usada cuando se azarisan
los datos antes de dividirlos para propósitos de evaluación.
Atributos de Clase
Los clasificadores en Weka, están diseñados para ser entrenados para predecir atributos de clase
simple, el cual es el objetivo de la predicción. Algunos clasificadores solo pueden aprender clases
nominales, otras solo numéricas (problemas de regresión), y otra, pueden aprender ambas.
Debajo de este cuadro de la ventana existe un menú desplegable que nos permitirá seleccionar un
atributo de nuestra muestra. Este atributo es el que actuará como resultado real de la clasificación.
Por descarte, las clases serán el último atributo en los datos. Si se requiere entrenar un clasificador
para predecir un atributo diferente, hay que hacer click en el cuadro, bajo el cuadro “Test options”
para obtener una lista (drop down list) de atributos para elegir.
-34-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Entrenamiento de Clasificadores
Cuando los clasificadores, las opciones de prueba y las clases ya están configuradas, el proceso de
aprendizaje empieza haciendo click en el botón “Start”. Mientras el clasificador está ocupado en
entrenamiento, el pájaro se mueve. Se puede detener el entrenamiento en cualquier momento con el
botón “Stop”. Una vez funcionando en la barra de estado aparecerá la información referente al
estado del experimento.
Cuando el entrenamiento está completo, la Weka situada en la esquina inferior derecha dejará de
bailar y eso indicará que el experimento ha concluido (figura 2.18); el área del clasificador de
salidas (Classifier output), a la derecha del “Display” está lleno de texto describiendo el resultado
del entrenamiento y de la prueba. Una nueva entrada (lista de resultados) aparece en el cuadro
“Result list”, miramos la lista debajo con resultados, pero antes investigar el texto que está en la
salida.
Figura 2.18: Weka habiendo aplicado un método de clasificación.
Texto de Salidas de Clasificador
Entonces una vez se ejecuta el clasificador seleccionado sobre los datos de la relación, en la
ventana de texto de la derecha aparece información de ejecución, el modelo generado con todos los
datos de entrenamiento y los resultados de la evaluación.
Por ejemplo, al predecir el atributo "presentado", con un árbol de decisión de tipo J48, aparece el modelo
textual siguiente:
J48 pruned tree
-----------------cal_prueba <= 0: NO (153.0)
cal_prueba > 0: SI (18649.0/2.0)
Number of Leaves : 2
Size of the tree : 3
Se obtiene a partir de los datos esta relación trivial, salvo dos únicos casos de error: los presentados son
los que tienen una calificación superior a 0.
-35-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
El texto en el que “Classifier output” (salidas del clasificador) tiene (scroll bars) barras de
selección, permitiendo buscar los resultados. Además, se puede agrandar la ventana Explorer, para
tener un área mayor mostrada. Las salidas pueden ser obtenidas (split) en diversas secciones:
Run
information: lista de información que muestra las opciones, nombre de relaciones, instancias,
atributos y modos de prueba de los tipos de aprendizaje (learning scheme) que tenían relación con el
proceso.
Classifier model (full training set) modelo total de clasificación: una representación textual del modelo de
clasificación que fue producido.
Summary (resumen): una lista de estadísticas, resumiendo cuan minucioso el clasificador pueda predecir
la clase verdadera de las instancias bajo el modo de pruebas.
Detailed accuracy by class (Se presentan detalles de exactitud para cada clase): un quiebre más detallado
por clase (detailed per-class break down) de clasificador de predicción (classifier prediction accuracy).
para cada uno de los valores que puede tomar el atributo de clase: el porcentaje de instancias con ese
valor que son correctamente predichas (TP: true positives), y el porcentaje de instancias con otros
valores que son incorrectamente predichas a ese valor aunque tenían otro (FP: false positives). Las otras
columnas, precision, recall, Fmeasure, se relacionan con estas dos anteriores.
Los parámetros de exactitud para cada clase son los siguientes:
La True Positive (TP) rate es la proporción de ejemplos que fueron clasificados como clase x, de
entre todos los ejemplos que de verdad tienen clase x, es decir, qué cantidad de la clase ha sido
capturada. En la matriz de confusión, es el valor del elemento de la diagonal dividido por la suma de
la fila relevante.
La False Positive (FP) rate es la proporción de ejemplos que fueron clasificados como clase x, pero
en realidad pertenecen a otra clase, de entre todos los ejemplos que no tienen clase x. En la matriz de
confusión, es la suma de la columna menos el valor del elemento de la diagonal dividido por la suma
de las filas de las otras clases.
La Precision es la proporción de ejemplos que de veras tienen clase x entre todos los que fueron
clasificados como clase x. En la matriz es el elemento de la diagonal dividido por la suma de la
columna relevante.
La F-Measure es simplemente 2*Precision*Recall/(Precision+Recall), una medida combinada de
precisión y recall.
Confusión matriz (Matriz de confusión): muestra cuantas instancias han sido asignadas a cada clase. La
matriz de confusión, o también tabla de contingencia, está formada por tantas filas y columnas como
clases hay. El número de instancias clasificadas correctamente es la suma de la diagonal de la matriz y el
resto están clasificadas de forma incorrecta. Comprobando el número de elementos no nulos fuera de la
diagonal principal tenemos una buena aproximación de la calidad del clasificador.
Por tanto, es una matriz con N2 posiciones, con N el número de valores que puede tomar la clase. En cada
fila i, i=1...N, aparecen las instancias que realmente son de la clase i, mientras que las columnas j, j=1...N,
son las que se han predicho al valor j de la clase.
En el ejemplo anterior, la matriz de confusión que aparece es la siguiente:
=== Confusion Matrix ===
a b <-- classified as
18647 0 | a = SI
2 153 | b = NO
Por tanto, los valores en la diagonal son los aciertos, y el resto de valores son los errores. De los 18647 alumnos
presentados, todos son correctamente clasificados, mientras que de los 155 no presentados, hay 153 correctamente
clasificados y 2 con error.
-36-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
La Lista de Resultados
Después de entrenar varios clasificadores, la lista de resultados tendrá varias entradas. En la zona
inferior-izquierda se encuentra la lista de resultados en la que aparecerán cada uno de los
experimentos que hayamos realizado. Si pulsamos el botón secundario sobre alguno de ellos
obtendremos opciones adicionales aplicables al experimento que hayamos seleccionado (figura
2.19). Éstas permiten visualizar los resultados obtenidos en diferentes variantes, incluyendo
gráficas, guardar modelos, etc.
Figura 2.19: Opciones adicionales de un experimento.
Estas opciones adicionales son:
•
View in main window (vista en ventana principal): muestra las salidas en la ventana principal
(igual que haciendo click izquierdo en la entrada (entry)).
•
View in separate window (visión en pantalla separada): abre una ventana independiente para
visualizar resultados..
•
Save result buffer (Guardar buffer de resultados): genera un diálogo, permitiendo guardar el
archivo de texto que contiene la salida de texto.
•
Load model (cargando el modelo): carga el objeto del modelo pre-entrenado de un archivo
binario.
•
Save model (guarda el modelo): guarda un objeto de modelo en un archivo binario. Los objetos
son guardados en JAVA.
•
Re-evaluate model on current test set (Enfrentará un modelo con el conjunto de muestra
actual) el modelo ya construido y probado su desempeño con los datos (data set) que fueron
especificados con el botón “Set…” bajo la opción “Supplied test set”.
•
Visualize clasiffier errors Se abrirá una nueva ventana (figura 2.20) en la que nos mostrará una
gráfica con los errores de clasificación17. Las instancias correctas serán representadas en forma
de cruces, y las no correctas serán representadas en cuadrados
17
Esta opción será sólo accesible si hemos configurado el clasificador para que almacene la
clasificación realizada
-37-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Figura 2.20: Gráfica de los errores de clasificación.
La ventana del modo gráfica está compuesta por 3 partes. En la parte superior las dos listas
desplegables indican el eje X y el eje Y de la gráfica. Es posible variarles a nuestro gusto y
obtener todas las combinaciones posibles.
Debajo de la lista desplegable del eje X se encuentra otra en la que podemos definir un atributo
que muestre el rango de variación del mismo en colores. El botón contiguo a ésta, en la misma
línea, sirve para definir el tipo de figura geométrica que queremos utilizar para seleccionar datos
en la propia gráfica. Interactuando en la misma seleccionamos un área (figura 2.21).
Una vez seleccionada a nuestro gusto con el botón Submit nos mostrará sólo los datos capturados
en el área de la figura que hemos trazado. El botón Reset sirve para volver a la situación inicial y
el botón Save es para guardar los valores de los datos18 en un fichero arff.
La barra de desplazamiento, denominada jitter, es muy interesante porque permite añadir un ruido
aleatorio (en función de lo que se desplace la barra) a los datos. Es útil cuando hay muchos datos
juntos y queremos separarlos para poder estimar la cantidad que hay.
18
Weka guardará todos los datos de ese apartado, no sólo los pertenecientes a dicha gráfica
-38-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Figura 2.21. Gráfica distribución de los atributos
En la parte media-derecha de la ventana de la gráfica (fig. 2.21) se muestra gráficamente, y de
una forma muy resumida, la distribución de cada uno de los atributos. Pulsando sobre ellos con
el botón principal del ratón definiremos el eje X y con el botón secundario el eje Y.
La última parte (la inferior) de la ventana que muestra gráficas es la leyenda. Pulsando con el
ratón en un elemento de la leyenda aparecerá una ventana (figura 2.22) que nos permitirá
modificar los colores en una extensa gama.
Figura 2.22: Selección del color para un atributo.
•
Visualize tree Esta opción mostrará un árbol de decisión, como el de la figura 1.23., generado por
el clasificador, en el caso que lo haya hecho. Genera una representación gráfica de la estructura
del modelo de clasificación, si es posible (solo está disponible con algunos clasificadores).
-39-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Figura 2.23: Visualización de árboles de decisión.
Se puede generar menú, haciendo click derecho en una zona en blanco, moviéndose por las
opciones, moviendo el Mouse (pan around by dragging the mouse) y ver las instancias de
entrenamiento en cada nodo, haciendo click en ellos. CTRL-click hace zoom en las vistas,
mientras que con SHIFT- dragging, una caja hace zoom in.
Las opciones que existen en esta ventana se despliegan pulsando el botón secundario sobre ella.
Éstas son:
− Center on Top Node centrará el gráfico en la ventana atendiendo a la posición del nodo superior. Esta opción es muy aconsejable si cambiamos el tamaño de la ventana.
− Fit to Screen Ajusta el gráfico a la ventana, no sólo la posición sino también su tamaño.
− Auto Scale Escala el gráfico de manera que no haya nodos que colisionen. Select Font Nos
permite ajustar el tamaño del tipo de letra del texto.
− Si pulsamos el botón secundario sobre un nodo del grafo nos dará la opción de Visualize the
node, si hay instancias que correspondan a ese nodo nos las mostrará.
•
Visualize margin curve Muestra en una curva la diferencia entre la probabilidad de la clase
estimada y la máxima probabilidad de otras clases. Genera un gráfico que ilustra las predicciones
del margen. El margen se define como la diferencia entre la predicción de probabilidad para la
clase actual y la probabilidad más alta que se puede predecir para otras clases.
Por ejemplo, logaritmos de loasting, pueden alcanzar mejores desempeños en pruebas de datos con
respecto a incrementar los márgenes de las datas de entrenamiento. El funcionamiento de la ventana es
igual que la del caso anterior.
•
Visualize thresold curve Muestra la variación de las proporciones de cada clase. Genera un
gráfico que muestra los “tradeoffs”en predicción, que son obtenidos variando los valores del
“threshold” de 0.5, la probabilidad que se predijo positiva (positive), debe ser mayor que 0.5 para
instancias que deben predecirse positivas. Un truco importante es que si situamos en el eje X los
coeficientes falsos positivos y en el eje Y los coeficientes de verdaderos positivos obtendremos
una curva ROC, y aparecerá sobre la gráfica el valor del área de ésta.
-40-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
•
Visualize cost curve Muestra una gráfica que indica la probabilidad de coste al vavariara
sensibilidad entre clases. Genera una gráfica que da una representación explícita de los costos
esperados, como los describen Drummond y Halte.
Las opciones son grilladas (greyed out) si no se aplica al set de resultados específicos.
1.4.2.1. Ejemplo Selección y configuración de clasificadores
Vamos a ilustrar la aplicación de algoritmos de clasificación a diferentes problemas de predicción
de atributos definidos sobre los datos de entrada en este ejemplo. El problema de clasificación
siempre se realiza sobre un atributo simbólico, en el caso de utilizar un atributo numérico se precisa
por tanto discretizarlo antes en intervalos que representarán los valores de clase.
En primer lugar efectuaremos análisis de predicción de la calificación en la prueba de selectividad a
partir de los siguientes atributos: año, convocatoria, localidad, opción, presentado y nota de
bachillerato. Se van a realizar dos tipos de predicciones: aprobados, e intervalos de clasificación.
Por tanto tenemos
que aplicar en
primer lugar una
combinación de
filtros que
elimine los
atributos no
deseados
relativos a
calificaciones
parciales y
asignaturas
opcionales, y un
filtro que
discretice la
calificación en la
prueba en dos
partes:
Obsérvese que se prefiere realizar las predicciones sobre la calificación en la prueba, puesto que la
calificación final depende explícitamente de la nota del bachillerato.
Clasificador “OneR”
Este es uno de los clasificadores más sencillos y rápidos, aunque en ocasiones sus resultados son
sorprendentemente buenos en comparación con algoritmos mucho más complejos. Simplemente
selecciona el atributo que mejor “explica” la clase de salida. Si hay atributos numéricos, busca los
umbrales para hacer reglas con mejor tasa de aciertos. Lo aplicaremos al problema de predicción de
aprobados en la prueba a partir de los atributos de entrada, para llegar al resultado siguiente:
-41-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Por tanto, el algoritmo llega a la conclusión que la mejor predicción posible con un solo atributo es
la nota del bachillerato, fijando el umbral que determina el éxito en la prueba en 6.55. La tasa de
aciertos sobre el propio conjunto de entrenamiento es del 72.5%.
Compárese este resultado con el obtenido mediante ejecución sobre instancias independientes.
-42-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Clasificador como árbol de decisión: J48
El algoritmo J48 de WEKA es una implementación del algoritmo C4.5, uno de los algoritmos de
minería de datos que más se ha utilizado en multitud de aplicaciones. No vamos a entrar en los
detalles de todos los parámetros de configuración, (ver sección 3), y únicamente resaltaremos uno
de los más importantes, el factor de confianza para la poda, confidence level, puesto que influye
notoriamente en el tamaño y capacidad de predicción del árbol construido.
Una explicación simplificada de este parámetro de construcción del árbol es la siguiente: para cada
operación de poda, define la probabilidad de error que se permite a la hipótesis de que el
empeoramiento debido a esta operación es significativo. Cuanto más baja se haga esa probabilidad,
se exigirá que la diferencia en los errores de predicción antes y después de podar sea más
significativa para no podar. El valor por defecto de este factor es del 25%, y conforme va bajando
se permiten más operaciones de poda y por tanto llegar a árboles cada vez más pequeños.
Otra forma de variar el tamaño del árbol es a través de un parámetro que especifica el mínimo
número de instancias por nodo, si bien es menos elegante puesto que depende del número absoluto
de instancias en el conjunto de partida.
Construiremos el árbol de decisión con los parámetros por defecto del algoritmo J48: se llega a un
clasificador con más de 250 nodos, con una probabilidad de acierto ligeramente superior al del
clasificador OneR.
-43-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Modifique ahora la configuración del algoritmo para llegar a un árbol más manejable, como el que
se presenta a continuación.
Obsérvese que este modelo es un refinamiento del generado con OneR, que supone una mejorar
moderada en las prestaciones. De nuevo los atributos más importantes son la calificación de
bachillerato, la convocatoria, y después el año, antes que la localidad o las opciones.
Analice las diferencias con evaluación independiente y validación cruzada, y compárelas con
las del árbol más complejo con menos poda.
Podría ser de interés analizar el efecto de las opciones y asignaturas seleccionadas sobre el éxito en
la prueba, para lo cual quitaremos el atributo más importante, nota de bachillerato. Llegamos a un
árbol en el que lo más importante es la primera asignatura optativa, en diferentes combinaciones
con el año y segunda asignatura optativa. Este resultado generado por el clasificador puede
comprobarse si se analizan los histogramas de cada variable y visualizando el porcentaje de
aprobados con el color, que esta variable es la que mejor separa las clases, no obstante, la precisión
apenas supera el 55%.
Otros problemas de clasificación pueden formularse sobre cualquier atributo de interés, a
continuación mostramos algunos ejemplos a título ilustrativo.
-44-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Clasifiación multinivel de las calificaciones
El problema anterior puede intentar refinarse y dividir el atributo de interés, la calificación final, en
más niveles, en este caso 5. Los resultados se muestran a continuación
OneR
J48
La precisión alcanzada es tan sólo del 60%, indicando que hay bastante incertidumbre una vez
generada la predicción con los modelos anteriores.
Predicción de la opción
Si dejamos todos los atributos en la
muestra y aplicamos el clasificador a
la opción cursado, se desvela una
relación trivial entre opción y
asignaturas en las opciones que
predice con prácticamente el 100% de
los casos.
-45-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
A continuación eliminamos estos designadores con un filtro de atributos. Si aplicamos el algoritmo
J48 sobre los datos filtrados, llegamos a un árbol de más de 400 nodos, y con muchísimo sobreajuste (observe la diferencia de error de predicción sobre el conjunto de entrenamiento y sobre un conjunto
independiente). Forzando la poda del árbol, llegamos al modelo siguiente:
Los atributos más significativos para separar las opciones son precisamente las calificaciones en las
asignaturas optativas, pero apenas predice correctamente un 43% de los casos. Por tanto, vemos
que no hay una relación directa entre opciones y calificaciones en la prueba, al menos relaciones
que se puedan modelar con los algoritmos de clasificación disponibles.
Si nos fijamos en detalle en las calificaciones en función de las opciones, podríamos determinar que
apenas aparecen diferencias aparecen en los últimos percentiles, a la vista de las gráficas siguientes:
-46-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Vemos que las diferencias no son significativas, salvo quizá en los últimos percentiles.
-47-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Predicción de localidad y opción
La clasificación se puede realizar sobre cualquier atributo disponible. Con el número de atributos
reducido a tres, localidad, opción y calificación (aprobados y suspensos), vamos a buscar modelos
de clasificación, para cada uno de los atributos:
Predicción de localidad
Predicción de opción
Es decir, la opción 1 y 2 aparecen mayoritariamente en Leganés, y las opciones 3 y 4 más en los
alumnos que aprobaron la prueba en Leganés. No obstante, obsérvese que los errores son tan
abrumadores (menos del 30% de aciertos) que cuestionan fuertemente la validez de estos modelos.
Mejora en la prueba
Un problema de clasificación interesante puede ser determinar qué alumnos tienen más "éxito" en
la prueba, en el sentido de mejorar su calificación de bachillerato con la calificación en la prueba.
Para ello utilizaremos el atributo "mejora", introducido en la sección 1.4.1.2.1. (“Filtros de añadir
expresiones”), y lo discretizamos en dos valores de la misma frecuencia (obtenemos una mediana
de -1.76, de manera que dividimos
los alumnos en dos grupos: los que
obtienen una diferencia menor a este
valor y superior a este valor, para
diferenciar los alumnos según el
resultado se atenga más o menos a
sus expectativas.
-48-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Evidentemente, para evitar construir
modelos triviales, tenemos que
eliminar los atributos relacionados
con las calificaciones en la prueba,
para no llegar a la relación que
acabamos de construir entre la
variable calculada y las originales.
Vamos a preparar el problema de
clasificación con los siguientes
atributros:
Attributes: 7
Año_académico
convocatoria
localidad
opcion1ª
nota_bachi
Presentado
mejora
Llegamos al siguiente árbol de clasificación.
Es decir, los atributos que más determinan el "éxito" en la prueba son: año académico, opción y
localidad. Para estos resultados tenemos una precisión, con evaluación sobre un conjunto
independiente, en torno al 58%, por lo que sí podríamos tomarlo en consideración.
-49-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
1.4.2.2. Ejemplo Predicción numérica
La predicción numérica se define en WEKA como un caso particular de clasificación, en el que la
clase es un valor numérico. No obstante, los algoritmos integrados para clasificar sólo admiten
clases simbólicas y los algoritmos de predicción numéricas, que aparecen mayoritariamente en el
apartado classifiers->functions, aunque también en classifiers->trees.
Vamos a ilustrar algoritmos de predicción numérica en WEKA con dos tipos de problemas. Por un
lado, "descubrir" relaciones deterministas que aparecen entre variables conocidas, como
calificación en la prueba con respecto a las parciales y la calificación final con respecto a la prueba
y bachillerato, y buscar otros modelos de mayor posible interés.
Relación entre calificación final y parciales
Seleccionamos los atributos con las 6
calificaciones parciales y la calificación en la
prueba:
Vamos a aplicar el modelo de predicción más popular: regresión simple, que construye un modelo
lineal del atributo clase a partir de los atributos de entrada: functions->LinearRegresion
Como resultado, aparece la
relación con los pesos relativos
de las pruebas parciales sobre la
calificación de la prueba:
Hay que observar que en los
problemas de predicción la
evaluación cambia, apareciendo
ahora
el
coeficiente
de
correlación y los errores medio
y medio cuadrático, en términos
absolutos y relativos. En este
caso
el
coeficiente
de
correlación es de 0.998, lo que
indica que la relación es de una
precisión muy notable.
-50-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Si aplicamos ahora esta función a la relación entre calificación final con calificación en la prueba y
nota de bachillerato (filtro que selecciona únicamente los atributos 15-17), podemos determinar la
relación entre estas variables: qué peso se lleva la calificación de bachillerato y de la prueba en la
nota final.
Vamos a hacerlo primero con los alumnos de una población pequeña, de Guadarrama (posición 12
del atributo localidad). Aplicamos los filtros correspondientes para tener únicamente estos alumnos,
y los atributos de calificaciones de la prueba, bachillerato y final:
Llegamos a 40 instancias:
-51-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Si aplicáramos regresión lineal
como en el ejemplo anterior,
obtenemos el siguiente
resultado:
El resultado deja bastante que desear porque la relación no es lineal. Para solventarlo podemos
aplicar el algoritmo M5P, seleccionado en WEKA como trees->m5->M5P, que lleva a cabo una
regresión por tramos, con cada tramo determinado a partir de un árbol de regresión.
Llegamos al siguiente resultado:
Que es prácticamente la relación
exacta utilizada en la actualidad:
60% nota de bachillerato y 40%
de la prueba, siempre que se
supere en ésta un valor mínimo de
4 puntos.
-52-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Si aplicamos este algoritmo a otros centros no siempre obtenemos este resultado, por una razón:
hasta 1998 se ponderaba al 50%, y a partir de 1999 se comenzó con la ponderación anterior.
Verifíquese aplicando este algoritmo sobre datos filtrados que contengan alumnos de antes de 1998
y de 1999 en adelante. En este caso, el algoritmo M5P no tiene capacidad para construir el modelo
correcto, debido a la ligera diferencia en los resultados al cambiar la forma de ponderación. Los
árboles obtenidos en ambos casos se incluyen a continuación:
Predicción de la calificación
Vamos a aplicar ahora este modelo para intentar construir un modelo aplicación más interesante, o,
al menos, analizar tendencias de interés. Se trata de intentar predecir la calificación final a partir de
los atributos de entrada, los mismos que utilizamos para el problema de clasificar los alumnos que
aprueban la prueba.
Si aplicamos el algoritmo sobre el conjunto
completo llegamos al siguiente modelo:
Obsérvese cómo trata el algoritmo los
atributos nominales para incluirlos en la
regresión: ordena los valores según el valor de
la magnitud a predecir (en el caso de
localidad, desde Collado hasta Los Peñascales
y en el de opción, ordenadas como 4º, 5º, 3º,
2º, 1º), y va tomando variables binarias
resultado de dividir en diferentes puntos,
determinando su peso en la función.
-53-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
En esta función lo que más pesa es la convocatoria, después la nota de bachillerato, y después
entran en juego la localidad, asignaturas optativas, y opción, con un modelo muy complejo.
Si
simplificamos
el
conjunto de atributos de
entrada, y nos quedamos
únicamente con el año,
opción,
nota
de
bachillerato,
y
convocatoria, llegamos a:
Este modelo es mucho
más manejable.
Compare los errores de predicción con ambos casos:
-54-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Correlación entre nota de bachillerato y calificación en prueba
Finalmente, es interesante a veces hacer un modelo únicamente entre dos variables para ver el
grado de correlación entre ambas. Continuando con nuestro interés por las relaciones entre
calificación en prueba y calificación en bachillerato, vamos a ver las diferencias por opción. Para
ello filtraremos por un lado los alumnos de opción 1 y los de opción 4. A continuación dejamos
únicamente los atributos calificación en prueba y nota de bachillerato, para analizar la correlación
de los modelos para cada caso.
Podemos concluir que para estas dos opciones el grado de relación entre las variables sí es
significativamente diferente, los alumnos que cursan la opción 1º tienen una relación más "lineal"
entre ambas calificaciones que los procedentes de la opción 4º
1.4.2.3. Ejemplo Aprendizaje del modelo y aplicación a nuevos datos
Para finalizar esta sección de clasificación, ilustramos aquí las posibilidades de construir y evaluar
un clasificador de forma cruzada con dos ficheros de datos. Seleccionaremos el conjunto atributos
siguiente: Año_académico, convocatoria, localidad, opcion1ª, des_Idioma, des_asig1, des_asig2,
des_asig3, cal_prueba, nota_bachi, Presentado. El atributo con la calificación, “cal_prueba”, lo
discretizamos en dos intervalos.
Vamos a generar, con el filtro de instancias dos conjuntos de datos correspondientes a los alumnos
de Getafe y Torrelodones. Para ello primero seleccionamos las instancias con el atributo localidad
con valor 10, lo salvamos (“datosGetafe”) y a continuación las instancias con dicho atributo con
valor 21 (“datosTorrelodones”).
-55-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Ahora vamos a generar los modelos de clasificación de alumnos con buen y mal resultado en la
prueba con el fichero de alumnos de la localidad de Torrelodones, para evaluarlo con los alumnos
de Getafe.
Para ello en primer lugar cargamos el fichero con los alumnos de Torrelodones que acabamos de
generar, “datosTorrelodones”, y lo evaluamos sobre el conjunto con alumnos de Getafe. Para ello,
seleccionaremos la opción de evaluación con un fichero de datos independiente, Supplied test set, y
fijamos con el botón Set, que el fichero de test es “datosGetafe”.
-56-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Obsérvese el modelo generado y los resultados:
Si ahora hacemos la operación inversa, entrenar con los datos de Getafe y evaluar con los de
Torrelodones, llegamos a:
Hay ligeras diferencias en los modelos generados para ambos conjuntos de datos (para los alumnos
de Torrelodones, lo más importante es tener una calificación de bachillerato superior a 6.8,
mientras que a los de Getafe les basta con un 6.5), y los resultados de evaluación con los datos
cruzados muestran una variación muy pequeña. El modelo construido a partir de los datos de
Torrelodones predice ligeramente peor los resultados de Getafe que a la inversa.
-57-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
1.4.3. Agrupamiento
La opción Cluster nos permite aplicar algoritmos de agrupamiento de instancias a nuestros datos.
Estos algoritmos buscan grupos de instancias con características "similares", según un criterio de
comparación entre valores de atributos de las instancias definidos en los algoritmos.
El mecanismo de selección, configuración y ejecución es similar a otros elementos: primero se
selecciona el algoritmo con Choose, se ajustan sus parámetros seleccionando sobre el área donde
aparece, y se después se ejecuta.
Pulsando la tercera pestaña, llamada Cluster, en la parte superior de la ventana accedemos a la
sección dedicada al clustering (figura 2.24).
Figura 2.24: El modo Cluster dentro del modo explorador.
Una vez que se ha realizado la selección y configuración del algoritmo, se puede pulsar el botón
Start, que hará que se aplique sobre la relación de trabajo. Los resultados se presentarán en la
ventana de texto de la parte derecha. Además, la ventana izquierda permite listar todos los
algoritmos y resultados que se hayan ejecutado en la sesión actual. Al seleccionarlos en esta lista de
visualización se presentan en la ventana de texto a la derecha, y además se permite abrir ventanas
gráficas de visualización con un menú contextual que aparece al pulsar el botón derecho sobre el
resultado seleccionado.
-58-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
En esta opción de Agrupamiento aparecen las siguientes opciones adicionales en la pantalla.
La caja de “Cluster Modes”, sirve apara elegir a qué se le va a aplicar cluster, y cómo evaluar los
resultados. Las primeras tres opciones, son iguales a los de clasificación: “USE training set,
Supplied test set y percentage split”; con la diferencia que los datos son asignados para Cluster, en
vez de tratar de predecir una clase específica. La cuarta opción o modo es el “Classes To Cluster
Evaluation”, que compara qué tan bien el cluster elegido calza con clases pre-asignadas de datos.
La caja drop down bajo estas opciones selecciona la clase, al igual que el panel “classify”.
Una opción propia de este apartado es la posibilidad de ver de una forma gráfica la asignación de
las muestras en clusters. En la caja de “Cluster Mode” hay una opción adicional, la “Store clusters
for visualization” (guarda para visualizar) que contiene caja de tickeado, determina si es posible o
no visualizar los cluster cuando el entrenamiento esté completo.
Activamos la opción Store cluster for
evaluation, ejecutando el experimento y
seguidamente, en la lista de resultados,
pulsando el botón secundario sobre el
experimento en cuestión y marcando la
opción Visualize cluster assignments con
esto obtendremos una ventana similar a
las del modo explorador para mostrar
gráficas en el que nos mostrará el
clustering realizado. Cuando se trabaje
con datasets demasiado grandes, pueden
existir problemas con la memoria, por lo
que podría ser de ayuda deshabilitar esta
opción.
Algunos atributos deberán ser ignorados cundo se hace “clustering”. El botón “Ignore attributes”
genera una pequeña ventana que permite escoger los atributos a ignorar. Al accionar esta opción
aparecen todos los atributos disponibles. Se pueden seleccionar con el botón izquierdo sobre un
atributo específico, o seleccionar grupos usando SHIFT para un grupo de atributos contiguos y
CONTROL para grupos de atributos sueltos. Para cancelar se hace con el botón “Cancel”, para
activar se hace a través del botón “select”. Así, la próxima vez que se haga clustering, los atributos
seleccionados serán ignorados.
La sección “cluster”, así como la sección “classify”, tienen botones Start/Stop, un área de resultado
de texto y una lista de resultados. Éstos se comportan igual que el contador de partes de
clasificación (classification counterparts). Haciendo click derecho en una entrada en la lista de
resultados, genera un menú similar, con la excepción que solo muestra una opción de visualización:
“Visualize Cluster Assigment”.
1.4.3. 1. Ejemplo Agrupamiento numérico
En primer lugar utilizaremos el algoritmo de agrupamiento K-medias, por ser uno de los más
veloces y eficientes, si bien uno de los más limitados. Este algoritmo precisa únicamente del número
de categorías similares en las que queremos dividir el conjunto de datos. Suele ser de interés repetir
la ejecución del algoritmo K-medias con diferentes semillas de inicialización, dada la notable
dependencia del arranque cuando no está clara la solución que mejor divide el conjunto de
instancias.
-59-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
En nuestro ejemplo, vamos a comprobar si el atributo “opción” divide naturalmente a los alumnos
en grupos similares, para lo que seleccionamos el algoritmo SimpleKMeans con parámetro
numClusters con valor 5. Los resultados aparecen en la ventana de texto derecha:
Nos aparecen los 5 grupos de ejemplos más similares, y sus centroides (promedios para atributos
numéricos, y valores más repetidos en cada grupo para atributos simbólicos).
En este caso es de interés analizar gráficamente como se distribuyen diferentes valores de los
atributos en los grupos generados. Para ello basta pulsar con botón derecho del ratón sobre el
cuadro de resultados, y seleccionar la opción visualizeClusterAssignments
-60-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Si seleccionamos combinaciones del atributo opción con localidad, nota o convocatoria podemos
ver la distribución de grupos:
A la vista de estos gráficos podemos concluir que el “parecido” entre casos viene dado
fundamentalmente por las opciones seleccionadas. Los clusters 0, 1 y 4 se corresponden con las
opciones 3, 4 y 1, mientras que los clusters 2 y 3 representan la opción 3 en las convocatorias de
junio y septiembre.
Aprovechando esta posibilidad de buscar grupos de semejanzas, podríamos hacer un análisis más
particularizado a las dos localidades mayores, Leganés y Getafe, buscando qué opciones y
calificaciones aparecen con más frecuencia.
Vamos a preparar los datos con filtros de modo que tengamos únicamente tres atributos: localidad,
opción, y calificación final. Además, discretizamos las calificaciones en dos grupos de la misma
frecuencia (estudiantes con mayor y menor éxito), y únicamente nos quedamos con los alumnos de
Leganés y Getafe. Utilizaremos para ello los filtros adecuados. A continuación aplicamos el
algoritmo K-medias con 4 grupos.
-61-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Vemos que los grupos nos muestran la presencia de buenos alumnos en Getafe en la opción 4, y
buenos alumnos en Leganés en la opción 1, siempre considerando estas conclusiones como
tendencias en promedio.
Gráficamente vemos la distribución de clusters por combinaciones de atributos:
-62-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Si consideramos que en Leganés hay escuelas de ingeniería, y en Getafe facultades de
Humanidades, podríamos concluir que podría ser achacable al impacto de la universidad en la zona.
El algoritmo EM proviene de la estadística y es bastante más elaborado que el K-medias, con el
coste de que requiere muchas más operaciones, y es apropiado cuando sabemos que los datos
tienen una variabilidad estadística de modelo conocido. Dada esta mayor complejidad, y el notable
volumen del fichero de datos, primero aplicaremos un filtro de instancias al 3% para dejar un
número de 500 instancias aproximadamente.
Para esto último iremos al preprocesado y
aplicamos un filtro de instancias, el filtro
Resample, con factor de reducción al 3%:
Una ventaja adicional del algoritmo de clustering EM es que permite además buscar el número de
grupos más apropiado, para lo cual basta indicar a –1 el número de clusters a formar, que es la
opción que viene por defecto. Esto se interpreta como dejar el parámetro del número de clusters
como un valor a optimizar por el propio algoritmo.
Tras su aplicación, este algoritmo determina que hay cinco clusters significativos en la muestra de
564 alumnos, y a continuación indica los centroides de cada grupo:
-63-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Al igual que antes, es interesante analizar el resultado del agrupamiento sobre diferentes
combinaciones de atributos, haciendo uso de la facilidad visualizeClusterAssignments
Por tanto podría concluirse que para este segundo algoritmo de agrupamiento por criterios
estadísticos y no de distancias entre vectores de atributos, predomina el agrupamiento de los
alumnos básicamente por tramos de calificaciones, independientemente de la opción, mientras que
en el anterior pesaba más el perfil de asignaturas cursado que las calificaciones.
Esta disparidad sirve para ilustrar la problemática de la decisión del criterio de “parecido” entre
instancias para realizar el agrupamiento.
1.4.3. 2. Ejemplo Agrupamiento simbólico
Finalmente, como alternativa a los algoritmos de agrupamiento anteriores, el agrupamiento
simbólico tiene la ventaja de efectuar un análisis cualitativo que construye categorías jerárquicas
para organizar los datos. Estas categorías se forman con un criterio probabilística de "utilidad",
llegando a las que permiten homogeneidad de los valores de los atributos dentro de cada una y al
mismo tiempo una separación entre categorías dadas por los atributos, propagándose estas
características en un árbol de conceptos.
Si aplicamos el algoritmo Cobweb con los parámetros por defecto sobre la muestra reducida de
instancias (dada la complejidad del algoritmo), el árbol generado llega hasta 800 nodos.
Vamos a modificar el parámetro cut-off, que
permite poner condiciones más restrictivas a la
creación de nuevas categorías en un nivel y
subcategorías.
La opción saveInstanceData es de gran utilidad
para después analizar la distribución de valores
de atributos entre las instancias de cada parte del
árbol de agrupamiento. Una vez ejecutado
Cobweb, genera un resultado como el siguiente:
-64-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Hay 3 grupos en un primer
nivel, y el segundo se
subdivide en otros dos. De
nuevo activando el botón
derecho sobre la ventana de
resultados, ahora podemos
visualizar el árbol
gráficamente:
Las opciones de visualización aparecen al pulsar el botón derecho en el fondo de la figura. Se
pueden visualizar las instancias que van a cada nodo sin más que pulsar el botón derecho sobre él.
Si nos fijamos en como quedan distribuidas las instancias por clusters, con la opción
visualizeClusterAssignments, llegamos a la figura:
-65-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Por tanto, vemos que de nuevo vuelve a pesar la opción como criterio de agrupamiento. Los nodos
hoja 1, 3, 4 y 5 se corresponden con las opciones cursadas 2, 3, 1 y 4 respectivamente. En un primer
nivel hay tres grupos, uno para la opción 2, otro para la opción 4 y otro que une las opciones 1 y 3.
Este último se subdivide en dos grupos que se corresponden con ambas opciones.
1.4.4. Búsqueda de Asociaciones
La cuarta pestaña (Asociate), muestra la ventana (figura 1.25) que nos permite aplicar métodos
orientados a buscar asociaciones entre datos. Los algoritmos de asociación permiten la búsqueda
automática de reglas que relacionan conjuntos de atributos entre sí. Son algoritmos no
supervisados, en el sentido de que no existen relaciones conocidas a priori con las que contrastar
la validez de los resultados, sino que se evalúa si esas reglas son estadísticamente significativas. Es
importante reseñar que estos métodos sólo funcionan con datos nominales.
Éste es sin duda el apartado más sencillo y más simple de manejar, carente de apenas opciones,
basta con seleccionar un método, configurarlo y verlo funcionar. La ventana de Asociación
(Associate en el Explorer), tiene los siguiente elementos:
-66-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Figura 1.25: El modo Asociación dentro del modo explorador.
El principal algoritmo de asociación implementado en WEKA es el algoritmo "Apriori". Este
algoritmo únicamente puede buscar reglas entre atributos simbólicos, razón por la que se requiere
haber discretizado todos los atributos numéricos.
1.4.4. 1. Ejemplo Búsqueda de Asociaciones
Por simplicidad, vamos a aplicar un filtro de discretización de todos los atributos numéricos en
cuatro intervalos de la misma frecuencia para explorar las relaciones más significativas. El
algoritmo lo ejecutamos con sus parámetros por defecto.
-67-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Las reglas que aparecen aportan poca información. Aparecen en primer lugar las relaciones triviales
entre asignaturas y opciones, así como las que relacionan suspensos en la prueba y en la
calificación final. En cuanto a las que relacionan alumnos presentados con idioma seleccionado son
debidas a la fuerte descompensación en el idioma seleccionado. La abrumadora mayoría de los
presentados a la prueba de idioma seleccionaron el inglés, como indica la figura siguiente:
-68-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Con objeto de buscar relaciones no conocidas, se filtrarán ahora todos los atributos relacionados
con descriptores de asignaturas y calificaciones parciales, quedando únicamente los atributos:
Año_académico
convocatoria
localidad
opcion1ª
cal_prueba
nota_bachi
En este caso, las reglas más significativas son:
1. nota_bachi='(8-inf)' 2129 ==> convocatoria=J 2105 conf:(0.99)
2. cal_prueba='(5.772-7.696]' nota_bachi='(6-8]' 2521 ==> convocatoria=J 2402
conf:(0.95)
3. cal_prueba='(5.772-7.696]' 4216 ==> convocatoria=J 3997 conf:(0.95)
Estas reglas aportan información no tan trivial: el 99% de alumnos con nota superior a 8 se
presentan a la convocatoria de Junio, así el 95% de los alumnos con calificación en la prueba entre
5.772 y 7. Es significativo ver que no aparece ninguna relación importante entre las calificaciones,
localidad y año de la convocatoria. También es destacado ver la ausencia de efecto de la opción
cursada.
Si preparamos los datos para dejar sólo cinco atributos,
Año_académico
convocatoria
localidad
opcion1ª
cal_final,
Con el último discretizado en dos grupos iguales (hasta 5.85 y 5.85 hasta 10), tenemos que de nuevo
las reglas más significativas relacionan convocatoria con calificación, pero ahora entran en juego
opciones y localidades, si bien bajando la precisión de las reglas:
1. opcion1ª=1 cal_final='(5.685-inf)' 2810 ==> convocatoria=J 2615 conf:(0.93)
2. localidad=LEGANES cal_final='(5.685-inf)' 2514 ==> convocatoria=J 2315 conf:(0.92)
3. Año_académico='(1998.4-2000.2]' cal_final='(5.685-inf)' 3175 ==> convocatoria=J 2890
conf:(0.91)
4. cal_final='(5.685-inf)' 9397 ==> convocatoria=J 8549 conf:(0.91)
5. opcion1ª=4 cal_final='(5.685-inf)' 2594 ==> convocatoria=J 2358 conf:(0.91)
6. Año_académico='(2000.2-inf)' cal_final='(5.685-inf)' 3726 ==> convocatoria=J 3376
conf:(0.91)
7. localidad=GETAFE cal_final='(5.685-inf)' 2156 ==> convocatoria=J 1951 conf:(0.9)
Al filtrar la convocatoria, que nos origina relaciones bastante evidentes, tendremos las reglas más
significativas entre localidad, año, calificación y opción. Como podemos ver, al lanzar el algoritmo
con los parámetros por defecto no aparece ninguna regla. Esto es debido a que se forzó como
umbral mínimo aceptable para una regla el 90%. Vamos a bajar ahora este parámetro hasta el 50%:
-69-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Best rules found:
1. opcion1ª=4 5984 ==> cal_final='(-inf-5.685]' 3390 conf:(0.57)
2. opcion1ª=1 5131 ==> cal_final='(5.685-inf)' 2810 conf:(0.55)
3. Año_académico='(2000.2-inf)' 7049 ==> cal_final='(5.685-inf)' 3726 conf:(0.53)
4. opcion1ª=2 4877 ==> cal_final='(5.685-inf)' 2575 conf:(0.53)
5. localidad=GETAFE 4464 ==> cal_final='(-inf-5.685]' 2308 conf:(0.52)
6. localidad=LEGANES 4926 ==> cal_final='(5.685-inf)' 2514 conf:(0.51)
7. Año_académico='(1998.4-2000.2]' 6376 ==> cal_final='(-inf-5.685]' 3201 conf:(0.5)
Por tanto, forzando los términos, tenemos que los estudiantes de las 2 primeras opciones tienen
mayor probabilidad de aprobar la prueba, así como los estudiantes de la localidad de Leganés. Los
estudiantes de Getafe tienen una probabilidad superior de obtener una calificación inferior. Hay que
destacar que estas reglas rozan el umbral del 50%, pero han sido seleccionadas como las más
significativas de todas las posibles. También hay que considerar que si aparecen estas dos
localidades en primer lugar es simplemente por su mayor volumen de datos, lo que otorga una
significatividad superior en las relaciones encontradas.
Si se consulta la bibliografía, el primer criterio de selección de reglas del algoritmo "A priori" es la
precisión o confianza, dada por el porcentaje de veces que instancias que cumplen el antecedente
cumplen el consecuente, pero el segundo es el soporte, dado por el número de instancias sobre las
que es aplicable la regla. En todo caso, son reglas de muy baja precisión y que habría que considerar
simplemente como ciertas tendencias.
-70-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
1.4.5. Selección de Atributos
Esta sección permite automatizar la búsqueda de subconjuntos de atributos más apropiados para
"explicar" un atributo objetivo, en un sentido de clasificación supervisada: permite explorar qué
subconjuntos de atributos son los que mejor pueden clasificar la clase de la instancia.
Esta selección "supervisada" aparece en contraposición a los filtros de preprocesado comentados en
la sección 1.4.2, que se realizan de forma independiente al proceso posterior, razón por la que se
etiquetaron como "no supervisados".
La pestaña Select Atributes nos permite acceder al área de selección atributos (figura 2.26). El
objetivo de estos métodos es identificar, mediante un conjunto de datos que poseen unos ciertos
atributos, aquellos atributos que tienen más peso a la hora de determinar si los datos son de una
clase u otra.
La selección supervisada de atributos tiene dos componentes:
Método de Evaluación (Attribute Evaluator): es la función que
determina la calidad del conjunto de atributos para discriminar
la clase.
Método de Búsqueda (Search Method): es la forma de realizar
la búsqueda de conjuntos. Como la evaluación exhaustiva de
todos los subconjuntos es un problema combinatorio
inabordable en cuanto crece el número de atributos, aparecen
estrategias que permiten realizar la búsqueda de forma eficiente
De los métodos de evaluación, podemos distinguir dos tipos: los métodos que directamente utilizan
un clasificador específico para medir la calidad del subconjunto de atributos a través de la tasa de
error del clasificador, y los que no.
- Los primeros, denominados métodos "wrapper", porque "envuelven" al clasificador para explorar
la mejor selección de atributos que optimiza sus prestaciones, son muy costosos porque necesitan
un proceso completo de entrenamiento y evaluación en cada paso de búsqueda.
- Entre los segundos podemos destacar el método "CfsSubsetEval", que calcula la correlación de la
clase con cada atributo, y eliminan atributos que tienen una correlación muy alta como atributos
redundantes.
En cuanto el método de búsqueda, vamos a mencionar por su rapidez el "ForwardSelection", que es
un método de búsqueda subóptima en escalada, donde elije primero el mejor atributo, después
añade el siguiente atributo que más aporta y continua así hasta llegar a la situación en la que añadir
un nuevo atributo empeora la situación. Otro método a destacar sería el "BestSearch", que permite
buscar interacciones entre atributos más complejas que el análisis incremental anterior. Este
método va analizando lo que mejora y empeora un grupo de atributos al añadir elementos, con la
posibilidad de hacer retrocesos para explorar con más detalle. El método "ExhaustiveSearch"
simplemente enumera todas las posibilidades y las evalúa para seleccionar la mejor
Por otro lado, en la configuración del problema debemos seleccionar qué atributo objetivo se
utiliza para la selección supervisada, en la ventana de selección, y determinar si la evaluación se
realizará con todas las instancias disponibles, o mediante validación cruzada.
-71-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Los elementos por tanto a configurar en esta sección se resumen en la figura siguiente
Figura 2.26: El modo de Selección de Atributos dentro del modo explorador
Para empezar un método de selección de atributos lo primero es seleccionar el método de evaluación de atributos, encargado de evaluar cada uno de los casos a los que se le enfrente y dotar a
cada atributo de un peso específico. El funcionamiento para seleccionar este método es el mismo
que con otros métodos en Weka, se selecciona el método con el botón Choose situado dentro del
cuadro Attribute evaluator. Una vez seleccionado podemos acceder a las propiedades del mismo
pulsando sobre el nombre de la etiqueta que muestra el nombre del método seleccionado.
El siguiente paso será elegir el método de búsqueda encargado de generar el espacio de pruebas. El
funcionamiento es el mismo al caso anterior.
Una vez seleccionado el método de evaluación y el de generación del espacio de pruebas sólo falta
elegir el método de prueba, el atributo que representa la clasificación conocida y pulsar Start.
Una vez acabado el experimento pulsando el botón secundario sobre la etiqueta del experimento en
la lista de experimentos realizados tenemos la opción de Visualize Reduced Data, que nos mostrará
los datos habiendo tomado los mejores atributos en una ventana como la del modo Visualización
(visualize).
La caja “Attribute Selections Mode” tiene dos opciones:
(worth of the attribute subset): el peor de los subconjuntos de atributos es
determinado usando el conjunto de entrenamiento de datos total (full set of training data).
: el peor de los subconjuntos de atributos está determinado por un proceso de
validación cruzada (cross-validation). Los compás “Fold” y “Seed” especifica el número de
registros (“Folds”) a usar y el “Random seed” organiza los datos.
-72-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Al igual que “Classify” existe un cuadro drop down donde se pueden especificar qué atributos tratar
(which attribute to treat as the class).
1.4.5.1. Ejemplo Selección de Atributos
Siguiendo con nuestro ejemplo, vamos a aplicar búsqueda de atributos para "explicar" algunos
atributos objetivo. Para obtener resultados sin necesidad de mucho tiempo, vamos a seleccionar los
algoritmos más eficientes de evaluación y búsqueda, CsfSubsetEval y ForwardSelection
Por ejemplo, para la calificación final tenemos 8 atributos
seleccionados:
Selected attributes: 5,6,7,10,12,14,17,18 : 8
nota_Lengua
nota_Historia
nota_Idioma
calif_asig1
calif_asig2
calif_asig3
cal_final
Presentado
y para la opción 1 atributo:
Selected attributes: 9 : 1
des_asig1
Por tanto, hemos llegado a los atributos que mejor explican ambos (la calificación en la prueba
depende directamente de las parciales, y la opción se explica con la 1ª asignatura), si bien son
relaciones bastante triviales. A continuación preparamos los datos para buscar relaciones no
conocidas, quitando los atributos referentes a cada prueba parcial. Dejando como atributos de la
relación:
Attributes: 7
Año_académico, convocatoria, localidad, opcion1ª, cal_prueba,
nota_bachi, Presentado
Para la calificación final llegamos a 2 atributos:
y para la opción 2:
Selected attributes: 6,7 : 2
nota_bachi
Presentado
Selected attributes: 3,5,6 : 3
localidad
cal_prueba
nota_bachi
No obstante, si observamos la figura de mérito con ambos problemas, que aparece en la ventana
textual de resultados, vemos que este segundo es mucho menos fiable, como ya hemos comprobado
en secciones anteriores.
1.4.6. Visualización
Una de las primeras etapas del análisis de datos puede ser el mero análisis visual de éstos, en
ocasiones de gran utilidad para desvelar relaciones de interés utilizando nuestra capacidad para
comprender imágenes. La herramienta de visualización de WEKA permite presentar gráficas 2D
que relacionen pares de atributos, con la opción de utilizar además los colores para añadir
información de un tercer atributo. Además, tiene incorporada una facilidad interactiva para
seleccionar instancias con el ratón.
-73-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Figura 1.27: El modo de Visualización dentro del modo explorador.
El modo visualización (figura 1.27) es un modo que muestra gráficamente la distribución de todos
los atributos mostrando gráficas en dos dimensiones, en las que va representando en los ejes todos
los posibles pares de combinaciones de los atributos. Este modo nos permite ver correlaciones y
asociaciones entre los atributos de una forma gráfica.
Pulsando doble click sobre cualquier gráfica se nos mostrará en una ventana nueva con el interfaz
para gráficas que ya explicamos cuando vimos las opciones de visualización en la lista de
resultados, una vez generado los modelos. Las opciones que ofrece este modo se activan mediante
las barras deslizantes. Las posibles opciones son:
-
define el tamaño del lado de cada una de las gráficas en píxeles, de 50 a 500.
define el tamaño del punto expresado en píxeles, de 1 a 10.
Añade un ruido aleatorio a las muestras, de manera que espacia las muestras que están físicamente muy próximas, esto tiene útilidad cuando se concentran tanto los puntos que no es
posible discernir la cantidad de éstos en un área.
-74-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Una vez seleccionados los cambios es imprescindible pulsar el botón Update para que se
representen de nuevo las gráficas. Otro botón útil, es el Select Atributes, que nos permite elegir los
atributos que se representarán en las gráficas. El último botón que se encuentra en esta ventana es el
Subsample que permite definir el tanto por ciento de muestras (que escogerá aleatoriamente) que
queremos representar.
Cambiando la Visual
Los puntos de los datos estarán ploteados en el área principal de la ventana. En la parte superior
hay dos botones de listas (drop down) para seleccionar los ejes del gráfico.
El de la izquierda, muestra los atributos del eje X, y el de la derecha el atributo del eje Y. En el
selector del eje X, existe una lista para seleccionar colores, esto permite cambiar el color de los
puntos basados en algún atributo seleccionado.
Bajo el área de graficado, existe una leyenda que describe qué significa cada color en la gráfica. Si
los valores son discretos, se pueden modificar los colores de cada uno haciendo click en ellas, y
haciendo una correcta selección en las ventanas emergentes.
A la derecha del área del gráfico existen una serie de “strips” horizontales, donde cada uno de estos
strips representa un atributo y los puntos muestran la distribución de los valores del atributo. Estos
valores están azarosamente “scattered” verticalmente, para ayudar a ver los puntos de
concentración. Se puede seleccionar qué ejes serán usados en el gráfico principal haciendo click en
las “strips”.Haciendo click izquierdo en los strip de atributos cambia el eje X para ese atributo, y
el eje Y, se cambia haciendo click derecho. Los ejes están marcados con las letras X e Y para
identificarlas. Sobre los strips de atributos, se muestra un “slider” (barra de deslizamiento) llamado
“jitter” que es un despliegue azaroso dado a todos los puntos de la gráfica. Arrastrándolo
(dragging) a la derecha aumenta el tamaño de “jitter”, que es útil para probar las concentraciones
de los puntos. Sin jitter millones de instancias no se verán diferentes (en un mismo punto o como
una sola instancia).
Seleccionan Instancias
Hay situaciones que es de ayuda seleccionar un subconjunto de datos al usar una herramienta de
visualización. Un caso especial de esto es el “User Classiffier”, que permite crear un clasificador
propio por medio de selecciones interactivas.
Bajo el botón selector del eje Y, existe un botón lista (drop down) para elegir un método de
selección. Un grupo de datos pueden seleccionarse de cuatro maneras:
Select instance: haciendo click en un punto individual genera una ventana que lista los
atributos. Si hay más de un punto en el mismo lugar, más de una lista aparecerá.
Rectangle: se puede crear un rectángulo arrastrando, así se seleccionan los puntos dentro de él.
Poligon: se puede crear un polígono de cualquier forma, que selecciona los puntos dentro de él.
Haciendo click izquierdo para agregar vértices del polígono y click derecho para completarlo. El
polígono se cerrará por orden de generar los puntos.
Polyline: se pueden generar líneas que distinguen los puntos de un lado y del otro. Haciendo
click izquierdo para fijar las vértices de las líneas y click derecho para terminar. En este caso
las figuras son abiertas.
-75-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Cuando el área graficada fue seleccionada con reclangle, polygon o polyline se torna gris. En este
momento al hacer click en el botón “submit” remueve todas las instancias de la gráfica excepto las
que están grises (áreas de selección). Haciendo click en botón “clear” borra el área de selección no
afectando la gráfica.
Cuando cualquier punto ha sido removido de la gráfica el botón “submit” cambia a botón “reset”.
Este botón deja sin efecto los actos previos de remover, y retorna al gráfico original con todos los
puntos incluidos. Finalmente, haciendo click en el botón “save” permite guardar las instancias
visibles en un archivo nuevo de extención. ARFF.
1.4.6. 1. Ejemplo Representación 2D de los datos
Las instancias se pueden visualizar en gráficas 2D que relacionen pares de atributos. Al seleccionar
la opción Visualize del Explorer aparecen todas los pares posibles de atributos en las coordenadas
horizontal y vertical. La idea es que se selecciona la gráfica deseada para verla en detalle en una
ventana nueva. En nuestro caso, aparecerán todas las combinaciones posibles de atributos.
Como primer ejemplo vamos a visualizar el rango de calificaciones finales de los alumnos a lo
largo de los años, poniendo la convocatoria (junio o septiembre) como color de la gráfica.
Vamos a visualizar ahora dos variables cuya relación es de gran interés, la calificación de la prueba
en función de la nota de bachillerato, y tomando como color la convocatoria (junio o septiembre).
-76-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
En esta gráfica podemos apreciar la relación entre ambas magnitudes, que si bien no es directa al
menos define una cierta tendencia creciente, y como la convocatoria está bastante relacionada con
ambas calificaciones.
Cuando lo que se relacionan son variables simbólicas, se presentan sus posibles valores a lo largo
del eje. Sin embargo, en estos casos todas las instancias que comparten cada valor de un atributo
simbólico pueden ocultarse (serían un único punto en el plano), razón por la que se utiliza la
facilidad de Jitter. Esta opción permite introducir un desplazamiento aleatorio (ruido) en las
instancias, con objeto de poder visualizar todas aquellas que comparten un par de valores de
atributos simbólicos, de manera que puede visualizarse la proporción de instancias que aparece en
cada región.
A modo de ejemplo se
muestra a continuación la
relación entre las tres
asignaturas optativas, y con
la opción cursada como
color
-77-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Puede verse una marcada
relación entre las asignaturas
opcionales, de manera que
este gráfico ilustra qué tipo
de asignaturas engloba cada
una de las cinco posibles
opciones cursadas.
Se sugiere preparar el siguiente gráfico, que relaciona la calificación obtenida en la prueba con la
localidad de origen y la nota de bachillerato, estando las calificaciones discretizadas en intervalos
de amplitud 2.
-78-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Aquí el color trae más información, pues indica en cada intervalo de calificaciones de la prueba, la
calificación en bachillerato, lo que permite ilustrar la "satisfacción" con la calificación en la prueba
o resultados no esperados, además distribuido por localidades.
1.4.6. 2. Ejemplo Filtrado “gráfico” de los datos
WEKA permite también realizar filtros de selección de instancias sobre los propios gráficos, con
una interacción a través del ratón para aislar los grupos de instancias cuyos atributos cumplen
determinadas condiciones. Esta facilidad permite realizar filtrados de instancias de modo interactivo
y más intuitivo que los filtros indicados en la sección 1.4.2.2.
Por ejemplo, a continuación se
indica la selección de alumnos
que obtuvieron una calificación
por debajo de sus expectativas
(calificación en la prueba
inferior a su nota en el
bachillerato), con la opción
Polygon.
Una vez realizada la selección,
la opción Submit permite
eliminar el resto de instancias, y
Save almacenarlas en un fichero.
Reset devuelve la relación a su
estado original.
Utilice
estas
facilidades
gráficas
para
hacer
subconjuntos de los datos con
los alumnos aprobados de las
opciones 1 y 2 frente a los de
las opciones 3, 4 y 5. Salve las
relaciones filtradas para a
continuación cargarlas y
mostrar los histogramas, que
aparecerán como se indica en
la figura siguiente.
-79-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
1.5. EXPERIMENTER
El modo experimentador (Experimenter) es un modo muy útil para aplicar uno o varios métodos de
clasificación sobre un gran conjunto de datos y, luego poder realizar contrastes estadísticos entre
ellos y obtener otros índices estadísticos.
1.5.1.
Configuración
Una vez abierto el modo experimentador obtendremos una ventana como la de la figura 1.27, que
corresponde a la sección Setup. Por defecto19 el modo experimentador está configurado en modo
simple, no obstante, esto puede variarse a modo avanzado pulsando el botón circular acompañado
con la etiqueta Advanced. Para empezar se explicará el modo simple y posteriormente se pasará a
explicar el modo avanzado.
Figura 1.27: El modo Experimentador, modo simple20
19
20
Hay diferentes versiones de Weka que se pueden conseguir en la red, por ser un programa de código
abierto, alguna instituciones o universidades ofrecen versiones mejordas. Es por esto que las ventanas y
cuadro de dialogo pueden variar.
Versión mejorada de la Universitat Politècnica de València, esta versión es la que se adjunta a estos
apuntes.
-80-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Lo primero a realizar es definir un fichero configuración que contendrá todos los ajustes, ficheros
involucrados, notas, etc, pertenecientes a un experimento. Con el botón Open podemos abrir uno ya
creado pero también podremos crear uno nuevo con el botón New. Una vez creado podemos
guardarlo (Weka por defecto no guarda nada), para lo que usaremos el botón Save21.
El siguiente paso es decidir dónde queremos almacenar los resultados, si es que queremos hacerlo.
En caso de decantarnos por no hacerlo, aunque Weka lo permite, luego no se podrán ver los
resultados obtenidos. Podemos archivar el resultado del experimento de tres formas distintas, en un
fichero ARFF, en un fichero CSV y en una base de datos. Para ello, simplemente debemos
seleccionar la opción que corresponda dentro del cuadro Results Destination y a continuación
elelegira ruta lógica dónde guardar dicho resultado.
Lo siguiente es definir el tipo de validación que tendrá el experimento, al igual que en el modo
explorer, tenemos tres tipos de validación: validación-cruzada estratificada, entrenamiento con un
porcentaje de la población tomando ese porcentaje de forma aleatoria y entrenamiento con un
porcentaje de la población tomando el porcentaje de forma ordenada.
Una vez completados los anteriores pasos, deberemos indicar a Weka qué archivos de datos
queremos que formen parte de nuestro experimento. Para ello en el cuadro Datasets tenemos un
botón llamado Add new... que nos permite especificar un archivo de datos a añadir o bien,
seleccionando un directorio, nos añadirá todos los archivos que contengan ese directorio de forma
recursiva. Junto a ese botón se encuentra la opción Use relative paths, que se utiliza para indicar a
Weka que almacene las referencias a los ficheros como referencias relativas no indirectas. Puede ser
útil si deseamos repetir el experimento en otro ordenador distinto con una estructura de ficheros
distinta.
En el cuadro denominado Iteration control definiremos el número de repeticiones de nuestro experimento, especificando si queremos que se realicen primero los archivos de datos o los
algoritmos. Debajo de este cuadro se encuentra la sección de algoritmos en el que con el botón Add
new... podremos añadir los algoritmos que ququeramos. Si queremos borrar alguno le
seleccionamos y pulsamos el botón Delete selected.
Si se desea se pueden añadir comentarios y notas al experimento; para ello, Weka dispone de un
cuadro de texto en la parte inferior de la ventana.
Con esto ya estaría configurado un experimento en modo simple. En el modo Advanced hay ciertas
diferencias tanto en los botones (ver figura 2.28) como en el uso.
21 Es importante señalar que aunque hayamos guardado una vez, cada vez que se realice un
cambio deberemos volver a guardar los cambios con Save
-81-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Figura 1.28: El modo experimentador, modo Advanced.
La principal diferencia es que el funcionamiento de este modo está orientado a realizar tareas específicas más concretas que un experimento normal, y una cierta funcionalidad existente en el
modo simple se ha traslado al modo avanzado, mostrándola más concreta y explícita al usuario.
El cuadro Destination especifica dónde guardará Weka el resultado del experimento. Su funcionalidad es la misma que la del modo simple, pero no su funcionamiento. En este caso deberemos
pulsar Choose y elegir en el árbol el tipo de método a utilizar para exportar los resultados (Base de
datos, fichero ARFF o fichero CSV). Una vez elegido pulsando sobre la etiqueta que indica el
método usado, se abrirá una ventana desplegable en donde configuraremos dicho método. Aunque
pueda parecer una complicación el cambio en la interfaz para realizar esta operación, ésta segunda
permite la adición de nuevos métodos sin variar la interfaz original.
-82-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Figura 1.29: 22Configuración de un experimento.
Ahora el cambio fundamental entre una interfaz y otra se basa en el Result Generator. En este
nuevo modo es necesario seleccionar con el botón Choose qué método generador de resultados
utilizaremos y seguidamente configurarle. Para ello es necesario seguir siempre el mismo
procedimiento, pulsar doble click sobre la etiqueta que identifica el método elegido.
Los 5 métodos que permite seleccionar Weka son:
CrossValidationResultProducer Genera resultados fruto de una validación cruzada. Tiene por
opciones:
- numfolds El número de particiones para la validación cruzada.
- outputFile Fichero donde queremos guardar cada una de las particiones que se realizarán en la
validación cruzada. Lo guarda codificado en formato Zip.
Nota: Weka tiene un “fallo” y éste es que al abrir la ventana de diálogo para seleccionar el fichero donde
queremos guardar, al elegir uno y pulsar Select, lo selecciona pero no cierra dicha ventana. Es por tanto
necesario pulsar Select y seguidamente cerrar la ventana.
- rawOutput Guarda los resultados “tal cual”, es decir sin ningún formato fijo. Esta opción es
interesante si queremos buscar errores en el programa (debug mode).
- splitEvaluator El método que seleccionemos para evaluar cada una de las particiones de la
validación cruzada. En él especificaremos, de la manera habitual, el clasificador a usar.
22
Utilizaremos una versión básica de Weka, más simple. Esta sólo posee 3 de las 4 internases. Se adjunta
con el material, solo se debe ejecutar el archivo weka intro.jar
-83-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
AveragingResultProducer Toma los resultados de un método generador de resultados (como
podría ser el anterior explicado, CrossValidationResultProducer) y cácalculaos promedios de
los resultados. Es útil, por ejemplo, para realizar una validación cruzada de muchas particiones
por separado y hallar los promedios. Tiene las siguientes opciones:
- calculateStdDevs Seleccionado calcula las desviaciones estándar.
- expectedResultsPerAverage Se elije el número de resultados que se esperan, para dividir la suma
de todos los resultados entre este número. Si por ejemplo realizamos una validación cruzada de 10
particiones y asignamos el valor de 10 nos dividirá el resultado de las sumas de cada partición
entre 10, es decir, en este caso la media aritmética.
- keyFieldname En esta opción se selecciona el campo que será distintivo y único de cada
repetición. Por defecto es “Fold” ya que cada repetición será de una partición distinta (Fold).
- resultProducer el método generador de resultados del que tomará los datos.
LearningRateResultProducer Llama a un método generador de resultados para ir repitiendo
el experimento variando el tamaño del conjunto de datos. Habitualmente se usa con un Avera
gingResultProducer y CrossValidationResultProducer para generar curvas de aprendizaje. Sus
opciones son:
- lowersize Selecciona el número de instancias para empezar. Si es 0 se toma como mínimo el
tamaño de stepSize.
- resultProducer Selecciona el método generador de resultados. Habitualmente para hacer curvas
de aprendizaje se usa el AveragingResultProducer.
- setsize Número de instancias a añadir por iteración.
- upperSize Selecciona el número máximo de instancias en el conjunto de datos. Si se elije -1 el
límite se marca en el número total de instancias.
RandomSplitResultProducer Genera un conjunto de entrenamiento y de prueba aleatorio para un
método de clasificación dado.
- outputfile Al igual que antes define el archivo donde se guardarán los resultados.
- randomizeData Si lo activamos cogerá los datos de forma aleatoria.
- rawOutput Activado proporciona resultados sin formato útiles para depurar el programa.
- splitEvaluator Selecciona el método de clasificación a usar.
- trainPercent Establece el porcentaje de datos para entrenar la muestra
DatabaseResultProducer De una base de datos toma los resultados que coinciden con los obtenidos
con un método generador de resultados (cualquiera de los anteriores). Si existen datos que no
aparezcan en la base de datos se calculan.
- cacheKeyName Selecciona el nombre del campo de la base de datos a utilizar para formar una
caché de la que coger los datos.
- databaseURL Dirección de la base de datos.
- resultproducer Método generador de resultados a utilizar.
- username Nombre de usuario para acceder a la base de datos.
- password Contraseña para acceder a la base de datos.
-84-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Una vez que ya está configurado el Result Generator podemos utilizar el Generator properties para
configurar de una forma más sencilla los parámetros seleccionados en el Result Generator. Para
activarlo, simplemente es necesario pulsar el botón que dentro del campo Generator properties
pone Disabled (desactivado). Una vez pulsado habrá pasado a Enabled (activado).
Una vez seleccionado aparecerá una figura 2.30, en la que podremos seleccionar (marcar con el
ratón y pulsar Select) algún atributo de los posibles del método. Una vez hecho esto, aparecerá en el
recuadro inferior, donde estaba el botón de activación, el valor actual de dicha variable. Escribiendo
un nuevo valor y pulsando Add podemos añadir uno o más valores y, seleccionándolos y pulsando
Delete borrarlos. Con el botón Select property. . . seleccionamos otros atributos.
Figura 1.30: Configurando las opciones de un método de generación de resultados.
En el caso de que el atributo a modificar sea un método, aparecerá un botón llamado Choose que
nos permitirá seleccionarlo y modificarlo. Esto es particularmente útil si queremos repetir un
experimento con varios clasificadores, pues seleccionado el atributo del clasificador a usar, con ese
menú podemos añadir tantos como queramos.
El cuadro runs permite seleccionar las iteraciones con la que se realizará el experimento.
1.5.1.1.
Weka distribuido
Una de las características más interesantes del modo experimentador es que permite distribuir la
ejecución de un experimento entre varios ordenadores mediante Java RMI. El modelo usado es el
cliente-servidor.
Como primer paso configuraremos un servidor para después explicar la configuración de los
clientes.
-85-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Configuración del Servidor
Los elementos a configurar en el servidor son los mismos que cualquier otro experimento pero
además de esto debemos activar el botón de activación del cuadro Distribuye experiment. Una vez
activado es necesario elegir el tipo de distribución, por fichero de datos (by data set), o por iteración
(by run). Un buen consejo es que cuando el número de archivos en el que realizar los experimentos
es pequeño la distribución se haga por iteraciones, ya que distribuirá cada una de las tareas
fundamentales de un experimento (por ejemplo, en una validación cruzada cada una de las
particiones); sin embargo, si usamos un conjunto de archivos grande es recomendable el uso de una
distribución por archivos.
Una vez seleccionado pulsaremos en el botón Hosts y obtendremos una ventana como la figura
2.31.
Figura 2.31: El modo experimentador, configuración de un experimento distribuido
En esta ventana introduciremos en la etiqueta cada uno de los ordenadores que queramos añadir y
con el enter lo añadiremos. También seleccionando una IP y pulsando Delete Selected nos da la
opción a borrar un host determinado. Para aceptar los cambios con cerrar la ventana es suficiente.
Con esto ya queda configurado el ordenador que actuará de servidor para la aplicación distribuida.
-86-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Configuración de un ordenador cliente
Lo primero es copiar el archivo remoteExperimentServer.jar situado en la carpeta raíz de Weka, en
el ordenador que actuará como cliente. Dicho archivo se encuentra codificado en Jar23 pero
debemos desempaquetarlo. Para ello se utiliza el siguiente mandato24
jar xvf remoteExperimentServer.jar
Con esto queda desempaquetado el archivo remoteExperimentServer.jar en el directorio actual.
Con esta operación habremos obtenido 3 ficheros: remoteEngine.jar, remote.policy y
DatabaseUtils.props. A continuación se hace una breve descripción de los mismos:
− DatabaseUtils.props Habitualmente, cuando se realiza un experimento distribuido lo normal y
más cómodo es que los datos estén en una base de datos común a todos los ordenadores que
participen en la ejecución del experimento. En este archivo se definen las bases de datos jdbc25,
en él lo primero que definiremos es el controlador (driver) de jdbc que utilizaremos, que
dependerá de la base de datos a utilizar. Las líneas que comiencen con “#” son comentarios. Lo
siguiente será determinar la dirección por la que son accesibles los datos.
− remote.policy Archivo que define la política de seguridad. En él se definen las restricciones de
acciones a realizar, los puertos y host a utilizar, etc.
− remoteEngine.jar Archivo jar en el que se encuentra el cliente para realizar experimentos de
forma remota.
Una vez configurados DatabaseUtils.props y remote.policy el siguiente paso es ejecutar el cliente,
para ello haremos uso del mandato (todo es la misma línea):
java -classpath remoteEngine.jar:/controlador_jdbc \ Djava.security.policy=remote.policy \ -Djava.rmi.server.codebase=
file:/ruta_al_dir_actual/remoteEngine.jar \ weka.experiment.RemoteEngine
Con esto ya estaría configurado y funcionando un cliente. El siguiente paso sería añadir tantos
clientes como deseemos.
23
24
25
Java ARchives. Este formato de archivos permite empaquetar multitud de ficheros en uno solo para poder
almacenar aplicaciones con muchos archivos y que su intercambio y ejecución sea más sencillo.
Se entiende que la máquina cliente tiene la máquina virtual Java correctamente instalada
jdbc es una tecnología que permite la interconexión de bases de datos con aplicaciones Java
-87-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
1.5.2.
Ejecución
La ventana para comenzar la ejecución del
experimento se obtiene pulsando la
segunda pestaña superior, etiquetada como
Run, obtendremos una ventana que será
similar a la de la figura 1.32.
Figura 1.32: El modo experimentador,
ventana de ejecución del experimento.
El funcionamiento es obvio, pulsar el
botón Start para comenzar el experimento
y el botón Stop si queremos detenerle en
plena ejecución. Un detalle importante es
que los experimentos no se pueden parar y
luego continuar en el punto en que se
pararon.
1.5.3.
Análisis de resultados
Pulsando la pestaña Analyse entraremos la
sección dedicada a analizar los datos
(figura 2.33). Ésta nos permite ver los
resultados de los experimentos, realizar
contrastes estadísticos, etc.
Figura 1.33: El modo experimentador,
ventana de análisis de resultados.
Lo primero a definir es el origen de los
datos de los resultados, con los botones
File, Database o Experiment (este último
procesa los resultados del experimento que
está actualmente cargado26).
Una vez hecho esto definiremos el test que queramos realizar; para ello, utilizaremos las opciones
que nos ofrece el cuadro Configure test. A continuación se realiza una breve descripción de las
mismas:
− Row key fields Selecciona el atributo o atributos que harán de filas en la matriz de resultados.
− Run fields Define el atributo que identifica cada una de las iteraciones.
− Column key fields Selecciona los atributos que actuarán de columnas en la matriz de resultados.
− Comparison fields El atributo que va a ser comparado en el contraste.
− Significance Nivel de significación para realizar el contraste estadístico. Por defecto es el 0,05.
26 Es importante señalar que para poder cargar los resultados de un experimento procesado es
necesario que hayamos definido un fichero de resultado de los datos
-88-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
− Test base Seleccionamos qué algoritmo de los utilizados (o el resumen, o el ranking) utilizaremos
de base para realizar el test.
− Show std. deviations Muestra las desviaciones estándar.
Una vez configurado ya sólo queda utilizar el botón Perform test con el que se realizará el test de la
t de Student, mostrando el resultado en el cuadro denominado Test Output. Con el botón Save
Output se permite guardar el contenido de la salida del test en un fichero de texto. También, si en la
lista de resultados pulsamos el botón secundario del ratón sobre algún elemento, nos mostrará el
resultado de ese test en una ventana separada.
Por ejemplo, queremos realizar una comparación entre dos clasificadores, ambos mediante SVM,
uno con el kernel lineal y otro gaussiano. Queremos comprobar si hay diferencias significativas
entre ambos métodos clasificando sobre la base de datos iris.arff que incluye Weka en el directorio
data. Para ello una vez realizado el experimento, en el modo análisis de resultados, realizamos un
test al 0,05 de confianza, comparando como atributo el porcentaje de acierto (percent correct) de
ambos clasificadores.
Realizamos el test y obtendremos un resultado como el siguiente:
Como se puede observar en la
línea 10, SVM con kernel
lineal (función 1) obtiene un
96,27 % (DE. 4,58) de acierto
frente a los 88,07 % (DE.
12.62) que se obtienen con un
kernel gaussiano. A la derecha
del todo aparece un asterisco
eso significa que el elemento a
comparar es Peor que el elemento base. Si hubiera
aparecido una “v” significaría
lo contrario.
Por tanto, concluimos que hay diferencias significativas entre ambos métodos. Además, en la línea
12, aparece un indicador del tipo (0/0/1) siendo (xx,yy,zz), xx el número de veces que el elemento a
comparar es mejor que el base, yy el número de veces que son iguales, y zz el número de veces que
es peor. En este caso sólo aparece un 1, debido a que sólo hemos comparado una medida, el
porcentaje de aciertos.
-89-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
1.6. KNOWLEDGE FLOW
Esta última interface de Weka es quizá la más cuidada y la que muestra de una forma más explícita
el funcionamiento interno del programa. Su funcionamiento es gráfico y se basa en situar en el
panel de trabajo (zona gris de la figura 2.34), elementos base (situados en la parte superior de la
ventana) de manera que creemos un “circuito” que defina nuestro experimento.
Figura 1.34: El modo Knowledge flow.
Para explicar este modo de funcionamiento se recurrirá a un ejemplo. Supongamos que queremos
clasificar mediante máquinas de vectores soporte la muestra (iris.arff) situada en el directorio data/
del programa.
Lo primero será añadir a nuestro “circuito” una fuente de los datos. Éstas se encuentran en el
apartado Datasources en la parte superior (ver figura 1.35) donde se puede observar que hay
cargadores de datos para arff, csv, c45 e instancias serializadas; no obstante, no los hay para bases
de datos. Esto es porque Weka es un programa en desarrollo y esta característica aún no está
implementada en el modo Knowledge flow.
Figura 1.35: Apartado Datasources
En este ejemplo utilizaremos el cargador arffloader. Para utilizarlo pulsaremos sobre él (ver figura
1.36), el icono del ratón pasará a convertirse en una cruz y podremos situar en la zona de trabajo
(zona gris) nuestro cargador. En cualquier momento, con el ratón, podremos arrastrarlo y situarlo
dónde creamos conveniente.
-90-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Figura 1.36: Icono del arffloader
Una vez lo hayamos situado es necesario configurarlo. Para ello, pulsando el botón secundario del
ratón aparecerá un menú desplegable con varias opciones. Para configurar el archivo arff que
cargará, pulsamos en edit/configure y aparecerá una ventana en la que seleccionaremos el archivo
pulsando doble click en la etiqueta del archivo. Hecho esto aparecerá una nueva ventana
desplegable. En nuestro caso accederemos a iris.arff. Si queremos borrar la configuración realizada
repetiremos el procedimiento anterior, pulsando en edit/delete.
Figura 1.37: Configurar el archivo arff
El siguiente paso será definir cuál es el atributo que define la clasificación correcta (habitualmente
suele ser el último). Para ello haremos uso del objeto Class asigner dentro de Evaluation que
realiza esta tarea. Lo situamos en la zona de trabajo y lo configuramos de la misma forma que el
objeto anterior.
-91-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Figura 1.38: Cargar el método de ClassAsigner.
Una vez ambos objetos estén situados y configurados deberemos unirles de manera que los datos
fluyan entre ambos. Abrimos el menú de opciones del cargador (botón secundario sobre el elemento
arffloader) y mediante la opción connection/dataset, Weka nos permitirá dibujar una flecha que
una ambos objetos (figura 1.39). Si queremos eliminarla pulsaremos el botón secundario sobre la
flecha y con la opción Delete será eliminada.
Figura 1.39: Knowledge flow. El Origen de los datos ya está definido.
En este punto, ya está definido por completo el origen de los datos. El siguiente hito será conseguir
realizar una validación cruzada que enfrentar al clasificador. Para ello existe el objeto
Crossvalida-tionfoldmaker dentro de Evaluation, que será el encargado de realizarnos cada una de
las particiones de la validación cruzada. Para configurarlo se utiliza el mismo sistema que antes,
pulsar botón secundario y configure. Para conectar el ClassAsigner con el
Crossvalidationfoldmaker, seleccionamos la opción connections/dataset y dibujamos una flecha al
igual que antes.
-92-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Figura 1.40: La validación ya está definido.
Ya sólo quedan añadir dos objetos más, el clasificador y algún objeto que nos facilite el resultado,
bien sea en modo texto o gráfico. A modo de ejemplo añadiremos dos clasificadores SVM con
distintos parámetros. Los objetos que corresponden a los clasificadores se encuentran en el apartado
Classifiers y son en este caso los SMO (que es el algoritmo que utiliza Weka para implementar las
SVM). Añadimos dos y los configuramos. Para conectarles pulsaremos en Crossvalidationfoldermaker botón secundario y seleccionaremos connections/testset uniendo el conjunto de prueba
del generador de pruebas con el clasificador. Es necesario también unir el conjunto de
entrenamiento (connections/trainingset).
Una vez que conectemos por duplicado el generador de particiones a los clasificadores obtendremos
el resultado de la figura 1.41.
Figura 1.41: Aún queda definir un elemento que nos muestre el resultado.
El último paso será añadir dos objetos de tipo textviewer, que nos permitirán ver el resultado de
forma textual. Para conectarlos a los clasificadores SMO haremos uso de la opción
connections/text. Para comenzar con la ejecución del experimento haremos uso de la opción
Actions/Start Loading dentro del arffloader, con esto es suficiente. Una vez hecho esto ya estaría
completada la primera prueba obteniéndose un circuito como el de la figura 1.42.
-93-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Figura 1.42: El experimento ya está completo.
Para poder observar los resultados, en nuestro caso, con la opción Actions/Show results veremos
los resultados de cada una de las particiones. De esta forma obtenemos una información mucho más
completa que la obtenida del modo explorador.
Esto no hace más que resaltar la necesidad de manejar Weka de una forma completa, porque la
comprensión de un sólo modo de funcionamiento es insuficiente para poder obtener el óptimo
rendimiento del programa.
1.7. ALMACENAMIENTO DE MODELOS EN WEKA
Entrenamiento Y Clasificación
La utilización real del aprendizaje automático comprende dos pasos:
•
•
Entrenamiento: se parte de unos datos conocidos o ejemplos de entrenamiento y se utilizan para
construir un modelo (por ejemplo, un árbol de decisión).
Clasificación: una vez creado el modelo con los datos conocidos, se utiliza el modelo para
clasificar nuevos datos, para los que no se conoce de antemano la clase.
En las prácticas anteriores únicamente se ha generado el modelo, pero no se ha utilizado para
clasificar datos desconocidos. En esta práctica se aprenderá como guardar los modelos y cómo
utilizarlos para clasificar nuevos ejemplos.
Ejemplo: Recomendación De Lentes De Contacto
Supongamos que se conocen datos sobre el tipo de lentes de contacto recomendadas en función de
ciertos datos: edad (3 valores), tipo de problema visual (2 valores), existencia de astigmatismo (2
valores) y nivel de producción de lágrimas (2 valores). Parte de estos ejemplos almacenados se
muestran a continuación:
Se trata de un ejemplo disponible en el
entorno weka:
“…\data\contactlenses.arff”
El objetivo es generar un modelo que se ajuste a los ejemplos de entrenamiento y posteriormente
usar el modelo para clasificar un ejemplo nuevo.
-94-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Una vez que entremos en la interfaz Simple CLI, teclearemos la instrucción:
java weka.classifiers.trees.J48 -t data/contact-lenses.arff -d data/mod.out
Figura 1.43. Ejecución y guardado de un modelo
Se trata de la misma instrucción utilizada en la práctica anterior para generar un árbol de decisión
con la diferencia de que el árbol se guarda como un modelo que se puede utilizar posteriormente
para clasificar nuevos ejemplos. La parte de la instrucción que permite hacer esto es:
-d data/mod.out
…e indica que el modelo se guarda en el fichero mod.out (podríamos haber dado cualquier otro
nombre al modelo). Es importante indicar la ruta de ubicación.
La forma de utilizar el modelo creado para clasificar un nuevo ejemplo es la siguiente:
1. En primer lugar, se debe crear un fichero .arff con el ejemplo (o los ejemplos) a clasificar. Dado
que la clase de estos nuevos ejemplos es desconocida, se indica con una interrogación. Crearemos
el siguiente fichero (la cabecera se puede copiar de data\contact-lenses.arff para ahorrar trabajo):
@relation nuevo
@attribute age {young, pre-presbyopic, presbyopic}
@attribute spectacle-prescrip {myope, hypermetrope}
@attribute astigmatism {no, yes}
@attribute tear-prod-rate {reduced, normal}
@attribute contact-lenses {soft, hard, none}
@data
young, hypermetrope, no, normal, ?
presbyopic, myope, yes, normal, ?
…y lo guardaremos como: ...\weka_java\data\nuevo.arff
2. En Segundo lugar, se debe lanzar WEKA para clasificar estos dos nuevos ejemplos de acuerdo
con el modelo guardado antes. Para ello se tecleará la siguiente instrucción:
java weka.classifiers.trees.J48 -T data/nuevo.arff -l data/mod.out -p 0
-95-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Figura 2.40. Uso del modelo guarado
Donde aparecen nuevos parámetros:
-T data/nuevo.arff indica el fichero de test (datos no clasificados a
-p 0 para mostrar sólo los resultados de la clasificación.
utilizar).
El resultado en pantalla será el siguiente:
0 soft 0.8333333333333334 ?
1 hard 1.0 ?
…e indica que el en el primer caso se deben recomendar lentillas blandas y en el segundo caso
lentillas duras. Los valores que aparecen a la derecha se refieren a la confianza de la clasificación,
pero no se usarán en esta práctica.
1.8. MODIFICANDO WEKA
Una de las características más interesantes de Weka es la posibilidad de modificar su código y
obtener versiones adaptadas con funcionalidades que no contengan las versiones oficiales. El
primer paso para poder modificar Weka es descargarse la última snapshot (versión en desarrollo)
que se encuentra en el servidor de versiones27 (CVS).
Para operar con dicho servidor es altamente recomendable utilizar algún programa que nos facilite
esta tarea. Un buen programa es el SmartCVS que es gratuito28 en su versión normal pero
totalmente funcional. Además, está programado en Java lo que lo hace multiplataforma.
Weka hace uso de la herramienta ant 29 para la compilación de este proyecto. Una vez que esté todo
instalado para compilar Weka haremos uso del mandato ant dentro del directorio donde tengamos la
versión en desarrollo y obtendremos un resultado como el siguiente:
La dirección del mismo es: pserver:cvs_anon@ cvs.scms.waikato.ac.nz:/usr/local/global-cvs/ml_cvs.
El sitio web del mismo es http://www.smartcvs.com.
29 Ant es una herramienta para la automatización de la compilación de proyectos Java. Está considerado el
make para Java. http://ant.apache.org/ant
27
28
-96-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Una vez compilado Weka, podremos ejecutar cada uno de los métodos que implementa por separado (ya que todos pueden ser accesibles vía consola porque tienen método main y paso de
parámetros por línea de mandato) o podemos cargar alguno de los interfaces que ofrece. Para poder
cargar la interfaz de selección de interfaces ordenaremos el mandato siguiente en el directorio
inmediatamente superior al de Weka:
java weka.gui.GUIChooser
La estructura de directorios de Weka está organizada en paquetes de forma que añadir, eliminar o
modificar elementos es una tarea sencilla. La estructura física de directorios es la siguiente:
associations Carpeta que contiene las clases que implementan los métodos para realizar asociaciones.
classification Contiene clases
tertius Contiene las clases para implementar el método tertius.
attributeSelection
classifiers Contiene la implementación de los clasificadores existentes en Weka.
bayes Clases para implementar clasificadores bayes como puede ser naivebayes.
net Clases en desarrollo para aplicar el clasificador bayes en búsquedas web.
evaluation Clases que evevalúanos resultados de un clasificador, como dibujar las matrices de
confusión, las curvas de coste, etc.
functions Contiene métodos de clasificación basados en funciones.
neural Métodos de clasificación basados en redes neuronales.
pace Métodos numéricos sobre datos (manipulación de matrices, funciones estadísticas)
supportVector Métodos de clasificación basados en máquinas de vectores soporte.
lazy Implementa clasificadores IB1, IBk, Kstar, LBR, LWL.
kstar Métodos necesarios para implementar Kstar.
meta Metaclasificadores.
misc Clasificadores que se encuentren identificados en otras categorías.
rules Contiene clases para implementar reglas de decisión.
car Carpeta que tiene métodos para realizar reglas de asociación sobre clases.
utils
part Clases para implementar reglas sobre estructuras parciales de árboles.
trees Contiene métodos para implementar árboles.
adtree Implementa árboles adtree
j48 Implementa árboles c45 y otros métodos útiles para tratar con éstos.
lmt Implementa árboles lmt
m5 Implementa árboles m5
clusterers Contiene las clases donde se implementa el clustering.
-97-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
core Paquete principal donde se encuentran las clases principales como Instance, Attribute, Option..., y las
clases que definen “habilidades” (Drawable, Copyable, Matchable,...).
converters Clases para convertir entre tipos de archivos y para cargar archivos de forma secuencial.
datagenerators Clases abstractas para generadores de datos y clases para representar tests.
estimators Estimadores de probabilidades condicionadas y de probabilidades simples de diferentes
distribuciones (Poisson, Normal...).
experiment Clases que implementan la entidad experimento. Así mismo también están las que modelan los
experimentos remotos.
filters Contiene filtros para aplicar a los datos para preprocesarlos.
unsupervised Filtros no supervisados.
attribute Filtros para aplicar a atributos.
instance Filtros para aplicar a instancias.
supervised Filtros supervisados. En la última versión oficial (3-4-2) de Weka esta opción no está activada,
se prevee que en sucesivas versiones lo esté.
attribute Filtros para aplicar a atributos.
instance Filtros para aplicar a instancias.
gui Contiene las clases que implementan las interfaces gráficas.
beans Clases básicas de Weka de tratamiento de datos y creación de entidades principales del
programa referentes a instancias (DataSource, TestsetListener, TetsetProducer, TrainingSet...).
icons Iconos y demás elementos visuales para aplicar a los beans y al knowledge flow.
boundaryvisualizer Métodos para crear instancias a partir de otras.
experiment Interfaz del modo experimentador.
explorer Interfaz del modo explorador.
graphvisualizer Clases para dibujar y mostrar gráficas.
icons Iconos y demás elementos visuales para aplicar al visor de gráficas.
streams Clases para realizar operaciones sobre flujos de datos, que habitualmente será sobre un
objeto de clase Instance, que es la clase que almacena las instancias.
treevisualizer Clases para elaborar árboles y mostrarlos de una forma gráfica.
visualizer Contiene clases que implementan los métodos para poder seleccionar atributos en las
gráficas y las clases principales para dibujar gráficas (Plot2d, VisualizePanel etc.).
− build.xml Archivo de reglas de compilación. Define qué archivos es necesario compilar y cómo hacerlo.
− TODO.xml Archivo de definición de tareas pendientes.
− TODO.dtd Archivo de definición de tipos. Define las construcciones permitidas para hacer listas de tareas
pendientes.
Creando un nuevo clasificador
Programar nuevos clasificadores para Weka es sencillo teniendo conocimientos de Java, ya que
Weka está orientado al desarrollo abierto y comunitario y eso se nota; no obstante, su estructura,
quizá algo enrevesada, en parte adolece un mal diseño. Para crear un nuevo clasificador han de
seguirse las siguientes pautas:
Lo primero es crear una nueva clase y situarla dentro de weka/classifiers/. Una vez creada la clase,
cualquier clasificador debe heredar de las clases:
− import weka.classifiers.*
− import weka.core.*
− import weka.util.*
-98-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Y debe extender la clase Classifier. Si el clasificador calcula la distribución de clases debe extender
también de DistributionClassifier.
Una vez completado esto, todo clasificador tiene que tener los siguientes métodos:
•
•
•
Este método debe implementar la
construcción del clasificador obteniendo como parámetro las instancias. Este método debe
inicializar todas las variables y nunca debe modificar ningún valor de las instancias.
float classifyInstance(Instance instancia). Clasifica una instancia concreta una vez que
el clasificador ya está construido. Devuelve la clase en la que se ha clasificado o
Instance.missingValue() si no se consigue clasificar.
double[] distributionForInstance(Instance instancia). Este método devuelve la
distribución de una instancia en forma de vector. Si el clasificador no ha logrado clasificar la
instancia dada devolverá un vector lleno de ceros. Si lo consigue y las clases son numéricas
devolverá el valor obtenido y en los demás casos devolverá un vector con las probabilidades de
cada elemento en cada clase.
void
buildClassifier(Instances
instancias).
Y, en según qué circunstancias, deberá implementar las siguientes interfaces:
•
•
•
•
•
•
•
Si el clasificador tiene un carácter incremental.
WeightedInstanceHandler Si el clasificador hace uso de los pesos de cada instancia.
Es muy útil conocer las clases Instance e Instances que son aquellas que almacenan (siempre con
doubles) todas las instancias, incluso las nominales que utilizan como índice la declaración del
atributo y las indexa según este orden. Los métodos más útiles de la clase Instance (se encuentra
en el paquete weka.core) son:
Instances classAttribute() Devuelve la clase de la que procede el atributo.
double classValue() Devuelve el valor de la clase del atributo.
double value(int i) Devuelve el valor del atributo que ocupa la posición i.
Enumeration enumerateAttributes() Devuelve una enumeración de los atributos que
contiene esa instancia.
double weight() Devuelve el peso de una instancia en concreto.
UpdateableClassifier
Y de la clase Instances:
•
•
•
Devuelve el número de instancias que contiene el conjunto de datos.
Instance instance(int) Devuelve la instancia que ocupa la posición i.
Enumeration enumerateInstances() Devuelve una enumeración de las instancias que posee el
conjunto de datos.
int numInstances()
-99-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
2. IMPLEMENTACIÓN DE LAS TÉCNICAS DE ANÁLISIS DE DATOS EN WEKA
WEKA se distribuye como software de libre distribución desarrollado en Java. Está constituido por
una serie de paquetes de código abierto con diferentes técnicas de preprocesado, clasificación,
agrupamiento, asociación, y visualización, así como facilidades para su aplicación y análisis de
prestaciones cuando son aplicadas a los datos de entrada seleccionados. Estos paquetes pueden ser
integrados en cualquier proyecto de análisis de datos, e incluso pueden extenderse con
contribuciones de los usuarios que desarrollen nuevos algoritmos.
2.1. Técnicas de Minería de Datos
Las técnicas de Minería de Datos intentan obtener patrones o modelos a partir de los datos
recopilados. Se clasifican en dos grandes categorías: supervisadas o predictivas y no supervisadas
o descriptivas:
Técnicas de Minería de Datos
Implementación en WEKA
Agrupamiento
No
supervisadas
Asociación
Numérico
Conceptual
Probabilístico
A Priori
Regresión
Predicción
Árboles de Predicción
Estimador de Núcleos
Tabla de Decisión
TÉCNICAS
Árboles de Decisión
Supervisadas
Clasificación
Inducción de Reglas
Bayesiana
Basado en Ejemplares
Redes Neuronales
weka.clusterers.SimpleKMeans.java
weka.clusterers.Cobweb.java.
weka.clusterers.EM.java
weka.associations.Apriori.java.
weka.classifers.LinearRegression.java
weka.classifers.LWR.java
weka.classifers.m5.M5Prime.java
weka.classifiers.KernelDensity
weka.classifiers.DecisionTable.java
weka.classifiers.ID3.java
weka.classifers.j48.J48.java
weka.classifers.DecisionStump.java
weka.classifers.OneR.java
weka.classifers.Prism.java
weka.classifers.j48.PART.java
weka.classifiers.NaiveBayesSimple.java
weka.classifiers.VFI.java
weka.classifiers.IBk.java
weka.classifers.kstar.KStar.java.
weka.classifiers.neural.NeuralNetwork.java.
Tabla 2.1.1. Algunas de las principales Técnicas de Minería de Datos
Una técnica constituye el enfoque conceptual para extraer la información de los datos, y, en
general es implementada por varios algoritmos. Cada algoritmo representa, en la práctica, la
manera de desarrollar una determinada técnica paso a paso, de forma que es preciso un
entendimiento de alto nivel de los algoritmos para saber cual es la técnica más apropiada para
cada problema. Asimismo es preciso entender los parámetros y las características de los algoritmos
para preparar los datos a analizar.
Las predicciones se utilizan para prever el comportamiento futuro de algún tipo de entidad
mientras que una descripción puede ayudar a su comprensión. De hecho, los modelos predictivos
pueden ser descriptivos (hasta donde sean comprensibles por personas) y los modelos
descriptivos pueden emplearse para realizar predicciones. De esta forma, hay algoritmos o
técnicas que pueden servir para distintos propósitos, por lo que la tabla anterior únicamente
representa para qué propósito son más utilizadas las técnicas. Por ejemplo, las redes de neuronas
pueden servir para predicción, clasificación e incluso para aprendizaje no supervisado.
-100-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
El aprendizaje inductivo no supervisado estudia el aprendizaje sin la ayuda del maestro; es decir,
se aborda el aprendizaje sin supervisión, que trata de ordenar los ejemplos en una jerarquía según
las regularidades en la distribución de los pares atributo-valor sin la guía del atributo especial
clase. Éste es el proceder de los sistemas que realizan clustering conceptual y de los que se dice
también que adquieren nuevos conceptos. Otra posibilidad contemplada para estos sistemas es la
de sintetizar conocimiento cualitativo o cuantitativo, objetivo de los sistemas que llevan a cabo
tareas de descubrimiento.
En el aprendizaje inductivo supervisado existe un atributo especial, normalmente denominado
clase, presente en todos los ejemplos que especifica si el ejemplo pertenece o no a un cierto
concepto, que será el objetivo del aprendizaje. Mediante una generalización del papel del atributo
clase, cualquier atributo puede desempeñar ese papel, convirtiéndose la clasificación de los
ejemplos según los valores del atributo en cuestión, en el objeto del aprendizaje. Expresado en
una forma breve, el objetivo del aprendizaje supervisado es: a partir de un conjunto de ejemplos,
denominados de entrenamiento, de un cierto dominio D de ellos, construir criterios para
determinar el valor del atributo clase en un ejemplo cualquiera del dominio. Esos criterios están
basados en los valores de uno o varios de los otros pares (atributo; valor) que intervienen en la
definición de los ejemplos. Dentro de este tipo de aprendizaje se pueden distinguir dos grandes
grupos de técnicas: la predicción y la clasificación.
2.2. CLUSTERING. (“Segmentación / Agrupamiento”)
También llamada agrupamiento, permite la identificación de tipologías o grupos donde los
elementos guardan gran similitud entre sí y muchas diferencias con los de otros grupos. Así se
puede segmentar el colectivo de clientes, el conjunto de valores e índices financieros, el espectro de
observaciones astronómicas, el conjunto de zonas forestales, el conjunto de empleados y de
sucursales u oficinas, etc. La segmentación está teniendo mucho interés desde hace ya tiempo dadas
las importantes ventajas que aporta al permitir el tratamiento de grandes colectivos de forma
pseudoparticularizada, en el más idóneo punto de equilibrio entre el tratamiento individualizado y
aquel totalmente masificado.
Las herramientas de segmentación se basan en técnicas de carácter estadístico, de empleo de
algoritmos matemáticos, de generación de reglas y de redes neuronales para el tratamiento de
registros. Para otro tipo de elementos a agrupar o segmentar, como texto y documentos, se usan
técnicas de reconocimiento de conceptos. Esta técnica suele servir de punto de partida para después
hacer un análisis de clasificación sobre los clusters.
2.2.1 Clustering Numérico (k-medias)
Uno de los algoritmos más utilizados para hacer clustering es el k-medias (kmeans), que se
caracteriza por su sencillez. Se trata de un algoritmo clasificado como Método de Particionado y
Recolocación. El nombre le viene porque representa cada uno de los clusters por la media (o media
ponderada) de sus puntos, es decir, por su centroide. Este método únicamente se puede aplicar a
atributos numéricos, y los outliers le pueden afectar muy negativamente.
Pseudo código del algoritmo de k-medias:
1.
2.
3.
4.
Elegir k ejemplos que actúan como semillas (k número de clusters).
Para cada ejemplo, añadir ejemplo a la clase más similar.
Calcular el centroide de cada clase, que pasan a ser las nuevas semillas
Si no se llega a un criterio de convergencia (por ejemplo, dos iteraciones no
cambian las clasificaciones de los ejemplos), volver a 2.
-101-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
En primer lugar se debe especificar por adelantado cuantos clusters se van a crear, éste es el
parámetro k, para lo cual se seleccionan k elementos aleatoriamente, que representaran el centro o
media de cada cluster. A continuación cada una de las instancias, ejemplos, es asignada al centro
del cluster más cercano de acuerdo con la distancia Euclidea que le separa de él. Para cada uno de
los clusters así construidos se calcula el centroide de todas sus instancias. Estos centroides son
tomados como los nuevos centros de sus respectivos clusters. Finalmente se repite el proceso
completo con los nuevos centros de los clusters. La iteración continúa hasta que se repite la
asignación de los mismos ejemplos a los mismos clusters, ya que los puntos centrales de los clusters
se han estabilizado y permanecerán invariables después de cada iteración. Para obtener los
centroides, se calcula la media [mean] o la moda [mode] según se trate de atributos numéricos o
simbólicos.
La representación mediante centroides tiene la ventaja de que tiene un significado gráfico y
estadístico inmediato. La suma de las discrepancias entre un punto y su centroide, expresado a
través de la distancia apropiada, se usa como función objetivo. La función objetivo, suma de los
cuadrados de los errores entre los puntos y sus centroides respectivos, es igual a la varianza total
dentro del propio cluster.
Por ejemplo se parte de un total de nueve ejemplos o instancias, se configura el algoritmo para que obtenga 3
clusters, y se inicializan aleatoriamente los centroides de los clusters a un ejemplo determinado. Una vez
inicializados los datos, se comienza el bucle del algoritmo. En cada una de las gráficas (figura 2.2.1.)
inferiores se muestra un paso por el algoritmo. Cada uno de los ejemplos se representa con un tono de color
diferente que indica la pertenencia del ejemplo a un cluster determinado, mientras que los centroides siguen
mostrándose como círculos de mayor tamaño y sin relleno. Por ultimo el proceso de clustering finaliza en el
paso 3, ya que en la siguiente pasada del algoritmo (realmente haría cuatro pasadas, si se configurara así)
ningún ejemplo cambiaría de cluster.
Figura 2.2.1. Ejemplo de clustering con k-medias.
-102-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
k-means en WEKA
El
algoritmo
de
k-medias
se
encuentra
implementado
en
la
clase
weka.clusterers.SimpleKMeans.java. Las opciones de configuración de que disponen son las que
vemos en la tabla.
Opción
Descripción
numClusters (2)
Número de clusters.
Semilla a partir de la cuál se genera el número aleatorio para
inicializar los centros de los clusters.
seed (10)
Tabla.2.2.1 Opciones de configuración para el algoritmo k-medias en WEKA.
El algoritmo es exactamente el mismo que el descrito anteriormente. A continuación se enumeran
los tipos de datos que admite y las propiedades de la implementación:
Admite
atributos simbólicos y numéricos.
obtener los centroides iniciales se emplea un número aleatorio obtenido a partir de la semilla
empleada. Los k ejemplos correspondientes a los k números enteros siguientes al número aleatorio
obtenido serán los que conformen dichos centroides.
En cuanto a la medida de similaridad, se emplea el mismo algoritmo que el que veremos más
adelante en el algoritmo KNN.
No se estandarizan los argumentos, sino que se normalizan.
xif − min f
Ecuación 2.2.1.
Max f − min f
Para
En la ecuación 2.2.1. xif será el valor i del atributo f, siendo minf el mínimo valor del atributo f
y Maxf el máximo.
2.2.2 Clustering Conceptual (COBWEB)
El algoritmo de k-medias se encuentra con un problema cuando los atributos no son numéricos, ya
que en ese caso la distancia entre ejemplares no está tan clara.
Para resolver este problema Michalski presenta la noción de clustering conceptual, que utiliza para
justificar la necesidad de un clustering cualitativo frente al clustering cuantitativo, basado en la
vecindad entre los elementos de la población. En este tipo de clustering una partición de los datos es
buena si cada clase tiene una buena interpretación conceptual (modelo cognitivo de jerarquías).
Una de las principales motivaciones de la categorización de un conjunto de ejemplos, que
básicamente supone la formación de conceptos, es la predicción de características de las categorías
que heredarán sus subcategorías. Esta conjetura es la base de COBWEB. A semejanza de los
humanos, COBWEB forma los conceptos por agrupación de ejemplos con atributos similares.
El objetivo de COBWEB es hallar un conjunto de clases o clusters (subconjuntos de ejemplos) que
maximice la utilidad de la categoría (partición del conjunto de ejemplos cuyos miembros son
clases).
-103-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Se caracteriza porque utiliza aprendizaje incremental, esto es, realiza las agrupaciones instancia a
instancia. Representa los clusters como una distribución de probabilidad sobre el espacio de los
valores de los atributos, generando un árbol de clasificación jerárquica en el que los nodos
intermedios definen subconceptos. Al principio, el árbol consiste en un único nodo raíz. Las
instancias se van añadiendo una a una y el árbol se va actualizando en cada paso. La actualización
consiste en encontrar el mejor sitio donde incluir la nueva instancia, operación que puede necesitar
de la reestructuración de todo el árbol (incluyendo la generación de un nuevo nodo anfitrión para la
instancia y/o la fusión/partición de nodos existentes) o simplemente la inclusión de la instancia en
un nodo que ya existía. La clave para saber cómo y dónde se debe actualizar el árbol la proporciona
una medida denominada utilidad de categoría, que mide la calidad general de una partición de
instancias en un segmento. La reestructuración que mayor utilidad de categoría proporcione es la
que se adopta en ese paso.
La descripción probabilística se basa en dos conceptos:
Predicibilidad:
Probabilidad condicional de que un suceso tenga un cierto atributo dada la clase:
P(Ai=Vij|Ck).
El mayor de estos valores corresponde al valor del atributo más predecible y es el de los miembros
de la clase (alta similaridad entre los elementos de la clase).
Previsibilidad:
Probabilidad condicional de que un ejemplo sea una instancia de una cierta clase,
dado el valor de un atributo particular:
P(Ck|Ai=Vij).
Un valor alto indica que pocos ejemplos de las otras clases comparten este valor del atributo, y el
valor del atributo de mayor probabilidad es el de los miembros de la clase (baja similaridad
interclase).
Estas dos medidas, combinadas mediante el teorema de Bayes, proporcionan una función que
evalúa la utilidad de una categoría (CU), que se muestra en la ecuación 2.2.2
ecuación 2.2.2
En esta ecuación n es el número de clases y las sumas se extienden a todos los atributos Ai y
sus valores Vij en cada una de las n clases Ck. La división por n sirve para incentivar tener
clusters con más de un elemento.
La utilidad de la categoría mide el valor esperado de valores de atributos que pueden ser
adivinados a partir de la partición sobre los valores que se pueden adivinar sin esa partición. Si la
partición no ayuda en esto, entonces no es una buena partición. El árbol resultante de este algoritmo
cabe denominarse organización probabilística o jerárquica de conceptos.
En la figura 2.2.2., se muestra un ejemplo de árbol que se podría generar mediante COBWEB. En la
construcción del árbol, incrementalmente se incorpora cada ejemplo al mismo, donde cada nodo es un
concepto probabilístico que representa una clase de objetos. COBWEB desciende por el árbol buscando el
mejor lugar o nodo para cada ejemplo. Esto se basa en medir en cuál se tiene la mayor ganancia de utilidad
de categoría.
-104-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Figura 2.2.2. Ejemplo de árbol generado por COBWEB.
Sin embargo, no se puede garantizar que se genere este árbol, dado que el algoritmo es sensible al orden en
que se introduzcan los ejemplos. En cuanto a las etiquetas de los nodos, éstas fueron puestas a posteriori,
coherentes con los valores de los atributos que determinan el nodo.
Cuando COBWEB incorpora un nuevo ejemplo en el nodo de clasificación, desciende a lo largo del
camino apropiado, actualizando las cuentas de cada nodo, y llevando a cabo por medio de los
diferentes operadores, una de las siguientes acciones:
• Incorporación: Añadir un nuevo ejemplo a un nodo ya existente.
• Creación de una nueva disyunción: Crear una nueva clase.
• Unión: Combinar dos clases en una sola.
• División: Dividir una clase existente en varias clases.
La búsqueda, que se realiza en el espacio de conceptos, es por medio de un heurístico basado en el
método de escalada gracias a los operadores de unión y división.
En la figura 2.2.3., se muestra el resultado de aplicar cada una de estas operaciones.
Figura 2.2.3: Operaciones de COBWEB.
-105-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
El algoritmo de COBWEB es el siguiente:
1. Nuevo Ejemplo: Lee un ejemplo e. Si no hay más ejemplos, terminar.
2. Actualiza raíz. Actualiza el cálculo de la raíz.
3. Si la raíz es hoja, entonces: Expandir en dos nodos hijos y acomodar en cada uno
de ellos un ejemplo; volver a 1.
4. Avanzar hasta el siguiente nivel: Aplicar la función de evaluación a varias
opciones para determinar, mediante la fórmula de utilidad de una categoría, el
mejor (máxima CU) lugar donde incorporar el ejemplo en el nivel siguiente de la
jerarquía. En las opciones que se evaluarán se considerará únicamente el nodo
actual y sus hijos y se elegirá la mejor opción de las siguientes:
a. Añadir e a un nodo que existe (al mejor hijo) y, si esta opción resulta
ganadora, comenzar de nuevo el proceso de avance hacia el siguiente nivel en
ese nodo hijo.
b. Crear un nuevo nodo conteniendo únicamente a e y, si esta opción resulta
ganadora, volver a 1.
c. Juntar los dos mejores nodos hijos con e incorporado al nuevo nodo combinado y,
si esta opción resulta ganadora, comenzar el nuevo proceso de avanzar hacia el
siguiente nivel en ese nuevo nodo.
d. Dividir el mejor nodo, reemplazando este nodo con sus hijos y, si esta opción
resulta ganadora, aplicar la función de evaluación para incorporar e en los
nodos originados por la división.
El algoritmo se puede extender a valores numéricos usando distribuciones gaussianas, ecuación
2.2.3. De esta forma, el sumatorio de probabilidades es ahora como se muestra en la ecuación 2.2.4.
ecuación 2.2.3
ecuación 2.2.4
Por lo que la ecuación de la utilidad de la categoría quedaría como se muestra en la ecuación 2.2.5.
ecuación 2.2.5
COBWEB en WEKA
El algoritmo de COBWEB se encuentra implementado en la clase weka.clusterers.Cobweb.java.
Las opciones de configuración de que disponen son las que vemos en la tabla:
Opción
acuity (100)
cutoff (0)
Descripción
Indica la mínima varianza permitida en un cluster
La utilidad de categoría se basa en una estimación de la media y la desviación estándar del
valor de los atributos, pero cuando se estima la desviación estándar del valor de un atributo
para un nodo en particular, el resultado es cero si dicho nodo sólo contiene una instancia.
Así pues, éste parámetro representa la medida de error de un nodo con una sola instancia,
es decir, establece la varianza mínima de un atributo.
Factor de poda.
Se utiliza para evitar el crecimiento desmesurado del número de segmentos. Indica el
grado de mejoría que se debe producir en la utilidad de categoría para que la instancia sea
tenida en cuenta de manera individual. En otras palabras: cuando no es suficiente el
incremento de la utilidad de categoría en el momento en el que se añade un nuevo nodo,
ese nodo se corta, conteniendo la instancia otro nodo ya existente.
Tabla 2.2.2. Opciones de configuración para el algoritmo COBWEB en WEKA.
-106-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Al algoritmo no hay que proporcionarle el número exacto de clusters que queremos, sino que en
base a los parámetros anteriormente mencionados encuentra el número óptimo.
La implementación de COBWEB en WEKA es similar al algoritmo explicado anteriormente.
Algunas características de esta implementación son:
Se
permiten atributos numéricos y simbólicos.
semilla para obtener números aleatorios es fija e igual a 42.
Permite pesos asociados a cada ejemplo.
1
.
Realmente el valor de cutoff 0.01 ×
2 π
En el caso de que el ejemplo que se desea clasificar genere, en un nodo determinado, un CU menor
al cutoff, se eliminan los hijos del nodo (poda).
La
(
)
2.2.3 Clustering Probabilístico (EM)
Los algoritmos de clustering estudiados hasta el momento presentan ciertos defectos entre los que
destacan la dependencia que tiene el resultado del orden de los ejemplos y la tendencia de estos
algoritmos al sobreajuste [overfitting]. Una aproximación estadística al problema del clustering
resuelve estos problemas. Desde este punto de vista, lo que se busca es el grupo de clusters más
probables dados los datos. Ahora los ejemplos tienen ciertas probabilidades de pertenecer a un
cluster. Se trata de obtener la FDP (Función de Densidad de Probabilidad) desconocida a la que
pertenecen el conjunto completo de datos. La base de este tipo de clustering se encuentra en un
modelo estadístico llamado mezcla de distribuciones [finite mixtures]. Cada distribución representa
la probabilidad de que un objeto tenga un conjunto particular de pares atributo-valor, si se supiera
que es miembro de ese cluster. Se tienen k distribuciones de probabilidad que representan los k
clusters.
La mezcla más sencilla se tiene cuando los atributos son numéricos con distribuciones gaussianas.
Cada distribución (normal) se caracteriza por dos parámetros: la media (µ) y la varianza (σ2).
Además, cada distribución tendrá cierta probabilidad de aparición p, que vendrá determinada por la
proporción de ejemplos que pertenecen a dicho cluster respecto del número total de ejemplos. En
ese caso, si hay k clusters, habrá que calcular un total de 3k-1 parámetros: las k medias, k varianzas
y k-1 probabilidades de la distribución dado que la suma de probabilidades debe ser 1, con lo que
conocidas k-1 se puede determinar la k-ésima. Si se conociera el cluster al que pertenece, en un
principio, cada uno de los ejemplos de entrenamiento sería muy sencillo obtener los 3k-1
parámetros necesarios para definir totalmente las distribuciones de dichos clusters, ya que
simplemente se aplicarían las ecuaciones de la media y de la varianza para cada uno de los clusters.
Además, para calcular la probabilidad de cada una de las distribuciones únicamente se dividiría el
número de ejemplos de entrenamiento que pertenecen al cluster en cuestión entre el número total de
ejemplos de entrenamiento. Una vez obtenidos estos parámetros, si se deseara calcular la
probabilidad de pertenencia de un determinado ejemplo de test a cada cluster, simplemente se
aplicaría el teorema de Bayes a cada problema concreto, con lo que quedaría la ecuación 2.2.6.
ecuación 2.2.6
En esta ecuación A es un cluster del sistema, x el ejemplo de test, pA la probabilidad del
cluster A y f(x;µA,σA) la función de la distribución normal del cluster A, que se expresa con
la ecuación 2.4.
-107-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Sin embargo, el problema es que no se sabe de qué distribución viene cada dato y se desconocen los
parámetros de las distribuciones. Por ello se adopta el procedimiento empleado por el algoritmo de
clustering k-medias, y se itera.
El algoritmo EM (Expectation Maximization) empieza adivinando los parámetros de las
distribuciones (se empieza adivinando las probabilidades de que un objeto pertenezca a una clase)
y, a continuación, los utiliza para calcular las probabilidades de que cada objeto pertenezca a un
cluster y usa esas probabilidades para re-estimar los parámetros de las probabilidades, hasta
converger.
Este algoritmo recibe su nombre de los dos pasos en los que se basa cada iteración: el cálculo de las
probabilidades de los grupos o los valores esperados de los grupos, mediante la ecuación 2.2.6,
denominado expectation; y el cálculo de los valores de los parámetros de las distribuciones,
denominado maximization, en el que se maximiza la verosimilitud de las distribuciones dados los
datos.
Para estimar los parámetros de las distribuciones se tiene que considerar que se conocen únicamente
las probabilidades de pertenencia a cada cluster, y no los clusters en sí. Estas probabilidades actúan
como pesos, con lo que el cálculo de la media y la varianza se realizan con las ecuaciones 2.2.7. y
2.2.8., respectivamente.
ecuación 2.2.7
ecuación 2.2.8
Donde N es el número total de ejemplos del conjunto de entrenamiento y wi es la probabilidad
de que el ejemplo i pertenezca al cluster A. La cuestión es determinar cuándo se finaliza el
procedimiento, es decir en que momento se dejan de realizar iteraciones. En el algoritmo kmedias se finalizaba cuando ningún ejemplo de entrenamiento cambiaba de cluster en una
iteración, alcanzándose así un “punto fijo” [fixed point].
En el algoritmo EM es un poco más complicado, dado que el algoritmo tiende a converger pero
nunca se llega a ningún punto fijo. Sin embargo, se puede ver cuánto se acerca calculando la
verosimilitud [likelihood] general de los datos con esos parámetros, multiplicando las
probabilidades de los ejemplos, tal y como se muestra en la ecuación 2.2.9.
ecuación 2.2.9
En esta ecuación j representa cada uno de los clusters del sistema, y pj la probabilidad de dicho
cluster. La verosimilitud es una medida de lo “bueno” que es el clustering, y se incrementa con
cada iteración del algoritmo EM. Se seguirá iterando hasta que dicha medida se incremente un
valor despreciable.
Aunque EM garantiza la convergencia, ésta puede ser a un máximo local, por lo que se recomienda
repetir el proceso varias veces, con diferentes parámetros iniciales para las distribuciones. Tras estas
repeticiones, se pueden comparar las medidas de verosimilitud obtenidas y escoger la mayor de
todas ellas.
En la figura 2.2.4., se muestra un ejemplo de clustering probabilístico con el algoritmo EM.
-108-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Figura 2.2.4. Ejemplo de clustering con EM.
En este experimento se introducen un total de doscientos ejemplos que constituyen dos distribuciones
desconocidas para el algoritmo. Lo único que conoce el algoritmo es que hay dos clusters, dado que este dato
se introduce como parámetro de entrada. En la iteración 0 se inicializan los parámetros de los clusters a 0
(media, desviación típica y probabilidad). En las siguientes iteraciones estos parámetros van tomando forma
hasta finalizar en la iteración 11, iteración en la que finaliza el proceso, por el incremento de la medida de
verosimilitud, tan sólo del orden de 10-4.
El modelo puede extenderse desde un atributo numérico como se ha visto hasta el momento, hasta
múltiples atributos, asumiendo independencia entre atributos. Las probabilidades de cada atributo se
multiplican entre sí para obtener una probabilidad conjunta para la instancia, tal y como se hace en
el algoritmo naive Bayesiano. También puede haber atributos correlacionados, en cuyo caso se
puede modelar con una distribución normal bivariable, en donde se utiliza una matriz de covarianza.
En este caso el número de parámetros crece según el cuadrado del número de atributos que se
consideren correlacionados entre sí, ya que se debe construir una matriz de covarianza. Esta
escalabilidad en el número de parámetros tiene serias consecuencias de sobreajuste.
En el caso de un atributo nominal con v posibles valores, se caracteriza mediante v valores
numéricos que representan la probabilidad de cada valor. Se necesitarán otros kv valores numéricos,
que serán las probabilidades condicionadas de cada posible valor del atributo con respecto a cada
cluster. En cuanto a los valores desconocidos, se puede optar por varias soluciones: ignorarlo en el
productorio de probabilidades; añadir un nuevo valor a los posibles, sólo en el caso de atributos
nominales; o tomar la media o la moda del atributo, según se trate de atributos numéricos o
nominales. Por último, aunque se puede especificar el número de clusters, también es posible dejar
que sea el algoritmo el que determine automáticamente cuál es el número de clusters mediante
validación cruzada.
-109-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
EM en WEKA
El algoritmo EM se encuentra implementado en la clase weka.clusterers.EM.java. Las opciones de
configuración de que disponen son las que vemos en la tabla:
Opción
Descripción
numClusters (-1)
maxIteration (100)
debug (False)
seed (100)
minStdDev (1e-6)
Número de clusters. Si es número es –1 el algoritmo determinará automáticamente el
número de clusters.
Número máximo de iteraciones del algoritmo si esto no convergió antes.
Muestra información sobre el proceso de clustering.
Semilla a partir de la cuál se generan los número aleatorios del algoritmo.
Desviación típica mínima admisible en las distribuciones de densidad.
Tabla 2.2.3. Opciones de configuración para el algoritmo EM en WEKA.
En primer lugar, si no se especifica el número de clusters, el algoritmo realiza un primer proceso
consistente en obtener el número óptimo de clusters. Se realiza mediante validación cruzada con 10
conjuntos [folders]. Se va aumentando el número de clusters hasta que se aumenta y empeora el
resultado. Se ejecuta el algoritmo en diez ocasiones, cada una de ellas con nueve conjuntos de
entrenamiento, sobre los que se ejecuta EM con los parámetros escogidos y posteriormente se
valida el sistema sobre el conjunto de test, obteniendo como medida la verosimilitud sobre dicho
conjunto. Se calcula la media de las diez medidas obtenidas y se toma como base para determinar si
se continúa o no aumentando el número de clusters.
El ajuste de los parámetros del modelo requiere alguna medida de su bondad, es decir, cómo de bien
encajan los datos sobre la distribución que los representa.
Una vez seleccionado el número óptimo de clusters, se procede a ejecutar el algoritmo EM sobre el
conjunto total de entrenamiento hasta un máximo de iteraciones que se configuró previamente si es
que el algoritmo no converge previamente.
El algoritmo EM, procede en dos pasos que se repiten de forma iterativa:
Expectation Utiliza los valores de los parámetros, iniciales o proporcionados por el paso
Maximization de la iteración anterior, obteniendo diferentes formas de la FDP buscada.
Maximization Obtiene nuevos valores de los parámetros a partir de los datos proporcionados
por el paso anterior.
Después de una serie de iteraciones, el algoritmo EM tiende a un máximo local. Finalmente se
obtendrá un conjunto de clusters que agrupan el conjunto de proyectos original. Cada uno de estos
cluster estará definido por los parámetros de una distribución normal.
La implementación que lleva a cabo del algoritmo EM lleva asociada la premisa de la
independencia de los atributos utilizados, nada más lejos de la realidad existente entre el esfuerzo y
los puntos de función.
En cuanto a los tipos de atributos con admite el algoritmo y algunas propiedades interesantes, éstas
son:
• En cuanto a los atributos, éstos pueden ser numéricos o simbólicos.
• Se entiende que se converge si en la siguiente iteración la verosimilitud aumenta en menos de 1e-6.
• No tiene en cuenta posibles correlaciones entre atributos.
-110-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
2.3. Reglas de Asociación
Este tipo de técnicas se emplea para establecer las posibles relaciones o correlaciones entre
distintas acciones o sucesos aparentemente independientes; pudiendo reconocer como la ocurrencia
de un suceso o acción puede inducir o generar la aparición de otros. Son utilizadas cuando el
objetivo es realizar análisis exploratorios, buscando relaciones dentro del conjunto de datos. Las
asociaciones identificadas pueden usarse para predecir comportamientos, y permiten descubrir
correlaciones y co-ocurrencias de eventos.
Debido a sus características, estas técnicas tienen una gran aplicación práctica en muchos campos
como, por ejemplo, el comercial ya que son especialmente interesantes a la hora de comprender los
hábitos de compra de los clientes y constituyen un pilar básico en la concepción de las ofertas y
ventas cruzada, así como del "merchandising". En otros entornos como el sanitario, estas
herramientas se emplean para identificar factores de riesgo en la aparición o complicación de
enfermedades. Para su utilización es necesario disponer de información de cada uno de los sucesos
llevados a cabo por un mismo individuo o cliente en un determinado período temporal. Por lo
general esta forma de extracción de conocimiento se fundamenta en técnicas estadísticas, como los
análisis de correlación y de varianza.
Uno de los algoritmos mas utilizado es el algoritmo A priori, que se presenta a continuación.
Algoritmo A Priori
La generación de reglas de asociación se logra basándose en un procedimiento de covering. Las
reglas de asociación son parecidas, en su forma, a las reglas de clasificación, si bien en su lado
derecho puede aparecer cualquier par opares atributo-valor. De manera que para encontrar ese tipo
de reglas es preciso considerar cada posible combinación de pares atributo-valor del lado derecho.
Para evaluar las reglas se emplean la medida del soporte [support], ecuación 2.3.1, que indica el
número de casos, ejemplos, que cubre la regla y la confianza [confidence], ecuación 2.3.2, que
indica el número de casos que predice la regla correctamente, y que viene expresado como el
cociente entre el número de casos en que se cumple la regla y el número de casos en que se aplica,
ya que se cumplen las premisas.
soporte( A ⇒ B ) = P( A ∩ B )
confianza( A ⇒ B ) = P(B | A) =
ecuación 2.3.1
P( A ∩ B )
P ( A)
ecuación 2.3.2
Las reglas que interesan son únicamente aquellas que tienen su valor de soporte muy alto, por lo
que se buscan, independientemente de en qué lado aparezcan, pares atributo-valor que cubran una
gran cantidad de ejemplos.
A cada par atributo-valor se le denomina item, mientras que a un conjunto de items se les denomina itemsets. Por supuesto, para la formación de item-sets no se pueden unir items referidos al mismo atributo pero
con distinto valor, dado que eso nunca se podría producir en un ejemplo. Se buscan item-sets con un máximo
soporte, para lo que se comienza con item-sets con un único item. Se eliminan los item-sets cuyo valor de
soporte sea inferior al mínimo establecido, y se combinan el resto formando item-sets con dos items. A su
vez se eliminan aquellos nuevos item-sets que no cumplan con la condición del soporte, y al resto se le
añadirá un nuevo item, formando item-sets con tres items. El proceso continuará hasta que ya no se puedan
formar item-sets con un item más. Además, para generar los item-sets de un determinado nivel, sólo es
necesario emplear los item-sets del nivel inferior (con n-1 coincidencias, siendo n el número de items del
nivel). Una vez se han obtenido todos los item-sets, se pasará a la generación de reglas. Se tomará cada itemset y se formarán reglas que cumplan con la condición de confianza. Debe tenerse en cuenta que un item-set
puede dar lugar a más de una regla de asociación, al igual que un item-set también puede no dar lugar a
ninguna regla.
-111-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Un ejemplo típico de reglas de asociación es el análisis de la cesta de la compra [market-basket analysis].
Básicamente consiste en encontrar asociaciones entre los productos que habitualmente compran los clientes,
para utilizarlas en el desarrollo de las estrategias mercadotécnicas. En la figura 2.3.1., se muestra un ejemplo
sencillo de obtención de reglas de asociación aplicado a este campo.
Figura 2.3.1. Ejemplo de obtención de reglas de asociación A Priori.
En esta imagen se muestra cómo se forman los item-sets a partir de los itemsets del nivel inferior, y cómo
posteriormente se obtienen las reglas de asociación a partir de los item-sets seleccionados. Las reglas en
negrita son las que se obtendrían, dado que cumplen con la confianza mínima requerida.
El proceso de obtención de las reglas de asociación que se comentó anteriormente se basa en el
algoritmo que se muestran a continuación:
1. Genera todos los items-sets con un elemento. Usa éstos para generar los de dos
elementos y así sucesivamente. Se toman todos los posibles pares que cumplen con
las medidas mínimas del soporte. Esto permite ir eliminando posibles combinaciones
ya que no todas se tienen que considerar.
2. Genera las reglas revisando que cumplan con el criterio mínimo de confianza.
Una observación interesante es que si una conjunción de consecuentes de una regla cumple con los
niveles mínimos de soporte y confianza, sus subconjuntos (consecuentes) también los cumplen. Por
el contrario, si algún item no los cumple, no tiene caso considerar sus superconjuntos. Esto da una
forma de ir construyendo reglas, con un solo consecuente, y a partir de ellas construir de dos
consecuentes y así sucesivamente.
-112-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Asociación A Priori en WEKA
La clase en la que se implementa el algoritmo de asociación A Priori es
weka.associations.Apriori.java. Las opciones que permite configurar son las que se muestran en la
tabla:
Opción
Descripción
numRules (10)
Número de reglas requerido.
Tipo de métrica por la que ordenar las reglas. Las opciones son
Confidence (confianza, ecuación 2.106), Lift (ecuación 2.107),
Leverage (ecuación 2.108) y Conviction (ecuación 2.109).
Mínimo valor de la métrica empleada. Su valor por defecto depende
del tipo de métrica empleada: 0.9 para Confidence, 1.1 para Lift y
Conviction y 0.1 para Leverage.
Constante por la que va decreciendo el soporte en cada iteración del
algoritmo.
Máximo valor del soporte de los item-sets. Si los itemsets tienen un
soporte mayor, no se les toma en consideración.
Mínimo valor del soporte de los item-sets.
Si se emplea, las reglas se validan para comprobar si su correlación es
estadísticamente significativa (del nivel requerido) mediante el test X2 .
En este caso, la métrica a utilizar es Confidence.
Si se activa, no se toman en consideración los atributos con todos los
valores perdidos.
Si se activa, se muestran los itemsets encontrados.
metricType (Confidence)
minMetric
delta (0.05)
upperBoundMinSupport (1.0)
lowerBoundMinSupport (0.1)
significanceLevel (-1.0)
removeAllMissingsCols (False)
-I (sólo modo texto)
Tabla 2.3.1. Opciones de configuración para el algoritmo de asociación A Priori en WEKA
En primer lugar, el algoritmo que implementa la herramienta WEKA es ligeramente distinto al
explicado anteriormente. Se muestra a continuación el algoritmo concreto.
Apriori (ejemplos, MS, mS) { /* MS: Máx. soporte; mS: Mín. soporte */
S = MS-delta
Mientras No Fin
Generar ItemSets en rango (MS, S)
GenerarReglas (ItemSets)
MS = MS-delta
S = S-delta
Si suficientes reglas O S menor que mS Entonces
Fin
}
GenerarReglas (ItemSets) {
Para cada ItemSet
Generar posibles reglas del ItemSet
Eliminar reglas según la métrica
}
Así, el algoritmo no obtiene de una vez todos los item-sets entre los valores máximo y mínimo
permitido, sino que se va iterando y cada vez se obtienen los de un rango determinado, que será de
tamaño delta.
Además, el algoritmo permite seleccionar las reglas atendiendo a diferentes métricas. Además de la
confianza, se puede optar por una de las siguientes tres métricas.
Lift:
Indica cuándo una regla es mejor prediciendo el resultado que asumiendo el resultado de
forma aleatoria. Si el resultado es mayor que uno, la regla es buena, pero si es menor que uno, es
peor que elegir un resultado aleatorio. Se muestra en la ecuación 2.3.3.:
lift ( A ⇒ B ) =
confianza ( A ⇒ B )
P (B )
-113-
ecuación 2.3.3
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Leverage:
Esta medida de una regla de asociación indica la proporción de ejemplos adicionales
cubiertos por dicha regla (tanto por la parte izquierda como por la derecha) sobre los cubiertos
por cada parte si fueran independientes. Se muestra en la ecuación 2.3.4.:
leverage( A ⇒ B ) = P( A ∩ B ) − P( A) ⋅ P(B )
ecuación 2.3.4
Convicción:
Es una medida de implicación. Es direccional y obtiene su máximo valor (infinito) si
la implicación es perfecta, esto es, si siempre que A ocurre sucede también B. Se muestra en la
ecuación 2.3.5.:
convicción( A ⇒ B ) =
P( A) ⋅ P(! B )
P( A∩! B )
ecuación 2.3.5
Por último, cabe destacar que esta implementación permite únicamente atributos simbólicos.
Además, para mejorar la eficiencia del algoritmo en la búsqueda de item-sets, elimina todos los
atributos que tengan sus valores desconocidos en todos los ejemplos.
TERTIUS en WEKA
El algoritmo TERTIUS disponible en WEKA es un algoritmo de descubrimiento de reglas de
asociación, sin embargo, difiere bastante del algoritmo Apriori. Por ejemplo, consideremos la típica
base de datos weather en su versión discretizada:
@relation weather.symbolic
@attribute outlook {sunny, overcast, rainy}
@attribute temperature {hot, mild, cool}
@attribute humidity {high, normal}
@attribute windy {TRUE, FALSE}
@attribute play {yes, no}
@data
sunny,hot,high,FALSE,no
sunny,hot,high,TRUE,no
overcast,hot,high,FALSE,yes
rainy,mild,high,FALSE,yes
rainy,cool,normal,FALSE,yes
rainy,cool,normal,TRUE,no
overcast,cool,normal,TRUE,yes
sunny,mild,high,FALSE,no
sunny,cool,normal,FALSE,yes
rainy,mild,normal,FALSE,yes
sunny,mild,normal,TRUE,yes
overcast,mild,high,TRUE,yes
overcast,hot,normal,FALSE,yes
rainy,mild,high,TRUE,no
Ejecutamos Apriori con los umbrales: minsup = 0.3 (es decir al menos cuatro instancias) y minconf
= 0.9, obtenemos las siguientes reglas:
1. humidity=normal windy=FALSE 4 ==> play=yes 4 conf:(1)
2. temperature=cool 4 ==> humidity=normal 4 conf:(1)
3. outlook=overcast 4 ==> play=yes 4 conf:(1)
Donde, el número que aparece a la izquierda es el soporte de la regla.
Si ejecutamos Tertius con las opciones por defecto las primeras reglas son:
1.
2.
3.
4.
5.
/*
/*
/*
/*
/*
0,633754
0,607625
0,607625
0,594071
0,590214
0,071429
0,000000
0,000000
0,214286
0,000000
*/
*/
*/
*/
*/
play = yes ==> outlook = overcast or humidity = normal
humidity = normal ==> temperature = cool or play = yes
temperature = cool ==> humidity = normal
humidity = normal ==> temperature = cool
outlook = sunny and humidity = high ==> play = no
Por lo que podemos ver que el resultado es bastante diferente. Dejando al margen los dos valores
que aparecen etiquetando a cada regla (y que discutiremos debajo), la implementación de Tertius en
WEKA permite hacer ciertas cosas diferentes a la implementación de Apriori. Así:
-114-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
• Podemos imponer que las reglas tengan estructura de clausulas de Horn, es decir, un único literal
en el consecuente, haciendo HornClauses = true. Si volvemos a ejecutar con esta opción obtenemos:
1.
2.
3.
4.
5.
/*
/*
/*
/*
/*
0,607625
0,594071
0,590214
0,486606
0,469374
0,000000
0,214286
0,000000
0,000000
0,000000
*/
*/
*/
*/
*/
temperature = cool ==> humidity = normal
humidity = normal ==> temperature = cool
outlook = sunny and humidity = high ==> play = no
outlook = sunny and play = no ==> humidity = high
outlook = overcast ==> play = yes
• Además podemos imponer la variable que queremos en el consecuente, haciendo classification =
true e indicando en classindex la variable que seleccionamos. Por ejemplo, si queremos Play
haremos classindex=5:
1.
2.
3.
4.
5.
/*
/*
/*
/*
/*
0,590214
0,469374
0,469374
0,439100
0,436395
0,000000
0,000000
0,000000
0,071429
0,214286
*/
*/
*/
*/
*/
outlook = sunny and humidity = high ==> play = no
outlook = overcast ==> play = yes
humidity = normal and windy = FALSE ==> play = yes
humidity = normal ==> play = yes
humidity = high ==> play = no
• También podemos obtener reglas sencillas o mas compactas indicando el número máximo de
literales que permitimos en una regla. Por defecto numberLiterals = 4.
El uso de estas opciones en Tertius junto con otras técnicas de minería de datos (p.e. clustering) y
de preprocesamiento, nos da una amplia variedad en las tareas a resolver.
Medidas usadas en Tertius
Las medidas usadas en Apriori de soporte y confianza no están exentas de críticas. Por ejemplo,
consideremos una base de datos con dos variables booleanas (B: jugar baloncesto y C:desayunar
cereales) y 5000 instancias distribuidas de la siguiente forma:
(B=t,C=t)
(B=t,C=f)
(B=f,C=t)
(B=f,C=f)
2000 instancias
1000 instancias
1750 instancias
250 instancias
Si consideramos las reglas:
B=t → C=t soporte=40%, confianza=67%
B=t → C=f soporte=20%, confianza=33%
Vemos que la primera regla a pesar de tener alto soporte y confianza no es en realidad nada útil, ya
que, nos dice que el 67% de los que juegan al baloncesto comen cereales, pero es que sin saber nada
acerca de baloncesto, la probabilidad a priori de comer cereales es del 75%, es decir, mayor. La
segunda regla, sin embargo, aunque tenga menor soporte y confianza es más interesante/útil.
Tertius no usa confianza para evaluar las reglas, sino una medida llamada confirmación (ecuación
2.3.6.), que se basa en considerar no sólo los datos a favor de una regla si no los datos en contra.
Así, hablaremos de instancias-en-contra para una regla como aquellas que satisfacen el antecedente
de la misma pero no el consecuente. Por ejemplo, para la regla B=t→C=t sus contra-instancias son
aquellas que contengan la instanciación (B=t,C=f).
En Tertius, si queremos calcular la confirmación de una regla A→B necesitamos calcular las
siguientes medidas para sus contra-instancias A, no(B).
Frecuencia observada: n( A, no( B) )
Frecuencia observada relativa: p ( A, no( B ) ) =
n( A, no( B ) )
N
n( A) ⋅ n(no( B) )
En este cálculo se asume que A y no(B) son independientes.
N
µ ( A, no( B) )
Frecuencia esperada relativa: π ( A, no( B ) ) =
, Número de veces que (A,no(B)) aparece en los datos.
N
Frecuencia esperada: µ ( A, no( B ) ) =
-115-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Novedad. Mide como de sorprendente/novedosa es una regla.
nov( A, no( B ) ) = π ( A, no( B ) ) − p ( A, no( B ) ) , donde N es el número de registros.
Confirmación:
υ/ ( A, no( B) ) = ± υ/ ( A, no( B) )2 =
π ( A, no( B) ) − p ( A, no( B) )
π ( A, no( B) ) − π ( A, no( B) )
ecuación 2.3.6
Está entre -0.25 y 0.25.
La medida de confirmación debe cumplir las siguientes propiedades:
Debe ser cero si la frecuencia esperada y la observada coinciden para las contra-instancias.
Debe decrecer monótonamente con la frecuencia observada de las contra-instancias.
Debe crecer monótonamente con la frecuencia observada p(no(consecuente)).
Por ejemplo, para las reglas analizadas anteriormente tendríamos:
Regla
Contra instancias
Freq. observada
Freq. observada
relativa
Freq. esperada
Freq. esperada
relativa
Novedad
Confirmación
y Tertius nos daría a la siguiente salida:
/* 0.226 0.400 */ B=t -> C=f
/* 0.221 0.200 */ B=t -> C=t
Donde el primer parámetro es la confirmación y el segundo la frecuencia observada de contra instancias. Lo
que es claro es que ahora la regla que indica que si se juega al baloncesto no se comen cereales es mas
interesante que la otra, como también indica el grado de novedad entre ambas reglas. De hecho, el grado de
novedad de la regla baloncesto → cereales, tiene novedad negativa, es decir, no es nada relevante tal y como
habíamos comentado antes.
2.4. La predicción
Es el proceso que intenta determinar los valores de una o varias variables, a partir de un conjunto
de datos.
La predicción de valores continuos puede planificarse por las técnicas estadísticas de regresión.
Se pueden resolver muchos problemas por medio de la regresión lineal, y puede conseguirse todavía
más aplicando las transformaciones a las variables para que un problema no lineal pueda convertirse
a uno lineal. A continuación se presenta una introducción intuitiva de las ideas de regresión lineal,
múltiple, y no lineal, así como la generalización a los modelos lineales.
Más adelante, dentro de la clasificación, se estudiarán varias técnicas de data mining que pueden
servir para predicción numérica. De entre todas ellas las más importantes se presentaran en la
clasificación bayesiana, la basada en ejemplares y las redes de neuronas. A continuación se
mostrarán un conjunto de técnicas que específicamente sirven para la predicción.
-116-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
2.4.1. Regresión Lineal
La regresión lineal es la forma más simple de regresión, ya que en ella se modelan los datos usando
una línea recta. Se caracteriza, por tanto, por la utilización de dos variables, una aleatoria, y
(llamada variable respuesta), que es función lineal de otra variable aleatoria, x (llamada variable
predictora), formándose la ecuación 2.4.1.
En esta ecuación la variación de y se asume que es constante, y a y b
son los coeficientes de regresión que especifican la intersección con
ecuación 2.4.1 el eje de ordenadas, y la pendiente de la recta, respectivamente
Estos coeficientes se calculan utilizando el método de los mínimos cuadrados que minimizan el
error entre los datos reales y la estimación de la línea.
Dados s ejemplos de datos en forma de puntos (x1, y1), (x2, x2),..., (xs, ys), entonces los coeficientes
de la regresión pueden estimarse según el método de los mínimos cuadrados con las ecuaciones
2.4.2 y 2.4.3.
ecuación 2.4.2
ecuación 2.4.3
Sxy es la covarianza
de x e y, y Sx2 la
varianza de x.
Los coeficientes a y b a menudo proporcionan buenas
aproximaciones a otras ecuaciones de regresión complicadas.
También es necesario saber cuán buena es la recta de regresión construida. Para ello, se emplea el
coeficiente de regresión (ecuación 2.4.4), que es una medida del ajuste de la muestra.
El valor de R2 debe estar entre 0 y 1. Si se acerca a 0 la
recta de regresión no tiene un buen ajuste, mientras que
si se acerca a 1 el ajuste es “perfecto”.
ecuación 2.4.4
En el ejemplo siguiente, para una muestra de 35 marcas de cerveza, se estudia la relación entre el grado de
alcohol de las cervezas y su contenido calórico. y se representa un pequeño conjunto de datos.
Figura 2.4.1. Regresión lineal simple.
El eje vertical muestra el número de calorías (por cada tercio de litro) y el horizontal el contenido de alcohol
(expresado en porcentaje). La nube de puntos es la representación de los datos de la muestra, y la recta es el
resultado de la regresión lineal aplicando el ajuste de los mínimos cuadrados.
En los siguientes apartados se mostrarán dos tipos de regresiones que amplían la regresión lineal
simple.
-117-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Regresión Lineal Múltiple
La regresión Lineal Múltiple es una extensión de regresión lineal que involucra más de una variable
predictora, y permite que la variable respuesta y sea planteada como una función lineal de un vector
multidimensional. El modelo de regresión múltiple para n variables predictoras sería como el que se
muestra en la ecuación 2.4.5.
ecuación 2.4.5
Para encontrar los coeficientes bi se plantea el modelo en términos de matrices, como se muestra en
la ecuación 2.4.6.
ecuación 2.4.6
En la matriz Z, las filas representan los m ejemplos disponibles para calcular la regresión, y las
columnas los n atributos que formarán parte de la regresión. De esta forma, zij será el valor que
toma en el ejemplo i el atributo j. El vector Y está formado por los valores de la variable
dependiente para cada uno de los ejemplos, y el vector B es el que se desea calcular, ya que se
corresponde con los parámetros desconocidos necesarios para construir la regresión lineal múltiple.
Representando con XT la matriz traspuesta de X y con X-1 la inversa de la matriz X, se calculará el
vector B mediante la ecuación 2.4.7
ecuación 2.4.7
Para determinar si la recta de regresión lineal múltiple está bien ajustada, se emplea el mismo
concepto que en el caso de la regresión lineal simple: el coeficiente de regresión. En este caso, se
utilizará la ecuación 2.4.8.
ecuación 2.4.8
Al igual que en el caso de la regresión simple, el valor de R2 debe estar entre 0 y 1, siendo 1 el
indicador de ajuste perfecto.
Una vez explicado el modo básico por el que se puede obtener una recta de regresión múltiple para
un conjunto de ejemplos de entrenamiento, a continuación se muestra, en la figura 2.4.2, un ejemplo
concreto en el que se muestra el proceso.
-118-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Figura 2.4.2: Ejemplo de obtención de una Regresión Lineal Múltiple.
Tal y como se muestra en la figura 2.4.2., en un primer momento se obtienen, a partir de los ejemplos de
entrenamiento, las matrices Z e Y, siendo el objetivo la matriz B. En el segundo paso se calcula los valores
de dicha matriz, que serán los coeficientes en la regresión. Por último, en un tercer paso se comprueba si la
recta generada tiene un buen ajuste o no. En este caso, como se muestra en la misma figura, el ajuste es
magnífico, dado que el valor de R2 es muy cercano a 1. Por último, en este ejemplo no se ha considerado el
término independiente, pero para que se obtuviese bastaría con añadir una nueva columna a la matriz Z con
todos los valores a 1.
Regresión Lineal en WEKA
Es en la clase weka.classifers.LinearRegression.java en la que se implementa la regresión lineal
múltiple. Las opciones que permite este algoritmo son las que se muestran en la tabla
Opción
AttributeSeleccionMethod (M5 method)
debug (False)
Descripción
Método de selección del atributo a eliminar de la regresión.
Las opciones son M5 Method, Greedy y None.
Muestra el proceso de construcción del clasificador.
Tabla 2.4.1. Opciones de configuración para el algoritmo de regresión lineal en WEKA.
La regresión lineal se construye tal y como se comentó anteriormente. Algunas propiedades de la
implementación son:
Admite
atributos numéricos y nominales. Los nominales con k valores se convierten en k-1
atributos binarios.
La
clase debe ser numérica.
Se
permite pesar cada ejemplo.
-119-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
En cuanto al proceso en sí, si bien se construye la regresión como se comentó anteriormente, se
sigue un proceso más complicado para eliminar los atributos. El algoritmo completo sería el
siguiente:
1. Construir regresión para los atributos seleccionados (en principio todos).
2. Comprobar la ecuación 2.4.8. sobre todos los atributos.
ci =
bi S i
Sc
ecuación 2.4.8
En la ecuación 2.4.8., SG es la desviación típica de la clase. Se elimina de la regresión el
atributo con mayor valor si cumple la condición ci>1.5. Si se eliminó alguno, volver a 1.
3. Calcular el error cuadrático medio y el factor Akaike tal y como se define en la ecuación
2.4.9
AIC = (m − p ) + 2 p
ecuación 2.4.9.
En la ecuación m es el número de ejemplos de entrenamiento, p el número de atributos
que forman parte de la regresión al llegar a este punto.
4. Escoger un atributo:
a. Si el método es Greedy, se generan regresiones lineales en las que se elimina un atributo
distinto en cada una de ellas, y se escoge la regresión con menor error medio absoluto.
b. Si el método es M5, se calcula el valor de ci (ecuación 2.64) para todos los atributos y se
escoge el menor. Se genera la regresión sin el atributo i y se calcula la regresión lineal
sin dicho atributo. Se calcula el error medio absoluto de la nueva regresión lineal.
c. Si el método es None, se finaliza el proceso.
5. Mejorar regresión. Se calcula el nuevo factor Akaike con la nueva regresión como es
muestra en la ecuación 2.4.10.
AIC =
MSE c
(m − pc ) + 2 p
MSE
ecuación 2.4.10
En la ecuación 2.4.10 MSEc es el error cuadrático medio absoluto de la nueva
regresión lineal y pc el número de atributos de la misma. Mientras, MSE es el valor
obtenido en el punto 3 y p el número de parámetros al llegar al mismo. Si el valor
nuevo de AIC es menor que el anterior, se actualiza éste como nuevo y se mantiene la
nueva regresión lineal, volviendo a intentar mejorarla (volver a 4). Si no es así, se
finaliza el proceso.
Regresión Lineal Ponderada Localmente
Otro método de predicción numérica es la regresión lineal ponderada localmente [Locally weighted
linear regresión]. Con este método se generan modelos locales durante el proceso de predicción
dando más peso a aquellos ejemplares de entrenamiento más cercanos al que hay que predecir.
Dicho de otro modo, la construcción del clasificador consiste en el almacenamiento de los ejemplos
de entrenamiento, mientras que el proceso de validación o de clasificación de un ejemplo de test
consiste en la generación de una regresión lineal específica, esto es, una regresión lineal en la que
se da más peso a aquellos ejemplos de entrenamiento cercanos al ejemplo a clasificar. De esta
forma, este tipo de regresión está íntimamente relacionado con los algoritmos basados en
ejemplares.
-120-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Para utilizar este tipo de regresión es necesario decidir un esquema de ponderación para los
ejemplos de entrenamiento, esto es, decidir cuánto peso se le va a dar a cada ejemplo de
entrenamiento para la clasificación de un ejemplo de test. Una medida usual es ponderar el ejemplo
de entrenamiento con la inversa de la distancia euclídea entre dicho ejemplo y el de test, tal y como
se muestra en ecuación 2.4.11.
ωi =
1
1 + d ij
ecuación 2.4.11
En esta ecuación ωi es el peso que se le otorgará al ejemplo de entrenamiento i para clasificar
al ejemplo j, y dij será la distancia euclídea de i con respecto a j.
Más crítico que la elección del método para ponderar es el “parámetro de suavizado” que se
utilizará para escalar la función de distancia, esto es, la distancia será multiplicada por la inversa de
este parámetro. Si este parámetro es muy pequeño sólo los ejemplos muy cercanos recibirán un gran
peso, mientras que si es demasiado grande los ejemplos muy lejanos podrían tener peso.
Un modo de asignar un valor a este parámetro es dándole el valor de la distancia del k-ésimo vecino
más cercano al ejemplo a clasificar. El valor de k dependerá del ruido de los datos. Cuanto más
ruido, más grande deberá ser k. Una ventaja de este método de estimación es que es capaz de
aproximar funciones no lineales. Además, se puede actualizar el clasificador (modelo incremental),
dado que únicamente sería necesario añadirlo al conjunto de entrenamiento. Sin embargo, como el
resto de algoritmos basado en ejemplares, es lento.
Regresión Lineal Ponderada Localmente en WEKA
El algoritmo se implementa en la clase weka.classifers.LWR.java. Las opciones que permite
configurar son las que se muestran en la tabla:
Opción
Descripción
weightingKernel (0)
debug (False)
KNN (5)
Indica cuál va a ser el método para ponderar a los ejemplos de entrenamiento:
0, lineal; 1, inverso; 2, gaussiano.
Muestra el proceso de construcción del clasificador y validación de los
ejemplos de test.
Número de vecinos que se tendrán en cuenta para ser ponderados y calcular la
regresión lineal. Si bien el valor por defecto es 5, si no se modifica o confirma
se utilizan todos los vecinos.
Tabla. Opciones de configuración para el algoritmo LWR en WEKA.
En primer lugar, las ecuaciones que se emplean en los métodos para ponderar a los ejemplos de
entrenamiento son: para el método lineal, la ecuación 2.4.12.; y para el método gaussiano, la
ecuación 2.4.13.
ω i = max (1.0001 − d ij ,0 ) ecuación 2.4.12.
ωi = e
− dij ⋅dij
ecuación 2.4.13.
El proceso que sigue el algoritmo es el que se comentó anteriormente. Algunas propiedades que hay
que mencionar sobre la implementación son:
Se
admiten atributos simbólicos y numéricos.
Se admiten ejemplos ya pesados, en cuyo caso, el peso obtenido del proceso explicado anteriormente se
multiplica por el peso del ejemplo.
Se toma como parámetro de suavizado la siguiente distancia mayor al del k-ésimo ejemplo más próximo.
Para la generación de la regresión lineal se emplea la clase explicada en el punto anterior, con los
parámetros por defecto y con los ejemplos pesados.
-121-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
2.4.2. Regresión No Lineal
En muchas ocasiones los datos no muestran una dependencia lineal. Esto es lo que sucede si, por
ejemplo, la variable respuesta depende de las variables independientes según una función
polinómica, dando lugar a una regresión polinómica que puede planearse agregando las
condiciones polinómicas al modelo lineal básico.
De está forma y aplicando ciertas transformaciones a las variables, se puede convertir el modelo no
lineal en uno lineal que puede resolverse entonces por el método de mínimos cuadrados. Por
ejemplo considérese una relación polinómica cúbica dada por:
y = a + b1 x + b2 x 2 + b3 x 3
ecuación 2.4.14.
Para convertir esta ecuación a la forma lineal, se definen las nuevas variables:
x1 = x
x2 = x 2
x3 = x 3
ecuación 2.4.15.
Con lo que la ecuación anterior puede convertirse entonces a la forma lineal aplicando los cambios
de variables, y resultando la ecuación 2.4.16, que es resoluble por el método de mínimos cuadrados
y = a + b1 x1 + b2 x 2 + b3 x3
ecuación 2.4.16.
No obstante, algunos modelos son especialmente no lineales como, por ejemplo, la suma de
términos exponenciales y no pueden convertirse a un modelo lineal. Para estos casos, puede ser
posible obtener las estimaciones del mínimo cuadrado a través de cálculos extensos en formulas
más complejas.
Los modelos lineales generalizados representan el fundamento teórico en que la regresión lineal
puede aplicarse para modelar las categorías de las variables dependientes. En los modelos lineales
generalizados, la variación de la variable y es una función del valor medio de y, distinto a la
regresión lineal dónde la variación de y es constante. Los tipos comunes de modelos lineales
generalizados incluyen regresión logística y regresión del Poisson. La regresión logística modela la
probabilidad de algún evento que ocurre como una función lineal de un conjunto de variables
independientes. Frecuentemente los datos exhiben una distribución de Poisson y se modelan
normalmente usando la regresión del Poisson.
Los modelos lineales logarítmicos aproximan las distribuciones de probabilidad
multidimensionales discretas, y pueden usarse para estimar el valor de probabilidad asociado con
los datos de las células cúbicas. Por ejemplo, suponiendo que se tienen los datos para los atributos
ciudad, artículo, año, y ventas. En el método logarítmico lineal, todos los atributos deben ser
categorías; por lo que los atributos estimados continuos (como las ventas) deben ser previamente
discretizados.
-122-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
2.4.3. Árboles de Predicción
Los árboles de predicción numérica son similares a los árboles de decisión, que se estudiarán más
adelante, excepto en que la clase a predecir es continua. En este caso, cada nodo hoja almacena un
valor de clase consistente en la media de las instancias que se clasifican con esa hoja, en cuyo caso
estamos hablando de un árbol de regresión, o bien un modelo lineal que predice el valor de la clase,
en cuyo caso se habla de árbol de modelos.
En el caso del algoritmo M5, se trata de obtener un árbol de modelos, si bien se puede utilizar para
obtener un árbol de regresión, por ser éste un caso específico de árbol de modelos.
Mientras que en el caso de los árboles de decisión se emplea la entropía de clases para definir el
atributo con el que dividir, en el caso de la predicción numérica se emplea la varianza del error en
cada hoja. Una vez construido el árbol que clasifica las instancias se realiza la poda del mismo, tras
lo cual, se obtiene para cada nodo hoja una constante en el caso de los árboles de regresión o un
plano de regresión en el caso de árboles de modelos. En éste último caso, los atributos que formarán
parte de la regresión serán aquellos que participaban en el subárbol que ha sido podado.
Al construir un árbol de modelos y definir, para cada hoja, un modelo lineal con los atributos del
subárbol podado suele ser beneficioso, sobre todo cuando se tiene un pequeño conjunto de
entrenamiento, realizar un proceso de suavizado [smoothing] que compense las discontinuidades
que ocurren entre modelos lineales adyacentes. Este proceso consiste en: cuando se predice el valor
de una instancia de test con el modelo lineal del nodo hoja correspondiente, este valor obtenido se
filtra hacia atrás hasta el nodo hoja, suavizando dicho valor al combinarlo con el modelo lineal de
cada nodo interior por el que pasa. Un modelo que se suele utilizar es el que se muestra en la
ecuación 2.4.17.
p' =
np + kq
n+k
ecuación 2.4.17.
En esta ecuación, p es la predicción que llega al nodo (desde abajo), p’ es la predicción filtrada
hacia el nivel superior, q el valor obtenido por el modelo lineal de este nodo, n es el número
de ejemplos que alcanzan el nodo inferior y k el factor de suavizado.
Para construir el árbol se emplea como heurística el minimizar la variación interna de los valores de
la clase dentro de cada subconjunto. Se trata de seleccionar aquel atributo que maximice la
reducción de la desviación estándar de error (SDR, [standard deviation reduction]) con la fórmula
que se muestra en la ecuación 2.4.18
SDR = SD ( E ) − ∑
i
Ei
E
SD( Ei )
ecuación 2.4.18.
En esta ecuación E es el conjunto de ejemplos en el nodo a dividir, Ej es cada uno de los
conjuntos de ejemplos que resultan en la división en el nodo según el atributo considerado, |E|
es el número de ejemplos del conjunto E y SD(E) la desviación típica de los valores de la
clase en E.
El proceso de división puede finalizar porque la desviación típica es una pequeña fracción (por
ejemplo, el 5%) de la desviación típica del conjunto original de instancias o porque hay pocas
instancias (por ejemplo, 2).
En la figura 2.4.3., se muestra un ejemplo de generación del árbol de predicción con el algoritmo M5. Para
ello se muestra en primer lugar los ejemplos de entrenamiento, en los que se trata de predecir los puntos que
un jugador de baloncesto anotaría en un partido.
-123-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Figura 2.4.3: Ejemplo de generación del árbol de predicción con M5.
En cada nodo del árbol se muestra la desviación típica de los ejemplos de entrenamiento que inciden en el
nodo (SD(E)) y la desviación estándar del error para el atributo y el punto de corte que lo maximiza, por lo
que es el seleccionado. Para obtener el atributo y el punto de corte se debe calcular la desviación estándar del
error para cada posible punto de corte. En este caso, la finalización de la construcción del árbol ocurre
porque no se puede seguir subdividiendo, ya que en cada hoja hay dos ejemplos (número mínimo permitido).
Por último, tras generar el árbol, en cada hoja se añade la media de los valores de la clase de los ejemplos
que se clasifican a través de dicha hoja. Una vez se ha construido el árbol se va definiendo, para cada nodo
interior (no para las hojas para emplear el proceso de suavizado) un modelo lineal, concretamente una
regresión lineal múltiple, tal y como se mostró anteriormente. Únicamente se emplean para realizar esta
regresión aquellos atributos que se utilizan en el subárbol del nodo en cuestión. A continuación se pasa al
proceso de poda, en el que se estima, para cada nodo, el error esperado en el conjunto de test. Para ello, lo
primero que se hace es calcular la desviación de las predicciones del nodo con los valores reales de la clase
para los ejemplos de entrenamiento que se clasifican por el mismo nodo.
Sin embargo, dado que el árbol se ha construido con estos ejemplos, el error puede desestimarse,
con lo que se compensa con el factor (n+v)(n-v), donde n es el número de ejemplos de
entrenamiento que se clasifican por el nodo actual y v es el número de parámetros del modelo lineal.
De esta forma, la estimación del error en un conjunto I de ejemplos se realizaría con la ecuación
2.4.19.
MAE es el error medio absoluto [mean absolute
error] del modelo, donde yi es el valor de la
clase para el ejemplo i y ŷ i la predicción del
modelo para el mismo ejemplo.
ecuación 2.4.19
Para podar el árbol, se comienza por las hojas del mismo y se va comparando el error estimado
para el nodo con el error estimado para los hijos del mismo, para lo cuál se emplea la ecuación
2.4.20.
ecuación 2.4.20.
En la ecuación 2.4.20, e(i) y e(d) son los errores estimados para los nodos hijo izquierdo y
derecho, |x| el número de ejemplos que se clasifica por el nodo x y n el número de ejemplos
que se clasifica por el nodo padre. Comparando el error estimado para el nodo con el error
estimado para el subárbol, se decide podar si no es menor el error para el subárbol.
-124-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
El proceso explicado hasta el momento sirve para el caso de que los atributos sean numéricos pero,
si los atributos son nominales será preciso modificar el proceso: en primer lugar, se calcula el
promedio de la clase en los ejemplos de entrenamiento para cada posible valor del atributo
nominal, y se ordenan dichos valores de acuerdo a este promedio. Entonces, un atributo nominal
con k posibles valores se transforma en k-1 atributos binarios. El i-ésimo atributo binario tendrá,
para un ejemplo dado, un 0 si el valor del atributo nominal es uno de los primeros i valores del
orden establecido y un 1 en caso contrario. Con este proceso se logra tratar los atributos nominales
como numéricos.
También es necesario determinar cómo se actuará frente a los atributos para los que faltan valores.
En este caso, se modifica ligeramente la ecuación 2.4.18 para llegar hasta la ecuación 2.4.21.
ecuación 2.4.21.
En esta ecuación c es el número de ejemplos con el atributo conocido.
Una vez explicadas las características de los árboles de predicción numérica, se pasa a mostrar el
algoritmo M5, cuyo pseudocódigo se muestra a continuación:
M5 (ejemplos) {
SD = sd(ejemplos)
Para cada atributo nominal con k-valores
convertir en k-1 atributos binarios
raíz = nuevo nodo
raíz.ejemplos = ejemplos
Dividir(raíz)
Podar(raíz)
Dibujar(raíz)
}
Dividir(nodo) {
Si tamaño(nodo.ejemplos)<4 O sd(nodo.ejemplos)<=0.05*SD Entonces
nodo.tipo = HOJA
Si no
nodo.tipo = INTERIOR
Para cada atributo
Para cada posible punto de división del atributo
calcular el SDR del atributo
nodo.atributo = atributo con mayor SDR
Dividir(nodo.izquierda)
Dividir(nodo.derecha)
}
Podar(nodo) {
Si nodo = INTERIOR
Podar(nodo.hijoizquierdo)
Podar(nodo.hijoderecho)
nodo.modelo = RegresionLinear(nodo)
Si ErrorSubarbol(nodo) > Error(nodo) Entonces
nodo.tipo = HOJA
}
ErrorSubarbol(nodo) {
l = nodo.izquierda
r = nodo.derecha
Si nodo = INTERIOR Entonces
ErrorSubarbol = (tamaño(l.ejemplos)*ErrorSubarbol(l) +
tamaño(r.ejemplos)*ErrorSubarbol(r))tamaño(nodo.ejemplos)
Si no
ErrorSubarbol = error(nodo)
}
-125-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
La función RegresionLinear generará la regresión correspondiente al nodo en el que nos
encontramos. La función error evaluará el error del nodo mediante la ecuación 2.4.20.
M5 en WEKA
La clase en la que se implementa el algoritmo M5 en la herramienta WEKA es
weka.classifers.m5.M5Prime.java. Las opciones que permite este algoritmo son las que se
muestran en la tabla:
Opción
Descripción
ModelType (ModelTree)
useUnsmoothed (False)
pruningFactor (2.0)
verbosity (0)
Permite seleccionar como modelo a construir entre un árbol de modelos, un
árbol de regresión o una regresión lineal.
Indica si se realizará el proceso de suavizado (False) o si no se realizará
(True).
Permite definir el factor de poda.
Sus posibles valores son 0, 1 y 2, y permite definir las estadísticas que se
mostrarán con el modelo.
Tabla. Opciones de configuración para el algoritmo M5 en WEKA.
En cuanto a la implementación concreta que se lleva a cabo en esta herramienta del algoritmo M5,
cabe destacar lo siguiente:
Admite
atributos simbólicos y numéricos; la clase debe ser, por supuesto, numérica.
Para la generación de las regresiones lineales se emplea la clase que implementa la regresión
lineal múltiple en WEKA.
El número mínimo de ejemplos que deben clasificarse a través de un nodo para seguir dividiendo
dicho nodo, definido en la constante SPLIT_NUM es 3.5, mientras la otra condición de parada, que
es la desviación típica de las clases en el nodo respecto a la desviación típica de todas las clases
del conjunto de entrenamiento, está fijada en 0.05.
En realidad no se intenta minimizar el SDR tal y como se definió en la ecuación 2.4.18, sino que se
intenta minimizar la ecuación 2.4.22, que se muestra a continuación.
n
n
SDR = 5 S 2 − i 5 S i2 − D 5 S D2 ecuación 2.4.22
n
n
En la ecuación 2.4.22, n es el número total de ejemplos, nI y nD el número de ejemplos del grupo izquierdo
y derecho respectivamente; y S, S2I y S2D la varianza del conjunto completo, del grupo izquierdo y del
grupo derecho respectivamente, definiéndose la varianza como se muestra en la ecuación 2.4.23.
S2 =
∑
n
X2
i =1 i
(∑ x )
−
2
n
i =1 i
n
n
ecuación 2.4.23
En la ecuación 2.4.23 n es el número de ejemplos y xi el valor de la clase para el ejemplo i.
cálculo del error de estimación para un nodo determinado, se modifica ligeramente hasta llegar
al que se muestra en la ecuación 2.4.24.
El
n + pv
e(l ) =
×
n−v
∑ ( yi − yˆ i )
i∈l
2


−  ∑ y i − yˆ i 
 i∈l

n
2
ecuación 2.4.24
En la ecuación 2.4.24., p es el factor de podado que es configurable y, por defecto es 2.
Por
último, la constante k empleada en el modelo de suavizado se configura con el valor 15.
-126-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
2.4.4. Estimador de Núcleos
Los estimadores de densidad de núcleo [kernel density] son estimadores no paramétricos. De entre
los que destaca el conocido histograma, por ser uno de los más antiguos y más utilizado, que tiene
ciertas deficiencias relacionadas con la continuidad que llevaron a desarrollar otras técnicas.
La idea en la que se basan los estimadores de densidad de núcleo es la siguiente. Si X es una
variable aleatoria con función de distribución F y densidad f, entonces en cada punto de continuidad
x de f se confirma la ecuación 2.4.22.
f ( x ) = lim h→0
1
(F (x + h ) − F (x − h )) ecuación 2.4.22.
2h
Dada una muestra X1,...,Xn proveniente de la distribución F, para cada h fijo, F(x+h)-F(x-h) se
puede estimar por la proporción de observaciones que están dentro del intervalo (x-h, x+h). Por lo
tanto, tomando h pequeño, un estimador natural de la densidad es el que se muestra en la ecuación
2.4.23, donde #A es el número de elementos del conjunto A.
1
fˆn,h ( x ) =
# {X i : X ∈ ( x − h, x + h )} ecuación 2.4.23.
2hn
Otra manera de expresar este estimador es considerando la función de peso w definida como se
muestra en la ecuación 2.4.24, de manera que el estimador de la densidad f en el punto x se puede
expresar como se expresa en la ecuación 2.4.25.
 1 si x < 1
w( x ) =  2
 0 en c.c.
ecuación 2.4.24.
1 n 1  x − Xi 
fˆn,h ( x ) = ∑ w

n i =1 h  h 
ecuación 2.4.25.
Pero este estimador no es una función continua, ya que tiene saltos en los puntos Xi±h y su derivada
es 0 en todos los otros puntos. Por ello se ha sugerido reemplazar a la función w por funciones más
suaves K, llamadas núcleos, lo que da origen a los estimadores de núcleos. El estimador de núcleos
de una función de densidad f calculado a partir de una muestra aleatoria X1,...,Xn de dicha densidad
se define según la ecuación 2.4.26.
1 n  x − Xi 
fˆn,h ( x ) =

∑ K
nh i =1  h 
ecuación 2.4.26.
En la ecuación 2.4.26, la función K se elige generalmente entre las funciones de densidad
conocidas, por ejemplo gaussiana, que se muestra en la ecuación 2.4.27, donde σ es la
desviación típica de la distribución y µ la media.
1
f ( x) =
2πσ
e
−
( x − µ )2
2σ 2
ecuación 2.4.27.
El otro parámetro de la ecuación 2.4.26 es h, llamado ventana, parámetro de suavizado o ancho de
banda, el cual determina las propiedades estadísticas del estimador: el sesgo crece y la varianza
decrece con h. Es decir que si h es grande, los estimadores están sobresuavizados y son sesgados, y
si h es pequeño, los estimadores resultantes están subsuavizados, lo que equivale a decir que su
varianza es grande.
-127-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Figura 2.4.4. Importancia del parámetro “tamaño de ventana” en el estimador de núcleos.
A pesar de que la elección del núcleo K determina la forma de la densidad estimada, la literatura
sugiere que esta elección no es crítica, al menos entre las alternativas usuales. Más importante es la
elección del tamaño de ventana. En la figura 2.4.1 se muestra cómo un valor pequeño para este
factor hace que la función de distribución generada esté subsuavizada. Mientras, al emplear un h
demasiado grande provoca el sobresuavizado de la función de distribución. Por último, empleando
el h óptimo se obtiene la función de distribución adecuada.
Para determinar un ancho de banda con el cual comenzar, una alternativa es calcular el ancho de
banda óptimo si se supone que la densidad tiene una forma específica. La ventana óptima en el
sentido de minimizar el error medio cuadrático integrado, definido como la esperanza de la integral
del error cuadrático sobre toda la densidad, depende de la verdadera densidad f y del núcleo K. Al
suponer que ambos, la densidad y el núcleo son normales, la ventana óptima resulta ser la que se
muestra en la ecuación 2.4.28.
ecuación 2.4.28.
En la ecuación 2.4.28 σ es la desviación típica de la densidad.
La utilización de esta h será adecuada si la población se asemeja en su distribución a la de la
normal; sin embargo si trabajamos con poblaciones multimodales se producirá una
sobresuavización de la estimación. Por ello se sugiere utilizar medidas robustas de dispersión en
lugar de σ, con lo cual el ancho de banda óptimo se obtiene como se muestra en la ecuación 2.4.29.
ecuación 2.4.29.
En la ecuación 2.4.29., IQR es el rango intercuartílico, esto es, la diferencia entre los percentiles 75 y 25.
Una vez definidos todos los parámetros a tener en cuenta para emplear un estimador de núcleos, hay
que definir cómo se obtiene, a partir del mismo, el valor de la variable a predecir, y, en función del
valor de la variable dependiente, x. Esto se realiza mediante el estimador de Nadaraya-Watson, que
se muestra en la ecuación 2.4.30.
 x − Xi 
Yi
h 
i =1
mˆ ( x) = E (Y | X = x ) = n
x−X 
∑ K  h r 
r =1
n
∑ K 
ecuación 2.4.30.
En la ecuación 2.4.30 x es el valor del atributo dependiente a partir del cual se debe obtener el valor de la variable
independiente y; Yi es el valor del atributo independiente para el ejemplo de entrenamiento i.
-128-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
En la figura 2.4.5, un ejemplo de su utilización tomando la variable temperatura como predictora y la
variable humedad como dependiente o a predecir.
Figura 2.4.5. Ejemplo de predicción con un estimador de núcleos.
En primer lugar se definen los parámetros que se van a emplear para el estimador de núcleos: la función
núcleo y el parámetro de suavizado. Posteriormente se puede realizar la predicción, que en este caso consiste
en predecir el valor del atributo humedad sabiendo que la temperatura es igual a 77. Después de completar el
proceso se determina que el valor de la humedad es igual a 82.97.
Aplicación a problemas multivariantes
Hasta el momento se han explicado las bases sobre las que se sustentan los estimadores de núcleos,
pero en los problemas reales no es una única variable la que debe tratarse, sino que han de tenerse
en cuenta un número indeterminado de variables. Por ello, es necesario ampliar el modelo
explicado para permitir la introducción de d variables. Así, supongamos n ejemplos Xi, siendo Xi
un vector d-dimensional. El estimador de núcleos de la función de densidad f calculado a partir de
la muestra aleatoria X1,...,Xn de dicha densidad se define como se muestra en la ecuación 2.4.31.
1
fˆn, H ( x) =
nH
∑ K (H −1 ( x − X i ) )
n
ecuación 2.4.31.
i =1
Tal y como puede verse, la ecuación 2.4.31., es una mera ampliación de la ecuación 2.4.26: en este
caso H no es ya un único valor numérico, sino una matriz simétrica y definida positiva de orden d×
d, denominada matriz de anchos de ventana. Por su parte K es generalmente una función de
densidad multivariante.
Por ejemplo, la función gaussiana normalizada en este caso pasaría a ser la que se muestra en la
ecuación 2.4.32.
f ( x) =
xT x
e 2
1
(2π )
d
2
-129-
ecuación 2.4.32.
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
De nuevo, es más importante definir una correcta matriz H que la función núcleo elegida. También
el estimador de Nadaraya-Watson, que se muestra en la ecuación 2.4.33, es una ampliación del visto
en la ecuación 2.4.30.
ecuación 2.4.33.
Tal y como se ve en la ecuación 2.4.33, el cambio radica en que se tiene una matriz de anchos de
ventana en lugar de un único valor de ancho de ventana.
Aplicación a problemas de clasificación
Si bien los estimadores de núcleo son diseñados para la predicción numérica, también pueden
utilizarse para la clasificación. En este caso, se dispone de un conjunto de c clases a las que puede
pertenecer un ejemplo determinado. Y estos ejemplos se componen de d variables o atributos. Se
puede estimar la densidad de la clase j mediante la ecuación 2.4.34, en la que nj es el número de
ejemplos de entrenamiento que pertenecen a la clase j, Yij será 1 en caso de que el ejemplo i
pertenezca a la clase j y 0 en otro caso, K vuelve a ser la función núcleo y h el ancho de ventana.
En este caso se ha realizado la simplificación del modelo multivariante, empleando en lugar de una
matriz de anchos de ventana un único valor escalar porque es el modelo que se utiliza en la
implementación que realiza WEKA de los estimadores de núcleo.
ecuación 2.4.34.
La probabilidad a priori de que un ejemplo pertenezca a la clase j es igual a Pj = n j / n Se puede
estimar la probabilidad a posteriori, definida mediante qj(x), de que el ejemplo pertenezca a j, tal y
como se muestra en la ecuación 2.4.35.
ecuación 2.4.35.
De esta forma, el estimador en este caso es idéntico al estimador de Nadayara-Watson.
Por último, se muestra un ejemplo de la aplicación de un estimador de núcleos a un problema de
clasificación: se trata de predecir el valor de la clase jugar a partir únicamente del atributo numérico
temperatura. Este ejemplo se muestra en la figura 2.4.6.
-130-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Figura 2.4.6.: Ejemplo de clasificación mediante un estimador de núcleos.
Al igual que para el problema de predicción, en primer lugar se definen los parámetros del estimador de
núcleos para, posteriormente, estimar la clase a la que pertenece el ejemplo de test. En este caso se trata de
predecir si se puede jugar o no al tenis teniendo en cuenta que la temperatura es igual a 77. Y la conclusión a
la que se llega utilizando el estimador de núcleos es que sí se puede jugar.
Kernel Density en WEKA
Es en la clase weka.classifiers.KernelDensity en la que se implementa el algoritmo de densidad de
núcleo. No se puede configurar dicho algoritmo con ninguna propiedad. Además, sólo se admiten
clases simbólicas, a pesar de que los algoritmos de densidad de núcleo, como se comentó
anteriormente nacen como un método de estimación no paramétrica (clases numéricas). A
continuación se muestran las principales propiedades de la implementación así como los atributos y
clases permitidas:
En cuanto a los atributos, pueden ser numéricos y simbólicos.
La
clase debe ser simbólica.
Como función núcleo [kernel] se emplea la distribución normal o gaussiana normalizada, esto es,
con media 0 y desviación típica 1.
tamaño de ventana se emplea h = 1 / n siendo n el número de ejemplos de entrenamiento.
Para clasificar el ejemplo Ai, para cada ejemplo de entrenamiento Aj se calcula la ecuación 2.4.36.:
Como
(
)
V ( Ai , A j ) = K dist ( Ai , A j ) × n × n
ecuación 2.4.36.
Es la distancia entre el ejemplo de test y uno de los ejemplos de entrenamiento. El resultado de
esta ecuación para el par Ai-Aj se sumará al resto de resultados obtenidos para la clase a la que
pertenezca el ejemplo Aj.
-131-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
El pseudocódigo del algoritmo implementado por WEKA es:
Kernel Density (ejemplo) {
Para cada ejemplo de entrenamiento (E) Hacer
prob = 1
c = clase de E
Para cada atributo de E (A) Hacer
temp = V(ejemplo, A)
Si temp < LB Entonces
prob = prob * LB
Si no
prob = prob * temp
probs[c] = probs[c] + prob
Normalizar(probs)
}
La clase que obtenga una mayor probabilidad será la que resulte ganadora, y la que se asignará al
ejemplo de test. En cuanto a la constante LB, se define en la ecuación 2.4.37.:
1
min es el número mínimo almacenable por un double en Java
y t el número de atributos de los ejemplos (incluida la clase).
LB = min t −1
ecuación 2.4.37.
2.5. LA CLASIFICACIÓN
La clasificación es el proceso de dividir un conjunto de datos en grupos mutuamente excluyentes,
de tal forma que cada miembro de un grupo esté lo mas cerca posible de otros y grupos diferentes
estén lo más lejos posible de otros, donde la distancia se mide con respecto a las variables
especificadas, que se quieren predecir.
El ejemplo empleado (Tabla 2.5.1) tiene dos atributos, temperatura y humedad, que pueden
emplearse como simbólicos o numéricos. Entre paréntesis se presentan sus valores numéricos.
Ejemplo
Vista
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Soleado
Soleado
Nublado
Lluvioso
Lluvioso
Lluvioso
Nublado
Soleado
Soleado
Lluvioso
Soleado
Nublado
Nublado
Lluvioso
Temperatura
Alta
Alta
Alta
Media
Baja
Baja
Baja
Media
Baja
Media
Media
Media
Alta
Media
(85)
(80)
(83)
(70)
(68)
(65)
(64)
(72)
(69)
(75)
(75)
(72)
(81)
(71)
Humedad
Viento
Jugar
Alta (85)
Alta (90)
Alta (86)
Alta (96)
Normal (80)
Normal (70)
Normal (65)
Alta (95)
Normal (70)
Normal (80)
Normal (70)
Alta (90)
Normal (75)
Alta (91)
No
Sí
No
No
No
Sí
Sí
No
No
No
Sí
Sí
No
Sí
No
No
Sí
Sí
Sí
No
Sí
No
Sí
Sí
Sí
Sí
Sí
No
Tabla 2.5.1. Ejemplo de problema de clasificación.
En los siguientes apartados se presentan y explican las principales técnicas de clasificación.
Además, se mostrarán ejemplos que permiten observar el funcionamiento del algoritmo, para lo que
se utilizará la tabla 2.5.1 que presenta un sencillo problema de clasificación consistente en, a partir
de los atributos que modelan el tiempo (vista, temperatura, humedad y viento), determinar si se
puede o no jugar al tenis.
-132-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
2.5.1. Tabla de Decisión
La tabla de decisión constituye la forma más simple y rudimentaria de representar la salida de un
algoritmo de aprendizaje, que es justamente representarlo como la entrada.
Estos algoritmos consisten en seleccionar subconjuntos de atributos y calcular su precisión
[accuracy] para predecir o clasificar los ejemplos. Una vez seleccionado el mejor de los
subconjuntos, la tabla de decisión estará formada por los atributos seleccionados (más la clase), en
la que se insertarán todos los ejemplos de entrenamiento únicamente con el subconjunto de atributos
elegido.
Si hay dos ejemplos con exactamente los mismos pares atributo-valor para todos los atributos del
subconjunto, la clase que se elija será la media de los ejemplos (en el caso de una clase numérica) o
la que mayor probabilidad de aparición tenga (en el caso de una clase simbólica).
La precisión de un subconjunto S de atributos para todos los ejemplos de entrenamientos se
calculará mediante la ecuación 2.5.1 para el caso de que la clase sea simbólica o mediante la
ecuación 2.5.2 en el caso de que la clase sea numérica:
ecuación 2.5.1
ecuación 2.5.2
Donde, en la ecuación 2.5.2, RMSE es la raíz cuadrada del error cuadrático medio [root mean
squared error], n es el número de ejemplos totales, yi el valor de la clase para el ejemplo i y
ŷ i el valor predicho por el modelo para el ejemplo i.
Como ejemplo de tabla de decisión, simplemente se puede utilizar la propia tabla 2.5.1, dado que si se
comenzase a combinar atributos y a probar la precisión de dicha combinación, se obtendría como resultado
que los cuatro atributos deben emplearse, con lo que la tabla de salida sería la misma. Esto no tiene por qué
ser así, ya que en otros problemas no serán necesarios todos los atributos para generar la tabla de decisión,
como ocurre en el ejemplo de la tabla 2.5.2 donde se dispone de un conjunto de entrenamiento en el que
aparecen los atributos sexo, y tipo (tipo de profesor) y la clase a determinar es si el tipo de contrato es o no
fijo.
Atributos
Clase
Ejemplo Nº
Sexo
Tipo
Fijo
1
2
3
4
5
6
7
8
9
10
Hombre
Mujer
Hombre
Mujer
Hombre
Mujer
Hombre
Mujer
Hombre
Mujer
Asociado
Catedrático
Titular
Asociado
Catedrático
Asociado
Ayudante
Titular
Asociado
Ayudante
No
Si
Si
No
Si
No
No
Si
No
No
11
Hombre
Asociado
No
Tabla 2.5.2. Determinación del tipo de contrato.
Si se toma como primer subconjunto el formado por el atributo sexo, y se eliminan las repeticiones resulta la
tabla 2.5.3
-133-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Ejemplo Nº
Sexo
Fijo
1
Hombre
No
2
3
4
Mujer
Hombre
Mujer
Si
Si
No
Tabla 2.5.3. Subconjunto 1
Con lo que se pone de manifiesto que la probabilidad de clasificar bien es del 50%. Si por el contrario se
elimina el atributo Sexo, quedará la tabla 2.5.4.
Ejemplo Nº
Tipo
Fijo
1
Asociado
No
2
3
4
Catedrático
Titular
Ayudante
Si
Si
No
Tabla 2.5.4. Subconjunto 2
Que tiene una precisión de aciertos del 100%, por lo que se deduce que ésta última tabla es la que se debe
tomar como tabla de decisión. El resultado es lógico ya que el atributo sexo es irrelevante a la hora de
determinar si el contrato es o no fijo.
Tabla de Decisión en WEKA
El algoritmo de tabla de decisión implementado en la herramienta WEKA se encuentra en la clase
weka.classifiers.DecisionTable.java. Las opciones de configuración de que disponen son las que
vemos en la tabla 2.5.5:
Opción
useIBk (False)
displayRules (False)
maxStale (5)
crossVal (1)
Descripción
Utilizar NN en lugar de la tabla de decisión si no la instancia a clasificar no
se corresponde con ninguna regla de la tabla.
Por defecto no se muestran las reglas del clasificador, concretamente la tabla
de decisión construida.
Indica el número máximo de conjuntos que intenta mejorar el algoritmo para
encontrar una tabla mejor sin haberla encontrado en los últimos n-1
subconjuntos.
Por defecto se evalúa el sistema mediante el proceso leave-one-out. Si se
aumenta el valor 1 se realiza validación cruzada con n carpetas.
Tabla 2.5.5. Opciones de configuración para el algoritmo de tabla de decisión en WEKA.
En primer lugar, en cuanto a los atributos que permite el sistema, éstos pueden ser tanto numéricos (que se
discretizarán) como simbólicos. La clase también puede ser numérica o simbólica. El algoritmo consiste en ir
seleccionando uno a uno los subconjuntos, añadiendo a cada uno de los ya probados cada uno de los
atributos que aún no pertenecen a él. Se prueba la precisión del subconjunto, bien mediante validación
cruzada o leave-one-out y, si es mejor, se continúa con él. Se continúa así hasta que se alcanza maxStale.
Para ello, una variable comienza siendo 0 y aumenta su valor en una unidad cuando a un subconjunto no se
le puede añadir ningún atributo para mejorarlo, volviendo a 0 si se añade un nuevo atributo a un subconjunto.
En cuanto al proceso leave-one-out, es un método de estimación del error. Es una validación cruzada en la
que el número de conjuntos es igual al número de ejemplos de entrenamiento. Cada vez se elimina un
ejemplo del conjunto de entrenamiento y se entrena con el resto. Se juzgará el acierto del sistema con el resto
de instancias según se acierte o se falle en la predicción del ejemplo que se eliminó. El resultado de las n
pruebas (siendo n el número inicial de ejemplos de entrenamiento) se promedia y dicha media será el error
estimado. Por último, para clasificar un ejemplo pueden ocurrir dos cosas. En primer lugar, que el ejemplo
corresponda exactamente con una de las reglas de la tabla de decisión, en cuyo caso se devolverá la clase de
dicha regla. Si no se corresponde con ninguna regla, se puede utilizar Ibk (si se seleccionó dicha opción) para
predecir la clase, o la media o moda de la clase según el tipo de clase del que se trate (numérica o simbólica).
-134-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
2.5.2. Árboles de Decisión
El aprendizaje de árboles de decisión está englobado como una metodología del aprendizaje
supervisado. La representación que se utiliza para las descripciones del concepto adquirido es el
árbol de decisión, que consiste en una representación del conocimiento relativamente simple y que
es una de las causas por la que los procedimientos utilizados en su aprendizaje son más sencillos
que los de sistemas que utilizan lenguajes de representación más potentes, como redes semánticas,
representaciones en lógica de primer orden etc. No obstante, la potencia expresiva de los árboles de
decisión es también menor que la de esos otros sistemas. El aprendizaje de árboles de decisión suele
ser más robusto frente al ruido y conceptualmente sencillo, aunque los sistemas que han resultado
del perfeccionamiento y de la evolución de los más antiguos se complican con los procesos que
incorporan para ganar fiabilidad. La mayoría de los sistemas de aprendizaje de árboles suelen ser no
incrementales, pero existe alguna excepción.
El primer sistema que construía árboles de decisión fue CLS, es un sistema desarrollado por
psicólogos como un modelo del proceso cognitivo de formación de conceptos sencillos. Su
contribución fundamental fue la propia metodología pero no resultaba computacionalmente
eficiente debido al método que empleaba en la extensión de los nodos. Se guiaba por una estrategia
similar al minimax con una función que integraba diferentes costes.
En 1979 Quinlan desarrolla el sistema ID3, conceptualmente es fiel a la metodología de CLS pero
le aventaja en el método de expansión de los nodos, basado en una función que utiliza la medida de
la información de Shannon. La versión definitiva, presentada por su autor Quinlan como un sistema
de aprendizaje, es el sistema C4.5. La evolución -comercial- de ese sistema es otro denominado C5
del mismo autor, del que se puede obtener una versión de demostración restringida en cuanto a
capacidades; por ejemplo, el número máximo de ejemplos de entrenamiento.
Representación de un árbol de decisión
Un árbol de decisión puede interpretarse esencialmente como una serie de reglas compactadas para
su representación en forma de árbol. Dado un conjunto de ejemplos, estructurados como vectores de
pares ordenados atributo-valor, de acuerdo con el formato general en el aprendizaje inductivo a
partir de ejemplos, el concepto que estos sistemas adquieren durante el proceso de aprendizaje
consiste en un árbol. Cada eje está etiquetado con un par atributo-valor y las hojas con una clase, de
forma que la trayectoria que determinan desde la raíz los pares de un ejemplo de entrenamiento
alcanzan una hoja etiquetada -normalmente- con la clase del ejemplo. La clasificación de un
ejemplo nuevo del que se desconoce su clase se hace con la misma técnica, solamente que en ese
caso al atributo clase, cuyo valor se desconoce, se le asigna de acuerdo con la etiqueta de la hoja a
la que se accede con ese ejemplo.
Problemas apropiados para este tipo de aprendizaje
Las características de los problemas apropiados para resolver mediante este aprendizaje dependen
del sistema de aprendizaje específico utilizado, pero hay una serie de ellas generales y comunes a la
mayoría y que se describen a continuación:
Que
la representación de los ejemplos sea mediante vectores de pares atributo-valor, especialmente cuando
los valores son disjuntos y en un número pequeño. Los sistemas actuales están preparados para tratar
atributos con valores continuos, valores desconocidos e incluso valores con una distribución de
probabilidad.
Que el atributo que hace el papel de la clase sea de tipo discreto y con un número pequeño de valores, sin
embargo existen sistemas que adquieren como concepto aprendido funciones con valores continuos.
Que las descripciones del concepto adquirido deban ser expresadas en forma normal disyuntiva.
-135-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Que
posiblemente existan errores de clasificación en el conjunto de ejemplos de entrenamiento, así como
valores desconocidos en algunos de los atributos en algunos ejemplos. Estos sistemas, por lo general, son
robustos frente a los errores del tipo mencionado.
A continuación se presentan tres algoritmos de árboles de decisión, los dos primeros diseñados por
los sistemas ID3 y C4.5; y el tercero un árbol de decisión muy sencillo, con un único nivel de
decisión.
2.5.2.1. El sistema ID3
El sistema ID3 es un algoritmo simple y, sin embargo, potente, cuya misión es la elaboración de un
árbol de decisión. El procedimiento para generar un árbol de decisión consiste, como se comentó
anteriormente en seleccionar un atributo como raíz del árbol y crear una rama con cada uno de los
posibles valores de dicho atributo. Con cada rama resultante (nuevo nodo del árbol), se realiza el
mismo proceso, esto es, se selecciona otro atributo y se genera una nueva rama para cada posible
valor del atributo. Este procedimiento continúa hasta que los ejemplos se clasifiquen a través de
uno de los caminos del árbol. El nodo final de cada camino será un nodo hoja, al que se le
asignará la clase correspondiente. Así, el objetivo de los árboles de decisión es obtener reglas o
relaciones que permitan clasificar a partir de los atributos.
En cada nodo del árbol de decisión se debe seleccionar un atributo para seguir dividiendo, y el
criterio que se toma para elegirlo es: se selecciona el atributo que mejor separe (ordene) los
ejemplos de acuerdo a las clases. Para ello se emplea la entropía, que es una medida de cómo está
ordenado el universo. La teoría de la información (basada en la entropía) calcula el número de bits
(información, preguntas sobre atributos) que hace falta suministrar para conocer la clase a la que
pertenece un ejemplo. Cuanto menor sea el valor de la entropía, menor será la incertidumbre y más
útil será el atributo para la clasificación.
La definición de entropía que da Shannon en su Teoría de la Información es: Dado un conjunto de
eventos A={A1, A2,..., An}, con probabilidades {p1, p2,..., pn}, la información en el conocimiento de
un suceso Ai (bits) se define en la ecuación 2.5.3, mientras que la información media de A (bits) se
muestra en la ecuación 2.5.4.
ecuación 2.5.3
ecuación 2.5.4
Si aplicamos la entropía a los problemas de clasificación se puede medir lo que se discrimina (se
gana por usar) un atributo Ai empleando para ello la ecuación 2.5.5., en la que se define la ganancia
de información.
ecuación 2.5.5
Siendo I la información antes de utilizar el atributo e I(Ai) la información después de utilizarlo. Se
definen ambas en las ecuaciones 2.5.6 y 2.5.7.
ecuación 2.5.6
ecuación 2.5.7
-136-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
En estas ecuaciones nc será el número de clases y nc el número de ejemplares de la clase c, siendo
n el número total de ejemplos. Será nv(Ai) el número de valores del atributo Ai, nij el número de
ejemplos con el valor j en Ai y nijk el número de ejemplos con valor j en Ai y que pertenecen a la
clase k.
Una vez explicada la heurística empleada para seleccionar el mejor atributo en un nodo del árbol de
decisión, se muestra el algoritmo ID3:
1.
2.
3.
4.
Seleccionar el atributo Ai que maximice la ganancia G(Ai).
Crear un nodo para ese atributo con tantos sucesores como valores tenga.
Introducir los ejemplos en los sucesores según el valor que tenga el atributo Ai.
Por cada sucesor:
a. Si sólo hay ejemplos de una clase, Ck, entonces etiquetarlo con Ck.
b. Si no, llamar a ID3 con una tabla formada por los ejemplos de ese nodo,
eliminando la columna del atributo Ai.
Por último, en la figura 2.5.1 se representa el proceso de generación del árbol de decisión para el problema
planteado en la tabla 2.5.1.
Figura 2.5.1. Ejemplo de clasificación con ID3.
En la figura 2.5.1 se muestra el árbol de decisión que se generaría con el algoritmo ID3. Además, para el
primer nodo del árbol se muestra cómo se llega a decidir que el mejor atributo para dicho nodo es vista. Se
generan nodos para cada valor del atributo y, en el caso de vista = Nublado se llega a un nodo hoja ya que
todos los ejemplos de entrenamiento que llegan a dicho nodo son de clase Sí. Sin embargo, para los otros dos
casos se repite el proceso de elección con el resto de atributos y con los ejemplos de entrenamiento que se
clasifican a través de ese nodo.
ID3 en WEKA
La clase en la que está codificado el algoritmo ID3 es weka.classifiers.ID3.java. En primer lugar,
en cuanto a la implementación, no permite ningún tipo de configuración. Esta implementación se
ajusta exactamente a lo descrito anteriormente. Lo único reseñable es que para determinar si un
nodo es hoja o no, se calcula la ganancia de información y, si la máxima ganancia es 0 se
considera nodo hoja, independientemente de que haya ejemplos de distintas clases en dicho nodo.
Los atributos introducidos al sistema deben ser simbólicos, al igual que la clase.
-137-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
2.5.2.2. El sistema C4.5
El ID3 es capaz de tratar con atributos cuyos valores sean discretos o continuos. En el primer caso,
el árbol de decisión generado tendrá tantas ramas como valores posibles tome el atributo. Si los
valores del atributo son continuos, el ID3 no clasifica correctamente los ejemplos dados. Por ello,
propuso el C4.5, como extensión del ID3, que permite:
Empleo del concepto razón de ganancia (GR, [Gain Ratio])
Construir árboles de decisión cuando algunos de los ejemplos presentan valores desconocidos
para algunos de los atributos.
3. Trabajar con atributos que presenten valores continuos.
4. La poda de los árboles de decisión.
5. Obtención de Reglas de Clasificación.
1.
2.
Razón de Ganancia
El test basado en el criterio de maximizar la ganancia tiene como sesgo la elección de atributos con
muchos valores. Esto es debido a que cuanto más fina sea la participación producida por los
valores del atributo, normalmente, la incertidumbre o entropía en cada nuevo nodo será menor, y
por lo tanto también será menor la media de la entropía a ese nivel. C4.5 modifica el criterio de
selección del atributo empleando en lugar de la ganancia la razón de ganancia, cuya definición se
muestra en la ecuación 2.5.8.
ecuación 2.5.8
Al término I(División Ai) se le denomina información de ruptura. En esta medida cuando nij tiende
a n, el denominador se hace 0. Esto es un problema aunque según Quinlan, la razón de ganancia
elimina el sesgo.
Valores Desconocidos
El sistema C4.5 admite ejemplos con atributos desconocidos tanto en el proceso de aprendizaje
como en el de validación. Para calcular, durante el proceso de aprendizaje, la razón de ganancia de
un atributo con valores desconocidos, se redefinen sus dos términos, la ganancia, ecuación 2.5.9, y
la información de ruptura, ecuación 2.5.10.
ecuación 2.5.9
ecuación 2.5.10
En estas ecuaciones, nic es el número de ejemplos con el atributo i conocido, y nid el número
de ejemplos con valor desconocido en el mismo atributo. Además, para el cálculo de las
entropía I(Ai) se tendrán en cuenta únicamente los ejemplos en los que el atributo Ai tenga un
valor definido.
-138-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
No se toma el valor desconocido como significativo, sino que se supone una distribución
probabilística del atributo de acuerdo con los valores de los ejemplos en la muestra de
entrenamiento. Cuando se entrena, los casos con valores desconocidos se distribuyen con pesos de
acuerdo a la frecuencia de aparición de cada posible valor del atributo en el resto de ejemplos de
entrenamiento. El peso ωij con que un ejemplo i se distribuiría desde un nodo etiquetado con el
atributo A hacia el hijo con valor j en dicho atributo se calcula mediante la ecuación 2.5.11, en la
que ωi es el peso del ejemplo i al llegar al nodo, esto es, antes de distribuirse, y p(A=j) la suma de
pesos de todos los ejemplos del nodo con valor j en el atributo A entre la suma total de pesos de
todos los ejemplos del nodo (ω).
ecuación 2.5.11
En cuanto a la clasificación de un ejemplo de test, si se alcanza un nodo con un atributo que el
ejemplo no tiene (desconocido), se distribuye el ejemplo (divide) en tantos casos como valores
tenga el atributo, y se da un peso a cada resultado con el mismo criterio que en el caso del
entrenamiento: la frecuencia de aparición de cada posible valor del atributo en los ejemplos de
entrenamiento. El resultado de esta técnica es una clasificación con probabilidades,
correspondientes a la distribución de ejemplos en cada nodo hoja.
Atributos Continuos
El tratamiento que realiza C4.5 de los atributos continuos está basado en la ganancia de
información, al igual que ocurre con los atributos discretos. Si un atributo continuo Ai presenta los
valores ordenados v1, v2,..., vn, se comprueba cuál de los valores zi =(vi + vi+1)/2 ; 1 ≤ j < n , supone
una ruptura del intervalo [v1, vn] en dos subintervalos [v1, zj] y [zj, vn] con mayor ganancia de
información. El atributo continuo, ahora con dos únicos valores posibles, entrará en competencia
con el resto de los atributos disponibles para expandir el nodo.
Para mejorar la eficiencia del algoritmo no se consideran todos los posibles puntos de corte, sino
que se tienen en cuenta las siguientes reglas:
1.
2.
3.
4.
Cada subintervalo debe tener un número mínimo de ejemplos (por ejemplo, 2).
No se divide el intervalo si el siguiente ejemplo pertenece a la misma clase que el actual.
No se divide el intervalo si el siguiente ejemplo tiene el mismo valor que el actual.
Se unen subintervalos adyacentes si tienen la misma clase mayoritaria.
Como se ve en el ejemplo de la figura 2.5.2, aplicando las reglas anteriores sólo es preciso probar
dos puntos de corte (66,5 y 77,5), mientras que si no se empleara ninguna de las mejoras que se
comentaron anteriormente se deberían haber probado un total de trece puntos. Como se ve en la
figura 2.5.2, finalmente se tomaría como punto de ruptura el 77,5, dado que obtiene una mejor
ganancia. Una vez seleccionado el punto de corte, este atributo numérico competiría con el resto de
atributos. Si bien aquí se ha empleado la ganancia, realmente se emplearía la razón de ganancia,
pero no afecta a la elección del punto de corte. Cabe mencionar que ese atributo no deja de estar
disponible en niveles inferiores como en el caso de los discretos, aunque con sus valores
restringidos al intervalo que domina el camino.
-139-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Figura 2.5.2. Ejemplo de tratamiento de atributos continuos con C4.5.
Poda del árbol de decisión
El árbol de decisión ha sido construido a partir de un conjunto de ejemplos, por tanto, reflejará
correctamente todo el grupo de casos. Sin embargo, como esos ejemplos pueden ser muy diferentes
entre sí, el árbol resultante puede llegar a ser bastante complejo, con trayectorias largas y muy
desiguales. Para facilitar la comprensión del árbol puede realizarse una poda del mismo. C4.5
efectúa la poda después de haber desarrollado el árbol completo (post-poda), a diferencia de otros
sistemas que realizan la construcción del árbol y la poda a la vez (pre-poda); es decir, estiman la
necesidad de seguir desarrollando un nodo aunque no posea el carácter de hoja.
En C4.5 el proceso de podado comienza en los nodos hoja y recursivamente continúa hasta llegar al
nodo raíz. Se consideran dos operaciones de poda en C4.5: reemplazo de sub-árbol por hoja
(subtree replacement) y elevación de sub-árbol (subtree raising). En la figura 2.5.3 se muestra en lo
que consiste cada tipo de poda.
Figura 2.5.3. Tipos de operaciones de poda en C4.5.
-140-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
En esta figura 2.5.3., tenemos el árbol original antes del podado (a), y las dos posibles acciones de
podado a realizar sobre el nodo interno C. En (b) se realiza subtree replacement, en cuyo caso el
nodo C es reemplazado por uno de sus subárboles. Por último, en (c) se realiza subtree raising: El
nodo B es sustituido por el subárbol con raíz C. En este último caso hay que tener en cuenta que
habrá que reclasificar de nuevo los ejemplos a partir del nodo C. Además, subtree raising es muy
costoso computacionalmente hablando, por lo que se suele restringir su uso al camino más largo a
partir del nodo (hasta la hoja) que estamos podando. Como se comentó anteriormente, el proceso de
podado comienza en las hojas y continúa hacia la raíz pero, la cuestión es cómo decidir reemplazar
un nodo interno por una hoja (replacement) o reemplazar un nodo interno por uno de sus nodos hijo
(raising). Lo que se hace es comparar el error estimado de clasificación en el nodo en el que nos
encontramos y compararlo con el error en cada uno de sus hijos y en su padre para realizar alguna
de las operaciones o ninguna.
Acontinuación se muestra el pseudocódigo del proceso de podado que se emplea en C4.5.
Podar (raíz) {
Si raíz No es HOJA Entonces
Para cada hijo H de raíz Hacer
Podar (H)
Obtener Brazo más largo (B) de raíz // raising
ErrorBrazo = EstimarErrorArbol (B, raíz.ejemplos)
ErrorHoja = EstimarError (raíz, raíz.ejemplos) // replacement
ErrorÁrbol = EstimarErrorArbol (raíz, raíz.ejemplos)
Si ErrorHoja <= ErrorÁrbol Entonces // replacement
raíz es Hoja
Fin Poda
Si ErrorBrazo <= ErrorÁrbol Entonces // raising
raíz = B
Podar (raíz)
}
EstimarErrorArbol (raíz, ejemplos) {
Si raíz es HOJA Entonces
EstimarError (raíz, ejemplos)
Si no
Distribuir los ejemplos (ej[]) en los brazos
Para cada brazo (B)
error = error + EstimarErrorArbol (B, ej[B])
}
De esta forma, el subtree raising se emplea únicamente para el subárbol más largo. Además, para
estimar su error se emplean los ejemplos de entrenamiento, pero los del nodo origen, ya que si se
eleva deberá clasificarlos él. En cuanto a la función EstimarError, es la función que estima el error
de clasificación de una hoja del árbol. Así, para tomar la decisión debemos estimar el error de
clasificación en un nodo determinado para un conjunto de test independiente. Habrá que estimarlo
tanto para los nodos hoja como para los internos (suma de errores de clasificación de sus hijos). No
se puede tomar como dato el error de clasificación en el conjunto de entrenamiento dado que,
lógicamente, el error se subestimaría.
Una técnica para estimar el error de clasificación es la denominada reduced-error pruning, que
consiste en dividir el conjunto de entrenamiento en n subconjuntos n-1 de los cuáles servirán
realmente para el entrenamiento del sistema y 1 para la estimación del error. Sin embargo, el
problema es que la construcción del clasificador se lleva a cabo con menos ejemplos. Esta no es la
técnica empleada en C4.5.
La técnica empleada en C4.5 consiste en estimar el error de clasificación basándose en los propios
ejemplos de entrenamiento. Para ello, en el nodo donde queramos estimar el error de clasificación,
se toma la clase mayoritaria de sus ejemplos como clase representante. Esto implica que habrá E
errores de clasificación de un total de N ejemplos que se clasifican a través de dicho nodo.
-141-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
El error observado será f=E/N, siendo q la probabilidad de error de clasificación del nodo y p=1-q
la probabilidad de éxito. Se supone que la función f sigue una distribución binomial de parámetro q.
Y lo que se desea obtener es el error e, que será la probabilidad del extremo superior con un
intervalo [f-z, f+z] de confianza c. Dado que se trata de una distribución binomial, se obtendrá e
mediante las ecuaciones 2.5.12 y 2.5.13.
ecuación 2.5.12
ecuación 2.5.13
Como factor c (factor de confianza) se suele emplear en C4.5 el 25%, dado que es el que mejores
resultados suele dar y que corresponde a un z=0.69.
Obtención de Reglas de Clasificación
Cualquier árbol de decisión se puede convertir en reglas de clasificación, entendiendo como tal una
estructura del tipo Si <Condición> Entonces <Clase>. El algoritmo de generación de reglas
consiste básicamente en, por cada rama del árbol de decisión, las preguntas y sus valores estarán
en la parte izquierda de las reglas y la etiqueta del nodo hoja correspondiente en la parte derecha
(clasificación). Sin embargo, este procedimiento generaría un sistema de reglas con mayor
complejidad de la necesaria. Por ello, el sistema C4.5 realiza un podado de las reglas obtenidas. Se
muestra a continuación el algoritmo completo de obtención de reglas:
ObtenerReglas (árbol) {
Convertir el árbol de decisión (árbol) a un conjunto de reglas, R
error = error de clasificación con R
Para cada regla Ri de R Hacer
Para cada precondición pj de Ri Hacer
nuevoError = error al eliminar pj de Ri
Si nuevoError <= error Entonces
Eliminar pj de Ri
error = nuevoError
Si Ri no tiene precondiciones Entonces
Eliminar Ri
}
En cuanto a la estimación del error, se realiza del mismo modo que para realizar el podado del árbol
de decisión.
ecuación 2.5.14
-142-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
C4.5 en WEKA (J48)
La clase en la que se implementa el algoritmo C4.5 en la herramienta WEKA es
weka.classifers.j48.J48.java. Las opciones que permite este algoritmo son las que se muestran en la
tabla
Opción
Descripción
minNumObj (2)
Número mínimo de instancias por hoja.
Una vez finalizada la creación del árbol de decisión se eliminan todas las
instancias que se clasifican en cada nodo, que hasta el momento se
mantenían almacenadas.
Con los atributos nominales también no se divide (por defecto) cada
nodo en dos ramas.
En caso de no activar la opción, se realiza la poda del árbol.
Se permite realizar el podado con el proceso subtree raising.
Factor de confianza para el podado del árbol.
Si se activa esta opción, el proceso de podado no es el propio de C4.5,
sino que el conjunto de ejemplos se divide en un subconjunto de
entrenamiento y otro de test, de los cuales el último servirá para estimar
el error para la poda.
Define el número de subconjuntos en que hay que dividir el conjunto de
ejemplos para, el último de ellos, emplearlo como conjunto de test si se
activa la opción reducedErrorPruning.
Si se activa esta opción, cuando se intenta predecir la probabilidad de que
una instancia pertenezca a una clase, se emplea el suavizado de Laplace.
saveInstanceData (False)
binarySplits (False)
unpruned (False)
subtreeRaising (True)
confidenceFactor (0.25)
reducedErrorPruning (False)
numFolds (3)
useLaplace (False)
Tabla 2.5.6. Opciones de configuración para el algoritmo C4.5 en WEKA.
El algoritmo J48 se ajusta al algoritmo C4.5 al que se le amplían funcionalidades tales como
permitir la realización del proceso de podado mediante reducedErrorPruning o que las divisiones
sean siempre binarias binarySplits. Algunas propiedades concretas de la implementación son las
siguientes:
primer lugar, en cuanto a los tipos de atributos admitidos, estos pueden ser simbólicos y
numéricos. Se permiten ejemplos con faltas en dichos atributos, tanto en el momento de
entrenamiento como en la predicción de dicho ejemplo. En cuanto a la clase, ésta debe ser
simbólica.
En
Se
permiten ejemplos con peso.
El
algoritmo no posibilita la generación de reglas de clasificación a partir del árbol de decisión.
Para
el tratamiento de los atributos numéricos el algoritmo prueba los puntos secuencialmente, con
lo que emplea tres de las cuatro opciones que se comentaron anteriormente. La cuarta opción, que
consistía en unir intervalos adyacentes con la misma clase mayoritaria no se realiza.
También
respecto a los atributos numéricos, cuando se intenta dividir el rango actual en dos
subrangos se ejecuta la ecuación 2.5.15.:
DivisiónMínima = 0.1 ×
nic
nc
ecuación 2.5.15
En esta ecuación nic es el número de ejemplos de entrenamiento con el atributo i conocido, y
nc el número de clases.
Además, si el resultado de la ecuación es menor que el número mínimo de ejemplos que debe
clasificarse por cada nodo hijo, se iguala a éste número y si es mayor que 25, se iguala a dicho
número.
-143-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Lo que indica este número es el número mínimo de ejemplos que debe haber por cada uno de los
dos nodos hijos que resultarían de la división por el atributo numérico, con lo que no se
considerarían divisiones que no cumplieran este dato.
El
cálculo de la entropía y de la ganancia de información se realiza con las ecuaciones:
G ( Ai ) =
nic
n2
(I − I ( Ai ) )
ecuación 2.5.16
nc
I = nic log 2 (nic ) − ∑ nc log 2 (nc )
ecuación 2.5.17
c =1
I ( Ai ) =
nv ( Ai )
nc
j =1
k =1
∑ nij log 2 (nij ) − I ij ; I ij = − ∑ nijk log 2 (nijk )
ecuación 2.5.18
En estas ecuaciones, nic es el número de ejemplos con el atributo i conocido, n el número total
de ejemplos, nc el número de ejemplos conocidos (el atributo i) con clase c, nij el número de
ejemplos con valory en el atributo i y nijk el número de atributos con valor j en el atributo i y
con clase k.
• Además, la información de ruptura se expresa como se muestra en la ecuación:
 nv ( Ai )

−  ∑ nij log 2 (nij )  − nic log 2 (nic ) + n log 2 (n)
 j =1



I (DivisiónAi ) =
n
ecuación 2.5.19
En la ecuación nij es el número de ejemplos con valor j en el atributo i, nic es el número de
ejemplos con valor conocido en el atributo i y n es el número total de ejemplos.
suavizado de Laplace se emplea en el proceso de clasificación de un ejemplar. Para calcular la
probabilidad de que un ejemplo pertenezca a una clase determinada en un nodo hoja se emplea la
ecuación:
El
P(k | E ) =
nk + 1
n+C
ecuación 2.5.20
En la ecuación nk es el número de ejemplos de la clase clasificados en el nodo hoja, n el
número total de ejemplos clasificados en el nodo y C el número de clases para los que hay
algún ejemplo clasificado en el nodo.
-144-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
2.5.2.3. Decision Stump (Árbol de un solo nivel)
Todavía existe un algoritmo más sencillo que genera un árbol de decisión de un único nivel. Se trata
de un algoritmo, [decision stump], que utiliza un único atributo para construir el árbol de decisión.
La elección del único atributo que formará parte del árbol se realizará basándose en la ganancia
de información, y a pesar de su simplicidad, en algunos problemas puede llegar a conseguir
resultados interesantes.
Árbol de Decisión de un solo nivel en WEKA
La clase en la que se implementa el algoritmo tocón de decisión en la herramienta WEKA es
weka.classifers.DecisionStump.java. Así, en WEKA se llama a este algoritmo tocón de decisión
[decisión stump]. No tiene opciones de configuración, pero la implementación es muy completa,
dado que admite tanto atributos numéricos como simbólicos y clases de ambos tipos también.
El árbol de decisión tendrá tres ramas: una de ellas será para el caso de que el atributo sea
desconocido, y las otras dos serán para el caso de que el valor del atributo del ejemplo de test sea
igual a un valor concreto del atributo o distinto a dicho valor, en caso de los atributos simbólicos,
o que el valor del ejemplo de test sea mayor o menor a un determinado valor en el caso de atributos
numéricos.
En el caso de los atributos simbólicos se considera cada valor posible del mismo y se calcula la
ganancia de información con el atributo igual al valor, distinto al valor y valores desconocidos del
atributo. En el caso de atributos simbólicos se busca el mejor punto de ruptura, tal y como se vio en
el sistema C4.5. Deben tenerse en cuenta cuatro posibles casos al calcular la ganancia de
información: que sea un atributo simbólico y la clase sea simbólica o que la clase sea numérica, o
que sea un atributo numérico y la clase sea simbólica o que la clase sea numérica. A continuación se
comenta cada caso por separado.
Atributo Simbólico y Clase Simbólica
Se toma cada vez un valor vx del atributo simbólico Ai como base y se consideran únicamente tres posibles
ramas en la construcción del árbol: que el atributo Ai sea igual a vx, que el atributo Ai sea distinto a vx o que
el valor del atributo A sea desconocido. Con ello, se calcula la entropía del atributo tomando como base el
valor escogido tal y como se muestra en la ecuación 2.60, en la que el valor de j en el sumatorio va desde 1 a
3 porque los valores del atributo se restringen a tres: igual a vx , distinto de vx o valor desconocido. En cuanto
a los parámetros, nij es el número de ejemplos con valor j en el atributo i, n el número total de ejemplos y nijk
el número de ejemplos con valor j en el atributo i y que pertenece a la clase k.
Atributo Numérico y Clase Simbólica
Se ordenan los ejemplos según el atributo Ai y se considera cada valor vx del atributo como posible punto de
corte. Se consideran entonces como posibles valores del atributo el rango menor o igual a vx, mayor a vx y
valor desconocido. Se calcula la entropía del rango tomando como base esos tres posibles valores
restringidos del atributo.
Atributo Simbólico y Clase Numérica
Se vuelve a tomar como base cada vez cada valor del atributo, tal y como se hacía en el caso Atributo
Simbólico y Clase Simbólica, pero en este caso se calcula la varianza de la clase para los valores del atributo
mediante la ecuación 2.5.21, donde Sj es la suma de los valores de la clase de los ejemplos con valor j en el
atributo i, SSj es la suma de los valores de la clase al cuadrado y Wj es la suma de los pesos de los ejemplos
(número de ejemplos si no se incluyen pesos) con valor j en el atributo.
ecuación 2.5.21
-145-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Atributo Numérico y Clase Numérica
Se considera cada valor del atributo como punto de corte tal y como se hacía en el caso Atributo Numérico y
Clase Simbólica. Posteriormente, se calcula la varianza tal y como se muestra en la ecuación 2.5.21.
En cualquiera de los cuatro casos que se han comentado, lo que se busca es el valor mínimo de la
ecuación calculada, ya sea la entropía o la varianza. De esta forma se obtiene el atributo que será
raíz del árbol de decisión y sus tres ramas. Lo único que se hará por último es construir dicho árbol:
cada rama finaliza en un nodo hoja con el valor de la clase, que será la media o la moda de los
ejemplos que se clasifican por ese camino, según se trate de una clase numérica o simbólica.
2.5.2.4. Error de un clasificador:
En cualquier estudio de investigación una cuestión clave es la fiabilidad de los procedimientos de
medida empleados. Tradicionalmente se ha reconocido una fuente importante de error de medida en
la variabilidad entre observadores. Consecuentemente, un objetivo de los estudios de fiabilidad debe
consistir en estimar el grado de dicha variabilidad.
En este sentido, dos aspectos distintos entran a formar parte típicamente del estudio de fiabilidad: de
una parte, el sesgo entre observadores (la tendencia de un observador a dar consistentemente
valores mayores que otro) y de otra, la concordancia entre observadores (hasta qué punto los
observadores coinciden en su medición).
La manera concreta de abordar el problema depende estrechamente de la naturaleza de los datos: si
éstos son de tipo continuo es habitual la utilización de estimadores del coeficiente de correlación
intraclase, mientras que cuando se trata de datos de tipo categórico el estadístico más empleado es
el índice kappa
Estadístico kappa
El estadístico kappa mide la coincidencia de la predicción con la clase real (1.0 significa que ha
habido coincidencia absoluta).
Supongamos que dos observadores distintos clasifican independientemente una muestra de n ítems
en un mismo conjunto de C categorías nominales. El resultado de esta clasificación se puede
resumir en una tabla como la tabla 2.5.7., en la que cada valor xij representa el número de ítems que
han sido clasificados por el observador 1 en la categoría i y por el observador 2 en la categoría j.
Observador 1
1
2
·
·
·
C
Total
1
X11
X21
·
·
·
Xc1
X.1
2
X12
X22
Xc2
X.2
Observador 2
…
…
…
…
…
C
X1c
X2c
·
·
·
Xcc
X.c
Total
X1
X2
·
·
·
XC
n
Tabla 2.5.7. Formato de los datos en un estudio de concordancia
Por ejemplo, podemos pensar en dos radiólogos enfrentados a la tarea de categorizar una muestra de
radiografías mediante la escala: "anormal, "dudosa", "normal". La tabla 2.5.8., muestra un conjunto de datos
hipotéticos para este ejemplo, dispuesto de acuerdo con el esquema de la tabla 2.5.7.
-146-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Radiólogo 1
Anormal
Dudosa
Normal
Total
Radiólogo 2
Dudosa
Normal
4
3
10
5
4
53
18
61
Anormal
18
1
2
21
Total
25
16
59
100
Tabla 2.5.8. Datos hipotéticos de clasificación de una muestra de 100 radiografías por dos
radiólogos.
Desde un punto de vista típicamente estadístico es más adecuado liberarnos de la muestra concreta
(los n ítems que son clasificados por los dos observadores) y pensar en términos de la población de
la que se supone que ha sido extraída dicha muestra. La consecuencia práctica de este cambio de
marco es que debemos modificar el esquema de la tabla 2.5.7., para sustituir los valores xij de cada
celda por las probabilidades conjuntas, que denotaremos por π ij (tabla 2.5.9.).
Observador1
1
2
·
·
·
C
Marginal
1
*11
n12
·
·
·
*C1
π .1
2
*12
*22
*C2
π .2
Observador 2
…
C
…
*1
…
1 2C
·
·
·
…
i CC
…
π .C
Marginal
π1
π2
·
·
·
πc
1
Tabla 2.5.9. Modificación del esquema de la Tabla 2.5.7. cuando se consideran las probabilidades
de cada resultado
Con el tipo de esquematización que hemos propuesto en las tablas 2.5.7. ó 2.5.9. es evidente que las
respuestas que indican concordancia son las que se sitúan sobre la diagonal principal. En efecto, si
un dato se sitúa sobre dicha diagonal, ello significa que ambos observadores han clasificado el ítem
en la misma categoría del sistema de clasificación. De esta observación surge naturalmente la más
simple de las medidas de concordancia que consideraremos: la suma de las probabilidades a lo largo
de la diagonal principal.
En símbolos, si denotamos dicha medida por π0, será: π 0 = ∑ π ii donde los índices del sumatorio van desde i
= 1 hasta i = C. Como es obvio, se cumple que 0 ≤ π 0 ≤ 1 correspondiendo el valor 0 a la mínima
concordancia posible y el 1 a la máxima.
Aunque este sencillo índice ha sido propuesto en alguna ocasión como medida de concordancia de
elección, su interpretación no está exenta de problemas. La tabla 2.5.10., ilustra el tipo de
dificultades que pueden surgir. En el caso A, π0 = 0.2, luego la concordancia es mucho menor que
en el caso B, donde π0 = 0.8. Sin embargo, condicionando por las distribuciones marginales se
observa que en el caso A la concordancia es la máxima posible, mientras que en el B es la mínima.
A
Observador 1
1
2
Marginal
Observador 2
1
2 Marginal
0.1 0.8
0.9
0 0.1
0.1
0.1 0.9
1
B
Observador 2
Observador 1 1 2 Marginal
1
0.8 0.1
0.9
2
0.1 0
0.1
Marginal
0.9 0.1
1
Tabla 2.5.10. Ejemplos de concordancia.
-147-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Por lo tanto, parece claro que la búsqueda se debe orientar hacia nuevas medidas de concordancia
que tengan en cuenta las distribuciones marginales, con el fin de distinguir entre dos aspectos
distintos de la concordancia, a los que podríamos aludir informalmente como concordancia absoluta
o relativa. El índice kappa representa una aportación en esta dirección, básicamente mediante la
incorporación en su fórmula de una corrección que excluye la concordancia debida exclusivamente
al azar (corrección que, como veremos, está relacionada con las distribuciones marginales).
Con la notación ya empleada en la tabla 2.5.9., el índice kappa, K , se define como
K=
∑ π ii − ∑ π i ∑ π i
1 − ∑ π iπ i
Donde los índices del sumatorio
van desde i = 1 hasta i = C.
Ecuación 2.5.22
Es instructivo analizar la expresión anterior. Observemos en primer lugar que si suponemos la
independencia de las variables aleatorias que representan la clasificación de un mismo ítem por los
dos observadores, entonces la probabilidad de que un ítem sea clasificado por los dos en la misma
categoría i es π i π i . Por lo tanto, si extendemos el sumatorio a todas las categorías, Σ π i π i es
precisamente la probabilidad de que los dos observadores concuerden por razones exclusivamente
atribuibles al azar.
En consecuencia, el valor de K simplemente es la razón entre el exceso de concordancia observado
más allá del atribuible al azar (Σ π i - Σ π i π i ) y el máximo exceso posible (1 - Σ π i π i ). La máxima
concordancia posible corresponde a K = 1. El valor K = 0 se obtiene cuando la concordancia
observada es precisamente la que se espera a causa exclusivamente del azar. Si la concordancia es
mayor que la esperada simplemente a causa del azar, K > 0, mientras que si es menor, K < 0. El
mínimo valor de K depende de las distribuciones marginales.
En el ejemplo de la tabla 2.5.10, K vale 0.024 en el caso A y -0.0216 en el B, lo que sugiere una
interpretación de la concordancia opuesta a la que sugiere el índice π0 (vide supra). Para comprender
resultados paradójicos como éstos, conviene recordar los comentarios que hacíamos más arriba acerca de las
limitaciones del índice π 0.
A la hora de interpretar el valor de κ es útil disponer de una escala como la siguiente, a pesar de su
arbitrariedad:
Valoración del Índice Kappa
Valor de k
< 0.20
0.21 – 0.40
0.41 – 0.60
0.61 – 0.80
0.81 – 1.00
Fuerza de la concordancia
Pobre
Débil
Moderada
Buena
Muy buena
A partir de una muestra se puede obtener una estimación, K, del índice kappa simplemente
reemplazando en la ecuación 2.5.22., las probabilidades por las proporciones muestrales
correspondientes:
∑  X ii n ∑  X i n  X i n  n∑ X ii − X i X i
= 2
K=
Ecuación 2.5.23
X i  X i 

n
−
X
X
∑
i
i
1− ∑


 n  n 
Con los datos de la tabla 2.5.8., se obtiene aplicando esta fórmula un valor de K = 0.66, que según
nuestra convención anterior calificaríamos como una buena concordancia.
-148-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
2.5.3. Reglas de Clasificación
Las técnicas de Inducción de Reglas surgieron hace más de dos décadas y permiten la generación y
contraste de árboles de decisión, o reglas y patrones a partir de los datos de entrada. La información
de entrada será un conjunto de casos donde se ha asociado una clasificación o evaluación a un
conjunto de variables o atributos. Con esa información estas técnicas obtienen el árbol de decisión
o conjunto de reglas que soportan la evaluación o clasificación.
En los casos en que la información de entrada posee algún tipo de “ruido" o defecto (insuficientes
atributos o datos, atributos irrelevantes o errores u omisiones en los datos) estas técnicas pueden
habilitar métodos estadísticos de tipo probabilístico para generar árboles de decisión recortados o
podados. También en estos casos pueden identificar los atributos irrelevantes, la falta de atributos
discriminantes o detectar "gaps" o huecos de conocimiento. Esta técnica suele llevar asociada una
alta interacción con el analista de forma que éste pueda intervenir en cada paso de la construcción
de las reglas, bien para aceptarlas, bien para modificarlas.
La inducción de reglas se puede lograr fundamentalmente mediante dos caminos: Generando un
árbol de decisión y extrayendo de él las reglas, como puede hacer el sistema C4.5 o bien mediante
una estrategia de covering, consistente en tener en cuenta cada vez una clase y buscar las reglas
necesarias para cubrir [cover] todos los ejemplos de esa clase; cuando se obtiene una regla se
eliminan todos los ejemplos que cubre y se continúa buscando más reglas hasta que no haya más
ejemplos de la clase.
A continuación se muestran una técnica de inducción de reglas basada en árboles de decisión, otra
basada en covering y una más que mezcla las dos estrategias.
2.5.3.1. Algoritmo 1R
El más simple algoritmo de reglas de clasificación para un conjunto de ejemplos es el 1R. Este
algoritmo genera un árbol de decisión de un nivel expresado mediante reglas. Consiste en
seleccionar un atributo (nodo raíz) del cual nace una rama por cada valor, que va a parar a un nodo
hoja con la clase más probable de los ejemplos de entrenamiento que se clasifican a través suyo.
Este algoritmo se muestra a continuación:
1R (ejemplos) {
Para cada atributo (A)
Para cada valor del atributo (Ai)
Contar el número de apariciones de cada clase con Ai
Obtener la clase más frecuente (Cj)
Crear una regla del tipo Ai -> Cj
Calcular el error de las reglas del atributo A
Escoger las reglas con menor error
}
La clase debe ser simbólica, mientras los atributos pueden ser simbólicos o numéricos. También
admite valores desconocidos, que se toman como otro valor más del atributo. En cuanto al error de
las reglas de un atributo, consiste en la proporción entre los ejemplos que cumplen la regla y los
ejemplos que cumplen la premisa de la regla.
En el caso de los atributos numéricos, se generan una serie de puntos de ruptura [breakpoint], que
discretizarán dicho atributo formando conjuntos. Para ello, se ordenan los ejemplos por el atributo
numérico y se recorren. Se van contando las apariciones de cada clase hasta un número m que
indica el mínimo número de ejemplos que pueden pertenecer a un conjunto, para evitar conjuntos
demasiado pequeños. Por último, se unen a este conjunto ejemplos con la clase más frecuente y
ejemplos con el mismo valor en el atributo.
-149-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
La sencillez de este algoritmo es un poco insultante. Tanto es así que 1R no tiene ningún elemento
de sofistificación y genera para cada atributo un árbol de profundidad 1, donde una rama está
etiquetada por missing si es que aparecen valores desconocidos (missing values) en ese atributo en
el conjunto de entrenamiento; el resto de las ramas tienen como etiqueta un intervalo construido de
una manera muy simple, como se ha explicado antes, o un valor nominal, según el tipo de atributo
del que se trate.
En la tabla 2.5.11., se presenta un ejemplo de 1R, basado en los ejemplos de la tabla 2.5.1.
atributo
vista
temperatura
humedad
viento
errores
error total
Soleado -* no Nublado -* si Lluvioso -* si
reglas
2/5 0/4 2/5
4/14
Alta -> no Media -> si Baja -> si
2/4 2/6 1/4
5/14
Alta -> no Normal -> si
3/7 1/7
4/14
Falso -* si Cierto -* no
2/8 3/6
5/14
Tabla 2.5.11 Resultados del algoritmo 1R.
Para clasificar según la clase jugar, 1R considera cuatro conjuntos de reglas, uno por cada atributo, que son
las mostradas en la tabla 2.5.11., en las que además aparecen los errores que se cometen. De esta forma se
concluye que como los errores mínimos corresponden a las reglas generadas por los atributos vista y
humedad, cualquiera de ellas es valida, de manera que arbitrariamente se puede elegir cualquiera de estos
dos conjuntos de reglas como generador de 1R.
1R en WEKA
La clase weka.classifers.OneR.java implementa el algoritmo 1R. La única opción configurable es la
que se muestra en la tabla
Opción
Descripción
minBucketSize (6)
Número mínimo de ejemplos que deben pertenecer a un
conjunto en caso de atributo numérico
Tabla. 2.5.12: Opciones de configuración para el algoritmo 1R en WEKA.
La implementación que se lleva a cabo en WEKA de este algoritmo cumple exactamente con lo
descrito anteriormente.
Como vemos, 1R es un clasificador muy sencillo, que únicamente utiliza un atributo para la
clasificación. Sin embargo, aún hay otro clasificador más sencillo, el 0R, implementado en
weka.classifers.ZeroR.java, que simplemente calcula la media en el caso de tener una clase
numérica o la moda, en caso de una clase simbólica. No tiene ningún tipo de opción de
configuración.
-150-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
2.5.3.2. Algoritmo PRISM
PRISM es un algoritmo básico de aprendizaje de reglas que asume que no hay ruido en los datos.
Sea t el número de ejemplos cubiertos por la regla y p el número de ejemplos positivos cubiertos
por la regla, lo que hace PRISM es añadir condiciones a reglas que maximicen la relación p/t
(relación entre los ejemplos positivos cubiertos y ejemplos cubiertos en total).
A continuación se muestra el algoritmo:
PRISM (ejemplos) {
Para cada clase (C)
E = ejemplos
Mientras E tenga ejemplos de C
Crea una regla R con parte izquierda vacía y clase C
Hasta R perfecta Hacer
Para cada atributo A no incluido en R y cada valor v de A
Considera añadir la condición A=v a la parte izquierda de R
Selecciona el par A=v que maximice p/t
(en caso de empates, escoge la que tenga p mayor)
Añadir A=v a R
Elimina de E los ejemplos cubiertos por R
Este algoritmo va eliminando los ejemplos que va cubriendo cada regla, por lo que las reglas
tienen que interpretarse en orden. Se habla entonces de listas de reglas [decision list].
En la figura 2.5.4., se muestra un ejemplo de cómo actúa el algoritmo. Concretamente se trata de la
aplicación del mismo sobre el ejemplo de la tabla 2.5.1.
Figura 2.5.4. Ejemplo de PRISM.
En la figura 2.5.4., se muestra cómo el algoritmo toma en primer lugar la clase Sí. Partiendo de todos los
ejemplos de entrenamiento (un total de catorce) calcula el cociente p/t para cada par atributo-valor y escoge
el mayor. En este caso, dado que la condición escogida hace la regla perfecta (p/t = 1), se eliminan los cuatro
ejemplos que cubre dicha regla y se busca una nueva regla. En la segunda regla se obtiene en un primer
momento una condición que no hace perfecta la regla, por lo que se continúa buscando con otra condición.
Finalmente, se muestra la lista de decisión completa que genera el algoritmo.
-151-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
PRISM en WEKA
La clase weka.classifers.Prism.java implementa el algoritmo PRISM. No tiene ningún tipo de
configuración posible. Únicamente permite atributos nominales, la clase debe ser también nominal
y no puede haber atributos con valores desconocidos. La implementación de esta clase sigue
completamente el algoritmo expuesto en el apartado 2.5.3.2.
2.5.3.3. Algoritmo PART
Uno de los sistemas más importantes de aprendizaje de reglas es el proporcionado por C4.5,
explicado anteriormente. Este sistema, al igual que otros sistemas de inducción de reglas, realiza
dos fases: primero, genera un conjunto de reglas de clasificación y después refina estas reglas para
mejorarlas, realizando así una proceso de optimización global de dichas reglas. Este proceso de
optimización global es siempre muy complejo y costoso computacionalmente hablando.
Por otro lado, el algoritmo PART es un sistema que obtiene reglas sin dicha optimización global.
Recibe el nombre PART por su modo de actuación: obtaining rules from PARTial decision trees, y
fue desarrollado por el grupo neozelandés que construyó el entorno WEKA.
El sistema se basa en las dos estrategias básicas para la inducción de reglas: el covering y la
generación de reglas a partir de árboles de decisión. Adopta la estrategia del covering (con lo que se
obtiene una lista de decisión) dado que genera una regla, elimina los ejemplares que dicha regla
cubre y continúa generando reglas hasta que no queden ejemplos por clasificar. Sin embargo, el
proceso de generación de cada regla no es el usual. En este caso, para crear una regla, se genera un
árbol de decisión podado, se obtiene la hoja que clasifique el mayor número de ejemplos, que se
transforma en la regla, y posteriormente se elimina el árbol.
Uniendo estas dos estrategias se consigue mayor flexibilidad y velocidad. Además, no se genera un
árbol completo, sino un árbol parcial [partial decisión tree]. Un árbol parcial es un árbol de decisión
que contiene brazos con subárboles no definidos. Para generar este árbol se integran los procesos de
construcción y podado hasta que se encuentra un subárbol estable que no puede simplificarse más,
en cuyo caso se para el proceso y se genera la regla a partir de dicho subárbol.
Este proceso se muestra a continuación:
Expandir (ejemplos) {
elegir el mejor atributo para dividir en subconjuntos
Mientras (subconjuntos No expandidos)
Y (todos los subconjuntos expandidos son HOJA) Expandir (subconjunto)
Si (todos los subconjuntos expandidos son HOJA)
Y (errorSubárbol >= errorNodo) deshacer la expansión del nodo y nodo es HOJ
El proceso de elección del mejor atributo se hace como en el sistema C4.5, esto es, basándose en la
razón de ganancia. La expansión de los subconjuntos generados se realiza en orden, comenzando
por el que tiene menor entropía y finalizando por el que tiene mayor. La razón de realizarlo así es
porque si un subconjunto tiene menor entropía hay más probabilidades de que se genere un subárbol
menor y consecuentemente se cree una regla más general. El proceso continúa recursivamente
expandiendo los subconjuntos hasta que se obtienen hojas, momento en el que se realizará una
vuelta atrás [backtracking]. Cuando se realiza dicha vuelta atrás y los hijos del nodo en cuestión son
hojas, comienza el podado tal y como se realiza en C4.5 (comparando el error esperado del subárbol
con el del nodo), pero únicamente se realiza la función de reemplazamiento del nodo por hoja
[subtree replacement]. Si se realiza el podado se realiza otra vuelta atrás hacia el nodo padre, que
sigue explorando el resto de sus hijos, pero si no se puede realizar el podado el padre no continuará
con la exploración del resto de nodos hijos (ver segunda condición del bucle “mientras”). En este
momento finalizará el proceso de expansión y generación del árbol de decisión.
-152-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Figura 2.5.5. Ejemplo de generación de árbol parcial con PART.
En la figura 2.5.5., se presenta un ejemplo de generación de un árbol parcial donde, junto a cada
brazo de un nodo, se muestra el orden de exploración (orden ascendente según el valor de la
entropía). Los nodos con relleno gris claro son los que aún no se han explorado y los nodos con
relleno gris oscuro los nodos hoja. Las flechas ascendentes representan el proceso de backtracking.
Por último, en el paso 5, cuando el nodo 4 es explorado y los nodos 9 y 10 pasan a ser hoja, el nodo
padre intenta realizar el proceso de podado, pero no se realiza el reemplazo (representado con el 4
en negrita), con lo que el proceso, al volver al nodo 1, finaliza sin explorar el nodo 2.
Una vez generado el árbol parcial se extrae una regla del mismo. Cada hoja se corresponde con una
posible regla, y lo que se busca es la mejor hoja. Si bien se pueden considerar otras heurísticas, en
el algoritmo PART se considera mejor hoja aquella que cubre un mayor número de ejemplos. Se
podría haber optado, por ejemplo, por considerar mejor aquella que tiene un menor error esperado,
pero tener una regla muy precisa no significa lograr un conjunto de reglas muy preciso.
Por último, PART permite que haya atributos con valores desconocidos tanto en el proceso de
aprendizaje como en el de validación y atributos numéricos, tratándolos exactamente como el
sistema C4.5.
PART en WEKA
La clase weka.classifers.j48.PART.java implementa el algoritmo PART. En la tabla 2.5.13., se
muestran las opciones de configuración de dicho algoritmo.
Opción
Descripción
minNumObj (2)
Número mínimo de instancias por hoja.
Con los atributos nominales también no se divide (por defecto) cada
nodo en dos ramas.
Factor de confianza para el podado del árbol.
Si se activa esta opción, el proceso de podado no es el propio de C4.5,
sino que el conjunto de ejemplos se divide en un subconjunto de
entrenamiento y otro de test, de los cuales el último servirá para estimar
el error para la poda.
Define el número de subconjuntos en que hay que dividir el conjunto de
ejemplos para, el último de ellos, emplearlo como conjunto de test si se
activa la opción reducedErrorPruning.
binarySplits (False)
confidenceFactor (0.25)
reducedErrorPruning (False)
numFolds (3)
Tabla 2.5.13. Opciones de configuración para el algoritmo PART en WEKA.
Como se ve en la tabla2.5.13., las opciones del algoritmo PART son un subconjunto de las
ofrecidas por J48, que implementa el sistema C4.5, y es que PART emplea muchas de las clases que
implementan C4.5, con lo que los cálculos de la entropía, del error esperado,... son los mismos.
-153-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
La implementación que se realiza en WEKA del sistema PART se corresponde exactamente con lo
comentado anteriormente, y más teniendo en cuenta que los implementadores de la versión son los
propios creadores del algoritmo.
Por último, en cuanto a los tipos de datos admitidos por el algoritmo, estos son numéricos y
simbólicos para los atributos y simbólico para la clase.
2.5.4. Clasificación Bayesiana
Los clasificadores Bayesianos son clasificadores estadísticos, que pueden predecir tanto las
probabilidades del número de miembros de clase, como la probabilidad de que una muestra dada
pertenezca a una clase particular.
La clasificación Bayesiana se basa en el teorema de Bayes, y los clasificadores Bayesianos han
demostrado una alta exactitud y velocidad cuando se han aplicado a grandes bases de datos.
Diferentes estudios comparando los algoritmos de clasificación han determinado que un clasificador
Bayesiano sencillo conocido como el clasificador “naive Bayesiano” es comparable en rendimiento
a un árbol de decisión y a clasificadores de redes de neuronas.
A continuación se explica los fundamentos de los clasificadores bayesianos y, más concretamente,
del clasificador naive Bayesiano. Tras esta explicación se comentará otro clasificador que, si bien
no es un clasificador bayesiano, esta relacionado con él, dado que se trata también de un
clasificador basado en la estadística.
2.5.4.1. Clasificador Naive Bayesiano
Lo que normalmente se quiere saber en aprendizaje es cuál es la mejor hipótesis (más probable)
dados los datos. Si denotamos P(D) como la probabilidad a priori de los datos, P(D | h) la
probabilidad de los datos dada una hipótesis, lo que queremos estimar es: P(hD), la probabilidad
posterior de h dados los datos. Esto se puede estimar con el teorema de Bayes, ecuación 2.5.24.
ecuación 2.5.24.
Para estimar la hipótesis más probable (MAP, [maximum a posteriori hipótesis]) se busca el mayor
P(h|D) como se muestra en la ecuación 2.5.25.
ecuación 2.5.25.
Ya que P(D) es una constante independiente de h. Si se asume que todas las hipótesis son
igualmente probables, entonces resulta la hipótesis de máxima verosimilitud (ML, [maximum
likelihood]) de la ecuación 2.5.26.:
ecuación 2.5.26.
El clasificador naive [ingenuo] Bayesiano se utiliza cuando se quiere clasificar un ejemplo descrito
por un conjunto de atributos (ai) en un conjunto finito de clases (V). Clasificar un nuevo ejemplo de
acuerdo con el valor más probable dados los valores de sus atributos. Si se aplica 2.5.26., al
problema de la clasificación se obtendrá la ecuación 2.5.27..
-154-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
ecuación 2.5.27.
Además, el clasificador naive Bayesiano asume que los valores de los atributos son
condicionalmente independientes dado el valor de la clase, por lo que se hace cierta la ecuación
2.5.28 y con ella la 2.5.29.
ecuación 2.5.28.
ecuación 2.5.29.
Los clasificadores naive Bayesianos asumen que el efecto de un valor del atributo en una clase dada
es independiente de los valores de los otros atributos. Esta suposición se llama “independencia
condicional de clase”. Ésta simplifica los cálculos involucrados y, en este sentido, es considerado
"ingenuo” [naive]. Esta asunción es una simplificación de la realidad.
A pesar del nombre del clasificador y de la simplificación realizada, el naive Bayesiano funciona
muy bien, sobre todo cuando se filtra el conjunto de atributos seleccionado para eliminar
redundancia, con lo que se elimina también dependencia entre datos.
En la figura 2.5.6., se muestra un ejemplo de aprendizaje con el clasificador naive Bayesiano, así como una
muestra de cómo se clasificaría un ejemplo de test. Como ejemplo se empleará el de la tabla 2.5.1.
Figura 2.5.6. Ejemplo de aprendizaje y clasificación con naive Bayesiano.
-155-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
En este ejemplo se observa que en la fase de aprendizaje se obtienen todas las probabilidades condicionadas
P(ai|vj) y las probabilidades P(vj). En la clasificación se realiza el productorio y se escoge como clase del
ejemplo de entrenamiento la que obtenga un mayor valor.
Algo que puede ocurrir durante el entrenamiento con este clasificador es que para cada valor de
cada atributo no se encuentren ejemplos para todas las clases. Supóngase que para el atributo ai y el
valor j de dicho atributo no hay ningún ejemplo de entrenamiento con clase k. En este caso,
P(aij|k)=0. Esto hace que si se intenta clasificar cualquier ejemplo con el par atributo-valor aij, la
probabilidad asociada para la clase k será siempre 0, ya que hay que realizar el productorio de las
probabilidades condicionadas para todos los atributos de la instancia. Para resolver este problema se
parte de que las probabilidades se contabilizan a partir de las frecuencias de aparición de cada
evento o, en nuestro caso, las frecuencias de aparición de cada terna atributo-valor-clase. El
estimador de Laplace, consiste en comenzar a contabilizar la frecuencia de aparición de cada terna a
partir del 1 y no del 0, con lo que ninguna probabilidad condicionada será igual a 0.
Una ventaja de este clasificador es la cuestión de los valores perdidos o desconocidos: en el
clasificador naive Bayesiano si se intenta clasificar un ejemplo con un atributo sin valor
simplemente el atributo en cuestión no entra en el productorio que sirve para calcular las
probabilidades.
Respecto a los atributos numéricos, se suele suponer que siguen una distribución Normal o
Gaussiana. Para estos atributos se calcula la media µ y la desviación típica σ obteniendo los dos
parámetros de la distribución N(µ,σ), que sigue la expresión de la ecuación 2.5.30, donde el
parámetro x será el valor del atributo numérico en el ejemplo que se quiere clasificar.
ecuación 2.5.30.
Naive Bayesiano en WEKA
El
algoritmo
naive
Bayesiano
se
encuentra
implementado
en
la
clase
weka.classifiers.NaiveBayesSimple.java. No dispone de ninguna opción de configuración. El
algoritmo que implementa esta clase se corresponde completamente con el expuesto anteriormente.
En este caso no se usa el estimador de Laplace, sino que la aplicación muestra un error si hay
menos de dos ejemplos de entrenamiento para una terna atributo-valor-clase o si la desviación
típica de un atributo numérico es igual a 0.
Una alternativa a esta clase que también implementa un clasificador naive Bayesiano es la clase
weka.classifiers.NaiveBayes.java. Las opciones de configuración de que disponen son las
mostradas en la tabla 2.5.14.:
Opción
Descripción
useKernelEstimator (False)
Emplear un estimador de densidad de núcleo para modelar los atributos
numéricos en lugar de una distribución normal.
Tabla 2.5.14.. Opciones de configuración para el algoritmo Bayes naive en WEKA.
En este caso, sin embargo, en lugar de emplear la frecuencia de aparición como base para obtener
las probabilidades se emplean distribuciones de probabilidad. Para los atributos discretos o
simbólicos se emplean estimadores discretos, mientras que para los atributos numéricos se emplean
bien un estimador basado en la distribución normal o bien un estimador de densidad de núcleo.
-156-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Se creará una distribución para cada clase, y una distribución para cada atributo-clase, que será
discreta en el caso de que el atributo sea discreto. El estimador se basará en una distribución normal
o kernel en el caso de los atributo-clase con atributo numérico según se active o no la opción
mostrada en la tabla.
En el caso de los atributos numéricos, en primer lugar se obtiene la precisión de los rangos, que por
defecto en la implementación será de 0,01 pero que se calculará siguiendo el algoritmo descrito,
mediante pseudocódigo:
Precisión (ejemplos, atributo) {
p = 0.01 // valor por defecto
// se ordenan los ejemplos de acuerdo al atributo numérico
Ordenar_ejemplos (ejemplos, atributo)
vUltimo = Valor(ejemplos(0), atributo)
delta = 0;
distintos = 0;
Para cada ejemplo (ej) de ejemplos
vActual = Valor (ej, atributo)
Si vActual <> vUltimo Entonces
delta = delta + (vActual – vUltimo)
vActual = vUltimo
distintos = distintos + 1
Si distintos > 0 Entonces
p = delta / distintos Devolver p
}
Una vez obtenida la precisión de los rangos, se crea el estimador basado en la distribución
correspondiente y con la precisión calculada. Se recorrerán los ejemplos de entrenamiento y de esta
forma se generará la distribución de cada atributo-clase y de cada clase.
Cuando se desee clasificar un ejemplo el proceso será el mismo que se comentó anteriormente, pero
obteniendo las probabilidades a partir de estas distribuciones generadas. En el caso de los atributos
numéricos, se calculará la probabilidad del rango [x-precisión, x+precisión], siendo x el valor del
atributo.
2.5.4.2. Votación por intervalos de características
Este algoritmo es una técnica basada en la proyección de características. Se le denomina “votación
por intervalos de características” (VFI, [Voting Feature Interval]) porque se construyen intervalos
para cada característica [feature] o atributo en la fase de aprendizaje y el intervalo
correspondiente en cada característica “vota” para cada clase en la fase de clasificación. Al igual
que en el clasificador naive Bayesiano, cada característica es tratada de forma individual e
independiente del resto. Se diseña un sistema de votación para combinar las clasificaciones
individuales de cada atributo por separado.
Mientras que en el clasificador naive Bayesiano cada característica participa en la clasificación
asignando una probabilidad para cada clase y la probabilidad final para cada clase consiste en el
producto de cada probabilidad dada por cada característica, en el algoritmo VFI cada característica
distribuye sus votos para cada clase y el voto final de cada clase es la suma de los votos obtenidos
por cada característica.
Una ventaja de estos clasificadores, al igual que ocurría con el clasificador naive Bayesiano, es el
tratamiento de los valores desconocidos tanto en el proceso de aprendizaje como en el de
clasificación: simplemente se ignoran, dado que se considera cada atributo como independiente del
resto. En la fase de aprendizaje del algoritmo VFI se construyen intervalos para cada atributo
contabilizando, para cada clase, el número de ejemplos de entrenamiento que aparecen en dicho
intervalo. En la fase de clasificación, cada atributo del ejemplo de test añade votos para cada clase
dependiendo del intervalo en el que se encuentre y el conteo de la fase de aprendizaje para dicho
intervalo en cada clase. A continuación se muestra este algoritmo:
-157-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Aprendizaje (ejemplos) {
Para cada atributo (A) Hacer
Si A es NUMÉRICO Entonces
Obtener mínimo y máximo de A para cada clase en ejemplos
Ordenar los valores obtenidos (I intervalos)
Si no /* es SIMBÓLICO */
Obtener los valores que recibe A para cada clase en ejemplos
Los valores obtenidos son puntos (I intervalos)
Para cada intervalo I Hacer
Para cada clase C Hacer
contadores [A, I, C] = 0
Para cada ejemplo E Hacer
Si A es conocido Entonces
Si A es SIMBÓLICO Entonces
contadores [A, E.A, E.C] += 1
Si no /* es NUMÉRICO */
Obtener intervalo I de E.A
Si E.A = extremo inferior de intervalo I Entonces
contadores [A, I, E.C] += 0.5
contadores [A, I-1, E.C] += 0.5
Si no
contadores [A, I, E.C] += 1
Normalizar contadores[] /* Σc contadores[A, I, C] = 1 */
}
clasificar (ejemplo E) {
Para cada atributo (A) Hacer
Si E.A es conocido Entonces
Si A es SIMBÓLICO
Para cada clase C Hacer
voto[A, C] = contadores[A, E.A, C]
Si no /* es NUMÉRICO */
Obtener intervalo I de E.A
Si E.A = límite inferior de I Entonces
Para cada clase C Hacer
voto[A, C] = 0.5*contadores[A,I,C] + 0.5*contadores[A,I-1,C]
Si no
Para cada clase C Hacer
voto[A, C] = contadores [A, I, C]
voto[C] = voto[C] + voto[A, C]
Normalizar voto[]/* Σc voto[C] = 1 */
}
En la figura 2.5.7., se presenta un ejemplo de entrenamiento y clasificación con el algoritmo VFI, en el que
se muestra una tabla con los ejemplos de entrenamiento y cómo el proceso de aprendizaje consiste en el
establecimiento de intervalos para cada atributo con el conteo de ejemplos que se encuentran en cada
intervalo. Se muestra entre paréntesis el número de ejemplos que se encuentran en la clase e intervalo
concreto, mientras que fuera de los paréntesis se encuentra el valor normalizado. Para el atributo simbólico
simplemente se toma como intervalo (punto) cada valor de dicho atributo y se cuenta el número de ejemplos
que tienen un valor determinado en el atributo para la clase del ejemplo en cuestión. En el caso del atributo
numérico, se obtiene el máximo y el mínimo valor del atributo para cada clase que en este caso son 4 y 7
para la clase A, y 1 y 5 para la clase B. Se ordenan los valores formándose un total de cinco intervalos y se
cuenta el número de ejemplos que se encuentran en un intervalo determinado para su clase, teniendo en
cuenta que si se encuentra en el punto compartido por dos intervalos se contabiliza la mitad para cada uno de
ellos. También se muestra un ejemplo de clasificación: en primer lugar, se obtienen los votos que cada
atributo por separado concede a cada clase, que será el valor normalizado del intervalo (o punto si se trata de
atributos simbólicos) en el que se encuentre el valor del atributo, y posteriormente se suman los votos (que se
muestra entre paréntesis) y se normaliza. La clase con mayor porcentaje de votos (en el ejemplo la clase A)
gana.
-158-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Figura 2.5.7. Ejemplo de aprendizaje y clasificación con VFI.
VFI en WEKA
El clasificador VFI se implementa en la clase weka.classifiers.VFI.java. Las opciones de
configuración de que dispone son las que se muestran en la tabla 2.5.15.:
Opción
Descripción
weightByConfidence (True)
bias (0.6)
Si se mantiene activa esta opción cada atributo se pesará
conforme la ecuación
Parámetro de configuración para el pesado por confianza
Tabla 2.5.15.. .Opciones de configuración para el algoritmo Bayes naive en WEKA.
El algoritmo que se implementa en la clase VFI es similar al mostrado anteriormente. Sin embargo,
sufre cambios sobretodo en el proceso de clasificación de un nuevo ejemplar:
La
normalización de los intervalos por clase se realiza durante la clasificación y no durante el
entrenamiento.
Si
se activa la opción de pesado por confianza, cada voto de cada atributo a cada clase se pesa
mediante la ecuación.
w( Ai ) = I ( Ai ) bias
−

=


(∑
)
lg(ni ) + n lg(n) 

n lg(2)

nC
n
i =0 i
bias
ecuación 2.5.31.
En la ecuación 2.5.31., I(Ai) es la entropía del atributo Ai, siendo n el número total de
ejemplares, nC el número de clases y ni el número de ejemplares de la clase i. El parámetro
bias es el que se configuró como entrada al sistema, tal y como se mostraba en la tabla 2.5.7.
En
cuanto a los atributos, pueden ser numéricos y simbólicos, mientras que la clase debe ser
simbólica.
-159-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Relacionado con este clasificador se encuentra otro que se implementa en la herramienta WEKA.
Se trata de la clase weka.classifiers.HyperPipes.java. Este clasificador no tiene ningún parámetro
de configuración y es una simplificación del algoritmo VFI: En este caso se almacena para cada
atributo numérico el mínimo y el máximo valor que dicho atributo obtiene para cada clase, mientras
que en el caso de los atributos simbólicos marca los valores que el atributo tiene para cada clase. A
la hora de clasificar un nuevo ejemplo, simplemente cuenta, para cada clase, el número de atributos
que se encuentran en el intervalo almacenado en el caso de atributos numéricos y el número de
atributos simbólicos con valor activado en dicha clase. La clase con mayor número de coincidencias
gana
2.5.5. Aprendizaje Basado en Ejemplares
El aprendizaje basado en ejemplares o instancias tiene como principio de funcionamiento, en sus
múltiples variantes, el almacenamiento de ejemplos: en unos casos todos los ejemplos de
entrenamiento, en otros solo los más representativos, en otros los incorrectamente clasificados
cuando se clasifican por primera vez, etc. La clasificación posterior se realiza por medio de una
función que mide la proximidad o parecido. Dado un ejemplo para clasificar se le clasifica de
acuerdo al ejemplo o ejemplos más próximos. El bias (sesgo) que rige este método es la
proximidad; es decir, la generalización se guía por la proximidad de un ejemplo a otros.
Se han enumerado ventajas e inconvenientes del aprendizaje basado en ejemplares, pero se suele
considerar no adecuado para el tratamiento de atributos no numéricos y valores desconocidos. Las
mismas medidas de proximidad sobre atributos simbólicos suelen proporcionar resultados muy
dispares en problemas diferentes.
A continuación se muestran dos técnicas de aprendizaje basado en ejemplares: el método de los kvecinos más próximos y el k estrella.
2.5.5.1. Algoritmo de los k-vecinos más próximos
El método de los k-vecinos más próximos está considerado como un buen representante de este tipo
de aprendizaje, y es de gran sencillez conceptual. Se suele denominar método porque es el esqueleto
de un algoritmo que admite el intercambio de la función de proximidad dando lugar a múltiples
variantes.
La función de proximidad puede decidir la clasificación de un nuevo ejemplo atendiendo a la
clasificación del ejemplo o de la mayoría de los k ejemplos más cercanos. Admite también
funciones de proximidad que consideren el peso o coste de los atributos que intervienen, lo que
permite, entre otras cosas, eliminar los atributos irrelevantes.
Una función de proximidad clásica entre dos instancias xi y xj , si suponemos que un ejemplo viene
representado por una n-tupla de la forma (a1(x), a2(x), ... , an(x)) en la que ar(x) es el valor de la
instancia para el atributo ar, es la distancia euclídea, que se muestra en la ecuación 2.5.32.
ecuación 2.5.32
En la figura 2.5.8., se muestra un ejemplo del algoritmo KNN para un sistema de dos atributos,
representándose por ello en un plano. En este ejemplo se ve cómo el proceso de aprendizaje consiste en el
almacenamiento de todos los ejemplos de entrenamiento. Se han representado los ejemplos de acuerdo a los
valores de sus dos atributos y la clase a la que pertenecen (las clases son + y -). La clasificación consiste en
la búsqueda de los k ejemplos (en este caso 3) más cercanos al ejemplo a clasificar. Concretamente, el
ejemplo a se clasificaría como -, y el ejemplo b como +.
-160-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Figura 2.5.8. Ejemplo de Aprendizaje y Clasificación con KNN.
Dado que el algoritmo k-NN permite que los atributos de los ejemplares sean simbólicos y
numéricos, así como que haya atributos sin valor [missing values] el algoritmo para el cálculo de la
distancia entre ejemplares se complica ligeramente. A continuación se muestra el algoritmo que
calcula la distancia entre dos ejemplares cualesquiera.
Distancia (E1, E2) {
dst = 0
n = 0
Para cada atributo A Hacer {
dif = Diferencia(E1.A, E2.A)
dst = dst + dif * dif
n = n + 1
}
dst = dst / n
Devolver dst
}
Diferencia (A1, A2) {
Si A1.nominal Entonces {
Si SinValor(A1) O SinValor(A2) O A1 <> A2 Entonces
Devolver 1
Si no
Devolver 0
} Si no {
Si SinValor(A1) O SinValor(A2) Entonces {
Si SinValor(A1) Y SinValor(A2) Entonces
Devolver 1
Si SinValor(A1) Entonces
dif = A2
Si no Entonces
dif = A1
Si dif < 0.5 Entonces
Devolver 1 – dif
Si no
Devolver dif
} Si no
Devolver abs(A1 – A2)
}
}
Además de los distintos tipos de atributos hay que tener en cuenta también, en el caso de los
atributos numéricos, los rangos en los que se mueven sus valores. Para evitar que atributos con
valores muy altos tengan mucho mayor peso que atributos con valores bajos, se normalizarán
dichos valores con la ecuación 2.5.33.
ecuación 2.5.33
En esta ecuación xif será el valor i del atributo f, siendo minf el mínimo valor del atributo f y
Maxf el máximo.
-161-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Por otro lado, el algoritmo permite dar mayor preferencia a aquellos ejemplares más cercanos al que
deseamos clasificar. En ese caso, en lugar de emplear directamente la distancia entre ejemplares, se
utilizará la ecuación 2.5.34.
ecuación 2.5.34
KNN en WEKA (IBk)
En WEKA se implementa el clasificador KNN con el nombre IBk, concretamente en la clase
weka.classifiers.IBk.java. Además, en la clase weka.classifiers.IB1.java hay una versión
simplificada del mismo, concretamente un clasificador NN [Nearest Neighbor], sin ningún tipo de
opción, en el que, como su propio nombre indica, tiene en cuenta únicamente el voto del vecino más
cercano. Por ello, en la tabla 2.5.16., siguiente se muestran las opciones que se permiten con el
clasificador IBk.
Opción
Descripción
KNN (1)
Número de vecinos más cercanos.
Los valores posibles son: No distance weighting, Weight by 1-distance y
Weight by 1/distance. Permite definir si se deben “pesar” los vecinos a la
hora de votar bien según su semejanza o con la inversa de su distancia con
respecto al ejemplo a clasificar
Si se activa esta opción, cuando se vaya a clasificar una instancia se
selecciona el número de vecinos (hasta el número especificado en la opción
KNN) mediante el proceso hold-one-out
Minimiza el error cuadrático en lugar del error absoluto para
el caso de clases numéricas cuando se activa la opción
crossValidate
Si es 0 el número de ejemplos de entrenamiento es
ilimitado. Si es mayor que 0, únicamente se almacenan los
n últimos ejemplos de entrenamiento, siendo n el número
que se ha especificado
Muestra el proceso de construcción del clasificador
No normaliza los atributos
distanceWeighting
(No distance weighting)
crossValidate (False)
meanSquared (False)
windowSize (0)
debug (False)
noNormalization False)
Tabla 2.5.16. Opciones de configuración para el algoritmo IBk en WEKA.
El algoritmo implementado en la herramienta WEKA consiste en crear el clasificador a partir de los
ejemplos de entrenamiento, simplemente almacenando todas las instancias disponibles (a menos
que se restrinja con la opción windowSize). Posteriormente, se clasificarán los ejemplos de test a
partir del clasificador generado, bien con el número de vecinos especificados o comprobando el
mejor k si se activa la opción crossValidate. En cuanto a los tipos de datos permitidos y las
propiedades de la implementación, estos son:
Admite
atributos numéricos y simbólicos.
Admite
clase numérica y simbólica. Si la clase es numérica se calculará la media de los valores de
la clase para los k vecinos más cercanos.
Permite
dar peso a cada ejemplo.
proceso de hold-one-out consiste en, para cada k entre 1 y el valor configurado en KNN,
calcular el error en la clasificación de los ejemplos de entrenamiento. Se escoge el k con un menor
error obtenido. El error cometido para cada k se calcula como el error medio absoluto o el
cuadrático si se trata de una clase numérica. El cálculo de estos dos errores se puede ver en las
ecuaciones siguientes. Si la clase es simbólica se tomará como error el número de ejemplos
fallados entre el número total de ejemplos.
El
-162-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
ecuación 2.5.35
ecuación 2.5.36
En las ecuaciones, yi es el valor de la clase para el ejemplo i e ŷi es el valor predicho por el
modelo para el ejemplo i. El número m será el número de ejemplos.
2.5.5.2. Algoritmo k-estrella
El algoritmo K* es una técnica de data mining basada en ejemplares en la que la medida de la
distancia entre ejemplares se basa en la teoría de la información.
Una forma intuitiva de verlo es que la distancia entre dos ejemplares se define como la complejidad
de transformar un ejemplar en el otro. El cálculo de la complejidad se basa en primer lugar en
definir un conjunto de transformaciones T={t1, t2, ..., tn , σ} para pasar de un ejemplo (valor de
atributo) a a uno b. La transformación σ es la de parada y es la transformación identidad (σ(a)=a).
El conjunto P es el conjunto de todas las posibles secuencias de transformaciones descritos en T*
que terminan en σ, y t (a ) es una de estas secuencias concretas sobre el ejemplo a. Esta secuencia
de transformaciones tendrá una probabilidad determinada de p (t ) , definiéndose la función de
probabilidad P*(b|a) como la probabilidad de pasar del ejemplo a al ejemplo b a través de cualquier
secuencia de transformaciones, tal y como se muestra en la ecuación 2.5.37.
ecuación 2.5.37
Esta función de probabilidad cumplirá las propiedades que se muestran en 2.5.38.
ecuación 2.5.38
La función de distancia K* se define entonces tomando logaritmos, tal y como se muestra en la
ecuación 2.5.39.
ecuación 2.5.39
Realmente K* no es una función de distancia dado que, por ejemplo K*(a|a) generalmente no será
exactamente 0, además de que el operador | no es simétrico, esto es, K*(a|b) no es igual que
K*(b|a). Sin embargo, esto no interfiere en el algoritmo K*. Además, la función K* cumple las
propiedades que se muestran en la ecuación 2.5.40.
ecuación 2.5.40
Una vez explicado cómo se obtiene la función K* y cuales son sus propiedades, se presenta a
continuación la expresión concreta de la función P* de la que se obtiene K*, para los tipos de
atributos admitidos por el algoritmo: numéricos y simbólicos.
-163-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Probabilidad de transformación para los atributos permitidos
En cuanto a los atributos numéricos, las transformaciones consideradas serán restar del valor a un
número n o sumar al valor a un número n, siendo n un número mínimo. La probabilidad de pasar de
un ejemplo con valor a a uno con valor b vendrá determinada únicamente por el valor absoluto de la
diferencia entre a y b, que se denominará x.
Se escribirá la función de probabilidad como una función de densidad, tal y como se muestra en la
ecuación 2.5.41, donde x0 será una medida de longitud de la escala, por ejemplo, la media esperada
para x sobre la distribución P*. Es necesario elegir un x0 razonable. Posteriormente se mostrará un
método para elegir este factor. Para los simbólicos, se considerarán las probabilidades de aparición
de cada uno de los valores de dicho atributo.
ecuación 2.5.41
Si el atributo tiene un total de n posibles valores, y la probabilidad de aparición del valor i del
atributo es pi (obtenido a partir de las apariciones en los ejemplos de entrenamiento), se define la
probabilidad de transformación de un ejemplo con valor i a uno con valor j como se muestra en la
ecuación 2.5.42.
ecuación 2.5.42
En esta ecuación s es la probabilidad del símbolo de parada (σ). De esta forma, se define la
probabilidad de cambiar de valor como la probabilidad de que no se pare la transformación
multiplicado por la probabilidad del valor de destino, mientras la probabilidad de continuar con el
mismo valor es la probabilidad del símbolo de parada más la probabilidad de que se continúe
transformando multiplicado por la probabilidad del valor de destino. También es importante, al
igual que con el factor x0, definir correctamente la probabilidad s. Y como ya se comentó con x0,
posteriormente se comentará un método para obtenerlo. También deben tenerse en cuenta la
posibilidad de los atributos con valores desconocidos. Cuando los valores desconocidos aparecen en
los ejemplos de entrenamiento se propone como solución el considerar que el atributo desconocido
se determina a través del resto de ejemplares de entrenamiento. Esto se muestra en la ecuación
2.5.43, donde n es el número de ejemplos de entrenamiento.
ecuación 2.5.43
Combinación de atributos
Ya se han definido las funciones de probabilidad para los tipos de atributos permitidos. Pero los
ejemplos reales tienen más de un atributo, por lo que es necesario combinar los resultados obtenidos
para cada atributo. Y para combinarlos, y definir así la distancia entre dos ejemplos, se entiende la
probabilidad de transformación de un ejemplar en otro como la probabilidad de transformar el
primer atributo del primer ejemplo en el del segundo, seguido de la transformación del segundo
atributo del primer ejemplo en el del segundo, etc.
De esta forma, la probabilidad de transformar un ejemplo en otro viene determinado por la
multiplicación de las probabilidades de transformación de cada atributo de forma individual, tal y
como se muestra en la ecuación 2.5.44.
ecuación 2.5.44
-164-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
En esta ecuación m será el número de atributo de los ejemplos. Y con esta definición la
distancia entre dos ejemplos se define como la suma de distancias entre cada atributo de los
ejemplos.
Selección de los parámetros aleatorios
Para cada atributo debe determinarse el valor para los parámetros s o x0 según se trate de un atributo
simbólico o numérico respectivamente. Y el valor de este atributo es muy importante. Por ejemplo,
si a s se le asigna un valor muy bajo las probabilidades de transformación serán muy altas, mientras
que si s se acerca a 0 las probabilidades de transformación serán muy bajas. Y lo mismo ocurriría
con el parámetro x0. En ambos casos se puede observar cómo varía la función de probabilidad P*
según se varía el número de ejemplos incluidos partiendo desde 1 (vecino más cercano) hasta n
(todos los ejemplares con el mismo peso).
Se puede calcular para cualquier función de probabilidad el número efectivo de ejemplos como se
muestra en la ecuación 2.5.45, en la que n es el número de ejemplos de entrenamiento y n0 es el
número de ejemplos con la distancia mínima al ejemplo a (para el atributo considerado). El
algoritmo K* escogerá para x0 (o s) un número entre n0 y n.
ecuación 2.5.45
Por conveniencia se expresa el valor escogido como un parámetro de mezclado [blending] b, que
varía entre b=0% (n0) y b=100% (n). La configuración de este parámetro se puede ver como una
esfera de influencia que determina cuantos vecinos de a deben considerarse importantes. Para
obtener el valor correcto para el parámetro x0 (o s) se realiza un proceso iterativo en el que se
obtienen las esferas de influencia máxima (x0 o s igual a 0) y mínima (x0 o s igual a 1), y se
aproximan los valores para que dicha esfera se acerque a la necesaria para cumplir con el parámetro
de mezclado.
En la figura 2.5.9., se presenta un ejemplo práctico de cómo obtener los valores para los parámetros x0 o s.
Se va a utilizar para ello el problema que se presentó en la tabla 2.5.1, y más concretamente el atributo Vista
con el valor igual a Lluvioso, de dicho problema.
-165-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Figura 2.5.9.: Ejemplo de obtención del parámetros de un atributo simbólico con el algoritmo K*.
En la figura 2.5.9., se muestra cómo el objetivo es conseguir un valor para s tal que se obtenga una esfera de
influencia de 6,8 ejemplos. Los parámetros de configuración necesarios para el funcionamiento del sistema
son: el parámetro de mezclado b, en este caso igual a 20%; una constante denominada EPSILON, en este
caso igual a 0,01, que determina entre otras cosas cuándo se considera alcanzada la esfera de influencia
deseada. En cuanto a la nomenclatura empleada, n será el número total de ejemplos de entrenamiento, nv el
número de valores que puede adquirir el atributo, y se han empleado abreviaturas para denominar los valores
del atributo: lluv por lluvioso, nub por nublado y sol por soleado.
-166-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Tal y como puede observarse en la figura 2.5.9., las ecuaciones empleadas para el cálculo de la
esfera y de P* no son exactamente las definidas en las ecuaciones definidas anteriormente. Sin
embargo, en el ejemplo se han empleado las implementadas en la herramienta WEKA por los
creadores del algoritmo. En cuanto al ejemplo en sí, se muestra cómo son necesarias 8 iteraciones
para llegar a conseguir el objetivo planteado, siendo el resultado de dicho proceso, el valor de s,
igual a 0,75341.
Clasificación de un ejemplo
Se calcula la probabilidad de que un ejemplo a pertenezca a la clase c sumando la probabilidad de a
a cada ejemplo que es miembro de c, tal y como se muestra en 2.5.46.
ecuación 2.5.46
Se calcula la probabilidad de pertenencia a cada clase y se escoge la que mayor resultado haya obtenido
como predicción para el ejemplo.
Figura 2.5.10. Ejemplo de clasificación con K*.
-167-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Una vez definido el modo en que se clasifica un determinado ejemplo de test mediante el algoritmo K*, en la
figura 2.5.10., se muestra un ejemplo concreto en el que se emplea dicho algoritmo. En el ejemplo se
clasifica un ejemplo de test tomando como ejemplos de entrenamiento los que se mostraron en la tabla 2.1,
tomando los atributos Temperatura y Humedad como numéricos. El proceso que se sigue para determinar a
qué clase pertenece un ejemplo de test determinado es el siguiente: en primer lugar, habría que calcular los
parámetros x0 y s que aún no se conocen para los pares atributo-valor del ejemplo de test. Posteriormente se
aplican las ecuaciones, que de nuevo no son exactamente las definidas anteriormente: se han empleado las
que los autores del algoritmo implementan en la herramienta WEKA. Una vez obtenidas las probabilidades,
se normalizan y se escoge la mayor de las obtenidas. En este caso hay más de un 99% de probabilidad a
favor de la clase no. Esto se debe a que el ejemplo 14 (el último) es casi idéntico al ejemplo de test por
clasificar. En este ejemplo no se detallan todas las operaciones realizadas, sino un ejemplo de cada tipo: un
ejemplo de la obtención de P* para un atributo simbólico, otro de la obtención de P* para un atributo
numérico y otro para la obtención de la probabilidad de transformación del ejemplo de test en un ejemplo de
entrenamiento.
K* en WEKA
La clase en la que se implementa el algoritmo K* en la herramienta WEKA es
weka.classifers.kstar.KStar.java. Las opciones que permite este algoritmo son las que se muestran
en la tabla 2.5.17.:
Opción
Descripción
entropicAutoBlend (False)
globalBlend (20)
missingMode (Average
column entropy curves)
Si se activa esta opción se calcula el valor de los parámetros x0 (o s)
basándose en la entropía en lugar del parámetro de mezclado.
Parámetro de mezclado, expresado en tanto por ciento
Define cómo se tratan los valores desconocidos en los ejemplos de
entrenamiento: las opciones posibles son Ignore the Instance with missing
value (no se tienen en cuenta los ejemplos con atributos desconocidos),
Treat missing value as maximally different (diferencia igual al del vecino
más lejano considerado), Normilize over the attributes (se ignora el atributo
desconocido) y Average column entropy curves
Tabla 2.5.1 7. Opciones de configuración para el algoritmo K* en WEKA.
Dado que los autores de la implementación de este algoritmo en WEKA son los autores del propio
algoritmo, dicha implementación se corresponde perfectamente con lo visto anteriormente.
Simplemente son destacables los siguientes puntos:
Admite
atributos numéricos y simbólicos, así como pesos por cada instancia.
Permite
que la clase sea simbólica o numérica. En el caso de que se trate de una clase numérica se
empleará la ecuación para predecir el valor de un ejemplo de test.
ecuación 2.5.47
En la ecuación 2.5.47., v(i) es el valor (numérico) de la clase para el ejemplo i, n el número
de ejemplos de entrenamiento, y P*(i|j) la probabilidad de transformación del ejemplo j en el
ejemplo i.
-168-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Proporciona
cuatro modos de actuación frente a pérdidas en los atributos en ejemplos de
entrenamiento.
Para el cálculo de los parámetros x0 y s permite basarse en el parámetro b o en el cálculo de la
entropía.
Las ecuaciones para el cálculos de P* y de la esfera de influencia no son las comentadas en la
explicación del algoritmo, sino las empleadas en los ejemplos de las figuras 2.5.9 y 2.5.10.
2.5.6. Redes de Neuronas
Las redes de neuronas constituyen una nueva forma de analizar la información con una diferencia
fundamental con respecto a las técnicas tradicionales: son capaces de detectar y aprender complejos
patrones y características dentro de los datos. Se comportan de forma parecida a nuestro cerebro
aprendiendo de la experiencia y del pasado, y aplicando tal conocimiento a la resolución de
problemas nuevos. Este aprendizaje se obtiene como resultado del adiestramiento ("training") y éste
permite la sencillez y la potencia de adaptación y evolución ante una realidad cambiante y muy
dinámica.
Una vez adiestradas las redes de neuronas pueden hacer previsiones, clasificaciones y
segmentación. Presentan además, una eficiencia y fiabilidad similar a los métodos estadísticos y
sistemas expertos, si no mejor, en la mayoría de los casos. En aquellos casos de muy alta
complejidad las redes neuronales se muestran como especialmente útiles dada la dificultad de
modelado que supone para otras técnicas. Sin embargo las redes de neuronas tienen el
inconveniente de la dificultad de acceder y comprender los modelos que generan y presentan
dificultades para extraer reglas de tales modelos. Otra característica es que son capaces de trabajar
con datos incompletos e, incluso, contradictorios lo que, dependiendo del problema, puede resultar
una ventaja o un inconveniente.
Las redes de neuronas poseen las dos formas de aprendizaje: supervisado y no supervisado;
derivadas del tipo de paradigma que usan: el no supervisado (usa paradigmas como los ART
“Adaptive Resonance Theory"), y el supervisado que suele usar el paradigma del
“Backpropagation".
El diseño de la red de neuronas consistirá, entre otras cosas, en la definición del número de
neuronas de las tres capas de la red. Las neuronas de la capa de entrada y las de la capa de salida
vienen dadas por el problema a resolver, dependiendo de la codificación de la información. En
cuanto al número de neuronas ocultas (y/o número de capas ocultas) se determinará por prueba y
error. Por último, debe tenerse en cuenta que la estructura de las neuronas de la capa de entrada se
simplifica, dado que su salida es igual a su entrada: no hay umbral ni función de salida.
• Proceso de adiestramiento (retropropagación)
Existen distintos métodos o paradigmas mediante los cuales estos pesos pueden ser variados durante
el adiestramiento de los cuales el más utilizado es el de retropropagación [Backpropagation]. Este
paradigma varía los pesos de acuerdo a las diferencias encontradas entre la salida obtenida y la que
debería obtenerse. De esta forma, si las diferencias son grandes se modifica el modelo de forma
importante y según van siendo menores, se va convergiendo a un modelo final estable.
-169-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
El error en una red de neuronas para un patrón [x= (x1, x2, …, xn), t(x)], siendo x el patrón de
entrada, t(x) la salida deseada e y(x) la proporcionada por la red, se define como se muestra en la
ecuación 2.5.48 para m neuronas de salida y como se muestra en la ecuación 2.5.49, para 1 neurona
de salida.
ecuación 2.5.48
ecuación 2.5.49
El método de descenso de gradiente consiste en modificar los parámetros de la red siguiendo la
dirección negativa del gradiente del error. Lo que se realizaría mediante 2.5.50.
ecuación 2.5.50
En la ecuación 2.88, w es el peso a modificar en la red de neuronas (pasando de wanterior a
wnuevo) y α es la razón de aprendizaje, que se encarga de controlar cuánto se desplazan los
pesos en la dirección negativa del gradiente. Influye en la velocidad de convergencia del
algoritmo, puesto que determina la magnitud del desplazamiento.
El algoritmo de retropropagación es el resultado de aplicar el método de descenso del gradiente a
las redes de neuronas. El algoritmo completo de retropropagación se muestra a continuación:
Paso 1: Inicialización aleatoria de los pesos y umbrales.
Paso 2: Dado un patrón del conjunto de entrenamiento (x, t(x)), se presenta el vector x a
la red y se calcula la salida de la red para dicho patrón, y(x).
Paso 3: Se evalúa el error e(x) cometido por la red.
Paso 4: Se modifican todos los parámetros de la red utilizando la ec.2.88.
Paso 5: Se repiten los pasos 2, 3 y 4 para todos los patrones de entrenamiento,
completando así un ciclo de aprendizaje.
Paso 6: Se realizan n ciclos de aprendizaje (pasos 2, 3, 4 y 5) hasta que se verifique el
criterio de parada establecido.
En cuanto al criterio de parada, se debe calcular la suma de los errores en los patrones de
entrenamiento. Si el error es constante de un ciclo a otro, los parámetros dejan de sufrir
modificaciones y se obtiene así el error mínimo. Por otro lado, también se debe tener en cuenta el
error en los patrones de validación, que se presentarán a la red tras n ciclos de aprendizaje. Si el
error en los patrones de validación evoluciona favorablemente se continúa con el proceso de
aprendizaje. Si el error no desciende, se detiene el aprendizaje.
-170-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Redes de Neuronas en WEKA
La clase en la que se implementan las redes de neuronas en weka es
weka.classifiers.neural.NeuralNetwork.java. Las opciones que permite configurar son las que se
muestran en la tabla 2.5.18.:
Opción
Descripción
momentum (0.2)
Factor que se utiliza en el proceso de actualización de los pesos. Se
multiplica este parámetro por el peso en el momento actual (el que se va a
actualizar) y se suma al peso actualizado
Determina el porcentaje de patrones que se emplearán como test del sistema.
De esta forma, tras cada entrenamiento se validará el sistema, y terminará el
proceso de entrenamiento si la validación da un valor menor o igual a 0, o si
se superó el número de entrenamientos configurado
validationSetSize (0)
nominalToBinaryFilter
(False)
learningRate (0.3)
hiddenLayers (a)
validationThreshold (20)
reset (True)
GUI (False)
autoBuild (True)
normalizeNumericClass
(True)
decay (False)
trainingTime (500)
normalizeAttributes (True)
randomSeed (0)
Transforma los atributos nominales en binarios
Razón de aprendizaje. Tiene valores entre 0 y 1.
Determina el número de neuronas ocultas. Sus posibles valores son:
‘a’=(atribs+clases)/2, ‘i’=atribs, ‘o’=clases, ‘t’=atribs+clases.
Si el proceso de validación arroja unos resultados en cuanto al error que
empeoran durante el n veces consecutivas (siendo n el valor de esta
variable), se detiene el aprendizaje.
Permite al sistema modificar la razón de aprendizaje automáticamente (la
divide entre 2) y comenzar de nuevo el proceso de aprendizaje si el proceso
de entrenamiento no converge.
Visualización de la red de neuronas. Si se activa esta opción se puede
modificar la red de neuronas, parar el proceso de entrenamiento en cualquier
momento, modificar parámetros como el de la razón de aprendizaje,...
El sistema construye automáticamente la red basándose en las entradas,
salidas y el parámetro hiddenLayers.
Normaliza los posibles valores de la clase si ésta es numérica, de forma que
estén entre –1 y 1.
La razón de ganancia se modifica con el ciclo de aprendizaje: α= α/n, donde
n es el número de ciclo de aprendizaje actual.
Número total de ciclos de aprendizaje.
Normaliza los atributos numéricos para que estén entre –1 y 1.
Semilla para generar los números aleatorios que inicializarán los parámetros
de la red.
Tabla 2.5.18. Opciones de configuración para las redes de neuronas en WEKA.
La implementación de redes de neuronas que se realiza en la herramienta se ciñe al algoritmo de
retropropagación. Algunas características que se pueden destacar de esta implementación son:
Se
admiten atributos numéricos y simbólicos.
Se admiten clases numéricas (predicción) y simbólicas (clasificación).
Permite la generación manual de redes que no se ciñan a la arquitectura mostrada anteriormente,
por ejemplo, eliminando conexiones de neuronas de una capa con la siguiente.
Como función sigmoidal se utiliza la restringida entre 0 y 1.
Los ejemplos admiten pesos: Cuando se aprende con dicho ejemplo se multiplica la razón de
aprendizaje por el peso del ejemplo. Todo esto antes de dividir la razón de aprendizaje por el
número de ciclo de aprendizaje si se activa decay.
-171-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
3. EJEMPLOS PRÁCTICOS DE ALGORITMOS EN WEKA
3.1. LANZAMIENTO DE DISTINTOS ALGORITMOS DE APRENDIZAJE DESDE WEKA.
En este apartado mostraremos la forma de lanzar distintos métodos de aprendizaje y la forma de
indicar sus parámetros, utilizando en todos los casos la misma base de datos. La base de datos se
encuentra en el 1directorio de WEKA: “…\data\weather.nominal.arff”
Se trata del problema que indica si una cierta persona practicará deporte en función de las
condiciones atmosféricas. En este caso se utiliza la versión de la base de datos en la que todos los
atributos son discretos (nominales) y se utiliza precisamente esta versión para que se puedan lanzar
todos los algoritmos de aprendizaje.
Los métodos que probaremos serán los siguientes:
A. Árbol de decisión
Se lanza desde MS-DOS (o desde Matlab anteponiendo ‘!’) con el siguiente comando:
java weka.classifiers.trees.J48 -t data/weather.nominal.arff –C 0.30
…y el principal parámetro a ajustar es el umbral de confianza para la poda, que en este caso se ha
-C 0.30
ajustado a 0.30:
El resultado se muestra de la forma siguiente (se elimina parte común a otros algoritmos):
J48 pruned tree
-----------------outlook = sunny
| humidity = high: no (3.0)
| humidity = normal: yes (2.0)
outlook = overcast: yes (4.0)
outlook = rainy
| windy = TRUE: no (2.0)
| windy = FALSE: yes (3.0)
N
umber of Leaves : 5
Size of the tree : 8
B. Vecino más cercano
El comando necesario para utilizar el método del vecino más cercano es el siguiente:
java weka.classifiers.lazy.IBk -t data/weather.nominal.arff –K 3
Donde el parámetro indica el número de vecinos considerado, que se ha fijado a 3:
-K 3
Y dado que este método no genera modelo propiamente dicho, el resultado no ofrece apenas
información (salvo la común al resto de algoritmos):
IB1 instance-based classifier
using 3 nearest neighbour(s) for classification
1
Junto con los apuntes se anexan todos los ficheros, con la versión de Weka mejorada se incluye la
colección de dataset que se bajo de la página oficial.
-172-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
C. Listas de reglas
Existen diversos algoritmos de generación de listas de reglas. Utilizaremos el método Prism, que no
admite ningún parámetro:
java weka.classifiers.rules.Prism -t data/weather.nominal.arff
El resultado es el siguiente:
Prism rules
---------If outlook = overcast then yes
If humidity = normal
and windy = FALSE then yes
If temperature = mild
and humidity = normal then yes
If outlook = rainy
and windy = FALSE then yes
If outlook = sunny
and humidity = high then no
If outlook = rainy
and windy = TRUE then no
D. Naive Bayes
El algoritmo Naïve Bayes se lanza de la forma siguiente:
java weka.classifiers.bayes.NaiveBayes -t data/weather.nominal.arff
java weka.classifiers.bayes.NaiveBayes -t data/weather.nominal.arff –K
Donde el parámetro –K (si está presente) indica que se estiman funciones de distribución de
probabilidad para los atributos mediante el método kernel (suma de gaussianas) en lugar de
considerar que cada atributo sigue una distribución gaussiana.
El resultado mostrado en pantalla es el siguiente:
Naive Bayes Classifier
Class yes: Prior probability = 0.63
outlook: Discrete Estimator. Counts = 3 5 4 (Total = 12)
temperature: Discrete Estimator. Counts = 3 5 4 (Total = 12)
humidity: Discrete Estimator. Counts = 4 7 (Total = 11)
windy: Discrete Estimator. Counts = 4 7 (Total = 11)
Class no: Prior probability = 0.38
outlook: Discrete Estimator. Counts = 4 1 3 (Total = 8)
temperature: Discrete Estimator. Counts = 3 3 2 (Total = 8)
humidity: Discrete Estimator. Counts = 5 2 (Total = 7)
windy: Discrete Estimator. Counts = 4 3 (Total = 7)
Se muestran las probabilidades a priori de las clases y también las estadísticas para cada atributo.
Con atributos discretos (como es el caso en este ejemplo, la opción –K no tiene ningún efecto).
-173-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
3.2. UN EJEMPLO SENCILLO
En particular, en este ejemplo, vamos a trabajar con los datos acerca de los días que se ha podido
jugar al tenis, dependiendo de diversos aspectos meteorológicos. El objetivo es poder determinar
(predecir) si hoy podremos jugar al tenis. Los datos de que disponemos están en el fichero:
“weather.arff” y son los siguientes:
Figura 3.2.1. Tabla de datos “Weather”
Abrimos el Weka y lanzamos el Explorer. Lo primero que vamos a hacer es cargar los datos en el
área de trabajo. Para ello, pincha en el botón “Open file” del entorno “preprocess”. Seleccionamos
el fichero “weather.arff” y si todo ha ido bien veremos la pantalla de la Figura 3.2.1.
Figura 3.2.1. Cargando el dataset Weather
-174-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Desde esta ventana podemos conocer bastantes detalles del dataset que acabamos de cargar. Por
ejemplo, el sistema nos indica que tenemos 14 registros con 5 atributos. En la Figura 3.2.2 podemos
observar que el atributo Outlook tiene tres valores diferentes (Sunny, Overcast y Rainy) siendo la
distribución de [5,4,5]. En el caso de los 5 registros donde el atributo Outlook=sunny, tenemos 3
con clase no y 2 con clase yes2, cuando Outlook=overcast los 4 registros son yes, y finalmente
cuando Outlook=rainy existen 3 con clase yes, y 2 con clase no.
Una vez cargado el fichero, ya estamos en disposición de aprender un modelo (en este caso un árbol
de decisión). Para ello, seleccionamos en la pestaña Classify.
Para este primer ejemplo vamos a utilizar el algoritmo clásico de aprendizaje de árboles de decisión
C4.5 (J48 es el nombre que se le da en Weka), Para ello pulsamos Choose, seleccionamos J48 en
Trees. Si pulsáramos sobre la ventana que contiene el nombre del método podríamos modificar los
parámetros específicos de este método. En este caso dejaremos los valores por defecto.
Por último seleccionamos como opción de evaluación (test options) la opción Use training set, y ya
estamos listos para ejecutar el método de aprendizaje. Para ello pulsamos el botón Start que
despierta al pájaro Weka de su letargo y realiza el aprendizaje del modelo predictivo, en este caso
un árbol de decisión.
Figura 3.2.2. Clasificación J48 del dataset Weather
2
Podemos conocer el significado de cada color seleccionando el atributo clase, en este caso play.
-175-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Si no ha habido problemas, el sistema nos muestra en la caja “Classifier Output” la siguiente
información:
=== Run information ===
Scheme:
Relation:
Instances:
Attributes:
Test mode:
weka.classifiers.trees.J48 -C 0.25 -M 2
weather
14
5
outlook
temperature
humidity
windy
play
10-fold cross-validation
=== Classifier model (full training set) ===
J48 pruned tree
-----------------outlook = sunny
|
humidity <= 75: yes (2.0)
|
humidity > 75: no (3.0)
outlook = overcast: yes (4.0)
outlook = rainy
|
windy = TRUE: no (2.0)
|
windy = FALSE: yes (3.0)
Number of Leaves
:
Size of the tree :
5
8
Time taken to build model: 0.02 seconds
=== Stratified cross-validation ===
=== Summary ===
Correctly Classified Instances
Incorrectly Classified Instances
Kappa statistic
Mean absolute error
Root mean squared error
Relative absolute error
Root relative squared error
Total Number of Instances
9
5
0.186
0.2857
0.4818
60
%
97.6586 %
14
=== Detailed Accuracy By Class ===
TP Rate
FP Rate
Precision
Recall
0.778
0.6
0.7
0.778
0.4
0.222
0.5
0.4
F-Measure
0.737
0.444
64.2857 %
35.7143 %
Class
yes
no
=== Confusion Matrix ===
a b
<-- classified as
7 2 | a = yes
3 2 | b = no
Como podemos observar Weka nos informa en primer lugar de algunos parámetros del dataset. A
continuación nos muestra de manera textual el modelo aprendido (en este caso el árbol de decisión).
-176-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Por ultimo nos incluye información sobre la evaluación del modelo. En este problema, el árbol
aprendido tiene una precisión máxima (100%) por lo que todas las medidas de error son 0. Además
podemos conocer más detalles de la distribución de los ejemplos por clase en la matriz de
confusión).
Podemos visualizar el árbol de una manera más atractiva si pulsamos el botón derecho sobre el
texto trees.J48 de la caja Result-list. Seleccionamos la opción Visualize Tree, y obtendremos el
árbol de decisión de la Figura 3.2.3.
Figura 3.2.3. Árbol representado gráficamente.
Además, la Figura 3.2.3 nos muestra para cada hoja cuántos ejemplos de la evidencia son cubiertos.
Con el botón derecho sobre el texto trees.J48 de la caja Result-list tendremos acceso otras opciones
más avanzadas para el análisis del modelo aprendido.
3.3. UN PROBLEMA DE CLASIFICACIÓN
Enunciado del problema. Selección de Fármaco
En este caso se trata de predecir el tipo de fármaco (drug) que se debe administrar a un paciente
afectado de rinitis alérgica según distintos parámetros/variables. Las variables que se recogen en
los historiales clínicos de cada paciente son:
· Age: Edad
· Sex: Sexo
· BP (Blood Pressure): Tensión sanguínea.
· Cholesterol: nivel de colesterol.
· Na: Nivel de sodio en la sangre.
· K: Nivel de potasio en la sangre.
Hay cinco fármacos posibles: DrugA, DrugB, DrugC, DrugX, DrugY. Se han recogido los datos del
medicamento idóneo para muchos pacientes en cuatro hospitales. Se pretende, para nuevos
pacientes, determinar el mejor medicamento a probar.
-177-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
En primer lugar vamos a cargar los datos del primer hospital fichero “...\data\
drug1n.arff”.
Resolución del problema
La primera pregunta que nos podemos hacer es ver qué fármacos son más comunes en general, para
ver si todos suelen ser igualmente efectivos en términos generales. Para ello seleccionamos el
atributo drug, y de esta manera vemos al distribución por clases. Podemos concluir que el fármaco
más efectivo es el Y, que se administra con éxito en casi la mitad de los pacientes. Una regla vulgar
sería aplicar el fármaco Y, en el caso que falle, el fármaco X, y así sucesivamente siguiendo las
frecuencias de uso con éxito.
Weka tiene un método que permite generar este modelo tan simple, es decir asignar a todos los
ejemplos la clase mayoritaria, recibe el nombre de ZeroR3 en la familia rules. Si vamos a la parte de
Classify y ejecutamos este modelo evaluamos sobre todos los datos de entrenamiento, veremos que
como era de esperar obtenemos un clasificador de precisión 45.5%.
Podemos utilizar métodos más complejos como el J48. Si probáis esta técnica veréis que se obtiene
el árbol de la Figura 3.1., que obtiene una precisión del 97%.
Figura 3.3.1. Árbol de decisión directamente sobre los datos
3
En el caso de regresión este método asigna la media aritmética a todos los casos predecir.
-178-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Como podemos observar, el árbol tiene bastantes reglas (en concreto 12). Podemos ver cuál es el
acierto (también denominado precisión o accuracy) de este árbol respecto a los datos de
entrenamiento. Sin embargo, en este caso tenemos un error de sólo el 3,5% sobre los datos de
entrenamiento. Este modelo es muchísimo mejor que sí sólo nos guiamos por la distribución, que
nos daría un error de más del 50% (el 54,5% de las veces el medicamento DRUGY no es el
adecuado). De todas maneras, es posible hacerlo mejor... ¿pero cómo? ¿con otro tipo de algoritmo
de aprendizaje, una red neuronal, por ejemplo.? Es posible que otros modelos (p.ej. las redes
neuronales) dieran mejor resultado (ya lo probaremos), pero el asunto aquí es que posiblemente no
hemos examinado suficientemente los datos de entrada.
Vamos a analizar, con más detenimiento, los atributos de entrada del problema. Es posible que se
puedan establecer mejores modelos si combinamos algunos atributos. Podemos analizar pares de
atributos utilizando diferentes gráficos.
Para comparar la relación entre atributos en Weka debemos acudir al entorno Visualize, donde
podemos realizar gráficas entre pares de atributos y ver si tienen alguna relación con las clases. De
entre todas las combinaciones posibles, destaca la que utiliza los parámetros de los niveles de sodio
y potasio (K y Na) ver Pulsando en la parte inferior sobre las clases, podemos cambiar los colores
asignados a las clases, mejorando la visualización del gráfico. Además podemos ampliar y ver con
más detalle alguna zona del gráfico con select instance y submit.
Figura 3.3.2.. Resultado de un nodo Gráfico (Na x K x Drug)
En este gráfico sí que se ven algunas características muy significativas. Parece haber una clara
separación lineal entre una relación K/Na alta y una relación K/Na baja. De hecho, para las
concentraciones K/Na bajas, el fármaco Y es el más efectivo de una manera clara y parece
mostrarse que por encima de un cierto cociente K/Na ese medicamento deja de ser efectivo y se
debe recurrir a los otros cuatro.
-179-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Podemos utilizar este conocimiento que acabamos de extraer para mejorar nuestros modelos.
Hemos establecido que el medicamento a administrar depende en gran medida del cociente entre
K/Na. Por tanto, vamos a realizar un nuevo modelo que utilice este cociente. Para ello, vamos a
crear un nuevo atributo derivado (también llamados atributos pick & mix) mediante el uso de los
filtros del entorno “preprocess”.
Seleccionamos esta parte de la aplicación, y pulsamos Choose en Filter. De entre todos los filtros
posibles elegimos Unsupervised.Attribute.Addexpression. Este atributo nos permite la creación de
nuevos atributos mediante la combinación de atributos ya existentes (Pick&Mix). Para configurar
este filtro pulsamos sobre la propia ventana del texto, y nos aparecen las opciones posibles. Sólo
tenemos que modificar la opción expression, asignandole el valor “a5/a6” (a5 corresponde a K y a6
corresponde a NA), y la opción name, donde colocamos el nombre del nuevo atributo “Na_to_Ka”.
Aceptamos con OK, y una vez configurado el filtro lo empleamos con apply. Veremos en ese
momento como aparece el nuevo atributo en la lista de atributos. Siempre podremos deshacer estos
cambios pulsando en undo.
A continuación, vamos a ver como funciona el nuevo atributo, para ello volvemos a aprender un
árbol de decisión J48 utilizando otra vez todos los datos para la evaluación. Atención que debemos
indicarle que la clase es el atributo drugs !!! ya que por defecto toma la clase como el último
atributo. Esto lo hacemos en la ventana de selección de la clase, en el entorno Classify. Ahora, si
examinamos el modelo aprendido tenemos lo siguiente:
Figura 3.3.3. Segundo modelo que utiliza el atributo derivado Na_to_K
Modelo mucho más simple y corto que el anterior, en el que se ve la importancia del atributo que
hemos creado Na_to_K. Además si analizamos su calidad vemos que el nuevo modelo un 100% de
precisión, con lo que el modelo es mucho más fiable que antes. No obstante, los árboles de decisión
pueden tener poda y tener porcentajes que no son del 100% ni siquiera con los mismos datos que se
han usado para el aprendizaje. De hecho si cambiamos el método de evaluación a validación
cruzada con 10 pliegues, podremos observar que la precisión baja ligeramente (99%). Sin embargo,
tal y como vimos en la parte de teoría, este método de evaluación es mucho más justo. Observad,
que el modelo que aparece corresponde al aprendizaje al modelo aprendido con todos los datos.
Weka muestra este modelo de manera sólo informativa, ya que no lo utiliza para la evaluación
-180-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Filtrado de atributos
En el árbol de decisión final se puede observar que no se utilizan todos los atributos para efectuar
una clasificación, esto indica que hay atributos que no son significativos para la resolución del
problema. Existen métodos como los árboles de decisión, a los cuales no les afecta de manera grave
la presencia de atributos no significativos, ya que en el propio mecanismo de aprendizaje realizan
una selección de atributos por su relevancia. Sin embargo, otros métodos no realizan este proceso,
por lo que si realizamos un filtrado de atributos previo al aprendizaje podremos mejorar de manera
relevante su precisión, y al mismo tiempo simplificamos los modelos.
Un ejemplo de método de aprendizaje que reduce su calidad ante la presencia de atributos no
relevantes, es el método Naive Bayes. Veamos que precisión obtiene este método, para ello
seleccionamos en Classify el método NaiveBayes y lo evaluamos con evaluación cruzada (10
pliegues). Este método obtiene una precisión de 91%, por lo tanto una precisión mucha más baja
que los árboles de decisión.
Bien, en este caso probablemente los atributos no relevantes están afectando a la calidad del
método. Veamos como podemos efectuar un filtrado de atributos. Para ello vamos a la sección
Select Attributes. Esta sección esta especializada en este proceso, y contiene una gran cantidad de
técnicas diversas para realizar la selección de atributos. Si recordamos la parte teórica, sabremos
que hay dos familias de técnicas: los wrappers, y los métodos de filtro. Dadas las características del
problema en este caso podemos probar con una técnica wrapper realizando una búsqueda
exhaustiva. Para ello, pulsamos Choose de AttributeEvaluator y seleccionamos el método
WrapperSubsetEval. Para configurarlo pulsamos en la ventana de texto. Vamos a utilizar el propio
Naive Bayes para el wrapper, por lo que seleccionaremos es método en classifier. Por otra parte en
SearchMethod, indicamos que queremos una búsqueda exhaustiva eligiendo ExhaustiveSearch.
De esta manera tendremos la herramienta configurada tal y como aparece en la Figura 3.4.
Figura 3.3.4. Filtrando atributos.
-181-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
A continuación ejecutamos el método de filtrado pulsando Start. Tras esperar un poco veremos, que
este método de filtraje nos recomienda usar los atributos: Age, Sex, BP. Cholesterol y Na_to_K.
Veamos si tiene razón, para ello volvemos a la pantalla preprocess, y eliminamos los atributos
descartados (Na y K)4, para ello los marcamos en la parte de Attributes, y pulsamos en Remove. En
realidad, podemos aplicar los filtros directamente al conjunto de datos si accedemos a los métodos a
través de Filter en la ventana Preprocess.
Finalmente, para conocer la precisión que obtiene NaiveBayes con este subconjunto de atributos,
volvemos a la ventana Classify, y seleccionamos el método NaiveBayes. Con validación cruzada
ahora se alcanzan 96.5 puntos de precisión.
Por ultimo, observa que también podemos utilizar los propios métodos de aprendizaje como
métodos de filtrado. Por ejemplo, si seleccionamos los atributos que utiliza el árbol de decisión:
Age, BP. Cholesterol y Na_to_K. obtenemos una precisión del 96.5% con NaiveBayes.
4
Por supuesto no debemos eliminar la clase.
-182-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
3.4. APRENDIZAJE SENSIBLE AL COSTE
En muchos problemas, nos encontraremos situaciones donde dependiendo el tipo de error que
cometamos tendremos un coste diferente asociado. Por ejemplo, suponed que en un entorno
bancario tenemos un modelo que nos recomienda si conceder o no un crédito a un determinado
cliente a partir de las características propias de ese cliente. Obviamente, y desde el punto de vista
del banco, es mucho más costoso que el sistema se equivoque dando un crédito a una persona que
no lo devuelve, que la situación contraria, denegar un crédito a un cliente que sí lo devolvería.
Para este tipo de problemas, la información sobre los costes de los errores viene expresada a través
de una matriz de coste. En este tipo de matrices recoge el coste de cada una de las posibles
combinaciones entre la case predicha por el modelo y la clase real.
Weka nos ofrece mecanismos para evaluar modelos con respecto al coste de clasificación, así como
de métodos de aprendizaje basados en reducir el coste en vez de incrementar la precisión.
Enunciado del problema. Otorgar un crédio
En este ejemplo vamos a utilizar el dataset “credit-g.arff”. Este conjunto de datos contiene 1.000
ejemplos que representan clientes de una entidad bancaria que demandaron un crédito. Existen siete
atributos numéricos y 13 nominales. Los atributos de cada objeto indican información sobre el
cliente en cuestión: estado civil, edad, parado, etc., así como información del crédito: propósito del
crédito, cantidad solicitada, etc. La clase es binaria e indica si el cliente puede ser considerado como
fiable para concederle el crédito o no.
Este dataset, trae información de los costes de clasificación errónea, en concreto la siguiente matriz
de coste:
Esta tabla indica que es 5 veces más costoso si se otorga un crédito a una persona que no lo
devuelve, que la situación contraria. Bien, vamos a ver cómo podemos evaluar los modelos con
respecto a la matriz de coste en Weka.
Resolución del problema
Vamos a la ventana Classify, y en Test Options, pulsamos More Options. Hablilitamos la opcion
Cost-Sensitive Evaluation. Pulsamos Set para introducir la matriz. Indicamos el número de clases, 2,
e introducimos la matriz de costes. Es importante que pulsemos enter tras escribir las cifras ya que
es bastante quisquillosa esta ventana. Finalmente cerramos todas las ventanas.
-183-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Empezamos con la clasificación más simple, asignar siempre la clase mayoritaria, (ZeroR).
Lanzamos la evaluación con validación cruzada de 10 pliegues. Y si todo ha ido bien, veremos que
se obtiene una precisión del 70 %, y un coste de de 1500 unidades. Era de esperar pues nos
equivocamos 300 veces pero en el peor de los casos. Es importante que confirméis que estáis
trabajando con la matriz de coste configurada correctamente. Esto lo podéis asegurar observando la
matriz de coste que aparece en el texto Classifier Output, en la parte Evaluation cost matrix. Si no
es la correcta, volved a configurarla, en ocasiones da mucha guerra esta ventana.
Probemos ahora con otro método, por ejemplo Naive Bayes. Para ello seleccionamos, NaiveBayes
de Bayes. En esta ocasión obtenemos una precisión de 75.4% y un coste de 850 unidades.
Mejoramos ambas medidas, sin embargo hemos de tener en cuenta que estos métodos están
ignorando la matriz de costes, por lo que se construyen de manera que intentan reducir el número de
errores. Weka, ofrece varias técnicas que permiten adaptar las técnicas a un contexto con costes.
Dos de estas técnicas están integradas CostSensitiveClassifier en Meta. Este paquete ofrece dos
técnicas bastante sencillas para que un método de aprendizaje sea sensible al contexto. La primera
versión consiste en que los modelos aprendidos asignen las clases de manera que se minimicen los
costes de clasificación errónea. Normalmente, esta asignación se realiza de manera que se reduzcan
los errores en la clasificación. La segunda técnica consiste en modificar los pesos asignados a cada
clase de manera que se da más importancia a los ejemplos que son susceptibles de cometer los
errores más costosos. Para optar entre estos métodos utilizamos la opción MinimizeExpectedCost. Si
fijamos esa opción como cierta, se utiliza la primera técnica (asignación de clase de coste mínimo),
si la dejamos como falsa, se utiliza la segunda (compensar los costes mediante los pesos de los
ejemplos).
Probemos como funcionan estos métodos. Seleccionad este paquete dejando ZeroR como
clasificador base. Además hemos de indicarle al método la matriz de coste que ha de utilizar en el
aprendizaje. Esto se hace, fijando CostMatrixSource como Use Explicit Matriz Cost. Y en Cost
Matriz introducimos la misma matriz de coste que hemos utilizado para la evaluación.
MinimizeExpectedCost lo dejamos como falso.
El esquema resultante sería:
weka.classifiers.meta.CostSensitiveClassifier -cost-matrix "[0.0 1.0; 5.0 0.0]" -S 1 -W
weka.classifiers.rules.ZeroR
Si lanzamos el método veremos que ahora en vez de tomar la clase mayoritaria para clasificar todos
los ejemplos, toma la clase minoritaria, de esta manera, aunque la precisión es muy baja (30%), el
coste total es menor 700.
Veamos que sucede si en vez de ZeroR utilzamos NaiveBayes y tomando la misma configuración
de CostSensitiveClassifier. Obtenemos, como es de esperar un resultado bastante mejor: 69% de
precisión y un coste de 530 unidades. Finalmente, si probamos el otro modo de convertir
NaiveBayes en un clasificador sensible al contexto (es decir cambiamos MinimizeExpectedCost a
True), todavía reducimos más el coste: Precisión 69.5% y coste 517 unidades.
-184-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Combinación de Modelos
Uno de los aspectos más destacados de Weka es la gran cantidad de métodos de combinación de
modelos que posee. Estos métodos mejoran la calidad de las predicciones mediante combinando las
predicciones de varios modelos. En realidad estos métodos implementan la estrategia de “cuatro
ojos ven más que dos”, aunque también es cierto que para que esta afirmación se cumpla los ojos
deben tener buena vista, y además no deben tener un comportamiento idéntico, ya que en ese caso
no habría mejora.
Por el contrario, utilizar métodos de combinación de modelos también tiene desventajas.
Principalmente, el modelo se complica, perdiendo comprensibilidad. Además, necesitamos más
recursos (tiempo y memoria) para el aprendizaje y utilización de modelos combinados. En este
ejemplo vamos a utilizar de nuevo el dataset “credit-g.arff”. Iniciamos el ejercicio cargando el
fichero “credit-g.arff”. A continuación, acudimos a la pantalla Classify. Vamos a ver que precisión
obtiene el método J48 en su configuración por defecto utilizando validación cruzada con 10
pliegues.
Para este problema, J48 obtiene una precisión de 70.5%, lo cual, aunque a priori no está mal, es
realmente un resultado muy pobre. Fijaos que utilizando el criterio de aceptar todos los créditos
tendríamos una precisión del 70%. Por lo tanto J48 casi no aporta nada a este problema.
Vamos a empezar con el método Bagging. Como sabeis esta técnica se fundamenta en construir un
conjunto de n modelos mediante el aprendizaje desde n conjuntos de datos. Cada conjunto de dato
se construye realizando un muestreo con repetición del conjunto de datos de entrenamiento.
Para seleccionar Bagging, pulsamos Choose y en Meta, tendremos el método Bagging. Vamos a
Configurarlo. En este caso las opciones más importantes son numIterations donde marcamos el
número de modelos base que queremos crear, y Classifier, donde seleccionamos el método base con
el cual deseamos crear los modelos base. Fijamos numIterations=20 y Classifier= J48.
De esta manera tendremos el método configurado de la siguiente manera:
weka.classifiers.meta.Bagging -P 100 -S 1 -I 20 -W weka.classifiers.trees.J48 -- -C 0.25 -M 2
Si lanzamos weka, observareis que obviamente le cuesta más (en realidad 20 veces más). Y ahora
obtenemos una precisión de 75%, hemos mejorado 5 puntos!!!. Puede parecer poco, pero pensad el
dinero que podría suponer una mejora de 5 puntos en el acierto en la predicción de créditos
impagados de una entidad bancaria
Veamos que pasa con Boosting. Esta técnica es bastante parecida al Bagging, aunque utiliza una
estrategia más ingeniosa ya que cada iteración intenta corregir los errores cometidos anteriormente
dando más peso a los datos que se han clasificado erróneamente.
Seleccionamos AdaBoostM1 en Meta. En este método las opciones más importantes son también
numIterations donde marcamos el número de iteraciones máximas (es decir de modelos base), y
Classifier, donde seleccionamos el método base con el cual deseamos crear los modelos base. Como
en caso anterior, fijamos numIterations=20 y Classifier= J48.
-185-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
De esta manera tendremos el método configurado de la siguiente manera:
weka.classifiers.meta.AdaBoostM1 -P 100 -S 1 -I 20 -W weka.classifiers.trees.J48 -- -C 0.25 -M 2
En este caso la mejora es más modesta, ya que nos quedamos en 71.6. Probemos a incrementar el
número máximo de iteraciones a 40. Como veréis, mejoramos un poco la predicción, ya que
llegamos a 73.5, eso sí, a base de dedicar más tiempo al aprendizaje.
3.5. UN PROBLEMA DE AGRUPACIÓN
Enunciado: Agrupación de Empleados
La empresa de software para Internet “Memolum Web” quiere extraer tipologías de empleados, con
el objetivo de hacer una política de personal más fundamentada y seleccionar a qué grupos
incentivar.
Las variables que se recogen de las fichas de los 15 empleados de la empresa son:
· Sueldo: sueldo anual en euros.
· Casado: si está casado o no.
· Coche: si viene en coche a trabajar (o al menos si lo aparca en el párking de la empresa).
· Hijos: si tiene hijos.
· Alq/Prop: si vive en una casa alquilada o propia.
· Sindic.: si pertenece al sindicato revolucionario de Internet
· Bajas/Año: media del nº de bajas por año
· Antigüedad: antigüedad en la empresa
· Sexo: H: hombre, M: mujer.
Los datos de los 15 empleados se encuentran en el fichero “empleados.arff”. Se intenta extraer
grupos de entre estos quince empleados.
Resolución del Problema
Vamos a utilizar un algoritmo de clustering para obtener grupos sobre esta población. En primer
lugar vamos a probar con tres grupos. Para ello acudimos a la ventana Cluster. Vamos a empezar a
trabajar con el algoritmo de Kmedias. Para ello en Clusterer, pulsamos Choose, y seleccionamos
SimpleKmeans. Lo configuramos definiendo como 3 el NumClusters.
-186-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Figura 3.5.1.. Determinando el número de clusters
Ahora podemos ejecutar el método pulsando Start.
Si examinamos el resultado conoceremos la suma media de errores cuadráticos de cada valor con
respecto a su centro. Además vemos qué características tiene cada cluster/conglomerados. A
continuación, se muestra de una manera más resumida a cómo lo muestra el Weka (que incluye
desviaciones):
Si pulsamos el botón derecho sobre SimpleKmeans de la parte de Result List Podremos ver a qué
Grupo va a parar cada ejemplo. Pero además, podemos estudiar cómo se asignan los ejemplos a los
clusters dependiendo de los atributos seleccionados para dibujar la gráfica.
-187-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
3.6. REGLAS DE ASOCIACIÓN Y DEPENDENCIAS
Vamos a estudiar ahora los datos del hundimiento del Titanic. Los datos se encuentran en el fichero
“titanic.arff” y corresponden a las características de los 2.201 pasajeros del Titanic. Estos datos son reales y
se han obtenido de: "Report on the Loss of the ‘Titanic’ (S.S.)" (1990), British Board of Trade Inquiry
Report_ (reprint), Gloucester, UK: Allan Sutton Publishing.
Para este ejemplo sólo se van a considerar cuatro variables:
· Clase (0 = tripulación, 1 = primera, 2 = segunda, 3 = tercera)
· Sexo (1 = hombre, 0 = mujer)
· Edad (1 = adulto, 0 = niño)
· Sobrevivió (1 = sí, 0 = no)
Para ello, vamos a ver que reglas de asociación interesantes podemos extraer de estos atributos. Para ejecutar
los métodos en Weka de reglas de asociaciación, seleccionamos la ventana de associate.
Entre otros, este sistema de minería de datos provee el paquete “WEKA.associations.Apriori” que contiene la
implementación del algoritmo de aprendizaje de reglas de asociación Apriori. Podemos configurar este
algoritmo con varias opciones: con la opción “UpperBoundMinSupport” indicamos el límite superior de
cobertura requerido para aceptar un conjunto de ítems. Si no se encuentran conjuntos de ítems suficientes
para generar las reglas requeridas se va disminuyendo el límite hasta llegar al límite inferior (opción
“LowerBoundMinSupport”). Con la opción “minMetric” indicamos la confianza mínima (u otras métricas
dependiendo del criterio de ordenación) para mostrar una regla de asociación; y con la opción “numRules”
indicamos el número de reglas que deseamos que aparezcan en pantalla. La ordenación de estas reglas en
pantalla puede configurarse mediante la opción “MetricType”, algunas opciones que se pueden utilizar son:
confianza de la regla, lift (confianza divido por el número de ejemplos cubiertos por la parte derecha de la
regla), y otras más elaboradas.
Veamos las reglas que extrae este algoritmo tomando los valores por defecto:
1. Clase=0 885 ==> Edad=1 885
2. Clase=0 Sexo=1 862 ==> Edad=1 862
3. Sexo=1 Sobrevivió?=0 1364 ==> Edad=1 1329
4. Clase=0 885 ==> Edad=1 Sexo=1 862
5. Clase=0 Edad=1 885 ==> Sexo=1 862
6. Clase=0 885 ==> Sexo=1 862
7. Sobrevivió?=0 1490 ==> Edad=1 1438
8. Sexo=1 1731 ==> Edad=1 1667
9. Edad=1 Sobrevivió?=0 1438 ==> Sexo=1 1329
10. Sobrevivió?=0 1490 ==> Sexo=1 1364
conf:(1)
conf:(1)
conf:(0.97)
conf:(0.97)
conf:(0.97)
conf:(0.97)
conf:(0.97)
conf:(0.96)
conf:(0.92)
conf:(0.92)
En cada regla, tenemos la cobertura de la parte izquierda y de la regla, así como la confianza de la regla.
Podemos conocer alguna regla interesante aunque otras los son menos. Por ejemplo, la regla 1 indica que,
como era de esperar toda la tripulación es adulta. La regla 2 nos indica lo mismo, pero teniendo en cuenta a
los varones. Parecidas conclusiones podemos sacar de las reglas 4, 5 y 6. La regla 3 nos indica que los
varones que murieron fueron en su mayoría adultos (97%). La regla 7 destaca que la mayoría que murieron
fueron adultos (97%). Y finalmente la 10 informa que la mayoría de los muertos fueron hombres (92%).
Cabe destacar que la calidad de las reglas de asociación que aprendamos muchas veces viene lastrada por la
presencia de atributos que estén fuertemente descompensados. Por ejemplo, en este caso la escasa presencia
de niños provoca que no aparezcan en las reglas de asociación, ya que las reglas con este ítemset poseen una
baja cobertura y son filtradas. Podemos mitigar parcialmente este fenómeno si cambiamos el método de
selección de reglas.
-188-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
EJERCICIOS DE AUTOCONTROL
Estas prácticas consisten en, dado un conjunto de datos (numéricos y/o nominales) referidos a un
problema cualquiera, aplicar algoritmos de inteligencia artificial que realizan un aprendizaje
automático para establecer patrones y modelos sobre esos datos y así extraer conclusiones sobre
ellos.
Los objetivos son practicar la implementación de las técnicas básicas de aprendizaje automático /
minería de datos en la herramienta Weka, comparar algunos de los algoritmos de aprendizaje, y
aprender a evaluar el resultado de la aplicación de un algoritmo.
Para ello se 1utilizará:
•
La biblioteca de clases de aprendizaje en Java llamada Weka, muy sencilla de utilizar,
desarrollada en la universidad de Waikato de Nueva Zelanda ([WF99] Ian H. Witten y Eibe
Frank. Data Mining. Practical Machine Learning Tools and Techniques with Java
Implementations, Morgan Kaufmann, 1999).
•
Conjuntos de datos reales sobre problemas variados, incluidos en Weka.
Los datos corresponden a una gran variedad de problemas diferentes. Hay dos tipos de conjuntos de
datos: datos numéricos (en los que los valores de las variables son números) y datos nominales (con
valores discretos nominales).
Ejemplos de conjuntos con datos nominales son:
- CLASIFICACION: Clasificación de setas (Mushroom.arff), Clasificación de animales (Zoo.arff)
- SOCIALES: Aprobación de créditos (Credit-a.arff), Votaciones en el Congreso de EEUU
(Vote.arff)
- ENFERMEDADES: Predicción de enfermedades (Breast-cancer.arff, Diabetes.arff, Heart-*.arff)
- RECONOCIMIENTO: Reconocimiento de audio (Vowel.arff), Reconocimiento de imágenes
(Letter.arff)
- MERCADO: Predicción del precio de los automóviles (Autos.arff)
Ejemplos de datos numéricos:
- CLASIFICACIÓN: Datos correspondientes a las siluetas de varios modelos de vehículos
(vehicle.arff), Clasificación de una silueta dentro de uno de cuatro posibles tipos.
- SOCIALES: Modelado de puntos/minuto en basket (BasketBall.arff), Tasa de homicidios en
Detroit (Detroit.arff), Predicción sobre huelgas (Strike.arff)
- ENFERMEDADES: Ecocardiograma (EchoMonths.arff)
- MERCADO: Predicciones sobre automóviles (Auto*.arff), Consumo de electricidad
(Elusage.arff), Consumo de gasolina (Gascons.arff), Valor de la vivienda en barrios de Boston
(Housing.arff)
- GEOLOGÍA: Datos sobre polución (Pollution.arff), Predicción sobre terremotos (Quake.arff).
1
Se adjunta a los apuntes Weka y dataset
-189-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Hay que modelar al menos dos problemas, uno de tipo nominal y otro de tipo numérico, de
cualquier categoría, utilizando los algoritmos que se estime oportuno.
En particular, con los datos nominales hay que emplear al menos dos de los siguientes algoritmos:
Árboles de decisión de un nivel (decision stump) weka.classifiers.DecisionStump
Clasificador 1R (OneR) weka.classifiers.OneR
Árboles de decisión de un nivel (decision stump) weka.classifiers.OneR
Tabla de decisión (decision table) weka.classifiers.DecisionTable-R
ID3 weka.classifiers.Id3
C4.5 weka.classifiers.j48.J48
PART weka.classifiers.j48.PART
Y con los datos numéricos hay que emplear al menos dos de los siguientes algoritmos:
Árboles de decisión de un nivel (decision stump) weka.classifiers.DecisionStump
Tabla de decisión (decision table) weka.classifiers.DecisionTable-R
Regresión lineal weka.classifiers.LinearRegression
M5' weka.classifiers.m5.M5Prime
Se pide:
•
•
Utilizando los datos de los problemas, crear los modelos estudiando diferentes estrategias
de entrenamiento utilizando los parámetros de cada algoritmo.
Análisis de resultados (textuales y gráficos) que da Weka, comentando la conclusión y las
diferencias entre los algoritmos que se han empleado.
-190-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
RESOLUCIÓN AUTOCONTROL
A. MODELOS DE ESTUDIO. Aquí utilizaremos dos conjuntos de datos1 y haremos variaciones
de los parámetros y utilizaremos diferentes estrategias de entrenamiento.
Aunque Weka es una potente herramienta tanto en el desarrollo de algoritmos de clasificación y
filtrado como en el preprocesado de los datos para que tengan una estructura adecuada, aquí
utilizaremos datos ya formateados, por lo que no es necesario el tratamiento previo de los mismos.
Conjunto de datos nominales zoo.arff
El primer conjunto de datos a estudiar se trata de un conjunto de datos nominales. En concreto es una base de
datos de un zoo imaginario creado por Richard Forsyth en 1990. Distingue 7 clases de animales, 17 atributos
(y además el nombre de la especie, único para cada muestra), 15 booleanos y 2 numéricos, y no hay valores
perdidos de algún atributo. Los atributos booleanos pueden tomar dos valores, verdadero o falso.
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
7. Attribute Information:
(name of attribute and type of value domain)
1. animal name: nombre del animal
Unique for each instance
2. hair pelo
Boolean
3. feathers plumas
Boolean
4. eggs huevos
Boolean
5. milk leche
Boolean
6. airborne volador
Boolean
7. aquatic acuático
Boolean
8. predator predador
Boolean
9. toothed con dientes
Boolean
10. backbone con espina dorsal Boolean
11. breathes respire
Boolean
12. venomous venenoso
Boolean
13. fins aletas de pez
Boolean
14. legs patas
Numeric (set of values: {0,2,4,5,6,8})
15. tail cola
Boolean
16. domestic doméstico
Boolean
17. catsize
Boolean
18. type
Numeric (integer values in range [1,7])
Hay una amplia gama de animales, (el autor decide incluir a la chica como una especie más) clasificados en
mamíferos, aves, reptiles, peces, anfibios, insectos y crustáceos.
1
Los ficheros se entregan junto con el material
-191-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
En concreto tenemos 101 instancias (que se corresponden con 101 tipos de animales).
Los datos que tenemos son:
Donde cada color corresponde a uno de los tipos existentes (type), en concreto: mamíferos (azul), pájaros
(rojo), reptiles (azul celeste), peces (gris), anfibios (rosa), insectos (verde) e invertebrados (amarillo).
1. Use training set
Veamos los resultados que se obtienen cuando estudiamos la calidad del clasificador prediciendo la clase de
las instancias de entrenamiento (Use training set) para los 3 algoritmos que hemos seleccionado: árboles de
decisión de un nivel, clasificador 1R y C4.5. Cabe esperar resultados similares por ser algoritmos basados en
árboles de decisión.
-192-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
- Árboles de decision de un nivel:
=== Run information ===
Scheme:
Test mode:
weka.classifiers.trees.DecisionStump
evaluate on training data
Esquema seguido
Modo de evaluación
=== Classifier model (full training set) ===
Árbol de decisión binario
Decision Stump
Classifications
milk = false : bird
milk != false : mammal
milk is missing : mammal
Distribución de las clases
Class distributions
milk = false
Las 7 clases posibles y su distribución
mammal bird
reptile fish
amphibian insect invertebrate
0.0
0.333 0.083
0.217 0.067
0.133
0.167
milk != false
mammal bird reptile fish amphibian insect invertebrate
1.0
0.0
0.0
0.0
0.0
0.0
0.0
milk is missing
mammal bird
reptile fish
amphibian insect invertebrate
0.406
0.198 0.050
0.129 0.040
0.790
0.099
Tiempo para construir el modelo
Time taken to build model: 0.02 seconds
=== Evaluation on training set ===
=== Summary ===
Correctly Classified Instances
Incorrectly Classified Instances
Kappa statistic
Mean absolute error
Root mean squared error
Relative absolute error
Root relative squared error
Total Number of Instances
61
40
0.4481
0.1332
0.2581
60.9052 %
78.3457 %
101
60.396
39.604
=== Detailed Accuracy By Class ===
TP Rate
1
1
0
0
0
0
0
FP Rate
0
0.494
0
0
0
0
0
Precision
1
0.333
0
0
0
0
0
Recall
1
1
0
0
0
0
0
F-Measure
1
0.5
0
0
0
0
0
-193-
Class
mammal
bird
reptile
fish
amphibian
insect
invertebrate
%
%
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
=== Confusion Matrix ===
a b
41 0
0 20
0 5
0 13
0 4
0 8
0 10
c
0
0
0
0
0
0
0
d
0
0
0
0
0
0
0
e
0
0
0
0
0
0
0
f
0
0
0
0
0
0
0
g
0
0
0
0
0
0
0
|
|
|
|
|
|
|
<-- classified as
a = mammal
b = bird
c = reptile
d = fish
e = amphibian
f = insect
g = invertebrate
El error de clasificación que se produce es un 39% de instancias mal clasificadas. Podemos ver que solo dos
de los elementos no nulos están en la diagonal principal (mamíferos y aves). El resto ha sido mal clasificado.
- OneR
=== Run information ===
Scheme:
Test mode:
weka.classifiers.rules.OneR -B 6
evaluate on training data
=== Classifier model (full training set) ===
animal:
aardvark
-> mammal
antelope
-> mammal
bass
-> fish
bear
-> mammal
boar
-> mammal
buffalo
-> mammal
calf
-> mammal
carp
-> fish
catfish
-> fish
cavy
-> mammal
cheetah
-> mammal
chicken
-> bird
chub
-> fish
clam
-> invertebrate
crab
-> invertebrate
crayfish
-> invertebrate
crow
-> bird
deer
-> mammal
dogfish
-> fish
dolphin
-> mammal
dove
-> bird
duck
-> bird
elephant
-> mammal
flamingo
-> bird
flea
-> insect
frog
-> amphibian
fruitbat
-> mammal
giraffe
-> mammal
girl
-> mammal
gnat
-> insect
goat
-> mammal
gorilla
-> mammal
gull
-> bird
haddock
-> fish
(101/101 instances correct)
hamster
hare
hawk
herring
honeybee
housefly
kiwi
ladybird
lark
leopard
lion
lobster
lynx
mink
mole
mongoose
moth
newt
octopus
opossum
oryx
ostrich
parakeet
penguin
pheasant
pike
piranha
pitviper
platypus
polecat
pony
porpoise
puma
pussycat
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
mammal
mammal
bird
fish
insect
insect
bird
insect
bird
mammal
mammal
invertebrate
mammal
mammal
mammal
mammal
insect
amphibian
invertebrate
mammal
mammal
bird
bird
bird
bird
fish
fish
reptile
mammal
mammal
mammal
mammal
mammal
mammal
Time taken to build model: 0 seconds
-194-
raccoon
reindeer
rhea
scorpion
seahorse
seal
sealion
seasnake
seawasp
skimmer
skua
slowworm
slug
sole
sparrow
squirrel
starfish
stingray
swan
termite
toad
tortoise
tuatara
tuna
vampire
vole
vulture
wallaby
wasp
wolf
worm
wren
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
mammal
mammal
bird
invertebrate
fish
mammal
mammal
reptile
invertebrate
bird
bird
reptile
invertebrate
fish
bird
mammal
invertebrate
fish
bird
insect
amphibian
reptile
reptile
fish
mammal
mammal
bird
mammal
insect
mammal
invertebrate
bird
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
=== Evaluation on training set ===
=== Summary ===
Correctly Classified Instances
Incorrectly Classified Instances
Kappa statistic
Mean absolute error
Root mean squared error
Relative absolute error
Root relative squared error
Total Number of Instances
=== Detailed Accuracy By Class ===
TP Rate
FP Rate
Precision
Recall
1
0
1
1
1
0
1
1
1
0
1
1
1
0
1
1
1
0
1
1
1
0
1
1
1
0
1
1
101
0
1
0
0
0
0
101
100
0
%
%
%
%
F-Measure
1
1
1
1
1
1
1
Class
mammal
bird
reptile
fish
amphibian
insect
invertebrate
=== Confusion Matrix ===
a b c d e f g
<-- classified as
41 0 0 0 0 0 0 | a = mammal
0 20 0 0 0 0 0 | b = bird
0 0 5 0 0 0 0 | c = reptile
0 0 0 13 0 0 0 | d = fish
0 0 0 0 4 0 0 | e = amphibian
0 0 0 0 0 8 0 | f = insect
0 0 0 0 0 0 10 | g = invertebrate
Ahora la clasificación ha sido perfecta. No hay elementos no nulos fuera de la matriz principal.
- C4.5
=== Run information ===
Scheme:
weka.classifiers.trees.J48 -C 0.25 -M 2
Test mode:
evaluate on training data
=== Classifier model (full training set) ===
J48 pruned tree
-----------------feathers = false
|
milk = false
|
|
backbone = false
|
|
|
airborne = false
|
|
|
|
predator = false
|
|
|
|
|
legs <= 2: invertebrate (2.0)
|
|
|
|
|
legs > 2: insect (2.0)
|
|
|
|
predator = true: invertebrate (8.0)
|
|
|
airborne = true: insect (6.0)
|
|
backbone = true
|
|
|
fins = false
|
|
|
|
tail = false: amphibian (3.0)
|
|
|
|
tail = true: reptile (6.0/1.0)
|
|
|
fins = true: fish (13.0)
|
milk = true: mammal (41.0)
feathers = true: bird (20.0)
Number of Leaves :
Size of the tree : 17
9
-195-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
El árbol resultante de aplicar el algoritmo se presenta aquí de forma textual.
Time taken to build model: 0.03 seconds
=== Evaluation on training set ===
=== Summary ===
Correctly Classified Instances
Incorrectly Classified Instances
Kappa statistic
Mean absolute error
Root mean squared error
Relative absolute error
Root relative squared error
Total Number of Instances
=== Detailed Accuracy By Class ===
TP Rate
FP Rate
Precision
Recall
1
0
1
1
1
0
1
1
1
0.01
0.833
1
1
0
1
1
0.75
0
1
0.75
1
0
1
1
1
0
1
1
100
1
0.987
0.0047
0.0486
2.1552 %
14.7377 %
101
F-Measure
1
1
0.909
1
0.857
1
1
99.0099 %
0.9901 %
Class
mammal
bird
reptile
fish
amphibian
insect
invertebrate
=== Confusion Matrix ===
a b c d e f g
<-- classified as
41 0 0 0 0 0 0 | a = mammal
0 20 0 0 0 0 0 | b = bird
0 0 5 0 0 0 0 | c = reptile
0 0 0 13 0 0 0 | d = fish
0 0 1 0 3 0 0 | e = amphibian
0 0 0 0 0 8 0 | f = insect
0 0 0 0 0 0 10 | g = invertebrate
2. Cross- validation con 10 folds
Ahora procedemos al estudio de los datos con 10 grupos, comprobando la calidad del clasificador. Cabe
señalar que los resultados que se obtienen con el árbol de decisión de un nivel no cambian respecto al caso
de usar todos los datos. En cuanto a los otros dos algoritmos, se detallan a continuación los parámetros más
relevantes. En el siguiente apartado discutiremos los resultados obtenidos.
-196-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
- OneR
Test mode:
10-fold cross-validation
=== Classifier model (full training set) ===
animal:
aardvark
-> mammal
antelope
-> mammal
bass
-> fish
bear
-> mammal
boar
-> mammal
buffalo
-> mammal
calf
-> mammal
carp
-> fish
catfish
-> fish
cavy
-> mammal
cheetah
-> mammal
chicken
-> bird
chub
-> fish
clam
-> invertebrate
crab
-> invertebrate
crayfish
-> invertebrate
crow
-> bird
deer
-> mammal
dogfish
-> fish
dolphin
-> mammal
dove
-> bird
duck
-> bird
elephant
-> mammal
flamingo
-> bird
flea
-> insect
frog
-> amphibian
fruitbat
-> mammal
giraffe
-> mammal
girl
-> mammal
gnat
-> insect
goat
-> mammal
gorilla
-> mammal
gull
-> bird
haddock
-> fish
(101/101 instances correct)
hamster
hare
hawk
herring
honeybee
housefly
kiwi
ladybird
lark
leopard
lion
lobster
lynx
mink
mole
mongoose
moth
newt
octopus
opossum
oryx
ostrich
parakeet
penguin
pheasant
pike
piranha
pitviper
platypus
polecat
pony
porpoise
puma
pussycat
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
mammal
mammal
bird
fish
insect
insect
bird
insect
bird
mammal
mammal
invertebrate
mammal
mammal
mammal
mammal
insect
amphibian
invertebrate
mammal
mammal
bird
bird
bird
bird
fish
fish
reptile
mammal
mammal
mammal
mammal
mammal
mammal
raccoon
reindeer
rhea
scorpion
seahorse
seal
sealion
seasnake
seawasp
skimmer
skua
slowworm
slug
sole
sparrow
squirrel
starfish
stingray
swan
termite
toad
tortoise
tuatara
tuna
vampire
vole
vulture
wallaby
wasp
wolf
worm
wren
Time taken to build model: 0 seconds
=== Stratified cross-validation ===
=== Summary ===
Correctly Classified Instances
Incorrectly Classified Instances
Kappa statistic
Mean absolute error
Root mean squared error
Relative absolute error
Root relative squared error
Total Number of Instances
43
58
0.045
0.1641
0.4051
74.8424 %
122.7774 %
101
-197-
42.5743 %
57.4257 %
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
mammal
mammal
bird
invertebrate
fish
mammal
mammal
reptile
invertebrate
bird
bird
reptile
invertebrate
fish
bird
mammal
invertebrate
fish
bird
insect
amphibian
reptile
reptile
fish
mammal
mammal
bird
mammal
insect
mammal
invertebrate
bird
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
=== Detailed Accuracy By Class ===
TP Rate
1
0
0
0
0.5
0
0
FP Rate
0.967
0
0
0
0
0
0
Precision
0.414
0
0
0
1
0
0
Recall
1
0
0
0
0.5
0
0
F-Measure
0.586
0
0
0
0.667
0
0
=== Confusion Matrix ===
a
41
20
5
13
2
8
10
b
0
0
0
0
0
0
0
c
0
0
0
0
0
0
0
d
0
0
0
0
0
0
0
e
0
0
0
0
2
0
0
f
0
0
0
0
0
0
0
g
0
0
0
0
0
0
0
|
|
|
|
|
|
|
<-- classified as
a = mammal
b = bird
c = reptile
d = fish
e = amphibian
f = insect
g = invertebrate
- C4.5
Test mode:
10-fold cross-validation
=== Classifier model (full training set) ===
J48 pruned tree
-----------------feathers = false
|
milk = false
|
|
backbone = false
|
|
|
airborne = false
|
|
|
|
predator = false
|
|
|
|
|
legs <= 2: invertebrate (2.0)
|
|
|
|
|
legs > 2: insect (2.0)
|
|
|
|
predator = true: invertebrate (8.0)
|
|
|
airborne = true: insect (6.0)
|
|
backbone = true
|
|
|
fins = false
|
|
|
|
tail = false: amphibian (3.0)
|
|
|
|
tail = true: reptile (6.0/1.0)
|
|
|
fins = true: fish (13.0)
|
milk = true: mammal (41.0)
feathers = true: bird (20.0)
Number of Leaves
:
Size of the tree :
9
17
Time taken to build model: 0 seconds
-198-
Class
mammal
bird
reptile
fish
amphibian
insect
invertebrate
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
=== Stratified cross-validation ===
=== Summary ===
Correctly Classified Instances
Incorrectly Classified Instances
Kappa statistic
Mean absolute error
Root mean squared error
Relative absolute error
Root relative squared error
Total Number of Instances
93
8
0.8955
0.0225
0.14
10.2478 %
42.4398 %
101
92.0792 %
7.9208 %
=== Detailed Accuracy By Class ===
TP Rate
1
1
0.6
1
0.75
0.625
0.8
FP Rate
0
0
0.01
0.011
0
0.032
0.033
Precision
1
1
0.75
0.929
1
0.625
0.727
Recall
1
1
0.6
1
0.75
0.625
0.8
F-Measure
1
1
0.667
0.963
0.857
0.625
0.762
Class
mammal
bird
reptile
fish
amphibian
insect
invertebrate
=== Confusion Matrix ===
a b
41 0
0 20
0 0
0 0
0 0
0 0
0 0
c d
0 0
0 0
3 1
0 13
1 0
0 0
0 0
e
0
0
0
0
3
0
0
f
0
0
1
0
0
5
2
g
0
0
0
0
0
3
8
|
|
|
|
|
|
|
<-- classified as
a = mammal
b = bird
c = reptile
d = fish
e = amphibian
f = insect
g = invertebrate
- Árbol de decisión binario
Test mode:
10-fold cross-validation
=== Classifier model (full training set) ===
Decision Stump
Classifications
milk = false : bird
milk != false : mammal
milk is missing : mammal
Class distributions
milk = false
mammal
0.000
milk != false
mammal
1.000
milk is missing
mammal
0.406
bird reptile fish amphibian insect invertebrate
0.333 0.083
0.217 0.067
0.133 0.167
bird reptile fish amphibian insect invertebrate
0.000 0.000
0.000 0.000
0.000 0.000
bird reptile fish amphibian insect invertebrate
0.198 0.050
0.129 0.040
0.079 0.099
Time taken to build model: 0 seconds
-199-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
=== Stratified cross-validation ===
=== Summary ===
Correctly Classified Instances
Incorrectly Classified Instances
Kappa statistic
Mean absolute error
Root mean squared error
Relative absolute error
Root relative squared error
Total Number of Instances
=== Detailed Accuracy By Class ===
TP Rate
FP Rate
Precision
Recall
1
0
1
1
1
0.494
0.333
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
===
a
41
0
0
0
0
0
0
Confusion
b c d
0 0 0
20 0 0
5 0 0
13 0 0
4 0 0
8 0 0
10 0 0
61
40
0.4481
0.1337
0.259
60.9785 %
78.5181 %
101
F-Measure
1
0.5
0
0
0
0
0
60.396
39.604
%
%
Class
mammal
bird
reptile
fish
amphibian
insect
invertebrate
Matrix ===
e f g
<-- classified as
0 0 0 | a = mammal
0 0 0 | b = bird
0 0 0 | c = reptile
0 0 0 | d = fish
0 0 0 | e = amphibian
0 0 0 | f = insect
0 0 0 | g = invertebrate
3. Percentage split (66% datos de entrenamiento, resto de test)
- Árbol de decisión binario
Test mode:
split 66% train, remainder test
=== Classifier model (full training set) ===
Decision Stump
Classifications
milk = false : bird
milk != false : mammal
milk is missing : mammal
Class distributions
milk = false
mammal
bird
0.000
0.330
milk != false
mammal
bird
1.000
0.000
milk is missing
mammal
bird
0.410
0.200
reptile fish amphibian insect invertebrate
0.080
0.220 0.070
0.130 0.170
reptile fish amphibian insect invertebrate
0.000
0.000 0.000
0.000 0.000
reptile fish amphibian insect invertebrate
0.050
0.130 0.040
0.080 0.100
Time taken to build model: 0 seconds
-200-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
=== Evaluation on test split ===
=== Summary ===
Correctly Classified Instances
Incorrectly Classified Instances
Kappa statistic
Mean absolute error
Root mean squared error
Relative absolute error
Root relative squared error
Total Number of Instances
=== Detailed Accuracy By Class ===
TP Rate
FP Rate
Precision
Recall
1
0
1
1
1
0.552
0.273
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
19
16
0.3939
0.1444
0.2742
64.8066 %
81.3879 %
35
F-Measure
1
0.429
0
0
0
0
0
54.2857 %
45.7143 %
Class
mammal
bird
reptile
fish
amphibian
insect
invertebrate
=== Confusion Matrix ===
a b c d e f g
<-- classified as
13 0 0 0 0 0 0 | a = mammal
0 6 0 0 0 0 0 | b = bird
0 1 0 0 0 0 0 | c = reptile
0 5 0 0 0 0 0 | d = fish
0 0 0 0 0 0 0 | e = amphibian
0 6 0 0 0 0 0 | f = insect
0 4 0 0 0 0 0 | g = invertebrate
- OneR
Test mode:
split 66% train, remainder test
=== Classifier model (full training set) ===
animal:
aardvark
antelope
bass
bear
boar
buffalo
calf
carp
catfish
cavy
cheetah
chicken
chub
clam
crab
crayfish
crow
deer
dogfish
dolphin
dove
duck
elephant
flamingo
flea
frog
fruitbat
giraffe
girl
gnat
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
mammal
mammal
fish
mammal
mammal
mammal
mammal
fish
fish
mammal
mammal
bird
fish
invertebrate
invertebrate
invertebrate
bird
mammal
fish
mammal
bird
bird
mammal
bird
insect
amphibian
mammal
mammal
mammal
insect
goat
gorilla
gull
haddock
hamster
hare
hawk
herring
honeybee
housefly
kiwi
ladybird
lark
leopard
lion
lobster
lynx
mink
mole
mongoose
moth
newt
octopus
opossum
oryx
ostrich
parakeet
penguin
pheasant
pike
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
mammal
mammal
bird
fish
mammal
mammal
bird
fish
insect
insect
bird
insect
bird
mammal
mammal
invertebrate
mammal
mammal
mammal
mammal
insect
amphibian
invertebrate
mammal
mammal
bird
bird
bird
bird
fish
-201-
piranha
pitviper
platypus
polecat
pony
porpoise
puma
pussycat
raccoon
reindeer
rhea
scorpion
seahorse
seal
sealion
seasnake
seawasp
skimmer
skua
slowworm
slug
sole
sparrow
squirrel
starfish
stingray
swan
termite
toad
tortoise
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
->
fish
reptile
mammal
mammal
mammal
mammal
mammal
mammal
mammal
mammal
bird
invertebrate
fish
mammal
mammal
reptile
invertebrate
bird
bird
reptile
invertebrate
fish
bird
mammal
invertebrate
fish
bird
insect
amphibian
reptile
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
tuatara
-> reptile
tuna
-> fish
vampire
-> mammal
vole
-> mammal
(101/101 instances correct)
vulture
wallaby
wasp
wolf
->
->
->
->
bird
mammal
insect
mammal
worm
wren
Time taken to build model: 0 seconds
=== Evaluation on test split ===
=== Summary ===
Correctly Classified Instances
Incorrectly Classified Instances
Kappa statistic
Mean absolute error
Root mean squared error
Relative absolute error
Root relative squared error
Total Number of Instances
13
22
0
0.1796
0.4238
80.6225 %
125.7661 %
35
37.1429 %
62.8571 %
=== Detailed Accuracy By Class ===
TP Rate
1
0
0
0
0
0
0
FP Rate
1
0
0
0
0
0
0
Precision
0.371
0
0
0
0
0
0
Recall
1
0
0
0
0
0
0
F-Measure
0.542
0
0
0
0
0
0
=== Confusion Matrix ===
a
13
6
1
5
0
6
4
b
0
0
0
0
0
0
0
c
0
0
0
0
0
0
0
d
0
0
0
0
0
0
0
e
0
0
0
0
0
0
0
f
0
0
0
0
0
0
0
g
0
0
0
0
0
0
0
|
|
|
|
|
|
|
<-- classified as
a = mammal
b = bird
c = reptile
d = fish
e = amphibian
f = insect
g = invertebrate
-202-
Class
mammal
bird
reptile
fish
amphibian
insect
invertebrate
-> invertebrate
-> bird
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
- C4.5
Test mode:
split 66% train, remainder test
=== Classifier model (full training set) ===
J48 pruned tree
-----------------feathers = false
|
milk = false
|
|
backbone = false
|
|
|
airborne = false
|
|
|
|
predator = false
|
|
|
|
|
legs <= 2: invertebrate (2.0)
|
|
|
|
|
legs > 2: insect (2.0)
|
|
|
|
predator = true: invertebrate (8.0)
|
|
|
airborne = true: insect (6.0)
|
|
backbone = true
|
|
|
fins = false
|
|
|
|
tail = false: amphibian (3.0)
|
|
|
|
tail = true: reptile (6.0/1.0)
|
|
|
fins = true: fish (13.0)
|
milk = true: mammal (41.0)
feathers = true: bird (20.0)
Number of Leaves
:
Size of the tree :
9
17
Time taken to build model: 0 seconds
=== Evaluation on test split ===
=== Summary ===
Correctly Classified Instances
Incorrectly Classified Instances
Kappa statistic
Mean absolute error
Root mean squared error
Relative absolute error
Root relative squared error
Total Number of Instances
33
2
0.926
0.0163
0.1278
7.3293 %
37.9199 %
35
94.2857 %
5.7143 %
=== Detailed Accuracy By Class ===
TP Rate
1
1
1
1
0
0.667
1
FP Rate
0
0
0
0
0
0
0.065
Precision
1
1
1
1
0
1
0.667
Recall
1
1
1
1
0
0.667
1
F-Measure
1
1
1
1
0
0.8
0.8
-203-
Class
mammal
bird
reptile
fish
amphibian
insect
invertebrate
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
=== Confusion Matrix ===
a
13
0
0
0
0
0
0
b
0
6
0
0
0
0
0
c
0
0
1
0
0
0
0
d
0
0
0
5
0
0
0
e
0
0
0
0
0
0
0
f
0
0
0
0
0
4
0
g
0
0
0
0
0
2
4
|
|
|
|
|
|
|
<-- classified as
a = mammal
b = bird
c = reptile
d = fish
e = amphibian
f = insect
g = invertebrate
Conjunto de datos nominales vehicle.arff
El segundo conjunto de datos que vamos a estudiar está compuesto por datos numéricos. Básicamente todo
lo explicado para los datos nominales del caso anterior seguirá siendo aplicable ahora. Sin embargo, al tratar
datos numéricos hay que tener en cuenta que Weka produce un conjunto distinto de medidas de prestaciones.
Los datos corresponden a las siluetas de varios modelos de vehículos. Los datos provienen del Instituto
Turing, en Escocia. Para clasificar una silueta dentro de uno de cuatro posibles tipos se utilizarán una serie
de parámetros extraídos de la silueta. El vehículo se puede observar desde diferentes ángulos.
Estos datos ya han sido objeto de estudio y se ha llegado a la conclusión de que la estructura en árbol es un
buen clasificador pero depende fuertemente de la orientación de los objetos, y agrupa vistas similares de
objetos. Los parámetros fueron extraídos de las siluetas mediante HIPS (Hierarchical Image Processing
System), que extrae una combinación de medidas independientes de la escala utilizando tanto las medidas
basadas en los momentos clásicos como una varianza escalada y otros parámetros estadísticos sobre los ejes
mayor y menor del vehículo, así como medidas heurísticas de oquedades, circularidad, vehículo compacto,
etc.
Los cuatro modelos tomados como referencia son: un bus de dos plantas, furgoneta Chevrolet, Saab 9000 y
Opel Manta 400. Esta elección se dio porque las siluetas del bus, la furgoneta y cualquiera de los coches son
claramente diferentes, pero sería más difícil distinguir los dos turismos. Las imágenes se tomaron con una
cámara apuntando hacia abajo con un ángulo de elevación fijo (34,2° sobre la horizontal). Los vehículos se
situaron sobre un fondo claro y se pintaron de negro mate para minimizar reflejos.
Todas las imágenes tenían la misma resolución (128x128), se tomaron con la misma cámara, en escala de 64
tonos de gris. Las imágenes fueron filtradas para producir siluetas binarias de los vehículos, hechas negativo,
limpiadas y almacenadas. Se realizaron más fotos rotando los vehículos, almacenándose al final un total de 2
juegos de 60 fotos por vehículo, cubriendo los 360° de rotación posibles. Después se realizaron dos tandas
más de 2 juegos de 60 fotos, salvo la van que tuvo 2 juegos de 46, a dos elevaciones diferentes (37,5° y
30,8°).
Los atributos que tendrán los datos serán por tanto:
-204-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
COMPACTNESS (average perim)**2/area
CIRCULARITY (average radius)**2/area
DISTANCE CIRCULARITY area/(av.distance from border)**2
RADIUS RATIO (max.rad-min.rad)/av.radius
PR.AXIS ASPECT RATIO (minor axis)/(major axis)
MAX.LENGTH ASPECT RATIO (length perp. max length)/(max length)
SCATTER RATIO (inertia about minor axis)/(inertia about major axis)
ELONGATEDNESS area/(shrink width)**2
PR.AXIS RECTANGULARITY area/(pr.axis length*pr.axis width)
MAX.LENGTH RECTANGULARITY area/(max.length*length perp. to this)
SCALED VARIANCE (2nd order moment about minor axis)/area
ALONG MAJOR AXIS
SCALED VARIANCE (2nd order moment about major axis)/area
ALONG MINOR AXIS
SCALED RADIUS OF GYRATION (mavar+mivar)/area
SKEWNESS ABOUT (3rd order moment about major axis)/sigma_min**3
MAJOR AXIS
SKEWNESS ABOUT (3rd order moment about minor axis)/sigma_maj**3
MINOR AXIS
KURTOSIS ABOUT (4th order moment about major axis)/sigma_min**4
MINOR AXIS
KURTOSIS ABOUT (4th order moment about minor axis)/sigma_maj**4
MAJOR AXIS
HOLLOWS RATIO (area of hollows)/(area of bounding polygon)
Tendremos 4 clases y un total de 846 instancias, además de 18 atributos.
-205-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Ahora los datos son:
Los colores corresponden con: bus (celeste), van (gris), Saab (rojo), Opel (azul). No hay atributos con
valores missing.
1) Use training test
- Árboles de decisión de un nivel
=== Run information ===
Scheme:
Test mode:
weka.classifiers.trees.DecisionStump
evaluate on training data
=== Classifier model (full training set) ===
Decision Stump
Classifications
ELONGATEDNESS <= 41.5 : saab
ELONGATEDNESS > 41.5 : van
ELONGATEDNESS is missing : bus
-206-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Class distributions
ELONGATEDNESS <= 41.5
opel
saab
bus
van
0.38481675392670156 0.387434554973822
0.22774869109947643 0.0
ELONGATEDNESS > 41.5
opel
saab
bus
van
0.1400862068965517 0.14870689655172414 0.2823275862068966 0.42887931034482757
ELONGATEDNESS is missing
opel
saab
bus
van
0.25059101654846333 0.2565011820330969 0.2576832151300236 0.23522458628841608
Time taken to build model: 0.03 seconds
=== Evaluation on training set ===
=== Summary ===
Correctly Classified Instances
Incorrectly Classified Instances
Kappa statistic
Mean absolute error
Root mean squared error
Relative absolute error
Root relative squared error
Total Number of Instances
347
499
0.2189
0.3372
0.4106
89.964 %
94.8494 %
846
41.0165 %
58.9835 %
=== Detailed Accuracy By Class ===
TP Rate
0
0.682
0
1
FP Rate
0
0.372
0
0.41
Precision
0
0.387
0
0.429
Recall
0
0.682
0
1
F-Measure
0
0.494
0
0.6
Class
opel
saab
bus
van
=== Confusion Matrix ===
a
b
0 147
0 148
0 87
0
0
c
d
<-- classified as
0 65 |
a = opel
0 69 |
b = saab
0 131 |
c = bus
0 199 |
d = van
- Tabla de decisión
=== Run information ===
Scheme:
Test mode:
weka.classifiers.rules.DecisionTable -X 1 -S 5
evaluate on training data
=== Classifier model (full training set) ===
Decision Table:
Number of training instances: 846
Number of Rules : 122
Non matches covered by Majority class.
Best first search for feature set,
terminated after 5 non improving subsets.
Evaluation (for feature selection): CV (leave one out)
Feature set: 1,2,6,12,19
-207-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Time taken to build model: 0.27 seconds
=== Evaluation on training set ===
=== Summary ===
Correctly Classified Instances
Incorrectly Classified Instances
Kappa statistic
Mean absolute error
Root mean squared error
Relative absolute error
Root relative squared error
Total Number of Instances
650
196
0.6913
0.1559
0.2792
41.5886 %
64.4893 %
846
76.8322 %
23.1678 %
=== Detailed Accuracy By Class ===
TP Rate
0.599
0.539
0.972
0.975
FP Rate
0.068
0.073
0.083
0.085
Precision
0.747
0.718
0.803
0.779
Recall
0.599
0.539
0.972
0.975
F-Measure
0.665
0.616
0.88
0.866
Class
opel
saab
bus
van
=== Confusion Matrix ===
a
b
c
d
127 42 23 20
41 117 26 33
0
4 212
2
2
0
3 194
|
|
|
|
<-a
b
c
d
classified as
= opel
= saab
= bus
= van
- M5’, Regresión lineal
Al tener como último atributo (el de salida) la clase, de tipo nominal, tanto el M5’ como la regresión lineal
no permiten procesar los datos. Por ello es necesario elegir alguna variable numérica para que clasifique en
función de ella, o transformar convenientemente los datos.
2. Cross validation con 10 folds
- Árboles de decisión de un nivel
Test mode:
10-fold cross-validation
=== Classifier model (full training set) ===
Decision Stump
Classifications
ELONGATEDNESS <= 41.5 : saab
ELONGATEDNESS > 41.5 : van
ELONGATEDNESS is missing : bus
-208-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Class distributions
ELONGATEDNESS <= 41.5
opel
saab
bus
van
0.38481675392670156 0.387434554973822
0.22774869109947643 0.0
ELONGATEDNESS > 41.5
opel
saab
bus
van
0.1400862068965517 0.14870689655172414 0.2823275862068966 0.42887931034482757
ELONGATEDNESS is missing
opel
saab
bus
van
0.25059101654846333 0.2565011820330969 0.2576832151300236 0.23522458628841608
Time taken to build model: 0.11 seconds
=== Stratified cross-validation ===
=== Summary ===
Correctly Classified Instances
Incorrectly Classified Instances
Kappa statistic
Mean absolute error
Root mean squared error
Relative absolute error
Root relative squared error
Total Number of Instances
338
508
0.2059
0.3374
0.4109
90.0076 %
94.9021 %
846
39.9527 %
60.0473 %
=== Detailed Accuracy By Class ===
TP Rate
0.245
0.401
0
1
FP Rate
0.15
0.235
0
0.41
Precision
0.354
0.37
0
0.429
Recall
0.245
0.401
0
1
F-Measure
0.29
0.385
0
0.6
Class
opel
saab
bus
van
=== Confusion Matrix ===
a
52
61
34
0
b
95
87
53
0
c
d
<-- classified as
0 65 |
a = opel
0 69 |
b = saab
0 131 |
c = bus
0 199 |
d = van
- Tabla de decisión
Test mode:
10-fold cross-validation
=== Classifier model (full training set) ===
Decision Table:
Number of training instances: 846
Number of Rules : 122
Non matches covered by Majority class.
Best first search for feature set,
terminated after 5 non improving subsets.
Evaluation (for feature selection): CV (leave one out)
Feature set: 1,2,6,12,19
Time taken to build model: 0.23 seconds
-209-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
=== Stratified cross-validation ===
=== Summary ===
Correctly Classified Instances
Incorrectly Classified Instances
Kappa statistic
Mean absolute error
Root mean squared error
Relative absolute error
Root relative squared error
Total Number of Instances
550
296
0.5335
0.198
0.3506
52.822 %
80.9939 %
846
65.0118 %
34.9882 %
=== Detailed Accuracy By Class ===
TP Rate
0.358
0.475
0.908
0.869
FP Rate
0.114
0.145
0.116
0.093
Precision
0.514
0.531
0.731
0.742
Recall
0.358
0.475
0.908
0.869
F-Measure
0.422
0.501
0.81
0.801
Class
opel
saab
bus
van
=== Confusion Matrix ===
a
b
c
d
76 74 39 23
58 103 26 30
6
7 198
7
8 10
8 173
|
|
|
|
<-a
b
c
d
classified as
= opel
= saab
= bus
= van
B. ANÁLISIS DE LOS RESULTADOS
Tanto de forma gráfica como textual pasaremos a comentar los aspectos más destacados de los
estudios realizados y las conclusiones que de ellos podemos derivar, así como las diferencias que se
obtienen entre los distintos algoritmos utilizados.
Para el primer conjunto de datos (zoo.arff) los resultados obtenidos son
- Use training set
Instancias clasificadas
correctamente (%)
Tiempo para construir el
modelo (s)
Kappa
statistic
60,396
0.11
0,4481
OneR
100
0
1
C4.5
99,0099
0.11
0,987
Tabla de decisión
98,0198
0.72
0,9739
PART
99,0099
0.16
0,987
Use training set
Árbol de decisión de un nivel
Como puede verse, se han incluido los resultados que se obtienen también con tablas de decisión y PART.
Podemos ver que en el primer caso la precisión es peor que en otros y el tiempo de ejecución es muy superior
a los demás. En el caso de PART los resultados son similares a los obtenidos con C4.5 pero algo más lentos.
Ésta es una razón para el descarte de estos dos algoritmos.
-210-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
En cuanto a la comparación de los tres sometidos a estudio, podemos ver que el OneR no comete ningún
error. Esto es lógico porque el algoritmo funciona probando todos los pares atributo-valor disponibles y
clasifica con los de menos error. Al tener ahora como conjunto de entrenamiento todos los datos no hay
posibilidad de fallo. Vemos que el C4.5 funciona bastante bien y que el árbol de decisión binario comete
muchos errores.
El árbol generado por el C4.5 es el siguiente:
- Cross – validation con 10 folds
Instancias clasificadas
correctamente (%)
Tiempo para construir el
modelo (s)
Kappa
statistic
Árbol de decisión de un nivel
60,396
0.11
0,4481
OneR
42,5743
0,05
0,045
C4.5
92,0792
0.06
0,8955
Tabla de decisión
91,0891
0.16
0,8811
PART
92,0792
0.06
0,8955
Cross – validation con 10 folds
Como vemos, de nuevo los resultados de PART son los mismos que los del C4.5. Ahora vemos que OneR no
funciona bien en la validación cruzada; como cabía esperar, generaliza mal, mientras que el árbol de decisión
no varía y C4.5 empeora pero muy poco.
El variar el número de grupos no afecta en los resultados de clasificación.
-211-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
En cuanto al error cometido, Weka ofrece una representación gráfica de los errores que comete el
clasificador. Las instancias clasificadas correctamente se representan por cruces y las erróneas por
cuadrados. Cada color identifica la clase a la que pertenece la instancia. Weka ofrece la posibilidad de ver
gráficamente en qué atributo comete más error o menos (por ejemplo cuánto se equivoca el clasificador
cuando estudiamos si las instancias tienen o no pelo, o tienen leche, o ponen huevos).
- árbol de decisión
- OneR
-212-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Al ver este gráfico se advierte que el OneR solo ha acertado clasificando mamíferos y a un par de anfibios.
- C4.5
Vemos que ahora se acierta mucho en la clasificación.
- Percentage split (66 % datos entrenamiento)
Instancias clasificadas
correctamente (%)
Tiempo para el construir
modelo (s)
Kappa
statistic
Árbol de decisión de un nivel
54,2857
0
0,3939
OneR
37,1429
0
0
C4.5
94,2837
0
0,926
Percentage split
Como vemos, al evaluar los algoritmos utilizando un porcentaje de los datos de test, es decir, sin tener a
priori información de clasificación sobre esos datos, aplicando directamente el algoritmo, los resultados son
algo peores en el caso del árbol binario (54 % frente al 60 % en los casos anteriores) . Para el OneR el
porcentaje de acierto también disminuye (de 42% a 37%) y sin embargo los resultados del C4.5 son mejores
(94% frente a 92%). Esto nos da a entender que éste es el mejor algoritmo de clasificación de los que hemos
estudiado.
Pasamos ahora a estudiar los datos referentes a las siluetas de los vehículos (vehicle.arff):
- Use training set
-213-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Use training set
Instancias clasificadas Tiempo para construir
correctamente (%)
el modelo (s)
Kappa
statistic
Árbol de decisión de un nivel
41,0165
0.11
0,2189
Tabla de decisión
76,8322
1.76
0,6913
Como vemos, la tabla de decisión da mejores resultados que el árbol, pero tarda bastante más.
- Cross validation con 10 folds
Cross validation con 10 folds
Instancias clasificadas Tiempo para construir
correctamente (%)
el modelo (s)
Kappa
statistic
Árbol de decisión de un nivel
39,9527
0
0,2059
Tabla de decisión
64,8936
1.87
0,5319
Al tratar ahora con datos numéricos disminuye el porcentaje de instancias clasificadas correctamente con el
árbol de decisión y con tabla de decisión respecto al caso anterior.
Weka permite de nuevo representar gráficamente el error de clasificación. Además se puede obtener
información exacta sobre cada instancia, en concreto el valor de sus parámetros y la estimación hecha por el
algoritmo.
Por ejemplo en el caso anterior obtenemos:
Como podemos ver, la instancia seleccionada es precisamente una de las mal clasificadas, ya que el
algoritmo ha considerado que era una furgoneta pero era un bus.
-214-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Además de visualizar los errores del clasificador, Weka permite también obtener gráficas de la curva
marginal (el margen se define como la diferencia entre la probabilidad prevista para la clase real y la mayor
probabilidad prevista para las otras clases), la curva umbral, que genera un gráfico ilustrando las diferencias
de predicción que se obtienen variando el umbral entre las clases, y la curva de coste. Todas estas curvas
también están disponibles para datos nominales, pero no son representativas en general al tener los atributos
valores de entre un conjunto dado y no ser reales. Ahora veremos algunas de estas curvas para nuestros
datos:
- Curva marginal, tabla de decisión
Podemos ver cómo en los
extremos la diferencia entre
la probabilidad prevista para
la clase y la probabilidad
para las otras clases es casi
de 1 en valor absoluto, es
decir son muy diferentes,
pero cuando el número de
instancias no es demasiado
bajo ni muy alto (menores a
600 instancias aprox.) la
evolución de la diferencia es
lineal, llegando a hacerse 0
para unas 400 instancias.
- Curva de umbral
(Threshold), tabla de decisión
Opel
Van
-215-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Saab
Bus
Para los dos turismos las curvas de umbral son similares. La precisión decae rápidamente cuando
aumentamos el recall, mientras que en la furgoneta la caída es mucho más suave y casi nula en el bus.
- Curvas de coste, tabla de decisión
Opel
Van
Saab
Bus
Podemos ver qué silueta cuesta más para ser clasificada. Como era de esperar, el sistema encuentra muchos
más problemas clasificando los dos turismos que distinguiendo entre un bus y una furgoneta.
-216-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Además podemos ver que para minimizar el coste en el caso de los turismos se requiere un umbral parecido
(0.2, 0.3), para la furgoneta el umbral es un poco mayor y para el autobús el umbral se sitúa por encima del
0.5. Parece que el umbral varía linealmente con el tamaño de los vehículos.
Para el árbol de decisión los resultados son:
- Curva marginal, árbol de decisión
Ahora las diferencias entre probabilidades son mucho menores, y tienden a 0 a medida que se aumenta el
número de instancias.
- Curva de umbral (Threshold), árbol de decisión
Opel
Van
-217-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Saab
Bus
Las curvas ahora son diferentes al caso de tablas de decisión. Salvo en el caso de la furgoneta, presentan un
crecimiento lineal, con más o menos pendiente, hasta alcanzar un punto de máxima precisión, y luego decae
de forma exponencial. El máximo se alcanza precisamente en valores altos del umbral. En cuanto a la
furgoneta, presenta un crecimiento lineal y un mínimo de precisión para el mínimo de umbral.
- Curvas de coste, árbol de decisión
Opel
Van
-218-
APRENDIZAJE AUTOMÁTICO CON WEKA – CÉSARI MATILDE
Saab
Bus
Podemos ver que los costes se agrupan en valores extemos del umbral y que se dan los mayores costes en
todos los casos precisamente en dichos extremos. Por otro lado los costes presentan una simetría que no se
daba en la tabla de decisión. Los costes son similares para el caso de los turismos, más dispersos para el caso
del bus y ligeramente asimétricos en el caso de la furgoneta.
Ahora sí se aprecian diferencias al incrementar el número de grupos. Los resultados obtenidos son:
N° grupos
Instancias clasificadas Tiempo para construir
correctamente (%)
el modelo (s)
Kappa
statistic
Árbol de decisión de un nivel
10
39,9527
0
0,2059
Tabla de decisión
10
64,8936
1.87
0,5319
Árbol de decisión de un nivel
20
39,1253
0.06
0,1949
Tabla de decisión
20
65,0118
1.92
0,5334
Árbol de decisión de un nivel
30
38,2979
0
0,1841
Tabla de decisión
30
65,8392
1.82
0,5445
Como puede verse, los resultados obtenidos con la tabla van mejorando paulatinamente mientras que los del
árbol de decisión van empeorando. Finalmente, si vemos los resultados que se obtienen destinando un 33 %
de los datos a test:
Instancias clasificadas Tiempo para construir
correctamente (%)
el modelo (s)
Kappa
statistic
Árbol de decisión de un nivel
39,5833
0.06
0,2127
Tabla de decisión
62,8472
2.09
0,5082
El porcentaje de acierto para árbol de decisión ha disminuido levemente, mientras que para tabla de decisión
el resultado es más lento y algo peor. Aún así la tabla de decisión ofrece un mejor resultado global que el
árbol de decisión de un nivel. Si lo comparamos con los resultados obtenidos clasificando datos nominales
podemos decir que en ese caso el clasificador por árbol de decisión binario era mejor que cuando clasifica
datos numéricos. En ambos casos la tabla de decisión daba mejores resultados, pero es más lenta y con
grandes volúmenes de datos la diferencia en el tiempo de ejecución se hace importante.
-219-