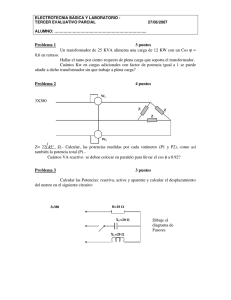
td i d * N td d *N ℜ = φ
Anuncio
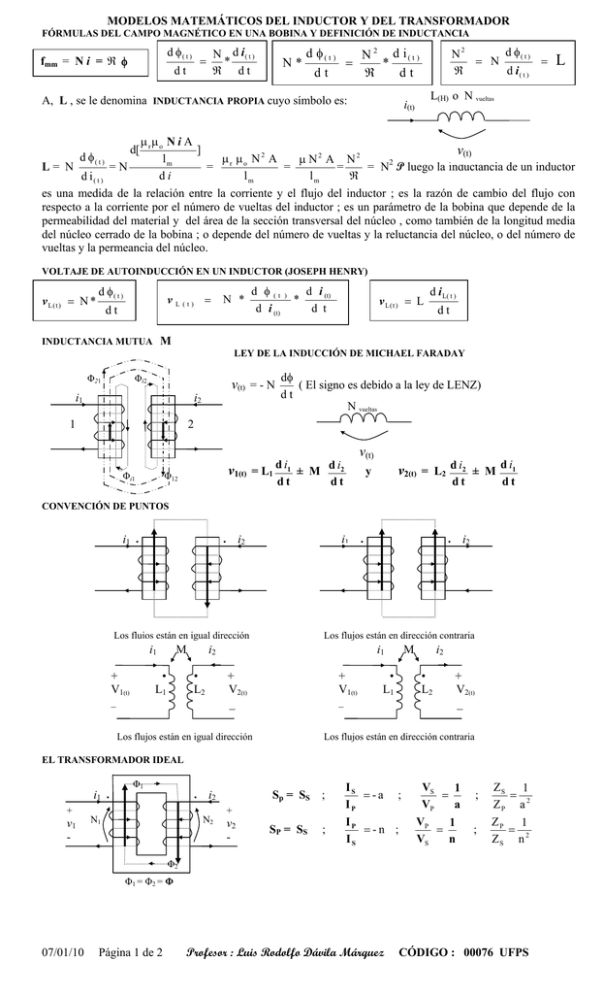
MODELOS MATEMÁTICOS DEL INDUCTOR Y DEL TRANSFORMADOR FÓRMULAS DEL CAMPO MAGNÉTICO EN UNA BOBINA Y DEFINICIÓN DE INDUCTANCIA d φ( t ) fmm = N i = ℜ φ N d i( t ) * ℜ dt = dt N* d φ( t ) d φ( t ) N2 = N = ℜ d i( t ) N 2 d i( t ) = * ℜ dt dt A, L , se le denomina INDUCTANCIA PROPIA cuyo símbolo es: L L(H) o N vueltas i(t) μrμo N i A ] v(t) d φ( t ) μr μo N 2 A lm μ N2 A N2 2 =N = L= N = = = N P luego la inductancia de un inductor di lm lm ℜ d i( t ) es una medida de la relación entre la corriente y el flujo del inductor ; es la razón de cambio del flujo con respecto a la corriente por el número de vueltas del inductor ; es un parámetro de la bobina que depende de la permeabilidad del material y del área de la sección transversal del núcleo , como también de la longitud media del núcleo cerrado de la bobina ; o depende del número de vueltas y la reluctancia del núcleo, o del número de vueltas y la permeancia del núcleo. d[ VOLTAJE DE AUTOINDUCCIÓN EN UN INDUCTOR (JOSEPH HENRY) v L( t ) = N * d φ( t ) v L (t) = dt N * d φ (t ) d i (t) * d i (t) v L( t ) = L d t d i L( t ) dt INDUCTANCIA MUTUA M LEY DE LA INDUCCIÓN DE MICHAEL FARADAY Φ21 Φi2 v(t) = - N i1 i2 1 dφ ( El signo es debido a la ley de LENZ) dt N vueltas 2 Φi1 v1(t) Φ12 v(t) di d i2 = L1 1 ± M dt dt v2(t) = L2 d i2 ± M d i1 y dt dt CONVENCIÓN DE PUNTOS i1 • i1 i2 • Los flujos están en igual dirección M i1 + V1(t) • L1 _ i2 • Los flujos están en dirección contraria i2 • L2 • M i1 + V2(t) _ + V1(t) _ • L1 i2 • L2 + V2(t) _ Los flujos están en dirección contraria Los flujos están en igual dirección EL TRANSFORMADOR IDEAL Φ1 i1 + v1 - • • N1 i2 N2 Sp = SS ; SP = SS ; + v2 - IS =-a ; IP IP =-n ; IS VS 1 = a VP VP 1 = n VS ; ; ZS 1 = ZP a 2 ZP 1 = 2 ZS n Φ2 Φ1 = Φ2 = Φ 07/01/10 Página 1 de 2 Profesor : Luis Rodolfo Dávila Márquez CÓDIGO : 00076 UFPS RELACIONES DE LAS VARIABLES ENTRE EL PRIMARIO Y EL SECUNDARIO IP + VP IS • • NS NP _ IP + VS _ + VP IS • NP _ IP • NS + VP VS + • • NS NP _ VS + N I VP N 1 = − P =a; P = − S = IS NP a VS NS N I VP N 1 =− P =a ; P = S = IS NP a VS NS N VP N P I 1 = =a ; P = S = VS N S IS NP a IS FÓRMULAS PARA EL PRIMARIO REFLEJADO EN EL SECUNDARIO n VP ; n2 ZP ; iP/n o VP/a ; ZP/a2 ; a iP FÓRMULAS PARA EL SECUNDARIO REFLEJADO EN EL PRIMARIO VS/n ; ZS/n2 ; n iS o a VS ; a2 ZS ; iS/a EL AUTOTRANSFORMADOR X Φ1 i1 • • + + • i2 + N2 v1 N 1 - ve v2 - • Z Φ1 = Φ2 = Φ X + Polaridad Aditiva • V2 V1 Y + I2 N2 Donde: Req p = Rp + a2 Rs ; - Z CIRCUITO EQUIVALENTE DEL TRANSFORMADOR REFERIDO A SU LADO SECUNDARIO a ip j Xeq p is a aVs(t) j XM Y + vS • Z EL TRANSFORMADOR REAL CIRCUITO EQUIVALENTE DEL TRANSFORMADOR REFERIDO A SU LADO PRIMARIO RC N2 - Z Req p I2 V2 - Z N1 ve vS - • I1 N1 ve ip Polaridad Sustractiva X + • I1 V1 Vp(t) Salida Φ2 - Y Entrada Vp (t) RC a2 a Xeq p = Xp + a2 Xs . Req s j Req s = Rs + j Xeq s XM a2 Rp a2 ; is Vs(t) Xeq s = Xs + Xp a2 FORMULARIO DEL TRANSFORMADOR REAL: REGULACIÓN EN EL SECUNDARIO VP =a VS ; IS = a IP 2 PCO = (Is) Req s ; ; Vp a RC ]2 ; Psal = Vs x Is Cos(θ) a2 Vp ] - Vs Psal a x 100% ; Eficiencia η = x 100% PCO + PNU + Psal Vs Pérdidas de Potencia en el cobre: PCO ; Pérdidas de Potencia en el núcleo: PNU ; Potencia de entrada: Pent Potencia de salida: PSal ; Regulación de voltaje: RV Pent = PCO + PNU + Psal 07/01/10 Página 2 de 2 ; RV = [ PNU = [ Profesor : Luis Rodolfo Dávila Márquez CÓDIGO : 00076 UFPS