Circuitos magnéticamente acoplados

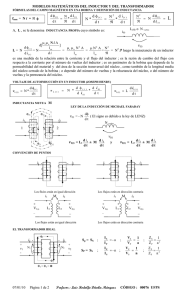
Circuitos Magnéticamente
Acoplados
Capítulo 14 Hayt
Inductancia Mutua
Los circuitos magnéticamente
acoplados poseen inductores para poder
transmitir la energía de un lugar a otro del
circuito. gracias a un fenómeno conocido
como inductancia mutua.
La inductancia mutua consiste en la
presencia de un flujo magnético común que
une a dos embobinados. En uno de los
cuales una excitación causa el cambio de
corriente y por tanto, un cambio de flujo
magnético. Como este flujo es común para
El voltaje producido en el segundo inductor es
proporcional a la razón de cambio de la
corriente del primer inductor y al valor del
segundo inductor.
Las relación entre la corriente del primer
inductor y el voltaje del segundo inductor es:
v 2 (t )  M
di 1 ( t )
2 ,1
M
dt
+
v2
-
El valor de la inductancia mutua se mide en henrys y
es siempre positivo, sin embargo, el valor del voltaje
producido en una inductancia debido al flujo
magnético de otra inductancia puede ser positivo o
negativo.
Como existen cuatro terminales involucradas en la
inductancia mutua, no se puede utilizar la convención
de signos que hemos utilizado en otros capítulos,
sino que ahora se tiene que utilizar la convención del
punto.
M
+
v2
-
Convención del Punto
• Una corriente
entrando a la
terminal punteada de
uno de los
inductores produce
un voltaje cuyo valor
positivo se encuentra
en la terminal
punteada del
segundo inductor.
• Una corriente
entrando a la
terminal no punteada
de un inductor
produce un voltaje
cuyo valor positivo
V2  M
V 2  M
di 1
V 2  M
dt
di 1
dt
V2  M
di 1
dt
di 1
dt
El voltaje inducido del cual hemos estado hablando, es
un
término independiente del voltaje que existe en el
inductor.
Por lo consiguiente, el voltaje total que existe en el
inductor,
va a formarse por la suma del voltaje individual y el
voltaje
1
2
mutuo.
V1  L
di
V2  L
di 2
dt
dt
M
di
M
di 1
dt
dt
De este modo también se definen los voltajes
en la frecuencia s,
V1   sL 1I1  sMI 2
V   sL 1I1  sMI 2
así como los voltajes en estado estable sinusoidal s
V 1   j  L 1 I 1  j  MI 2
La convención del punto, nos evita tener que
dibujar el sentido en el que está enrollado el
inductor, de tal manera que los puntos colocados
en el mismo lugar en los dos inductores indican
que los flujos producidos por estos son aditivos
(se suman), y los puntos colocados en distinto
lugar en los inductores indican que los flujos se
restan.
Energía
Para encontrar la energía almacenada
podemos encontrar la energía que existe en
cada uno de los inductores asumiendo
primero que la corriente i2 es cero mientras
que la corriente aumenta hasta un valor
determinado después mantenemos fijo i1 y
aumentamos a i2 hasta valor fijo.

t1
0
v1i1 dt 

I1
0
L1i1 di 1 
1
2
2
1 1
LI
por un razonamiento similar se encuentra
que la energía en el segundo inductor al
iniciar el incremento de i2 es:
1
2
L
2
2I2
Sin embrago mientras i2 aumenta i1
transmite energía al sistema
independientemente de que i1
permanezca constante pues al
aumentar i2 existe un voltaje y por
tanto el inductor consumirá
se tiene entonces que, al aumentar i2, i1 deja en
el sistema la energía:

t2
t1
M
di 2
1, 2
dt
i1 dt  M
1, 2
I1 I 2
Por lo tanto la energía total es:
1
2
2
1 1
L I

1
2
L2 I
2
2
 M 1, 2 I 1 I 2
De haber iniciado este análisis con i2
y terminado con i1 habríamos llegado
a la misma expresión excepto que se
habría utilizado el coeficiente M21 por
lo tanto al despejar observamos que:
M21=M12
Si consideramos que alguna de las
corrientes entra por un punto mientras
que la otra no encontramos que la
energía
almacenada
es:
1
1
2
2
L 1I 1 
L
2
2
2 I 2  MI
2 I1
Considerando que la energía no puede ser
negativa M tiene un valor máximo:
M 
L 1L 2
El cual es el promedio geométrico de los
inductores. Definimos ahora el coeficiente de
acoplamiento k como:
k 
M
L 1L 2
Transformador Lineal
Existen dos elementos prácticos que utilizan la
inductancia mutua: El transformador lineal y el
ideal. El primero de ellos es sumamente utilizado
en los sistemas de comunicaciones.
Primero asumimos que el transformador es lineal,
es decir que no posee ningún material magnético
que elimine su linealidad.En muchas aplicaciones
se conecta el primario en un circuito en
resonancia mientras que el secundario muchas
veces también esta en resonancia. Esto tiene
como ventaja que se pueden realizar circuitos con
respuestas de picos anchos y caídas bruscas lo
cual se utilizan en sistemas de filtrado.
Podemos observar en el siguiente circuito que
una impedancia en el secundario se refleja en
el primario según la relación:
2
Z in  R 1  sL 1 
R
2
22
2
2
 M R 22
 X
2
22

2
j  M X 22
2
2
R 22  X 22
Para el caso en el que el circuito conectado al
primario y el secundario son circuitos en
resonancia idénticos, es decir con los mismos
valores de inductancia, capacitancia y
resistencia entonces se observa que existe
una frecuencia de resonancia en el circuito es
cual es w0. Sin embargo, si el acoplamiento es
alto a una frecuencia superior existe también
resonancia lo mismo que a una frecuencia
inferior. Esto es lo que causa que el ancho de
banda de paso sea un poco mayor que en
circuito RLC
Este es el equivalente de un
transformador lineal en el cual se muestra
que el valor de cada inductor es L-M y el
que une es de M. En el caso de que
alguna de las corrientes entre por una
terminal en la que no haya un punto
entonces se sustituye el valor por menos
M.
El Transformador Ideal
El transformador ideal es una útil aproximación
de un transformador altamente acoplado, cuyo
coeficiente de acoplamiento se acerca a la unidad
y las reactancias inductivas primaria y secundaria
son muy grandes en comparación con las
impedancias terminales.
Una aproximación al transformador ideal son los
transformadores con núcleos de fierro.
Existe un concepto nuevo dentro del tema que
hablamos, la razón del número de vueltas “a”. La
inductancia individual de cualquiera de los
inductores es proporcional al número de vueltas
del alambre.
La relación anterior es válida solamente si el flujo
De lo anterior podemos ver que la
proporcionalidad entre la inductancia y el
cuadrado del número de vueltas es la siguiente:
L2
L1

N2
N1
2
2
a
2
Existen varios detalles para reconocer un
transformador ideal en diagrama:
--el uso de líneas verticales entre los dos inductores
para
indicar el uso de placas de fierro.
--el valor unitario del coeficiente de acoplamiento
--la presencia del símbolo 1:a que representa la
razón del
número de vueltas de N1 a N2.
Características del Transformador Ideal.
--La habilidad que tiene para cambiar la magnitud de una
impedancia.
Si en el primario se tienen 100 vueltas y en el secundario
se tienen 10000 vueltas entonces la impedancia decrece
en un factorde 100.
Se tiene la siguiente relación:
a 
V2
V1

N2
N1
Con lo cual se pueden simplificar los cálculos
para conocer el voltaje en el secundario a partir
del número de vueltas en el transformador.
Para las corrientes observas que la
relación es:
I1
 a
I2
En el caso de las
Z1 impedancias
Z2
Z in 
a^2Z
1
ZL
a
2
Z2
Entonces se tiene que:
FIN