Factorización LU - elara.supersitio.net

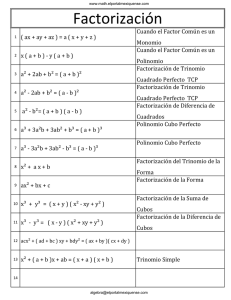
UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN
FACULTAD DE INGENIERÍA MECÁNICA Y ELÉCTRICA
Factorización LU
El método de descomposición LU se utiliza para resolver ciertos sistemas de ecuaciones
lineales. Consiste en escribir la matriz de coeficientes como el producto de una matriz
triangular inferior L y una matriz triangular superior U.
Definición
Sea A una matriz que se puede factorizar de la forma A=LU, donde L es una matriz
triangular inferior y U una matriz triangular superior. A esta factorización se le llama una
descomposición LU de A.
Ejemplo 1
Encuentre la factorización LU de A.
⎡ 4 −2 1 ⎤
A = ⎢⎢ 20 − 7 12⎥⎥
⎢⎣− 8 13 17⎥⎦
⎡ 4 − 2 1 ⎤ A1, 2(−5 ) ⎡4 − 2 1 ⎤
⎡4 − 2 1 ⎤
(
)
(
)
2
−
3
⎢
⎥
⎢
⎥
A
A
3
⎯→ ⎢0 3 7 ⎥ ⎯⎯2 ,⎯
⎯→⎢⎢0 3
U = ⎢ 20 − 7 12⎥ ⎯⎯1, 3⎯
7 ⎥⎥
⎢⎣− 8 13 17 ⎥⎦
⎢⎣0 9 19⎥⎦
⎢⎣0 0 − 2⎥⎦
El tamaño de L es de 3x3 y está formada por los factores (con signo contrario) que se
utilizaron para generar los ceros en la matriz U
⎡ 1 0 0⎤
L = ⎢⎢ 5 1 0⎥⎥
⎢⎣− 2 3 1⎥⎦
En consecuencia
⎡ 4 −2 1⎤
⎡ 1 0 0⎤ ⎡4 − 2 1 ⎤
⎢
⎥
7 ⎥⎥
A = ⎢ 20 − 7 12⎥ = LU = ⎢⎢ 5 1 0⎥⎥ ⎢⎢0 3
⎢⎣− 8 13 17 ⎥⎦
⎢⎣− 2 3 1⎥⎦ ⎢⎣0 0 − 2⎥⎦
Ejemplo 2
Encuentre la factorización LU de A.
1
1 ⎤
⎡ 4
⎢
A = ⎢− 12 2 − 4⎥⎥
⎢⎣ 20 − 5 10 ⎥⎦
ALGEBRA LINEAL
1
M.C. JOSÉ MANUEL ROCHA NÚÑEZ
M.C. ELIZABETH GPE. LARA HERNÁNDEZ
UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN
FACULTAD DE INGENIERÍA MECÁNICA Y ELÉCTRICA
1
1 ⎤ A1, 2(3 ) ⎡4 1
1⎤
⎡ 4
⎡4 1 1 ⎤
( −5 ) ⎢
(2 ) ⎢
⎢
⎥
⎥
A
A
1, 3
2,3
⎯→ ⎢0
− 1⎥ ⎯⎯ ⎯→ ⎢0 5 − 1⎥⎥
5
U = ⎢− 12 2 − 4⎥ ⎯⎯ ⎯
⎢⎣ 20 − 5 10 ⎥⎦
⎢⎣0 − 10 5 ⎥⎦
⎢⎣0 0 3 ⎥⎦
El tamaño de L es de 3x3 y está formada por los factores (con signo contrario) que se
utilizaron para generar los ceros en la matriz U
0 0⎤
⎡1
⎢
L = ⎢− 3 1 0⎥⎥
⎢⎣ 5 − 2 1⎥⎦
En consecuencia
1
1⎤
0 0⎤ ⎡4 1 1 ⎤
⎡ 4
⎡1
⎢
⎥
⎢
A = ⎢− 12 2 − 4⎥ = LU = ⎢− 3 1 0⎥⎥ ⎢⎢0 5 − 1⎥⎥
⎢⎣ 20 − 5 10 ⎥⎦
⎢⎣ 5 − 2 1⎥⎦ ⎢⎣0 0 3 ⎥⎦
Teorema
Si A es una matriz mxn que puede reducirse a la forma de escalón U solo con eliminaciones,
entonces A tiene una factorización LU. En particular, A puede factorizarse como
A=LU
Aquí, L es una matriz triangular inferior de mxm donde solo hay números 1 en la diagonal
principal. El (i, j ) -ésimo elemento lij (i > j ) de L proviene de la operación Ri − lij R j → Ri ,
que se usó para obtener 0 en esta posición durante la reducción.
Se tiene el siguiente sistema de ecuaciones
Ax = b
Si se puede factorizar la matriz A, mxn en la forma
A = LU
Entonces el sistema se transforma en
LUx = b
Primero se despeja y de la ecuación, resolviendo la ecuación mediante sustitución directa
Ly = b
Y a continuación se despeja x de la ecuación resolviendo mediante sustitución hacia atrás
Ux = y
ALGEBRA LINEAL
2
M.C. JOSÉ MANUEL ROCHA NÚÑEZ
M.C. ELIZABETH GPE. LARA HERNÁNDEZ