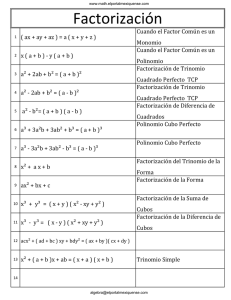
Factorización Estrategia Factor común y por agrupación Factorización Factorización de diferencia de cuadrados y cubos Factorización de trinomios Factor a bx z a bx z ab y x z b y x z Factorización Operación necesaria para re-escribir una expresión algebraica como producto de factores simples 2 2 ma mb m(a b)(a b) Son factores Expresión algebraica que multiplica a otra expresión, Esos factores pueden ser también numéricos Caso I. Factor Común Esta formado por el divisor común en todos los términos de una expresión algebraica. 2 2 ma mb 2 3x y x 2 2 2 4 24a xy 36x y a(x 1) b(x 1) Como Factorizar: •Identificar el máximo término común. Se tomara el máximo común divisor ,en el caso de un potencia la que tenga el menor exponente . Dividir cada término de la expresión algebraica original entre el máximo término común Caso I. Factor Común Resolviendo los ejemplos: Ejemplo 2 ma 2 mb 3x2 y x Máx. factor común m x 24a2 xy2 36x2 y 4 12xy 2 a(x 1) b(x 1) x 1 Segund Factorización o factor 2 b m(a2 b2 ) 3xy 1 x(3xy 1) 2 a 2 2 2 2a2 3xy2 12xy (2a 3xy ) a b (x 1)(a b) Factorización por agrupación de términos Ocurre cuando no existe un máximo común divisor para todos los términos , pero al agrupar convenientemente , los términos Algebraicos de cada grupo si lo tienen. Requiere factorizar dos veces de manera consecutiva ax abx b 2 3m 6mn 4m8n 2am n 12an 2a m •Agrupar términos con factores comunes, usando la propiedad asociativa, se puede Conmutar si es necesario • Factorizar en cada grupo, los factores comunes • Identificar el máximo término común polinomio, como en el último ejemplo. •Dividir la expresión algebraica entre el máximo término común Factor común por agrupación de términos Resolviendo los ejemplos: ax a bx b (ax a) (bx b) (a b)(x 1) a(x 1) b(x 1) procedimiento trinomio cuadrado perFecto (Conocimiento previo) Resultado del siguiente producto notable: 2 (a b) 2 2 a 2ab b o, 2 (a b) 2 2 a 2ab b trinomio de la Forma (Conocimiento previo) 2 x cx d Resultado del siguiente producto notable: 2 (x a)(x b) x (a b)x ab Donde: c a b y d ab Factor Común por Agrupación de Términos Resolviendo los ejemplos: 3m2 6mn 4m 8n (3m 4)(m 2n) (3m2 6mn) (4m 8n) 3m(m 2n) 4(m 2n) procedimiento Factor común por agrupación de términos Resolviendo los ejemplos: 2am n 1 2an 2a m (2a 1)(m n 1) (2am 2an 2a) (m n 1) 2a(m n 1) (m n 1) procedimiento caso ii. Factorización de trinomios Trinomio Cuadrado Perfecto Determinar si es Trinomio cuadrado perfecto Obtener la raíz cuadrada del primer y tercer términos 2 2 a 2ab b 2 x 2x 1 Observar el signo del segundo término 2 2 4a x 12ax 9 • Escribir el binomio al cuadrado Factorización de trinomios Resolviendo ejemplos: 2 2 a 2ab b ¿ es TCP ? Sí a2 a b2 b 2ab 2 (a b) procedimiento Factorización de trinomios Resolviendo ejemplos: ¿ es TCP ? 2 2 4a x 12ax 9 Sí 4a2 x 2 2ax 93 12ax 2 (2ax 3) procedimiento Factorización de trinomios Trinomio de la forma 2 x 12x 20 2 2 9a x 39ax 30 3ax -10 3ax -3 (3ax-10) (3ax-3) 2 x cx d •Obtener la raíz cuadrada del primer término •Determinar dos números que sumados sean igual a c y que multiplicados sean igual a d •Escribir el producto de binomios Factorización de trinomios Resolviendo ejemplos: 2 x 12x 20 x2 x 10 2 12 (10)(2) 20 (x 10)(x 2) procedimiento Factorización de trinomios Resolviendo ejemplos: 2 2 9a x 39ax 30 9a2 x 2 3ax 10 3 13 (10)(3) 30 (3ax 3)(3ax 10) 3(ax 1)(3ax10) procedimiento diFerencia de cuadrados (conoocimiento previo) Resultado del siguiente producto notable: (a b)(a b) a 2 b2 (a b) (a b) = (a b) (a b) 2 a 2 b = Factorización de la diFerencia de cuadrados 2 2 a b 2 a 1 9 16x 2 •Identificar la diferencia de cuadrados •Obtener la raíz cuadrada del primer y segundo términos 6 x 2x 1 y 2 •Escribir el producto de binomios conjugados Factorización de la diFerencia de cuadrados Resolviendo ejemplos: 6 9 16x 93 16x6 4x 3 3 3 (3 4x )(3 4x ) procedimiento Factorización de la Diferencia de Cuadrados Resolviendo ejemplos: (x 1)2 x 1 2 2 x 2x 1 y y2 y (x 1 y)(x 1 y) procedimiento suma y diFerencia de cubos (Conocimiento previo) Resultado del siguiente producto notable: 3 3 2 2 (a b)(a ab b ) a b o bien, 2 2 (a b)(a ab b ) 3 3 a b Factorización de la suma o diFerencia de cubos 3 3 a b •Identificar si es suma o diferencia de cubos 3 a 1 •Obtener la raíz cúbica del primer y segundo términos 6 27 64x •Escribir el producto del binomios por trinomio correspondiente Factorización de la suma o diFerencia de cubos Resolviendo ejemplos: 3 a 1 diferencia 3 3 a a 3 1 1 2 (a 1)(a a1) procedimiento Factorización de la suma o diFerencia de cubos Resolviendo ejemplos: 6 27 64x suma 3 27 3 3 64x6 4x 2 2 2 4 (3 4x )(9 12x 16x ) procedimiento estrategia general 1. 2. Factorizar todos los factores comunes. Observar el número de términos entre paréntesis (o en la expresión original). Si hay: I. II. Cuatro términos: factorizar por agrupación. Tres términos: probar si es tcp y factorizar así; si no es tcp, emplear el caso general. III. Dos términos y cuadrados: buscar la diferencia de cuadrados y factorizarla. IV. Dos términos y cubos: buscar la suma o diferenica de cubos y factorizar. 3. Asegurarse de que la expresión está factorizada completamente.