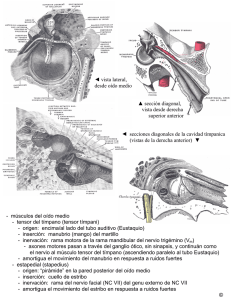
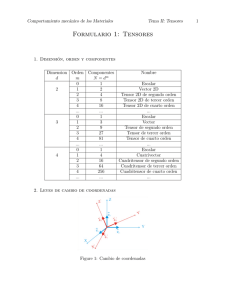
Elementos de Matemáticas
Anuncio

Estabilidad IV-a Capítulo 0: Elementos de Matemáticas Capítulo 0 ELEMENTOS DE MATEMATICAS 0 - 1 : INTRODUCCION El presente capítulo no es más que un sintético resumen de conceptos y fórmulas útiles para el estudio de la asignatura Estabilidad IV-a de la carrera de Ingeniería Civil de la U.N.N.E. Se referirá a elementos del área de vectores, tensores, transformaciones lineales, operadores y matrices. Dado el objetivo utilitario que se persigue nos referiremos exclusivamente a coordenadas cartesianas ortogonales del espacio tridimensional que coincide con el espacio físico. En correspondencia con la tendencia de la bibliografía se introduce la Notación Indicial, que si bien puede dificultar al principio la lectura del estudiante, facilita enormemente los desarrollos y la implementación de los cálculos. Se ha tratado de unificar una nomenclatura que, siendo fácilmente adaptable a la utilizada por los estudiantes en cursos anteriores, permita (aunque en el curso realicemos los desarrollos en forma clásica) aplicar la notación a quienes así lo prefieran. Aspiramos con la presente facilitar el cursado de la asignatura sin pretender suplir el dictado de las clases teórico-prácticas, ni que sea un texto de la materia. 0 - 2 : MAGNITUDES ESCALARES Existen magnitudes como la longitud, el volumen, la densidad, la energía, la temperatura, etc., que quedan perfectamente determinadas por un número real, y que puede ser representada por un segmento aplicado a partir de un origen sobre una recta. Diremos que estamos ante un Escalar y el número que representa a la magnitud es independiente del sistema de coordenadas adoptado. 0 - 3 : VECTORES Existen otras magnitudes como las fuerzas, la velocidad, la aceleración, etc., que no pueden ser representadas por un número real, ya que tiene como característica una intensidad, una dirección y un sentido. Estamos ante magnitudes vectoriales y deben ser representadas por vectores. Recordaremos aquí algunos elementos de la teoría de vectores que nos serán útiles para definir nomenclaturas y para su posterior x3 utilización en el curso. P(b1 , b2, b3) En primer lugar nos referiremos a un sistema de ejes cartesianos ortogonales x 1 , x 2 , x 3 , como el b de la figura definido por una base de versores e1; e2; e3 b3 e3 . o En este sistema el segmento orientado OP e2 x2 b1 e1 b2 que define al vector b tendrá las componentes b1, b2, b3, que no son más que las proyecciones de b sobre los tres ejes coordenados. b1 Facultad de Ingeniería - U.N.N.E. 1 Estabilidad IV-a Capítulo 0: Elementos de Matemáticas ⎡b 1 ⎤ ⎢ ⎥ b = (b 1 , b 2 , b 3 ) = ⎢b 2 ⎥ = bi ⎢b ⎥ ⎣ 3⎦ i = 1, 2, 3 b = b 1 ⋅ e1 + b 2 ⋅ e 2 + b 3 ⋅ e 3 x3 x’3 α33 x’2 α23 α21 α32 α31 Veamos que pasa con una rotación de ejes (transformación lineal) donde denominamos con x i ⋅ (x 1 x 2 x 3 ) a los ejes originales y x ' i ⋅(x '1 x ' 2 x ' 3 ) a los nuevos ejes rotados. Denominamos con αij al ángulo entre los ejes x'i y xj y con aij al coseno de dicho ángulo. cos(x ' i , x j ) = cos α ij = a ij α22 α13 x2 α11 α12 Con los 9 elementos se puede formar una Matriz de Rotación (Matriz de Transformación Ortogonal) que denominaremos A=(aij) x1 x’1 ⎡a 11 a 12 a 13 ⎤ ⎢ ⎥ A = ⎢a 21 a 22 a 23 ⎥ ⎢a a a ⎥ ⎣ 31 32 33 ⎦ Ejes x'1 x'2 x'3 tal que: x1 a11 a21 a31 x2 a12 a22 a32 x3 a13 a23 a33 La matriz de rotación se denomina ortogonal pues cumple con las siguientes propiedades: 3 a) ∑a j=1 ij ⋅ a kj = 1 si i = k ij ⋅ a kj = 0 si i ≠ k 3 b) ∑a j=1 c) Determinante de A = |A| = 1 d) A-1= AT (matriz inversa de A = Matriz transpuesta de A) Veamos como referirnos y que relación existe entre sus componentes al pasar el vector b=(b1; b2; b3) = (bi)del sistema de referencia xi al x3 x'i. Las nuevas coordenadas (b'i) serán: x’3 x’2 b’ 3 b’ 2 b'1 = a 11 b1 + a 12 b 2 + a 13 b 3 b’1 P b' 2 = a 21 b1 + a 22 b 2 + a 23 b 3 x2 b' 3 = a 31 b1 + a 32 b 2 + a 33 b 3 Según las reglas del cálculo matricial se puede expresar al vector b en las nuevas coordenadas mediante el producto matricial: x1 x’1 Facultad de Ingeniería - U.N.N.E. 2 Estabilidad IV-a Capítulo 0: Elementos de Matemáticas ⎡b'1 ⎤ ⎡a 11 a 12 a 13 ⎤ ⎡b1 ⎤ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ 3 ⎢ ⎢ ⎥ b' 2 = a 21 a 22 a 23 ⎥ * ⎢b 2 ⎥ b' = A ⋅ b donde b' i = ∑ a ij ⋅ b i ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ j=1 ⎢ b ' ⎥ ⎢a a a ⎥ ⎢ b ⎥ ⎣ 3 ⎦ ⎣ 31 32 33 ⎦ ⎣ 3 ⎦ Es este el momento indicado para introducir la Notación indicial o de Einstein, que básicamente consiste en las siguientes reglas: a) Un índice puede aparecer una o dos veces en un término dado: Cuando un índice aparece una vez en un término (no aparece repetido) se entiende que este índice toma los valores de rango (Ej.: 1, 2, 3 en el espacio de tres dimensiones): (xi) = (x1, x2, x3) b= bi = (b1, b2, b3) ƒ(xi) = ƒ(x1, x2, x3) Cuando un índice aparece dos veces en un término se interpretará que ese índice toma todos los valores de su rango, sumándose los términos que resulten (Convención de sumatoria) 3 b = b i ⋅ e i = b1 ⋅ e1 + b 2 ⋅ e 2 + b 3 ⋅ e 3 = ∑ b i ⋅ e i i =1 b ⋅ c = (b i ⋅ c i ) = b1 ⋅ c1 + b 2 ⋅ c 2 + b 3 ⋅ c 3 = ∑ b i ⋅ c i = ∑ b j ⋅ c j = (b j ⋅ c j ) 3 3 i =1 j=1 Es evidente que este tipo de notación permite eliminar el símbolo de sumatoria dándolo por sobreentendido y también cambiar los índices sin alterar el resultado. La repetición de un índice más de dos veces no es aplicable a la convención de sumatoria, no teniendo sentido una expresión del tipo ui · vii b) También especificaremos una notación para la diferenciación (Derivación), utilizando una coma ( , ) y a continuación un subíndice indicando que existe una derivada parcial y el eje respecto del cual se deriva. Tomemos como ejemplo el operador nabla ∇( ). ∂( ) ∂( ) ∂( ) + e3 ⋅ + e2 ⋅ ∇( ) = e1 ⋅ ∂x 3 ∂x 2 ∂x 1 ∂( ) Según convención de suma ∇( ) = e i ⋅ ∂x i Según convención de diferenciación ∇( ) = e i ⋅ ( ), i Otro ejemplo sería: ∂b1 ∂b 2 ∂b 3 ∂b i + + = = b i ,i = b1,1 + b 2 ,2 + b 3 ,3 ∂x 1 ∂x 2 ∂x 3 ∂x i c) El símbolo δij (Delta de Kroenecker) representa una matriz especial y simétrica (matriz unidad) ⎡1 0 0⎤ ⎥ ⎢ δ ij = ⎢0 1 0⎥ = I δij = δji ⎢0 0 1⎥ ⎦ ⎣ Facultad de Ingeniería - U.N.N.E. 3 Estabilidad IV-a Capítulo 0: Elementos de Matemáticas donde δij = 1 si i = j y δij = 0 si i ≠ j Retomando el tema Vectores, daremos ahora una "Definición Analítica de Vectores" mediante el siguiente Teorema Fundamental: "La condición necesaria y suficiente para que tres escalares b1 b2 b3 (bi) sean componentes de un vector b, es que por un cambio de ejes coordenados ortogonales de origen fijo, ellos se transformen según las mismas fórmulas que las coordenadas del punto" b'1 = a 11 b1 + a 12 b 2 + a 13 b 3 ∴b'i = aij · bj b' 2 = a 21 b 1 + a 22 b 2 + a 23 b 3 b' 3 = a 31 b1 + a 32 b 2 + a 33 b 3 Es posible, a través de esta definición analítica del vector plantear toda la teoría de vectores, propiedades, operaciones, etc., a las cuales estamos tan habituados los Ingenieros. 0 - 4 : TENSOR CARTESIANO DE 2° ORDEN Consideremos el espacio ordinario de tres dimensiones referido al triedro de ejes cartesianos ortogonales (x1; x2; x3) y supongamos los x3 dos vectores: P u = (u1, u2, u3) = ui x3 v = (v1, v2, v3) = vi O x2 x1 x1 x2 los cuales bajo una rotación de ejes cuya matriz de transformación es: ⎡a 11 a 12 a 13 ⎤ ⎢ ⎥ A = (aij) = ⎢a 21 a 22 a 23 ⎥ ⎢ ⎥ ⎢a a a ⎥ ⎣ 31 32 33 ⎦ Se transformarán según: u 'i = a i1 u 1 + a i2 u 2 + a i3 u 3 = a ih u h v' j = a j1 v1 + a j2 v 2 + a j3 v 3 = a jk v k Consideremos ahora los 9 productos (ui ⋅ vj) ⎡u 1 v1 u 1 v 2 u 1 v 3 ⎤ (u i ⋅ v j ) = ⎢⎢u 2 v1 u 2 v 2 u 2 v 3 ⎥⎥ ⎢u v u v u 3 v 3 ⎥⎦ 3 2 ⎣ 3 1 Las cuales mediante una rotación de ejes se transforman según la siguiente regla: u ' i ⋅v' j = (a i1 u 1 + a i2 u 2 + a i3 u 3 )(a j1 v 1 + a j2 v 2 + a j3 v 3 ) u ' i ⋅v' j = a ih ⋅ a jk ⋅ u h ⋅ v k donde como h y k van de 1 a 3 constituyen 9 sumandos (3 x 3). El conjunto de los 9 productos (ui, vj) se denomina producto tensorial de los vectores (ui); (vj) y cumplen con las propiedades que caracterizan al "Tensor de 2° orden" que en forma similar al caso de los Vectores podemos definir en forma analítica de la siguiente manera: Facultad de Ingeniería - U.N.N.E. 4 Estabilidad IV-a Capítulo 0: Elementos de Matemáticas "dadas las 9 cantidades tij ⎡ t 11 ⎢ T = (t ij ) = ⎢ t 21 ⎢t ⎣ 31 t 12 t 22 t 32 t 13 ⎤ ⎥ t 23 ⎥ t 33 ⎥⎦ se dice que son componentes de un vector cartesiano de 2° orden cuando por un cambio de coordenadas se transforma según la ley: t ' ij = a ih ⋅ a jk ⋅ t h ⋅k (9 sumandos) " donde es inmediato que se interpreta: thk = componente del tensor en los ejes x i ⋅ (x 1 ; x 2 ; x 3 ) t'ij = componente del tensor en los ejes x 'i ⋅(x '1 ; x ' 2 ; x '3 ) aih, ajk = cosenos directores entre los ejes rotados y los ejes originales. De la misma forma se podrían definir Tensores Cartesianos de 3°, 4°,..., n° orden dando origen a una teoría de tensores en la cual el tensor de enésimo orden se transforma mediante una ley en que el producto es de n. cosenos directores. Bajo esta premisa podemos considerar que el tensor de 2° orden (tij) tiene 32 componentes (9) y que los vectores con 31 componentes son tensores de 1er orden y los escalares con 30 componentes son tensores de orden cero. 0 - 4 . 1 : PROPIEDADES Y OPERACIONES CON TENSORES DE 2° ORDEN 0 - 4 . 1 . 1 : Igualdad Dos tensores A = (aij) y B = (bij) son iguales cuando sus respectivos componentes son iguales aij = bij 0 - 4 . 1 . 2 : Adición Solo definida para tensores del mismo orden (en este caso 2° orden). El tensor suma (o diferencia) de otros es un nuevo tensor que tiene por componentes la suma (o diferencia) de las componentes respectivas, obteniéndose un tensor del mismo orden. Sean los tensores T = (tij) y S = (sij) será M = (mij) la suma; M= T ± S si mij = tij ± sij 0 - 4 . 1 . 3 : Multiplicación: a) Multiplicación por un escalar λ Da como resultado un tensor del mismo orden cuyas componentes son obtenidas como el producto escalar por los componentes respectivos λ ⋅ T = λ ⋅ (t ij ) = (λ ⋅ t ij ) b) Producto de tensores (o Tensorial) El producto de dos tensores da un Tensor cuyo orden es la suma del orden de ambos tensores y cuyas componentes son los productos de las componentes de los dos tensores. Facultad de Ingeniería - U.N.N.E. 5 Estabilidad IV-a Capítulo 0: Elementos de Matemáticas Consideremos un tensor de primer orden U = (ui) y uno de segundo orden T = (tij). El tensor producto de tercer orden será: s ijk = u i ⋅ t jk 0 - 4 . 1 . 4 : Contracción Dado un tensor de orden ≥ 2, igualando dos índices y sumando respecto del índice igualado, se obtiene un tensor en el que han desaparecido estos índices y cuyo orden es 2 grados inferior al original. Por ejemplo el tensor tijk da origen a: uk = tii k Al tensor resultante se lo denomina Tensor Contraído y en este caso tendrá componentes: u 1 = t 111 + t 221 + t 331 u 2 = t 112 + t 222 + t 332 u 3 = t 113 + t 223 + t 333 0 - 4 . 1 . 5 : Tensores Simétricos de 2° Orden Diremos que un tensor es simétrico si se cumple que: T = (tij) tij = tji denominándose antisimétrico si tij = -tji y se representan por matrices que son respectivamente simétricas y antisimétricas respecto a su diagonal principal. Como en el curso utilizaremos tensores simétricos de segundo orden, veamos algunas de sus propiedades sin plantear las demostraciones: a) Para cada tensor simétrico T = (tij) hay un vector dado por el Producto Interno que está asociado a cada dirección (definida por un versor ni ó vector unitario) en ese punto. vi = tij · nj Nótese que el tensor tij puede considerarse como un operador vectorial lineal que asocia a cada dirección definida por su versor nj un vector vi donde no necesariamente nj y vi son vectores colineales. Si por el contrario para una dirección nj determinada, el vector vi resultante es colineal con nj se cumplirá: v i = t ij ⋅ n j = λ ⋅ n i denominándose a nj "dirección principal de T = (tij)" Utilizando el Delta de Kroenecker podemos decir: n i = δ ij ⋅ n j siendo o bien t ij ⋅ n j = λ ⋅ δ ij ⋅ n j (t ij − λ ⋅ δ ij ) ⋅ n j = 0 Facultad de Ingeniería - U.N.N.E. 6 Estabilidad IV-a Capítulo 0: Elementos de Matemáticas que expresada en forma desarrollada equivale a: (t 11 − λ ) ⋅ n 1 + t 12 ⋅ n 2 + t 13 ⋅ n 3 = 0 t 21 ⋅ n 1 + (t 22 − λ ) ⋅ n 2 + t 23 ⋅ n 3 = 0 t 31 ⋅ n 1 + t 32 ⋅ n 2 + (t 33 − λ ) ⋅ n 3 = 0 Sistema de 3 ecuaciones homogéneas donde, si se conocen las componentes tij del tensor tendremos 4 incógnitas λ, n1, n2, n3 que definen la dirección principal. La solución trivial de un sistema es ni = 0 (n1 = n2 = n3 = 0), que no se comparece con la condición: ∴ ni ⋅ ni =1 n 12 + n 22 + n 32 = 1 al ser ni los cosenos directores del versor n = ni Para que el sistema de ecuaciones tenga una solución distinta a la trivial el determinante de la matriz de los coeficientes debe ser nulo (Roche-Frobenius): t ij − λδ ij = 0 que explicitada se expresa: (t 11 − λ ) t 12 t 13 t 21 (t 22 − λ ) t 31 t 32 t 23 = 0 (t 33 − λ ) Desarrollado, el determinante conduce a una ecuación algebraica de tercer grado (Ecuación secular o característica) λ3 − I1λ2 + I 2 λ − I 3 = 0 donde los escalares I1, I2, I3: I 1 = t 11 + t 22 + t 33 = t ii (traza de T) t 22 t 23 t 32 t 33 t 11 t 13 t 31 t 33 t 11 t 12 t 21 t 22 t 11 t 12 I 2 = t 21 t 22 t 23 = t ij = det (t ij ) t 31 t 32 t 33 I2 = + + = 1 (t ii ⋅ t jj − t ij ⋅ t ji ) 2 t 13 se denominan Invariantes de 1°, 2° y 3er orden del tensor tij, por no variar al producirse un cambio de ejes de referencia. Facultad de Ingeniería - U.N.N.E. 7 Estabilidad IV-a Capítulo 0: Elementos de Matemáticas Las soluciones (reales) λ1 λ2 λ3 se denominan valores principales o autovalores de tij y a las tres direcciones ni correspondientes con los λi se las denomina direcciones principales, siendo ortogonales entre si. Cuando el tensor tij se refiere a ejes coordenados coincidentes con las direcciones principales la matriz que los representa es diagonal: ⎡λ 1 0 0 ⎤ ⎥ ⎢ T = ⎢0 λ 2 0 ⎥ ⎥ ⎢ ⎢0 0 λ ⎥ 3⎦ ⎣ 0 - 5 : MATRICES - TRANFORMACIONES LINEALES 0 - 5 . 1 : TRANSFORMACIÓN LINEAL Como siempre estamos en el espacio afín R3 de 3 dimensiones y sean xi (i = 1, 2, 3) las coordenadas de sus puntos. Se llama Transformación Lineal de R3 en R'3 a toda transformación de los puntos del primer espacio R3 en los del segundoR'3 definida por ecuaciones lineales y homogéneas de la forma: 3 x ' i = ∑ a ij ⋅ x j = a ij ⋅ x j j=1 donde los coeficientes aij son constantes y forman la matriz: ⎡a 11 a 12 a 13 ⎤ ⎢ ⎥ A = ⎢a 21 a 22 a 23 ⎥ = (a ij ) ⎢a ⎥ ⎣ 31 a 32 a 33 ⎦ que se llama Matriz de Transformación y tiene una correspondencia biunívoca con la transformación lineal definida. En realidad una transformación lineal general tiene término independiente, pero aquí solo trataremos las transformaciones lineales homogéneas. 0 - 5 . 1 . 1 : Producto de transformaciones lineales Sea la transformación lineal A(aij) de R3 a R'3 y la nueva transformación B(bij) de R'3 a R''3 definida por: 3 x ' ' k = ∑ b ki ⋅ x 'i = b ki ⋅ x 'i j=1 ⎡b11 b12 b13 ⎤ ⎥ ⎢ o sea la matriz: B = ⎢b 21 b 22 b 23 ⎥ = (b ki ) ⎥ ⎢ ⎥ ⎢b ⎣ 31 b 32 b 33 ⎦ Se llama Transformación Lineal Producto B.A a la transformación de R3 en R''3 resultante de realizar sucesivamente la transformación A y luego la B siendo; 3 3 i =1 i =1 x ' ' k = ∑ b ki ⋅ x ' i = ∑ 3 ∑b j=1 ki ⋅ a ij ⋅ x j = b ki ⋅ a ij ⋅ x j k = 1, 2, 3 lo cual representa una transformación lineal C cuya matriz será: Facultad de Ingeniería - U.N.N.E. 8 Estabilidad IV-a Capítulo 0: Elementos de Matemáticas ⎡c11 c12 c13 ⎤ ⎢ ⎥ C = ⎢c 21 c 22 c 23 ⎥ con ⎢c ⎥ ⎣ 31 c 32 c 33 ⎦ que responde a la Ley de Producto de Matrices. 3 c ij = ∑ b ih ⋅ a hj = b ih ⋅ a hj h =1 Si convenimos en representar con: ⎡x 1 ⎤ ⎡ x '1 ⎤ ⎡ x ' '1 ⎤ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ x = (x i ) = ⎢ x 2 ⎥ x ' = (x ' i ) = ⎢ x ' 2 ⎥ x ' ' = (x ' ' i ) = ⎢ x ' ' 2 ⎥ ⎢x ⎥ ⎢x' ⎥ ⎢x ' ' ⎥ ⎣ 3⎦ ⎣ 3⎦ ⎣ 3⎦ a las matrices columnas x, x' y x'', las transformaciones lineales se pueden expresar: x ' = A.x x ' ' = B.x ' x ' ' = B.A.x = C.x En general y cumpliendo las condiciones para que se pueda realizar el producto de matrices se cumple: - Propiedad Asociativa: A.(B.C ) = (A.B).C - Propiedad Conmutativa: No es en general válida: A.B ≠ B.A salvo casos particulares. 0 - 5 . 1 . 2 : Adición y sustracción - Producto por un escalar - La suma y resta está definida por: A ± B = (a ij ± b ij ) - La adición es asociativa y conmutativa A + B + C = (A + B) + C = A + (B + C ) = A + (C + B) - Cumpliendo con las condiciones para que se pueda realizar el producto, es válida la propiedad distributiva: A ⋅ (B ± C ) = A ⋅ B ± A ⋅ C - (A ± B) ⋅ C = A ⋅ C ± B ⋅ C El producto de una matriz A por un escalar λ se define; λ ⋅ A = (λ.a ij ) = A ⋅ λ 0 - 5 . 1 . 3 : Matriz Transpuesta Se llama matriz transpuesta AT de la matriz A, a la que resulta de permutar las filas por columnas: T T A = (a ij ) A T = a ij a ij = a ji ( ) Facultad de Ingeniería - U.N.N.E. 9 Estabilidad IV-a Capítulo 0: Elementos de Matemáticas cumpliéndose que: (A ± B)T = A T ± B T (A ⋅ B)T = B T ⋅ A T 0 - 5 . 1 . 4 : Transformaciones y Matrices Inversas Solo definidas para Matrices Cuadradas como las que estamos tratando y sea la transformación lineal; x' = A ⋅ x siendo A no singular, o sea: det A = A = a ij ≠ 0 . Se podrá definir la matriz inversa A-1 y la transformación inversa tales que: A −1 ⋅ A = A ⋅ A −1 ⎡1 0 0⎤ ⎥ ⎢ = I = ⎢0 1 0 ⎥ ⎢0 0 1⎥ ⎦ ⎣ Será: A −1 ⋅ x ' = (A −1 ⋅ A ) ⋅ x = I ⋅ x x = A −1 ⋅ x ' A −1 = ⎛⎜ a *ji ⎞⎟ ⎝ ⎠ xj = ∑ T a* ⋅ x' ji i con adj a ji a*ji = A 0 - 5 . 1 . 5 : Otras Propiedades de las Matrices (A ⋅ B)−1 = B −1 ⋅ A −1 (A ) −1 −1 (A ) T −1 =A = (A −1 ) T Matriz simétrica: Matriz antisimétrica: aij = aji aij = -aji Teniendo en cuenta que: 1 A s = (A + A T ) es simétrica y 2 1 A a = (A − A T ) es antisimétrica 2 1 1 A = (A + A T ) + (A − A T ) = As + Aa . Suma de una matriz simétrica mas 2 2 una antisimétrica. Facultad de Ingeniería - U.N.N.E. 10 Estabilidad IV-a Capítulo 0: Elementos de Matemáticas 0 - 5 . 1 . 6 : Transformaciones y Matrices Ortogonales Ha sido tratado en el tema (0-3) al definir la Matriz de Rotación A = (aij) como una Matriz Ortogonal. Una transformación lineal pueda interpretarse de dos maneras: a) La transformación "afin" que cambia las coordenadas xi a otras coordenadas x'i referidas al mismo sistema de coordenadas. b) La transformación "alias'' en la que se supongan que xi y x'i son las coordenadas del mismo punto del espacio referido a sistemas coordenados diferentes. Podemos decir: "Las transformaciones lineales que definen cambios de sistemas de coordenadas cartesianas ortogonales en otros del mismo tipo son transformaciones lineales ortogonales" Su Matriz A = (aij) cumple con las siguientes propiedades: 3 a) ∑ a ij ⋅a kj = δ ik j=1 3 ∑ a ji ⋅a jk = δ ik j=1 -1 b) A = AT c) det A = |A| = ± 1 (–si se invierten algunos ejes) d) adj aij = ± aji (–si se invierten algunos ejes) 0 - 5 . 1 . 7 : Transformación de los Componentes del Tensor de Segundo Orden Aplicando el álgebra matricial calcularemos las nuevas componentes (t'ij) de un tensor T = (thk) al efectuar una rotación de los ejes originales (x1; x2; x3) mediante la Matriz de Rotación ortogonal A= (aij) y su inversa y transpuesta AT = (aTij) = (aji) . De (0 - 4): t'ij = aih ajk thk Multipliquemos A·T = C Multipliquemos C·AT = D Luego será Facultad de Ingeniería - U.N.N.E. cij = aih·thj dij = cik·aTkj = (aih·thk)·aTkj dij = aih·ajk·thk = t'ij T'=A T·AT 11