Afternotes 27- Sistemas de ecuaciones diferenciales I: modelización

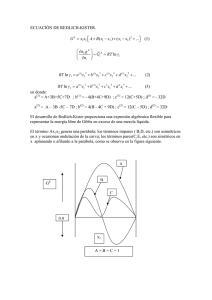
Sistemas de ecuaciones diferenciales I:
Modelización matemática y tipos de interacción
entre especies
José Luis López Fernández
11 de enero de 2012
Sólo puedo decir que la vida es lucha, lo pone en los libros de ciencias naturales. Lucha entre congéneres, contra los elementos, por el alimento, la luz, el agua y el aire,
una combinación de estrategias ofensivas y defensivas que nos conduce circularmente
desde el no ser hasta el dejar de ser. Todo lo que no sea así entendido carece de vida
[. . . ] todos los órdenes vegetales y animales están permanentemente en pie de guerra,
combatiendo por mantener la vida, escondiénose de sus predadores y depredando a
sus presas, a veces de forma individual, otras en grupo, pero siempre guerreando sobre
este planeta en que sólo pueden cohabitar los más dotados
(Fragmento de la novela Un estado del malestar, de Joaquín Berges)
En Afternotes 25 ya esbozamos un primer modelo que consideraba la interacción (subliminal) entre dos especies (pájaros y gusanos), a pesar de que, por
simplicidad en la presentación, solo la ecuación para los gusanos era tenida en
cuenta. En aquel caso la interacción entre ambas especies respondía a un modelo de depredación, en el que la única información de que disponíamos consistía
en que la población de gusanos se veía mermada a un ritmo proporcional a su
propio tamaño en cada instante de tiempo.
En esta lección atenderemos a la formulación completa de los modelos matemáticos pertinentes cuando dos poblaciones distintas1 interactúan en el mismo
hábitat. Es decir, diseñaremos una ecuación diferencial por cada una de las
especies que participan en la interacción, de modo que el sistema general de
ecuaciones diferenciales que vendrá a representar finalmente tal experiencia interactiva responderá al siguiente esquema:
x0 (t) = a + bx(t) + cy(t) x(t) ,
y 0 (t) = d + ex(t) + f y(t) y(t) ,
(1)
donde a, b, c, d, e, f ∈ R son los parámetros biológicos del modelo. Tales sistemas reciben el nombre de sistemas de Lotka–Volterra. El significado de las
1 Por simplicidad consideraremos únicamente dos poblaciones, si bien los mismos argumentos son válidos para cualquier número de especies interactuando entre sí
1
constantes es el siguiente:
a y d representan las tasas de crecimiento intrínsecas asociadas a las poblaciones x e y, respectivamente;
b y f son los coeficientes de autoinfluencia (sobre su propio crecimiento)
de las poblaciones representadas por x e y, respectivamente;
por último, las cantidades c y e son los coeficientes de influencia cruzados
de la especie y sobre la especie x y de la especie x sobre la especie y,
respectivamente.
Es interesante observar que las dos ecuaciones que conforman el sistema (1)
responden a un esquema logístico. En efecto, proceden de la siguiente escritura:
x
+ cyx ,
x0 = r1 x 1 −
K1
y
y 0 = r2 y 1 −
+ exy ,
K2
r2
r1
, f = −K
(verifíquese).
sin más que haber elegido a = r1 , d = r2 , b = − K
1
2
Si a continuación planteamos todas las posibilidades en lo referente al signo
que pueden adoptar los coeficientes de influencia cruzada c y e (+, 0, ó −), llegamos a nueve configuraciones de interacción posibles (de seis formas distintas)
entre ambas especies, como aparece contemplado en la siguiente tabla:
+
0
−
+
Mutualismo
Comensalismo
Antagonismo
0
Comensalismo
Neutralismo
Amensalismo
−
Antagonismo
Amensalismo
Competencia
Algunos ejemplos de estos tipos de interacción son los siguientes:
La relación simbiótica entre un hongo y un alga da lugar a un organismo
que recibe el nombre de liquen. Se trata de un ejemplo de mutualismo
forzoso, pues de otro modo no tendría presencia en la naturaleza dicho
organismo. Otro ejemplo lo constituyen los insectos que favorecen el ciclo
polinizador (las abejas, sin ir más lejos) a cambio de alimento para sus
crías.
Cualquier modelo de presa y depredador (por ejemplo, el ya comentado
de algunas familias de pájaros que se alimentan de gusanos que viven
en los árboles) constituye un ejemplo de antagonismo. También lo es
cualquier relción de parasitismo: la garrapata en el perro, la solitaria en
el ser humano, . . .
2
Cualesquiera dos especies que compartan hábitat en pugna por el alimento
(animales) o por la luz y el agua (vegetales) ilustran el modo de interacción
en competencia.
La rémora se adhiere al tiburón para ingerir los restos de las presas que
no son aprovechados por éste. Es un claro ejemplo de comensalismo. Del
mismo modo proceden los animales carroñeros: hienas, buitres, . . .
Los árboles de mayor tamaño impiden en algunos bosques la captura de
luz por parte de matorrales o arbustos que viven a ras de suelo. Se trata
de un ejemplo de amensalismo, pues nada aporta el matorral a favor ni
en contra del árbol.
Por último, para ilustrar la relación de neutralismo podríamos escoger
una especie de animales carnívoros y cualquier especie vegetal que convivan en el mismo hábitat (bajo una especie de pacto de no agresión).
Para ilustrar lo expuesto elijamos el siguiente sistema de ecuaciones diferenciales de Lotka–Volterra:
x0 = 12 − 5x + 2y x ,
y 0 = 24 − 4x − 2y y .
(2)
Los valores de los coeficientes de influencia cruzada son c = +2 y e = −4, lo
cual quiere decir que la presencia de la especie y favorece el desarrollo de la
especie x pero, por contra, la presencia de x perjudica el desarrollo de y. Se
trata, por consiguiente, de un caso de antagonismo. Para entender en profundidad el efecto último de la interacción es conveniente analizar qué le sucedería
separadamente a cada una de las poblaciones en ausencia de la otra.
Ausencia de la especie y: Se trata del caso en que y = 0, luego la
segunda de las ecuaciones en (2) no aporta ninguna información relevante
(0 = 0), mientras que la primera de ellas se reduce a
x0 = (12 − 5x)x .
(3)
Los puntos de equilibrio de (3) son x = 0 y x = 2,4, luego cualquier
solución cuyo dato inicial x0 se encuentre entre ambos puntos de equilibrio
(por ejemplo, x0 = 1) verifica que es creciente (x0 = (12 − 5 · 1) · 1 = 7 >
0), por lo que a largo plazo tenderá hacia el valor de la correspondiente
capacidad de carga: K1 = 2,4.
Ausencia de la especie x: Ahora x = 0, luego es la primera de las
ecuaciones en (2) la que no aporta información relevante. La segunda, sin
embargo, se lee
y 0 = (24 − 2y)y .
(4)
Los puntos de equilibrio de (4) son y = 0 e y = 12, luego cualquier solución
cuyo dato inicial x0 se encuentre entre ambos puntos de equilibrio (por
3
ejemplo, y0 = 1) verifica que es creciente (y 0 = (24−2·1)·1 = 22 > 0), por
lo que a largo plazo tenderá hacia el valor de la correspondiente capacidad
de carga: K2 = 12.
Ambas especies conviven e interactúan: Entonces, como vimos con
anterioridad, la especie x sale beneficiada (c = +2) mientras que y es pejudicada (e = −4). La intuición biológica nos dicta que el comportamiento
conjunto de ambas especies a largo plazo debe traducirse en una capacidad
de carga mayor que 2,4 para la especie x (fruto del beneficio obtenido a
costa de y) y menor que 12 para la especie de y (fruto del perjuicio provocado por la presencia de x). Esto será motivo de estudio en las siguientes
lecciones.
4