AD3
Anuncio
EJERCICIOS DE AD3
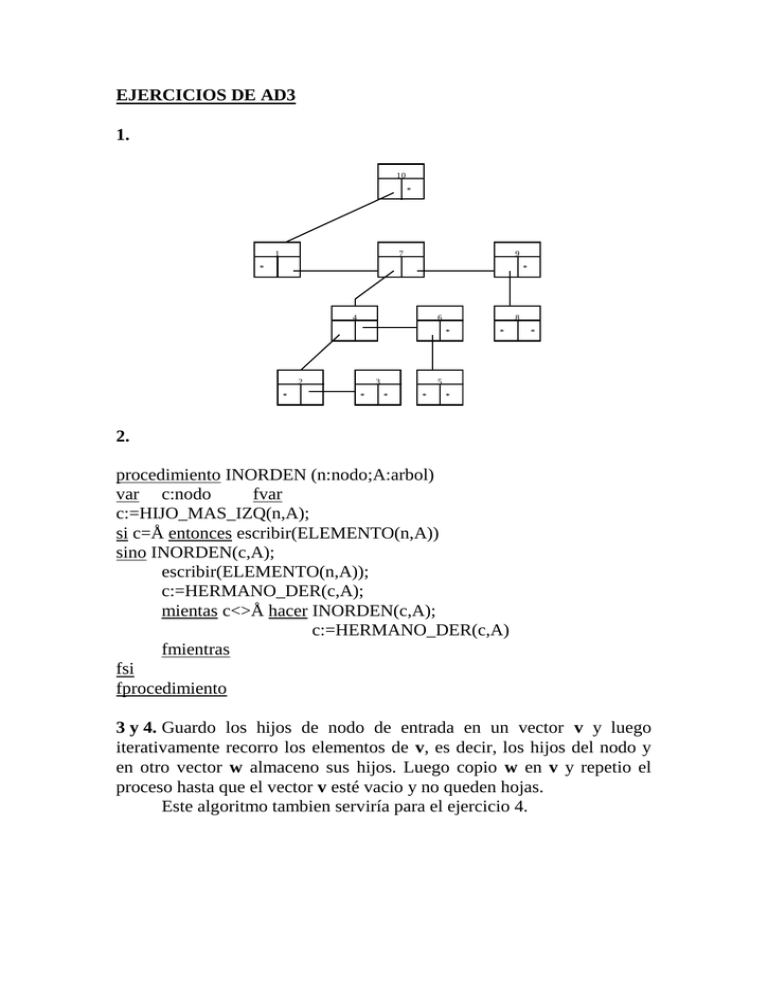
1.
10
*
1
7
9
*
*
4
6
8
*
2
*
3
*
*
*
5
*
*
*
2.
procedimiento INORDEN (n:nodo;A:arbol)
var c:nodo
fvar
c:=HIJO_MAS_IZQ(n,A);
si c=Å entonces escribir(ELEMENTO(n,A))
sino INORDEN(c,A);
escribir(ELEMENTO(n,A));
c:=HERMANO_DER(c,A);
mientas c<>Å hacer INORDEN(c,A);
c:=HERMANO_DER(c,A)
fmientras
fsi
fprocedimiento
3 y 4. Guardo los hijos de nodo de entrada en un vector v y luego
iterativamente recorro los elementos de v, es decir, los hijos del nodo y
en otro vector w almaceno sus hijos. Luego copio w en v y repetio el
proceso hasta que el vector v esté vacio y no queden hojas.
Este algoritmo tambien serviría para el ejercicio 4.
procedimiento RECORRE (n:nodo; A:arbol);
var v,w:vector [1..maxnodos] de enteros
i,j,k:enteros
fvar
para k:=1 hasta maxnodos hacer
v[k]:=0; w[k]:=0;
fpara
v[1]:=n; altura:=0 ;
mientras v[1]<>0 hacer
i:=1;
mientras v[i]<>0 hacer
c:=HIJO_IZQ(v[i]);
j:=1;
mientras c<>Å hacer
w[j]:=c;
c:=HERMANO_DER(w[j]);
j:=j+1
fmientras
i:=i+1;
fmientras
w[j]:=0; k::=1;
mientras w[k]<>0 hacer
v[k]:=w[k];
fmientras
v[k]:=0;
altura:=altura+1;
fmientras
5. Para resolver la operación HIJO_MAS_IZQ(n) en una representación
mediante vectores, en la cual los nodos estan ordenados, habría que
recorrer el vector,desde la posición n hasta maxnodos-1, hasta encontrar
el primer nodo cuya dirección sea la del nodo n.
k:=n;
mientras v[k]<>n AND k<maxnodos hacer
k:=k+1;
fmientras
{ HIJO_MAS_IZQ(n)=k }
6. Implementado con vectores:
1.- Encontrar el HIJO_MAS_IZQ del nodo padre, es decir, el
hermano más a la izquierda del nodo que nos dan.
2.- Recorrer el vector mirando en el campo v[k].hijo_izq hasta
hallar el valor del nodo obtenido en el punto 1.Esto se puede hacer de la siguiente manera:
procedimiento PADRE(n:nodo;A:arbol);
var k:entero fvar
k:=1;
mientras v[k].hijo_izq<>n AND v[k].hermano_der<>n hacer
si v[k].hermano_der=n entonces PADRE(v[k].hermano_der,A)
sino k:=k+1;
fmientras
devuelve k
{ PADRE(n)=k }






