El análisis de problemas de sistemas dinámicos complejos ha

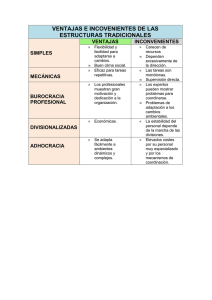
Influencia del Pensamiento Sistémico en la enseñanza de
sistemas dinámicos planos
Juarez Gustavo Adolfo; Navarro Silvia Inés
Facultad de Ciencias Exactas y Naturales - Universidad Nacional de Catamarca
juarezgustavoadolfo@yahoo.com.ar
RESUMEN
El análisis de sistemas dinámicos complejos llevó a múltiples
científicos ha generar nuevas formas de pensamiento y acciones
con el fin de contribuir en la búsqueda de soluciones y alcances para
profundizar el comportamiento de dichos sistemas. A esta nueva
forma de pensar y actuar se conoce como Pensamiento Sistémico,
entendiéndose como la habilidad de ver al mundo como un sistema
complejo, en el que todos los componentes del sistema están
conectados entre sí, comprendiendo la ciencia en relación con su
comportamiento y estructura a lo largo del tiempo. Considerando
la naturaleza dinámica de ciertos modelos matemáticos, y que los
sistemas dinámicos son la base principal del pensamiento sistémico,
los sistemas dinámicos planos permiten analizar fenómenos
mediante el comportamiento en simulaciones de modelos en
dinámica de sistemas.
La resolución de problemas que modelan Sistemas Dinámicos,
requieren de la aplicación de Sistemas de Ecuaciones Funcionales,
en particular los lineales planos. Estas ecuaciones pueden
resolverse en forma directa o bien pueden analizarse mediante
simulación.
En este contexto, emerge el objeto de investigación del presente
trabajo, mediante el análisis cualitativo de tales sistemas y su
simulación, que implícitamente se utiliza en la enseñanza de las
Ciencias Experimentales que se sustentan en la simulación de
modelos matemáticos dinámicos.
Palabras claves: modelos matemáticos dinámicos, dinámica de
sistemas, sistemas dinámicos planos.
Revista Electrónica Iberoamericana de Educación en Ciencias y Tecnología
— Volumen 4, Número 3, Diciembre 2013. Página 21—
Juarez Gustavo Adolfo; Navarro Silvia Inés; Influencia del Pensamiento Sistémico en la enseñanza de sistemas
dinámicos planos
Influences of the Systemic Thought in the Teaching of Systems
Dynamic Planes
ABSTRACT
The systems analysis dynamic complexes took to multiple scientists
it is necessary to generate new thought forms and stocks with the
purpose of contributing in the search of solutions and reaches to
deepen the behavior of this systems. To this new form of to think
and to be acted knows as Systemic Thought, understanding each
other as the ability of seeing to the world like a complex system, in
which all the components of the system are connected to each
other, understanding the science in connection with their behavior
and structure along the time. Whereas clause the dynamic nature of
certain mathematical models, and that the dynamic systems are the
main base of the systemic thought, the systems dynamic planes
allow to analyze phenomena by means of the behavior in
simulations of models in dynamics of systems.
The resolution of problems that model Dynamic Systems, requires
of the application of Systems of Functional Equations, in particular
the lineal planes. These equations can be solved in direct form or
they can be analyzed by means of simulation.
In this context, the object of investigation of the present work
emerges, by means of the qualitative analysis of such systems and
its simulation that implicitly is used in the teaching of the
Experimental Sciences that are sustained in the simulation of
dynamic mathematical models.
Key word: dynamic mathematical models, dynamics systems,
systems dynamic planes.
INTRODUCCIÓN
En la presente publicación pretendemos conjugar conceptos
tales como innovación, tecnología, aprendizaje, sistemas dinámicos complejos,
modelado matemático dinámico, simulación entre otros, temas estos que son
Revista Electrónica Iberoamericana de Educación en Ciencias y Tecnología
— Volumen 4, Número 3, Diciembre 2013. Página 22—
Juarez Gustavo Adolfo; Navarro Silvia Inés; Influencia del Pensamiento Sistémico en la enseñanza de sistemas
dinámicos planos
objetos a discutir en éstas Séptimas Jornadas Universitarias de Educación en la
Ciencia y en la Tecnología y forman parte de nuestra labor en investigación.
En efecto, desde la Matemática Aplicada, la Simulación y la
Modelización Matemática han permitido acercar los conocimientos a problemas
de la realidad, y en particular su importancia radica en poder mostrar la forma en
que tales resultados pueden aplicarse a las distintas disciplinas. Pero mas
importante aún resulta ver que el planteo dado por la Dinámica de Sistema ha
permitido analizar comportamientos de fenómenos mediante visualizaciones
amplias del entorno de un problema, es lo que nos lleva a conjugar en este
trabajo tales conceptos en los Sistemas Dinámicos Planos.
MARCO TEÓRICO
En su Obra La Quinta Disciplina Senge Peter (Director de
Pensamiento de Sistemas y Aprendizaje Organizacional de la Sloan School of
Management del MIT) manifiesta que:
“Desde muy temprana edad nos enseñan a analizar los problemas, a
fragmentar el mundo. Al parecer esto facilita las tareas complejas, pero sin
saberlo pagamos un precio enorme. Cuando intentamos ver la imagen general,
tratamos de ensamblar nuevamente los fragmentos, enumerar y organizar
todas las piezas. El Pensamiento Sistémico permite destruir la ilusión de que el
mundo está compuesto por fuerzas separadas y desconectadas.
Cuando en la mañana fría y clara de diciembre de 1903, en Kitty Hawk, Carolina
del Norte, la aeronave de Wilbur y Orville Wright demostró que era posible
volar con máquinas de motor, se inventaba el aeroplano, pero pasaron más de
treinta años hasta que la aviación comercial pudiera servir al público general.
Los ingenieros dicen que se ha inventado una idea nueva cuando se demuestra
que funciona en el laboratorio. La idea se transforma en innovación solo
cuando se puede reproducir sin contratiempos, en gran escala y a costos
prácticos. Si la idea tiene suficiente importancia (teléfono, ordenador digital ó
aviación comercial) se denomina innovación básica, y crea una industria nueva
Revista Electrónica Iberoamericana de Educación en Ciencias y Tecnología
— Volumen 4, Número 3, Diciembre 2013. Página 23—
Juarez Gustavo Adolfo; Navarro Silvia Inés; Influencia del Pensamiento Sistémico en la enseñanza de sistemas
dinámicos planos
o modifica la existente. Bajo estos términos las organizaciones existentes ya se
han inventado y falta ahora innovar.
En ingeniería cuando una idea pasa de la invención a la innovación, confluyen
diversas tecnologías de componentes.
En la actualidad, cinco nuevas tecnologías de componentes convergen para
innovar las organizaciones inteligentes. Brindan una dimensión vital para la
construcción de organizaciones con auténtica capacidad de aprendizaje. Estas
son conocidas como disciplinas: pensamiento sistémico, dominio personal,
modelos mentales, construcción de una visión compartida y aprendizaje en
equipo.
El pensamiento sistémico es un marco conceptual, un cuerpo de conocimientos
y herramientas que se ha desarrollado en los últimos cincuenta años, para que
los patrones totales resulten más claros, y para ayudarnos a modificarlos”.
Por otro lado, para Araceli Javier (Catedrático de Ingeniería de
Sistemas y Automática, en la Escuela Superior de Ingenieros de la Universidad de
Sevilla) en su Obra Dinámica de Sistemas, reconoce a estos diciendo:
“...formalmente hablamos de un sistema como de un objeto dotado de
alguna complejidad, formado por partes coordinadas, de modo que el
conjunto posea una cierta unidad, que es precisamente el sistema. Así,
hablamos del sistema planetario, formado por los planetas unidos mediante
las fuerzas gravitatorias; de un sistema económico, formado por agentes
económicos, relacionados entre sí por el intercambio de bienes y servicios; de
un sistema ecológico, formado por distintas poblaciones, relacionadas
mediante cadenas alimentarias o vínculos de cooperación; de una empresa,
como sistema, en la que los distintos departamentos se coordinan en la
organización empresarial; de una máquina, cuyas diferentes partes
interactúan para lograr el fin para el que ha sido concebida. Este es el uso del
término sistema que vamos a adoptar”.
Revista Electrónica Iberoamericana de Educación en Ciencias y Tecnología
— Volumen 4, Número 3, Diciembre 2013. Página 24—
Juarez Gustavo Adolfo; Navarro Silvia Inés; Influencia del Pensamiento Sistémico en la enseñanza de sistemas
dinámicos planos
De esta manera enmarcamos nuestros problemas dentro de los
sistemas dinámicos complejos, en donde la búsqueda de soluciones y alcances
para profundizar el comportamiento de dichos sistemas se realiza bajo esta
disciplina: Pensamiento Sistémico.
Por Pensamiento Sistémico, se considera a la habilidad de ver al
mundo como un sistema complejo, en el que todos los componentes del sistema
están conectados entre sí, comprendiendo la ciencia en relación con su
comportamiento y estructura a lo largo del tiempo.
Considerando la naturaleza dinámica de ciertos modelos
matemáticos, y que los sistemas dinámicos son la base principal del pensamiento
sistémico que ayudan a simular comportamientos, resultan así que los sistemas
dinámicos planos permiten analizar un fenómeno mediante el comportamiento
en la simulación de modelos en dinámica de sistemas.
Según
Kuznetsov
(1995)
un
sistema
dinámico
es
la
representación matemática de un proceso determinístico. Si se conoce la ley que
gobierna su evolución y su estado inicial, se puede predecir cualquier estado
futuro del sistema. Todos los posibles estados del sistema se pueden representar
por puntos en algún conjunto X llamado espacio de estados.
La evolución del sistema dinámico supone un cambio de estado
en un tiempo t  T , donde T es un conjunto ordenado. Dependiendo de la
naturaleza de T , se pueden clasificar los sistemas dinámicos en dos grupos:

Sistemas dinámicos de tiempo continuo, si T 

Sistemas dinámicos de tiempo discreto, si T 
Una órbita es el conjunto de puntos que definen la evolución de
un sistema en el espacio de estados a partir de un estado inicial x0 .
Figura 1: A la izquierda órbita de un sistema continuo, a la derecha órbita de un sistema discreto.
Revista Electrónica Iberoamericana de Educación en Ciencias y Tecnología
— Volumen 4, Número 3, Diciembre 2013. Página 25—
Juarez Gustavo Adolfo; Navarro Silvia Inés; Influencia del Pensamiento Sistémico en la enseñanza de sistemas
dinámicos planos
Es precisamente en este contexto en el que emerge el objeto de
investigación, que plantea la formulación del Estudio comparativo de sistemas
lineales planos discretos y continuos aplicados a Modelos Matemáticos
Dinámicos, a través del análisis cualitativo de tales sistemas y sus simulaciones y
la actividad de la enseñanza de tales sistemas.
Por lo tanto, el objetivo del presente trabajo es aportar a la
comunicación con la sociedad, dando a conocer resultados, preocupaciones e
investigaciones en relación con el estado actual de la enseñanza de las Ciencias
Experimentales que se sustentan en la simulación de modelos matemáticos
dinámicos.
La metodología sistémica suministra también un lenguaje que
aporta nuevas formas de ver los problemas complejos. Las herramientas que
aporta la dinámica de sistemas -desde los diagramas de influencias hasta los
modelos informáticos- nos van a permitir ver los sistemas que pueblan nuestro
entorno mediante una óptica diferente que nos descubrirá aspectos en los que
posiblemente no hayamos reparado y que, de este modo, nos permite alcanzar
una visión más rica de la realidad. [Araceli J. (1995)]
De allí que, tratar los problemas dinámicos desde la Dinámica de
Sistemas ha sido un desafío que brinda excelentes resultados mas aun en
sistemas complejos que pueden además estudiarse en su comportamiento
cualitativo a través de su forma gráfica cuando es posible, y esto se logra
mediante los diagramas de plano fase del sistema.
METODOLOGÍA
Todo lo dicho hasta aquí puede ser advertido con un ejemplo.
Para ello partamos de nuestro ejemplo de propagación de una epidemia basado
en el articulo Ciencia en Tiempos de Cólera de Verónica Grünfeld (IB-CNEA 1994);
que posteriormente fuera discretizado y simulado en Vensim 5.4 bajo Dinámica
de Sistemas en Ecuaciones en Diferencias por los autores de este articulo en
Revista Electrónica Iberoamericana de Educación en Ciencias y Tecnología
— Volumen 4, Número 3, Diciembre 2013. Página 26—
Juarez Gustavo Adolfo; Navarro Silvia Inés; Influencia del Pensamiento Sistémico en la enseñanza de sistemas
dinámicos planos
Epidemiología Matemática: Aprendiendo modelos por contagio (ver figura 2);
luego evolucionara tal propuesta por Juan Martín García en su obra Teoría y
Ejercicios Prácticos en Dinámica de Sistemas y que finalmente usando el software
Stella v.8, lo han recreado otros integrantes del grupo de Dinámica de Sistemas
de Centroamérica y Perú.
Figura 2: Diagrama de Forrester del modelo en dinámica de sistemas del modelo epidemiológico SIR.
Para el modelo de la figura 2 el comportamiento del número de
infectados en el sistema se observa en la figura 3.
Figura 3: Comportamiento del número de infectados mediante el sistema plano en el modelo SIR
La evolución del modelo desde el punto de vista del pensamiento
sistémico hace que se considere variables adicionales que determinan al
Revista Electrónica Iberoamericana de Educación en Ciencias y Tecnología
— Volumen 4, Número 3, Diciembre 2013. Página 27—
Juarez Gustavo Adolfo; Navarro Silvia Inés; Influencia del Pensamiento Sistémico en la enseñanza de sistemas
dinámicos planos
problema desde un aspecto más real. Así es como a partir del modelo anterior,
Juan Martín García en su obra Teoría y Ejercicios Prácticos en Dinámica de
Sistemas, muestra su propuesta en la figura 4, incorporando la posibilidad de
mortalidad y vacunación al problema, y extendiendo con ello al modelo de tipo
SIRS, mediante una tasa de exposición no nula.
Figura 4: Modelo epidemiológico bajo dinámica de sistema propuesto por Juan Martín García en Teoría
y Ejercicios Prácticos en Dinámica de Sistemas (2003)
Para
tal
modelo
epidemiológico
de
la
figura
4,
el
comportamiento del modelo compartamental se muestra en la figura 5, mientras
que el sistema plano se muestra en la figura 6.
Epidemia JMG
1,000
750
500
250
0
0
10
susceptibles : Current
infectados : Current
20
30
40
50
60
70
80
Time (Month)
recuperados : Current
90
Figura 5: Comportamiento de las variables del modelo epidemiológico
de la figura 4
Revista Electrónica Iberoamericana de Educación en Ciencias y Tecnología
— Volumen 4, Número 3, Diciembre 2013. Página 28—
100
Juarez Gustavo Adolfo; Navarro Silvia Inés; Influencia del Pensamiento Sistémico en la enseñanza de sistemas
dinámicos planos
Infectados vs Susceptibles
200
150
100
50
0
213
328
442
557
susceptibles
671
786
900
infectados : Current
Figura 6: Sistema plano de las variables infectados vs susceptibles del modelo epidemiológico de la
figura 4
RESULTADOS Y DISCUSIÓN
Los sistemas dinámicos planos generalmente se enseñan desde
un simple sistema de ecuaciones diferenciales, con pocas variables y con
funciones que permitan una fácil resolución, pero que en la gráfica de plano fase
resulta muy inmediata y su valor de equilibrio puede ser determinado
rápidamente. El planteo de problemas bajo dinámica de sistemas permite señalar
variables que en un simple modelo se desprecian y por ello la busqueda de
valores de equilibrio para el sistema son más complejas y lo adecuado es plantear
simulaciones en donde los diagramas de plano fase permitan hallar tales
equilibrios. En tal caso la dinámica de sistema brinda un resultado más completo
y real. La destreza de la modelización se ve facilitada por los diagramas de
Forrester, y con ello la simulación dinámica es un excelente recurso didáctico
para la enseñanza de los sistemas dinámicos.
CONCLUSIÓN
La dinámica de sistemas es una herramienta para el estudio y
modelización de sistemas dinámicos, permitiendo el tratamiento cualitativo de un
Revista Electrónica Iberoamericana de Educación en Ciencias y Tecnología
— Volumen 4, Número 3, Diciembre 2013. Página 29—
Juarez Gustavo Adolfo; Navarro Silvia Inés; Influencia del Pensamiento Sistémico en la enseñanza de sistemas
dinámicos planos
modelo matemático más realista en donde las múltiples variables participan, y
esto se logra bajo la modelización basada en el pensamiento sistémico. Si a ello
agregamos la interpretación gráfica dada a partir de los planos fases, es
inmediato analizar el comportamiento a largo plazo de un sistema. Por otro lado,
podemos concluir que un modelo de dinámica de sistemas es un sistema
dinámico.
REFERENCIAS
Araceli Javier. (1995). Dinámica de Sistemas. Madrid. Editorial ISDEFE.
Habermann, Richard. (1998). Mathematical Models. Mechanical Vibrations, Population
Dynamics, and Traffic Flow. New Jersey. SIAM - Prentice Hall.
Juarez Gustavo, Navarro Silvia. (2005). Ecuaciones en Diferencias con aplicaciones a
modelos en sistemas dinámicos. Catamarca. Editorial Sarquís.
Martín García Juan. (2003). Teoría y Ejercicios Prácticos en Dinámica de Sistemas.
Barcelona. Edición del autor.
Martín García Juan. (2008). Ejercicios Avanzados en Dinámica de Sistemas. Barcelona.
Barcelona. Edición del autor.
Senge Peter. (1992). La Quinta Disciplina. El arte y la práctica de la organización abierta
al aprendizaje. Barcelona. Ediciones Juan Granica, S.A.
Tovar Pérez, Andrés. (2001). Identificador Gráfico de Bifurcaciones IGB – versiones 4 y
5.
Bogotá.
Recuperado
el
15
de
noviembre
de
http://www.docentes.unal.edu.co/atovarp/docs/IGB/01 sistemas%20din%E1micos.pdf
Revista Electrónica Iberoamericana de Educación en Ciencias y Tecnología
— Volumen 4, Número 3, Diciembre 2013. Página 30—
2012,
de