ondas mecánicas
Anuncio

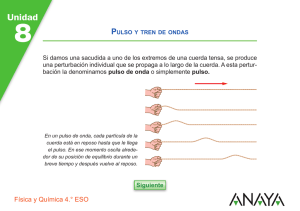
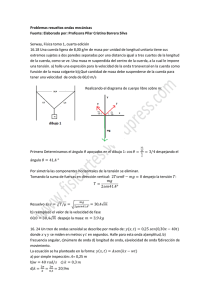
ONDAS MECÁNICAS Profesor BRUNO MAGALHAES I. ONDAS MECÁNICAS En Física se estudian dos tipos de ondas: Las Ondas Mecánicas y las Ondas Electromagnéticas. Una Onda Mecánica es la propagación de una perturbación a través de un medio físico. Al lanzar una piedra al agua, a partir del punto de entrada de la piedra elementos de agua se mueven horizontal y verticalmente (con un desplazamiento neto nulo, vuelven a su posición original) transfiriendo energía de unos a otros elementos y se propaga una onda a través del agua que viaja en su superficie en forma de circunferencia. Al sacudir verticalmente hacia arriba y hacia abajo el extremo de una cuerda, los elementos de la cuerda se mueven hacia arriba y hacia abajo (con un desplazamiento neto nulo, vuelven a su posición original) y se propaga una onda a través de la cuerda que viaja horizontalmente. Al perturbar el aire mediante algún mecanismo, elementos de aire oscilan en la misma dirección de la perturbación, empujándose unos a otros (con un desplazamiento neto nulo, vuelven a su posición original) y se propaga una onda en la misma dirección de la perturbación, denominada onda de sonido. Mientras las ondas mecánicas necesitan un medio físico de para poder viajar, las ondas electromagnéticas se propagan en vacío a la velocidad de la luz. Se generan acelerando partículas, donde se radia una onda debido a campos eléctricos y magnéticos que oscilan. Ejemplos de estas últimas son las ondas de radio y televisión, luz visible, rayos X, etc. En resumen las ondas mecánicas requieren de: Un mecanismo de perturbación, el cual es la fuente de la onda. Un medio físico que se perturba y puede propagar la onda. Es importante diferenciar el movimiento de las partículas físicas del medio perturbado al movimiento de la onda, la onda viaja a través del medio, las partículas del medio no viajan. Esta es la característica fundamental del movimiento de las ondas, transfieren energía a distancia, mas no materia. Como ejemplo, consideremos una cuerda larga bajo una tensión, y con una sola sacudida se forma un pulso (onda) que se desplaza con una rapidez determinada a lo largo de la cuerda, dicha rapidez y la altura del pulso dependen de las propiedades físicas del medio, como la tensión de la cuerda y su masa por unidad de longitud, lo cual demostraremos mas adelante. Pulso v La cuerda es el medio a través del cual viaja el pulso hacia la derecha con una velocidad definida, la forma del pulso no sufre modificación en su viaje a través de la cuerda. (En la realidad el pulso cambia de forma y gradualmente se extiende durante el movimiento y se dispersa, no consideraremos el fenómeno de dispersión del pulso) Si movemos repetidamente el extremo de la cuerda, se forman varios pulsos que conforma una onda viajera, la cual es una perturbación periódica que se desplaza en el medio, con rasgos distintos a un solo pulso de onda. I.1 ONDAS TRANSVERSALES Considerando el movimiento de los elementos del medio físico través del cual se propagan, las ondas se clasifican en transversales y longitudinales. Analizando el movimiento de un elemento P de la cuerda: Los elementos de la cuerda se mueven perpendicularmente (hacia arriba y abajo) a la dirección de la onda que viaja hacia la derecha. Las ondas viajeras o pulsos en los cuales los elementos del medio perturbado se mueven perpendicularmente (transversalmente) a la dirección de propagación de la onda se denominan ondas transversales. Si sacudimos un resorte largo longitudinalmente (hacia la derecha e izquierda) se comprimen unas espiras y se estiran (estrechan) otras en regiones del resorte, dichas regiones se desplazan a lo largo del resorte formando una onda viajera, donde los elementos del medio se mueven paralelamente a la dirección de propagación de la onda. Las ondas viajeras o pulsos en los cuales los elementos del medio perturbado se mueven paralelamente a la dirección de propagación de la onda se denominan ondas longitudinales. En la naturaleza, existen ondas mixtas, en las cuales los elementos del medio perturbado de propagación experimentan desplazamientos transversales y longitudinales a la dirección de la onda, como las ondas en la superficie del agua. I.1.1 ONDAS TRANSVERSALES VIAJERAS Considerando un pulso que se desplaza hacia la derecha en una cuerda larga, tomamos una instantánea del pulso (una foto) en t=0, podemos representar la forma y posición del pulso por medio de una función matemática que depende del tiempo “t” y la coordenada “x”. Esta función describe la posición transversal “y” de un elemento de la cuerda: t=0 y(x ,0) = f (x) t>0 Como la rapidez del pulso es v, el pulso ha viajado una distancia vt en “x” transcurrido un tiempo t, suponiendo que la forma del pulso no cambia con el tiempo, la forma del pulso en t es la misma que en t=0. Con lo cual podemos decir que un elemento de la cuerda en x para t tiene la misma posición y que un elemento situado en x-vt en t=0: y (x ,t) = y (x – vt , 0) De forma general, tomando como sistema de referencia de origen en O (marco estacionario en O) podemos representar la posición transversal “y” para todas las posiciones “x” y tiempos “t”, como: y ( x , t ) = f ( x – vt ) Función de Onda Viajera que se desplaza a la derecha De forma análoga, si el pulso se desplaza hacia la izquierda, las posiciones “y” de los elementos de la cuerda están descritos por: y ( x , t ) = f ( x + vt ) Función de Onda Viajera que se desplaza a la izquierda I.1.2 ONDAS TRANSVERSALES SENOIDALES Si al extremo de una cuerda en tensión conectamos un mecanismo de oscilación vertical periódica y constante (generando un movimiento armónico simple), dicho extremo también oscila verticalmente y se transfiere energía a los demás elementos de la cuerda, creando pulsos idénticos que conforman una onda viajera senoidal (función de onda resultante igual a la función senØ), la cual es una de las más importantes y fundamentales en el estudio del movimiento de ondas. Todos los elementos de la cuerda (por ejemplo el punto P) oscilan verticalmente con una frecuencia igual a la frecuencia de oscilación del mecanismo vibratorio conectado. Si tomamos una fotografía de la onda en algún tiempo, por ejemplo: Crestas Valles Los puntos más altos de desplazamiento de los elementos de la cuerda se denominan Crestas de la onda. Así mismo, Los puntos más bajos se denominan Valles. La distancia desde la posición original de un elemento de la cuerda (y=0) hasta la cresta se llama Amplitud “A” de la onda. La distancia de una cresta a la siguiente se llama Longitud “λ” de la onda, la cual es la mínima distancia entre dos puntos idénticos. Si graficamos la posición “y” de un elemento de la cuerda en el tiempo, se tiene: El intervalo de tiempo en el cual ocurren dos crestas sucesivas (o dos puntos idénticos cualesquiera) se llama Período “T”, el cual es el tiempo en el cual un elemento completa un ciclo (igual en toda la cuerda y constante) El número de crestas (o valles, u otro punto cualquiera) que ocurren en un punto por unidad de tiempo se denomina Frecuencia “f”, donde la frecuencia es el inverso del período (f=1/T). Para t=0, la función de onda debe ser del tipo y(x,0) = Asen(ax), donde A es la amplitud y a es una constante a determinar. Para x=0, se tiene que y(0,0) = Asen(0) = 0, El siguiente valor de x para el cual y=0 es en x=λ/2: y ( λ , 0 ) = A sen( a λ ) = 0 2 2 Lo cual ocurre si a(λ/2) = л, entonces a=2л/λ y ( x , 0 ) = A sen( 2л x ) λ Conocido el valor de la constante a, si la onda se mueve a la derecha con rapidez v constante (cuyo valor determinará en el próximo punto), la función de onda para un tiempo posterior será: y ( x , t ) = A sen 2л (x – vt) λ La onda viaja una distancia λ en un período T (v= λ /T): y ( x , t ) = A sen 2л ( x – t ) λ T Se definen dos nuevas cantidades, k=2л/λ como número de onda angular y w=2л/T como frecuencia angular: y ( x , t ) = A sen (kx – wt) Función de Onda Senoidal Podemos expresar la rapidez v de una onda senoidal utilizando v=λ/T, f=1/T y w=2л/T: v= λf = w/k Rapidez de Onda Senoidal La ecuación anterior de función de onda senoidal considera que y=0 para t=0 y x=0, lo cual no necesariamente siempre ocurre, si agregamos un término Ø a la ecuación llamado constante de fase, nos indica la posición inicial “y” para x=0 y t=0: y ( x , t ) = A sen (kx – wt + Ø ) Expresión general para Onda Senoidal viajera a la derecha Analizando el movimiento de los elementos de la cuerda: y ( x , t ) = A sen (kx – wt + Ø ) La rapidez transversal (en “y”) por definición es: vy= dy / dt La aceleración transversal (en “y”) por definición es: ay= dvy / dt vy= dy/dt (x=constante) = ∂y/∂t = – w A cos(kx – wt+Ø) Vy máx= w A ay= dvy/dt (x=constante) = ∂vy/∂t = – w2 A sen(kx – wt+Ø) ay máx= w2 A Rapidez transversal de los elementos de la cuerda Aceleración transversal de los elementos de la cuerda I.2 RAPIDEZ DE ONDAS EN CUERDAS Considerando un pulso que se mueve a la derecha con una rapidez constante v (no consideramos el fenómeno de dispersión) en una cuerda que esta sometida a una tensión T determinada (si no existe ninguna tensión en la cuerda no se puede propagar una onda a través de ella) Analizando el movimiento un elemento de la cuerda ∆s como muestra la figura, forma un arco aproximado de radio R: Dicho elemento solo tiene aceleración vertical, la cual es radial o centrípeta debido a que es un movimiento de forma curvilínea (arco de radio R). Amplificando el elemento y elaborando su diagrama de fuerzas: v Efectuando sumatoria de fuerzas en los ejes coordenados, en un marco inercial de referencia junto con la onda (marco con velocidad constante, viajamos con la onda) considerando una velocidad v tangencial en ese elemento ∆s: ΣFx = TcosØ – TcosØ = 0 (El elemento solo oscila verticalmente) ΣFy = –2TsenØ = –maR Si la altura del pulso es pequeña comparada con la longitud de la cuerda, el ángulo Ø es pequeño y senØ~Ø. Si suponemos además que la tensión no es afectada por el pulso (T es la misma en todos los puntos de la cuerda: ΣFy = 2TØ = maR aR=v2/R y m=µ∆s Donde µ es la densidad lineal de masa de la cuerda (masa por unidad de longitud), la cual al multiplicar por la longitud del elemento ∆s (arco de circunferencia, L=R2Ø) arroja el valor de la masa m de dicho elemento. ΣFy = 2TØ = maR 2TØ = µ(R2Ø) v2 R v= T µ 2TØ = µ∆s v2 R T = µ v2 Velocidad (rapidez) de una onda en una cuerda Es importante señalar que el análisis anterior no considera una forma particular para el pulso (forma general), cualquier pulso generado en una cuerda bajo las condiciones supuestas viaja con dicha velocidad sin que cambie su forma en el tiempo. Empíricamente se puede demostrar lo anterior, la velocidad de cualquier onda que se propaga en un medio físico sigue la expresión: v= Propiedades elásticas del medio Propiedades inerciales del medio I.3 ENERGÍA EN ONDAS Una de las características fundamentales de las ondas es que transfieren energía, si colgamos una masa en una cuerda estirada (bajo tensión) y viaja un pulso por la cuerda: Al pasar la onda por el punto donde está la masa, le transfiere en energía cinética que se transforma en energía potencial (sube y baja) y viceversa. Si consideramos una onda senoidal en una cuerda, la fuente de energía es algún mecanismo que genera la onda, el cual realiza trabajo sobre el extremo de la cuerda, y la energía se propaga a través de toda su longitud. Analizando el movimiento de una elemento de cuerda de masa ∆m y una longitud ∆x, su energía cinética es: Ec = 1 ∆m vy2 2 Ec = 1 (µ∆x) vy2 2 dEc = 1 (µdx) vy2 2 Si ∆x tiende a cero: Donde vy es la velocidad transversal del elemento, vy = –wAcos(kx–wt+Ø) dEc = 1 µw2A2cos2(kx–wt+Ø)dx 2 Si integramos esta expresión en una longitud de onda λ, se obtiene la energía cinética total de todos los elementos diferenciales de la cuerda en una longitud de onda: Para simplificar la solución, podemos realizar la integración para t=0 y Ø=0, el resultado final es una constante y no es afectado por dichos valores, como se demostrará a continuación: λ 0 λ λ dEc = 1 µw2A2cos2(kx)dx = 1 µw2A2 cos2(kx)dx 2 2 0 0 Por métodos de integración: Ecλ = 1 2 µw2A2 x + sen2kx 2 4k λ/2 λ 0 = 1 µw2A2λ 4 Además de energía cinética, en una longitud de onda existe energía potencial de todos los elementos del medio (por los desplazamientos y fuerzas verticales desde la posición de equilibrio), si efectuamos el mismo análisis se obtiene que la energía potencial total es el mismo valor que la energía cinética total: Epλ = 1 µw2A2λ 4 Como energía mecánica es igual a cinética más potencial, la energía total de los elementos de la cuerda en una longitud de onda es: Emλ= 1 µw2A2λ + 1 µw2A2λ = 1 µw2A2λ 4 4 2 Si esta es energía total en una longitud de onda (que corresponde a un período de oscilación), como la onda viaja a través de la cuerda la tasa de transferencia de energía o potencia de la onda es: P =E =1 2 t µw2A2 λ T v P = 1 µw2A2 v 2 Potencia de una Onda I.4 ECUACIÓN DE ONDA Las funciones y(x,t) que representan las ondas que viajan en una cuerda, son soluciones particulares de una ecuación general que describe el movimiento de todas las ondas viajeras en una cuerda, llamada ecuación de onda. Consideremos una cuerda bajo una tensión T a través de la cual pasa cualquier tipo de onda viajera, y analicemos un pequeño segmento de la cuerda de longitud ∆x: ΣFy = TsenØB – TsenØA = may Al ser Ø pequeño, senØ ~ tanØ, la tangente de un ángulo se mide como ∆y/∆x, para elementos infinitesimales tanØ=dy/dx, como “y” depende de dos variables (tiempo y coordenada en “x”), analizamos la tangente parcialmente respecto a “x”: ΣFy = T(senØB – TsenØA) = T [(∂y/∂x)B – [(∂y/∂x)A] = may Tomamos la masa del elemento como µ∆x y ay=(∂2y/∂t2) µ∆x ∂2y = T [(∂y/∂x)B – [(∂y/∂x)A] ∂t2 µ ∂2y = [(∂y/∂x)B – [(∂y/∂x)A] T ∂t2 ∆x Recordando la definición de la derivada, de cualquier función: ∂f = lim f(x+∆x) – f(x) ∆x ∂x 0 ∆x Asociando esta última expresión con la anterior: µ ∂ 2y = ∂ 2 y T ∂t2 ∂x2 Ecuación de onda para una cuerda Utilizando v= T/µ ∂2 y = 1 ∂2 y ∂x2 v2 ∂t2 Ecuación de onda general A pesar de obtener esta ecuación a partir de una onda transversal en una cuerda, esta expresión se aplica a varios tipos de ondas viajeras, como ondas longitudinales de sonido y ondas electromagnéticas. I.5 REFLEXIÓN Y TRANSMISIÓN DE ONDAS Cuando existe un cambio en el medio físico a través del cual se propaga una onda, como cambio en la densidad del medio, un borde o una frontera con características que modifican el viaje de la onda a través del medio, ocurre reflexión y/o transmisión de la onda. Si consideramos un pulso que viaja a través de una cuerda que está rígidamente unida a un soporte fijo en un extremo , el pulso experimenta reflexión: Si consideramos un pulso que viaja a través de una cuerda que está libre de moverse verticalmente en un extremo mediante de un anillo sin fricción (como muestra la figura), el pulso experimenta reflexión: En los dos casos anteriores la frontera es totalmente fija o totalmente libre, si tenemos un caso intermedio, por ejemplo, una cambio de menor a mayor densidad en la cuerda, parte del pulso se transmite y parte se refleja: O un cambio de mayor a menor densidad en la cuerda: