Capitulo 7 part 2

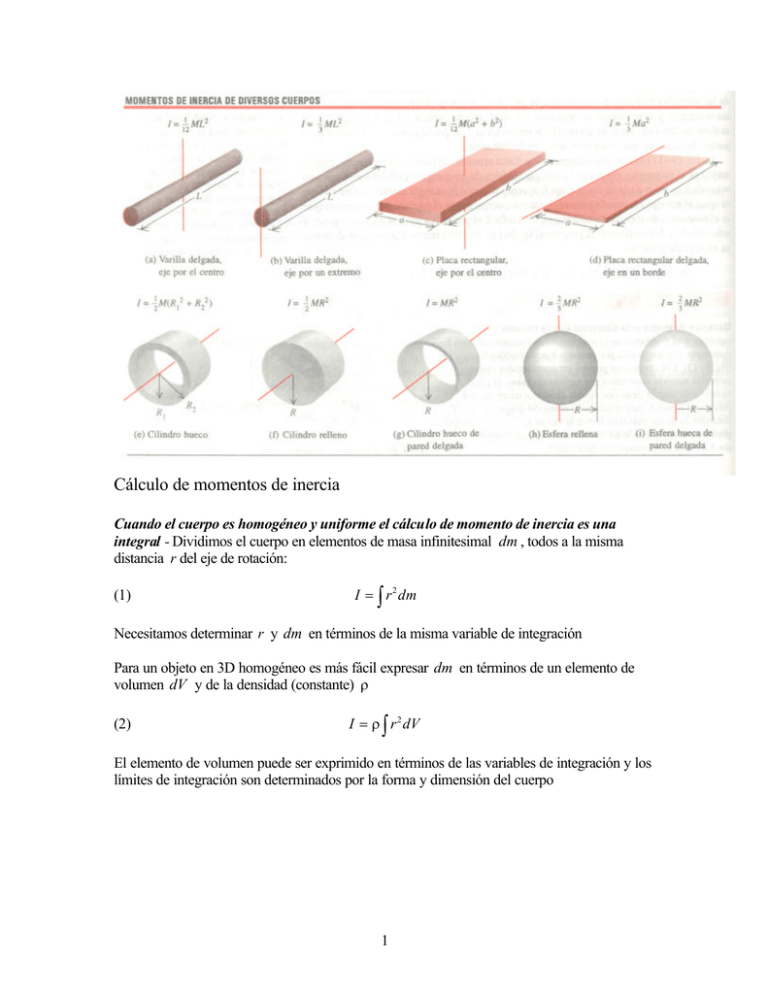
Cálculo de momentos de inercia
Cuando el cuerpo es homogéneo y uniforme el cálculo de momento de inercia es una
integral - Dividimos el cuerpo en elementos de masa infinitesimal dm , todos a la misma
distancia r del eje de rotación:
(1)
I = ∫ r 2 dm
Necesitamos determinar r y dm en términos de la misma variable de integración
Para un objeto en 3D homogéneo es más fácil expresar dm en términos de un elemento de
volumen dV y de la densidad (constante) ρ
(2)
I = ρ ∫ r 2 dV
El elemento de volumen puede ser exprimido en términos de las variables de integración y los
límites de integración son determinados por la forma y dimensión del cuerpo
1
Ejemplo #1 Barra delgada uniforme
Sección de masa dm de longitud dx a una
distancia x de O
Densidad uniforme:
dm dx
=
M
L
⇒ dm =
M
dx
L
Usando I = ∫ r 2 dm :
M
I = ∫ x dm =
L
2
∫
L −h
−h
L−h
M  x3 
1
x dx ⇒ I =
= M L2 − 3Lh + 3h2
 
L  3  −h
3
2
(
)
1
Para h = 0 (extremo izquierda) I = ML2 , la misma respuesta para h = L
3
L
1
⇒ I = ML2 , mucho mas bajo (de hecho un mínima) :
2
12
2
dI
L
d I
= − 3L + 6h = 0 ⇒ h = , y
= +6 > 0
dh
2
dh 2
Si el eje pasa por el centro: h =
2
Ejemplo #2 Cilindro hueco o relleno
Escogemos como elemento de volumen una capa
cilíndrica delgada de radio r y espesor dr con
longitud L
El volumen es similar a una lámina plana de espesor
dr longitud L y anchura 2π r .
⇒ dm = ρ dV = ρ 2π rLdr
I = ∫ r 2 dm = ∫ r 2 ρ 2π rLdr
R2
R1
R2
⇒ I = 2πρ L∫ r 3dr =
R1
2πρ L 4
πρ L 2
R2 − R14 =
R2 − R12
4
2
(
)
(
)( R
2
2
+ R12
)
Como el volumen esta dado por: V = π L ( R22 − R12 )
La masa es igual a: M = ρV = ρπ L ( R22 − R12 ) ⇒ I =
Si el cilindro no es hueco: R1 = 0 y R2 = R ⇒ I =
(
1
M R22 + R12
2
)
1
MR 2
2
Si la pared es muy delgada: R1 ≈ R2 = R ⇒ I = MR 2
Podríamos haber predicho este último resultado, porque en un cilindro de pared delgada, toda
la masa está a la misma distancia r = R
⇒ I = ∫ r 2 dm = R 2 ∫ dm = MR 2
Observe que el momento de inercia depende solamente de la distribución radial de la masa no
de su distribución a la largo del eje
3
Ejemplo #3 Esfera uniforme de radio R
Dividimos la esfera en discos delgados de espesor dx con radio r = R 2 − x 2
El volumen: dV = π r 2 dx = π ( R 2 − x 2 ) dx ;
Del Ej. 9.12: dI =
1 2
1
r dm =
2
2
(
R 2 − x2
La masa: dm = ρ dV = ρπ ( R 2 − x 2 ) dx
) πρ ( R − x ) dx 
⇒ dI =
2
2
πρ 2
R − x2
2
(
2
)
2
dx
Integrando de x = 0 a x = R , obtenemos el momento de inercia del hemisferio derecho
Por simetría, el momento de inercia total debe ser el doble:
I =2
πρ
2
∫ (R
R
0
2
)
2
− x 2 dx ⇒ I =
8πρ 5
R
15
4
Como M = ρV = ρ π R3
3
⇒I =
2
MR 2
5
Observe que el momento de inercia de una esfera sólido de masa M y radio R es menor que
el de un cilindro sólido con misma masa y radio
La razón es que una proporción mayor de la masa de la esfera es cerca del eje è
distribución simétrica tiene menos inercia
4
Traslación y rotación combinadas: relación de energía
En el espacio-tiempo los objetos rígidos tiene al
mismo tiempo movimiento de traslación y
rotación è la energía es la suma de de la energía
de los dos movimientos (equipartición de
energía)
Cada movimiento de un cuerpo rígido puede
representarse como una combinación de un
movimiento de traslación del centro de masa y
un movimiento de rotación alrededor de un eje
que pasa por el centro de masa del cuerpo
(referencial relativo)
La energía cinética de un cuerpo rígido con movimiento de traslación y rotación es la suma
1
1
2
de una parte Mvcm
asociado al centro de masa y una parte I cmω 2 asociada al movimiento
2
2
de las partículas en torno de un eje pasando por el centro de masa
K=
(3)
1
1
2
Mvcm
+ I cmω 2
2
2
Demostración
Consideramos el movimiento de una partícula de masa mi :
r r
r
vi = vcm + v′i
r
Donde v′i es la velocidad de rotación relativa al centro de
1
r r
masa – su energía cinética Ki = mi ( vi ⋅ vi ) se decompone en
2
Ki =
1
r
r
r
r
1 r r
r r r r
mi ( vcm + vi′ ) ⋅ ( vcm + vi′ ) = [vcm ⋅ vcm + 2vcm ⋅ vi′ + vi′ ⋅ vi′]
2
2
=
1 2
r r
 v + 2vcm ⋅v i′ + vi′2 

cm

2
5
La energía cinemática total es la suma sobre todas las partículas
(4)
1
r
r
1
2
K = ∑ Ki = ∑ mivcm
+ vcm ⋅ ∑ mi v 'i + ∑ mi v′i 2
i
i 2
i
i 2
En el segundo términos la expresión
r
∑mv'
i
i
= 0 porque es la velocidad del centro de masa
i
relativo al centro de masa
En el primero término
∑m
i
= M y como por definición vi′ = rω
⇒ vi′2 = ri2ω 2
i
i
(5)
K=
1
 2 1

1
1
2
mi  vcm
+ ∑ miri2 ω 2 = Mvcm
+ I cmω 2
∑

2 i
2i
2
2


Un caso particular importante = rodar sin deslizar
En cualquier instante podemos pensar que la rueda gira alrededor de un eje de rotación
instantáneo que pasa por el punto de contacto en el suelo
Como el punto que toca el suelo debe ser momentáneamente en reposo:
r
r
r
r
r r
v1 = 0 , ⇒ v1′ + vc m = 0 o v1′ = −vcm ⇒ v1′ = Rω
La condición para rodar sin deslizar
(6)
vcm = Rω
6
En torno del eje de rotación en contacto con el suelo ⇒ K =
1
I1ω 2
2
Pero por el teorema de los ejes paralelos: I1 = I cm + MR 2
⇒K=
(
)
1
1
1
1
1
1
2
I1ω 2 =
I cm + MR 2 ω 2 = I cmω 2 + MR 2ω 2 = I cmω 2 + Mvcm
2
2
2
2
2
2
Ejemplo #4 - Casco cilíndrico hueco que rueda
El cilindro tiene una masa M un radio R y rapidez vcm
I cm = MR 2 y por la condición vcm = Rω ⇒ ω =
vcm
R
2
1
1
v 
2
2
La energía cinética: K = Mvcm
+ MR2  cm  = Mvcm
2
2
 R 
(
)
La mitad de la energía es traslacional y la otra es rotacional
Si el cuerpo cambia de altura, debemos incluir el potencial gravitacional U = Mgycm
Demostración:
Para un cuerpo rígido la energía potencial de un elemento de masa mi es mi gyi
La energía potencial gravitacional total es: U = ∑ mig yi = g ∑ mi yi
i
∑m y ∑ m y
=
M
∑m
i
Por definición del centro de masa:
i
i
i
i
i
i
i
= ycm ⇒ ∑ mi yi = Mycm
i
i
Donde ycm es la coordenada vertical del centro de masa del sistema
De modo que para un cuerpo de masa total M, la energía potencial gravitatoria es
(7)
U = Mgycm
La inercia es solamente la suma de las masas, no depende de su distribución en el
espació – todo se pasa como si la masa total estaba concentrada en un punto = centro
de masa del sistema
7
Ejemplo #5 - Cuerpos rodantes
Consideramos diversos cuerpos rígidos de misma masa M rolando sobre un plano inclinado.
¿Cual cuerpo llegara a bajo del plano el primero?
Asumimos que los cuerpos no resbalan y que no hay fricción
Como cada cuerpo parte del reposo a altura h
Arriba: K1 = 0 y U1 = Mgh
Abajo: U 2 = 0 y K2 =
Sin resbalar ⇒ ω =
1
1
2
Mvcm
+ I cmω 2
2
2
vcm
R
Los momentos de inercia puede se escribir como I cm = cMR 2 donde 0 < c < 1 depende de la
geometría del cuerpo
Aplicamos el principio de la conservación de la energía:U1 + K 1 = U2 + K2
2
1
1
v
1
2
2
Mgh = Mvcm
+ cMR2 cm2 = (1 + c ) Mvcm
2
2
R
2
2 gh
(1 + c )
⇒ vcm =
8
La velocidad lineal no depende de la masa o del radio
Depende de la distribución de masa en torno de un eje pasando por el centro de masa
•
Un cuerpo con c menos tienes mayores velocidades lineal
•
Por orden de velocidad lineal creciente I cm = cMR 2
1. cilindro hueco con pared delgada ( c = 1 ⇒ v cm = gh )
2
⇒ vcm =
3
2. esfera hueca con pared delgada ( c =
3. cilindro sólido ( c =
4. esfera sólida ( c =
1
⇒ vcm =
2
4 gh
)
3
2
10 gh
⇒ vcm =
)
5
7
9
6 gh
)
5
r
Por un cuerpo rígido con masa M , la aceleración linear acm es la misma que si toda la masa
estaba concentrada en un punto
(8)
r
∑F
ext
r
= Macm
Similarmente, para el movimiento de rotación alrededor del centro de masa
(9)
∑τ ext = Icmα
La relación es valida aunque el eje de rotación se mueve si :
1. El eje que pasa por el centro de masa es un eje de simetría
2. El eje no debe cambiar de dirección
Cabe señalar que en general este eje de rotación móvil no esta en reposo en un marco de
referencia inercial
Si el cuerpo tiene movimiento de traslación y rotación necesitamos dos ecuaciones
independientes para resolver los problemas dinámicamente
10
Ejemplo #6 - Esfera rodante
Una bola de bolos sólido rueda sin resbalar por la rampa de retorno
La rampa hace un ángulo β con el piso - buscamos la aceleración acm
La ecuación del movimiento de traslación:
∑F
x
= Mgsenβ + ( − f ) = Mac m
El momento de inercia de la bola: I cm =
2
MR 2
5
Solo la fuerza de fricción produce un momento de
torsión
La ecuación del movimiento de rotación: ∑ τ = fR = I cmα =
Sin resbalar ⇒ acm = Rα deducimos que f =
2
MR 2α
5
2
Macm
5
2
Despejamos f en la ecuación de traslación Mgsenβ − Macm = Macm
5
⇒ acm =
5
gsenβ
7
Substituimos en la expresión por la fricción: f =
La aceleración es
2 5
 2
M  gsenβ  = Mgsenβ
5 7
 7
5
de su valor si la bola pudiera deslizarse sin fricción
7
11
Como f es la fuerza de fricción estática, podemos deducir cual seré el coeficiente de
fricción µ s mínimo necesario para evitar el deslizamiento
La fuerza normal η = Mg cos β è La fuerza máxima de fricción estática es µsη
2
f 7 Mg senβ 2
⇒ µs = =
= tan β
η
Mg cos β
7
Al aumentar el ángulo µ s debe ser mayor
Cuando la bola comienza a resbalar vcm ≠ Rω y acm ≠ Rα
Tenemos dos ecuaciones por tres incógnitas acm , f y α
Necesitamos considerar la fricción cinemática
Si la bola desciende una distancia h al bajar la rampa su desplazamiento es
La rapidez de la bola en la basa vcm =
h
senβ
10
2
gh esto es el mismo resultado que antes con c =
7
5
12
Fricción por rodamiento
Si la superficie y el cuerpo son rígidos no hay fricción por rodamiento
Pero si la superficie es amontona delante de la esfera, por estas deformaciones la fuerza de
contactos sobre la esfera actúan en un área y la fuerza normal ejerce un momento de
torsión que se opone a la rotación
Además hay cierto deslizamiento debido a la deformación causando una perdida de energía
Esto es la fricción por rodamiento (otro ejemplo es un cuerpo deformable como un
neumático)
13