Anuncio

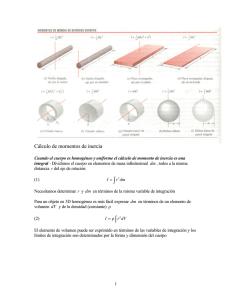
4.- Se tiene un sistema de partículas formado por tres masas puntuales de valores m1 = m, m2 = 3m y m3 = 2m. La posición de las masas en el instante inicial y las fuerzas externas a las que se ven sometidas (de módulo constante F) son las que se muestran en la figura. El centro de masas (CM) se está trasladando con una velocidad VCM = 3 i (m/s) con respecto a O. a) ¿Puede el CM describir una trayectoria curva?. Calcular el momento lineal del sistema con respecto a O, ¿es contante?. ¿Se conserva el momento angular del sistema con respecto a O?. G ∑F ext G = M aCM G ∑F ext G G G = F (− j ) + F j = 0 ⇒ aCM = 0 - El CM no puede describir una trayectoria curva (aceleración normal no nula) porque se mueve sin aceleración. G G G G - Momento lineal p = M vCM M = m1 + m2 + m3 = 6m vCM = 3 i G G G G G G p = 6m3i = 18 m i (kg m / s ) aCM = 0 ⇒ vCM cte ⇒ p cte G G G G G G dL G - ¿Momento angular L cte? = ∑τ ext = F (− j ) × 3 j + Fj × 4 i ≠ 0 dt G L no se conseva porque los momentos de las fuerzas externas no se cancelan. b) Si en un instante dado las velocidades de las masas m1 y m2 son respectivamente v1 = - 12 j y v2 = 6 i + 8 j (en m/s), calcular la energía cinética interna del sistema en ese instante. Ec = Ecint + Ecorb Ecorb = 1 1 2 = 27 m ; Ec = ∑ mi vi2 M vCM 2 2 G G v1 = −12 j G G G v2 = 6 i + 8 j v1 = 12 v2 = 100 vCM = 3 G G Calculamos v3 a partir de la definición de vCM (cte) G G G G G G G G m1v1 + m2 v2 + m3v3 m (−12 j ) + 3 m (6 i + 8 j ) + 2 m v3 G vCM = = = 3i 6m 6m G G G G G G G G G −12 j + 18 i + 24 j + 2v3 = 18 i ⇒ 12 j + 2v3 = 0 ⇒ v3 = − 6 j Ec = 1 1 1 m122 + 3m100 + 2m 62 = 258m 2 2 2 Ecint = Ec − Ecorb = 258m − 27 m = 231m ( J ) c) Calcular el vector posición del CM en función del tiempo. G G G G rCM = ∫ vCM dt = r0 + vCM t G G G ya que vCM es constante vCM = 3i . G r0 vector posición del CM en t = 0 G G G G G G G G G m1r01 + m2 r02 + m3 r03 m 3 j + 3m (−2 j ) + 2m 4i 8i − 3 j 4 G 1 G r0 = = = = i− j 6m 6m 6 3 2 G ⎛4 4G 1 G G ⎞G 1G rCM = i − j + 3 t i = ⎜ + 3 t ⎟ i − j ( m) 3 2 2 ⎝3 ⎠ d) Si además actuáse sobre m2 otra fuerza externa de valor F= - 2 F i calcular la aceleración del CM. Razonar si se conservan entonces el momento lineal y el momento angular del sistema. G G - ∑ Fext = M aCM G G Fext −2 Fi − F G G i (m / s 2 ) ⇒ aCM = = = M 6m 3m G G dp G = ∑ Fext ≠ 0 ⇒ p no se conserva dt G G G G G G G - ∑τ ext = 4i × Fj + ( −2 j × 2 F (−i ) ) = 4 F k − 4 F k = 0 G G dL G = ∑τ ext = 0 ⇒ L sí se conserva dt