Sistemas Digitales I - Sistemas Digitales UIS

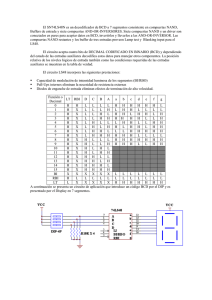
UNIVERSIDAD INDUSTRIAL DE SANTANDER
Sistemas Digitales I
Taller No1
Profesor: Carlos A. Fajardo
Mayo de 2015
Temas: Representación digital de los Datos, Algebra de Boole, Funciones Lógicas, Introducción a
VHDL, Implementación de circuitos combinacionales usando VHDL.
Profesor: Carlos A. Fajardo
Sección 1: Representación digitales de los datos.
1. Realice las siguientes conversiones:
a.
b.
c.
d.
e.
100,1562510 a Binario punto fijo con el mínimo de bits posible.
C1420000FLOAT a Decimal
-125,610 a flotante precisión simple
-1210 a Complemento a 2 con 5 bits
9172 a BCD
2. Realice las siguientes operaciones en la base indicada, mostrando claramente los acarreos:
a.
b.
c.
d.
e.
4356 +255 6
2234 + 3324
1328 +276 8
2637 + 5627
A26B12 + 5AAB12
3. Encuentre, si es posible, el valor de la base x en la que se encuentra escrito el siguiente
número (x es número entero positivo):
a. 321x = 2125
b. 198x = 4447
4. Realice las operaciones indicadas en complemento a 2 con 6 bits. (Sugerencia: primero
escriba los números en complemento a 2 y luego realice las operaciones).
a. -1010 + 3010
b. -1A16+ 1216
5. Realice las operaciones indicadas: Primero en punto fijo (3:3). Segundo en complemento a 2
con 6 bits. (Sugerencia: primero escriba los números en complemento a 2 y luego realice las
operaciones).
a. -2.2510 + 2.510
b. -3.14 + 2.24
6. Determine el rango de valores numéricos que pueden escribirse en palabras de 8 bits si el
número está escrito en:
a. Signo y magnitud
b. Complemento a 2
c. BCD
d. Punto fijo con 3 bits en la parte entera y 5 bits en la parte decimal
7. Determine el rango de valores numéricos que pueden escribirse en palabras de 16 bits si el
número está escrito en:
a. Signo y magnitud
b. Complemento a 2
c. BCD
d. Punto fijo con 12 bits en la parte entera y 4 bits en la parte decimal
1
Profesor: Carlos A. Fajardo
Sección 2: Algebra de Boole y Funciones Lógicas
8. Diseñe un circuito SOP, empleando el menor número de compuertas AND, OR y NOT. La
entrada al circuito es un número en BCD y la salida debe indicar si el número es divisible entre
3.
9. Diseñe un circuito SOP, empleando el menor número de compuertas AND, OR y NOT, cuya
entrada sea un número de 3 bits en complemento a 2 y su salida sea su correspondiente
representación en magnitud y signo.
10. Usando mapas de Karnaugh encuentre la mínima expresión POS (Producto de Sumas) de la
función F.
F( A, B ,C , D )   m (0,1,5,7,13,15)
11. Usando mapas de Karnaugh encuentre la mínima expresión SOP (suma de productos) de la
función F. Donde d, son condiciones no importa (don’t care).
F( A, B ,C , D )   m (0,1,2)   d (3,8,9,10,11,12 )
12. Implemente la siguiente función boolena con el mínimo posible de compuertas AND, OR y
NOT.
̅ 𝑪 + 𝑨𝑩
̅𝑪
̅ + 𝑨𝑩𝑪 + 𝑨
̅𝑩
̅𝑪
𝐹(𝐴,𝐵,𝐶) = 𝑨𝑩
13. Implemente la siguiente función boolena con el mínimo posible de compuertas AND, OR y
NOT.
̅𝑪
𝐹(𝐴,𝐵,𝐶) = 𝑨 𝑥𝑜𝑟 𝑪 + 𝑨𝑩 + 𝑨𝑩
14. Usando mapas de Karnaugh encuentre la mínima expresión POS (Producto de Sumas) de la
función F. Donde d, son condiciones no importa (don’t care).
F( A, B ,C , D )   m (5,7,13,15)   d (0,4,8,12 )
15. Usando mapas de Karnaugh encuentre la mínima expresión POS (Producto de Sumas) de la
función F.
F( A, B ,C , D , E )   m (0,2,5,7,13,15,21,23,29,31)
16. Usando mapas de Karnaugh encuentre la mínima expresión POS (Producto de Sumas) de la
función F. Donde d, son condiciones no importa (don’t care).
F( A, B ,C , D )   m (0,2,11,13,14,15,27,26)   d (,8,10,16,18,24,26,30)
17. Implemente la función G( A, B ,C , D ) 

m
(2,4,7,13,14) , utilizando
a. Un multiplexor de 8 a 1
2
Profesor: Carlos A. Fajardo
b. Un multiplexor de 4 a 1
18. Implemente la función G( A, B ,C , D , E ) 
 (0,2,3,4,11,17,24,25,27,30,31) utilizando un multiplexor
de 8 a 1
19. Diseñe un circuito SOP, empleando el menor número de compuertas AND, OR y NOT, cuya
entrada sea un número de 3 bits en signo y magnitud y la salida sea su correspondiente
representación en complemento a 2.
20. Diseñe un circuito POS, empleando el menor número de compuertas AND, OR y NOT, cuya
entrada sea un número de 3 bits en complemento a 2 y la salida sea su correspondiente
representación en signo y magnitud.
21. Diseñe un decodificador de 2 a 4 de lógica negada con enable activo en bajo. El diseño debe
utilizar el mínimo posible de compuertas lógicas AND, OR y NOT.
22. Diseñe un comparador de dos números de tres bits cada uno, el cual debe indicar si los dos
números son iguales. (La salida debe ser 1 si A y B son iguales y 0 si son diferentes). Ver figura
1.
Figura 1: Comparador de igualdad
23. Diseñe un comparador de dos números de tres bits cada uno, el cual debe indicar si un número
es mayor (La salida F debe ser 1 si A es mayor que B o 0 si es menor o igual, ver figura 2).
Figura 2: Comparador Mayor que.
24. Diseñe un multiplexor de 2 a 1, usando únicamente compuertas NOR.
contener el mínimo posible de compuertas NOR.
Su diseño debe
3
Profesor: Carlos A. Fajardo
25. El display de 7 segmentos de la figura 3, requiere un nivel BAJO para encender cada segmento
(ánodo común). Diseñar un circuito POS con el mínimo de compuertas posibles cuya entrada
sea un número en BCD y la salida sea la lógica del segmento B.
Figura 3: Display de 7 segmentos
26. El display de 7 segmentos de la figura 3, requiere un nivel BAJO para activar cada segmento
(ánodo común). Diseñar un circuito SOP con el mínimo de compuertas posibles cuya entrada
sea un número en BCD y la salida sea la lógica del segmento G.
27. El display de 7 segmentos de la figura 3, requiere un nivel ALTO para activar cada segmento
(cátodo común). Diseñar un circuito SOP con el mínimo de compuertas posibles cuya entrada
sea un número en BCD y la salida sea la lógica del segmento D.
4
Profesor: Carlos A. Fajardo
Sección 3: Implementación de funciones combinacionales en VHDL
Ejercicios 28 – 31:Suponga que usted es un sintetizador de VHDL y debe sintetizar los siguientes
circuitos. Ustede debe:


Verificar la sintaxis, si la descripción VHDL tiene errores indique cuáles son.
Si la descripción NO tiene errores de sintaxis muestre el RTL. El diagrama RTL debe estar en
función de bloques combinacionales como sumadores, restadores, comparadores,
multiplexores, compuertas lógicas, etc.
28.
29.
5
Profesor: Carlos A. Fajardo
30.
31.
6
Profesor: Carlos A. Fajardo
7
Profesor: Carlos A. Fajardo
Respuestas a los ejercicios seleccionados
1.
a.
b.
c.
d.
e.
1100100,000101
-12,125
C2FB3333
10100
1001 0001 0111 0010
3.
a. Base 4
b. Base 11
5.
101,110
a. 010,100
̅̅̅̅̅̅̅̅̅̅̅
000,010
100,110
b. 010,100
̅̅̅̅̅̅̅̅̅̅̅
111,010
6.
a. 𝐹 = 𝐵𝐷
b. 𝐹 = 𝐵̅
c. 𝐹 = 𝐴̅𝐵̅𝐶̅ + 𝐵𝐷
7.
A2
0
0
0
0
1
1
1
1
A1
0
0
1
1
0
0
1
1
A0
0
1
0
1
0
1
0
1
F3 F2 F1 F0
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
1 1 0 0
1 0 1 1
1 0 1 0
1 0 0 1
𝐹3
𝐹2
𝐹1
𝐹0
= 𝐴2
= 𝐴2 ̅̅̅
𝐴1 ̅̅̅
𝐴0
= 𝐴2 ̅̅̅
𝐴1 𝐴0 + ̅̅̅
𝐴2 𝐴1 + 𝐴1 ̅̅̅
𝐴0
= 𝐴0
8
Profesor: Carlos A. Fajardo
17.
18. Error de sintanxis.
9