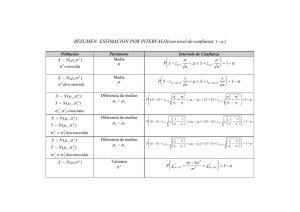
contrastes de hipotesis e intervalos de confianza

PRÁCTICAS Nº 10 Y 11
CONTRASTES DE HIPOTESIS E
INTERVALOS DE CONFIANZA
ESTADÍSTICA E INTRODUCCIÓN A LA ECONOMETRÍA
2º LADE
CURSO 2008-09
Profesorado:
Prof. Dra. Mª Dolores González Galán
Prof. M ª Mar Romero Miranda
Prof. Mª Teresa Álvarez Bravo
Prof. Antonio Hernández Moreno
Prof. Miguel Ángel Rivas Carrasco
Estadística e Introducción a la Econometría
Práctica 10
Para el desarrollo de esta práctica seguiremos la ayuda del programa SPSS y utilizaremos como
ejemplos los datos de los ejercicios 5.12 y 5.18 del libro de Casas Sánchez, J.M. (1998):Problemas de
estadística. Descriptiva, probabilidad e inferencia, Edit. Pirámide.
1.
PRUEBA DE HIPÓTESIS E INTERVALO DE CONFIANZA PARA LA
MEDIA DE UNA POBLACIÓN NORMAL.
Analizar/ Comparar Medias/ Prueba T para una muestra
El procedimiento Prueba T para una muestra contrasta si la media de una sola variable
difiere de una constante especificada. Nos permite realizar dicho contraste así como
obtener un intervalo de confianza para la diferencia promedio.
Ejercicio 5.12: Los niveles de audiencia (en miles de personas) de un programa de
televisión, medidos en 10 emisiones elegidas aleatoriamente, han sido los siguientes: 682,
553, 555, 666, 657, 649, 522, 568, 700, 552. Suponiendo que los niveles de audiencia
siguen una distribución normal, ¿Se podría afirmar, con un 95% de confianza, que la
audiencia media del programa es de 600.000 espectadores por programa?
Tal como se ha estudiado en teoría, el contraste sobre la media (µ) de una población
normal con varianza desconocida se basa en la distribución t de Student tal como se
indica a continuación:
Estadística e Introducción a la Econometría
Práctica 10
Sabemos también que el intervalo de confianza al 100(1-α)% para la media (µ) de una
población normal viene dado por la expresión:
S´
S´ ⎤
⎡
−
+
x
t
x
t
;
n −1,α / 2
n −1,α / 2
⎢
⎥
n
n⎦
⎣
Procedimiento en SPSS:
Creamos nuestro fichero titulado Ejercicio Audiencia Programa Televisión que contiene
los datos de los niveles de audiencia, en una variable que llamaremos “Audiencia”. Tras
esto hacemos:
Estadística e Introducción a la Econometría
Pinchando sobre el botón Opciones, se nos despliega la siguiente ventana:
Práctica 10
Estadística e Introducción a la Econometría
Práctica 10
Resultado:
Estadísticos para una muestra
Error típ. de la
N
Niveles de audiencia (en
Media
10
Desviación típ.
610,40
media
66,076
20,895
miles de personas) de un
programa de televisión
Donde el error típico de la media es =
S´
n
Prueba para una muestra
Valor de prueba = 600
95% Intervalo de confianza para la
diferencia
Diferencia de
t
Niveles de audiencia (en
gl
,498
Sig. (bilateral)
9
,631
medias
10,400
Inferior
Superior
-36,87
miles de personas) de un
programa de televisión
(1): CONTRASTE
(2): INTERVALO DE CONFIANZA
(1): CONTRASTE:
Resuelve el siguiente contraste de hipótesis:
Ho: Nº medio de espectadores del programa = 600
H1: Nº medio de espectadores del programa ≠ 600
Es decir:
Ho: µ espectadores = 600
Ho: µ espectadores – 600 = 0
H1: µ espectadores ≠ 600
H1: µ espectadores – 600 ≠ 0
57,67
Estadística e Introducción a la Econometría
Práctica 10
El estadístico de prueba es:
t=
x − µ0
S´/ n
=
610,4 − 600
66,076 / 10
= 0,4977
La distribución t de Student en este caso tiene 9 grados de libertad y es:
t0,025= 2,262
p = 2P(t ≥ 0,4978) = 0,63061
Como el valor del nivel crítico del contraste es: p=0.63061 que es mayor que α=0.05 ⇒ el
estadístico de prueba no se encuentra en la región crítica y, por tanto, no habría suficiente
evidencia estadística como para rechazar Ho, es decir, aceptamos la hipótesis nula, de
modo que, con un 95% de confianza, podemos decir que la audiencia media del programa
es de 600.000 espectadores.
En SPSS, nos fijamos en la significación (bilateral, en este caso) o p-valor, que es 0,631
el cual comparamos con α, que en este caso hemos tomado α = 0,05. Como p > α, ya
que, 0,631 > 0,05 concluiríamos, que no podemos rechazar la hipótesis nula, por lo que
se podría aceptar que el número medio de espectadores del programa de televisión es de
600.000.
Estadística e Introducción a la Econometría
Práctica 10
(2): INTERVALO DE CONFIANZA
Podemos también construir un Intervalo de Confianza para la media sabiendo que:
t=
x−µ
~ t n −1
S
n
⎛
I.C. (µ, 1-α) = ⎜⎜ x − t n − 1 ,1 − α
⎝
/2
S
, x + t n − 1 ,1 − α
n
/2
S
n
⎞
⎟⎟
⎠
En nuestro caso, el SPSS nos da un Intervalo de Confianza para la diferencia, es decir,
para (µ-600), el cual viene dado por (-36,87; 57,67).
Para construir el intervalo de confianza para la media, tendremos que hacer (-36,87 +
600; 57,67 + 600) = (563,13; 657,67).
Otra forma de resolver el contraste planteado sobre la media sería viendo si el valor
600 se encuentra o no dentro del intervalo de confianza construido. Como si se encuentra,
podríamos afirmar que con un 95% de confianza, la audiencia media del programa es de
600.000 espectadores.
Estadística e Introducción a la Econometría
2.
Práctica 10
PRUEBA DE HIPÓTESIS E INTERVALO DE CONFIANZA PARA LA
DIFERENCIA DE MEDIAS EN POBLACIONES NORMALES.
Analizar/ Comparar Medias/ Prueba T para muestras independientes
(Estudiaremos sólo el caso en que las muestras sean independientes)
El procedimiento Prueba T para muestras independientes compara las medias de dos
grupos de casos. Para esta prueba, lo ideal es que los sujetos se asignen aleatoriamente
a dos grupos, de forma que cualquier diferencia en la respuesta sea debida al tratamiento
(o falta de tratamiento) y no a otros factores. Este caso no ocurre si se comparan los
ingresos medios para hombres y mujeres. El sexo de una persona no se asigna
aleatoriamente. En estas situaciones, debe asegurarse que las diferencias en otros
factores no enmascaren o resalten una diferencia significativa entre las medias. Las
diferencias de ingresos medios pueden estar sometidas a la influencia de factores como
los estudios y no solamente al sexo.
El programa calcula la t para varianzas iguales y distintas y realiza el contraste para las
varianzas. Para el contraste sobre las varianza el SPSS no usa la prueba F, sino la de
Levene que no asume normalidad y se puede usar para comparar varias varianzas.
Nos permite obtener además de la prueba, un intervalo de confianza para la diferencia de
medias, para lo cual debemos distinguir los casos en que:
a)
se asumen varianzas iguales:
Estadística e Introducción a la Econometría
I.C. al 100(1-α)%
para µx- µy
Práctica 10
⎡
1 1
1 1⎤
+ ; ( x − y ) + tn + m−2,α / 2 s
+ ⎥
⎢( x − y ) − tn + m−2,α / 2 s
n
m
n
m⎦
⎣
Siendo:
s=
b)
(n − 1) S´2x + (m − 1) S´2y
n+m−2
1-α
α/2
α/2
− t n + m − 2 ,α
/2
0
t n +m − 2,α / 2
no se asumen varianzas iguales:
I.C. al 100(1-α)%
para µx- µy
2
2
⎡
S´2x S´y
S´2x S´y ⎤
⎢(x − y ) − Zα / 2
⎥
+ ; (x − y) + Zα / 2
+
n
m
n
m
⎢⎣
⎥⎦
Estadística e Introducción a la Econometría
Práctica 10
Ejercicio 5.18: Se seleccionan dos muestras aleatorias e independientes del número de
puestos de trabajo creados en el último mes por diferentes empresas de dos sectores
económicos. La información suministrada por las muestras es la siguiente:
Sector A: nº de empleos: 13, 14, 21, 19, 15, 15
Sector B: nº de empleos: 18, 19, 20, 22, 31, 26.
Con el fin de conocer el impacto de las nuevas modalidades de contratación en ambos
sectores y suponiendo que el número de empleos creados siguiera en ambos sectores
distribuciones normales con varianzas iguales: ¿Podríamos afirmar con un 99% de
confianza, que ambos sectores son similares en cuanto al número medio de empleos
creados en el último mes?
Lo primero que haremos será crear nuestro fichero titulado Ejercicio Empleos por
Sectores que contiene los datos anteriores, en una variable que llamaremos “Empleos”.
Tras esto hacemos:
Estadística e Introducción a la Econometría
Procedimiento:
Práctica 10
Estadística e Introducción a la Econometría
Práctica 10
Resultados:
Estadísticos de grupo
Error típ. de la
Sector
N
Media
Nº de empleos creados en el Sector A
último mes en el
Sector B
Desviación típ.
media
6
16,17
3,125
1,276
6
22,67
4,967
2,028
correspondiente Sector
Prueba de muestras independientes
Prueba de
Levene para la
igualdad de
varianzas
Prueba T para la igualdad de medias
99% Intervalo de
Error típ.
Sig.
F
Nº de empleos
Se han asumido
Sig.
1,263
t
,287 -2,713
gl
Diferencia
confianza para la
de la
diferencia
(bilateral) de medias diferencia Inferior Superior
10
,022
-6,500
2,396 -14,092
1,092
-2,713 8,423
,025
-6,500
2,396 -14,422
1,422
creados en el último varianzas
mes en el
correspondiente
Sector
iguales
No se han
asumido
varianzas
iguales
(1): Cont. Igualdad var.
(2): Cont. Igualdad medias
(3): Int. Confza.
(1): CONTRASTE SOBRE IGUALDAD DE VARIANZAS
Se plantea el contraste sobre la igualdad de varianzas:
Ho: Varianza del nº medio de empleos creados en el último mes en el Sector A =
Varianza del nº medio de empleos creados en el último mes en el Sector B
H1: Varianza del nº medio de empleos creados en el último mes en el Sector A ≠
Varianza del nº medio de empleos creados en el último mes en el Sector B
Estadística e Introducción a la Econometría
Práctica 10
Es decir:
Ho: σ2EmpleoscreadosSectorA = σ2EmpleoscreadosSectorB
H1: σ2EmpleoscreadosSectorA ≠ σ2EmpleoscreadosSectorB
O equivalentemente:
Ho: σ2EmpleoscreadosSectorA - σ2EmpleoscreadosSectorB = 0
H1: σ2EmpleoscreadosSectorA - σ2EmpleoscreadosSectorB ≠ 0
Para dicho contraste, el SPSS nos da una significación de (p=) 0,287 > 0,01 (=α), por lo
que no habría suficiente evidencia estadística como para rechazar la hipótesis nula, es
decir, que asumiríamos entonces igualdad de varianzas.
Al asumir igualdad de varianzas, nos fijaríamos pues sólo en la fila “Se han asumido
varianzas iguales” (
)
Seguidamente, pasaríamos a resolver el contraste sobre igualdad de medias.
(2): CONTRASTE SOBRE IGUALDAD DE MEDIAS:
Se plantea en este caso el contraste:
Ho: Nº medio empleos creados en último mes en Sector A = Nº medio empleos creados
en último mes en Sector B
H1: Nº medio empleos creados en último mes en Sector A ≠ Nº medio empleos
creados en último mes en Sector B
Es decir:
Ho: µEmpleoscreadosSectorA = µEmpleoscreadosSectorB
H1: µEmpleoscreadosSectorA ≠ µEmpleoscreadosSectorB
O equivalentemente:
Estadística e Introducción a la Econometría
Práctica 10
Ho: µEmpleoscreadosSectorA - µEmpleoscreadosSectorB = 0
H1: µEmpleoscreadosSectorA - µEmpleoscreadosSectorB ≠ 0
El estadístico en este caso resulta ser:
t=
(16,16 − 22,66)
(5)3,125 + (5)4,966
2
6+6−2
2
= −2,713
1 1
+
6 6
Y la distribución una t-Student con 10 grados de libertad:
0,99
− tα /2=-3,169
0
tα /2 =3,169
cuyo nivel crítico del contraste es : p = 2 P(t ≥ −2,713) = 0,022
Como este nivel crítico p=0,022 es mayor que α=0.01, el estadístico de prueba no
pertenece a la región crítica y, por tanto, se acepta la hipótesis nula de igualdad de
medias.
En SPSS, asumiendo pues varianzas iguales, nos fijaríamos en que la significación que
tenemos para la igualdad de medias es 0,022 que no es inferior a 0,01, por lo que
concluiríamos que con un nivel de confianza del 99 %, no hay suficiente evidencia
estadística como para rechazar la igualdad de medias, es decir, podemos suponer que el
número medio de empleos creados en el último mes en los sectores A y B son similares.
Estadística e Introducción a la Econometría
Práctica 10
(3): INTERVALO DE CONFIANZA:
Podemos, tal como hemos visto, construir un Intervalo de Confianza para la diferencia de
medias, el cual nos lo proporciona igualmente el SPSS.
En nuestro ejemplo el intervalo de confianza para la diferencia de medias a un nivel de
confianza del 99 % sería (-14,092, 1,092).
Por último, comentar que para resolver el contraste sobre la igualdad de medias en
el caso de muestras independientes, también podemos hacerlo fijándonos en el intervalo
de confianza que nos proporciona el SPSS, para lo cual tendríamos que ver si dicho
intervalo contiene el valor 0 o no: si no contiene al 0, habría diferencia de medias. En caso
de contenerlo, se asume que las medias son iguales.
En nuestro caso, como el valor 0 se encuentra dentro del intervalo de confianza
construido, con un 99% de confianza, puede admitirse la similaridad en la creación de
puestos de trabajo en estos dos sectores.
Estadística e Introducción a la Econometría
Práctica 10
EJERCICIOS
EJERCICIO 1: Fichero de SPSS “Employee data”
a) ¿Se podría afirmar con una confianza del 95 % que el salario inicial medio es igual a
20.000? Hallar un intervalo de confianza para la media.
b) Resolver usando el SPSS y con un nivel de confianza del 99 % el siguiente contraste
sobre la media, e indicar así mismo un intervalo de confianza para la media:
Ho: µSalarioActual = 32.800
H1: µSalarioActual ≠ 32.800
EJERCICIO 2: Fichero “Terreno.sav”
a) ¿Se podría afirmar que el consumo medio a 120 km/h es igual para los vehículos de 4 y
6 cilindros, con un nivel de confianza del 95 %? ¿Y con un 99 %? Dar un intervalo de
confianza en ambos casos y compararlos.
b) ¿Se podría afirmar que el consumo urbano medio es igual para los vehículos de 4 y 6
cilindros, con un nivel de confianza del 95 %? ¿Qué tipo de vehículo tiene un consumo
medio urbano mayor, los de 4 o los de 6 cilindros? Dar un intervalo de confianza.