Distribucion_T
Anuncio

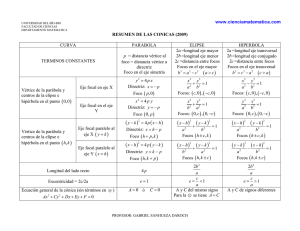
Distribución T Si el tamaño de la muestra es pequeño, los valores de s^2 fluctúan considerablemente de muestra a muestra y la distribución de la variable aleatoria (promedio -µ)/(s/n^1/2) se desvía en forma apreciable de la distribución normal estándar. se trata entonces de la distribución T donde, (promedio -µ)/(s/n^1/2) La distribución T se asemeja a la distribución Z en que ambas son simétricas alrededor de la media cero. Ambas distribuciones tienen forma de campana, pero la distribución t, varía más; cuando el tamaño de la muestra es grande, es decir cuando n ∞ las dos distribuciones son iguales. Ejemplo: Un fabricante de focos afirma que su producto durará un promedio de 500 horas de trabajo. Para conservar este promedio, esta persona verifica 25 focos cada mes. Si el valor de t cae entre –t0.05 y t0.05 , el se encuentra satisfecho con esta afirmación. Qué conclusión deberá sacar de una muestra que tiene media= 518 horas y una desviación estándar de s=40 horas? En la tabla de distribución t, se encuentra t0.05 para 24 grados de libertad. El fabricante esta satisfecho con esta afirmación si una muestra de 25 focos da un valor entre -1.711 u 1.711 (estos valores se encuentran en la tabla t). Si µ= 500, entonces t=(518 -500)/(40/25^1/2)=2.25 que es un valor superior a 1.711. La probabilidad de obtener un valor t con V=24 grados de libertad, igual o mayor a 2.25 es aproximadamente 0.02.