Apuntes Derivada de una función

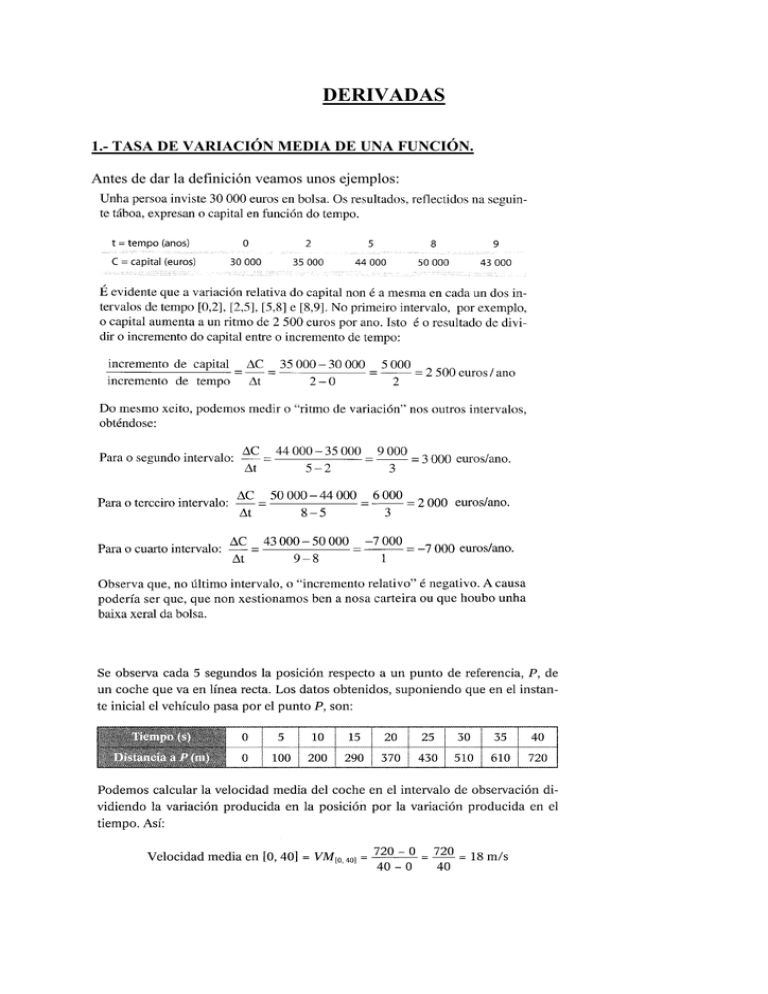
DERIVADAS
1.- TASA DE VARIACIÓN MEDIA DE UNA FUNCIÓN.
Antes de dar la definición veamos unos ejemplos:
Definición:
2.- TASA DE VARIACIÓN INSTANTÁNEA. DEFINICIÓN DE DERIVADA DE UNA
FUNCIÓN EN UN PUNTO.
Una función es derivable en un intervalo si lo es en
todos sus puntos.
3.- EL PROBLEMA DE LA TANGENTE. INTERPRETACIÓN GEOMÉTRICA DE
LA DERIVADA DE UNA FUNCIÓN EN UN PUNTO.
Para dar una interpretación geométrica del concepto de derivada necesitamos utilizar la tangente a una
curva en un punto.
La definición intuitiva de que la tangente a una curva en un punto es la recta que toca a la curva sólo
en ese punto sólo es válida para la circunferencia y curvas similares: cerradas y convexas (“sin
baches”) como puede verse en las figuras.
Para el caso general hace falta una nueva definición que sea válida siempre y que corresponda a la
idea intuitiva en los casos en que ésta pueda aplicarse. Veamos cual es:
Para poder hallar la ecuación de esa recta tangente en el punto de coordenadas (a, f(a)), si la
escribimos en forma punto-pendiente:
y – f(a) = m(x – a)
necesitamos saber el valor de la pendiente m. Si la recta tangente es la posición límite de las secantes,
su pendiente será el límite de las pendientes de las secantes, con lo que:
f(a + h) − f(a)
h
f(a + k) − f(a)
P2..........sec nº 2..........α2......... m 2 = tg α 2 =
k
P1..........sec nº 1..........α1......... m1 = tg α1 =
...............................................................................................
....................................................................................................
cuando ese punto variable llegue a coincidir con P tendremos la
recta tangente, cuya pendiente será:
P........tangente...........α......... m = tg α = lim
h → 0
f(a + h) − f(a)
= f ´ (a)
h
4.- DERIVADAS LATERALES.
Como una derivada es un límite, para que exista han de existir y coincidir los límites
laterales que, en este caso, se llaman derivadas laterales de la función en el punto:
la derivada por la izquierda de la función f en el punto a es (si existe)
f (a + h ) − f (a )
f − ´ (a ) = lim −
h → 0
h
la derivada por la derecha de la función f en el punto a es (si existe)
f (a + h ) − f ( a )
f + ´(a ) = lim +
h → 0
h
Evidentemente una función será derivable en un punto si y sólo si existen sus derivadas por la
izquierda y por la derecha en ese punto y coinciden.
5.- ECUACIÓN DE LA TANGENTE A UNA FUNCIÓN EN UN PUNTO. ECUACIÓN
DE LA NORMAL.
Como vimos en la interpretación geométrica de la derivada, ésta es la pendiente de la
recta tangente a la función (realmente a la gráfica de la función) en el punto de coordenadas
(a, f(a)), por lo que la ecuación de esa tangente será
y – f(a) = f ´(a)·(x – a)
Se llama recta normal a la función en el punto (a, f(a)) a la perpendicular a la recta
tangente en ese punto. Por tanto, teniendo en cuenta que si dos rectas son perpendiculares el
−1
producto de sus pendientes vale – 1 (m1·m2 = - 1), la pendiente de la recta normal será
f ´ (a )
(si f ´(a) ≠ 0), y la ecuación de la normal será:
−1
y − f (a ) =
⋅ (x − a )
f ´(a )
Si f ´(a) = 0 la recta tangente será horizontal y de ecuación y = f(a). En ese caso la
recta normal es vertical y de ecuación x = a.
6.- RELACIÓN ENTRE CONTINUIDAD Y DERIVABILIDAD.
TEOREMA: Si una función f es derivable en un punto a es continua en ese punto.
f será continua en a si: 1) ∃ lim f ( x ), 2) ∃ f (a ), 3) lim f ( x ) = f (a )
x →a
Por ser derivable en a
x→a
∃ f ´ (a ) = lim
x → a
f ( x ) − f (a )
, luego tiene que existir todo lo que
x−a
interviene en ese límite, en concreto f(a).
Además, en caso de existir el límite, será:
 f ( x ) − f (a )

lim f ( x ) − f (a ) = lim [ f ( x ) − f (a ) ] = lim 
⋅ ( x − a ) =
x → a
x → a
x → a
 x−a

f ( x ) − f (a )
= lim
⋅ lim ( x − a ) = f ´ (a ) ⋅ 0 = 0
x → a
x → a
x−a
por tanto existe lim f ( x ) y además coincide con f(a), con lo que se cumplen las tres
x → a
condiciones así que f es continua en a.
Pero el que una función sea continua en un punto no es suficiente para que sea
derivable en ese punto
7.- DEFINICIÓN DE FUNCIÓN DERIVADA. DERIVADAS SUCESIVAS.
8.- REGLAS DE DERIVACIÓN.
Obtener la expresión de la función derivada de una función dada implica calcular el
límite que define a esa función derivada en un punto genérico usando la expresión que define
a la función original; es decir, calcular
y ´ = f ´ (x) = lim
h→0
f(x + h) − f(x)
h
Pero calcular ese límite cada vez que deseemos obtener la derivada de una función resulta
bastante engorroso y, por ello, se obtienen (aunque no las demostraremos) unas expresiones o
fórmulas generales que permiten obtener fácilmente la derivada de cualquier función. Esas
fórmulas o reglas de derivación son las siguientes:
Derivadas de las funciones trigonométricas inversas
DERIVACIÓN LOGARÍTMICA: Es un método que permite calcular fácilmente muchas
derivadas y que consiste en tomar logaritmos neperianos en los dos miembros de la función y
derivar a continuación.
Ejemplo:
y = x sen x
Ln (y) = ln (x sen x)
Ln (y) = sen x Α ln x
1
1
y ′ = cosx ⋅ ln x + ⋅ sen x
y
x
1


y ′ = cos x ⋅ ln x + ⋅ sen x  ⋅ y
x


1


y ′ = cos x ⋅ ln x + ⋅ sen x  ⋅ x sen x
x


DERIVACIÓN IMPLÍCITA: Es un método que se emplea cuando resulta difícil escribir la
función a derivar en la forma y = f(x).
Ejemplo:
2xΑy2 + 3y = 5
2y2 + 2yΑy´Α2x + 3y´ = 0