iii.3 extensiones radicales
Anuncio

III.3 ACCIONES DE GRUPOS Y RESOLUBILIDAD.
G un grupo finito.
Acción de un grupo G sobre un conjunto X (notación: G y X); órbita de x ∈ X (notación: orb(x)); estabilizador de x
(notación: Gx ); G actúa transitivamente sobre X.
Tma.III.6. Sea f (X) ∈ F [X] y sea E/F c. de d. de f (X) sobre F . Sea X := {α ∈ E | f (α) = 0}. Entonces,
(i) f (X) irreducible implica Gal(E/F ) y X transitivamente;
(ii) si f (X) no tiene raı́ces múltiples y Gal(E/F ) y X transitivamente entonces f (X) es irreducible.
Cor.1. Sea F un cuerpo que contenga una raı́z n-ésima primitiva de la unidad,
f (X) = xn − c ∈ F [X].
Entonces existe un homomorfismo inyectivo
ψ : Gal(f ) → Z/nZ.
Además, ψ es isomorfismo si y solo si f (X) es irreducible.
Obs. Si F contiene una raı́z n-ésima primitiva de la unidad entonces la caracterı́stica de F no divide a n.
Cor.2. Sea p primo y F un cuerpo que contenga una raı́z p-ésima primitiva de la unidad. Sea E/F cuerpo de descomposición de
f (X) = xp − c ∈ F [X].
Entonces, o bien f (X) se descompone sobre F y |Gal(E/F )| = 1, o f (X) es irreducible sobre F y Gal(E/F ) ∼
= Z/pZ.
Cor.3. Sea p primo y F un cuerpo. X p − c ∈ F [X] es irreducible sobre F si y solo si c 6∈ F p .
Tma.III.7. Sea G y X y x ∈ X. Entonces
|orb(x)| = [G : Gx ].
Si |X| = n y G y X transitivamente entonces |G| = n|Gx |, en particular n divide a |G|.
Subgrupo transitivo de Sn .
Obs. Si G es un subgrupo transitivo de Sn entonces n divide al |G|.
Tma.III.8. Sea H ≤ G de ı́ndice n. Entonces existe un homomorfismo
ϕ : G → Sn
con Ker(ϕ) ⊆ H.
Cor.1. S5 no tiene subgrupos de orden 30, ni de orden 40.
Cor.2. S5 = hσ, τ i, para cualquier 5-ciclo σ y cualquier transposición τ .
Serie normal de un grupo, grupo resoluble.
Conmutador de x, y ∈ G (notación [x, y]); subgrupo conmutador o derivado de un grupo G (notación G0 ).
Obs.(i) G0 E G y G/G0 abeliano;
(ii) N E G y G/N abeliano si y solo si G0 ⊆ N (G0 es el mı́nimo subgrupo normal de G tal que el cociente es abelaino).
El n-ésimo subgrupo conmutador de G (notación G(n) ).
Tma.III.9. G es un grupo resoluble si y solo si existe n ∈ N tal que G(n) = {1}.
Cor.1. Sea G resoluble. Entonces,
(i) H ≤ G implica H resoluble;
(ii) si ϕ : G → H es un homomorfismo de grupos entonces ϕ(G) es un grupo resoluble; en particular, N E G implica
G/N resoluble.
Cor.2. Sea N E G. N y G/N resolubles si y solo si G resoluble.
Cor.3. Sn es resoluble si y solo si n ≤ 4.
Cor.4. Sea H ≤ S5 resoluble. Entonces |H| ≤ 24.
Cor.5. Sea G un grupo no trivial y resoluble. Entonces existe H E G de ı́ndice primo.
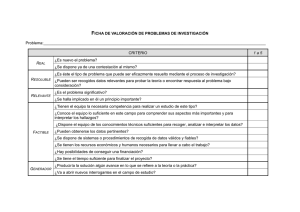
Subgrupos de S4
Elementos de S5
ord.
tipo de iso. #
E
Estr. cicl. # ord.
Elementos de S4
1
trivial
1
sı́
Estr. cicl. # ord. A4
(a)
1
1
2
Z/2Z
9
no
(a)
1
1
sı́
(ab) 10
2
3
Z/3Z
4
no
(ab)
6
2 no
(abc) 20
2
4 Z/2Z × Z/2Z, Z/4Z y V
7 1 sı́ y 6 no
(abc)
8
3
sı́
(abcd) 30
4
6
S3
4
no
(abcd)
6
4 no
(abcde) 24
5
8
D4
3
no
(ab)(cd)
3
2
sı́
(ab)(cd) 15
2
12
A4
1
sı́
(ab)(cde) 20
6
24
S4
1
sı́
10
A5
sı́
no
sı́
no
sı́
sı́
no