transformaciones lineales

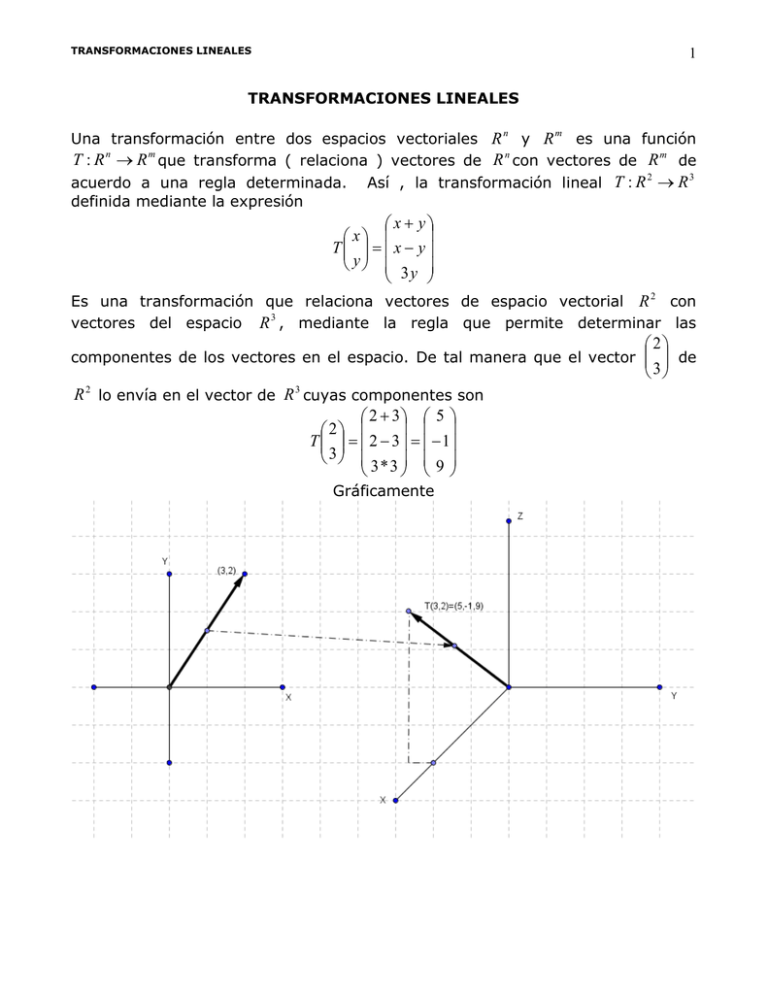
TRANSFORMACIONES LINEALES
1
TRANSFORMACIONES LINEALES
Una transformación entre dos espacios vectoriales R y R es una función
T : R n  R m que transforma ( relaciona ) vectores de R n con vectores de R m de
2
3
acuerdo a una regla determinada. Así , la transformación lineal T : R  R
definida mediante la expresión
n
m
 x  y

 x 
T     x  y 
 y   3y 


Es una transformación que relaciona vectores de espacio vectorial R con
3
vectores del espacio R , mediante la regla que permite determinar las
2
 2
componentes de los vectores en el espacio. De tal manera que el vector   de
 3
R 2 lo envía en el vector de R 3 cuyas componentes son
 2  3  5 
  
 2 
T     2  3     1
 3  3*3   9 

  
Gráficamente
TRANSFORMACIONES LINEALES
2
Ejemplo. Evaluar las transformaciones dadas en los puntos indicados.
 x  x  y
 , determine
y 
  2    3  5   8
1 1  1  2 
   
   
T    
; T    

5

5

5
1
1
  
  
  
 1
2
2
a) dado T : R  R definida por T    
 y 
 1  1  2   3 
   
T    
2
2
  
  2
Gráficamente tenemos:
 2x  y 

 x 
   3y  2z 
3
4
b) Dada la T : R  R definida por T  y   
 , evaluar
 z   xy  z 
   2z  3 


 2 *1  3   5 
  
1 
   3 * 3  2 *1  7 
T  3  
 4 
1
*
3

1
1 
   2 *1  3    1

  
;
 2*2  3   7 
  
 2 
  3*3  2 * 4  1 
T  3  
  10 
2
*
3

4
 4 
   2 * 4  3   5 

  
TRANSFORMACIONES LINEALES
3
TRANSFORMACIONES LINEALES
Sean V y W dos espacios vectoriales. Una transformación lineal de V en W es
una función T : V  W tal que para todos los vectores u, v V , y cualquier
escalar k , se verifican las siguientes propiedades.
1)
T (u  v)  T (u)  T (v)
2) T (ku)  kT(u)
Dada una transformación entre dos espacios vectoriales, para determinar si
esta es lineal, debemos comprobar que se cumplen las dos propiedades de
linealidad.
2
2
Ejemplo.
Demuestre que la transformación T : R  R
definida por
 x  x  2y
 es lineal.
T    
y
x

3
y
  

2
Para verificar las propiedades, tomemos dos vectores de R , sean
u 
v 
u   1  y v   1  y sea un escalar k, por definición de operaciones entre
 u2 
 v2 
 u1  v1 
 ku 
 y ku   1  luego
vectores tenemos que : u  v  
 u 2  v2 
 ku2 
 u  v   u  v  2(u 2  v2 )   (u1  2v1 )  (u 2  2v2 ) 
  

T (u  v)  T  1 1    1 1
u

v
u

v

3
(
u

v
)
(
u

3
v
)

(
u

3
v
)
2
2 
1
2
2 
 2 2  1 1
 1
 u  2v1   u 2  2v2 
  
  T (u )  T (v)
T (u  v)   1
 u1  3v1   u 2  3v2 
 ku   ku  2ku2   k (u1  2u 2 ) 
 u  2u 2 
  
  k  1
  kT (u )
T (ku)  T  1    1
 ku2   ku1  3ku2   k (u1  3u 2 ) 
 u1  3u 2 
Como se cumplen las dos propiedades, decimos que la transformación dada es
lineal.
TRANSFORMACIONES LINEALES
4
Ejemplo 2. Demuestre que la transformación
T : R 3  R 2 definida por
 x
  x z
 es lineal.
T  y   
y

z

z 
 
2
Para verificar las propiedades, tomemos dos vectores de R , sean
 u1 
 v1 
 
 
u   u 2  y v   v 2  y sea un escalar k, por definición de operaciones entre
u 
v 
 3
 3
 u1  v1 


vectores tenemos que : u  v   u 2  v 2 
u  v 
 3 3
 ku1 


y ku   ku2  luego
 ku 
 3
 u1  v1 

  (u  v )  (u3  v3 )   (u1  u3 )  (v1  v3 ) 
  

T (u  v)  T  u 2  v2    1 1
(
u

v
)

(
u

v
)
(
u

u
)

(
v

v
)
3
3 
3
1
3 
 2
u  v   2 2
 3 3
 u  u  v  v 
T (u  v)   1 3    1 3   T (u )  T (v)
 u 2  u3   v1  v3 
 ku1 

  ku  ku3   k (u1  u3 ) 
u u 
  
  k  1 3   kT (u )
T (ku)  T  ku2    1
 u 2  u3 
 ku   ku2  ku3   k (u 2  u3 ) 
 3
Luego la transformación es lineal.
Ejercicio. Sea A una matriz m x n . demuestre que la transformación
T : M nxk  M mxk
definida por T ( B)  AB es lineal.
Ejercicio. Determine si
la transformación lineal
 x
   x  y  2z 

 y 
T     2 x  4 w  es lineal.
z
   y  2 z  w 
 w
 
T : R 4  R 3 definida por
TRANSFORMACIONES LINEALES
5
PROPIEDADES DE LAS TRANSFORMACIONES LINEALES.
Sea T : V  W una transformación lineal. Entonces.
a) T (0V )  0W
b) T (v)  T (v)
n
m
DEFINICION. Sea T : R  R una transformación lineal. Sea e1 , e2 , e3 ,..., en la
n
base estándar del espacio vectorial R y sea A  T (e1 ), T (e2 ), T (e3 )......, T (en ) la
matriz cuyas columnas son las imágenes de e1 , e2 , e3 ,..., en entonces T ( x)  Ax
n
Para todo x  R . La matriz A se llama la matriz de la transformación.
3
2
Ejemplo. Encuentre la matriz de la transformación T : R  R definida por
 x
   x  2y
 .
T  y   
y

3
z


z
 
3
La base estándar del espacio vectorial R esta dada por los vectores
1
0
0
 
 
 
e1   0  , e2   1  , e3   0  y evaluando la transformación tenemos:
0
0
1
 
 
 
1
   1  2(0)   1 
   
T  0   
 0   0  3(0)   0 
 
0
 0
   0  2(1)    2 
   0  2(0)   0 
    ; T  0   
   
; T  1   
 0  1  3(0)   1 
 1   0  3(1)   3 
 
 
1  2 0

Luego la matriz de transformación es : A  
0
1
3


4
3
Ejemplo. Encuentre la matriz de transformación de T : R  R
x
   x  2 y  2z 

 y 
T     2 x  4w  .
z
   y  2 z  w 
 w
 
4
La base estándar del espacio vectorial R es:
TRANSFORMACIONES LINEALES
1
 
0
e1   
0
 
0
 
0
 
1
, e2    ,
0
 
0
 
6
0
 
0
e3    ,
1
 
0
 
0
 
0
e4    , Evaluando la transformación
0
 
1
 
tenemos:
1  2(0)  2(0)   1 

  
T e1    2(1)  4(0)    2  ,
 0  2(0)  0   0 

  
 0  2(0)  2(1)    2 

  
T (e3 )   2(0)  4(0)    0 
 0  2(1)  0    2 

  
 0  2(1)  2(0)   2 

  
T e2    2(0)  4(0)    0 
 1  2(0)  0   1 

  
0
 
; T e4    4 
1
 
luego la matriz de la
transformación es:
1 2  2 0


A   2 0 0 4
0 1  2 1


EJERCICIO0. ENCUENTRE LA MATRIZ
TRANSFORMACIONES LINEALES.
ASOCIADA
 x  2y 


x


2
3
A) T : R  R DEFINIDA POR T     2 x  y 
 y   3x  2 y 


B)
 x   x  2y  z 
  

T : R 3  R 3 DEFINIDA POR T  y    2 x  4 y  2 z 
 z    3x  6 y  2 z 
  

2x  y



 x 
   4 x  2 y  3z 
3
4
C) T : R  R DEFINIDA POR T  y   

 z    6x  3 y  9z 
   4x  y  2z 


A
LAS
SIGUIENTES
TRANSFORMACIONES LINEALES
7
TEOREMA: Sean V y W dos espacios vectoriales. Una transformación de V en
W es una función T : V  W es lineal si preserva la combinación lineal entre
elementos de ambos espacios es decir, si para todos los vectores vi  V , y
cualquier escalar k i  R ,con i  1,2,3....,n se verifica la siguiente propiedad.
T (k1v1  k 2 v2  k 3 v3  .....  k n vn )  k1T (v1 )  k 2T (v2 )  k 3T (v3 )  ...... k 4T (v4 )
Es decir:
 n
 n
T   k i vi    k i T (vi )
 i 1
 i 1
2
3
Ejemplo. Aplicar el teorema para demostrar que la transformación T : R  R
 x  2y 

 x 
definida por T     2 x  4 y  es lineal.
 y   y  2x 


 x1 
 x2 
Solución. Sean u1    y u 2    dos vectores de R2 y sean los escalares
 y1 
 y2 
k1 ;k 2 . Una combinación lineal de los vectores es de la forma:
x 
x  k x k x 
k1u1  k 2u 2  k1  1   k 2  2    1 1 2 2 
 y1 
 y2   k1 y1  k 2 y2 
Luego:
k x k x 
T k1u1  k 2 u 2   T  1 1 2 2 
 k1 y1  k 2 y2 
 k1 x1  k 2 x2  2(k1 y1  k 2 y 2 ) 


T k1u1  k 2 u 2    2k1 x1  k 2 x 2   4(k1 y1  k 2 y 2 ) 
 k x  k x  4( k y  k y ) 
1 1
2 2
 1 1 2 2

 k1 x1  2k1 y1  k 2 x2  2k 2 y 2 


T k1u1  k 2 u 2    2k1 x1  4k1 y1  2k 2 x2  4k 2 y 2 
 k y  2k x  k y  2k x 
1 1
2 2
2 2 
 1 1
 x  2y 

 x 
T 1    2 x  4 y 
 y   y  2x 


TRANSFORMACIONES LINEALES
8
 k1 x1  2k1 y1   k 2 x2  2k 2 y 2 ) 

 

T k1u1  k 2 u 2    2k1 x1  4k1 y1    2k 2 x2  4k 2 y 2 ) 
 k y  2k x   k y  2k x ) 
1 1   2 2
2 2 
 1 1
 x1  2 y1 
 x2  2 y 2 ) 




T k1u1  k 2 u 2   k1  2 x1  4 y1   k 2  2 x2  4 y 2 ) 
 y  2x 
 y  2x ) 
1 
2 
 1
 2
T k1u1  k 2 u 2   k1T u1   k 2T u 2 
Como preserva la combinación lineal , entonces cumple con el teorema y es
consecuencia es una transformación lineal.
Ejercicio aplicar el teorema de la conservación de la linealidad para verificar si
las siguientes transformaciones son lineales:
 x  x  y 
2
2

a) T : R  R definida por T    
 y   2 y  3z 
 x
   2 y  3x 
3
2

b) T : R  R definida por T  y   
y

3
z

z 
 
T 2 :V W
Teorema. Sean U , V y W espacios vectoriales y T1 : U  V
transformaciones lineales definidos entre ellos. Entonces la transformación
T : U  W definida por T  T 2  T1 también es una transformación lineal. E4n
otras palabras la compuesta de dos transformaciones lineales, es otra
transformación lineal.
2
3
3
4
Ejemplo. Si T1 : R  R y T 2 : R  R dos transformaciones lineales definidas
 x  2y 

 x 
por T 1    2 x  4 y 
 y   y  2x 


 2x  y 

 x 
   y  2z 
y T 2 y   
 determine la transformación
 z   4z  x 
   z  2x 


compuesta y demuestre que es lineal.
2
4
La transformación compuesta T : R  R esta definida por: T  T 2  T1 luego
TRANSFORMACIONES LINEALES
9
 2( x  2 y )  (2 x  4 y ) 

 x  2y  

  (2 x  4 y )  2( y  2 x) 
  x 
 x
 x
T    T 2  T 1   T 2 T 1    T 2 2 x  4 y   

 y
 y
  y 
 y  2 x   4( y  2 x)  ( x  2 y ) 

  ( y  2 x)  2( x  2 y ) 


 2x  4 y  2x  4 y   4x  8 y 

 

 x   2x  4 y  2 y  4x   6x  2 y 
T    


 y   4 y  8x  x  2 y   6 y  7 x 
 y  2x  2x  4 y   5 y 

 

 4x  8 y 


 x   6x  2 y 
T    

 y   6 y  7x 
 5y 


Verifiquemos que es una transformación lineal.
 x1 
 x2 
Sean u1    y u 2    dos vectores de R2 y sean los escalares
 y1 
 y2 
k1 ;k 2 . Una combinación lineal de los vectores es de la forma:
x 
x  k x k x 
k1u1  k 2u 2  k1  1   k 2  2    1 1 2 2  luego
 y1 
 y2   k1 y1  k 2 y2 
k x k x 
T k1u1  k 2 u 2   T  1 1 2 2 
 k1 y1  k 2 y2 
 4(k1 x1  k 2 x2 )  8(k1 y1  k 2 y 2 ) 


 6(k1 x1  k 2 x2 )  2(k1 y1  k 2 y 2 ) 
T k 2 u1  k 2 u 2   
6(k y  k y )  7(k1 x1  k 2 x2 ) 
 1 1 2 2



5
(
k
y

k
y
)
1 1
2 2


 4k1 x1  4k 2 x2  8k1 y1  8k 2 y 2 


6
k
x

6
k
x

2
k
y

2
k
y

2 2
1 1
2 2
T k 2 u1  k 2 u 2    1 1
6k y  6k 2 y 2  7 k1 x1  7 k 2 x2 
 1 1



5
k
y

5
k
y
1 1
2 2


TRANSFORMACIONES LINEALES
10
 4k1 x1  8k1 y1  4k 2 x2  8k 2 y 2 


 6k1 x1  2k1 y1  6k 2 x2  2k 2 y 2 
T k 2 u1  k 2 u 2   
6k y  7 k1 x1  6k 2 y 2  7 k 2 x 2 
 1 1



5
k
y

5
k
y
1 1
2 2


 4k1 x1  8k1 y1   4k 2 x2  8k 2 y 2 

 

 6k1 x1  2k1 y1   6k 2 x2  2k 2 y 2 
T k 2 u1  k 2 u 2   

6k1 y1  7 k1 x1   6k 2 y 2  7 k 2 x2 

 


 

5
k
y
5
k
y
1 1
2 2

 

 4 x1  8 y1 
 4 x2  8 y 2 




6
x

2
y
6
x

2
y


1
2
T k 2 u1  k 2 u 2   k1  1
 k2  2

6 y  7 x1
6 y  7 x2 
 1

 2

 5y

 5y

1
2




T k 2 u1  k 2 u 2   k1T (u1 )  k 2T (u 2 )
T 2 :V W
TEOREMA: Sean U , V y W espacios vectoriales y T1 : U  V
transformaciones lineales definidos entre ellos. Y sean A y B las matrices
asociadas a las transformaciones lineales, entonces la matriz BA es la matriz
asociada a la transformación compuesta T  T 2  T1 .
EJEMPLO.
COMPUEBE
EL
TRANFOTMACIONES LINEALES.
TEOREMA
PARA
LAS
SIGUIENTES
 x y 


x


T1 : R 2  R 3 DEFINIDA POR T 1    x  y  la matriz asociada es :
 y   2x  3y 


1 0 

 1
0 
A   T 1  T 1      1  0 
1  2  0
  0


 0  1   1 1 

 

 0  1     1  1
 0  3   2 3 

 

 x
   x yz 
 la matriz asociada es :
T 2 : R 3  R 2 DEFINIDA POR T 2 y   

2
x

2
y

2
z

z 
 
TRANSFORMACIONES LINEALES
11
 1
0
0
  
 
   1 1 1 

B   T 2 0  T 2 1  T 2 0    

2
2

2


 0
0
1
 
 
  
La matriz BA es:
1 1 
  2
5 
 1  1 1 
 1  1  

BA  
  2 2  2  2 3    4  10 


Ahora la transformación compuesta es: T  T 2  T1 esta definida por
 x y 

  ( x  y )  ( x  y )  (2 x  3 y 
  x 
 x

T    T 2 T 1    T 2 x  y   
 y
  y 
 2 x  3 y    2( x  y )  2( x  y )  2(2 x  3 y ) 


 x   2x  5 y 
 y la matriz asociada es:
T    
y

4
x

10
y
)
  

 1
5 
 0  2
 como se puede ver las matrices asociadas BA y
C   T   T     
0
1

4

10
  

  
C son iguales.