Determinación de una fórmula

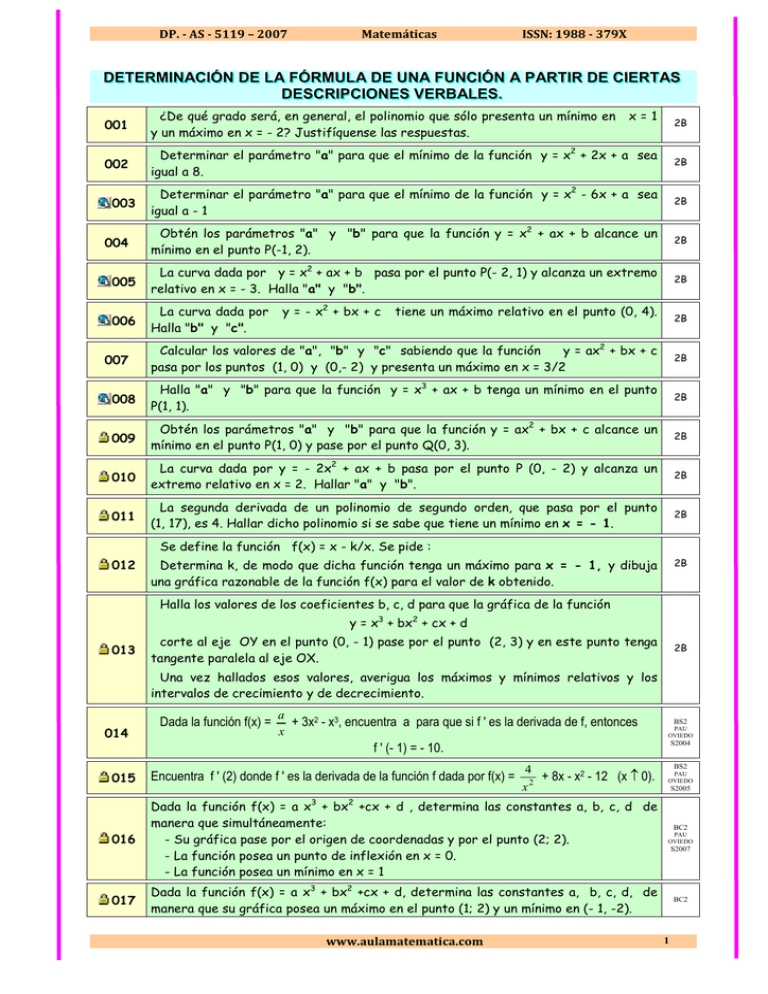
DP. - AS - 5119 – 2007
Matemáticas
ISSN: 1988 - 379X
D
DE
ETTE
ER
RM
MIIN
NA
AC
CIIÓ
ÓN
ND
DE
E LLA
A FFÓ
ÓR
RM
MU
ULLA
AD
DE
EU
UN
NA
A FFU
UN
NC
CIIÓ
ÓN
NA
AP
PA
AR
RTTIIR
RD
DE
EC
CIIE
ER
RTTA
AS
S
D
E
S
C
R
I
P
C
I
O
N
E
S
V
E
R
B
A
L
E
S
.
DESCRIPCIONES VERBALES.
001
¿De qué grado será, en general, el polinomio que sólo presenta un mínimo en
y un máximo en x = - 2? Justifíquense las respuestas.
002
Determinar el parámetro "a" para que el mínimo de la función y = x2 + 2x + a sea
igual a 8.
2B
Determinar el parámetro "a" para que el mínimo de la función y = x2 - 6x + a sea
igual a - 1
2B
Obtén los parámetros "a" y "b" para que la función y = x2 + ax + b alcance un
mínimo en el punto P(-1, 2).
2B
005
La curva dada por y = x2 + ax + b pasa por el punto P(- 2, 1) y alcanza un extremo
relativo en x = - 3. Halla "a" y "b".
2B
006
La curva dada por
Halla "b" y "c".
003
004
y = - x2 + bx + c
x=1
2B
tiene un máximo relativo en el punto (0, 4).
2B
Calcular los valores de "a", "b" y "c" sabiendo que la función
y = ax2 + bx + c
pasa por los puntos (1, 0) y (0,- 2) y presenta un máximo en x = 3/2
2B
008
Halla "a" y "b" para que la función y = x3 + ax + b tenga un mínimo en el punto
P(1, 1).
2B
009
Obtén los parámetros "a" y "b" para que la función y = ax2 + bx + c alcance un
mínimo en el punto P(1, 0) y pase por el punto Q(0, 3).
2B
010
La curva dada por y = - 2x2 + ax + b pasa por el punto P (0, - 2) y alcanza un
extremo relativo en x = 2. Hallar "a" y "b".
2B
011
La segunda derivada de un polinomio de segundo orden, que pasa por el punto
(1, 17), es 4. Hallar dicho polinomio si se sabe que tiene un mínimo en x = - 1.
2B
007
Se define la función f(x) = x - k/x. Se pide :
012
2B
Determina k, de modo que dicha función tenga un máximo para x = - 1, y dibuja
una gráfica razonable de la función f(x) para el valor de k obtenido.
Halla los valores de los coeficientes b, c, d para que la gráfica de la función
y = x3 + bx2 + cx + d
013
corte al eje OY en el punto (0, - 1) pase por el punto (2, 3) y en este punto tenga
tangente paralela al eje OX.
2B
Una vez hallados esos valores, averigua los máximos y mínimos relativos y los
intervalos de crecimiento y de decrecimiento.
014
Dada la función f(x) =
a
+ 3x2 - x3, encuentra a para que si f ' es la derivada de f, entonces
x
BS2
PAU
OVIEDO
S2004
f ' (- 1) = - 10.
015
Encuentra f ' (2) donde f ' es la derivada de la función f dada por f(x) =
3
016
017
4
x2
+ 8x - x2 - 12 (x ≠ 0).
BS2
PAU
OVIEDO
S2005
2
Dada la función f(x) = a x + bx +cx + d , determina las constantes a, b, c, d de
manera que simultáneamente:
- Su gráfica pase por el origen de coordenadas y por el punto (2; 2).
- La función posea un punto de inflexión en x = 0.
- La función posea un mínimo en x = 1
PAU
OVIEDO
Dada la función f(x) = a x3 + bx2 +cx + d, determina las constantes a, b, c, d, de
manera que su gráfica posea un máximo en el punto (1; 2) y un mínimo en (- 1, -2).
BC2
www.aulamatematica.com
BC2
S2007
1
DERIVADAS. APLICACIONES.
018
019
Calcula el punto de inflexión de la función y = 2x3- 6x2 + 4 y la ecuación de la recta
tangente en el mencionado punto de inflexión.
2B
Calcula el punto de inflexión de la función y = -x3+ 3x y la ecuación de la recta
tangente en el mencionado punto de inflexión.
2B
DETERMINACIÓN DE LA FÓRMULA DE UNA FUNCIÓN A PARTIR DE GRÁFICAS.
001
Dadas las siguientes gráficas, haz un ESBOZO de las posibles representaciones
gráficas de las derivadas. Razona las respuestas
GRÁFICA 1
002
GRÁFICA 2
003
GRÁFICA 5
2B
GRÁFICA 6
Dadas las siguientes gráficas, haz un ESBOZO de las posibles representaciones
gráficas de las derivadas. Razona las respuestas
GRÁFICA 7
004
GRÁFICA 3
Dadas las siguientes gráficas, haz un ESBOZO de las posibles representaciones
gráficas de las derivadas. Razona las respuestas
GRÁFICA 4
2B
GRÁFICA 8
2B
GRÁFICA 9
Dadas la siguiente gráfica, haz un ESBOZO
de las posible representación gráfica de la
derivada. Razona la respuesta.
2B
2
005
La gráfica de la FUNCIÓN DERIVADA de
f(x) es la siguiente:
2B
1
(a) Una de estas cuatro gráficas es un esbozo de f(x). ¿Cuál de ellas? Argumenta tu respuesta.
GRÁFICA 1
GRÁFICA 2
GRÁFICA 3
2
1
1
1
(b) Halla la expresión analítica de la función f'(x) y de la función f(x).
2
www.aulamatematica.com
GRÁFICA 4
DP. - AS - 5119 – 2007
006
Matemáticas
ISSN: 1988 - 379X
La gráfica de la FUNCIÓN DERIVADA de
f(x) es la siguiente:
2B
(a) Una de estas cuatro gráficas es un esbozo de f(x). ¿Cuál de ellas? Argumenta tu respuesta.
GRÁFICA 1
GRÁFICA 2
GRÁFICA 3
GRÁFICA 4
1
1
(b) Halla la expresión analítica de la función f'(x) y de la función f(x).
007
La gráfica de la FUNCIÓN DERIVADA de
f(x) es la siguiente:
2B
(a) Una de estas cuatro gráficas es un esbozo de f(x). ¿Cuál de ellas? Argumenta tu respuesta.
GRÁFICA 1
GRÁFICA 2
GRÁFICA 3
GRÁFICA 4
(b) Halla la expresión analítica de la función f'(x) y de la función f(x).
008
La gráfica de la FUNCIÓN DERIVADA de
f(x) es la siguiente:
2B
(a) Una de estas cuatro gráficas es un esbozo de f(x). ¿Cuál de ellas? Argumenta tu respuesta.
GRÁFICA 1
GRÁFICA 2
GRÁFICA 3
GRÁFICA 4
(b) Halla la expresión analítica de la función f'(x) y de la función f(x).
009
La gráfica de la FUNCIÓN DERIVADA de
f(x) es la siguiente:
2B
(a) Una de estas cuatro gráficas es un esbozo de f(x). ¿Cuál de ellas? Argumenta tu respuesta.
GRÁFICA 1
GRÁFICA 2
GRÁFICA 3
www.aulamatematica.com
GRÁFICA 4
3
DERIVADAS. APLICACIONES.
(b) Halla la expresión analítica de la función f'(x) y de la función f(x).
010
Sea f: R → R. Si f'(x) = x – x2 , ¿cuál de las siguientes gráficas podría
corresponder a f(x)? Argumenta tu respuesta. Si nos dicen además que f(1) = 3, ¿Se
podría hallar f? Justifíquese la respuesta.
GRÁFICA 1
0.5
0.5
1
GRÁFICA 3
0.5
1
1
Dada la siguiente gráfica, determina la
fórmula que las representa
2B
Dada la siguiente gráfica, determina la
fórmula que las representa
2B
013
Dada la siguiente gráfica, determina la
fórmula que las representa
2B
014
Dada la siguiente gráfica, determina la
fórmula que las representa
2B
015
Dada la siguiente gráfica, determina la
fórmula que las representa
2B
016
Dada la siguiente gráfica, determina la
fórmula que las representa
2B
011
012
4
GRÁFICA 2
2B
PAU
Málaga
J2005
www.aulamatematica.com
DP. - AS - 5119 – 2007
017
Matemáticas
ISSN: 1988 - 379X
Dadas las siguientes funciones de la TABLA I, asocia a cada una de ellas la función
derivada de la TABLA II
GRÁFICA 1
GRÁFICA 2
GRÁFICA 3
GRÁFICA 4
GRÁFICA 5
GRÁFICA 6
GRÁFICA 7
GRÁFICA 8
GRÁFICA 9
GRÁFICA 10
2B
TABLA I
GRÁFICA A
GRÁFICA B
GRÁFICA C
GRÁFICA D
GRÁFICA E
GRÁFICA F
GRÁFICA G
GRÁFICA H
GRÁFICA I
GRÁFICA J
TABLA II
(1) x2/2 – x3/3
(6) – x4 + 3x2 + 1
(A) 4x
(F) x – x2
(2) x4 – 3x2 + 2
(7) – 2 x2 + 1
(B) – 2
(G) – 1/x2
(3) 3x3 + x2 – x + 1
(8) – 2x + 1
(C) 4x3 – 6x
(H) – 4x3 + 6x
(4) 2x2 + 1
(9) 2x2 + 3x – 1
(D) 4x2 + 3
(I) – 1 si x < 0 ; 1 si x > 0
www.aulamatematica.com
(5) | x |
(10) 1/x
(E) – 4x
(J) 9x2 + 2x – 1
5